2. 中海油田服务股份有限公司, 天津 300450;
3. 中国石油化工股份有限公司胜利油田分公司 勘探开发研究院, 山东 东营 257100;
4. 昆仑能源投资(山东)有限公司, 山东 青岛 266500
2. China Oilfield Services Limited, Tianjin 300450, China;
3. SINOPEC(China Petrochemical Corporation) Shengli Oil Field Exploration and Development Research Institute, Dongying 257100, China;
4. Kunlun Energy Investment(Shangdong) Co., Ltd., Qingdao 266500, China
在油气勘探、开发的钻井施工中,常遇到地层复杂、坚硬,岩石可钻性级别上升,钻井效率降低;随着钻井工艺技术的发展,大位移井、水平井所占的比例越来越大,钻柱自身重力和岩屑床等引起的托压、黏卡问题严重[1]。针对这些问题,国外NOV(National Oilwell Varco)公司研发了一种水力振荡器[2-4],并在国内外各钻井现场应用,取得了不错的效果[5-7]。国内也进行了此类工具的研发,其中包括工具结构的改进和相关实验研究[8-12]。但由于对此类工具工作性能的理论研究比较薄弱,国内的振荡器研究并未取得理想效果。综合国内外水力振荡器的应用及发展情况[8-14],在前人的基础上对该类工具工作性能进行理论研究和水力脉冲计算,并对振动冲击性能影响因素进行分析,目的是为它在钻井现场的应用提供理论支撑和为提高钻速及优化水力脉冲工具提供指导意义。
1 振荡冲击器的结构及工作原理分析振荡冲击器的关键性技术在于如何产生轴向振荡冲击。因为钻井采用的是钻井液循环工艺,所以轴向振荡冲击的动力方式选择液动方式,把一部分钻井液流体的能量转化为振动冲击机械能。
1.1 振荡冲击器基本结构组成振荡冲击器主要由振荡部分、动力部分和盘阀(动盘阀与定盘阀)组成,其结构如图 1所示[2]。
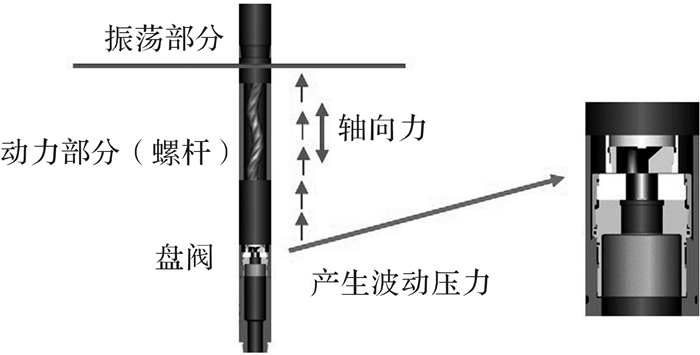
|
| 图 1 振荡冲击器结构示意图 Fig.1 Structure diagram of oscillation impacter |
振荡冲击器工作的基本原理为:当钻井液流过动力部分(螺杆)时,部分液体的动能转化为机械能,驱动盘阀旋转,使得过流面积发生周期性变化,产生压力脉冲;工具的振荡部分将压力脉冲转化成冲击振动,从而实现钻进过程中的减阻降摩冲击。
此类工具实现冲击功能的关键在于利用螺杆钻具定转子特有的行星运动改变盘阀的过流面积。
1.2 盘阀运动分析水力脉冲发生装置由定盘阀和动盘阀组成,定盘阀有一偏心距为e的圆孔,动盘阀的圆孔在中心,且动、定盘阀的圆孔作为过流孔,半径为r,面积相同,如图 2所示。定盘阀安装在螺杆马达的定子上;动盘阀与螺杆相接,可随螺杆马达的行星运动而规律运动。
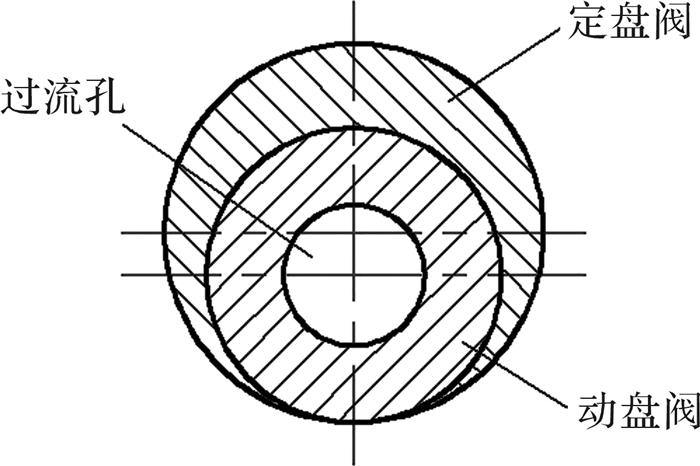
|
| 图 2 定盘阀和动盘阀 Fig.2 Dynamic disc valve and stable disc valve |
盘阀运动基于螺杆马达转子在定子内运动规律:转子围绕着中心轴作偏心距为e的运动,即在形成定转子密封共轭条件下,转子始终围绕定子作偏心距为e的旋转运动。在运动的过程中,动盘阀的位置不一样,所形成的的过流面积也不一样。如图 3为盘阀运动示意图,当动盘阀与定盘阀的过流孔重合时,过流面积最大;当动盘阀转过90°时,过流面积随着盘阀的运动变小;当动盘阀转过180°时,过流面积最小,但不会出现全闭状态,防止了憋泵的产生;当动盘阀转过270°时,过流面积又开始变大。因此,动盘阀随螺杆马达的定子运动时,过流面积从最大到最小,再从最小到最大,不断地发生周期性的变化,进而引起盘阀附近水泥浆的压力变化,形成水力脉冲。
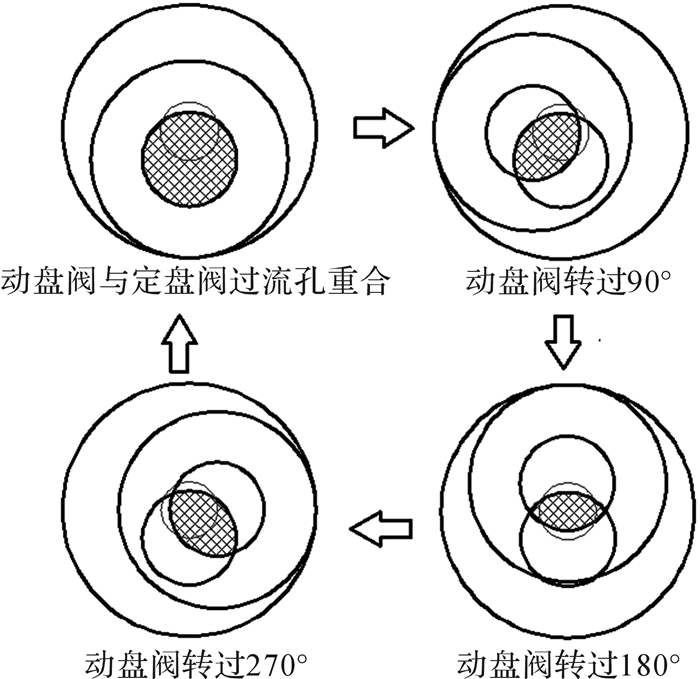
|
| 图 3 盘阀运动示意图 Fig.3 Disc valve movement diagram |
假设开始时定盘阀和动盘阀的过流孔重合,此时过流面积最大。过流孔的半径为r,过流区域中心O1与中心轴存在偏心距e,动盘阀绕中心轴作行星运动,运动速度与螺杆的运动速度ω相同。动盘阀绕中心轴作行星运动时,动盘阀圆心O2的轨迹为圆心为O点的圆,过流面积具体的变化过程如图 4所示。
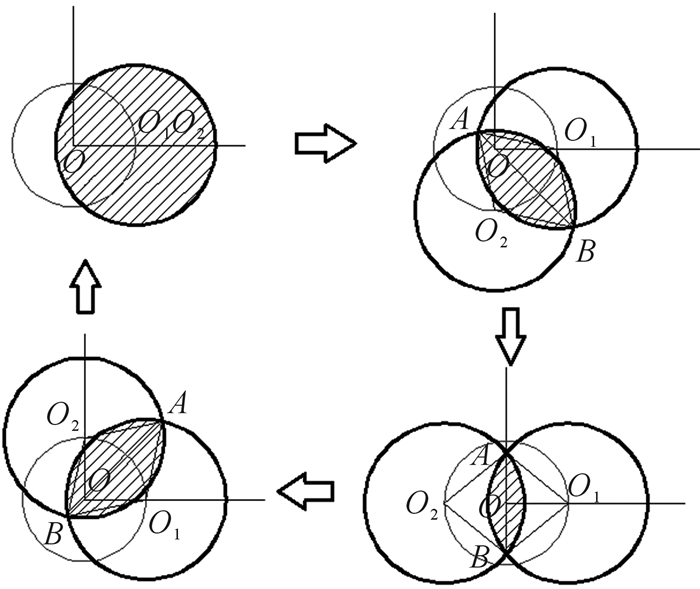
|
| 图 4 过流面积变化示意图 Fig.4 Schematic diagram of flow area change |
现推导过流面积变化的方程。
假设过流区域与定、动盘阀过流孔的交点为A,B。O1与O2之间的距离2L为:
| $ 2L = 2e\left| {\sin \left( {wt/2} \right)} \right| $ | (1) |
则三角形ABO1和三角形ABO2的面积为:
| $ {S_1} = Lr\sin \theta $ | (2) |
式中:θ=arccos(L/r)
扇形ABO1和扇形ABO2的面积为:
| $ {S_2} = \theta {r^2} $ | (3) |
得过流面积随时间的变化方程为:
| $ \begin{array}{*{20}{c}} {S = 2\left( {{S_2} - {S_1}} \right) = 2\left[ {{r^2}\arccos \frac{{e\left| {\sin \left( {wt/2} \right)} \right|}}{r} - } \right.}\\ {\left. {\left( {e\sin \left( {wt/2} \right)\sqrt {{r^2} - {e^2}{{\sin }^2}\left( {wt/2} \right)} } \right)} \right]} \end{array} $ | (4) |
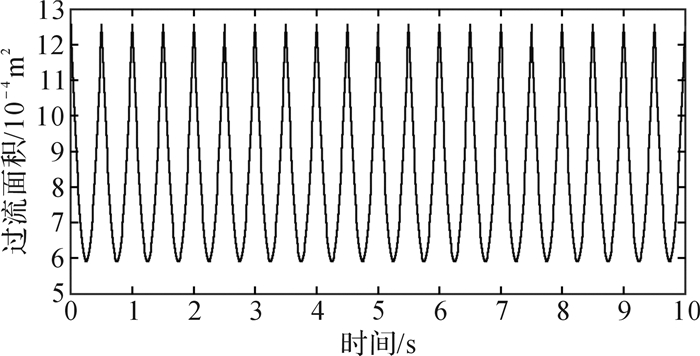
取过流孔半径r=20 mm,偏心距e=8.6 mm,用MATLAB软件编制程序,通过计算可得过流面积的变化规律,如图 5所示。
|
| 图 5 过流面积变化规律 Fig.5 Change rule of flow area |
由图 5可以看出过流面积呈周期性变化。当定盘阀和动盘阀的过流孔重合时,过流面积最大,对应图中的波峰;当动盘阀转过180°,此时过流面积最小,对应图中的波谷;当动盘阀随螺杆马达不断转动时,过流面积呈连续的周期性的变化。
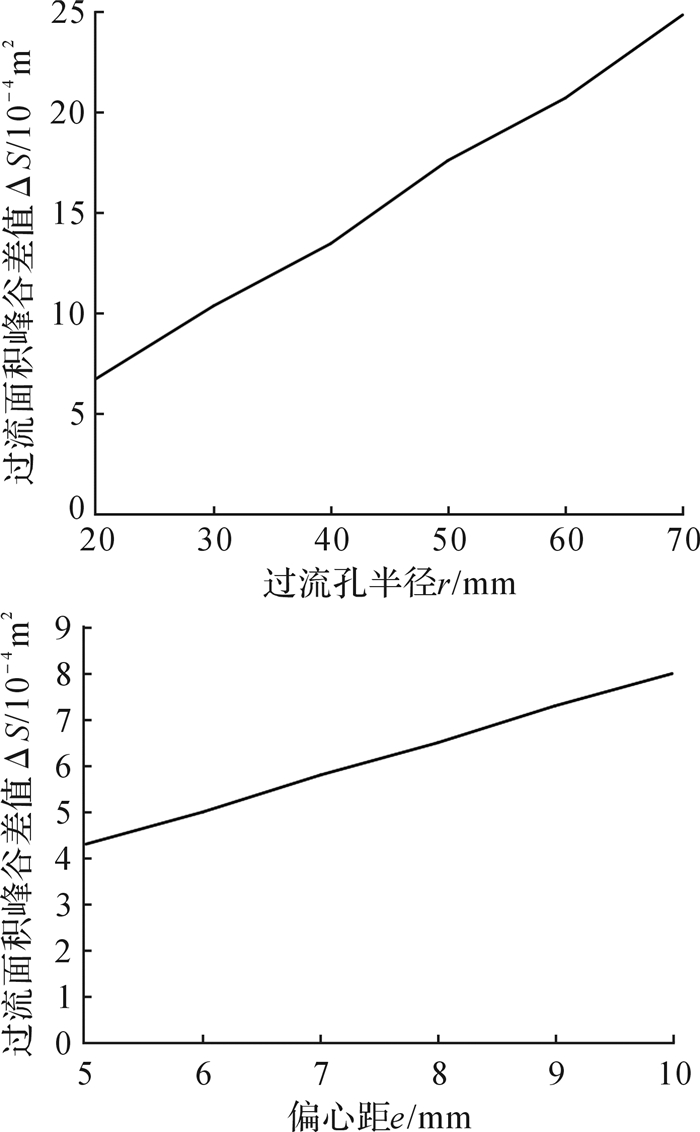
1.4 过流面积变化影响因素分析盘阀过流孔的参数主要有过流孔半径r和偏心距e。改变过流孔的参数,分析数据可得出过流面积的峰谷差值ΔS均随过流孔半径r、偏心距e的增大而增大,基本呈正线性相关,如图 6所示。
|
| 图 6 过流面积峰谷差值ΔS随参数r和e的变化曲线 Fig.6 The change curve of flow area difference valve between the maximum and minimum with parameter r and e |
根据流体力学可知,盘阀过流面积变化使得液体流速发生变化,进一步引起压强大幅度波动,这种流动参数(压力、速度等)随时间变化的流动,称为不稳定流(或非定常流)[15-18]。在大多数情况下波动压力是有害的,但振荡冲击器是利用波动压力的能量实现脉动冲击, 故波动压力理论分析和脉冲计算在研究振荡器时就尤为关键。
产生水力脉冲的物理原因主要是由于液体具有惯性和压缩性, 液体惯性企图维持其原有的运动状态[13]:过流面积减小时,由于惯性作用,后方流体会对前方流体不断挤压,使其压力上升;同理,过流面积增大时,阀片处压力会减小。振荡器过流面积的周期变化就会产生周期性的波动压力,这就是振荡器产生振荡冲击的根本原因。
2.2 波动压力理论分析模型盘阀过流面积周期性变化,但盘阀不会出现完全封闭的状态,所以应按间接水击处理进行。基于此,波动压力理论分析和计算时需注意以下几点:
1) 由于过流面积变化,流体运动为非稳定流,不能按稳定流计算。
2) 由于盘阀运动过程中,没有过流孔完全封闭的情况,所产生的水击为间接水击,不能看作直接水击进行计算。
3) 产生的波动压力是连续的,并不断地在液体中进行传递,不能认为波动压力只在振荡器内部传递。
由于波动压力计算比较复杂,为了便于分析,忽略影响较小的因素,作适当的模型简化:
1) 盘阀处过流面积发生变化,振荡器内腔的过流面积为恒定值。
2) 振荡器和钻杆为圆柱形,可将钻井液在振荡器和钻杆中的流动看作一维流动[1]。
3) 振荡器的运动部件主要为脉冲发生装置,认为在振荡器内腔其他地方不引起波动压力,以确保计算准确性。
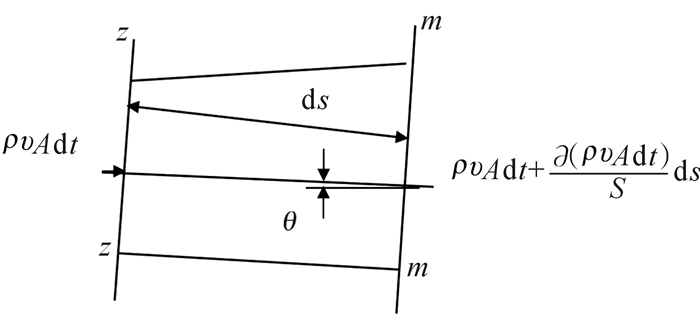
根据《工程流体力学》[15],对微元控制体进行分析,如图 7所示,得一元不稳定流的基本方程为连续性方程和运动方程。
|
| 图 7 微元控制体分析示意图 Fig.7 Microelement control analysis diagram |
连续性方程为:
| $ - \frac{{\partial \left( {\rho vA} \right)}}{{\partial x}} = \frac{{\partial \left( {\rho A} \right)}}{{\partial t}} $ | (5) |
单位质量的流体运动微分方程为:
| $ g\frac{{\partial H}}{{\partial x}} + v\frac{{\partial v}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + \frac{{4{\tau _0}}}{{\rho D}} = 0 $ | (6) |
压力波速方程为:
| $ a = \sqrt {\frac{E}{\rho }} /\sqrt {1 + \frac{E}{{{E_0}}}\frac{D}{d}} $ | (7) |
式中:E为钻井液的弹性系数,Pa;E0为管材的弹性系数,Pa;ρ为钻井液的密度,kg/m3;d为管材壁厚,m,H为水头,m;x为长度,m; v为液体速度,m/s;t为时间,s;a为压力波速,m/s;D为直径,m;g为重力加速度,m/s2。
波动压力的基本方程可由一元不稳定流的基本方程得出。根据一元不稳定流的连续性方程(5)可推导波动压力的连续方程为:
| $ \frac{{\partial H}}{{\partial t}} + v\frac{{\partial H}}{{\partial x}} + \frac{{{a^2}}}{g}\frac{{\partial v}}{{\partial x}} = 0 $ | (8) |
根据液体流动时力的平衡条件可得:
| $ {\tau _0} = \frac{{\rho \lambda }}{8}v\left| v \right| $ | (9) |
根据一元不稳定流的运动方程,将τ0代入式(7)可推导波动压力的运动方程为:
| $ g\frac{{\partial H}}{{\partial x}} + v\frac{{\partial v}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + \frac{\lambda }{{2D}}v\left| v \right| = 0 $ | (10) |
式中λ为达西摩擦系数(即水力摩阻系数)。
2.3 波动压力数值计算由于二次摩擦项的存在,目前还无法得到波动压力的解析式,只能用数值方法进行求解。最常用的一种数值方法为特征线解法[11]。
在数值计算中需要设置边界条件,本文中边界条件设置处为钻井泵和盘阀处。
钻井泵边界条件为:若泵的压力能保持稳定,则H为定常值即初始值; 若不能稳定, 则可根据泵的特性曲线建立泵的特征方程,一般情况下,泵的特征方程可用二次方程表示:
| $ H = {a_1} + {a_2}Q + {a_3}{Q^2} $ | (11) |
盘阀处边界条件为:
| $ Q = \mu S\sqrt {2g{H_t}} $ | (12) |
式中:Q为排量,m3/s;μ为盘阀的流量系数,在过流面积变化时近似地认为是常数;Ht为盘阀处在t时刻的水头,在引起压力波的过程中是变化的;S为盘阀的过流面积。
将式(4)代入可得:
| $ \begin{array}{l} Q = 2\left\{ {{r^2}\arccos \frac{{e\left| {\sin \left( {wt/2} \right)} \right|}}{r} - } \right.\\ \;\;\;\;\;\;\;\left. {\left[ {e\sin \left( {wt/2} \right)\sqrt {{r^2} - {e^2}{{\sin }^2}\left( {wt/2} \right)} } \right]} \right\}\mu \sqrt {2g{H_t}} \end{array} $ | (13) |
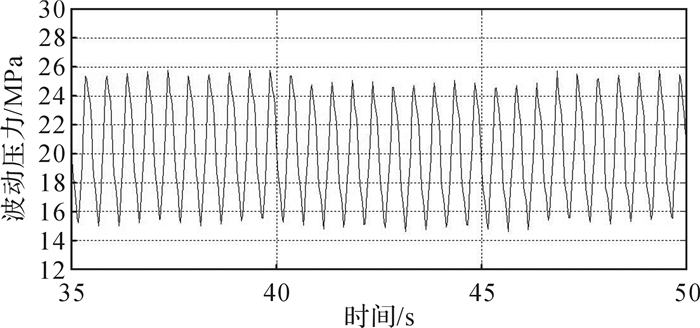
取初始泵压为20 MPa,利用MATLAB进行数值计算,得出盘阀处波动压力变化曲线,如图 8所示。
|
| 图 8 盘阀处压力随时间的变化曲线 Fig.8 Change curve of disc valve pressure with time |
从结果可以看出:当过流面积最小时,波动压力为峰值;当过流面积最大时,波动压力为波谷;波动压力的频率与过流面积的变化频率一致。从波形上看接近于正弦变化,产生的是连续柔和的压力,这样的稳定变化有利于延长工具的使用寿命。
3 振动冲击性能分析振动冲击性能主要表现为波动频率和波动压力。现主要分析盘阀的偏心距e和过流孔半径r对波动频率和波动压力的影响,为振荡器的优化提供依据和指导。
3.1 波动频率变化规律波动频率和过流面积的变化频率一致,螺杆的转速与盘阀的转速相同,螺杆的转速与钻井泵的排量有固定关系,所以泵的排量决定振荡器的工作频率。
螺杆马达的参数主要有转子偏心距ez、转子截面直径Dz和定子导程T,螺杆马达的转速和工作排量关系为:
| $ n = \frac{Q}{{4{e_{\rm{z}}}{D_{\rm{z}}}T}} $ | (14) |
式中n为转子转速,r/min。
由式(14)可得波动频率与排量呈正线性相关。因此,当钻井泵排量确定后,频率受螺杆马达参数影响,不受盘阀参数的影响。
3.2 波动压力变化规律其他条件不变,改变偏心距e和过流孔半径r, 得到波动压力的变化曲线如图 9所示。
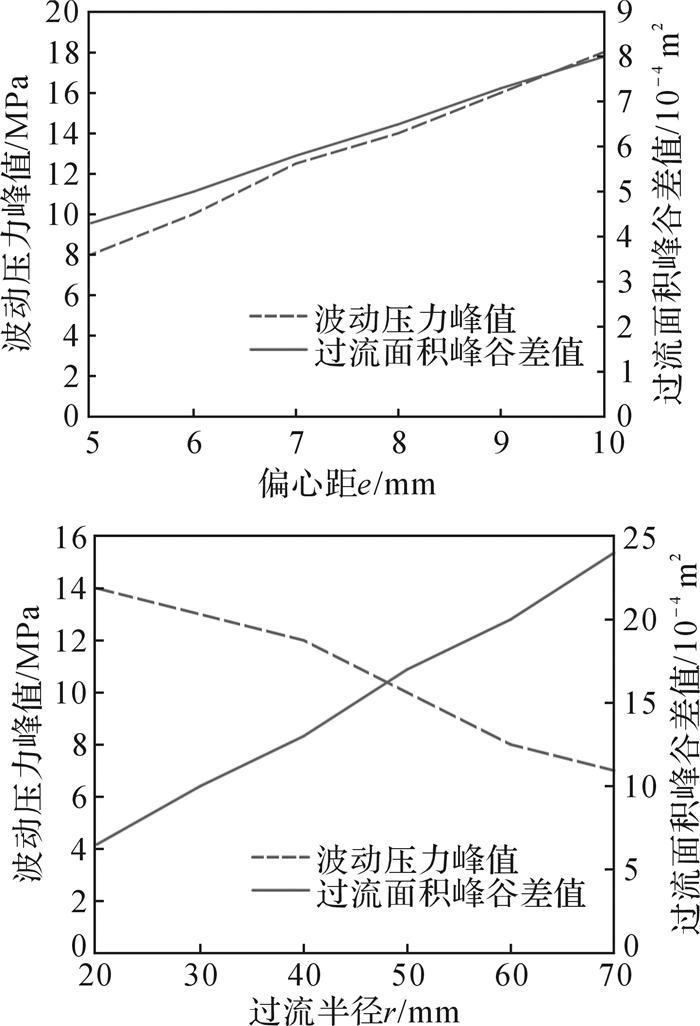
|
| 图 9 盘阀参数对波动压力峰值的影响 Fig.9 The influence of disc valve parameters on fluctuating pressure peak |
由图 9分析可得:当偏心距增大时,过流面积峰谷差值随之增大,波动压力峰值也随之增大;当过流孔半径增大时,过流面积峰谷差值随之增大,但波动压力峰值反而降低。其原因为:过流孔半径增大时,过流孔处的局部阻尼系数减小,导致波动压力峰值随之减小。若想获得较高的波动压力峰值,应在条件允许时增大偏心距和减小过流孔半径。
4 盘阀结构参数优化方法因为影响此类冲击振荡器性能的关键零部件主要是脉冲发生装置,所以对其主要参数进行优化分析。
4.1 盘阀结构最优目标函数的建立在旋转转速一定的条件下,盘阀振动产生的单位时间冲击功越大,其破岩效果越好,为此在振荡器设计过程中应该使冲击功达到最大。冲击功的大小可以表示为:
| $ W = \frac{{nFl}}{{60}} $ | (15) |
式中:W为单位时间冲击功,J;F为冲击力,N;l为振动行程,m。
单位时间的冲击次数和波动频率一致,由螺杆马达的转速决定,可由(14)确定。振荡器驱动装置(螺杆马达)的参数确定后,根据不同井段钻井水力参数Q确定优化步骤[19],波动频率也随之确定。因此冲击功的大小由冲击力决定,冲击力的大小表示为:
| $ F = \Delta pA $ | (16) |
式中:Δp为波动压差,MPa;A为活塞面积;m2。
波动压差的大小主要取决于过流面积的改变量,根据瞬变流理论和薄壁圆孔节流理论,波动压力波谷和波峰之间的差值目标函数表达式为:
| $ \Delta p = \frac{{\rho {Q^2}\left( {S_0^2 - S_{\rm{t}}^2} \right)}}{{2{\mu ^2}S_0^2S_{\rm{t}}^2}} $ | (17) |
式中:S0为盘阀最大过流面积,m2;St为盘阀最小过流面积,m2。
根据目标函数,在具体的工况下优选出流量Qopt后,提高Δp的方法是:在满足不憋泵的条件下, 使盘阀过流面积变化尽量小。
4.2 盘阀结构参数优化步骤由于地层不同,破岩机制不同,所需的破碎功(波动压差Δp)也不尽相同。根据试验和经验公式, 将目标波动压差Δp代入波动压力波谷和波峰之间的差值目标函数表达式,对盘阀的过流孔半径r和偏心距e进行优化,得到与不同地层、不同井段匹配的盘阀最优面积。针对不同的工况,可根据以下步骤进行脉冲发生装置的结构优化:
1) 在一口井施工以前,根据《钻井工程理论与技术》对钻井每个井段所采取的钻井泵工作参数(排量、泵压、泵功率等)进行设计[19],确定其最优组合;
2) 根据试验和经验公式确定目标冲击功,使活塞的面积大小固定,再由公式(16)得到目标波动压差;
3) 目标波动压差确定后,根据公式(17)确定过流面积最大值和最小值;
4) 根据过流面积最大值和最小值,利用所编程序或软件选出适用的盘阀过流孔半径r和偏心距e。
5 试验采用优质合金钢加工动、定盘阀,加工的样机盘阀参数见表 1。
| 参数 | 动盘阀过流孔 | 定盘阀过流孔 |
| 直径/mm | 40 | 40 |
| 偏心距/mm | 0 | 8.6 |
| 最大面积/mm2 | 1 256 | 1 256 |
| 最小面积/mm2 | 596 | 596 |
对振荡冲击器进行了试装配,形成了一套样机,如图 10所示。

|
| 图 10 振荡冲击器样机 Fig.10 Oscillation impacter prototype |
模拟现场钻井工艺,钻井泵提供清水作为循环介质,构成循环系统;模拟垂直井井筒深为20 m,泵压近似看作是振荡冲击器的压耗。对样机整机进行试验,泵压为5 MPa时,整个工具压耗为5 MPa,选用的螺杆马达的压耗设计值为3 MPa,可得盘阀部分的平均压耗大约为2 MPa,与数值计算得到的结果(见图 11)吻合,证明理论计算的合理性和可行性。
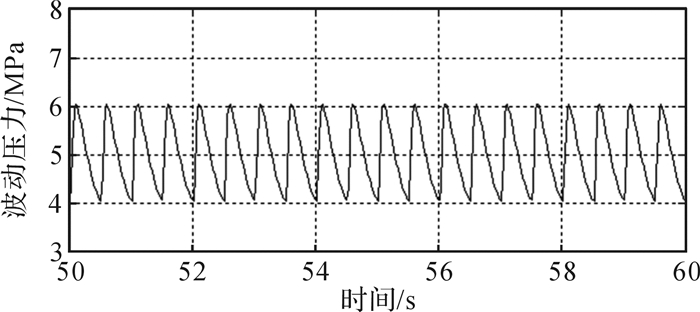
|
| 图 11 盘阀处波动压力数值计算结果 Fig.11 Numerical calculation results of fluctuating pressure at the disc valve |
1) 对振荡冲击器的工作性能进行了理论分析,首次引入瞬变流数值计算方法,建立了此工具所产生波动压力的计算模型,并进行了MATLAB编程和计算,计算结果表明该工具可以引起波动压力,并得出了波动压力变化曲线。
2) 基于理论分析和MATLAB计算,得出了偏心距e和过流孔半径r对振荡器性能影响规律,为其性能优化提供依据;建立了该工具产生振动冲击的目标函数,并给出了优化的步骤。
3) 在室内进行了测试试验,试验结果与理论计算结果相吻合,证明了理论分析和数值计算的合理性。
4) 研究结果为钻井现场应用提供理论支撑,对振荡冲击器在工程技术上的应用提出了创新性的优化方法。
| [1] |
董学成, 熊继有, 王国华, 等.
振荡冲击器工作特性研究[J]. 机械工程学报, 2014, 50(21): 197–205.
DONG Xue-cheng, XIONG Ji-you, WANG Guo-hua, et al. Study on running characteristic of oscillation impacter for oil-drilling[J]. Journal of Mechanical Engineering, 2014, 50(21): 197–205. |
| [2] | BARTON S P, BAEZ F, ALALI A. Drilling performance improvements in gas shale plays using a novel drilling agitator device[C]//The North American Unconventional Gas Conference and Exhibition, Woodlands, Texas, Jun. 14-16, 2011. https://www.sciencedirect.com/science/article/pii/S0920410517305788 |
| [3] | MELAMED Y, KISELEV A, GELFGAT M, et al. Hydraulic hammer drilling technology:developments and capabilities[J]. Journal of Energy Resources Technology, 2000, 122(1): 1–7. DOI:10.1115/1.483154 |
| [4] | LANE P Skyles, YOSEF A Amiraslani. Converting static friction to drill further and fast in directional holes[C]//IADC/SPE Drilling Conference and Exhibition, San Diego, California, Mar. 6-8, 2012. |
| [5] |
胥豪, 牛洪波, 唐洪林, 等.
水力振荡器在新场气田新沙21-28H井的应用[J]. 天然气工业, 2013, 33(3): 64–67.
XU Hao, NIU Hong-bo, TANG Hong-lin, et al. Application of hydraulic oscillators to the development of Well Xinsha 21-28H in the Xinchang Gas Field·western Sichuan Basin[J]. Natural Gas Industry, 2013, 33(3): 64–67. DOI:10.3787/j.issn.1000-0976.2013.03.014 |
| [6] |
张璀, 张金成, 王甲昌.
AG-Itator水力振荡器及其在我国的试验应用[J]. 探矿工程(岩土钻掘工程), 2015, 42(7): 54–57.
ZHANG Cui, ZHANG Jin-cheng, WANG Jia-chang. Experimental application of AG-Itator hydraulic oscillator in China[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2015, 42(7): 54–57. |
| [7] |
刘志坚, 李榕.
172mm水力振荡器在川西中浅水平井的应用[J]. 天然气技术与经济, 2012, 6(6): 37–39.
LIU Zhi-jian, LI Rong. Application of hydraulic oscillator with 172mm to medium-to-shallow horizon-tall wells, western Sichuan Basin[J]. Nature Gas Technology and Economy, 2012, 6(6): 37–39. |
| [8] |
罗朝东, 鄢标, 夏成宇, 等.
水力振荡器性能影响因素试验研究[J]. 石油机械, 2016, 44(1): 25–28.
LUO Chao-dong, YAN Biao, XIA Cheng-yu, et al. Experimental study on the factors impacting the performance of the hydraulic oscillator[J]. China Petroleum Machinery, 2016, 44(1): 25–28. |
| [9] |
张辉, 于文涛, 陈忠帅, 等.
水力脉冲轴向振荡减阻工具研制[J]. 石油矿场机械, 2014, 43(7): 73–77.
ZHANG Hui, YU Wen-tao, CHEN Zhong-shuai, et al. Development of hydropulse axial-oscillation friction-reduce tool[J]. Oil Field Equipment, 2014, 43(7): 73–77. |
| [10] |
王杰, 夏成宇, 冯定, 等.
新型涡轮驱动水力振荡器设计与实验研究[J]. 工程设计学报, 2016, 23(4): 391–395.
WANG Jie, XIA Cheng-yu, FENG Ding, et al. Design and experimental study on a new type of turbine driven hydraulic oscillator[J]. Chinese Journal of Engineering Design, 2016, 23(4): 391–395. |
| [11] |
张辉, 吴仲华, 蔡文军.
水力振荡器的研制及现场试验[J]. 石油机械, 2014, 42(6): 12–15.
ZHANG Hui, WU Zhong-hua, CAI Wen-jun. Development and field testing of hydraulic oscillator[J]. China Petroleum Machinery, 2014, 42(6): 12–15. |
| [12] |
付加胜, 李根生, 史怀忠, 等.
井下振动减摩技术研究进展[J]. 石油机械, 2012, 40(10): 6–10, 45.
FU Jia-sheng, LI Gen-sheng, SHI Huai-zhong, et al. Research progress of the downhole vibration antifriction technology[J]. China Petroleum Machinery, 2012, 40(10): 6–10, 45. |
| [13] | CARLOS R J, CARLOSV M A, CARVALHO D J L, et al. A new type of hydraulic hammer compatible with conventional drilling fluids[C]//SPE Annual Technical Conference and Exhibition, Denver, Colorado, Oct. 5-8, 2003. |
| [14] | STAYSKO R, FRANCIS B, COTE B. Fluid hammer drives down well costs[C]//SPE/IADC Drilling Conference and Exhibition, Amsterdam, Mar. 1-3, 2011. |
| [15] |
袁恩熙.
工程流体力学[M]. 北京: 石油工业出版社, 1986: 221-222.
YUAN En-xi. Engineering fluid mechanics[M]. Beijing: Petroleum Industry Press, 1986: 221-222. |
| [16] |
王树人.
水击理论与水击计算[M]. 北京: 清华大学出版社, 1981: 20-24.
WANG Shu-ren. Theory of water hammer and water hammer calculation[M]. Beijing: Tsinghua University Press, 1981: 20-24. |
| [17] |
张国忠.
管道瞬变流动分析[M]. 青岛: 中国石油大学出版社, 1994: 27-29.
ZHANG Guo-zhong. Pipeline transient flow analysis[M]. Qingdao: China University of Petroleum Press, 1994: 27-29. |
| [18] | WYLIE E B, STREETER V L. 瞬变流[M]. 索丽生, 译. 北京: 中国水利电力出版社, 1983: 22-24. WYLIE E B, STREETER V L. Transient flow[M]. Translated by SUO Li-sheng. Beijing: China Water & Power Press, 1983: 22-24. |
| [19] |
陈廷根, 管志川.
钻井工程理论与技术[M]. 青岛: 中国石油大学出版社, 2000: 139-142.
CHEN Ting-gen, GUAN Zhi-chuan. The theory and technology of drilling engineering[M]. Qingdao: China University of Petroleum Press, 2000: 139-142. |


