准确识别穿戴者的运动意图是实现外骨骼机器人精准控制的重要前提条件。目前,国内众多下肢外骨骼机器人还无法进行精确的人机协同行走,其主要原因是缺少能够准确判断使用者运动意图的感知系统,从而无法采用更合理高效的控制策略[1-2]。因此,研究具有高响应、高精度的外骨骼机器人的人体运动状态感知系统迫在眉睫。
国外在外骨骼机器人感知系统研究方面一直位居前列。BLEEX(Berkeley lower extremity exoskeleton)外骨骼机器人感知系统通过在穿戴者下肢安装一系列物理信号传感器[如惯性测量单元(inertial measurement unit, IMU)、倾角仪、力敏电阻器(force sensing resistor, FSR)],分别获取人体关节的角度和足底压力作为外骨骼动力学模型的输入量,并采用灵敏度放大控制[3-4]。但是,IMU传感器和FSR传感器存在滞后性等缺点,灵敏度放大控制能准确控制机器人的重要前提是建立高精度的动态模型,而动态模型与穿戴者穿上外骨骼机器人后的实际情况之间存在很大差异。HAL外骨骼采用能检测脑电信号(electroencephalogram, EEG)和肌电信号(electromyography, EMG)等的生物传感器来获取穿戴者的运动意图[5-8],然而这类信号通常比较微弱,对环境变化十分敏感,因此采集难度较大,采集质量不高,这在一定程度上限制了HAL外骨骼在复杂环境下的工作能力。
上述文献中提及的外骨骼机器人的人体运动感知系统均是采用单一的控制模式,没有考虑到人机系统所处的步态相与控制方法之间的适用性和优化配置问题。要实现更为柔顺、精确的控制,需要根据不同的步态模型,采用不同的针对性的控制方法。采用人体关节姿态角度、人机交互力和足底压力等关键特征来进行综合判断,能更精确识别步态相。
为更准确地获取穿戴者的步态特征,需要对下肢多传感器信号特征进行融合感知。本文提出了基于支撑相选择位置控制、摆动相选择交互力导纳控制的人机协同控制方法,设计了基于多信息融合的感知系统,以人体关节角度、人机交互力和足底压力为感知量,利用变增益卡尔曼滤波算法和Savitzky-Golay滤波算法分别进行处理,获得步态信息的关键特征。
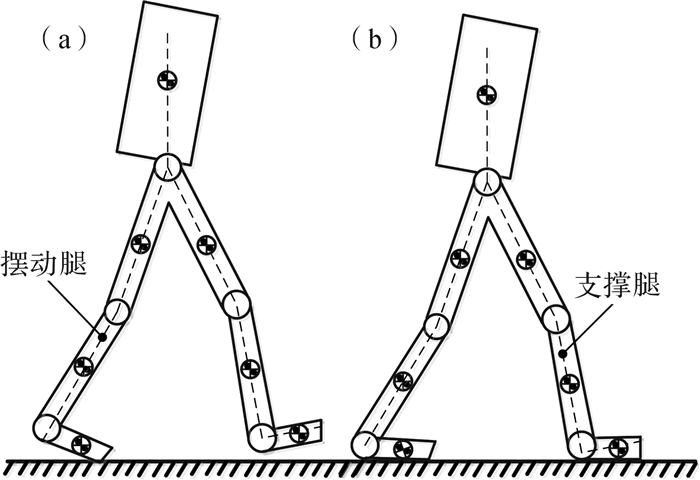
1 控制方法及感知参数的确定基于人行走过程中腿部呈现交替触地的变化,下肢动态模型将分为支撑腿、摆动腿以及双腿支撑三种步态相。下肢外骨骼机器人只在矢状面内驱动髋关节和膝关节即可满足最基本的运动需求,因此下肢外骨骼机器人可以简化成顶端固定的刚性七连杆模型,如图 1所示。
|
| 图 1 下肢动态模型 Fig.1 Dynamic model of lower limb |
支撑相选择位置控制、摆动相选择交互力导纳控制的人机协同控制方法是鉴于:支撑腿在行走过程中的主要作用是承载外骨骼重力,其位置状态改变不明显,故采用位置控制方法;而摆动腿位置状态变化剧烈,其自由运动几乎不受外骨骼影响,故采用导纳控制。
基于以上分析,下肢外骨骼机器人采用基于步态相的控制方法:将人体关节的姿态角度、人机交互力和足底压力作为多信息融合感知系统的感知参数,综合判断步态相,当判断为支撑相时,采用位置控制,当判断为摆动相时,采用导纳控制。
2 多信息融合感知系统 2.1 下肢关节角度采集多信息融合感知系统将4个IMU传感器分别置于穿戴者的大腿、小腿上,以测量下肢髋关节和膝关节在行走过程中摆动的角度,如图 2所示。IMU传感器的安装位置以及它测量的髋关节和膝关节角度,以顺时针摆动方向为关节角度的正方向。

|
| 图 2 IMU传感器安装位置及测量的关节角度 Fig.2 Installation location of IMU sensor and measurement angle of joints |
人机交互力为穿戴者与外骨骼间的相互作用力。在理想的人机耦合协同运动模型中,穿戴者和外骨骼之间不存在相互作用力。但在实际运动过程中,人机之间的跟随动作总是会存在一定程度的滞后,这种滞后导致了人机交互力的产生,故人机交互力的大小与外骨骼的跟随灵敏度有关,这种关系使得人机交互力适合作为导纳控制的输入量。
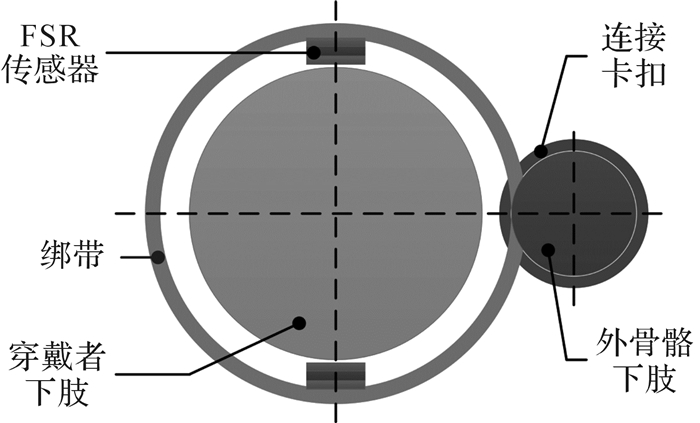
以往对人体交互力的研究主要集中在触觉传感器的研发上,而其中仅有小部分应用于对下肢外骨骼人机交互力的测量。Rossi等自主研发了触觉传感器来测量下肢康复机器人与穿戴者间的相互作用,获得了良好的实验结果[9],但该触觉传感器制作难度大,成本昂贵。对比各类力传感器的结构、测量原理以及安装形式后,本文决定采用灵敏度高、柔韧性好、重复性强、质量轻、体积小、成本低的压敏电阻FSR薄膜传感器,来测量人机交互力。穿戴者与外骨骼机器人通过绑带连接时FSR传感器的安装位置如图 3所示。
|
| 图 3 FSR传感器安装位置 Fig.3 Installation location of FSR sensor |
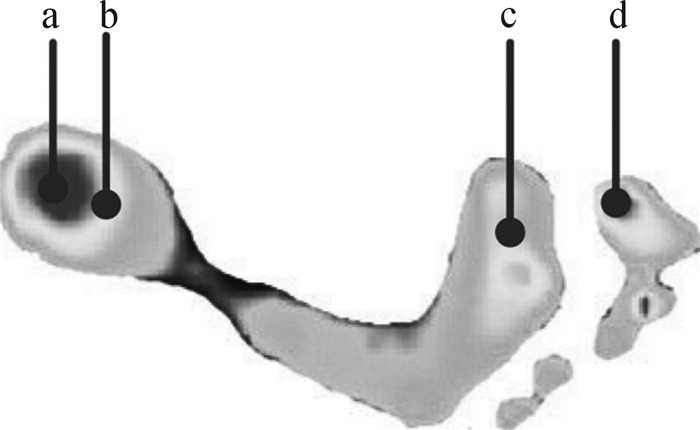
足底压力直接反映了人-外骨骼系统与外界环境的特征,对研究下肢的行走步态相有很好的借鉴作用[10]。如图 4所示,足底的结构复杂,在不同的步态相下,各部位的受力大小不一样。因此,要精确地检测足底压力,必须对足底各部位的受力情况有充分的了解,合理设计足底压力传感器的数量和布置的位置,符合足底压力的分布与变化情况。
|
| 图 4 足底压力分布 Fig.4 Distribution of plantar pressure |
在图 4中,足底被划分为4个受力区:脚跟受力区a、外侧脚根部分受力区b、第1趾跖受力区c以及脚尖受力区d。为了便于安装以及准确地测量相应区域的受力,将4个FSR传感器封装好,分别置于鞋垫的相应位置,制成传感鞋垫。
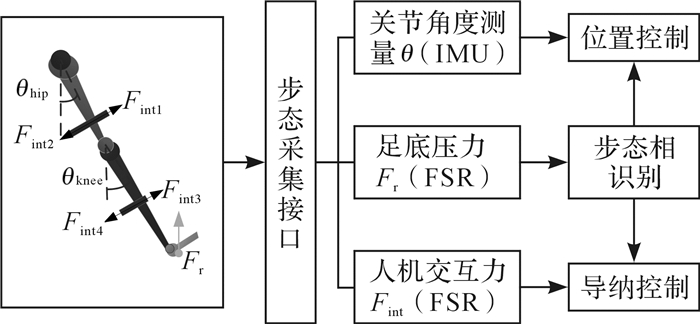
2.4 多信息融合感知系统架构文献[10]表明,仅仅利用人体关节角度、人机交互力和足底压力等数据和特征,不能直接获取步态相,需要对各个压力传感器信号进行多信息融合处理,提取各个信号的特征来进行综合判断。多信息融合感知系统采用STM32作为控制器,共采集穿戴者的4个下肢关节角度数据、8个足底压力信号以及8个人机交互力信号,进行数据融合处理以识别步态相位,并根据所处相位采用相应的控制方法,其系统原理框架如图 5所示。
|
| 图 5 基于多信息融合的下肢外骨骼机器人感知系统原理框架 Fig.5 Framework of sensing system for lower limb exoskeleton robot based on multi-information fusion |
由于无法直接从IMU传感器检测的角速度和角加速度等数据中直接获取人体的关节角度,加上FSR传感器受到人机之间的摩擦或者相对运动的影响,难以对原始数据进行精确判断,因此必须对传感器采集的数据进行解算和预处理。
3.1 变增益卡尔曼滤波算法卡尔曼滤波理论以最小均方差为估计准则,融合了加速度计的稳定性与陀螺仪的瞬时高精度,是实现数据融合和快速跟踪的最佳方法[11-15]。
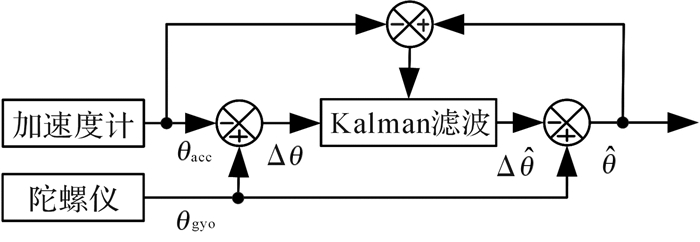
本文解算关节角度采用的是基于变噪声率的卡尔曼滤波算法,其主要特点是:随着迭代的变化, 噪声率也将变化。该算法的原理框图如图 6所示。
|
| 图 6 变增益卡尔曼滤波算法原理框图 Fig.6 Block diagram of the variable-gain Kalman filter algorithm |
根据变增益卡尔曼滤波算法原理,结合下肢关节角度的测量,可得:
| $ \left[\begin{array}{l} \Delta {{\hat \theta }_k}\\ \Delta {{\hat b}_k} \end{array} \right] = \left[\begin{array}{l} \Delta \hat \theta _k^-\\ \Delta \hat b_k^- \end{array} \right] + \left[\begin{array}{l} {K_1}\\ {K_2} \end{array} \right](\Delta {\theta _k} -\Delta \hat \theta _k^ -) $ | (1) |
| $ \left[\begin{array}{l} \Delta \hat \theta _{k + 1}^-\\ \Delta \hat b_{k + 1}^- \end{array} \right] = \left[\begin{array}{l} 1\;\;\;\Delta t\\ 0\;\;\;1 \end{array} \right]\left[\begin{array}{l} \Delta {{\hat \theta }_k}\\ \Delta {{\hat b}_k} \end{array} \right] $ | (2) |
式中:K1, K2分别代表Δθ, Δb的增益; Δ
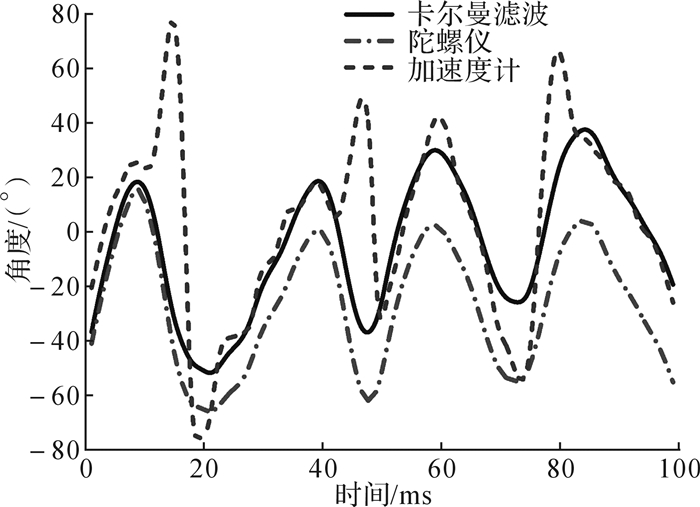
从图 7可以看出,在初始阶段,陀螺仪的积分误差小,其积分角度值与卡尔曼滤波算法解算结果基本相同,但随着误差积累,两者相差越来越大;振动对加速度的测量影响很大,但加速度计长时间测量精度好;变增益卡尔曼角度解算算法发挥了加速度计持久的稳定特性以及综合了陀螺仪瞬时测量精度水平高的优势,具有优异的处理效果。
|
| 图 7 变增益卡尔曼滤波算法效果对比 Fig.7 Comparison of the effect of variable-gain Kalman filter algorithm |
足底与地面产生的脉冲性冲击和鞋内水平方向或垂直方向存在的摩擦噪声,都会干扰FSR传感器信号从而造成明显的测量误差[10]。采用基于最小二乘原理的平滑Savitzky-Golay滤波算法,设一个一维数据x(n),其中n∈[-m, m],构建一个N阶多项式(N≤2m+1)拟合这组数据:
| $ p(n) = {a_0} + {a_1}n + {a_2}{n^2} + \cdots {a_N}{n^N} = \sum\limits_{j = 0}^N {{a_j}{n^j}} $ | (3) |
通过最小二乘法理论拟合的残差,结合微积分可得:
| $ \mathop N\limits_{j = 0}^M \left( {\sum\limits_{n =-m}^m {{n^{i + j}}} } \right)\;\;{a_j} = \sum\limits_{n =-m}^m {{n^i}x(n), \mathit{i}{\rm{ = 0, 1, }} \cdots {\rm{, }}\mathit{N}} $ | (4) |
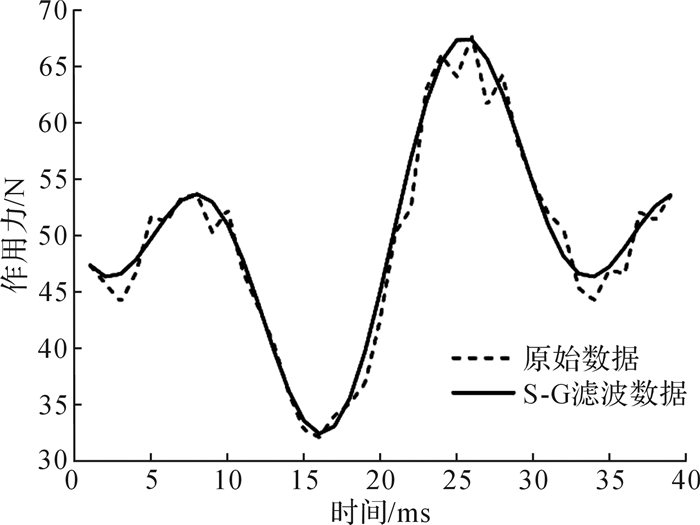
根据式(4),通过求解多项式的系数,即可算出每一项滤波的数值。如图 8所示,采用该算法对FSR传感器信号进行预处理,可滤除纹波扰动对信号的影响。
|
| 图 8 FSR传感器信号滤波前后对比 Fig.8 Comparison of FSR sensor signal before and after filtering |
在人机协同行走的过程中,人体关节角度、人机交互力和足底压力均有较为明显的变化,这些数据含有大量的运动特征信息。全面深入地分析这些数据,并进行数据融合,获取步态特征,有助于更深入地开发步态相识别算法和后期控制算法。
4.1 髋关节角度数据分析图 9和图 10为一名身高为1.78 m的成年中国男子,以4 km/h速度在水平路面上行走的步态数据。

|
| 图 9 髋关节角速度和角度信号曲线 Fig.9 Curve of angular velocity and angle of hip joints |
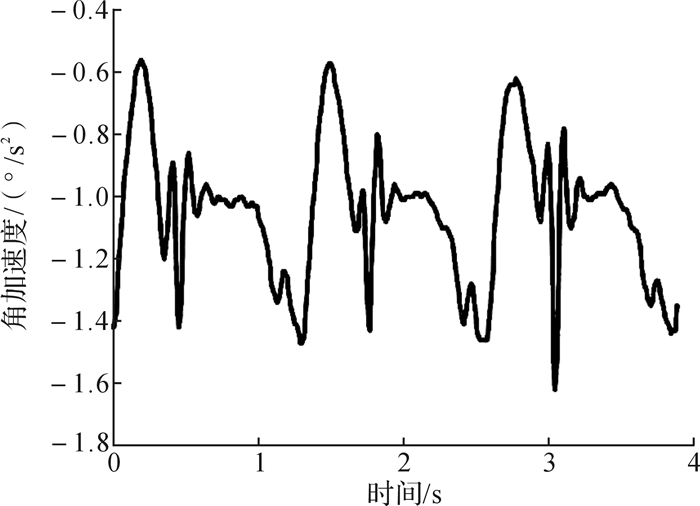
|
| 图 10 髋关节角加速度信号曲线 Fig.10 Curve of angular acceleration of hip joints |
从图中可以看出:角加速度明显受到振动干扰,其特征值无法获得。而对于角速度信号,虽然在支撑相存在一些不规则的变化,但是在整个过程中呈现很好的周期性,相同的变化大小和位置使其特征值容易获取。在支撑相和摆动相,角度信号曲线区分非常明显,且呈现严格的周期性,可以用于步态相的识别。
单独对1个周期内髋关节角度信号曲线进行分析:穿戴者开始时处于站立状态,其起始点角度基本为零;当右脚开始行走时,角度随之增大,脚跟触地时为图 9中曲线的第1个波峰,脚尖离地时为第1个波谷。但是,脚跟着地和脚尖离地这2种步态通常并非恰好对应角度的最大值与最小值,对于同一穿戴者,它们以相同的时间间隔分别落后和超前于角度最大值与最小值发生的时刻。
4.2 膝关节角度数据分析与髋关节角加速度一样,膝关节矢状面上的角加速度信号受振动干扰很大,不具可用性。因此,只对膝关节的角速度和角度信号曲线进行详细分析。
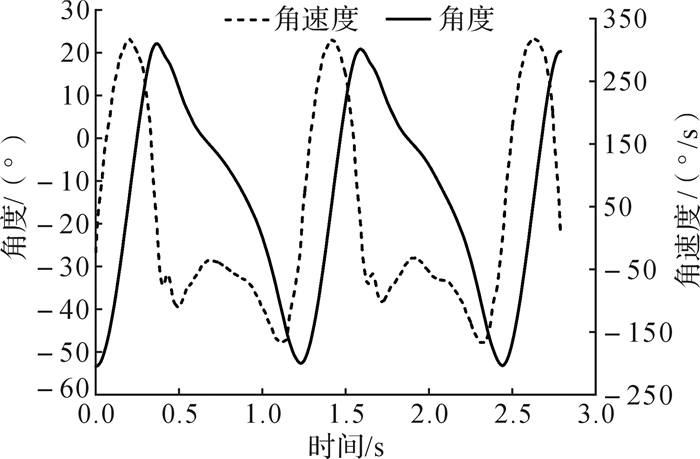
如图 11所示:膝关节的正向最大角(约为25°)小于负向最大角(约为55°);角速度相差较大,但在摆动相为正值,在支撑相为负值,在支撑相与摆动相切换时(脚跟着地、脚尖离地)接近零。
|
| 图 11 膝关节角度和角速度信号曲线 Fig.11 Curve of angle and angular velocity of knee joints |
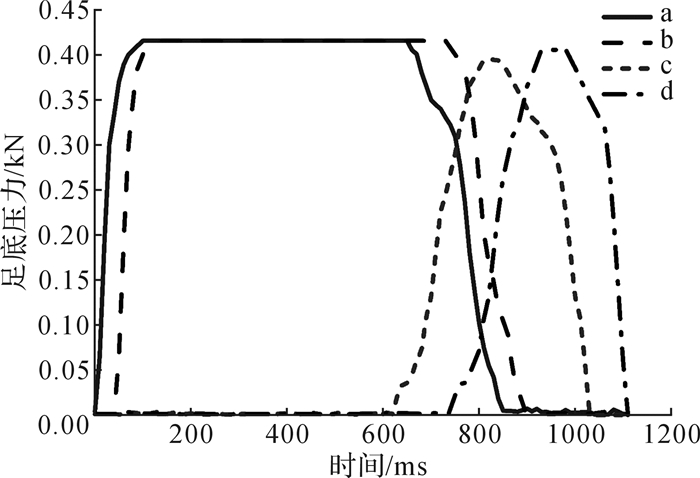
由图 12可知,穿戴者在行走过程中,足底压力变化是连续不间断的,且没有突变。各传感器压力峰值为:Fa和Fb大致相等,Fd次之,Fc最小,这是因为a处和b处的传感器都位于脚跟位置附近,且相隔距离不大。大约在200 ms时脚跟着地,距离踝关节最近的a处FSR先采集到压力,随着足绕脚跟旋转,b处FSR采集到压力;当脚尖着地时,d处FSR才会采集到压力,并且其压力信号会随着脚尖瞬间离地而快速地降低为零;c处FSR采集的压力信号变化可以看作是Fb与Fd之间的过渡,变化不大且缓和。4个足底压力传感器依次平稳输出压力数据,通过融合这4个信号进行步态相识别。
|
| 图 12 单周期内足底压力变化曲线 Fig.12 Curve of plantar pressure in a single cycle |
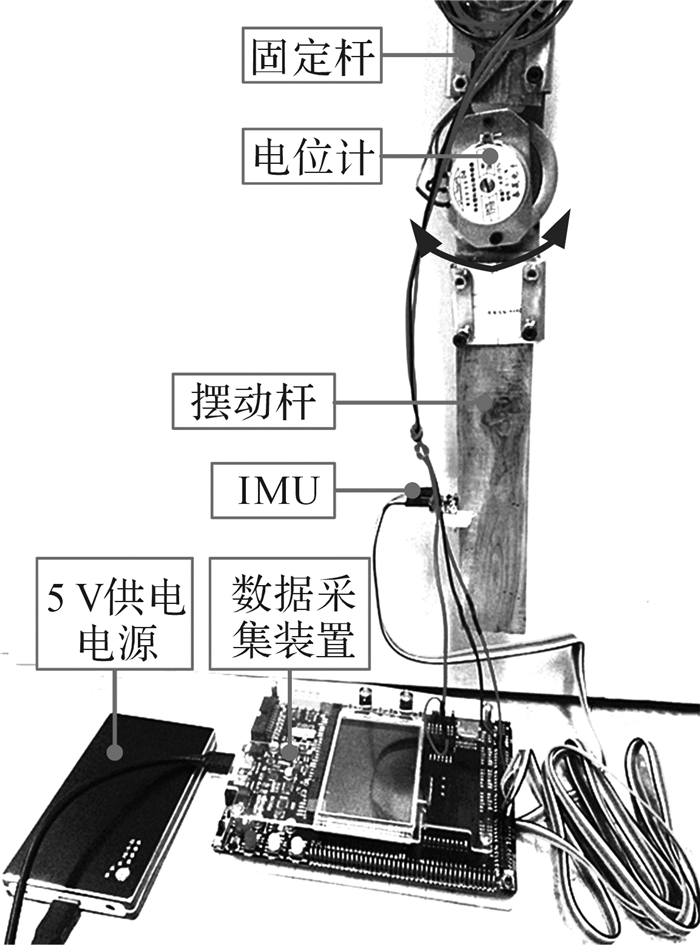
如图 13所示,姿态角度解算算法验证装置是一个由固定杆和摆动杆组成的简单二连杆结构,其中摆动杆可以绕连接处在竖直平面内摆动,电位计安装在两杆之间,IMU传感器安装在摆动杆上,电位计和IMU传感器供电线和信号传输线连接至下肢步态数据采集模块。
|
| 图 13 姿态角度解算算法验证装置 Fig.13 Verification device of attitude angle processing algorithm |
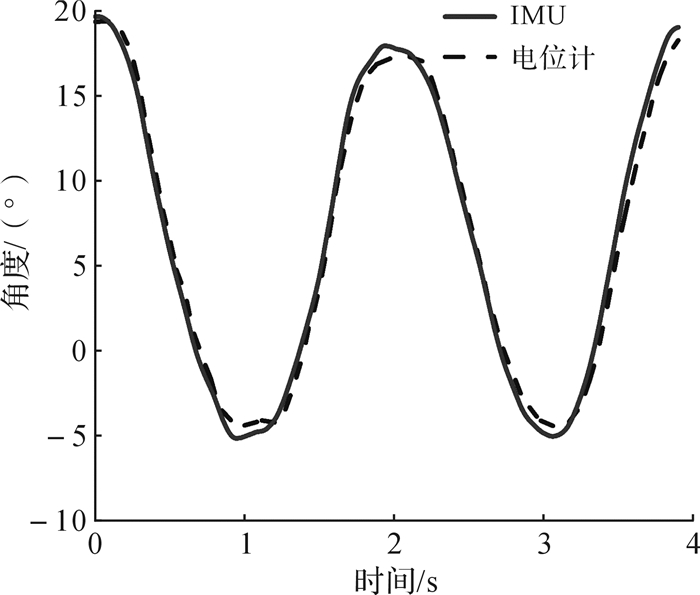
图 14所示为电位计获得的角度变化曲线和使用变增益卡尔曼滤波算法解算出的姿态角度曲线,可以发现这2条曲线基本上是重合的,两者之间误差很小,验证了该算法是准确可靠的。
|
| 图 14 电位计及IMU传感器测得的角度数据曲线 Fig.14 Curve of angle data measured by potentiometer and IMU sensor |
同时,为了验证该算法在不同行走速度下的稳定性,在不同驱动速度下,进行了5组对比实验,得到了实验结果与该算法所得结果的平均相对误差,如表 1所示。
| (°) | |||||
| 组别 | 驱动速度/(°/s) | ||||
| 10 | 20 | 30 | 40 | 50 | |
| 第1组 | 0.06 | 0.07 | 0.07 | 0.06 | 0.08 |
| 第2组 | 0.07 | 0.06 | 0.07 | 0.10 | 0.06 |
| 第3组 | 0.09 | 0.08 | 0.07 | 0.07 | 0.08 |
| 第4组 | 0.09 | 0.07 | 0.08 | 0.09 | 0.08 |
| 第5组 | 0.09 | 0.08 | 0.08 | 0.09 | 0.09 |
从表 1中看出:电位计与IMU传感器测得角度的平均相对误差均小于或者等于0.09°,且最小值为0.06°。由此可以说明,基于变增益卡尔曼滤波的角度解算算法的解算结果精度高、稳定性好。
5.2 交互力感知方法验证如图 15所示为人机交互力验证装置。绑带上装有2个FSR传感器,它们与下肢步态数据采集模块连接。将绑带固定在下肢外骨骼右肢小腿上,穿戴者穿上外骨骼服。外骨骼右肢小腿与穿戴者右肢小腿通过绑带绑在一起。FSR1和FSR2分别位于穿戴者小腿的前后两侧。穿戴者小腿动作起来,驱动外骨骼下肢前后摆动。FSR1和FSR2分别测量穿戴者作前摆运动与后摆运动时受到的相互作用力,得到的数据保存至实验装置的采集模块。

|
| 图 15 人机交互力验证装置 Fig.15 Verification device for human-robot interaction force |
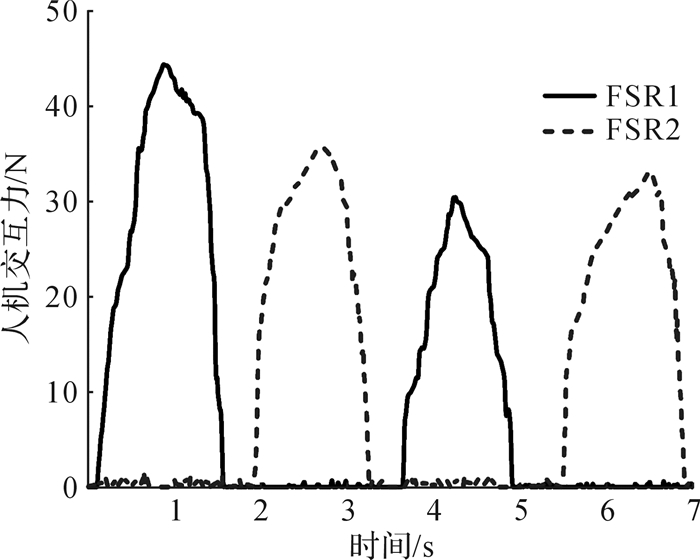
图 16为实验测得的人机交互力。从图 16可以看出,穿戴者每次摆动大腿及小腿的步幅和步高不同,导致了FSR压力传感器所测得的法向重力分量大小也有所不同,这使得2条曲线中4个峰值大小有所不同。当穿戴者向前摆腿时,理论上只有FSR1受力,但FSR2实际上也会受到拉应力,反之亦然。在运动过程中,人机之间的接触摩擦力作用在FSR上,所以,2条曲线会在0 N处有很小的波动,但这种波动是可以忽略不计的,因此FSR对人机交互力的感知不会受到影响。实验结果说明了FSR传感器可以很好地感知人机交互力,验证了该人机交互力感知方法是可靠的、有效可行的。
|
| 图 16 人机交互力曲线 Fig.16 Curve of human-robot interaction force |
1) 采用支撑相选择位置控制、摆动相选择交互力导纳控制且根据步态相状况实时切换的人机协同控制方法,依此方法确定关节角度、下肢人机交互力以及足底压力为控制方法所需的控制输入量,即作为基于多信息融合感知系统的感知量。
2) 搭建了一套基于多信息融合的下肢外骨骼机器人感知系统,利用变增益卡尔曼滤波算法解算IMU传感器采集的人体关节角度数据,利用Savitzky-Golay滤波算法对FSR传感器采集的压力数据进行预处理,获得步态特征,为更深层次的步态识别算法提供特征数据支持。
3) 通过实验对变增益卡尔曼角度解算算法和人机交互力感知方式进行了验证,说明了基于多信息融合感知系统的设计开发是可行、可靠的。
| [1] |
李俊杰. 外骨骼步态检测系统的研究与实现[D]. 成都: 电子科技大学自动化工程学院, 2013: 1-3.
LI Jun-jie. Research and implementation of the exoskeleton gait detection system[D]. Chengdu: University of Electronic Science and Technology of China, School of Automation Engineering, 2013: 1-3. |
| [2] |
孙建, 余永, 葛运建.
可穿戴型下肢助力机器人感知系统研究[J]. 微纳电子技术, 2007, 44(7): 353–357.
SUN Jian, YU Yong, GE Yun-jian, et al. Research on sensing systems of wearable power assist leg[J]. Micronanoelectronic Technology, 2007, 44(7): 353–357. |
| [3] | STEGER R, KIM S H, KAZEROONI H. Control scheme and networked control architecture for the Berkeley lower extremity exoskeleton (BLEEX)[C]//Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, Florida, May 15-19, 2006. |
| [4] | KAZEROONI H, STEGER R, HUANG L. Hybrid control of the Berkeley lower extremity exoskeleton (BLEEX)[J]. The International Journal of Robotics Research, 2006, 25(5/6): 561–573. |
| [5] | HAYASHI T, KAWAMOTO H, SANKAI Y. Control method of robot suit HAL working as operator's muscle using biological and dynamical information[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, Alberta, Aug. 2-6, 2005. https://link.springer.com/chapter/10.1007/978-3-319-12922-8_2 |
| [6] | KAWAMOTO H, SANKAI Y. Power assist method based on phase sequence and muscle force condition forhal[J]. Advanced Robotics, 2005, 19(7): 717–734. DOI:10.1163/1568553054455103 |
| [7] | SUZUKI K, MITO G, KAWAMOTO H, et al. Intention-based walking support for paraplegia patients with robot suit HAL[J]. Advanced Robotics, 2007, 21(12): 1441–1469. |
| [8] | TSUKAHARA A, KAWANISHI R, HASEGAWA Y, et al. Sit-to-stand and stand-to-sit transfer support for complete paraplegic patients with robot suithal[J]. Advanced Robotics, 2010, 24(11): 1615–1638. DOI:10.1163/016918610X512622 |
| [9] | De ROSSI S M, VITIELLO N, LENZI T, et al. Soft artificial tactile sensors for the measurement of human-robot interaction in the rehabilitation of the lower limb[C]//Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Aug. 31-Sep. 4, 2010. |
| [10] |
杨金江. 助力型下肢外骨骼机器人多信号融合感知系统研究[D]. 杭州: 浙江大学机械工程学院, 2016: 30-31.
YANG Jin-jiang. Research on the multi-sensor fusion sensing system for lower exoskeleton robot[D]. Hangzhou: Zhejiang University, School of Mechanical Engineering, 2016: 30-31. |
| [11] | CIKAJLO I, MATJAČIĆ Z, BAJD T. Efficient FES triggering applying Kalman filter during sensory supported treadmill walking[J]. Journal of Medical Engineering & Technology, 2008, 32(2): 133–144. |
| [12] | BENNETT T, JAFARI R, GANS N. An extended Kalman filter to estimate human gait parameters and walking distance[C]//American Control Conference, Washington, DC, Jun. 17-19, 2013. |
| [13] | COOPER G, SHERET I, MCMILLIAN L, et al. Inertial sensor-based knee flexion/extension angle estimation[J]. Journal of Biomechanics, 2009, 42(16): 2678–2685. DOI:10.1016/j.jbiomech.2009.08.004 |
| [14] | JAKOB C, KUGLER P, HEBENSTREIT F, et al. Estimation of the knee flexion-extension angle during dynamic sport motions using body-worn inertial sensors[C]//Proceedings of the 8th International Conference on Body Area Networks, Boston, Massachusetts, Sep. 30-Oct. 2, 2013. |
| [15] | KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45. DOI:10.1115/1.3662552 |



