2. 湖南长河机械有限公司, 湖南 长沙 410600
2. Hunan Changhe Machinery Co., Ltd., Changsha 410600, China
长螺旋钻机是一种适用于建筑基础工程中成孔作业的施工机械,因施工时噪声低、污染小、作业速度快、作业人员少而得到广泛应用。长螺旋钻机主要由钻杆、纵移机构、鹅头、桅杆、斜撑、回转平台、机身及动力头等组成。钻机钻杆为螺旋叶片钻杆,钻进时土料可沿叶片排到地面上。钻杆的上下运动,可通过动力头的驱动实现。动力头在桅杆滑轨上滑动,保证了其钻孔的垂直度。长螺旋钻机的提钻过程中同时伴随着CFG压灌桩施工,而桅杆的提钻稳定性不仅直接影响成桩质量和施工效率[1-2],还涉及施工的安全性。由此可见,保证长螺旋钻机提钻工况下其桅杆的稳定性对钻孔施工有着很重要的作用。目前,对此类稳定性问题的研究较多,如:Timoshenk等[3]给出了等截面柱和几种简单的变截面柱的稳定性精确解;Rahai等[4]使用修正的振动模态法和能量法研究了非等截面混合结构的稳定性;楼梦麟等[5]提出了基于Ritz函数展开的模态摄动法来求解变截面压杆稳定性问题的半解析法。鉴于变截面梁的复杂性和多样性,其他学者相继提出了多种变截面梁单元稳定性的求解方法[6-9]。随着工程机械的广泛应用,国内外很多学者对起重机吊臂的稳定性进行了研究[10-13],但对长螺旋钻机稳定性的研究却很少见。文献[14]虽然对提钻工况下旋挖钻机(单斜撑作用)进行受力分析,却并未深入研究其稳定性。
长螺旋钻机现有的提钻方式有2种:直接提钻和回转提钻。回转提钻工况下会发生螺旋钻杆卡钻、停钻等状况,而直接提钻会产生真空负压使孔坍塌,甚至使桅杆失稳,发生安全事故[15]。因此,本文对直接提钻工况下双斜撑长螺旋钻机桅杆稳定性进行分析,建立了桅杆失稳特征方程及直接提钻失稳临界值。针对ZLH43ZL(TB)-D180长螺旋钻机桅杆,通过对比本文推导结果与采用ANSYS有限元方法所得结果,验证本文推导表达式的正确性,并进一步分析主副斜撑点位置参数λ1,λ2,桅杆截面惯性矩I和主卷扬钢丝绳角度θ对直接提钻工况下双斜撑长螺旋钻机桅杆的失稳临界值Fcr的影响。
1 双斜撑长螺旋钻机结构及其工作原理双斜撑长螺旋钻机的结构如图 1所示。长螺旋钻机的单个作业流程为:通过变幅油缸2将桅杆4举升到竖直位置,由主斜撑12和副斜撑13将桅杆总成4、动力头总成5以及鹅头6稳定支撑在机身11上,之后由滑动在桅杆滑轨中的动力头总成5驱动空心螺旋钻杆3向下运动。待达到钻进深度后,主卷扬10回转,通过鹅头6中的滑轮组使动力头和钻杆向上运动,钻杆的上口与水泥灌注设备连接,同时进行水泥灌注和排土。

|
| 1—纵移机构;2—变幅油缸;3—空心螺旋钻杆;4—桅杆总成;5—动力头总成;6—鹅头;7—支腿油缸;8—配重;9—驾驶室;10—主卷扬;11—机身;12—主斜撑;13—副斜撑 图 1 双斜撑长螺旋钻机结构 Fig.1 The structure of continuous flight auger driller with double braces |
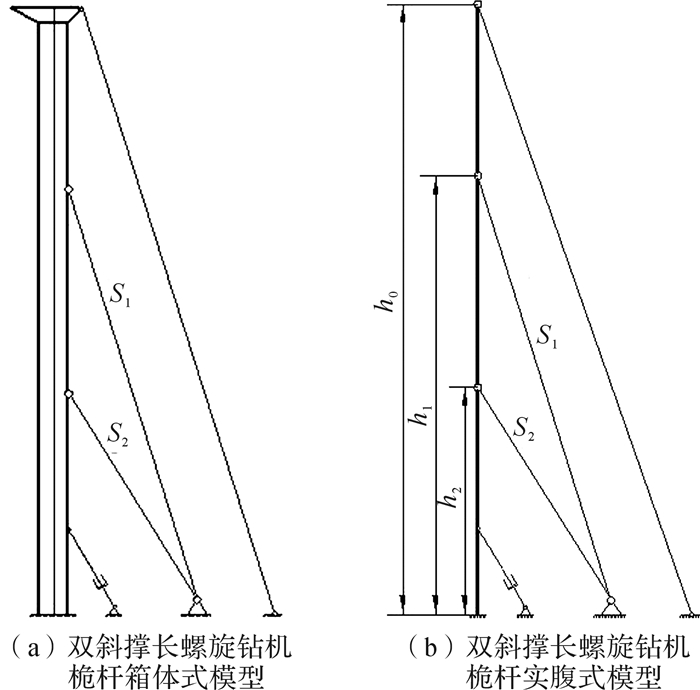
直接提钻工况下双斜撑长螺旋钻机桅杆箱体式模型及等效后的实腹式模型如图 2所示,记桅杆总高为h0,主、副斜撑点到桅杆根部高度为hi,长度为Si,i=1, 2。其中:主、副斜撑点位置引起的桅杆形心轴的偏心对桅杆稳定性影响很小,故在桅杆实腹式等效时直接将两斜撑点移动至桅杆形心轴;桅杆根部与机身焊接,故可将桅杆根部视为固定端;螺旋钻机桅杆、斜撑结构和受力均具有对称性,故双斜撑长螺旋钻机桅杆提钻稳定性分析可以简化为平面内稳定性分析。同时由胡均平等[16]对长螺旋钻机变幅机构的研究可知:起杆变幅油缸在起杆完毕后,无杆腔压力基本为0,因此在下述建模中忽略变幅油缸对桅杆受力的影响。
|
| 图 2 直接提钻工况下双斜撑长螺旋钻机桅杆力学分析模型 Fig.2 Mechanical analysis model of the mast of continuous flight auger driller with two braces under direct-drill-lifting condition |
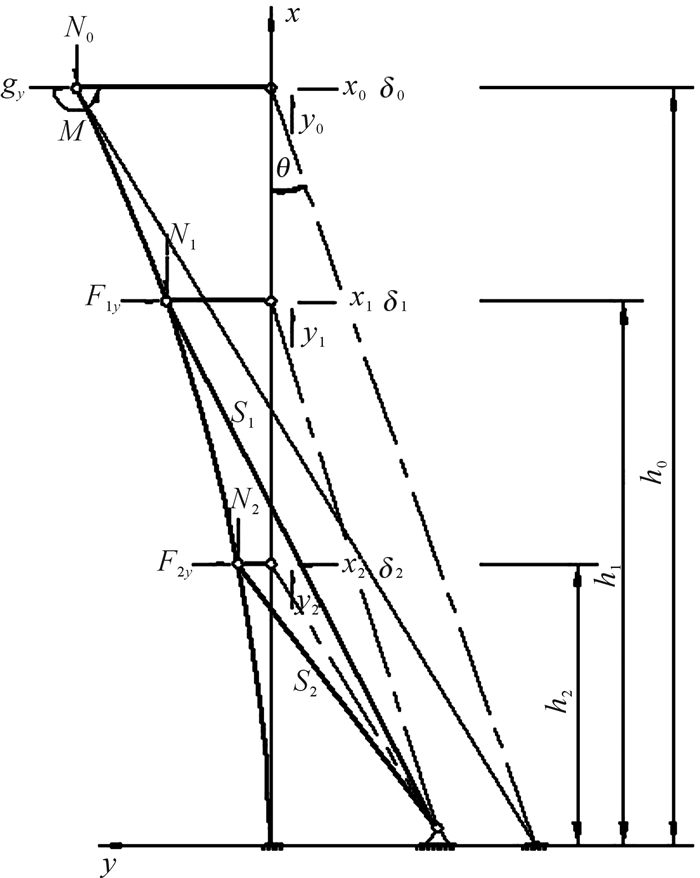
以桅杆根部形心为原点,以桅杆轴为x轴,建立桅杆坐标系如图 3所示。记直接提钻工况下双斜撑长螺旋钻机桅杆发生失稳时,桅杆顶部产生侧向位移为δ0;鹅头处滑轮组传动比为z,其左端到桅杆轴心的距离为b1;提钻力为F;主卷扬钢丝绳与桅杆轴心夹角为θ;钢丝绳力为g,沿x,y轴分力为gx,gy。
|
| 图 3 直接提钻工况下双斜撑长螺旋钻机桅杆稳定性分析 Fig.3 Stability analysis of the mast of continuous flight auger driller with double braces under direct-drill-lifting condition |
记直接提钻工况下桅杆顶部总轴力为N0,总偏心力矩为M, 则由长螺旋钻机鹅头结构的特性可得:
| $ \left\{ \begin{array}{l} M = F\left( {{\delta _0} + {b_1}} \right)\\ {g_y} = g\sin \theta = \frac{F}{z}\sin \theta \\ {N_0} = F + {g_x} = F\left( {1 + \frac{1}{z}\cos \theta } \right) \end{array} \right. $ | (1) |
记主、副斜撑点侧向位移为δi,斜撑平面内拉力为Fi,i=1, 2。则其轴向分力Ni及侧向分力Fiy为:
| $ \left\{ \begin{array}{l} {N_i} = \frac{{{h_i}}}{{{S_i}}}{F_i},i = 1,2\\ {F_{iy}} = \frac{{{\delta _i}}}{{{S_i}}}{F_i},i = 1,2 \end{array} \right. $ | (2) |
由于斜撑产生的侧向分力Fiy可用斜撑点处的侧向位移线性表示,故可将它视为弹性力,采用文献[17]提出的等效弹性支座法进行推导,记主、副斜撑点处等效侧向刚度
| $ {F_{iy}} = {k_i}{\delta _i},i = 1,2 $ | (3) |
设各段桅杆的y轴惯性矩为Ii,弹性模量为E,则第i段桅杆的挠曲微分方程为:
| $ \left\{ \begin{array}{l} E{I_0}{{y''}_0} = {N_0}\left( {{\delta _0} - {y_0}} \right) - {g_y}\left( {{h_0} - {x_0}} \right) + M\\ E{I_1}{{y''}_1} = {N_0}\left( {{\delta _0} - {y_1}} \right) - {g_y}\left( {{h_0} - {x_1}} \right) + M + \\ \;\;\;\;\;\;\;\;\;\;\;{N_1}\left( {{\delta _1} - {y_1}} \right) - {F_{1y}}\left( {{h_1} - {x_1}} \right)\\ E{I_2}{{y''}_2} = {N_0}\left( {{\delta _0} - {y_2}} \right) - {g_y}\left( {{h_0} - {x_2}} \right) + M + \\ \;\;\;\;\;\;\;\;\;\;\;{N_1}\left( {{\delta _1} - {y_2}} \right) - {F_{1y}}\left( {{h_1} - {x_2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{N_2}\left( {{\delta _2} - {y_2}} \right) - {F_{2y}}\left( {{h_2} - {x_2}} \right) \end{array} \right. $ | (4) |
需要注意的是0≤h2≤h1≤h0,将式(3)代入式(4)中,化简后得:
| $ \left\{ \begin{array}{l} E{I_0}{{y''}_0} + {P_0}{y_0} = {P_0}\left( {{\delta _0} + \frac{{{h_0} - {x_0} - {b_1}}}{{1 + \frac{{\sin \theta }}{z}}}} \right)\\ E{I_1}{{y''}_1} + {P_1}{y_1} = {k_1}{\delta _1}\left[ {{P_1} + {k_1}\left( {{h_1} + {x_1}} \right) + \frac{{{h_1} - {x_1}}}{{1 + \frac{{\sin \theta }}{z}}}} \right]\\ E{I_2}{{y''}_2} + {P_2}{y_2} = {k_2}\left( {{h_2} + {x_2}} \right){\delta _2} + \left( {{k_1}{\delta _1} + {k_2}{\delta _2}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{P_2} - {k_2}\left( {{h_2} + {x_2}} \right) + \frac{{{h_2} - {x_2}}}{{1 + \frac{{\sin \theta }}{z}}}} \right] \end{array} \right. $ | (5) |
式中:Pi为桅杆各段的总轴力,P0=N0,P1=N0+N1,P2=N0+N1+N2;δ0表示桅杆顶部水平位移。
记中间量
| $ \left\{ \begin{array}{l} {y_0} = {A_0}\cos \left( {{\omega _0}{x_0}} \right) + {B_0}\sin \left( {{\omega _0}{x_0}} \right) + {\delta _0} \cdot \\ \;\;\;\;\;\;\;\left[ {1 + \frac{{{h_0} - {x_0} - {b_1}}}{{{h_0}\left( {1 + \frac{{\sin \theta }}{z}} \right)}}} \right]\\ {y_1} = {A_1}\cos \left( {{\omega _1}{x_1}} \right) + {B_1}\sin \left( {{\omega _1}{x_1}} \right) + \frac{{{h_1} - {x_1}}}{{{h_0}\omega _1^2}} \cdot \\ \;\;\;\;\;\;\;{\delta _0} + \frac{{{k_1}{\delta _1}}}{{{k_1} + {k_2}}}\left[ {1 + \frac{{{h_1} - {x_1}}}{{{h_1}\left( {1 + \frac{{\sin \theta }}{z}} \right)}}} \right]\\ {y_2} = {A_2}\cos \left( {{\omega _2}{x_2}} \right) + {B_2}\sin \left( {{\omega _1}{x_1}} \right) - \frac{{{h_1} - {x_2}}}{{{h_0}\omega _2^2}} \cdot \\ \;\;\;\;\;\;\;{\delta _1} + \frac{{{k_1}{\delta _1} + {k_2}{\delta _2}}}{{{k_1} + {k_2}}}\left[ {1 + \frac{{{h_2} - {x_2}}}{{{h_2}\left( {1 + \frac{{\sin \theta }}{z}} \right)}}} \right] + \\ \;\;\;\;\;\;\frac{{{h_0} - {x_2}}}{{{h_0}}}{\delta _0} \end{array} \right. $ | (6) |
利用边界条件及变形协调方程可将挠曲微分方程通解中的未知量Ai,Bi写为桅杆顶部和双斜撑点位移δi的线性表达式,即[Ai Bi]T=Ri·[δ0 δ1 δ2]T, 其中Ri为转换矩阵。
引入无量纲轴力系数εi=ωihi,则桅杆顶部和主、副斜撑点处总轴力可表示为Pi=εi2EIi/hi2。当桅杆根部满足位移边界条件x2=0时,y2=y′2=0,代入桅杆挠曲微分方程,可得:
| $ {\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} { - 1}&{\frac{{{h_1}}}{{{h_0}\omega _2^2}} - {k_1}{a_1}}&{ - {k_2}{a_1}}\\ {\frac{1}{{{h_0}{\omega _2}}}}&{ - \frac{1}{{{h_0}\omega _2^3}} + {k_1}{a_2}}&{ - {k_2}{a_2}} \end{array}} \right] $ | (7) |
式中:
| $ {a_1} = \frac{{\left( {2z + \sin \theta } \right)}}{{\left( {{k_1} + {k_2}} \right)\left( {z + \sin \theta } \right)}} $ |
| $ {a_2} = \frac{z}{{{\omega _2}{h_2}}} \cdot \frac{1}{{\left( {{k_1} + {k_2}} \right)\left( {z + \sin \theta } \right)}} $ |
桅杆段在副斜撑点处满足变形协调条件,即有:当x1=0,x2=h2时,y1=y2且y′1=y′2,代入桅杆挠曲微分方程,可得:
| $ {\mathit{\boldsymbol{R}}_1} = \frac{1}{{{\omega _1}}}\left[ {\begin{array}{*{20}{c}} {\cos {\varepsilon _2}}&{\sin {\varepsilon _2}}\\ { - {\omega _2}\sin {\varepsilon _2}}&{{\omega _2}\cos {\varepsilon _2}} \end{array}} \right] \cdot {\mathit{\boldsymbol{R}}_2} + \frac{1}{{{\omega _1}}}{\mathit{\boldsymbol{U}}_1} $ | (8) |
| $ {\mathit{\boldsymbol{U}}_1} = \left[ {\begin{array}{*{20}{c}} {\frac{{\omega _1^2\left( {{h_0} - {h_2}} \right) - {h_1}}}{{{h_0}\omega _1^2}}}&{\frac{{{h_2} - {h_1}}}{{{h_0}\omega _2^2}} + \frac{{{k_1}z}}{{{a^3}}}}&{\frac{{{k_2}}}{{{k_1} + {k_2}}}}\\ {\frac{{1 - \omega _1^2}}{{{h_0}\omega _1^2}}}&{\frac{1}{{{h_0}\omega _2^2}} - \frac{{2{k_1}z}}{{{a_4}}}}&{ - \frac{{{k_2}}}{{{a_4}}}} \end{array}} \right] $ | (9) |
式中:
| $ {a_3} = \left( {{k_1} + {k_2}} \right)\left( {2z + \sin \theta } \right) $ |
| $ {a_4} = \left( {{k_1} + {k_2}} \right)\left( {z + \sin \theta } \right){h_2} $ |
桅杆段在主斜撑点处满足变形协调条件,即有:当x0=0,x1=h1时,y0=y1且y′0=y′1,代入桅杆挠曲微分方程,可得:
| $ {\mathit{\boldsymbol{R}}_0} = \frac{1}{{{\omega _0}}}\left[ {\begin{array}{*{20}{c}} {\cos {\varepsilon _1}}&{\sin {\varepsilon _1}}\\ { - {\omega _1}\sin {\varepsilon _1}}&{{\omega _1}\cos {\varepsilon _1}} \end{array}} \right] \cdot {\mathit{\boldsymbol{R}}_1} + \frac{1}{{{\omega _0}}}{\mathit{\boldsymbol{U}}_0} $ | (10) |
| $ {\mathit{\boldsymbol{U}}_0} = \left[ {\begin{array}{*{20}{c}} {\frac{{{h_1}z - {h_0}\left( {2z + \sin \theta } \right)}}{{{h_0}\left( {z + \sin \theta } \right)}}}&{\frac{{{k_1}}}{{{k_1} + {k_2}}}}&0\\ {\frac{{z\left( {\omega _1^2 - 1} \right) - \sin \theta }}{{\left( {z + \sin \theta } \right)\omega _1^2{h_0}}}}&{\frac{{{k_1}z{a_5}}}{{{h_0}}}}&0 \end{array}} \right] $ | (11) |
式中:
| $ {a_5} = \frac{1}{{\left( {{k_1} + {k_2}} \right)\left( {z + \sin \theta } \right)}} $ |
同时桅杆顶部及主、副斜撑点处满足边界条件:当x0=h0时,y0=δ0;当x1=h1时,y1=δ1;当x2=h2时,y2=δ2。从而可得关于桅杆顶部及主、副斜撑点侧向位移δi的线性方程组K·δ=0,其中系数矩阵K的具体表达式为:
| $ \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{U}}_{3 \times 3}} + \left[ {\begin{array}{*{20}{c}} { - \frac{{{h_1}z}}{{{a_7}{h_0}}}}&0&1\\ 0&{ - {a_6}}&1\\ {\frac{{{b_1} - {h_2}}}{{{h_0}}}}&{{a_6} - \frac{{{h_1} - {h_2}}}{{\omega _2^2{h_0}}}}&{ - {a_6}} \end{array}} \right] $ | (12) |
式中:
| $ \mathit{\boldsymbol{r}}{\left( {{\mathit{\boldsymbol{U}}_{3 \times 3}}} \right)_i} = \left[ {\begin{array}{*{20}{c}} {\cos {\varepsilon _i}}&{\sin {\varepsilon _i}} \end{array}} \right] \cdot {\mathit{\boldsymbol{R}}_i},i = 0,1,2 $ |
| $ {a_6} = \frac{{{k_1}}}{{{k_1} + {k_2}}} $ |
| $ {a_7} = z + \sin \theta $ |
若直接提钻工况下双斜撑长螺旋钻机桅杆失稳形态存在,即桅杆顶部及双斜撑点侧向位移δi存在非零解,则有系数矩阵行列式det K=0,故直接提钻工况下双斜撑长螺旋钻机桅杆失稳特征方程为det K=0。记主斜撑点与桅杆高度比值λ1=h1/h0,副斜撑点与主斜撑点高度比值λ2=h2/h1,则失稳特征方程化简后表达如下:
| $ \det \mathit{\boldsymbol{K}} = \frac{{{c_0}\omega _0^2 + {c_1}\omega _1^2 + {c_2}}}{{{c_3}\omega _2^2 + {c_4}}} = 0 $ | (13) |
式中:
| $ {c_0} = {\omega _1}\varepsilon _2^2\left( {{\lambda _1}{h_2} + \frac{{z + \sin \theta }}{{\csc \theta + 1}} + 1} \right) + {\omega _1}\cos {\varepsilon _1} $ |
| $ \begin{array}{l} {c_1} = {\omega _0}\left( {{k_1} + {k_2}} \right)\cos {\varepsilon _0} + \left( {{\lambda _1} - \omega _1^2{h_0}{h_1}} \right)\sin {\varepsilon _1} + {\omega _2}{\lambda _2} \cdot \\ \;\;\;\;\;\;\left( {{h_0} - {h_2}} \right)\left( {{\omega _2}{h_2}\cos {\varepsilon _2} - \sin {\varepsilon _2}\cos {\varepsilon _2}} \right) + \frac{{1 - {\lambda _1}}}{{{h_0}}} \end{array} $ |
| $ \begin{array}{l} {c_2} = \varepsilon _2^2{h_2}\left( {1 + {\lambda _2}} \right)\cos {\varepsilon _1} + {\omega _1}{h_1}\left( {1 + {\lambda _1}} \right) \cdot \left( {{\lambda _1}\cos {\varepsilon _0} - } \right.\\ \;\;\;\;\;\;\left. {{\omega _0}{h_0}\sin {\varepsilon _0}} \right) - {\lambda _2}\left( {1 - {b_1}} \right) \cdot \left( {z + \sin \theta } \right) \end{array} $ |
| $ {c_3} = \left( {1 + {\lambda _2}} \right)\left( {{k_1} + {k_2}} \right)\left( {z + \sin \theta } \right){h_2} $ |
| $ {c_4} = \left( {1 + {k_1}{\lambda _1}} \right)\left( {{h_0} - {h_2}} \right){\omega _1} $ |
式(13)是关于桅杆轴力P0=N0,P1=N0+N1,P2=N0+N1+N2的超越方程,而特定幅值下主、副斜撑受力Fi与其轴向分力Ni(i=1, 2)是确定的,相应中间量ωi和εi(i=1, 2)也是确定的,因此失稳特征方程实质上是单变量方程,所有变量均与直接提钻工况的提钻力F相关。某特定拔钻状态下,主、副斜撑点位置参数λ1,λ2,主卷扬钢丝绳与桅杆轴心夹角θ都是确定的,代入式(13)即可得出各段桅杆对应的临界轴力Pi, cr=εi, cr2EIi/hi2,从而由式(1)进一步确定直接提钻工况提钻失稳临界力
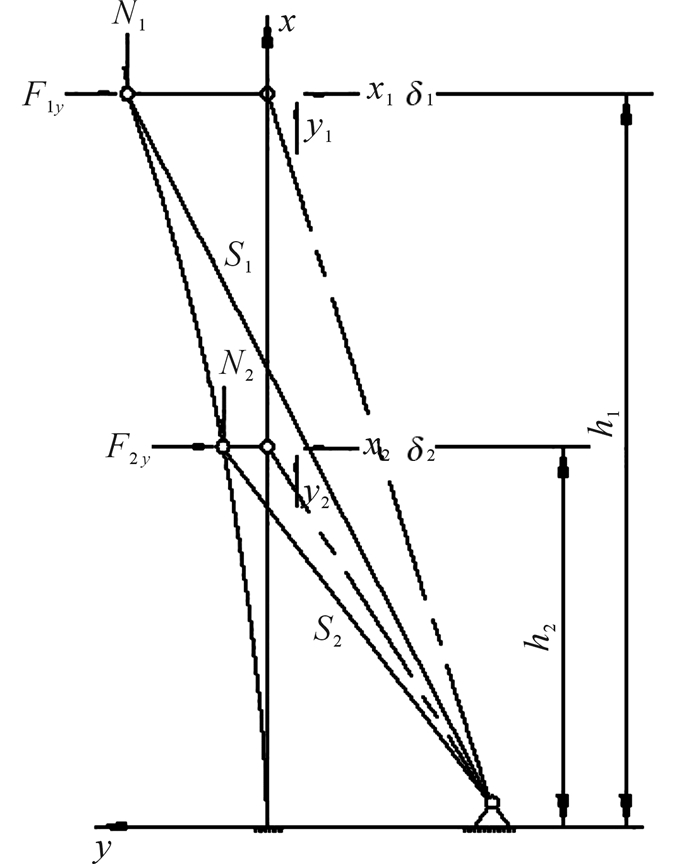
当双斜撑长螺旋钻机桅杆无主斜撑以上部分时,则有N0=F=g=0,b1=δ0=0,λ1=1,且此段截面惯性矩I0=0。此时双斜撑长螺旋钻机桅杆的稳定性分析模型如图 4所示,而桅杆失稳特征方程简化为:
| $ \tan {\varepsilon _1}\tan {\varepsilon _2} - \frac{{{\omega _1}{\mathit{\boldsymbol{I}}_1}}}{{{\omega _2}{\mathit{\boldsymbol{I}}_2}}}\left[ {1 + \omega _1^2{h_1}\left( {z + \sin \theta } \right)} \right] = 0 $ | (14) |
|
| 图 4 λ1=1时直接提钻工况下双斜撑螺旋钻机桅杆的稳定性分析模型 Fig.4 Stability analysis model of the mast of continuous flight auger driller with double braces under direct-drill-lifting condition while λ1=1 |
此时主卷扬钢丝绳夹角θ=0,鹅头定滑轮传动比z=0,代入式(14)可得:
| $\tan {\varepsilon _1}\tan {\varepsilon _2} - \frac{{{\omega _1}{\mathit{\boldsymbol{I}}_1}}}{{{\omega _2}{\mathit{\boldsymbol{I}}_2}}} = 0 $ | (15) |
式(15)与文献[18]中起重臂固支点无侧向刚度时的稳定判定方程式一致。
4 直接提钻工况下双斜撑长螺旋钻机桅杆稳定性数值分析为分析直接提钻工况下影响长螺旋钻机桅杆稳定性的因素,以湖南长河机械有限公司研制的新型ZLH43ZL(TB)-D180双斜撑长螺旋钻机桅杆为例进行稳定性分析。其中,桅杆总高度h0=43.310 m,鹅头处滑轮组传动比z=8,其左端到桅杆轴心的距离b1=1.369 m。取桅杆等截面,即有I0=I1=I2=I,桅杆材料弹性模量E=210 GPa。
由失稳特征表达式(13)可知:直接提钻工况下,双斜撑长螺旋钻机桅杆的失稳临界力Fcr与斜撑点位置参数λ1和λ2、主卷扬钢丝绳夹角θ、桅杆截面惯性矩I等因素有关。取不同的λ1,λ2,θ,I代入双斜撑螺旋钻机桅杆失稳表达式中,可得桅杆失稳计算长度系数
| λ1 | θ=1° | θ=5° | θ=10° | θ=15° | |||||||||||
| 本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
||||
| 0.0 | 9.450 3 | 9.561 6 | -1.164 0 | 9.051 0 | 8.993 1 | 0.643 8 | 8.872 1 | 8.789 3 | 0.942 1 | 8.670 1 | 8.544 6 | 1.468 8 | |||
| 0.2 | 8.467 1 | 8.564 4 | -1.136 0 | 8.104 3 | 8.159 8 | -0.680 2 | 8.012 1 | 7.998 0 | 0.176 3 | 7.882 2 | 7.901 3 | -0.241 7 | |||
| 0.4 | 6.125 9 | 6.241 8 | -1.856 0 | 5.717 2 | 5.809 1 | -1.582 2 | 5.617 1 | 5.703 4 | -1.513 1 | 5.555 3 | 5.465 7 | 1.639 3 | |||
| 0.6 | 3.414 7 | 3.474 4 | -1.718 0 | 3.242 3 | 3.304 1 | -1.870 4 | 3.210 9 | 3.210 1 | 0.024 9 | 3.092 1 | 3.101 1 | -0.290 2 | |||
| 0.8 | 3.038 6 | 3.095 2 | -1.828 0 | 2.890 1 | 2.902 1 | -0.413 5 | 2.807 6 | 2.805 4 | 0.078 4 | 2.747 3 | 2.734 5 | 0.468 1 | |||
| 1.0 | 4.067 3 | 4.111 7 | -1.079 0 | 3.833 1 | 3.905 1 | -1.843 7 | 3.805 4 | 3.785 4 | 0.528 3 | 3.774 1 | 3.745 2 | 0.771 7 | |||
| λ2 | θ=1° | θ=5° | θ=10° | θ=15° | |||||||||||
| 本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
本文方 法计算 |
ANSYS 计算 |
相对误 差/% |
||||
| 0.0 | 3.838 6 | 3.900 7 | -1.592 0 | 3.602 1 | 3.609 3 | -0.199 5 | 3.505 1 | 3.464 3 | 1.177 7 | 3.447 6 | 3.388 4 | 1.747 1 | |||
| 0.2 | 3.022 2 | 3.038 3 | -0.529 9 | 2.899 7 | 2.948 9 | -1.668 4 | 2.787 4 | 2.778 6 | 0.316 7 | 2.702 7 | 2.678 7 | 0.896 0 | |||
| 0.4 | 2.380 9 | 2.354 9 | 1.104 1 | 2.300 3 | 2.298 7 | 0.069 6 | 2.237 7 | 2.241 2 | -0.156 2 | 2.207 6 | 2.181 9 | 1.177 9 | |||
| 0.6 | 2.118 1 | 2.155 5 | -1.735 1 | 2.063 8 | 2.074 6 | -0.520 6 | 2.004 3 | 2.037 8 | -1.643 9 | 1.968 9 | 1.972 1 | -0.162 3 | |||
| 0.8 | 2.501 4 | 2.549 1 | -1.871 2 | 2.423 2 | 2.401 6 | 0.899 4 | 2.350 5 | 2.377 8 | -1.148 1 | 2.307 9 | 2.290 9 | 0.742 1 | |||
| 1.0 | 3.193 7 | 3.169 7 | 0.757 2 | 3.097 6 | 3.078 7 | 0.613 9 | 2.986 4 | 3.012 1 | -0.853 2 | 2.932 6 | 2.890 6 | 1.453 0 | |||
由表 1、表 2可知,本文解析法结果与ANSYS数值结果的相对误差均在2%以内,验证了本文推导的桅杆矢稳特征方程的正确性。造成误差的主要原因有以下2点:1)主、副斜撑通过斜撑上下铰座和销轴分别与桅杆和机身相连,在直接提钻工况下,斜撑、销轴甚至机身的微小变形均会对双斜撑长螺旋钻机桅杆的稳定性产生影响,这种影响会体现在ANSYS分析结果中,却无法在推导表达式中体现;2)动力头通过滑道与桅杆侧身的滑轨相连,而滑轨滑道间的间隙对直接提钻工况下双斜撑长螺旋钻机桅杆的稳定性影响也难以体现在推导表达式中。基于此,本文所推导的直接提钻工况下双斜撑长螺旋钻机桅杆失稳特征表达式可用于理论研究和优化设计中。
图 5所示为当I=0.003 8 m4,θ=10°时桅杆失稳计算长度系数u随主、副斜撑点位置参数λ1,λ2的变化曲线。由图 5(a)可知:当λ2=0时,即桅杆只受单斜撑作用时,随着λ1逐渐增大,桅杆的失稳计算长度系数u先减小后增大,即提钻工况下桅杆的失稳临界力先增大后减小。且有当λ1=0.6~0.8时,桅杆失稳临界力Fcr接近最大,此时Fcr, max与Fcr, min的比值接近5,即直接提钻工况下有无斜撑作用对长螺旋钻机桅杆稳定性影响极大。由图 5(b)可知:当λ1=0.8时,随着λ2的增大(双斜撑作用),桅杆的失稳计算长度系数u先减小后增大,即直接提钻工况下桅杆的失稳临界力随λ2的增大先增大后减小。且当λ2=0.4~0.6时,失稳临界力接近最大。此时Fcr, max与Fcr, min的比值接近3,这说明对于直接提钻工况下的长螺旋钻机,双斜撑相比单斜撑作用对其桅杆稳定性的影响要大。由图 5(c)可知:当λ1=0.6~0.8, λ2=0.4~0.6时,桅杆取得理论最优失稳临界值,即此时桅杆的抗失稳能力最强。

|
| 图 5 I=0.003 8 m4, θ=10°时失稳计算长度系数u随主、副斜撑点位置参数的变化曲线 Fig.5 The variation curve of the instability calculation length coefficient u with position parameters of the main and the auxiliary support while I= 0.003 8 m4 and θ=10° |
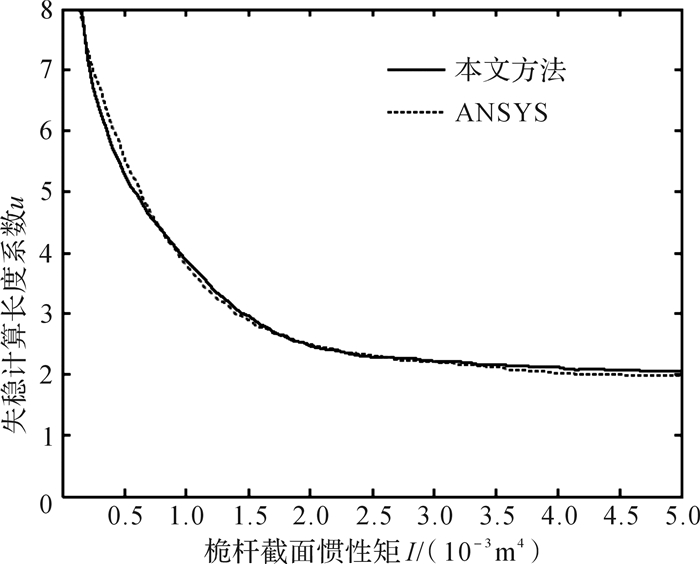
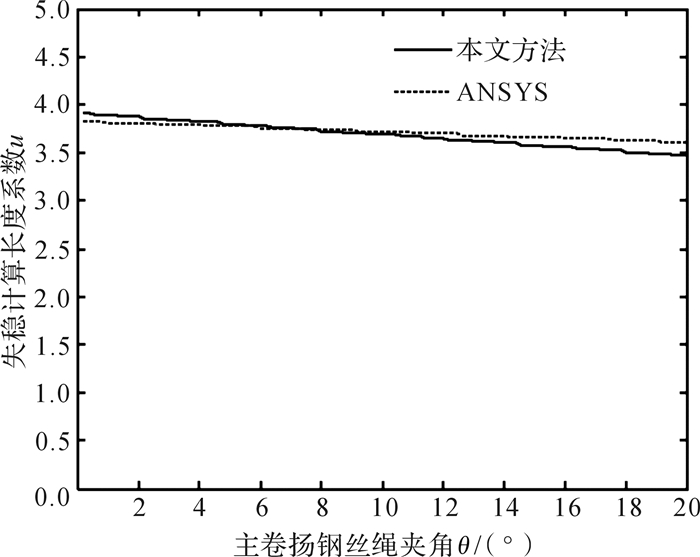
图 6所示为当θ=10°,λ1=0.8,λ2=0.5时失稳计算长度系数u随桅杆截面惯性矩I的变化曲线,由图可知:随着I不断增大,桅杆失稳计算长度系数u逐渐减小,即桅杆的失稳临界力逐渐增大,且有当0 < I < 0.003 m4时,桅杆的失稳临界力增大迅速,当I≥0.003 m4后,桅杆的失稳临界力增大放缓。图 7所示为当I=0.003 8 m4,λ1=0.8,λ2=0.5时失稳计算长度系数u随主卷扬钢丝绳夹角θ的变化曲线。考虑到安装主卷扬的机身长度有限,此处取0°≤θ≤20°。由图可知:随着θ不断增大,桅杆失稳计算长度系数u逐渐减小,即桅杆的失稳临界力逐渐增大,但增长十分缓慢,并不显著。同时由图 5和图 6可知,本文解析法结果与ANSYS数值结果相差无几,这也验证了本文推导的失稳特征表达式的正确性。
|
| 图 6 θ=10°, λ1=0.8,λ2=0.5时失稳计算长度系数u随桅杆截面惯性矩I的变化曲线 Fig.6 The variation curve of the instability calculation length coefficient u with the mast section inertia moment I while θ=10°, λ1=0.8 and λ2=0.5 |
|
| 图 7 I= 0.003 8 m4, λ1=0.8,λ2=0.5时失稳计算长度系数u随主卷扬钢丝绳夹角θ的变化曲线 Fig.7 The variation curve of the instability calculation length coefficient u with the main hoisting wire rope angle θ while I= 0.003 8 m4, λ1=0.8 and λ2=0.5 |
1) 建立了直接提钻工况下双斜撑长螺旋钻机桅杆的稳定性分析模型,推导出桅杆失稳特征表达式,并采用ANSYS有限元分析验证了所推导的表达式的正确性。
2) 直接提钻工况下双斜撑长螺旋钻机桅杆的失稳临界值Fcr与主、副斜撑点位置参数λ1,λ2,桅杆截面惯性矩I和主卷扬钢丝绳角度θ等因素有关;随着λ1和λ2的逐渐增大,失稳临界值Fcr先增大后减小,且λ1对Fcr的影响甚于λ2;随着I的增大,失稳临界值Fcr先迅速增大,后逐渐平缓;随着θ(0°≤θ≤20°)不断增大,失稳临界值Fcr缓慢增大。
3) 桅杆失稳特征表达式可用于求解直接提钻工况下双斜撑长螺旋钻机桅杆失稳临界值的最优化问题以及其他类似结构的稳定性及轻量化设计,并对长螺旋钻机回转提钻的桅杆稳定性研究有重要的参考价值。
| [1] |
刘利民.
谈CFG桩施工工艺及常见问题处理[J]. 山西建筑, 2012, 38(34): 71–73.
LIU Li-min. Discussion on CFG pile construction technology and common problem treatment[J]. Shanxi Architecture, 2012, 38(34): 71–73. DOI:10.3969/j.issn.1009-6825.2012.34.040 |
| [2] |
王茂桑.
影响长螺旋CFG压灌桩成桩质量的几个因素[J]. 山西建筑, 2005, 31(8): 58–59.
WANG Mao-sang. Factors influencing the construction quality of long auger drilling CFG pressure grouting pile[J]. Shanxi Architecture, 2005, 31(8): 58–59. |
| [3] | TIMOSHENKO S P, GERE J M. Theory of elastic stability[M]. New York: McGraw-Hill, 1961: 134-141. |
| [4] | RAHAI A R, KAZEMI S. Buckling analysis of non-prismatic columns based on modified vibration modes[J]. Communications in Nonlinear Science and Numerical Simulation, 2006, 13(8): 1721–1735. |
| [5] |
楼梦麟, 李建元.
变截面压杆稳定问题半解析解[J]. 同济大学学报, 2004, 32(7): 857–860.
LOU Meng-lin, LI Jian-yuan. Semi-analtical approach for stability of variable cross-section compression bars[J]. Journal of Tongji University, 2004, 32(7): 857–860. |
| [6] | LI Guo-qiang, LI Jin-jun. A tapered Timoshenko-Euler beam element for analysis of steel portal frames[J]. Journal of Constructional Steel Research, 2002, 58(12): 1531–1544. DOI:10.1016/S0143-974X(02)00003-2 |
| [7] | BAKER G. Exact deflection in nonprismatic members[J]. Computer & Structures, 1996, 61(3): 515–528. |
| [8] |
卞敬玲, 王小岗.
变截面压杆稳定计算的有限单元法[J]. 武汉大学学报(工学版), 2002, 35(4): 102–104.
BIAN Jing-ling, WANG Xiao-gang. FEM for calculating stability of variable cross-section compression bars[J]. Engineering Journal of Wuhan University, 2002, 35(4): 102–104. |
| [9] |
宋启根, 徐梁, 宋丹.
变截面梁柱刚度方程的Bessel函数解[J]. 计算力学学报, 2001, 18(3): 355–357.
SONG Qi-gen, XU Liang, SONG Dan. Solution of stiffness equations of beam-column with varying section by Bessel function[J]. Chinese Journal of Computational Mechanics, 2001, 18(3): 355–357. |
| [10] |
陈策, 兰朋, 陆念力.
对称双拉绳作用下起重机吊臂起升平面外稳定性分析[J]. 工程机械, 2014, 45(8): 34–38.
CHEN Ce, LAN Peng, LU Nian-li. Outer stability analysis of crane boom lifting plane under dual draft wire rope[J]. Construction Machinery and Equipment, 2014, 45(8): 34–38. |
| [11] |
刘士明, 陆念力, 孟丽霞.
牵绳非保向力作用下的起重臂稳定性分析[J]. 哈尔滨工业大学学报, 2014, 46(3): 26–29.
LIU Shi-ming, LU Nian-li, MENG Li-xia. Stability analysis of telescopic booms under pull-rope follower force[J]. Journal of Harbin Institute of Technology, 2014, 46(3): 26–29. DOI:10.11918/hitxb20140305 |
| [12] | WANG An-lin, JIANG Tao, DONG Ya-ning, et al. Study on structural instability of large crawler crane boom structure[C]//Proceedings of the 20093rd International Conference on Teachning and Computational Science, Heidelberg: Springer Verlag, 2012: 401-406. |
| [13] |
张宏生, 陆念力.
动臂式塔机变截面吊臂的整体稳定性分析[J]. 哈尔滨工业大学学报, 2010, 42(9): 1394–1397.
ZHANG Hong-sheng, LU Nian-li. Global stability analysis of the tapered luffing jib of tower crane[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1394–1397. DOI:10.11918/j.issn.0367-6234.2010.09.010 |
| [14] |
康辉梅, 何清华, 谢嵩岳, 等.
提钻工况下旋挖钻机的受力分析[J]. 工程力学, 2010, 27(10): 214–218.
KANG Hui-mei, HE Qing-hua, XIE Song-yue, et al. Mechanics analysis of rotary drilling rig under drilling-bucket-lifting conditions[J]. Engineering Mechanics, 2010, 27(10): 214–218. |
| [15] |
庞浩. 长螺旋钻机提钻力学行为及提钻液压控制系统研究[D]. 长沙: 中南大学机电工程学院, 2008: 8-17.
PANG Hao. Research on the mechanical behaviour and hydraulic control system of drill-lifting-condition of continuous flight auger driller[D]. Changsha: Central South University, College of Mechanical and Electrical Engineering, 2008: 8-17. |
| [16] |
胡均平, 李科军.
螺旋钻机变幅时机液耦合动力学的键合图建模[J]. 中南大学学报(自然科学版), 2016, 47(2): 495–502.
HU Jun-ping, LI Ke-jun. Dynamics model of mechanical-hydraulic coupling of auger driller during luffing motion by bond gragh[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 495–502. DOI:10.11817/j.issn.1672-7207.2016.02.020 |
| [17] |
孟晓平, 陆念力, 李良.
非保向力作用下起重机吊臂起升平面外整体稳定性特征方程及应用[J]. 哈尔滨建筑大学学报, 1997, 30(2): 99–103.
MENG Xiao-ping, LU Nian-li, LI Liang. Crane jib out-of-the-lifting-plane stability characteristic equation and its use under follower forces[J]. Journal of Harbin University of Civil Engineering and Architecture, 1997, 30(2): 99–103. |
| [18] |
王腾飞, 兰朋, 陆念力.
计及支座柔性的双拉杆起重臂平面外稳定性[J]. 华南理工大学学报(自然科学版), 2015, 43(6): 71–76.
WANG Teng-fei, LAN Peng, LU Nian-li. Out-of-plane stability of crane jib with double rods considering flexibility of fixed joint[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(6): 71–76. |



