球罐是一种存储气体、液体的球形压力容器,凭借其优异的力学性能,在石油化工、交通运输、航空航天等领域得到了十分广泛的应用。大型球罐多由若干块球壳板焊接而成(见图 1),作为存储易燃易爆介质的容器,其焊接质量需满足非常高的要求,建完投产和使用中的球罐,均须依照国家相关规定进行定期检修。

|
| 图 1 大型球罐结构图 Fig.1 Structure diagram of large spherical tank |
目前,国内大部分大型球罐内部定检仍采用在球罐内部搭设脚手架的方式,只有少部分采用球罐内部检修专用设备[1-7]。对一个1 000 m3的大型球罐进行开罐检查,若按照搭设满堂脚手架的方式进行,采用钢结构脚手架杆,需要长度为6 m的钢管约500根,连接卡子2 500~3 000个,一次搭设周期约15 d,该方式存在劳动强度大、检修周期长、安全性差、返修困难、易造成罐体二次损伤等问题。
球罐内部检修设备是特种检修设备研究领域一大热点。法国普鲁旺斯机器制造厂为设计的大型球罐研制了一种专用球罐内部检修回转吊篮;湖北特种设备安全检验检测研究院研发了HBTJ-1A型球罐检验联合工作平台[8]。从相关研究现状来看,由于实际工程应用中各球罐结构参数不同,检测环境差异大,很多设计方案普适性差,难以实现平稳运行、精确定位等目标。同时,复杂的装配结构也给球罐内部检修带来了很大麻烦。
为解决上述问题,本文设计了一种新的大型球罐内部检修工作台,该检修工作台采用顶、底部双向牵引和顶部水平回转相结合的结构,保证载人工作篮能够快速定位至球罐内壁所有检修工作点,并运用MATLAB和ADAMS对工作台主要结构进行动、静力学仿真分析,验证工作台设计的合理性。
1 检修工作台功能需求及其性能指标 1.1 检修工作台功能需求依据《固定式压力容器安全技术监察规程》(TSG21—2016)[9],在役金属压力容器安全状况等级为3级的,一般每3~6年必须进行开罐检查,检测人员携带检测设备进入球罐内部,检查罐体球壳板焊接质量,通常100%射线探伤Ⅱ级为合格。球罐内壁表面没有支架,因此对焊缝进行射线探伤时要求载人工作篮可携带检测人员和检测设备平稳运行、精确定位至球罐内壁检测点附近。具体功能需求如下:
1) 设备承载:载人工作篮可承受检测人员及设备的有效载荷;
2) 运动可行域:载人工作篮可运行并定位至球罐内壁所有检测工作点;
3) 装卸性:零件可通过球罐顶部或底部人孔进出球罐内部,方便装配、拆卸;
4) 安全性:设备运行平稳,有安全保障装置,保证检测人员、设备安全;
5) 经济实用性:设备可重用,提高检修效率,不对球罐内壁造成二次损伤。
1.2 检修工作台性能指标大型球罐内部检修工作台具有负载惯量大、平稳性要求高、装卸速度要求快、定位精度要求高等特点,运用相似性理论[10],参考工程应用相关实例,结合球罐结构参数和功能需求,确定检修工作台的性能指标,如表 1所示。
| 性能指标 | 数值 | 单位 |
| 设备总高度 | 23.5 | m |
| 额定球罐直径 | 20 | m |
| 额定回转角速度 | 3 | (°/s) |
| 额定变幅升降角速度 | 0.5 | (°/s) |
| 水平回转工作范围 | 0~360 | (°) |
| 变幅升降工作范围 | -80~80 | (°) |
| 回转支撑臂长度 | 7.8 | m |
| 载人工作篮尺寸(长×宽×高) | 1.5×1×1.3 | m |
| 额定工作载荷 | 250 | kg |
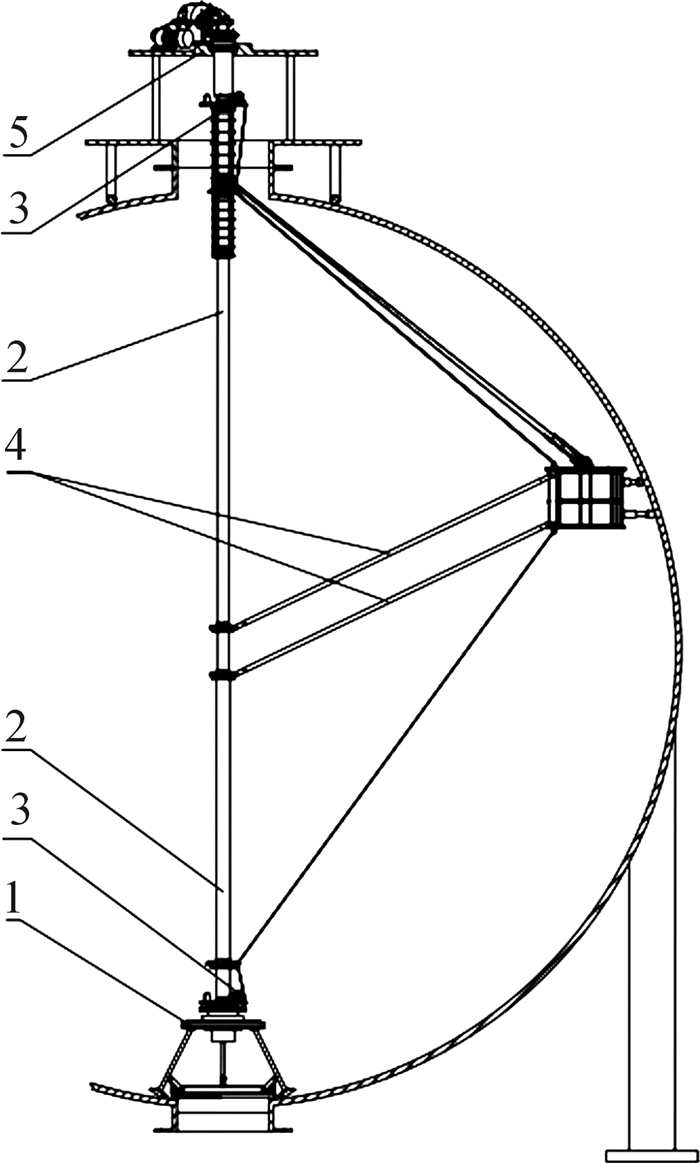
本文设计的大型球罐内部检修工作台由底部支承平台、中央支撑立柱、升降牵引装置、回转支撑平台和顶部回转平台构成。底部支承平台与球罐底部人孔配合定位;中央支撑立柱为多节结构,分别通过端部法兰连接固定,装配于底部支承平台正上方;升降牵引装置分为顶部和底部两部分,装配于以中央支撑立柱为基础的牵引装置支架上;回转支撑平台装配于中央支撑立柱中部,上、下回转支撑臂,载人工作篮和中央支撑立柱共同构成平面四杆机构,保证载人工作篮始终保持水平运行;顶部回转平台位于中央支撑立柱正上方,装配于球罐顶部人孔法兰上,其上设有水平回转传动系统,驱动整个检修工作台水平回转。检修工作台结构如图 2所示。
|
| 1—底部支承平台;2—中央支撑立柱;3—升降牵引装置;4—回转支撑平台;5—顶部回转平台 图 2 大型球罐内部检修工作台结构示意图 Fig.2 Structure diagram of interior overhaul workbench of large spherical tank |
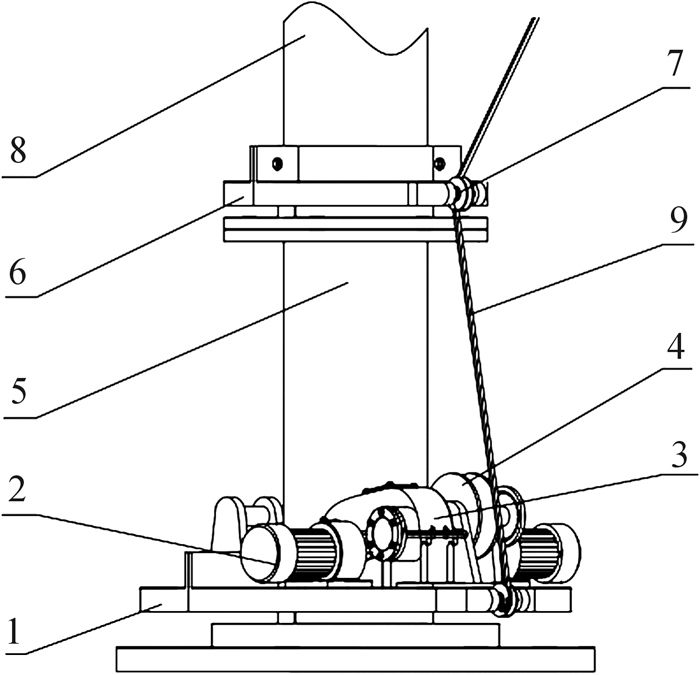
升降牵引装置装配于以中央支撑立柱为基础的牵引装置支架上,分为顶部和底部两组。它由牵引电机、减速箱、制动器、卷筒、钢绳和滑轮构成[11],底部牵引装置如图 3所示。
|
| 1—牵引装置支架;2—牵引电机;3—减速箱;4—卷筒;5—立柱1;6—滑轮支架;7—滑轮;8—立柱2;9—钢绳 图 3 底部牵引装置结构示意图 Fig.3 Structure diagram of bottom pulling device |
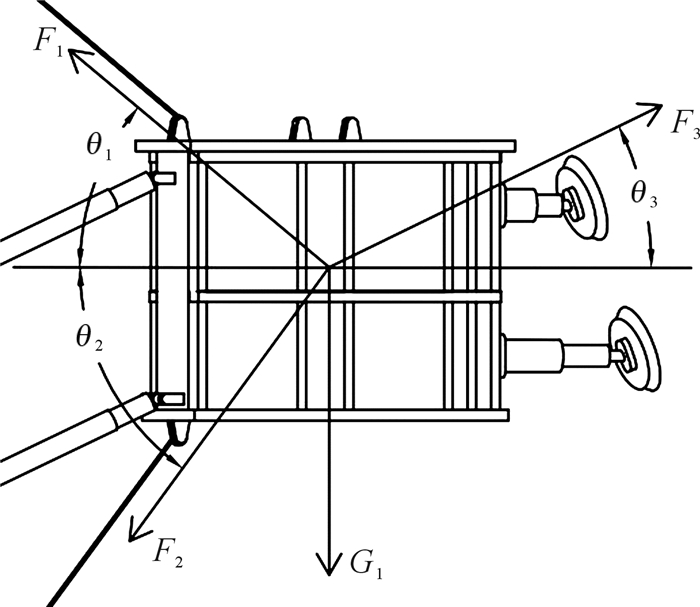
载人工作篮在顶部、底部牵引钢绳联合作用下实现升降,将载人工作篮及负载简化为一质点,在重力G1、变幅升降牵引力F1、牵引张力F2、回转支撑臂支撑力F3共同作用下,其受力状态如图 4所示。
|
| 图 4 载人工作篮受力示意图 Fig.4 Force diagram of manned workbasket |
在竖直和水平方向上建立平衡方程:
| $ \left\{ \begin{array}{l} {F_1}\sin {\theta _1} + {F_3}\sin {\theta _3} = {F_2}\sin {\theta _2} + {G_1}\\ {F_1}\cos {\theta _1} + {F_2}\cos {\theta _2} = {F_3}\cos {\theta _3} \end{array} \right. $ | (1) |
式中:θ1为顶部牵引钢绳仰角,θ2为底部牵引角,θ3为回转支承臂俯仰角,θ1,θ2和θ3随载人工作篮高度变化而变化。
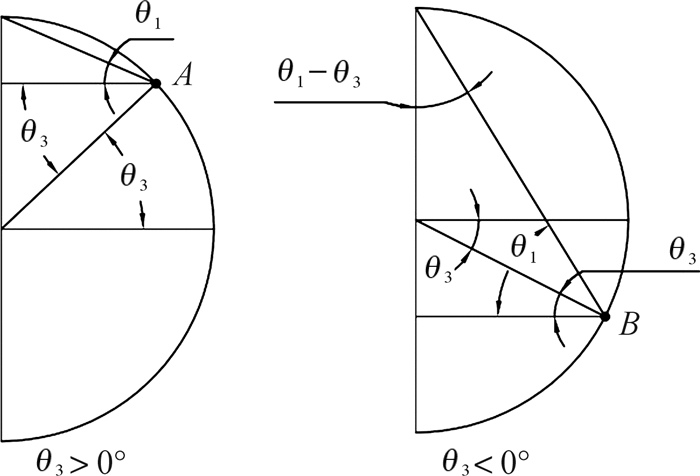
底部牵引钢绳仅提供牵引张力,可按照θ1和θ2互余近似拟合计算。易知,θ1,θ3成比例变化,当载人工作篮运动至A,B位置(其中A位置表示载人工作篮处于球罐上半部分时的任意位置,B位置表示载人工作篮处于球罐下半部分时的任意位置)时,θ1,θ3的关系如图 5所示。
|
| 图 5 载人工作篮在A,B位置时的角度关系 Fig.5 Angle relationship of manned workbasket at position A and B |
分析图 5中θ1, θ3的比例关系易知:2θ1+θ3π/2,且θ1和θ2互余,因此可得:
| $ \left\{ \begin{array}{l} {\theta _2} = {\rm{ \mathsf{ π} }}/2 - {\theta _1}\\ {\theta _3} = {\rm{ \mathsf{ π} }}/2 - 2{\theta _1} \end{array} \right. $ | (2) |
联立式(1)和(2)得:
| $ \left\{ \begin{array}{l} {F_1}\sin {\theta _1} + {F_3}\cos 2{\theta _1} = {F_2}\cos {\theta _1} + {G_1}\\ {F_1}\cos {\theta _1} + {F_2}\sin {\theta _1} = {F_3}\sin 2{\theta _1} \end{array} \right. $ | (3) |
载人工作篮质量为250 kg,设计性能指标中要求载人工作篮可承受250 kg的额定工作载荷,因此,载人工作篮及负载总重G1=5 kN,额定牵引张力F2=5 kN。在载人工作篮升降过程中,变幅升降牵引力F1由顶部牵引装置提供,牵引张力F2由底部牵引装置提供。
由式(3)易知,变幅升降牵引力F1随顶部牵引钢绳仰角θ1变化而变化。设计性能指标中变幅升降范围即回转支承臂俯仰角θ3∈[-80°, 80°],由式(2)易得θ1∈[5°, 85°],联立式(3)可得:
F1sinθ1+(F1cosθ1+5sinθ1)cot 2θ1=5cosθ1+5
令y=F1,x=θ1,可得F1与θ1的函数关系如图 6所示。
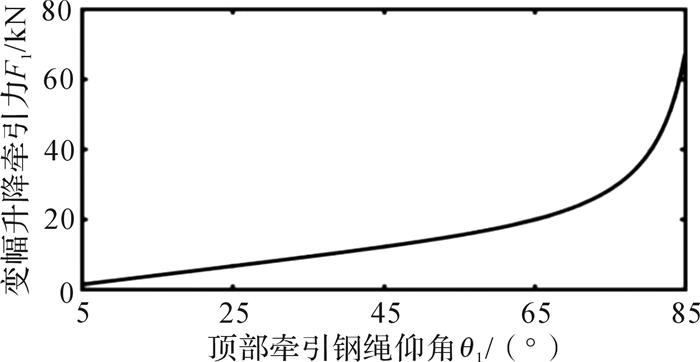
|
| 图 6 F1和θ1的函数关系 Fig.6 Function relationship of F1and θ1 |
分析图 6易得,在θ1∈[5°, 85°]时,变幅升降牵引力F1单调递增,并在θ1=85°处取得极大值,F1max=67.1 kN。顶部最大牵引载荷Fq1=F1max=67.1 kN,顶部的牵引装置滑轮组倍率a1=1,顶部的牵引钢绳最大静拉力Smax1、牵引钢绳破断拉力Fp1、卷筒的计算直径D11、卷筒直径D1、卷筒长度L01可由式(4)确定:
| $ \left\{ \begin{array}{l} {S_{\max }} = \frac{{{F_{\rm{q}}}}}{{a{\eta _2}\eta }}\\ {F_{\rm{p}}} \ge {n_1}{S_{\max }}\\ {D_{1\min }} \ge hd\\ {L_0} = 1.1\left[ {\frac{{Ha + {Z_0}{\rm{ \mathsf{ π} }}{D_1}}}{{{\rm{ \mathsf{ π} }}n\left( {D + nd} \right)}}} \right]d \end{array} \right. $ | (4) |
式中:η2为变幅滑轮组效率,η为导向滑轮组效率,h为机构工作级别与钢绳相关系数,n1为安全系数,d为钢绳直径,H为牵引钢绳最大变化长度,n为卷绕圈数,Z0为附加安全圈数。
查阅资料[12]选取相关参数η2=0.96,η=0.98,h=14,n1=3.5,H=18 000 mm,n=3,Z0=2,代入式(4)计算,并按照安全系数法选取顶部钢绳直径d1,易得:
| $ \left\{ \begin{array}{l} {S_{\max 1}} = 71.3\;{\rm{kN}},{F_{{\rm{p1}}}} = 250\;{\rm{kN,}}{d_1} = 20\;{\rm{mm}}\\ {D_1} = 260\;{\rm{mm}},{D_{11}} = 280\;{\rm{mm}},{L_{01}} = 145\;{\rm{mm}} \end{array} \right. $ |
将上述结果代入式(5),计算顶部制动装置的制动力矩Mb1和牵引电机的额定功率Pjc1:
| $ \left\{ \begin{array}{l} {{M'}_{\max }} = \frac{{{F_{\rm{q}}}{D_1}}}{{2{i_{\rm{b}}}a}}\eta {\eta ^2}{\eta ^{\rm{b}}}\\ {M_{\rm{b}}} \ge {K_{\rm{b}}}{{M'}_{\max }}\\ {v_{\rm{a}}} = \frac{H}{{{t_{\rm{a}}}}}\\ {P_{\rm{j}}} = \frac{{{F_{\rm{q}}}{v_{\rm{a}}}}}{{1\;000 \times 60 \times a\eta {\eta ^2}{\eta ^{\rm{b}}}}}\\ {P_{{\rm{jc}}}} \ge {K_{{\rm{jc}}}}{P_{\rm{j}}} \end{array} \right. $ | (5) |
式中:M′max为最大变幅牵引制动力矩,ib为卷筒与制动器轴间传动比,ηb为变幅机构传动效率,Kb为制动安全系数,va为钢绳平均线速度,ta为总卷绕时间,Pj为最大变幅牵引力矩,Kjc为稳态负载平均系数。
依据设计性能指标中顶部最大变幅升降速度和变幅升降工作范围可求出ta=5.5 min,查阅资料[13]选取相关参数:ηb=0.96,ib=25,Kb=1.5,Kjc=1,代入式(5),计算得:
| $ \left\{ \begin{array}{l} {v_{{\rm{a1}}}} = 3.27\;{\rm{m}}/\min ,{{M'}_{\max 1}} = 340\;{\rm{N}} \cdot {\rm{m}},{P_{{\rm{j1}}}} = 4.1\;{\rm{kW}}\\ {M_{{\rm{b1}}}} = 510\;{\rm{N}} \cdot {\rm{m}},{P_{{\rm{jc1}}}} = 4.1\;{\rm{kW}} \end{array} \right. $ |
因此,所选顶部牵引装置牵引电机额定功率应大于等于4.1 kW,顶部牵引装置制动器额定制动力矩应大于等于510 N·m。
底部牵引装置提供牵引张力F2=5 kN,底部最大牵引载荷Fq2=F2=5 kN,底部的牵引装置滑轮组倍率a2=1。底部的牵引钢绳最大静拉力Smax2、牵引钢绳破断拉力Fp2、卷筒的计算直径D12、卷筒直径D2、卷筒长度L02,可由式(4)确定。查阅行业资料选取相关参数η2=0.96,η=0.98,h=14,n1=3.5,H=17 000 mm,n=3,Z0=2,代入式(4)计算,并按照安全系数法选取底部钢绳直径d2,易得:
| $ \left\{ \begin{array}{l} {S_{\max 2}} = 5.3\;{\rm{kN}},{F_{{\rm{p2}}}} = 18.55\;{\rm{kN,}}{d_2} = 8\;{\rm{mm}}\\ {D_2} = 110\;{\rm{mm}},{D_{12}} = 118\;{\rm{mm}},{L_{02}} = 125\;{\rm{mm}} \end{array} \right. $ |
将上述结果代入式(5),计算底部制动装置制动力矩Mb2和牵引电机额定功率Pjc2,依据设计性能指标中底部最大变幅升降速度和变幅升降工作范围可求出ta=5.5 min,选取相关参数:ηb=0.96,ib=5,Kb=1.5,Kjc=1,代入式(5),计算得:
| $ \left\{ \begin{array}{l} {v_{{\rm{a2}}}} = 3.1\;{\rm{m}}/\min ,{{M'}_{\max 2}} = 50.6\;{\rm{N}} \cdot {\rm{m}},{P_{{\rm{j2}}}} = 1660\;{\rm{W}}\\ {M_{{\rm{b2}}}} = 75.9\;{\rm{N}} \cdot {\rm{m}},{P_{{\rm{jc2}}}} = 1.8\;{\rm{kW}} \end{array} \right. $ |
因此,所选底部牵引装置牵引电机额定功率应大于等于1.8 kW,底部牵引装置制动器额定制动力矩应大于等于75.9 N·m。
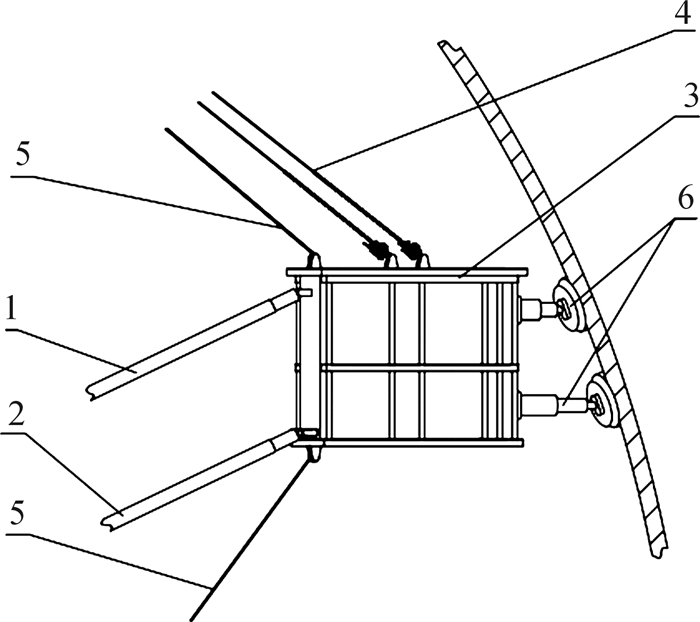
2.3 回转支撑平台的设计与分析回转支撑平台装配于中央支撑立柱中部,主要由上、下回转支撑臂和载人工作篮构成。上、下回转支撑臂一端分别与立柱3和立柱4上装配的上、下回转支撑臂支架铰接,另一端与载人工作篮铰接。上、下回转支撑臂,载人工作篮和中央支撑立柱共同构成平面四杆机构,保证载人工作篮在运动过程中始终保持水平。载人工作篮顶部设有安全锁紧装置,后部固连牵引钢绳,前部设有由气压推杆和球面吸盘构成的柔性贴壁装置,其中,气压推杆为上下两组,一端装配于载人工作篮上,另一端球铰接于球面吸盘上。回转支撑平台结构如图 7所示。
|
| 1—上回转支撑臂;2—下回转支撑臂;3—载人工作篮;4—安全锁紧装置;5—牵引钢绳;6—柔性贴壁装置 图 7 回转支撑平台结构示意图 Fig.7 Structure diagram of revolving supporting platform |
上、下回转支撑臂的外载有载人工作篮载荷Fa、中央支撑立柱载荷Fb、回转支撑臂自重Gb和回转惯性力Fg。静止状态下,回转支撑臂轴向受压, 载人工作篮载荷Fa和回转支撑臂支撑力F3为相互作用力,中央支撑立柱载荷Fb和载人工作篮载荷Fa为一对平衡力,其受力如图 8所示。

|
| 图 8 回转支撑臂受力示意图 Fig.8 Force diagram of revolving supporting arm |
回转支撑臂支撑力F3随回转支承臂俯仰角θ3变化,θ3∈-80°, 80°,联立式(3)可得:
| $ \left\{ \begin{array}{l} {F_3}\sin {\theta _3} + \left( {{F_3}\cos {\theta _3} - 5\sin {\theta _4}} \right)\tan {\theta _4} = 5\cos {\theta _4} + 5\\ {\theta _4} = \left( {{\rm{ \mathsf{ π} }}/2 - {\theta _3}} \right)/2 \end{array} \right. $ |
令y=F3,x=θ3,可得F3和θ3的函数关系如图 9所示。
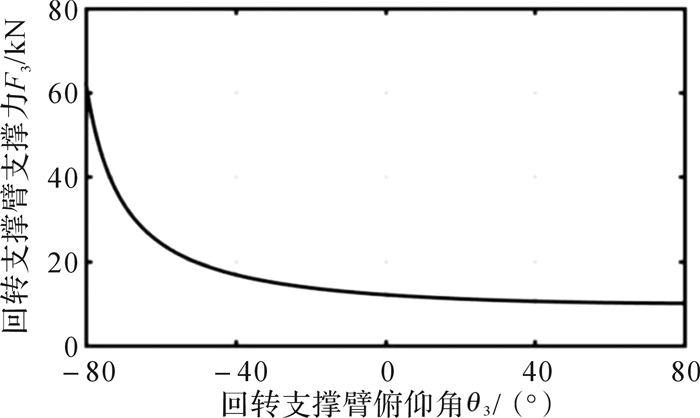
|
| 图 9 F3和θ3的函数关系 Fig.9 Function relationship of F3and θ3 |
分析图 9易得,回转支撑臂支撑力F3单调递减,在θ3=-80°处取得极大值,F3max=62.4 kN,载人工作篮载荷Famax=62.4 kN。假设均匀受载,每根回转支撑臂载荷Fmax=31.2 kN,回转支撑臂长L1=7.8 m,回转支撑臂平均直径Db和壁厚Tb由式(6)确定:
| $ \left\{ \begin{array}{l} {\sigma _{{\rm{a1}}}} = \frac{F}{A} = \frac{{{F_{\max }}}}{{{\rm{ \mathsf{ π} }}{T_{\rm{b}}}{D_{\rm{b}}}}}\\ {F_{{\rm{c1}}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}EI}}{{{L^2}}} = \frac{{{{\rm{ \mathsf{ π} }}^3}E\left( {T_{\rm{b}}^2 + D_{\rm{b}}^2} \right){T_{\rm{b}}}{D_{\rm{b}}}}}{{8L_{\rm{b}}^2}}\\ {\sigma _{{\rm{c1}}}} = \frac{{{F_{{\rm{c1}}}}}}{A} = \frac{{{{\rm{ \mathsf{ π} }}^2}E\left( {T_{\rm{b}}^2 + D_{\rm{b}}^2} \right)}}{{8L_{\rm{b}}^2}}\\ {\sigma _{{\rm{a1}}}} \le \left[ \delta \right]\\ {\delta _{{\rm{c1}}}} \le \left[ \delta \right] \end{array} \right. $ | (6) |
式中:σa1为回转支撑臂压应力,Fc1为回转支撑臂临界压力,σc1为回转支撑臂临界应力,回转支撑臂选用弹性模量E=206×109 Pa,许用压应力[δ]=305×106 Pa的低合金高强度结构钢。使用MATLAB迭代优化[14],可得平均直径Db=100 mm,壁厚Tb=20 mm,回转支撑臂总重Gb=3.84 kN。
运动状态下,回转支撑平台还承受载人工作篮载荷惯性力Fg1和回转支撑臂自重惯性力Fg2,由式(7)确定:
| $ \left\{ \begin{array}{l} {F_{{\rm{g1}}}} = \frac{{{G_1}\upsilon {\rm{ \mathsf{ π} }}R}}{{30gt}}\\ {F_{{\rm{g2}}}} = \frac{{{G_{\rm{b}}}\upsilon {\rm{ \mathsf{ π} }}}}{{30gt}} \times \frac{{{L_1} + 2b}}{2} \end{array} \right. $ | (7) |
载人工作篮及负载总重G1=5 kN,载人工作篮载荷到回转中心距离R=8.82 m,额定转速υ=0.5 r/min,重力加速度g=9.8 N/kg,回转启制动时间t=0.5 s,回转支撑臂总重Gb=3.84 kN,回转支撑臂根部销轴到回转中心的距离b=0.27 m,回转支撑臂长L1=7.8 m,易得Fg1=0.461 6 kN,Fg2=0.324 3 kN。回转面内,简化为一端固定一端悬臂,按式(8)对回转支撑臂根部进行弯曲正应力校核:
| $ \left\{ \begin{array}{l} {\sigma _{{\rm{b}}\max }} = \frac{{{{\left| M \right|}_{\max }}{y_{\max }}}}{{{I_{\rm{z}}}}} = \frac{{{{\left| M \right|}_{\max }}}}{{{W_{\rm{z}}}}} \le \left[ \sigma \right]\\ {\left| M \right|_{\max }} = \frac{1}{2}{L_1}{F_{{\rm{g}}2}} + {F_{{\rm{g}}1}}{L_1}\\ {W_{\rm{z}}} = \frac{{{\rm{ \mathsf{ π} }}D_{\rm{b}}^3}}{{32}}\left( {1 - {\alpha ^4}} \right) \end{array} \right. $ | (8) |
式中:回转支撑臂外径Db=105×10-3 m,内外径之比α=19/21。易得,惯性力Fg1, Fg2产生的弯曲正应力最大值σbmax=129.8×106 Pa,满足强度条件。
2.4 中央支撑立柱的设计与分析中央支撑立柱位于底部支承平台正上方,为两端带法兰的多节空心圆柱结构。自底向顶为立柱1、立柱2、立柱3、立柱4和立柱5,各段立柱及顶、底部回转轴分别由端部法兰上的螺栓组紧固连接。
立柱1外径Dc1=300 mm、壁厚Tc1=20 mm、长Lc1=925 mm;立柱2外径Dc2=300 mm、壁厚Tc2=20 mm、长Lc2=6 300 mm;立柱3外径Dc3=250 mm、壁厚Tc3=20 mm、长Lc3=1 025 mm;立柱4外径Dc4=250 mm、壁厚Tc4=20 mm、长Lc4=9 500 mm;立柱5外径Dc5=250 mm、壁厚Tc5=20 mm、长Lc5=2 175 mm。
中央支撑立柱承载升降牵引装置和回转支撑平台,其上承受的载荷主要有:顶部回转支承水平力Fh1、底部回转支承水平力Fh2、变幅升降牵引力反力F4、牵引张力反力F5、回转支撑臂支撑反力F6、底部支撑力F7、中央支撑立柱及其上载荷重力Gc、顶部回转驱动力矩T1、回转惯性阻力矩T2、摩擦阻力矩T3等,为压弯扭组合受力状态,如图 10所示。
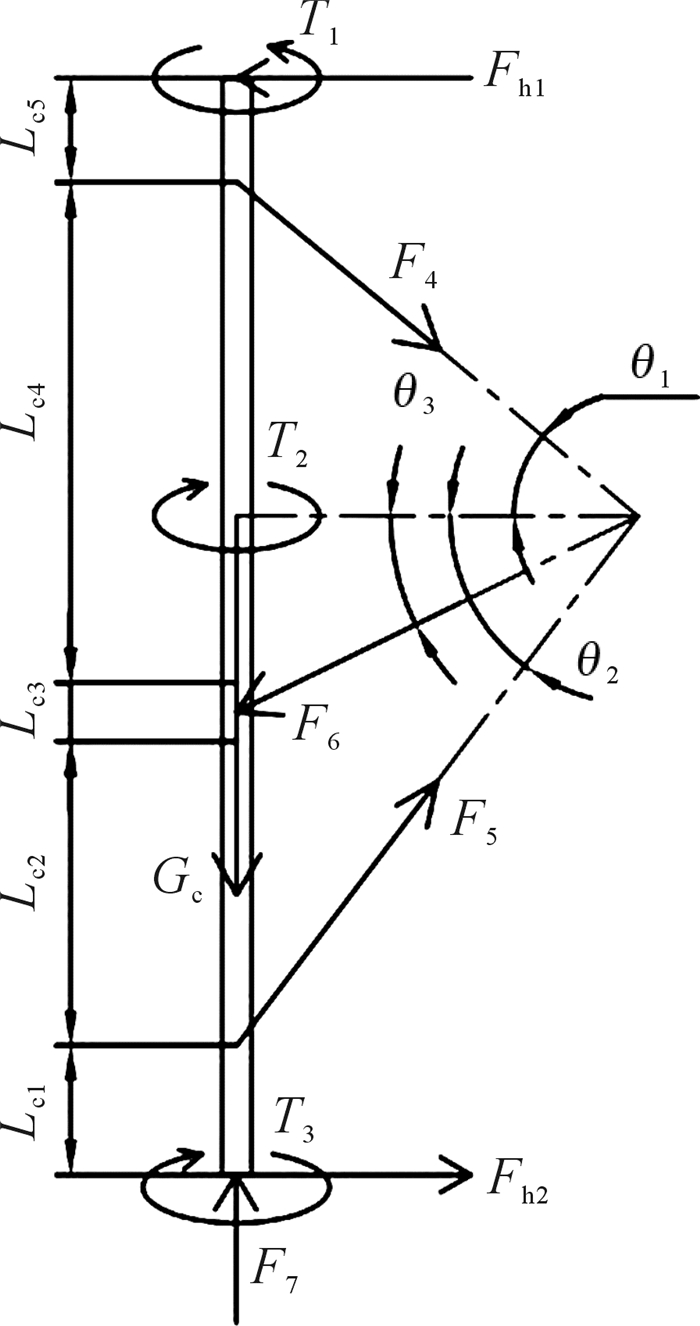
|
| 图 10 中央支撑立柱受力示意图 Fig.10 Force diagram of central supporting column |
将载荷沿横向分解,变幅升降牵引力反横向力F4x随顶部牵引钢绳仰角θ1变化,θ1∈[5°, 85°],由式(3)易得:
| $ {F_{{\rm{4x}}}}\sin {\theta _1} + \left( {{F_{{\rm{4x}}}}\cos {\theta _1} + 5\sin {\theta _1}} \right)\cot 2{\theta _1} = 5\cos {\theta _1} + 5 $ |
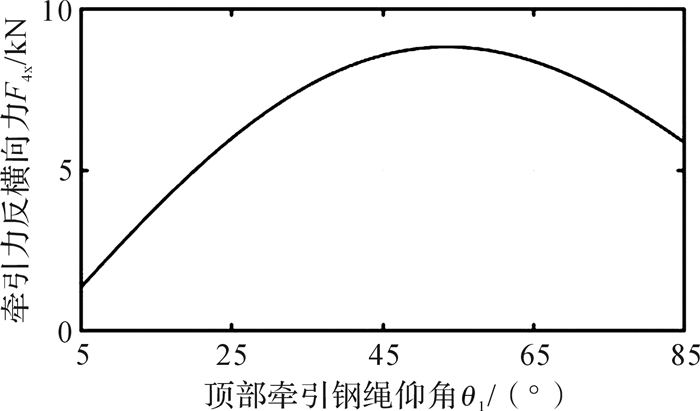
令y=F4x=F4cosx,x=θ1,F4x与θ1的函数关系如图 11所示。
|
| 图 11 θ1和F4x的函数关系 Fig.11 Function relationship of F4x and θ1 |
分析图 11易得,变幅升降牵引力反横向力F4x在θ1=53.6°处取得极大值,F4xmax=8.8 kN,且牵引张力反横向力F5x随顶部牵引钢绳仰角θ1单调递增,因此回转支撑臂支撑反横向力F6x在此处取得极大值,F6xmax=13.0 kN,此时牵引张力反横向力F5x=2.97 kN,顶部回转支承水平力Fh1=2.93 kN,底部回转支承水平力Fh2=4.15 kN,以上5个横向力共同作用,产生倾覆力矩Mc,计算得立柱3中心处倾覆力矩取得最大值, Mcmax=52 300 N·m。按式(9)对立柱3端部连接螺栓组进行设计校核:
| $ \left\{ \begin{array}{l} 不压溃条件:{\sigma _{{\rm{pmax}}}} = \frac{{Z{F_0}}}{A} + \frac{M}{W} \le {\sigma _{{\rm{pp}}}}\\ 不分离条件:{\sigma _{{\rm{pmin}}}} = \frac{{Z{F_0}}}{A} - \frac{M}{W} \ge 0\\ {\sigma _{{\rm{pp}}}} = \frac{{{\sigma _{\rm{s}}}}}{{1.25}}\\ {F_{\max }} = \frac{{M{r_{\max }}}}{{r_1^2 + r_2^2 + \cdots + r_n^2}}\\ {F_2} = {F_0} + \frac{{{c_{\rm{b}}}}}{{{c_{\rm{b}}} + {c_{\rm{m}}}}}{F_{\max }}\\ {d_1} \ge \sqrt {\frac{{4 \times 1.3{F_2}}}{{{\rm{ \mathsf{ π} }}\left[ \sigma \right]}}} \end{array} \right. $ | (9) |
螺栓个数Z=6,倾覆力矩M=52 300 N·m,抗弯截面系数W=8.59×10-3 m3,受压面积A=0.125 m2,许用压应力σpp=2.88×108 Pa,螺栓中心到对称轴线距离r1=r2=…=r6=0.187 5 m,相对刚度cb/(cb+cm)=0.25,预紧力F0=130 kN。选取性能等级为9.8的M30高强度螺栓,d1=26.211 mm≥25.52 mm,满足设计要求。
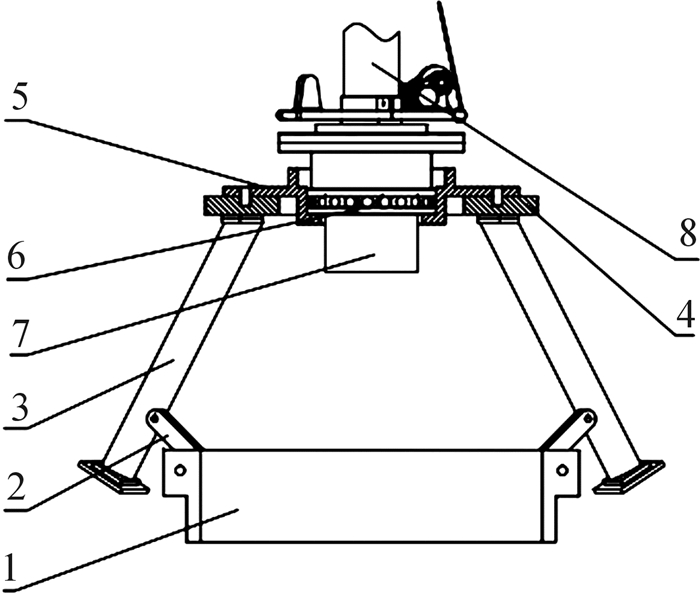
2.5 底部支承平台的设计与分析底部支承平台由固定部分和回转部分构成。其中:固定部分包括定位卡环、紧固拉杆、机座支腿和底部机座;回转部分则包括回转支座、回转支承和底部回转轴。底部支承平台结构如图 12所示。
|
| 1—定位卡环;2—紧固拉杆;3—机座支腿;4—底部机座;5—回转支座;6—回转支承;7—回转轴;8—中央支撑立柱 图 12 底部支承平台结构示意图 Fig.12 Structure diagram of bottom supporting platform |
底部支承平台由2块半圆带凸台的定位卡环与球罐底部人孔配合定位;定位卡环周向均布3根紧固拉杆,紧固拉杆另一端与机座支腿下部侧耳铰接;机座支腿下端由球面垫铁贴合球罐内壁,上端由螺栓与底部机座连接;回转支座由螺栓与底部机座连接,内设回转支承;底部回转轴下部与回转支承配合,上端法兰与立柱下端法兰由螺栓紧固连接。
升降牵引装置、回转支撑平台和中央支撑立柱由底部支承平台承载,载人工作篮运动过程中产生的动载荷较小,可忽略不计。由图 10易知,底部支撑力F7与中央支撑立柱及载荷重力Gc为一对相反力。中央支撑立柱及载荷重力Gc为回转支撑臂总重(Gb=3.84 kN),载人工作篮及负载总重(G1=5 kN),升降牵引装置总重(G2=7.5 kN),立柱总重(G3=32.36 kN),顶、底部回转轴总重(G4=8.5 kN)之和,即:
| $ {F_7} = {G_{\rm{c}}} = {G_{\rm{b}}} + {G_{\rm{1}}} + {G_{\rm{2}}} + {G_{\rm{3}}} + {G_4} = 57.2\;{\rm{kN}} $ |
底部支撑力F7与底部机座压力为相互作用力,假设均匀受载,每根支腿压力Fd=22 kN,长度Ld=1.55 m,平均直径Dd和壁厚Td可由式(10)确定:
| $ \left\{ \begin{array}{l} {\sigma _{{\rm{a2}}}} = \frac{F}{A} = \frac{{{F_{\rm{d}}}}}{{{\rm{ \mathsf{ π} }}{T_{\rm{d}}}{D_{\rm{d}}}}}\\ {F_{{\rm{c2}}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}EI}}{{{L^2}}} = \frac{{{{\rm{ \mathsf{ π} }}^3}E\left( {T_{\rm{d}}^2 + D_{\rm{d}}^2} \right){T_{\rm{d}}}{D_{\rm{d}}}}}{{8L_{\rm{d}}^2}}\\ {\sigma _{{\rm{c2}}}} = \frac{{{F_{{\rm{c2}}}}}}{A} = \frac{{{{\rm{ \mathsf{ π} }}^2}E\left( {T_{\rm{d}}^2 + D_{\rm{d}}^2} \right)}}{{8L_{\rm{d}}^2}}\\ {\sigma _{{\rm{a2}}}} \le \left[ \delta \right]\\ {\delta _{{\rm{c2}}}} \le \left[ \delta \right] \end{array} \right. $ | (10) |
式中:σa2为机座支腿压应力,Fc2为机座支腿临界压力,σc2为机座支腿临界应力。
机座支腿材料选用弹性模量E=206×109 Pa,许用压应力[δ]=250×106 Pa的低合金高强度结构钢。通过MATLAB迭代优化,可得机座支腿平均直径Dd=100 mm,壁厚Td=10 mm,长度Ld=1.55 m。
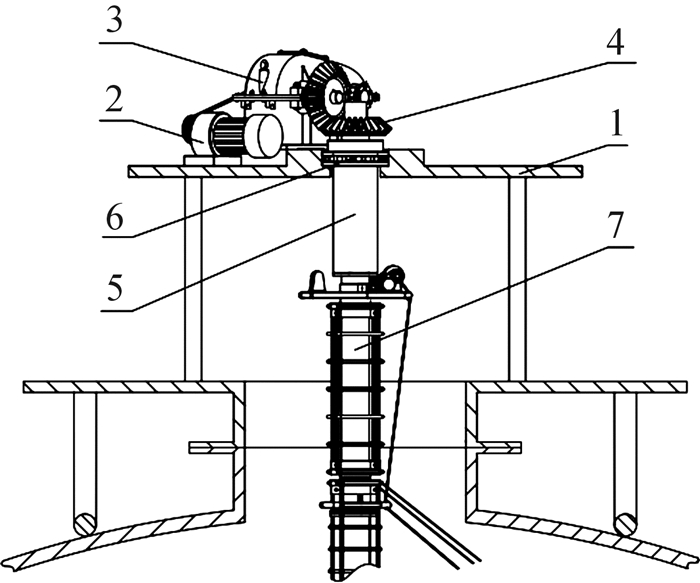
2.6 顶部回转平台的设计与分析顶部回转平台位于中央支撑立柱正上方,装配于球罐顶部人孔法兰上,由球罐体承载。其上设有水平回转传动系统,驱动检修工作台水平回转。水平回转传动系统由回转电机、减速箱、一对啮合锥齿轮、顶部回转轴和回转支承构成。顶部支座上设有回转电机和减速箱,减速箱输出轴通过啮合锥齿轮与顶部回转轴上端相连;顶部回转轴中部与装配于顶部支座内的回转支承配合;顶部回转轴下端法兰与立柱5上端法兰通过螺栓连接。顶部回转平台结构如图 13所示。
|
| 1—顶部支座;2—回转电机;3—齿轮减速箱;4—啮合锥齿轮;5—顶部回转轴;6—回转支承;7—立柱5 图 13 顶部回转平台结构示意图 Fig.13 Structure diagram of top revolving platform |
回转支承包括顶部和底部两部分,作用于其上的载荷主要包括:自重、回转惯性载荷及驱动啮合力等,可分解为垂直力V、水平力H和力矩M,由于采用顶、底部两组回转支承,力矩M较小忽略不计。底部回转支承承载中央支撑立柱及其载荷,因此底部垂直力V2等于中央支撑立柱及其载荷重力Gc,底部水平力H2等于底部回转支承水平力Fh2,大小为:
| $ \left\{ \begin{array}{l} {V_2} = {G_{\rm{c}}} = {G_{\rm{b}}} + {G_{\rm{1}}} + {G_{\rm{2}}} + {G_{\rm{3}}} + {G_{\rm{4}}} = 57.2\;{\rm{kN}}\\ {H_2} = {F_{{\rm{h2}}}} = 4.15\;{\rm{kN}} \end{array} \right. $ |
顶部回转支承仅受水平力,顶部垂直力V1为0,顶部水平力H1等于顶部回转支承水平力Fh1,大小为:
| $ \left\{ \begin{array}{l} {V_1} = 0\\ {H_1} = {F_{{\rm{h1}}}} = 2.93\;{\rm{kN}} \end{array} \right. $ |
水平回转传动系统驱动检修工作台水平回转时,需克服的回转阻力矩包括回转惯性阻力矩T2和摩擦阻力矩T3。摩擦阻力矩T3又包括顶部摩擦阻力矩T31和底部摩擦阻力矩T32,可由式(11)确定:
| $ \left\{ \begin{array}{l} {T_3} = {T_{31}} + {T_{32}}\\ {T_{31}} = {T_{32}} = \mu \frac{{{D_0}}}{2}\left( {\sum {{N_{{\rm{vm}}}}} + \sum {{N_{\rm{h}}}} } \right)\\ \sum {{N_{{\rm{vm}}}}} = 1.414V\\ \sum {{N_{\rm{h}}}} = {k_{\rm{h}}}H \end{array} \right. $ | (11) |
当量摩擦系数μ=0.012,回转支承轨道中心圆直径D0=0.6 m,∑Nvm为垂直力V和力矩M对滚动体的法向压力绝对值和,∑Nh为水平力H对滚动体的切向压力绝对值和,滚动接触系数kh=1.79时,可得底部摩擦阻力矩T32=317.9 N·m,顶部摩擦阻力矩T31=18.9 N·m,摩擦阻力矩T3=336.8 N·m。
回转惯性阻力矩T2包括载人工作篮及负载惯性阻力矩T21、回转支撑臂惯性阻力矩T22和中央支撑立柱惯性阻力矩T23,由式(12)确定:
| $ \left\{ \begin{array}{l} {T_2} = {T_{21}} + {T_{22}} + {T_{23}}\\ {T_{21}} = {J_1}\frac{\upsilon }{{9.55t}} = \frac{{{G_1}{R^2}}}{g}\frac{\upsilon }{{9.55t}}\\ {T_{22}} = {J_2}\frac{\upsilon }{{9.55t}} = \frac{{{G_{\rm{b}}}}}{{3g}}\left( {{b^2} + bR' + {{R'}^2}} \right)\frac{\upsilon }{{9.55t}}\\ {T_{23}} = {J_3}\frac{\upsilon }{{9.55t}} = \frac{{\left( {{G_3} + {G_4}} \right){{R''}^2}}}{{2g}}\frac{\upsilon }{{9.55t}} \end{array} \right. $ | (12) |
式中:J1为载人工作篮及负载转动惯量,J2为回转支撑臂转动惯量,J3为立柱及回转轴转动惯量。
载人工作篮及负载总重G1=5 kN,载人工作篮载荷到回转中心距离R=8.82 m,额定转速υ=0.5 r/min,重力加速度g=9.8 N/kg,回转启制动时间t=5 s,回转支撑臂总重Gb=3.84 kN,回转支撑臂根部销轴到回转中心距离b=0.27 m,回转支撑臂末端到回转中心距离R′=8.07 m,立柱总重G3=32.36 kN,顶、底部回转轴总重G4=8.5 kN,立柱及回转轴回转半径R″=0.29 m,计算得回转惯性阻力矩T2=4 994 N·m。等效静阻力矩T1,等效功率Pe由式(13)确定:
| $ \left\{ \begin{array}{l} {T_1} = {T_2} + {T_3}\\ {P_{\rm{e}}} = \frac{{{T_1}\upsilon }}{{9550{\eta _{\rm{e}}}}} \end{array} \right. $ | (13) |
额定转速υ=0.5 r/min,传动效率ηe=0.6,机构平稳运动的等效静阻力矩T1=5 330.8 N·m,等效功率Pe=450 W。因此,机构平稳运动时,水平回转传动系统的输出功率应大于等于450 W。
3 检修工作台工作原理及运动仿真分析 3.1 检修工作台的工作原理 3.1.1 检修工作台装配过程首先,由装配人员或吊车将顶部支座、卷扬机及牵引钢绳等组件运送至球罐顶部人孔附近,并进行装配;待顶部支座及牵引设备装配完毕后,利用牵引设备,从球罐底部人孔依次将各组件吊装入球罐内部,并置于罐底;待相关组件吊装完毕后,自底向顶依次进行底部支承平台、中央支撑立柱、回转支撑平台、升降牵引装置的装配,其中,各段中央支撑立柱和回转支撑平台可拆分为多个子部件分别送入罐体;待罐内相关组件装配完毕后,拆除顶部支座上的牵引设备,安装顶部水平回转传动系统,完成检修工作台装配。
3.1.2 检测人员进入载人工作篮过程若检修人员由底部人孔进入球罐,底部升降牵引装置主动牵引,顶部从动牵引,牵引钢绳带动载人工作篮在竖直面内下降,待载人工作篮下降至下极限位置,停止牵引,检修人员从罐底进人载人工作篮;若检修人员由顶部人孔进入球罐,顶部升降牵引装置主动牵引,底部从动牵引,牵引钢绳带动载人工作篮在竖直面内上升,待载人工作篮上升至上极限位置,停止牵引,检修人员从顶部支座进入顶部人孔,经顶部人梯进入载人工作篮。
3.1.3 载人工作篮回转升降过程载人工作篮水平回转时,顶、底部升降牵引装置停止牵引,安全锁紧装置锁紧,顶部支座上的回转电机驱动齿轮减速箱输入轴,齿轮减速箱输出轴驱动锥齿轮2,锥齿轮2与锥齿轮1啮合传动,驱动顶部回转轴,带动载人工作篮水平回转。
载人工作篮竖直升降时,顶、底部升降牵引装置进行主、从动牵引,牵引钢绳带动载人工作篮在竖直面内升降,载人工作篮升降至指定位置后,停止牵引,同时安全锁紧装置自动锁紧,柔性贴壁装置伸出贴合球罐内壁,检修人员即可开始检修工作。
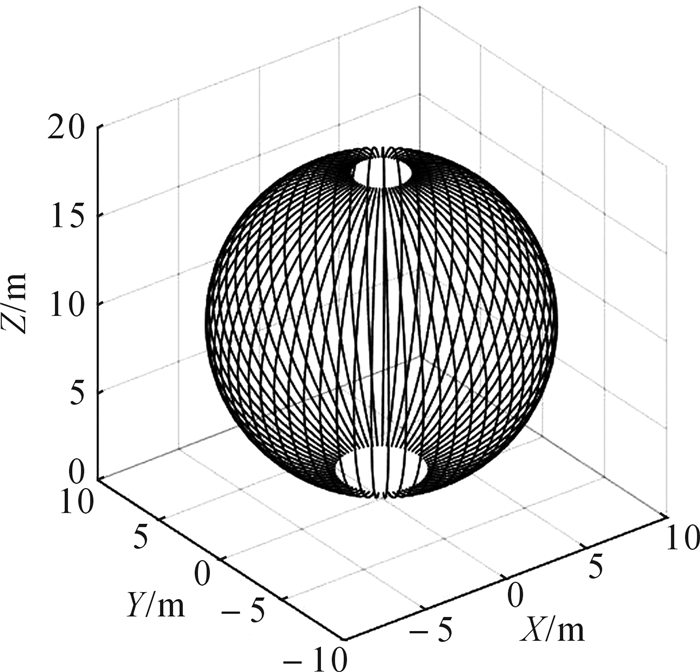
3.2 检修工作台运动仿真分析为保证载人工作篮能够平稳运行并精确定位至球罐内壁所有检修工作点,球罐内部检修工作台采用顶、底部双向牵引与顶部水平回转相结合的方式驱动载人工作篮运行。载人工作篮的运动由竖直升降运动和水平回转运动合成,设计规定变幅升降工作范围θ3∈[-80°, 80°],水平回转工作范围θ4∈[0°, 360°],依据相关参数建立载人工作篮质心的运动学方程,运用MATLAB进行仿真分析,求解运动学方程,可得载人工作篮质心的运动轨迹[15-16],如图 14所示。
|
| 图 14 载人工作篮质心的运动轨迹 Fig.14 Moving trail of manned workbasket centroid |
运用ADAMS对检修工作台竖直升降和水平回转两种运动状态进行仿真分析[17],以得到载人工作篮质心位移、角速度随时间变化的曲线。
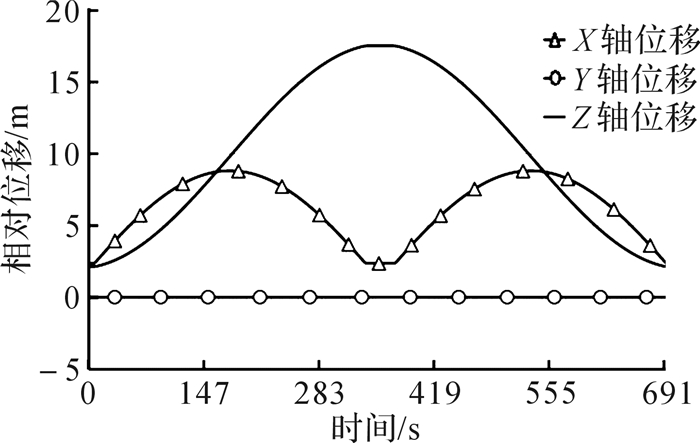
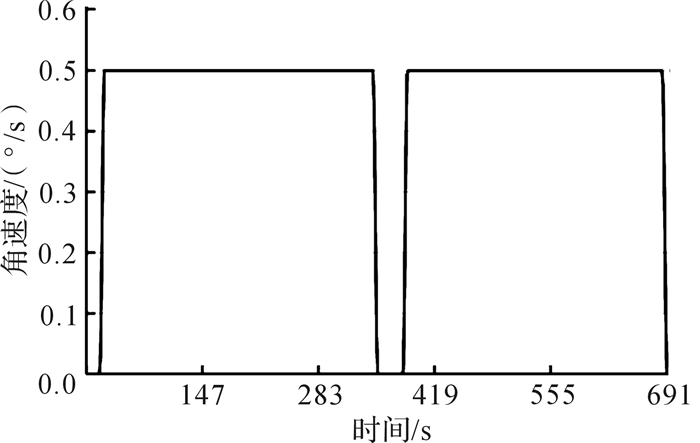
为保证检修人员及设备安全,载人工作篮竖直升降过程不能过快,且不能出现过大的角速度、角加速度突变,因此,竖直升降运动启停采用匀加速、匀速、匀减速的控制方式。以球罐底部人孔圆心为原点,参照图 14建立参考坐标系,竖直升降运动从载人工作篮下极限位置起始,顶部升降牵引装置主动牵引,底部从动牵引,载人工作篮以0.1°/s2的角加速度作匀加速运动,经5 s加速,回转支撑臂竖直回转1.25°,载人工作篮质心沿X轴方向移动0.189 m,沿Z轴方向上升0.036 m;待达到额定变幅升降速度(0.5°/s)后,匀速运行315 s可到达上极限位置附近;最后,载人工作篮以-0.1°/s2的角加速度作匀减速运动,经5 s匀减速,停于上极限位置,反之实现下降过程。检修工作台竖直升降运动的仿真结果如图 15、图 16所示。
|
| 图 15 检修工作台竖直升降运动时位移—时间曲线 Fig.15 Displacement—time curve of overhaul workbench under up-and-down motion |
|
| 图 16 检修工作台竖直升降运动时角速度—时间曲线 Fig.16 Palstance—time curve of overhaul workbench under up-and-down motion |
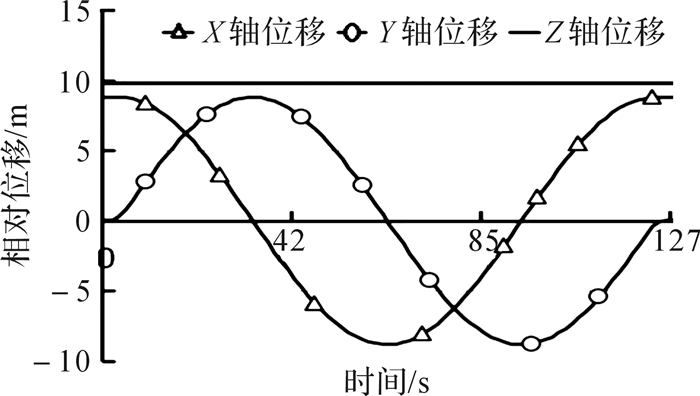
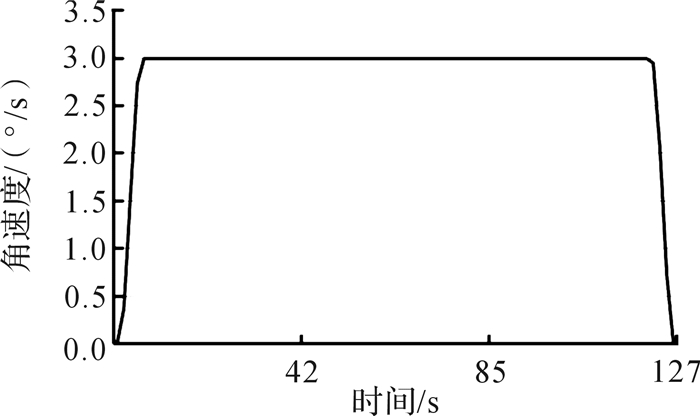
同理,水平回转运动过程不能过快,且不能出现过大的角速度、角加速度突变。回转过程中,当载人工作篮质心回转角速度恒定时,回转线速度随载人工作篮质心高度(Z轴方向)变化而变化,且在载人工作篮质心与球罐体球心等高处达到最大值。因此,水平回转运动从载人工作篮质心与球罐体球心等高位置起始,顶部支座上的回转电机驱动整个装置水平回转,载人工作篮以0.5°/s2的角加速度作匀加速运动,经6 s匀加速,水平回转9°,载人工作篮质心沿X轴方向移动0.12 m,沿Y轴方向移动1.38 m;待达到额定水平回转速度(3°/s)后,匀速运行114 s可回到起始位置附近;最后,载人工作篮以-0.5°/s2的角加速度作匀减速运动,经6 s匀减速,回转1周停于起始位置。检修工作台水平回转运动的仿真结果如图 17、图 18所示。
|
| 图 17 检修工作台水平回转运动时位移—时间曲线 Fig.17 Displacement—time curve of overhaul workbench under revolving motion |
|
| 图 18 检修工作台水平回转运动角速度—时间曲线 Fig.18 Palstance—time curve of overhaul workbench under revolving motion |
从以上仿真结果能够看出,载人工作篮竖直升降和水平回转运动过程中,角速度曲线连续,在匀加速、匀减速引起角速度突变位置,角速度曲线存在一段非线性扰动,但因角速度、角加速度变化较小,对整体运行平稳性影响不大,运动位移曲线平滑,表明在整个工作过程中载人工作篮运行相对平稳;通过分析载人工作篮质心运动轨迹曲线,易得设备运动可行域能够覆盖球罐内壁所有检修工作点,达到设计要求。
4 结束语针对大型球罐内部定检维修中存在的劳动强度大、周期长、返修困难、易二次损伤等问题,从具体功能需求出发,完成了大型球罐内部检修工作台主要结构的设计,采用顶、底部双向牵引和顶部水平回转相结合的结构,保证载人工作篮能够快速定位至球罐内壁所有检修工作点,运用MATLAB和ADAMS对检修工作台运动进行仿真分析,仿真结果验证了检修工作台理论设计的合理性,满足设计要求。
| [1] | URBAN V H, WIEN G. Spherical tank servicing:a complex job[J]. Oil Gas European Magazine, 2007, 33(1): 39. |
| [2] |
黄金祥.
5000 m3球罐安装中三角架弧梯及PA检测技术的应用[J]. 石油化工设备, 2010, 39(6): 61–63.
HUANG Jin-xiang. Application for arc ladder with tripod and PA nondestructive test technology for the erection of 5000 m3 spherical tank[J]. Petro-chemical Equipment, 2010, 39(6): 61–63. |
| [3] | LUO Yu, ZHANG Zhong-liang, JIAO Xiang-dong, et al. Research status and key technology of all-position welding robots on spherical tank[J]. Electric Welding Machine, 2016, 46(10): 25–30. |
| [4] |
杨玉国.
TOFD超声成像检测技术在厚壁加氢反应器检验中的应用[J]. 石油化工设备, 2010, 39(3): 82–85.
YANG Yu-guo. Application of TOFD ultrasonic imaging technology on thickness wainscot hydrogen-reactor[J]. Petro-chemical Equipment, 2010, 39(3): 82–85. |
| [5] |
蒋力培, 焦向东, 薛龙, 等.
大型钢制球罐的高效自动焊关键技术研究[J]. 机械工程学报, 2003, 39(8): 146–150.
JIANG Li-pei, JIAO Xiang-dong, XUE Long, et al. Key points of high efficient automatic welding technique for large scale spherical steel tank[J]. Journal of Mechanical Engineering, 2003, 39(8): 146–150. |
| [6] |
闫家振, 赵世刚, 樊雪燕, 等.
浅析塔架内载人服务篮的结构与技术特点[J]. 机械研究与应用, 2016, 29(1): 200–201.
YAN Jia-zhen, ZHAO Shi-gang, FAN Xue-yan, et al. Structural and technical characteristics of the manned service basket in derrick[J]. Mechanical Research & Application, 2016, 29(1): 200–201. |
| [7] |
沈青青. 磁粉探伤爬壁检测机器人的设计与研究[D]. 杭州: 浙江工业大学机械工程学院, 2014: 2-17.
SHEN Qing-qing. Design and research of wall-climbing & inspecting robot based on magnetic particle inspection[D]. Hangzhou: Zhejiang University of Technology, College of Mechanical Engineering, 2014: 2-17. |
| [8] |
吴遵红, 陈晓, 杨笑蜂, 等. 一种可自由移动的球罐检验联合工作台: CN201575887U[P]. 2010-09-08.
WU Zun-hong, CHEN Xiao, YANG Xiao-feng, et al. A free move spherical tank inspection workbench: CN201575887U[P]. 2010-09-08. |
| [9] |
国家质量监督检验检疫总局. 固定式压力容器安全技术监察规程: TSG 21-2016[S]. 北京: 新华出版社, 2016: 48-95.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Supervision regulation on safety technology for stationary pressure vessel: TSG 21-2016[S]. Beijing: Xinhua Publishing House, 2016: 48-95. |
| [10] |
彭天好, 王光耀, 张义龙, 等.
基于相似理论的采煤机模拟螺旋滚筒的设计[J]. 工程设计学报, 2016, 23(4): 322–326.
PENG Tian-hao, WANG Guang-yao, ZHANG Yi-long, et al. Design of shearer simulated spiral drum based on similarity theory[J]. Chinese Journal of Engineering Design, 2016, 23(4): 322–326. |
| [11] |
张青, 张瑞军.
工程起重机结构与设计[M]. 北京: 化学工业出版社, 2008: 29-177.
ZHANG Qing, ZHANG Rui-jun. Structure and design of engineering crane[M]. Beijing: Chemical Industry Press, 2008: 29-177. |
| [12] |
卜一德.
起重吊装计算及安全技术[M]. 北京: 中国建筑工业出版社, 2008: 32-159.
BU Yi-de. Crane hoisting calculation and security technology[M]. Beijing: China Architecture & Building Press, 2008: 32-159. |
| [13] |
成大先.
机械设计手册(第2卷)[M]. 北京: 化学工业出版社, 2007: 8-85.
CHENG Da-xian. Handbook of mechanical design (Volume 2)[M]. Beijing: Chemical Industry Press, 2007: 8-85. |
| [14] |
宋守许, 刘明, 柯庆镝, 等.
基于强度冗余的零部件再制造优化设计方法[J]. 机械工程学报, 2013, 49(9): 121–127.
SONG Shou-xu, LIU Ming, KE Qing-di, et al. Component optimization design for remanufacturing based on residual strength[J]. Journal of Mechanical Engineering, 2013, 49(9): 121–127. |
| [15] |
赵华慧, 李云伍, 曾庆庆, 等.
基于MATLAB的旋耕机运动仿真分析[J]. 西北农林科技大学学报(自然科学版), 2016, 44(1): 230–234.
ZHAO Hua-hui, LI Yun-wu, ZENG Qing-qing, et al. Simulation of rotary tiller based on MATLAB[J]. Journal of Northwest A & F University (Natural Science Edition), 2016, 44(1): 230–234. |
| [16] | WANG K, ZHOU J. Kinematical analysis and simulation of high-speed plate carrying manipulator based on MATLAB[J]. Engineering, 2012, 4(12): 850–856. DOI:10.4236/eng.2012.412108 |
| [17] |
任斌, 赵广慧, 夏征, 等.
基于UG与ADAMS的水平定向钻牙轮扩孔器联合运动仿真研究[J]. 机械设计, 2017, 34(6): 30–35.
REN Bin, ZHAO Guang-hui, XIA Zheng, et al. Motion simulation of horizontal directional drilling roller reamer based on UG and ADAMS[J]. Journal of Machine Design, 2017, 34(6): 30–35. |



