无砟轨道工程在我国铁路建设中陆续开展,其施工机械的研制也随之全面展开[1-3]。我国自主研制的轮胎式变跨龙门吊[4]、MEY12型轮胎式变跨龙门吊[5]、可变跨铺板龙门吊[6]等设备为铁路建设领域填补了一项技术空白。但目前国内研究工作主要集中在产品研制和结构设计上,对于设备结构力学性能的研究甚少。为了完善结构设计,提高设备设计效率,有必要对其结构性能进行力学研究。
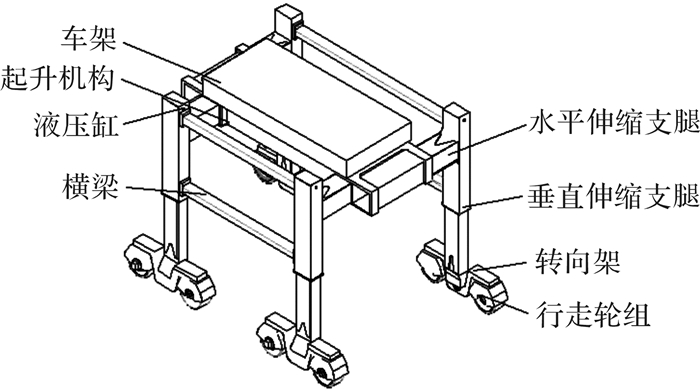
无轨伸缩式门式起重机是国内新型的无砟轨道施工吊装设备,用于吊装轨道板、轨排等构件。图 1所示为其结构简图,起重机主体结构由车架、起升机构、液压缸、横梁、行走轮组、转向架、垂直伸缩支腿、水平伸缩支腿等组成。其工作原理为:当起重机移动到施工地点后,行走轮组通过转向架偏摆一定角度到合适位置,垂直支腿通过液压缸伸长支撑在隧道上,水平支腿打开,便可吊运轨道板或轨排等。该起重机扩展性能好,可实现变跨、变高、倾斜起吊等功能,以适应不同工况的施工要求,且操作灵活,提高了吊装作业的效率和质量。其垂直支腿内外套之间、水平支腿与车架之间均通过滑块(板)实现相互支撑、导向与传递载荷等功能[7]。图 2为起重机单条支腿结构简图,水平支腿与车架接触处有上、下两个滑板和左、右两个滑块,垂直支腿内外套之间设置前、后、左、右四个滑板。滑块(板)受力复杂,易产生应力集中[8-9],因此有必要对其进行力学分析。
|
| 图 1 无轨伸缩式门式起重机结构简图 Fig.1 The trackless telescopic gantry crane structure diagram |

|
| 图 2 无轨伸缩式门式起重机支腿结构简图 Fig.2 The trackless telescopic gantry crane leg structure diagram |
由图 2可知,无轨伸缩式门式起重机伸缩支腿间滑块(板)和与之相对应的接触面构成面-面接触对,是典型的非线性接触问题。在处理此类接触问题时,非线性接触分析可以更加接近工程实际,但是接触参数设置复杂,且计算存在不收敛情况,而节点耦合分析为线性分析,计算成本低,不存在收敛问题。本文在ANSYS中构建该起重机的接触模型和节点耦合模型,考虑接触刚度和摩擦系数对计算结果的影响,通过比较2种模型各接触部位等效应力值的差异,以探讨采用节点耦合线性分析代替非线性接触分析的可行性。
1 基于接触对的接触分析 1.1 无轨伸缩式门式起重机有限元模型的建立以某公司研发的起重量为12 t的变跨度无轨伸缩式门式起重机为例,结合图 1、图 2知,其两侧支腿共有32个滑块(板),由于各支腿结构及载荷均对称,接触情况一致,因此以下分析只列出单条支腿接触对的计算结果。用接触对1,…,4表示水平支腿与车架之间的滑块(板);接触对5,…,8表示垂直支腿内、外套之间的滑板,接触对位置如图 2所示。
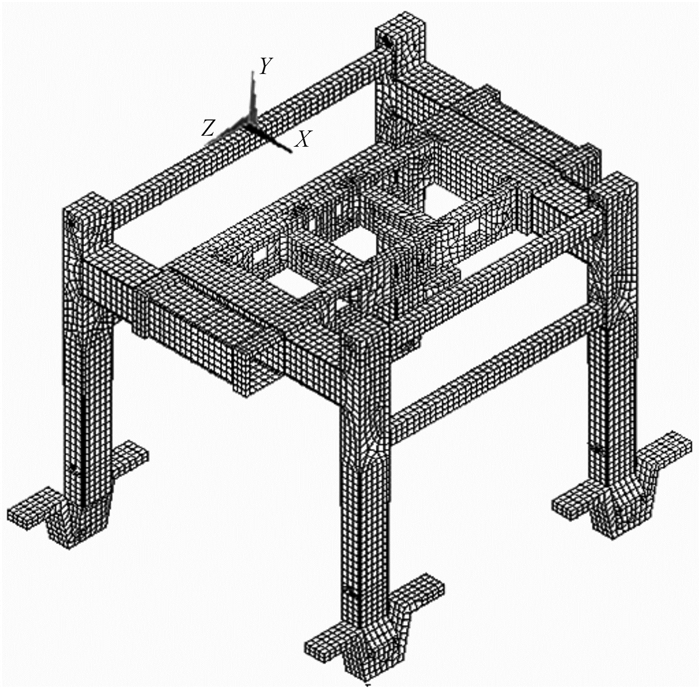
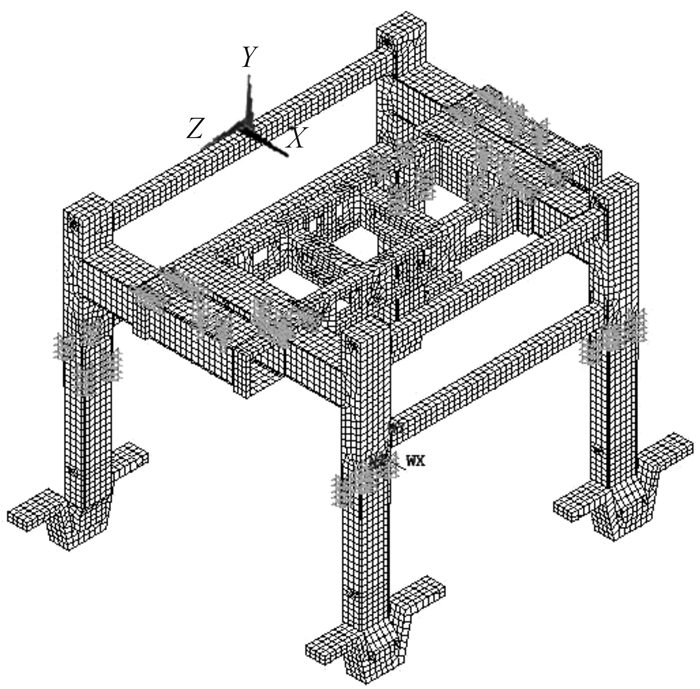
建模时,利用ANSYS中的APDL语言定义无轨伸缩式门式起重机各参数,采用Solid45单元模拟接触对滑块(板),Shell63模拟其余板结构,Beam188模拟伸缩液压缸,通过约束X, Y, Z三个方向的平动自由度来模拟液压缸铰接处的铰接,有限元模型如图 3所示。整个系统离散成121 652个单元,其中52 768个为壳单元,68 882个为实体单元,2个为质量单元。所用材料Q345钢的弹性模量E=2.1×1011N/m2,泊松比μ=0.3,材料密度ρ=7 850 kg/m3。
|
| 图 3 无轨伸缩式门式起重机有限元分析模型 Fig.3 The finite element model for trackless telescopic gantry crane |
在定义接触对时,采用接触单元Conta173与目标单元Targe170构成面-面接触对。伸缩支腿滑块(板)的接触为刚体-柔体接触,选择较刚面滑块(板)外表面为目标单元,较柔面与滑块(板)相对的接触面的内表面为接触单元,接触单元和目标单元通过共享实常数建立接触对[10]。在定义接触分析参数时,为保证计算收敛,选择易得到良态矩阵的增广拉格朗日算法,为避免收敛太慢或发散,采用不带自适应下降的牛顿-拉普森迭代方式,打开自动时间步长来设置精确时间步长,打开线性搜索使迭代稳定化。模型计算工况为各支腿处于全伸的状态,考虑模型结构自重,在起升机构与车架接触位置施加额定起升载荷。
1.2 接触刚度的选取在接触分析中,接触刚度的大小决定了2个表面之间的穿透量[11]。在构建接触对时,为了使接触面之间不发生相互穿透,需要设置合理的接触刚度来保持接触平衡。接触刚度取较大值可以提高计算精度,但会引起刚度矩阵病态,从而导致计算不收敛;小的接触刚度可以保证计算收敛性,但计算精度不高[12]。一般来说,应在保证计算收敛的前提下选择较大的接触刚度。为了研究接触刚度对起重机水平支腿与车架之间、垂直支腿内外套之间各接触滑块(板)应力计算结果的影响,选择不同的接触刚度进行计算。各接触对等效应力、接触应力随接触刚度的变化曲线见图 4、图 5所示。

|
| 图 4 各接触对等效应力随接触刚度变化曲线 Fig.4 The curve of equivalent stress with the change of contact stiffness for each contact pair |
|
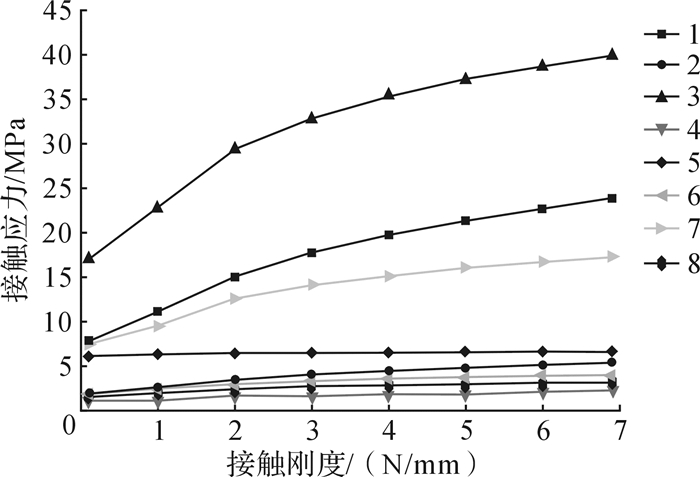
| 图 5 各接触对接触应力随接触刚度变化曲线 Fig.5 The curve of contact stress with the change of contact stiffness for each contact pair |
由图 4、图 5知,随着接触刚度的增大,起重机水平支腿与车架之间、垂直支腿内外套之间各接触滑块(板)等效应力和接触应力逐渐趋于稳定。但随着接触刚度的增加,模型计算耗时会显著增加,使计算不易于收敛。因此,在保证计算收敛及计算精度前提下,此处选择接触刚度k=5 N/mm进行接触分析。
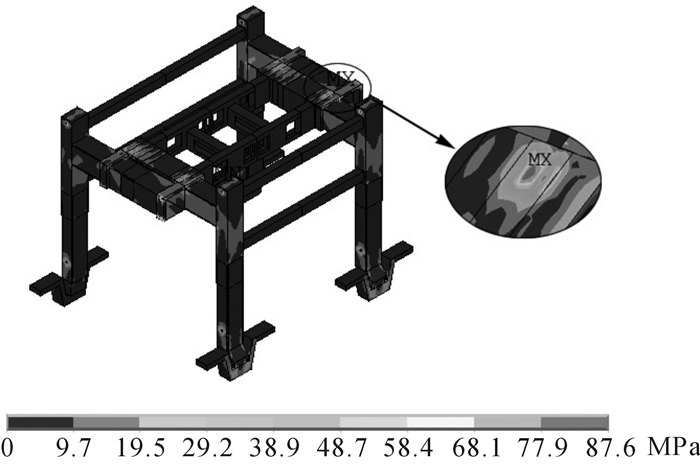
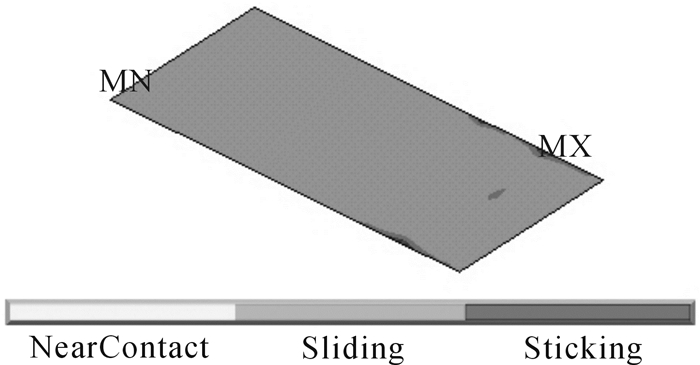
1.3 接触模型分析结果起重机接触模型的等效应力见图 6,其最大应力出现在车架施加起升载荷处,为87.6 MPa,此处既受较大的弯矩,也受较大的接触压力,但应力小于Q345钢的许用应力值345/1.34=257 MPa[13]。此处滑板接触状态见图 7,接触状态主要是滑动接触,只有边缘存在少量的粘和接触,说明接触刚度选择合理,计算精度高。
|
| 图 6 无轨伸缩式门式起重机接触模型等效应力图 Fig.6 Trackless telescopic gantry crane contact model equivalent stress |
|
| 图 7 最大等效应力处滑板接触状态 Fig.7 Slider contact status at the maximun equivalent stress |
非线性接触分析涉及状态非线性,求解困难,且设置接触对相关参数较为繁琐[14],而节点耦合分析是不存在以上问题的,其计算成本比接触分析低,在实际工程应用中通常采用节点耦合的方式简化计算[15-17]。节点耦合模型是将接触面之间部分节点设置为刚性连接,以此获得相同的节点自由度[18]。因节点耦合区域不合理可能会导致计算精度不高,文献[19]研究了如何确定耦合区域的问题,为高效确定耦合区域提供了参考。本文中,依靠经典的材料力学、弹性力学等方法计算出模型初始耦合区域,将初始耦合区域代入有限元模型,通过提取各耦合节点处位移及受力情况来判断各接触对在耦合区域的耦合位置,经过试算,其最终的耦合区域如图 8所示。在水平支腿接触对处耦合X, Y, Z方向自由度,由于垂直方向结构自重由液压缸承受,垂直支腿只承受起升载荷所产生的弯矩,因此垂直支腿只对X, Z方向进行耦合。
|
| 图 8 无轨伸缩式门式起重机有限元分析节点耦合模型 Fig.8 Node coupling model for finite element analysis of trackless telescopic gantry crane |
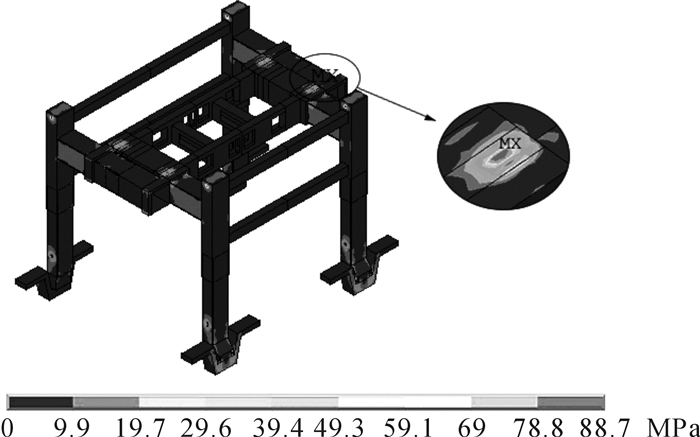
图 9为起重节点耦合模型等效应力图,支腿各接触对的等效应力值如表 1所示。由图 9可以看出节点耦合模型最大等效应力出现在车架施加起升载荷处,位置与接触模型分析结果一致,计算结果为88.7 MPa。
| 接触对 | 节点耦合模型等效应力/MPa | 接触模型等效应力/MPa | 两模型相对误差/% |
| 1 | 70.6 | 82.1 | 14.0 |
| 2 | 20.1 | 28.1 | 28.5 |
| 3 | 33.6 | 46.0 | 27.0 |
| 4 | 31.8 | 47.2 | 32.6 |
| 5 | 22.9 | 21.0 | 9.0 |
| 6 | 27.9 | 45.4 | 38.5 |
| 7 | 16.4 | 13.8 | 18.8 |
| 8 | 30.2 | 44.6 | 32.3 |
|
| 图 9 无轨伸缩式门式起重机节点耦合模型等效应力图 Fig.9 Trackless telescopic gntry crane node coupling model equivalent stress |
根据图 6、图 9两种模型的计算结果可知,起重机最大等效应力相差1.3%,结果差异不大。根据表 1可知,支腿各接触对的等效应力值存在差异,主要原因是2种模型接触部位的相对滑动量存在差异。
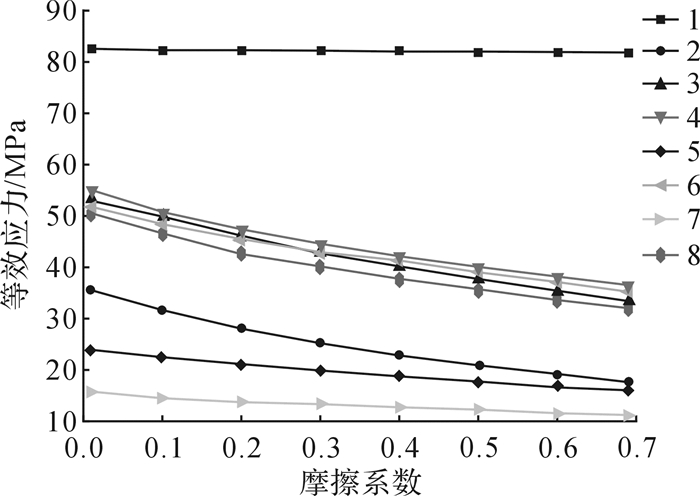
在接触分析中,摩擦系数是一个重要的接触参数,直接决定接触面之间的相对滑动量[20],摩擦系数取值较大,接触面之间相对滑动越小。节点耦合模型是将接触面间节点设置为刚性连接,忽略了摩擦因素,使接触面之间不存在相对滑动,而接触模型分析考虑了摩擦系数,接触区域存在相对滑动,导致2种模型接触部位等效应力存在差异。为了探究接触面之间的相对滑动对各接触部位等效应力和接触应力的影响,在接触模型中,采用不同的摩擦系数值进行分析,得到摩擦系数对起重机水平支腿与车架之间以及垂直支腿内外套之间各接触滑块(板)等效应力和接触应力的影响关系曲线,如图 10、图 11所示。
|
| 图 10 接触模型中各接触对等效应力与摩擦系数关系曲线 Fig.10 The relationship between the equivalent stress and the friction coefficient of each contact pair in the contact model |
|
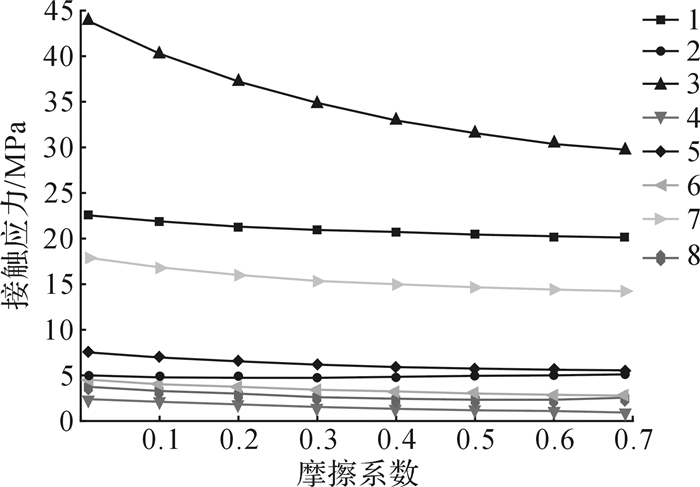
| 图 11 接触模型中各接触对接触应力与摩擦系数关系曲线 Fig.11 The relationship between the contact stress and the friction coefficient of each contact pair in the contact model |
由图 10、图 11可知,当摩擦系数从0.01变化至0.7时,各接触位置等效应力与接触应力逐渐趋近稳定,说明随着摩擦系数的增加,各接触区域相对滑动趋近于零,接触状态逐渐达到了平衡,所以各接触位置等效应力与接触应力不再有显著改变。
对比表 1与图 10可知,接触对5与7处节点耦合模型等效应力与摩擦系数取0.01时的接触模型计算结果相近,由于这2对接触对均为垂直支腿的内外侧滑板,较支腿其他滑板而言,其主要承受载荷为吊重所产生的弯矩,此处滑板因承受较大接触压力导致接触面之间的相对滑动几乎为零,所以此时接触模型与无相对滑动的节点耦合模型相近,因此可以用节点耦合分析代替接触分析。除接触对5与7外,其余各处耦合模型等效应力与摩擦系数取0.7的接触模型计算结果相近,由于这几处接触对接触不紧密,存在相对滑动,所以随着摩擦系数的增加,接触面之间相对滑动减少,接触模型计算结果逐渐趋近于节点耦合模型。
4 结论1) 2种模型下接触部位存在相对滑动量是等效应力值存在差异的原因,根据接触部位的相对滑动在接触分析中选择合适的摩擦系数可减小差异。当接触区域接触不紧密存在相对滑动时,选择较大的摩擦系数可使2种模型计算结果相近;当接触区域相对滑动很小时,接触模型计算结果与节点自由度耦合模型差异不大。
2) 对比无轨伸缩式门式起重机接触模型与自由度耦合模型等效应力计算结果,最大等效应力差1.3%,结果差异不大,说明节点耦合分析能较好地模拟接触分析。在实际工程中,对于精度要求不高的计算,可采用基于节点自由度耦合模型这种简化方式来代替接触分析,以简化计算。
| [1] |
赵国祝. 双块式无砟轨道快速施工综合技术及配套设备、工装技术[D]. 西安: 西安建筑科技大学土木工程学院, 2012: 15-21.
ZHAO Guo-zhu. The comprehensive technique and the matched equipment, the tooling technology which are used in the fast construction of the double-block ballastless track[D]. Xi'an: Xi'an University of Architecture and Technology, School of Civil Engineering, 2012: 15-21. http://cdmd.cnki.com.cn/Article/CDMD-10703-1012045293.htm |
| [2] |
卿三惠, 胡健, 陈叔.
京津城际高速铁路无砟轨道施工技术及装备创新[J]. 高速铁路技术, 2010, 1(1): 61–65.
QING San-hui, HU Jian, CHEN Shu. Construction technology and equipment innovation for ballastless track of Beijing-Tianjin intercity high speed railway[J]. High-Speed Railway Technology, 2010, 1(1): 61–65. |
| [3] |
陈叔, 史渡, 龚成光.
CRTS-Ⅱ型板式无碴轨道施工成套设备国产化研制[J]. 建设机械技术与管理, 2008, 21(6): 66–71.
CHEN Shu, SHI Du, GONG Cheng-guang. Development of homeland whole set equipment of CRTS-slab ballastless track construction[J]. Construction Machinery Technology and Management, 2008, 21(6): 66–71. |
| [4] |
王浩.
轮胎式变跨龙门吊的设计[J]. 铁道建筑技术, 2012(8): 109–112.
WANG Hao. Design of rubber tire type crane with variable span[J]. Railway Construction Technology, 2012(8): 109–112. |
| [5] |
刘继平, 李晓钢.
无砟轨道铺装设备的设计研究[J]. 铁道工程学报, 2007, 24(s1): 191–194.
LIU Ji-ping, LI Xiao-gang. Research on the design for laying equipment of ballastless track[J]. Journal of Railway Engineering, 2007, 24(s1): 191–194. |
| [6] |
卿三惠, 陈叔, 胡建.
高速铁路CRTSⅡ型板式无砟轨道施工关键设备及施工技术研究[J]. 铁道工程学报, 2008, 25(7): 22–27.
QING San-hui, CHEN Shu, HU Jian. Research on key equipment and construction technology of CRTSⅡslab ballastless track construction for high speed railway[J]. Journal of Railway Engineering, 2008, 25(7): 22–27. |
| [7] |
胡青春, 倘广垒, 谢文牧.
箱型伸缩臂滑块接触应力的显著性分析[J]. 现代制造工程, 2015(12): 109–112.
HU Qing-chun, CHANG Guang-lei, XIE Wen-mu. Sensitivity analysis of the slider's contact stress of the telescopic boom based on orthogonal design[J]. Modern Manufacturing Engineering, 2015(12): 109–112. DOI:10.3969/j.issn.1671-3133.2015.12.023 |
| [8] |
李小平, 郑建标, 郧建国.
随车起重机伸缩臂的非线性接触有限元分析[J]. 现代制造工程, 2014(6): 68–71.
LI Xiao-ping, ZHEN Jian-biao, YUN Jian-guo. Nonlinear contact finite element analysis on the telescopic boom of a truck-mounted crane[J]. Modern Manufacturing Engineering, 2014(6): 68–71. |
| [9] |
李志敏. 伸缩吊臂滑块局部应力分析及变化规律研究[D]. 成都: 西南交通大学机械工程学院, 2009: 47-48.
LI Zhi-min. Localized stress analysis and variation law of telescopic crane slider[D]. Chengdu: Southwest Jiaotong University, School of Mechanical Engineering, 2009: 47-48. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1688920 |
| [10] |
张洪伟, 高相胜, 张庆余.
ANSYS非线性有限元分析方法及范例应用[M]. 北京: 中国水利水电出版社, 2013: 161-162.
ZHANG Hong-wei, GAO Xiang-shen, ZHANG Qing-yu. ANSYS nonlinear finite element analysis method and its application[M]. Beijing: China Water Conservancy and Hydropower Press, 2013: 161-162. |
| [11] |
张涔涔. 伸缩臂式履带起重机支腿滑块接触分析[D]. 大连: 大连理工大学机械工程学院, 2012: 24-25.
ZHANG Cen-cen. Contact analysis on outrigger's sliders of telescopic crawler crane[D]. Dalian: Dalian University of Technology, School of Mechanical Engineering, 2012: 24-25. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012393868.htm |
| [12] |
林雪. 箱型伸缩臂滑块的接触分析及规律研究[D]. 大连: 大连理工大学机械工程学院, 2011: 22-23.
LIN Xue. Analysis of contact problems and study of regularity on telescopic boom's sliders[D]. Dalian: Dalian University of Technology, School of Mechanical Engineering, 2011: 22-23. http://cdmd.cnki.com.cn/Article/CDMD-10141-1011109170.htm |
| [13] |
王金诺, 于兰峰.
起重运输机械金属结构[M]. 北京: 中国铁道出版社, 2002: 43-47.
WANG Jin-nuo, YU Lan-feng. Hoisting and conveying machinery metal structure[M]. Beijing: China Railway Press, 2002: 43-47. |
| [14] |
程兵, 于兰峰, 符康, 等.
地坑式架车机托头接触问题的有限元分析[J]. 铁道科学与工程学, 2017, 14(2): 364–369.
CHENG Bing, YU Lan-feng, FU Kang, et al. Finite element analysis of the contact problem on the head of underfloor lifting system[J]. Journal of Railway Science and Engineering, 2017, 14(2): 364–369. |
| [15] |
纪爱敏, 彭铎.
QY25K型汽车起重机伸缩吊臂的有限元分析[J]. 工程机械, 2003, 34(1): 19–21.
JI Ai-min, PENG Duo. QY25K type truck crane telescopic boom finite element analysis[J]. Construction Machinery, 2003, 34(1): 19–21. |
| [16] |
纪爱敏, 彭铎, 刘木南.
三种工况下大型吊臂的有限元分析[J]. 工程机械, 2006, 37(2): 30–33.
JI Ai-min, PENG Duo, LIU Mu-nan. Finite element analysis of large boom under three working conditions[J]. Construction Machinery, 2006, 37(2): 30–33. |
| [17] | XU G, HAN X, ZUO B, et al. Study on different treatment ways of slider joint for solid-webbed telescopic jib[J]. MATEC Web of Conferences, 2015, 31: 26–27. |
| [18] |
王高一, 吴新跃, 毛艳蕾.
装配体结构动态分析中不同连接方法对比分析[J]. 机械传动, 2016, 40(5): 125–127.
WANG Gao-yi, WU Xin-yue, MAO Yan-lei. Comparison and analysis of different connection methods in structure dynamic analysis of assemblies[J]. Mechanical Transmission, 2016, 40(5): 125–127. |
| [19] |
于瀚翔, 于兰峰, 李少鹏.
基于有限元法的高空作业车伸缩臂接触分析[J]. 机械科学与技术, 2014, 33(12): 1773–1776.
YU Han-xiang, YU Lan-feng, LI Shao-peng. Finite element analysis of the contact problem on the telescopic boom of hydraulic aerial cage[J]. Mechanical Science and Technology, 2014, 33(12): 1773–1776. |
| [20] |
何君毅, 林祥都.
工程结构非线性问题的数值解法[M]. 北京: 国防工业出版社, 1994: 83-84.
HE Jun-yi, LIN Xiang-du. Numerical methods for nonlinear problem of engineering structures[M]. Beijing: National Defense of Industry Press, 1994: 83-84. |



