2. 中国煤炭科工集团太原研究院有限公司, 山西 太原 030006
2. Taiyuan Research Institute Co., Ltd., China Coal Technology and Engineering Group, Taiyuan 030006, China
履带车辆在行驶过程中接地比压小,通过性能好,牵引附着能力较强,且克服障碍及转向能力强。这些优点使其在现代军事、农业、建筑业等领域发挥着十分重要的作用[1]。然而,随着现代履带车辆对机动性要求的不断提高,车辆在斜坡行驶、软地急转弯等恶劣工况下,履带板、履带连接销轴及驱动链轮承受较大的挤压弯曲应力,容易发生履带板变形、销轴断裂及驱动轮断齿等故障[2-3]。因此,需加强履带行走装置的刚度和强度以提高其行驶平稳性。近年来,诸多学者对履带车辆行走系统的动力学特性进行了研究。Park等[4]建立了一个数学模型来确定地面特性和履带车辆主要设计因素之间存在的机械关系, 并预测了履带车辆在松软地面上的牵引性能。Wang等[5]基于车辆与地面间的滑动摩擦理论,针对履带车辆在硬质地面上的稳定转向性能作了研究。Le[6]分析了履带车辆在软地面上的稳定转向性能。西班牙塞维利亚大学的Galvin等[7]通过建立地面-履带的边界元模型,研究了履带张紧力对车辆行驶过程中履带与地面间的作用关系的影响。Bekker[8]通过建立地面模型,推导出地面的压力—沉陷量关系,并研究了地面承受压力时的应力—应变关系。卢进军等[9]利用RecurDyn多体动力学软件建立履带车辆模型,并对履带车辆在软、硬两种路面情况下的高速转向性能进行仿真分析。黄雪涛等[10]基于ADAMS建立了履带车辆多体动力学模型,对履带车辆行驶过程中履带张紧力的变化情况进行理论估算和动力学仿真验证。王红岩等[11]通过建立两侧履带与地面相互作用的模型,对其转向过程进行了分析及试验研究。文献[12-13]基于RecurDyn多体动力学软件建立履带车辆模型,并对其行走装置进行仿真分析。孟磊等[14]建立了以行动系统为主的车辆-履带动力学模型和车辆-试验台架动力学模型(不含履带),利用仿真结果对比了2种模型在不同车速、不同路况下车体质心垂向振动加速度功率谱密度曲线的变化情况,从而分析出履带对车体振动的影响。张宏等[15]针对连续采煤机履带销轴折断、驱动轮轮齿断裂及履带板断裂等常见失效形式,作了动力学特性分析和疲劳寿命分析。
综上,国内外学者的研究重点主要集中在地面特性对履带车辆行走系统牵引力性能、车辆转向性能和行驶稳定性的影响,履带滑移和滑转对车辆转向性能的影响,以及影响履带张紧力的因素。但是,针对链环不均匀系数对履带行驶机构平顺性影响的研究较少。因此,本文首先研究履带链环不均匀系数的影响因素,并通过相关理论分析与RecurDyn动力学仿真相结合的方法研究了不均匀系数对车辆行驶平顺性的影响,以期为履带车辆行驶平顺性的研究提供可靠依据。
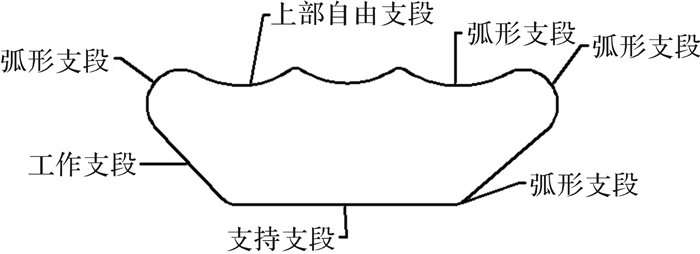
1 履带链环运动不均匀性理论分析履带链环的构成包括自由支段、弧形支段和支持支段,如图 1所示。自由支段是自由悬置在两拖链轮之间的部分履带,弧形支段是位于导向轮、拖链轮及支重轮上的部分履带,支持支段是与地面接触的部分履带。另外,被牵引力拉紧的自由支段称为工作支段[16]。
|
| 图 1 履带链环的构成 Fig.1 Composition of the track link |
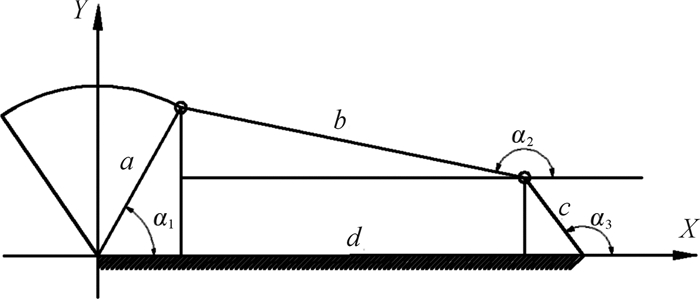
连接销是指连接自由支段和弧形支段两处履带板的销轴。任意一个四链节系统动力学分析如图 2,其中:a,c表示弧形支段;b表示自由支段;固定段d表示履环体; α1=θa+Δθa,θ2=θb+Δθb,θ3=θc+Δθc,θa, θb, θc分别是履带链节a, b, c的起始位置,Δθa, Δθb, Δθc是履带链节a, b, c旋转角位移。
|
| 图 2 四链节系统动力学分析 Fig.2 Four link system dynamics analysis |
假设链节的最初位置由θa, θb, θc决定,由X, Y方向投影方程得到:
| $ \begin{array}{l} {l_a}\cos \left( {{\theta _a} + \Delta {\theta _a}} \right) + {l_b}\cos \left[ {{\rm{ \mathsf{ π} }} - \left( {{\theta _b} + \Delta {\theta _b}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{l_c}\cos \left[ {{\rm{ \mathsf{ π} }} - \left( {{\theta _c} + \Delta {\theta _c}} \right)} \right] = {l_d} \end{array} $ | (1) |
| $ \begin{array}{l} {l_a}\sin \left( {{\theta _a} + \Delta {\theta _a}} \right) - {l_b}\sin \left[ {{\rm{ \mathsf{ π} }} - \left( {{\theta _b} + \Delta {\theta _b}} \right)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{l_c}\sin \left[ {{\rm{ \mathsf{ π} }} - \left( {{\theta _c} + \Delta {\theta _c}} \right)} \right] = 0 \end{array} $ | (2) |
化简,得:
| $ {l_a}\sin {\theta _a}\Delta {\theta _a} - {l_b}\sin {\theta _b}\Delta {\theta _b} - {l_c}\sin {\theta _c}\Delta {\theta _c} = 0 $ | (3) |
| $ {l_a}\cos {\theta _a}\Delta {\theta _a} - {l_b}\cos {\theta _b}\Delta {\theta _b} - {l_c}\cos {\theta _c}\Delta {\theta _c} = 0 $ | (4) |
假定cos Δθa=1, sin Δθa=Δθa,得:
| $ \Delta {\theta _b} = - \frac{{{l_a}}}{{{l_b}}}\frac{{\sin \left( {{\theta _c} - {\theta _a}} \right)}}{{\sin \left( {{\theta _c} - {\theta _b}} \right)}} \cdot \Delta {\theta _a} $ |
| $ \Delta {\theta _c} = - \frac{{{l_a}}}{{{l_c}}}\frac{{\sin \left( {{\theta _b} - {\theta _a}} \right)}}{{\sin \left( {{\theta _b} - {\theta _c}} \right)}} \cdot \Delta {\theta _a} $ |
式中la,lb,lc,ld分别表示链节a, b, c和履环体d的长度。
由此,得出链节b和c的旋转角位移与四链节系统初始位置有关。要使链节b处于被拉紧的状态,θa和θc必须位于同一象限,而且θa和θb应该小于180°。当履带链环节距远小于驱动轮半径的时候,θa和θc非常接近,可以近似认为θb≈0。因此,履带链环的自由支段在运动过程中属于直进运动。
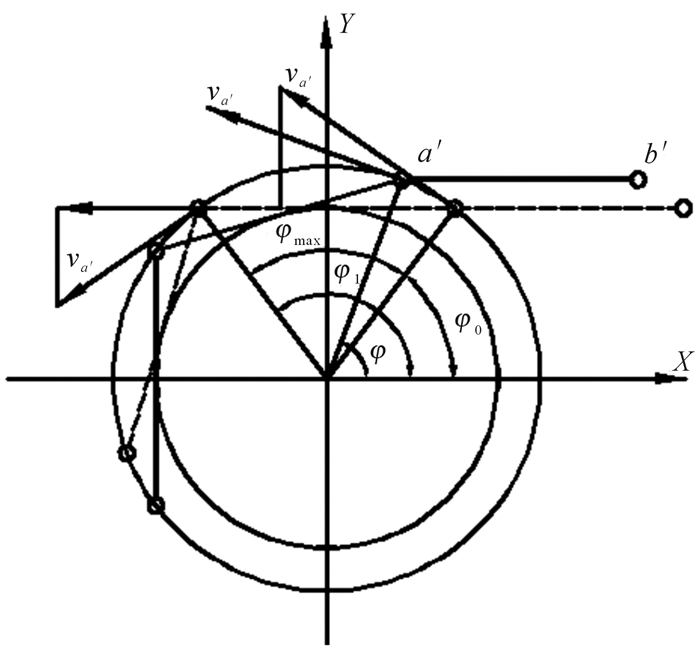
1.2 履带链环不均匀系数履带链环的运动过程是不等速运动,因此只能考虑履带链环运动的平均速度。图 3中va′=R′ω, 为弧形支段与自由支段两处履带板的连接销a′的圆周速度。
|
| 图 3 连接销圆周速度 Fig.3 Circumferential speed of link pin |
在履带链环相对于地面的运动中,自由支段以不变的端点铰链圆周速度作直线运动,弧形支段沿着圆周运动。假设支持支段与地面没有相对滑动,则履带链环的水平速度为:
| $ {v_{a'x}} = R'\omega \sin \varphi $ | (5) |
式中:φ是连接销a′的起始角度;ω是驱动轮角速度;R′是驱动轮分度圆半径。
当φ=φ0或φ=φ1时,得到速度va′x的最小值; 当φ=90°时, 得到速度va′x的最大值:
| $ \left\{ \begin{array}{l} {v_{a'x\min }} = R'\omega \sin {\varphi _0} = R'\omega \cos \frac{{{\varphi _{\max }}}}{2} = R\omega \\ {v_{a'x\max }} = R'\omega \end{array} \right. $ | (6) |
式中:
履带链环不均匀系数表示车轮行驶不均匀性及行驶装置上的动力负荷和车辆发动传动装置的动力负荷[16]。不均匀系数β为:
| $ \beta = \frac{{{v_{a'x\max }}}}{{{v_{a'x\min }}}} = \frac{{R'}}{R} $ | (7) |
式中R是驱动轮根圆半径。若用链节节距z表示不均匀系数[16],则有:
| $ \beta = \sqrt {1 + {{\left( {\frac{z}{{2R}}} \right)}^2}} $ | (8) |
由公式(8)可看出履带链环不均匀系数由链节节距和驱动轮的根圆半径决定。
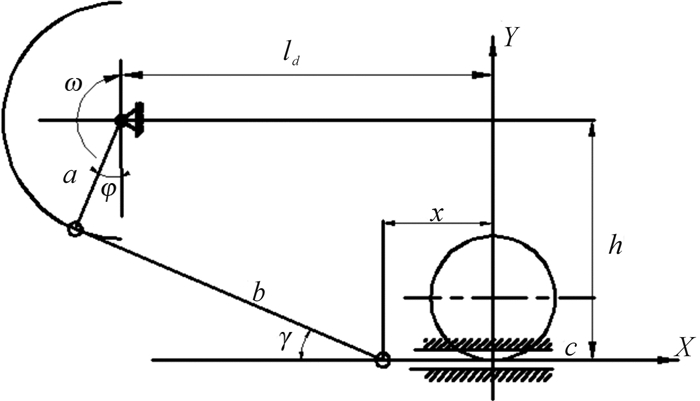
1.3 履带后部支段运动学分析如图 4,假定履带链环在理想的刚性地面上运动,其履环体相对地面的速度为v。当履带链环对履环体作相对运动时,假设履环体是固定的(此时后部支段被认为是曲柄滑块),在链节a以角速度ω作旋转运动过程中,链节c作直线运动,其速度与履环体速度大小相等,方向相反。
|
| 图 4 履带后部支段运动学分析 Fig.4 Kinematics analysis of the rear section of track |
现确定角速度ω和线速度v的关系:
| $ \left\{ \begin{array}{l} x = {l_d} + {l_a}\sin \varphi - {l_b}\cos \gamma \\ {l_b}\cos \gamma = \sqrt {l_b^2 - {{\left( {h - {l_a}\cos \varphi } \right)}^2}} \end{array} \right. $ | (9) |
对时间t微分可得:
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = {l_a}\cos \varphi \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} + {l_a}\frac{{\left( {h - {l_a}\cos \varphi } \right)\sin \varphi }}{{\sqrt {l_b^2 - {{\left( {h - {l_a}\cos \varphi } \right)}^2}} }} \cdot \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} $ |
化简, 得:
| $ v = \left[ {\cos \varphi + \frac{{\left( {h - {l_a}\cos \varphi } \right)\sin \varphi }}{{\sqrt {l_b^2 - {{\left( {h - {l_a}\cos \varphi } \right)}^2}} }}} \right]{l_a}\omega $ | (10) |
令:
| $ f\left( \varphi \right) = \left[ {\cos \varphi + \frac{{\left( {h - {l_a}\cos \varphi } \right)\sin \varphi }}{{\sqrt {l_b^2 - {{\left( {h - {l_a}\cos \varphi } \right)}^2}} }}} \right]{l_a} $ |
得:
| $ v = f\left( \varphi \right)\omega $ | (11) |
式中:f(φ)是表示链式履带链环运动不均匀性的函数。后支重轮的直径越大, f(φ)值越小,车辆行驶平顺性越好。
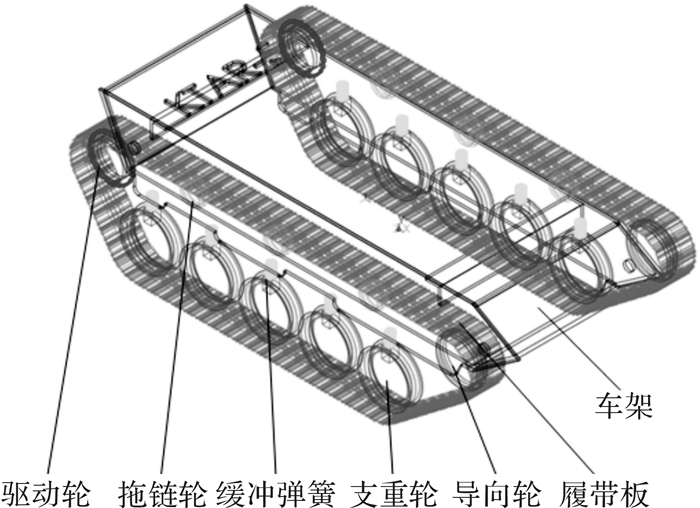
2 履带车辆系统动力学模型建立 2.1 履带车辆模型在Solidworks中建立履带车辆模型,并将其导入多体动力学仿真软件RecurDyn子系统Track(LM),配合履带模块子系统中驱动轮、支重轮、拖链轮、履带板以及地面模型联合建立履带车辆动力学模型。给驱动轮添加约束及旋转速度或转矩来驱动履带车辆,在支重轮与车体之间加入弹簧缓冲装置,在拖链轮与车体之间添加转动副。该仿真模型中一侧履带主要部件有:1个后置驱动轮、5个支重轮、3个拖链轮、1个导向轮和73块履带板。整机仿真的主要参数:履带中心距B=755 mm,履带板宽L=70 mm,履带板节距为25.4 mm,驱动轮直径为86 mm,整车采用双驱动模式,最大速度可达到0.35 m/s(角速度为8.14 rad/s),如图 5所示。在驱动轮的旋转副施加驱动函数STEP(Time, 0.1, 0, 1, -8.14)[17],表示在前0.1 s内,驱动轮转速为0,车辆由于自重在路面上达到静平衡;在0.1-1 s内,车辆由0加速到8.14 rad/s,随后保持匀速行驶。
|
| 图 5 履带车辆模型 Fig.5 The model of tracked vehicle |
在RecurDyn中,路面由无数个矩形单元构成,每个矩形单元都有记忆功能,包括最大沉陷量和最大压力,通过剪应变和剪切力可计算正压力和摩擦力。履带板与地面之间的压力是通过计算接触力实现的。RecurDyn中接触力的公式[18]为:
| $ {f_n} = k{\delta ^{{m_1}}} + c\frac{{\dot \delta }}{{\left| {\dot \delta } \right|}}{\left| {\dot \delta } \right|^{{m_2}}}{\delta ^{{m_3}}} $ | (12) |
式中:k为接触强度;c为阻尼系数;m1为刚度指数;m2为阻尼指数;m3为缺口指数,通常使m3>1来弥补穿透力非常小时,由负阻尼导致的接触力为负的现象;δ为穿透深度;
摩擦力ff=μ|fn|,其中:μ是摩擦系数,摩擦系数的确定与接触位置的相对速度有关;fn为法向接触力。
在路面模型中,考虑加载卸载过程,履带车辆与地面的相互作用是通过计算正压力实现的。基于Bekker提出的压力—沉陷量关系式,在加载、卸载-重复加载两种过程中分别有:
| $ {p^1}\left( \varepsilon \right) = \left( {{K_c}/\lambda + {K_\varphi }} \right){\varepsilon ^n} $ | (13) |
| $ {p^2}\left( \varepsilon \right) = {p_{\rm{u}}} - \left( {{k_{\rm{u}}} + {A_{\rm{u}}}{\varepsilon _{\rm{u}}}} \right)\left( {{\varepsilon _{\rm{u}}} - \varepsilon } \right) $ | (14) |
式中:p1(ε)为加载接地压力;Kc为土壤内聚力的变形模量;Kφ为土壤内摩擦力的变形模量;ε为沉陷量;λ为载荷面短边;n为土壤的变形指数;p2(ε)为卸载接地压力;ku为卸载-加载曲线斜率;Au为土壤对加载卸载过程的响应参数;pu为卸载起始压力;εu为卸载起始沉陷量。
剪应力—剪切位移关系可通过由Janosi和Hanamoto提出的指数函数来描述:
| $ \tau = \left( {{\gamma _n} + p\tan {\alpha _{\rm{n}}}} \right)\left( {1 - {{\rm{e}}^{j/k}}} \right) $ | (15) |
式中:j是剪切位移;γn和αn分别为内聚力和内剪切力的角度;k为剪切力的变形模数。
本次仿真选用重黏土路面(参数如表 1)中的坑路面和平板路面两种路面。
| 土壤参数 | 数值 | 单位 |
| 土壤内聚力变形模量 | 5.173 7 | Pa |
| 土壤内摩擦力变形模量 | 0.633 86 | Pa |
| 变形指数 | 0.13 | - |
| 内聚力 | 0.068 95 | N |
| 剪切角 | 34 | (°) |
| 剪切变形模数 | 25 | mm |
| 下沉率 | 0.05 | - |
本次研究主要针对履带车辆动力学及履带链环运动不均匀性,经理论推算得知影响履带链环不均匀系数的主要参数为履带链节距和驱动轮的半径。分别从履带板与地面作用力、履带板与驱动轮作用力和支重轮与地面作用力三方面分析不均匀系数对车辆行驶平顺性的影响。
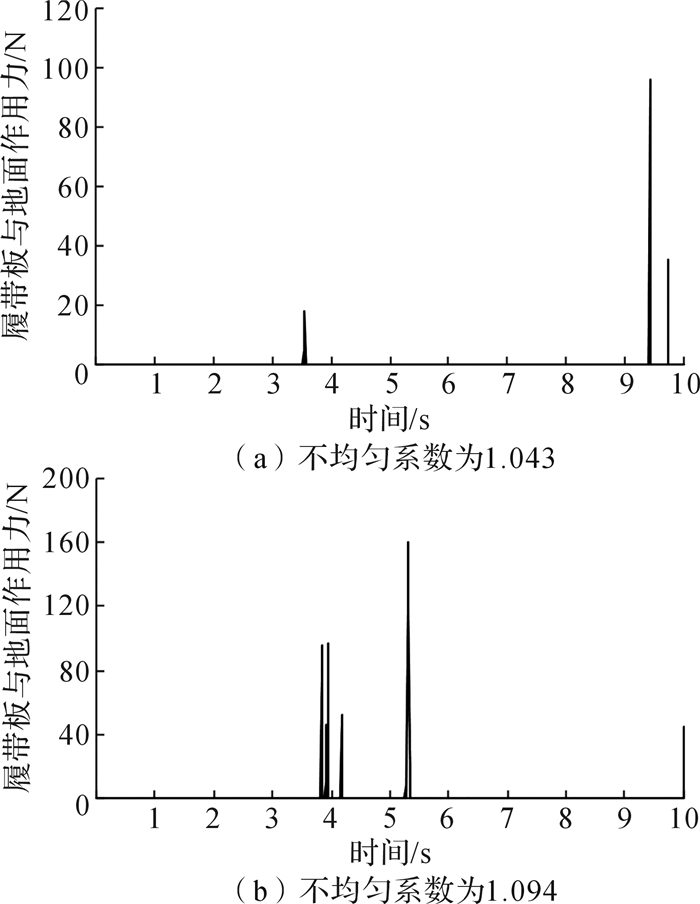
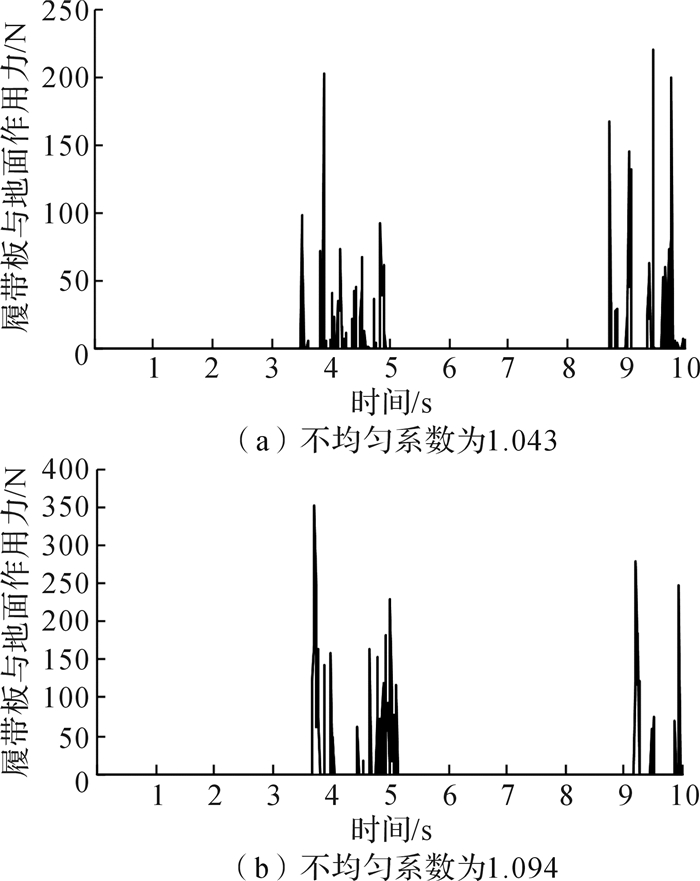
3.1 履带板与地面间作用力选取履带车辆行走装置的一块履带板作为研究对象,在坑路面和平路面两种路况下,分别得出不均匀系数为1.043和1.094两种情况下的履带板与地面相互作用力,如图 6和图 7所示。
|
| 图 6 坑路面时履带板与地面作用力 Fig.6 Force between the tracked plate and the ground on pit pavement |
|
| 图 7 平路面履带板与地面作用力 Fig.7 Force between the tracked plate and the ground on level road |
从图 6和图 7中可以看出:在0—3.6 s阶段,履带板与地面间平均作用力为0,这是由于仿真选取的履带板处在自由支段,履带行驶过程中该支段不与地面接触。在坑路面中,路面相同而不均匀系数有变化,而且过坑时选取的履带板不一定与路面接触,所以导致(a)、(b)两种情况下受力阶段不同,但是可以看出(a)中平均受力要小于(b)的。由此可以看出不均匀系数减小有利于履带板与地面作用力的减小,从而提高车辆行驶平顺性。图 7为平路面仿真结果,从中可以看出(a)和(b)两种情况整体趋势一致,但是图中出现多个峰值,这是由于履带板与地面刚接触时受到了冲击力,该冲击力是由大到小再到大的过程,符合加载—卸载—加载循环作用下土壤压力变化规律[19]。而且同样可以看出,不均匀系数小的情况下履带板受力越小,即车辆行驶平顺性高。
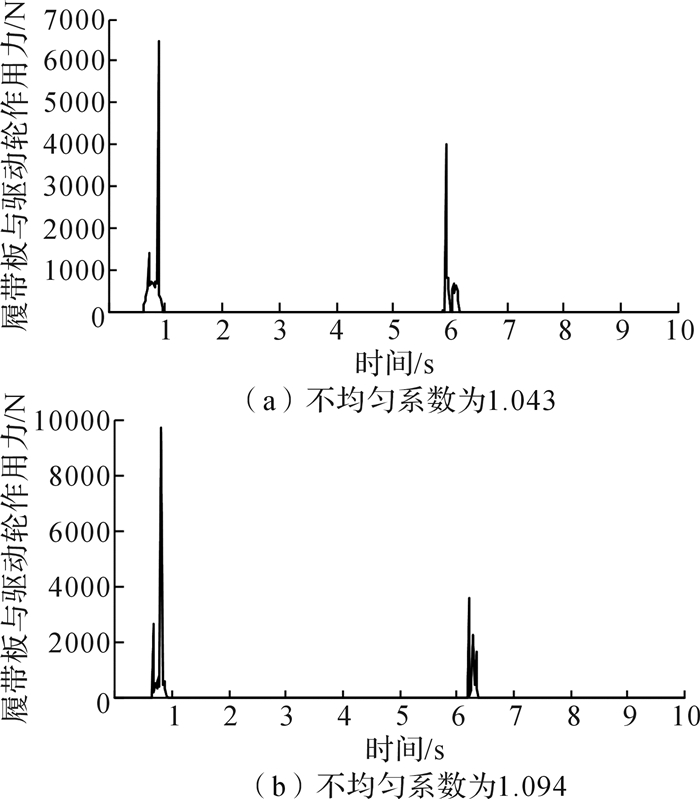
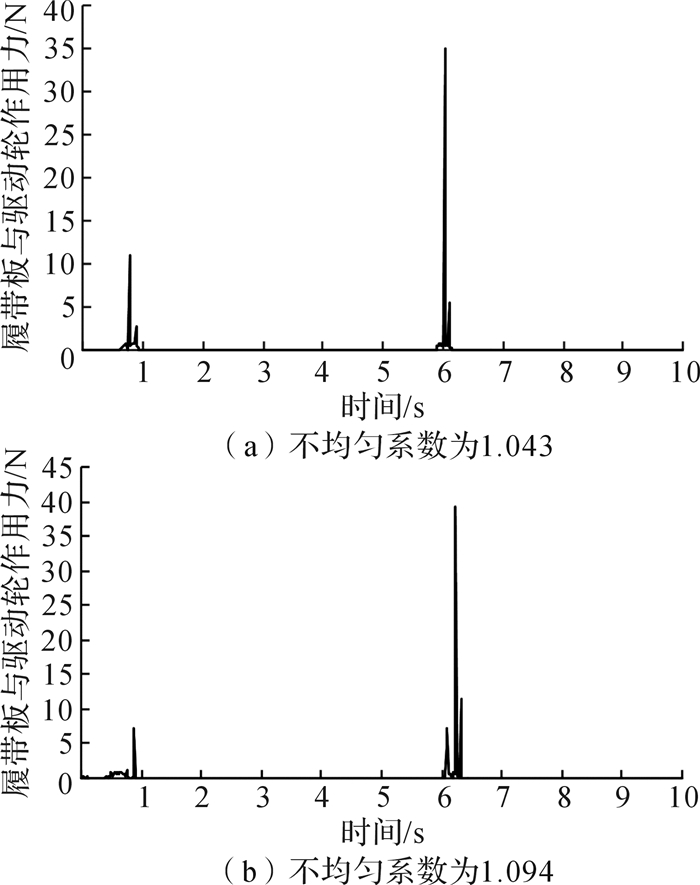
3.2 履带板与驱动轮间作用力选取工作支段的一块履带板为研究对象,在运动过程中,该履带板与驱动轮接触碰撞2次,因此在2种路况下履带板与驱动轮的作用力出现2段波动,代表了履带析与驱动轮两次啮合的全过程,仿真结果如图 8和图 9所示。
|
| 图 8 坑路面履带板与驱动轮作用力 Fig.8 Force between tracked plate and driving wheel on pit pavement |
|
| 图 9 平路面履带板与驱动轮作用力 Fig.9 Force between tracked plate and driving wheel on level road |
图 8和图 9中,最大峰值的出现是由于履带板与驱动轮初始啮合碰撞造成瞬时冲击力较大而引起的。在图 8中可以看到:不均匀系数为1.043时,0.5-1 s内履带板与驱动轮最大作用力约为6 500 N,不均匀系数为1.094时中最大作用力接近10 000 N。而在第2次啮合碰撞中,比较两者的平均作用力发现(b)的大于(a)。在平路面的情况下,在0.5-1 s阶段,(a)和(b)中的履带板与驱动轮作用力相差不大,而在6-6.5 s阶段履带板与驱动轮第2次啮合时,(b)中的平均作用力明显比(a)中作用力大。上述分析结果表明,在同一路面下,减小不均匀系数,有利于减小履带板与驱动轮的作用力,从而提高履带车行驶平顺性。
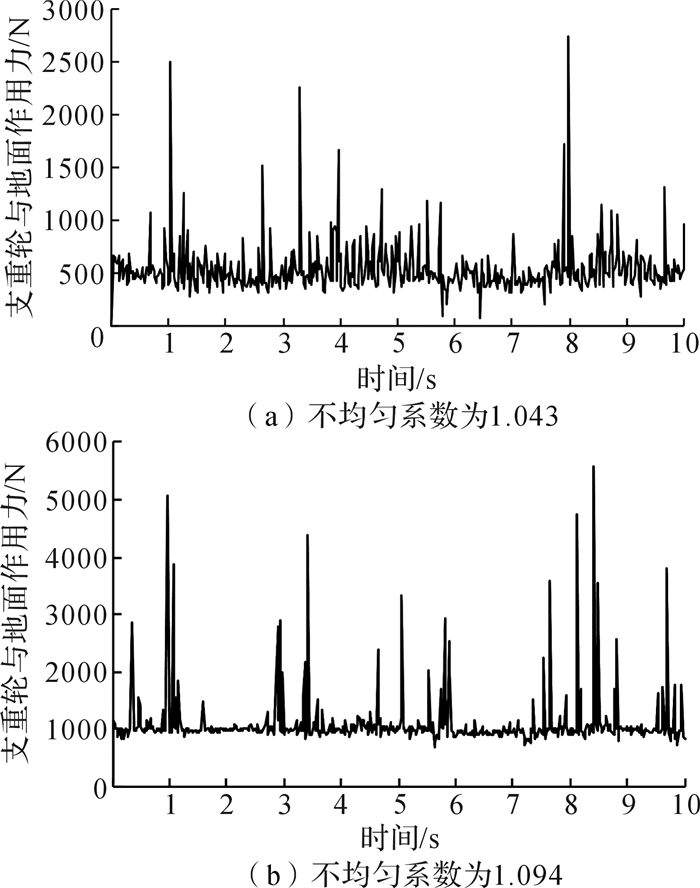
3.3 支重轮与地面间作用力选取工作支段和支持支段相交处支重轮为研究对象,把连接支重轮与车体的转动副的受力近似为支重轮与地面的受力情况,在2种路况下的仿真结果如图 10和图 11所示。
|
| 图 10 坑路面支重轮与地面作用力 Fig.10 The force between the supporting wheel and the ground on pit pavement |
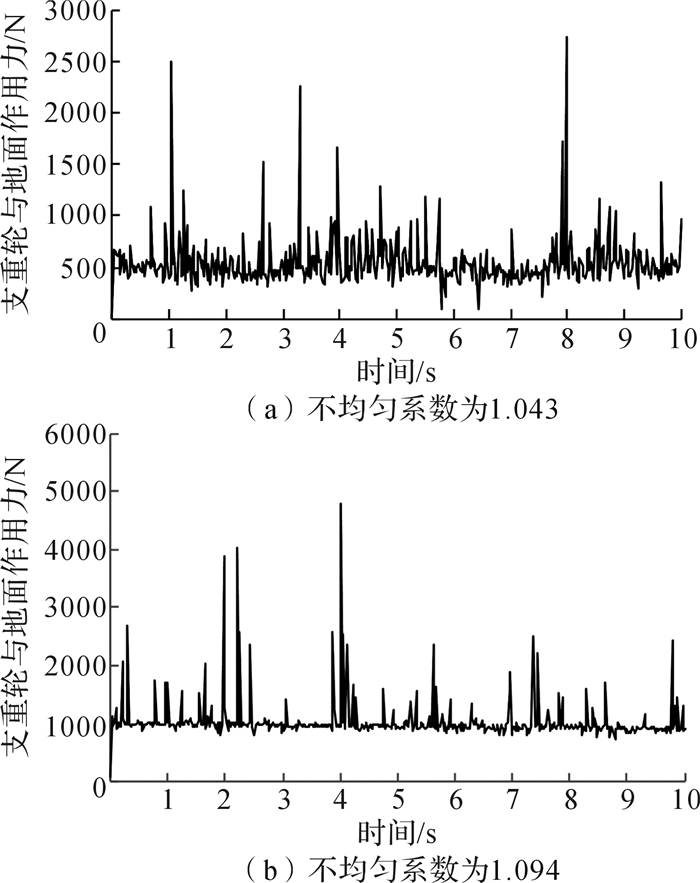
|
| 图 11 平路面支重轮与地面作用力 Fig.11 The force between the supporting wheel and the ground on level road |
从图 10和图 11中看出,不论是平路面还是坑路面,支重轮与地面作用力曲线变化趋势大致相同。在坑路面情况中,不均匀系数为1.043时的支重轮与地面平均作用力和1.094时的相比,前者是后者的一半,平路面情况与坑路面相似。比较图 10(a)和图 11(a)发现,两曲线类似,而且受力相差不大。结果表明:相同不均匀系数情况下,路况对支重轮受力几乎没有影响;而相同路面时,不均匀系数小的情况下,支重轮受地面的垂直支持力较小。
综合以上结果可知不均匀系数越小,履带车的行驶平顺性越好,因此在实际设计过程中应尽可能减小不均匀系数,可通过减小链节距或者增大链轮的半径来实现,以确保车辆平稳行驶。
4 结论针对履带车链环不均匀系数对车辆行驶平顺性的影响问题,建立履带车辆模型并借助RecurDyn动力学软件进行仿真分析。在坑路面和平路面两种情况下,改变不均匀系数的大小,对比分析履带车行走装置某些部件受力的变化情况。通过分析得出如下结论:
1) 履带链环不均匀系数与履带链节距和驱动轮半径有关。通过减小链节距或增大轮半径均可以减小履带链环不均匀系数。
2) 相同路况下,减小不均匀系数,可以减小履带板与地面作用力、履带板与驱动轮作用力及支重轮受地面的垂直支持力,从而提高履带车行驶的平顺性。
3) 不同路况、同一不均匀系数的情况下,并非路面情况越恶劣,支重轮所受地面支持力越大。因此,提高履带车辆行驶平顺性要从改进行走装置来考虑。
| [1] |
刘斌, 王志福.
履带车辆动力学系统发展综述[J]. 四川兵工学报, 2014, 35(1): 68–73.
LIU Bin, WANG Zhi-fu. Review of the development of tracked vehicle dynamic system[J]. Journal of War Industry in Sichuan, 2014, 35(1): 68–73. |
| [2] |
陈媛媛. 履带车辆行动系统动力学仿真分析[D]. 沈阳: 沈阳理工大学机械工程学院, 2012: 5-7.
CHEN Yuan-yuan. Dynamic simulation analysis of tracked vehicle motion system[D]. Shenyang: Shenyang University of Science and Engineering, School of Mechanical Engineering, 2012: 5-7. http://cdmd.cnki.com.cn/Article/CDMD-10144-1013140832.htm |
| [3] |
张宏, 张晓鸥, 赵秀梅, 等.
连续采煤机行走系统的动载荷分析方法[J]. 机械设计与制造, 2015(7): 44–47.
ZHANG Hong, ZHANG Xiao-ou, ZHAO Xiu-mei, et al. Dynamic load analysis method of walking system for continuous miner[J]. Mechanical Design and Manufacture, 2015(7): 44–47. |
| [4] | PARK W Y, CHANG Y C, LEE S S, et al. Prediction of the tractive performance of a flexible tracked vehicle[J]. Journal of Terra Mechanics, 2008, 45(1/2): 13–23. |
| [5] | WONG J Y, CHIANG C F. A general theory for skid-steering of tracked vehicles of firm ground[J]. Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering, 2001, 215(3): 343–355. DOI:10.1243/0954407011525683 |
| [6] | LE Anh Tuan. Modelling and control of tracked vehicles[D]. Sydney: University of Sydney, Department of Mechanical and Mechatronic Engineering, 1999: 183-196. http://www.acfr.usyd.edu.au/?publicationid=162&displaypage=2 |
| [7] | GALVIN P, ROMERO A, DOMINGUEZ J, et al. Fully three-dimensional analysis of high-speed train-track soil-structure dynamic interaction[J]. Journal of Sound and Vibration, 2010, 329(24): 5147–5163. DOI:10.1016/j.jsv.2010.06.016 |
| [8] | BEKKER M G. Introduction to terrain-vehicle systems[M]. Ann Arbor: University of Michigan Press, 1969: 71-85. |
| [9] |
卢进军, 魏来生, 赵韬硕, 等.
基于RecurDyn的履带车辆高速转向动力学仿真研究[J]. 现代机械, 2008(1): 10–12.
LU Jin-jun, WEI Lai-sheng, ZHAO Tao-shuo, et al. Dynamics simulation of tracked vehicle high speed steering based on RecruDyn[J]. Modern Machine, 2008(1): 10–12. |
| [10] |
黄雪涛, 顾亮, 吕唯唯, 等.
履带张紧力及其影响因素分析[J]. 兵工学报, 2014, 35(7): 1110–1118.
HUANG Xue-tao, GU Liang, LÜ Wei-wei, et al. Factors of track tension and impact analysis[J]. Journal of War Industry, 2014, 35(7): 1110–1118. |
| [11] |
王红岩, 王钦龙, 芮强, 等.
高速履带车辆转向过程分析与试验验证[J]. 机械工程学报, 2014, 50(16): 162–172.
WANG Hong-yan, WANG Qin-long, RUI Qiang, et al. Steering process analysis and test verification of high speed tracked vehicle[J]. Journal of Mechanical Engineering, 2014, 50(16): 162–172. |
| [12] |
陈安成, 穆希辉, 杜峰坡, 等.
基于RecurDyn的小型履带车的建模与仿真[J]. 机械设计, 2013, 30(10): 36–38.
CHEN An-cheng, MU Xi-hui, DU Feng-po, et al. Modeling and simulation of a small tracked vehicle based on RecurDyn[J]. Mechanical Design, 2013, 30(10): 36–38. DOI:10.3969/j.issn.1001-2354.2013.10.009 |
| [13] |
骆清国, 司东亚, 龚正波, 等.
基于RecurDyn的履带车辆动力学仿真[J]. 车辆与动力技术, 2011(4): 26–29.
LUO Qing-guo, SI Dong-ya, GONG Zheng-bo, et al. Dynamic simulation of tracked vehicles based on RecurDyn[J]. Vehicle and Power Technology, 2011(4): 26–29. |
| [14] |
孟磊, 李晓雷, 邱实, 等.
履带对履带车辆车体振动影响的分析[J]. 车辆与动力技术, 2015(4): 1–5.
MENG Lei, LI Xiao-lei, QIU Shi, et al. Analysis of the influence of caterpillar tracks on the vibration of tracked vehicle body[J]. Vehicle and Power Technology, 2015(4): 1–5. |
| [15] |
张宏, 张晓鸥, 石涛, 等.
连采机履带行走装置动力学特性与疲劳寿命分析[J]. 煤炭科学技术, 2016, 44(11): 111–115.
ZHANG Hong, ZHANG Xiao-ou, SHI Tao, et al. Dynamic characteristics and fatigue life analysis of crawler walking mechanism of continuous mining machine[J]. Coal Science and Technology, 2016, 44(11): 111–115. |
| [16] |
AHTOHOB A C. 履带行驶装置原理[M]. 魏宸官, 译. 北京: 国防工业出版社, 1957: 45-50.
AHTOHOB A C. Principle of crawler driving device[M]. Translated by WEI Chen-guan. Beijing: National Defense Industry Press, 1957: 45-50. |
| [17] |
段宝钢. 多履带车辆建模研究与仿真分析[D]. 大连: 大连理工大学机械工程学院, 2011: 32-33.
DUAN Bao-gang. Modeling and simulation analysis of multi tracked vehicle[D]. Dalian: Dalian University of Science and Engineering, School of Mechanical Engineering, 2011: 32-33. http://cdmd.cnki.com.cn/Article/CDMD-10141-1011108892.htm |
| [18] |
焦晓娟, 张湝渭, 彭斌彬.
RecurDyn多体系统优化仿真技术[M]. 北京: 清华大学出版社, 2010: 178-179.
JIAO Xiao-juan, ZHANG Jie-wei, PENG Bin-bin. Technology of optimization and simulation on RecurDyn multi-body system[M]. Beijing: Tsinghua University Press, 2010: 178-179. |
| [19] |
张宏, 康鹏, 宋扬, 等.
滑动式履带行走系统动力学建模方法与试验[J]. 振动、测试与诊断, 2015, 35(1): 70–75.
ZHANG Hong, KANG Peng, SONG Yang, et al. Dynamic modeling method and experiment of sliding track walking system[J]. Vibration, Measurement and Diagnosis, 2015, 35(1): 70–75. |



