随着科技的进步,半实物仿真作为一种降低系统研制费用和周期的手段,被广泛应用到各种高精度、复杂的控制领域,在位置控制系统中尤为适用。考虑到高精度位置控制系统中复杂的工况条件,借助于半实物仿真的优势[1-3],建立一个能够准确反映位置控制变化的数学模型和控制算法就显得至关重要。
近年来,对于高精度的控制需求越来越迫切,在位置的精准控制方面,传统的控制方法已经很难达到要求,新控制方法的研究已成为当下研究的热点[4-7]。文献[8]采用T-S模糊控制与PID结合的方法,降低了阶跃输入的上升时间和调节时间;文献[9]建立了T-S数学模型,通过仿真验证控制算法的正确性和有效性;文献[10]中采用经遗传算法优化参数后的速度前馈-位移PI反馈算法来实现液压缸位置的控制,将控制误差保持在较小的范围内;文献[11]采用分段模糊PID控制策略,获得最优PID参数,但在系统响应速度增加的同时整体误差偏大;文献[12]采用了速度和位移双闭环的位置控制技术,相比于单闭环控制,位置精度得到了一定的提高;文献[13-15]对系统的PID控制参数进行了优化,提高了控制系统的鲁棒性和稳定性,但是PID控制器设计复杂,系统的响应速度并没有显著提高。同时一些新型的智能建模方法在控制系统中也得到了应用,如最小二乘法、BP神经网络、支持向量机等[16-19]。这些算法或模型设计都较为复杂,对模型精度的要求很高,且实验条件难以满足,理论跟实验结果差距较大。
基于分析,笔者在圆弧滑轨系统设计过程中,针对轨道小车运行惯量大、响应速度不快、末端位置定位误差大等问题,设计了一套双轨式机械滑动结构。对轨道小车的运行过程进行建模,设计了一种前馈控制与传统PID控制相结合的前馈-PID控制系统。该控制系统由电流环、速度环和位置环组成,速度环采用PI控制,用来消除余差,位置环将前馈控制引入控制系统中,结合PID反馈控制器,不仅消除了系统余差,减小了系统的跟踪误差,还提高了系统响应速度,满足了对被试件高精度定位的要求。
1 高速大行程圆弧滑轨简介高速大行程圆弧滑轨主要是作为一个承载平台,对链路天线性能进行测试。在圆弧移动平台上可完成:被试件沿弧形轨道移动, 沿直线模组上下运动,以及自身的上下摆动和左右摆动。圆弧段的加工方式为分组加工,每组弧段的弧度都有差别,将各个弧段组装在一起,形成一个完整的圆弧轨道。直线段轨道结构构成主要有四部分:基座、垫板、导轨和齿条。图 1所示为滑轨的组成与安装示意图.该平台的被试件(天线)的自由度及相应坐标系如图 2所示。

|
| 图 1 高速大行程圆弧滑轨组成与安装流程 Fig.1 Composition and installation flow of high-speed large-stroke circular slide |
|
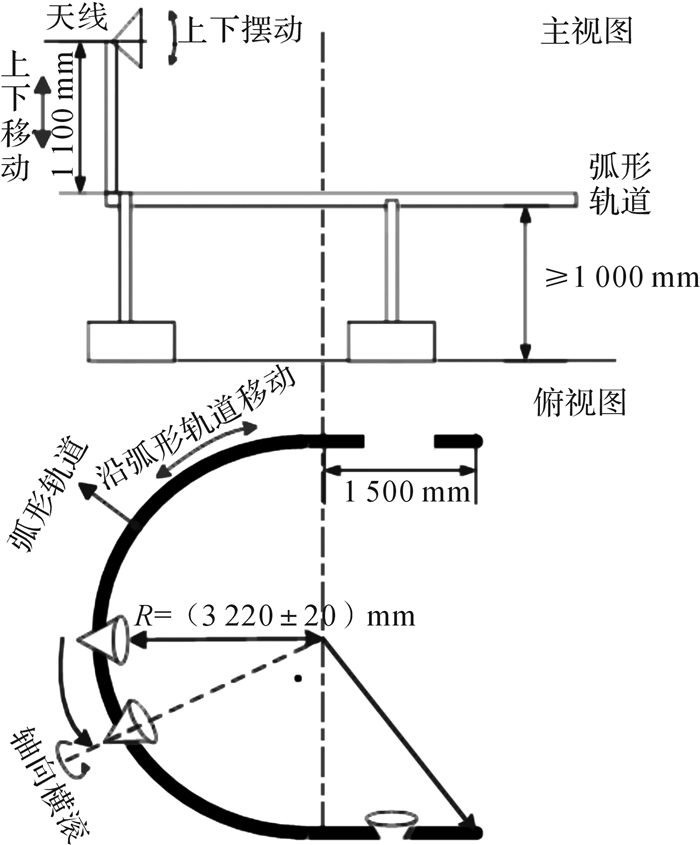
| 图 2 天线运动自由度示意图及相应坐标系 Fig.2 Schematic diagram of the movement freedom of the antenna and the corresponding coordinate system |
被试件(天线)固定在圆弧滑轨平台的竖直导轨上,可以沿竖直导轨上下移动,自身也可以作左右摆动和上下摆动,竖直导轨固定在一个载重小车上,小车可在圆弧滑轨上运动,要求天线在运动时一直对准圆弧中心(被测产品安放位置)。为了减小天线性能的测试误差,小车需按已设置好的控制方案停到指定位置,并保证位置误差小于1 mm。如图 2所示,圆弧滑轨分为3个部分,分别是2段长为1 500 mm的直线导轨和1段半径为3 220 mm的半圆弧导轨,圆弧滑轨段作为影响被试件测试精度的主要段落,其位置控制精度将直接影响天线的测试精度,两边直线段可作为加、减速段,同时也作为测试区域。负载小车有3种运行状态:匀加速、匀速和匀减速。在圆弧滑轨上,每隔500 mm会安装一个霍尔元件,小车底部装有磁性较高的磁铁,使小车通过时能够激发霍尔元件产生信号。示波器的2个表笔连在霍尔元件上,接收2个元件的信号,从而可以计算出小车运行的速度。
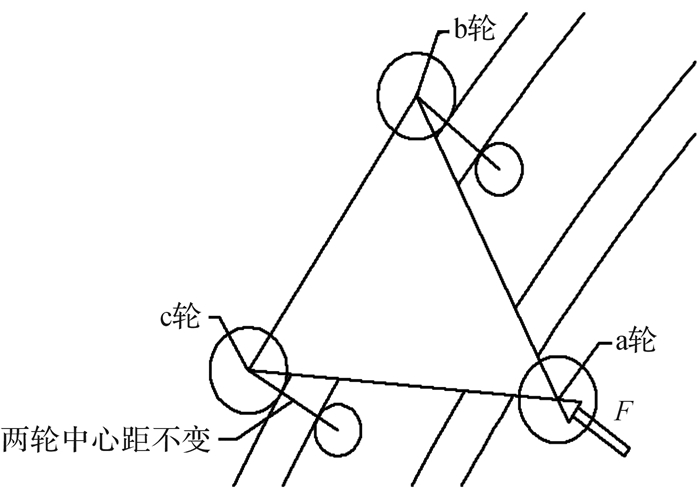
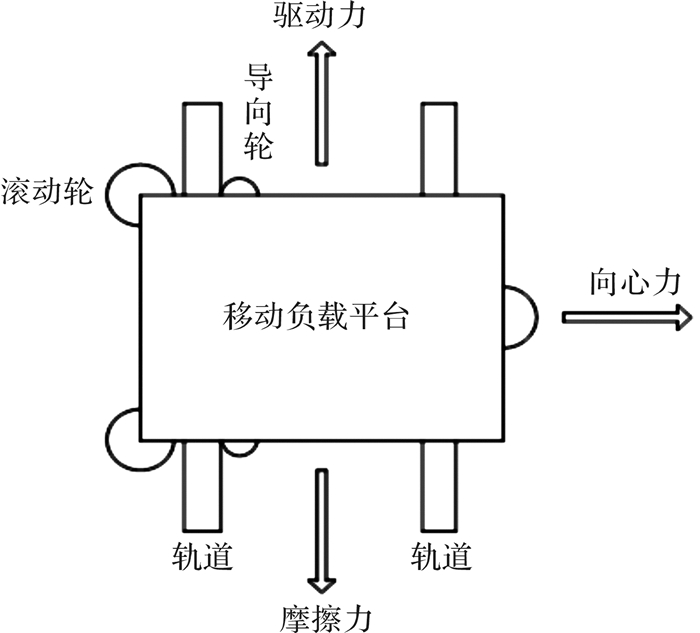
为确保负载小车在轨道上运行平稳,则需要设计一种切合实际的移动机构。笔者将导轨设计成双轨式,分为内、外导轨,负载小车通过螺栓安装在滑轨两侧,导轨的弧度与基座两侧的弧度一致。负载小车的运动机构设计成三角式滚轮机构,滚动轮b,c在外轨外侧配合,滚动轮a在内轨外侧配合。同时,负载小车在过渡段行驶时,所受力的大小和方向会发生一些突变,从而影响到小车的运动轨迹,在此过程中,负载小车会受到向心力作用发生偏转,使系统运行不稳,一旦偏转角过大,则可能发生脱轨或卡壳。所以在外轨内侧设计2个导向轮,分担小车变向时的受力,使小车运行更为平稳,图 3所示是负载小车滚动轮与导向轮布置示意图,其中a轮、b轮、c轮为滚动轮,外轨内侧为2个导向轮,其中c轮上的弹簧机构可以起到缓冲作用,使负载小车运行更加平稳。图 4所示是负载小车运行时的受力示意图,负载小车是由伺服电机提供动力。图 5所示为设计的负载小车移动机构及其齿轮机构的三维模型。
|
| 图 3 负载小车滚动轮与导向轮布置示意图 Fig.3 Arrangement diagram of rolling wheel and guide wheel of load truck |
|
| 图 4 负载小车运行时受力示意图 Fig.4 Load truck running force diagram |

|
| 图 5 负载小车移动机构及其齿轮机构的三维模型 Fig.5 Three-dimensional model of load truck moving mechanism and its gear mechanism |
在滑轨系统运行过程中,有很多因素会影响小车的运行,从而对天线的性能测试造成影响。电机作为动力源,驱动小车运行,电机正常运行需要有与之相匹配的驱动器进行驱动。电机运行时,需对驱动器的参数进行设置,结合减速器的使用,使系统满足各个工况下要达到的性能要求。同时在小车运行的过程中,小车与导轨间的摩擦、阻尼不能忽略,因为它们会影响小车最终所停的精确位置,从而影响到天线测试性能。所以,需要对整个滑轨系统建立精确的数学模型,从而保证整个系统能够达到控制需求。
2.1 电机数学模型电机作为整个圆弧滑轨平台的动力源,其转速变化直接影响小车运行过程中的控制性能,从而影响到最终的定位精度。根据滑轨平台运行要求,笔者所选用的是安川伺服电机E-V系列SGM7G-13AFC61,与之相匹配的驱动器是SGD7S-120A00A002。电机输入为电压,输出为转速。建立电机的数学模型时,忽略电机内部的电枢反应,以及电机磁滞和涡流效应所带来的影响。所选伺服电机相关参数如表 1所示。
| 参数 | 量值 |
| 额定转速v | 1 500 r/min |
| 额定角加速度a | 3 790 rad/s2 |
| 线圈电阻Ra | 59 Ω |
| 转矩系数Cm | 0.891 |
| 反电势系数Ce | 1.2 |
电机的电压平衡方程为:
| $ {U_{\rm{d}}}\left( t \right) = R{i_{\rm{d}}}\left( t \right) + L\frac{{{\rm{d}}{i_{\rm{d}}}\left( t \right)}}{{{\rm{d}}t}} + {E_{\rm{d}}} $ | (1) |
反电动势方程为:
| $ {E_{\rm{d}}} = {C_{\rm{e}}}n\left( t \right) $ | (2) |
式中:Ed为电枢反电势;R为电枢电路的电阻;L为电枢电路的电感;Ce为电机反电势系数;id(t)为电机回路的电流;n(t)为电机的转速。
电机轴上的转矩平衡方程为:
| $ {T_{\rm{e}}}\left( t \right) - {T_{\rm{L}}}\left( t \right) = J\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} $ | (3) |
式中:Te(t)为电枢电流产生的电磁转矩;TL(t)为折算到电机轴上的负载转矩;J为电动机的转动惯量;ω(t)为电机输出的角速度。
角速度ω(t)与转速n(t)之间的关系为:
| $ \omega \left( t \right) = \frac{{2{\rm{ \mathsf{ π} }}n}}{{360}} $ | (4) |
转动惯量为:
| $ J = \frac{{G{D^2}}}{{4g}} $ | (5) |
式中GD2为转子飞轮转矩。
将式(4),(5)代入式(3),整理得:
| $ {T_{\rm{e}}}\left( t \right) - {T_{\rm{L}}}\left( t \right) = \frac{{G{D^2}}}{{375}} \cdot \frac{{{\rm{d}}n}}{{{\rm{d}}t}} $ | (6) |
电机的电磁转矩为:
| $ {T_{\rm{e}}}\left( t \right) = {C_{\rm{m}}}{i_{\rm{d}}}\left( t \right) $ | (7) |
令:
| $ {T_{\rm{l}}} = \frac{L}{R},{T_{\rm{m}}} = \frac{{G{D^2}R}}{{375{C_{\rm{e}}}{C_{\rm{m}}}}} $ | (8) |
式中:Tl为电枢回路的电磁时间常数,Tm为机电时间常数。
将式(6), (7), (8)代入式(1)和式(3)中,并进行拉普拉斯变换,在零初始条件下得:
| $ \begin{array}{l} {U_{\rm{d}}}\left( s \right) = {T_{\rm{m}}}\left( s \right)\left( {{T_{\rm{l}}}s + 1} \right)s{E_{\rm{d}}}\left( s \right) + {E_{\rm{d}}}\left( s \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{R{T_{\rm{L}}}\left( s \right)}}{{{C_{\rm{m}}}}}\left( {{T_{\rm{l}}}s + 1} \right) \end{array} $ | (9) |
伺服电机中电感L很小,通常可以忽略不计,可表示为Tl=L/R≈0,将此式代入式(9)得:
| $ {U_{\rm{d}}}\left( s \right) = {T_{\rm{m}}}\left( s \right)s{E_{\rm{d}}}\left( s \right) + {E_{\rm{d}}}\left( s \right) + \frac{{R{T_{\rm{L}}}\left( s \right)}}{{{C_{\rm{m}}}}} $ | (10) |
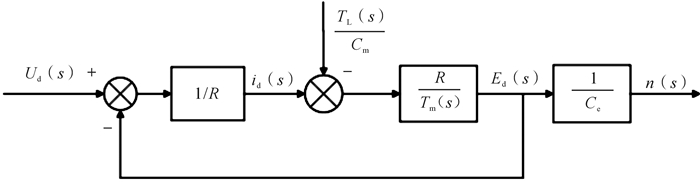
负载小车电机电流闭环结构如图 6所示。
|
| 图 6 负载小车电机电流闭环结构 Fig.6 Motor current closed-loop structure of load truck |
减速器作为一个齿轮传动机构,其输出转速和伺服电机的输出转速呈比值关系,所以其数学模型可以简化为一个比例环节。
齿轮转速为:
| $ {n_1}\left( s \right) = \frac{{v \times 60}}{{{\rm{ \mathsf{ π} }}d}} = \frac{{0.5 \times 60}}{{{\rm{ \mathsf{ π} }} \times 0.032}} = 298\;{\rm{r/}}\min $ |
其中d为主动轮与从动轮的直径,d=0.032 m。
电机的额定转速为:
| $ {n_2}\left( s \right) = 1500\;{\rm{r/}}\min $ |
齿轮的传动比为:
| $ \frac{{{n_1}\left( s \right)}}{{n\left( s \right)}} = \frac{1}{i} = \frac{1}{5} $ |
式中:n1(s)为减速器输出的转速;n(s)为电机的输出转速;i为减速比。
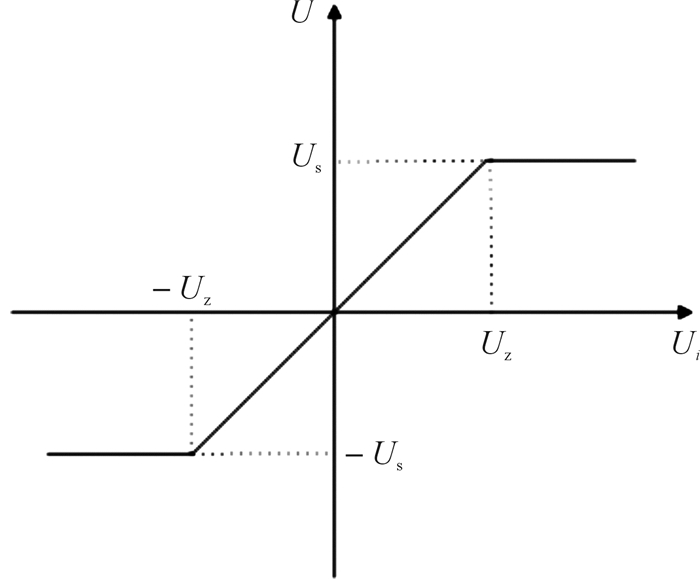
2.3 伺服驱动器模型本系统对电机的控制采用PWM调速技术[20]。驱动器模型主要包括2个环节:比例环节以及饱和非线性环节,其中比例环节为电机的工作电压与调制波幅值电压的比值。故本次分析时,将该模型简化成比例饱和环节,其特性图如图 7所示,其中Us为电机的工作电压, Uz为调制波的幅电压。
|
| 图 7 PWM功率放大特性图 Fig.7 PWM power amplification characteristic diagram |
将该环节简化为比例模型,其传递函数为:
| $ {K_{{\rm{PWM}}}} = {U_{\rm{s}}}/{U_{\rm{z}}} $ |
在电机带动齿轮运动时,电机轴和齿轮均要承载一定的惯量,它们均会对电机轴产生力矩,对于旋转运动,折合到电机轴上的总惯量为:
| $ {J_{\rm{z}}} = J + {J_1}/i_1^2 + {J_2}/i_2^2 $ | (11) |
式中:Jz为系统总惯量,J1为主传动轴的惯量,J2为从动轴的惯量,i1为电机轴与主传动轴之间的转速比,i2为电机轴与从动轴之间的转速比,i1=i2=5。
总惯量产生的转矩为:
| $ {T_J} = {J_{\rm{z}}}{\rm{d}}\omega \left( t \right)/{\rm{d}}t $ | (12) |
因整个设备较为复杂,设备运行时会产生惯性作用,这部分惯性作用产生的转矩折算到电机轴上为:
| $ {T_{\rm{g}}} = mar/i = \frac{{m{r^2}}}{i}\frac{{{\rm{d}}\omega \left( t \right)}}{{{\rm{d}}t}} $ | (13) |
式中:m为移动机构的质量,r为齿轮半径。
2.5 阻尼矩模型轨道小车运行时,小车会受到阻尼作用,阻尼力会对电机轴产生一定的转矩,其中阻尼力大小与轨道小车的运行速度成正比,阻尼力的方向与速度方向相反。该部分转矩折算到电机轴上为:
| $ {T_c} = cv = cr\omega \left( t \right) = \frac{{c{r^2}}}{i}\frac{{{\rm{d}}\omega \left( t \right)}}{{{\rm{d}}t}} $ | (14) |
式中c为阻尼系数。
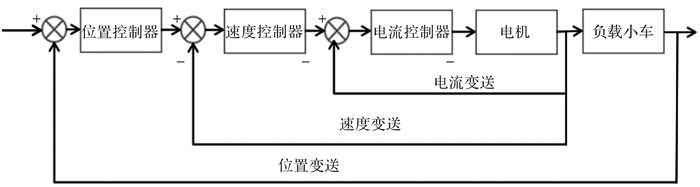
2.6 滑轨位置控制系统传递函数模型 2.6.1 滑轨位置控制模型通过直流伺服电机、减速器、功率放大器可以对负载小车的运行速度进行精确控制,同时对小车启动和制动过程进行最优的调控,再结合最外环的位置控制,就可以对负载小车的最终定位进行控制,实现对负载小车精确控制的目的。滑轨位置控制系统的框图如图 8所示。
|
| 图 8 圆弧滑轨位置控制系统框图 Fig.8 Block diagram of circular slide position control system |
如图 8所示,整个系统由3个闭环回路组成,3个环路构成了一个完整的串级控制系统,电流环包含在速度环中,可将它看成一个整体,作为副回路,位置环作为主回路。在速度环中,负载小车的速度是由电机和减速器共同作用来控制的,而伺服电机具有响应速度快、精度高的优点,所以速度环可以很好地对应于主回路进行随动控制。整个系统响应速度快,具有一定的抗干扰能力和自适应能力,能对被控对象——负载小车——进行比较精准的控制。
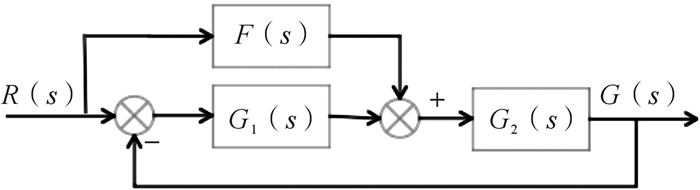
将图 8简化为拥有速度环和位置环的串级控制系统后,位置环的控制对象可以等效为位置传递函数G1(s)和速度传递函数G2(s)的串联,在此基础上,引入前馈控制。系统复合控制框图如图 9所示,其中F(s)为前馈补偿函数。
|
| 图 9 系统复合控制框图 Fig.9 Composite control block diagram of system |
整个位置控制回路的闭环传递函数为:
| $ G\left( s \right) = \frac{{F\left( s \right){G_2}\left( s \right) + {G_1}\left( s \right){G_2}\left( s \right)}}{{1 + {G_1}\left( s \right){G_2}\left( s \right)}} $ | (15) |
根据不变性原理,当F(s)=1/G2(s)时,G(s)=1,这样就可以让输出完全复现输入时的信号,提高控制精度。
2.6.2 传递函数求解在整个系统设计过程中,笔者对速度环采用PI控制,位置环采用PID控制,在控制过程中电流环包含在速度环中,因此只需求得速度环传递函数G2(s)即可。
速度环传递函数G2(s)表示的是电机输入电压与电机输出转速之间的关系。通过上述所建立的各个模型,电机的总负载转矩为各个模块的转矩总和,其表达式为:
| $ {T_{\rm{L}}}\left( t \right) = {J_{\rm{z}}}\frac{{{\rm{d}}\omega \left( t \right)}}{{{\rm{d}}t}} + \frac{{\left( {m + c} \right){r^2}}}{i}\frac{{{\rm{d}}\omega \left( t \right)}}{{{\rm{d}}t}} $ | (16) |
对式(16)进行拉氏变换:
| $ {T_{\rm{L}}}\left( s \right) = {J_{\rm{z}}}s\omega \left( s \right) + \frac{{\left( {m + c} \right){r^2}}}{i}s\omega \left( s \right) $ | (17) |
联立方程(10)和(17),得到以电机电压为输入、负载小车运行速度为输出的传递函数,其表达式为:
| $ {G_2}\left( s \right) = \frac{r}{5}\frac{1}{{\left[ {\frac{{60}}{{2{\rm{ \mathsf{ π} }}}}{C_{\rm{e}}}{T_{\rm{m}}} + {J_{\rm{z}}}\frac{R}{{{C_{\rm{m}}}}} + \frac{{R\left( {m + c} \right){r^2}}}{{i{C_{\rm{m}}}}}} \right]s + \frac{{60}}{{2{\rm{ \mathsf{ π} }}}}{C_{\rm{e}}}}} $ | (18) |
电机转速从0加速到1 500 r/min时需要用时t=ω/α=6.596 ms,电机机电时间常数Tm=63.2%×t=4.17 ms。电机轴上的系统总惯量Jz=2.599×10-3 kg·m2。整个移动轨道车质量m=180 kg。
重力引起的摩擦力为:
| $ {f_g} = \mu mg = 0.2 \times 180 \times 10 = 36{\rm{N}} $ |
设备在圆弧滑轨上所受的向心力为:
| $ {F_x} = m{v^2}/r = 180 \times {0.5^2}/3.22 = 13.98{\rm{N}} $ |
向心力所引起的摩擦力为:
| $ {f_x} = \mu {F_x} = 0.28{\rm{N}} $ |
总摩擦力为:
| $ {F_f} = {f_g} + {f_x} = 36.28{\rm{N}} $ |
阻尼系数取总阻力的10%,c=3.628。
结合电机参数,求得传递函数:
| $ {G_3}\left( s \right) = \frac{1}{{0.236s + 1}} $ | (19) |
前馈补偿函数:
| $ F\left( s \right) = 0.236{s^2} + 2s + 1 $ | (20) |
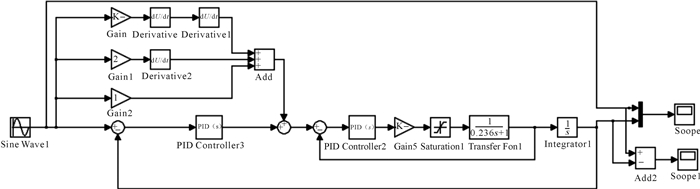
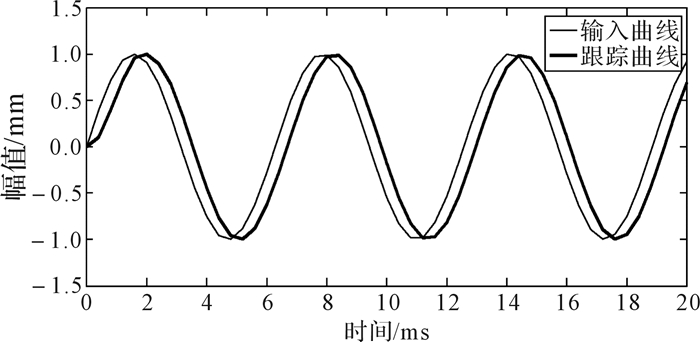
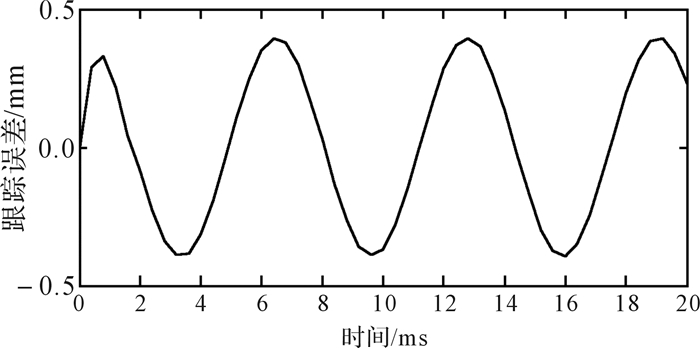
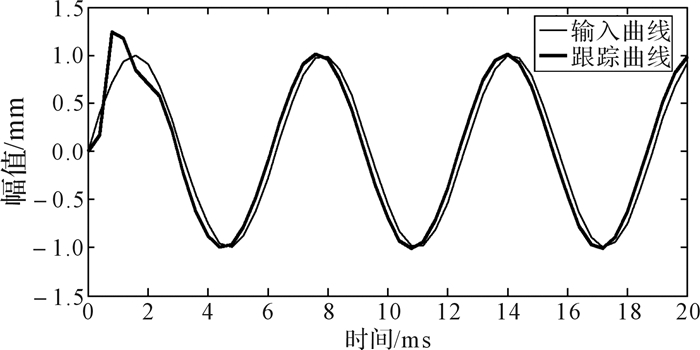
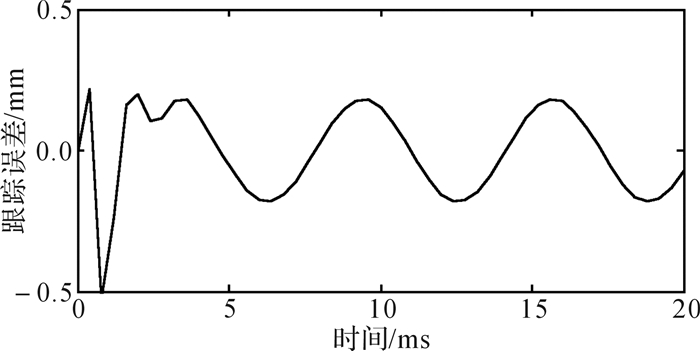
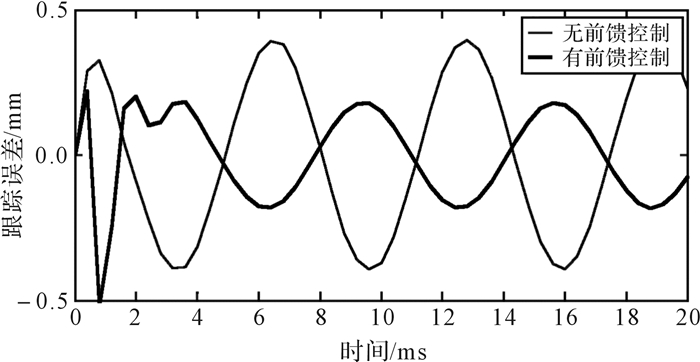
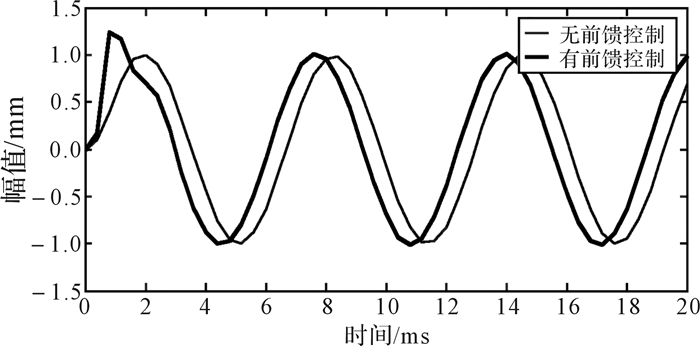
根据建立的滑轨系统模型,在MATLAB中构建Simulink仿真模型,采用正弦曲线进行跟踪,正弦输入信号为1 Hz正弦曲线, 图 10为搭建的圆弧滑轨位置控制系统仿真模型。图 11、图 12分别是无前馈控制和有前馈控制时的跟踪曲线,从图中可以看出,无前馈控制时跟踪曲线滞后较多,有前馈控制时跟踪曲线有较小的超前,总体来说有前馈控制时跟踪曲线跟踪度较好;图 13、图 14分别是无前馈控制和有前馈控制时的跟踪误差曲线,图 15是两者跟踪误差曲线的对比。从图 15中可以看出,无前馈控制时,误差范围在[-0.4, 0.4]mm;有前馈控制时,在0—3 ms内跟踪度稍差,之后系统较稳定后,误差范围在[-0.18, 0.18] mm。比较两者的跟踪误差曲线,可以得出有前馈控制时的跟踪精度比无前馈控制时提高了1.2倍,证明了前馈控制系统的可行性和精确性。图 16为2种状态下系统响应时间曲线,从图中可以看出有前馈控制比无前馈控制有一个明显的超前作用,有前馈控制时系统响应时间为2 ms,无前馈控制时系统响应时间为3 ms,系统响应速度提升16.7%。
|
| 图 10 圆弧滑轨位置控制系统Simulink仿真模型 Fig.10 Simulink simulation model for position control system of circular rail |
|
| 图 11 无前馈控制时系统跟踪曲线 Fig.11 System tracking curve without feedforward control |
|
| 图 12 有前馈控制时系统跟踪曲线 Fig.12 System tracking curve with feedforward control |
|
| 图 13 无前馈控制时系统跟踪误差曲线 Fig.13 System tracking error curve without feedforward control |
|
| 图 14 有前馈控制时系统跟踪误差曲线 Fig.14 System tracking error curve with feedforward control |
|
| 图 15 系统跟踪误差曲线对比 Fig.15 Comparison of system tracking error curve |
|
| 图 16 系统响应时间曲线对比 Fig.16 Comparison of system response time curves |
图 17为搭建的实验平台。在上述仿真的基础上, 经过重复实验,其运行关系可以表达为:
| $ S = \left\{ \begin{array}{l} x,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < x \le 1500\;{\rm{mm}}\\ 1500 + \frac{{k \times l\left( {x - 1500} \right)}}{{3220 \times {\rm{ \mathsf{ π} }}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1500 < x \le 3200{\rm{ \mathsf{ π} }}\;{\rm{mm}}\\ k \times l + x - 3220 \times {\rm{ \mathsf{ π} }},\;\;\;\;\;\;\;\;1500 + 3220{\rm{ \mathsf{ π} }} < x \le 3000 + 3220{\rm{ \mathsf{ π} }}\;{\rm{mm}} \end{array} \right. $ |

|
| 图 17 圆弧滑轨位置控制实验平台 Fig.17 Experimental platform for position control of circular rail |
其中:x为输入目标位置;S为理论上小车所能到达的位置,k为负载小车运行完整个圆弧段伺服电机所转的总圈数;l为伺服电机每旋转一圈,负载小车在滑轨上移动的距离。经过多次实验,测得k=216.15,l=46.8 mm。
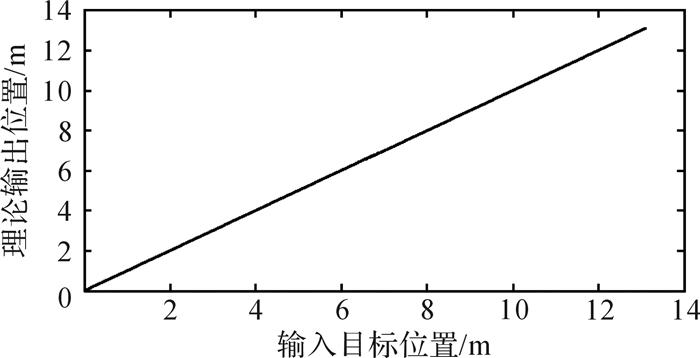
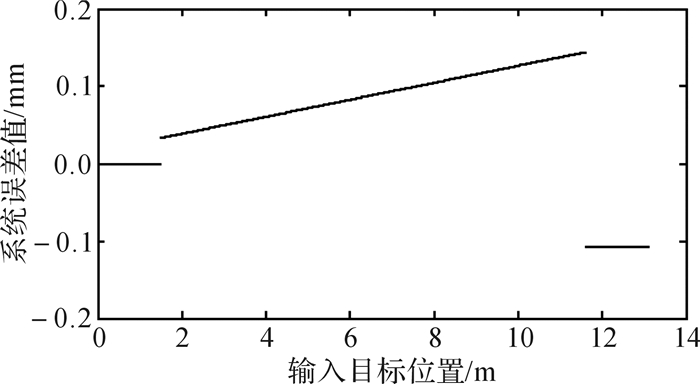
图 18为小车位置拟合曲线,图 19为小车理论位置误差曲线,从图中可以看出,小车理论位置误差范围为[-0.2, 0.2] mm,在系统许可范围内。
|
| 图 18 负载小车理论位置拟合曲线 Fig.18 Theoretical position fitting curve of load truck |
|
| 图 19 负载小车理论位置误差曲线 Fig.19 Theoretical position error curve of load truck |
采集小车在不同位置的数据,取100组进行误差分析。数据如表 2所示。
| mm | |||||
| 组别 | 初始位置 | 终止位置 | 实际行程 | 理论行程 | 误差 |
| 1 | 0 | 700.1 | 700.1 | 700 | 0.1 |
| 2 | 500 | 1 800.2 | 1 299.9 | 1 200 | -0.1 |
| 3 | 1 000 | 2 999.8 | 1 999.8 | 2 000 | -0.2 |
| 4 | 2 300 | 3 450.3 | 1 150.3 | 1 150 | 0.1 |
| 5 | 4 800 | 8 030.7 | 3 230.7 | 3 230 | 0.3 |
| … | … | … | … | … | … |
| 100 | 5 000 | 13 000.5 | 8 000.5 | 8 000 | 0.5 |
所取样本的标准偏差为:
| $ {S_x} = \sqrt {\sum {{{\left( {{x_{末}} - {x_{初}}} \right)}^2}} } = 0.48\;{\rm{mm}} $ |
仪器的不确定度为:
| $ {\Delta _{仪}} = 0.5\;{\rm{mm}} $ |
合成的不确定度为:
| $ {\Delta _x} = \sqrt {S_x^2 + \Delta _x^2} = 0.69\;{\rm{mm}} < 1\;{\rm{mm}} $ |
笔者在对圆弧滑轨负载小车位置进行控制时,针对小车在滑轨上的运动特性,设计了一套双轨式机械滑动结构,提高了小车运行时的稳定度,并对小车运行的各个环节进行了建模,得到了小车位置控制的传递函数,利用前馈-PID控制,搭建Simulink仿真模型,利用正弦曲线进行跟踪,仿真结果表明:在无前馈控制的情况下,跟踪误差范围为[-0.4, 0.4] mm,引入前馈控制后,跟踪误差为[-0.18, 0.18] mm,系统跟踪精度提高了1.2倍,并且系统的响应速度提高了16.7%。搭建实验平台进行实验,采集数据,拟合出小车运动位置曲线,并与理论输入值进行对比,理论位置误差范围保持在[-0.2, 0.2] mm,取其中100组数据进行误差分析,误差为0.69 mm,系统的理论误差与实际误差皆小于1 mm,满足整个系统的设计要求。研究结果为滑轨系统的机械设计和性能测试提供了有效的参考数据,可促进轨道系统测试的工业自动化。
| [1] |
黄建强, 鞠建波.
半实物仿真技术研究现状及发展趋势[J]. 舰船电子工程, 2011, 31(7): 5–7, 25.
HUANG Jian-qiang, JU Jian-bo. Research status and development trend of hardware-in-the-loop simulation technology[J]. Ship Electronic Engineering, 2011, 31(7): 5–7, 25. |
| [2] | XU Kai, LÜ Yan, JIN Guang, et al. Design of semi physical simulation for small satellite by virtual display[J]. Applied Mechanics and Materials, 2012, 130/134: 2684–2687. |
| [3] | PENG Min. Semi physical simulation of diesel generator set rotational speed control[J]. Applied Mechanics and Materials, 2013, 389: 563–567. DOI:10.4028/www.scientific.net/AMM.389 |
| [4] | JEONG Seok-kwon, YOU Sam-sang. Precise position synchronous control of multi-axis servo system[J]. Mechatronics:The Science of Intelligent Machines, 2008, 18(3): 129–140. |
| [5] | CHENG Guo-yang, PENG Ke-mao, CHEN Ben M, et al. Discrete-time mode switching control with application to a PMSM position servo system[J]. Mechatronics:The Science of Intelligent Machines, 2013, 23(8): 1191–1201. |
| [6] |
孙春亚, 吴楝华, 喜冠南, 等.
电液伺服模糊PID位置控制系统设计及应用[J]. 机械设计与制造, 2016(6): 155–157, 62.
SUN Chun-ya, WU Lian-hua, XI Guan-nan, et al. Design and application of electro-hydraulic servo fuzzy PID position control system[J]. Machinery Design & Manufacture, 2016(6): 155–157, 62. |
| [7] |
喜冠南, 吴楝华, 孙春亚, 等.
运用PID算法的电液伺服位置控制系统实验[J]. 现代制造工程, 2016(6): 153–156, 29.
XI Guan-nan, WU Lian-hua, SUN Chun-ya, et al. Experiments on electro-hydraulic servo position control system using PID algorithm[J]. Modern manufacturing engineering, 2016(6): 153–156, 29. |
| [8] |
高嵩, 王磊, 陈超波, 等.
TS-PID算法的直流伺服控制系统[J]. 西安工业大学学报, 2016, 36(1): 14–20.
GAO Song, WANG Lei, CHEN Chao-bo, et al. DC servo control system based on TS-PID algorithm[J]. Journal of Xi'an University of Technology, 2016, 36(1): 14–20. |
| [9] |
袁铸钢, 苏哲, 张强, 等.
水泥分解炉出口温度T-S建模[J]. 控制工程, 2016, 23(2): 211–217.
YUAN Zhu-gang, SU Zhe, ZHANG Qiang, et al. T-S modeling for calciner outlet temperature[J]. Control Engineering of China, 2016, 23(2): 211–217. |
| [10] |
高钦和, 刘志浩, 牛海龙.
参数优化的高速开关阀控液压缸位置控制研究[J]. 机械科学与技术, 2015, 34(6): 903–909.
GAO Qin-he, LIU Zhi-hao, NIU Hai-long. Controlling position of hydraulic cylinder with high-speed on-off valve parameters optimized[J]. Mechanical Science and Technology, 2015, 34(6): 903–909. |
| [11] |
吴楝华, 喜冠南, 孙春亚, 等.
电液伺服泵控系统的速度控制实验研究[J]. 组合机床与自动化加工技术, 2016(9): 61–63, 67.
WU Lian-hua, XI Guan-nan, SUN Chun-ya, et al. Experimental study on speed control of electro-hydraulic servo pump control system[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(9): 61–63, 67. |
| [12] |
赵典, 强宝明, 王卫辉, 等.
基于双闭环系统的起重机位置控制技术研究[J]. 计算机测量与控制, 2012, 20(11): 2965–2967.
ZHAO Dian, QIANG Bao-ming, WANG Wei-hui, et al. Research of gantry crane position control technology based on double-closed loops system[J]. Computer Measurement & Control, 2012, 20(11): 2965–2967. |
| [13] |
邹金红, 朱玉川.
基于复合前馈控制的交流位置伺服系统动态特性[J]. 电机与控制应用, 2011, 38(1): 29–42.
ZOU Jin-hong, ZHU Yu-chuan. Dynamic characteristic in permanent magnet AC synchronous servo motor position servo system based on compound feedforward control[J]. Electric Machines & Control Application, 2011, 38(1): 29–42. |
| [14] |
邓昌奇, 廖辉.
基于前馈控制的交流伺服系统精确定位的研究[J]. 武汉大学学报, 2013, 46(3): 405–408.
DENG Chang-qi, LIAO Hui. Research on precise positioning of AC servo system based on feedforward control[J]. Journal of Wuhan University, 2013, 46(3): 405–408. |
| [15] |
杨文刚.
适用于多种积分过程的鲁棒PID控制器设计方案[J]. 控制工程, 2016, 23(4): 538–543.
YANG Wen-gang. A robust PID controller design method for multiple kinds of integrating systems[J]. Control Engineering of China, 2016, 23(4): 538–543. |
| [16] | ZERZUCHA P, DASZYKOWSKI M, WALCZAK B. Dissimilarity partial least squares applied to non-linear modeling problems[J]. Chemometrics and Intelligent Laboratory Systems, 2012, 110(1): 156–162. DOI:10.1016/j.chemolab.2011.11.005 |
| [17] | MARIA H, PENTTI K. Bayesian network modeling of Port State Control inspection findings and ship accident involvement[J]. Expert Systems with Applications, 2014, 41(4): 1632–1646. DOI:10.1016/j.eswa.2013.08.060 |
| [18] |
朱坚民, 齐北川, 沈正强, 等.
基于神经网络补偿控制的PID双闭环球杆位置控制[J]. 系统仿真学报, 2014, 26(5): 1032–1039.
ZHU Jian-min, QI Bei-chuan, SHEN Zheng-qiang, et al. Double closed-loop PID position control of ball-and-beam system based on neural network compensation control[J]. Journal of System Simulation, 2014, 26(5): 1032–1039. |
| [19] |
朱坚民, 谢平, 黄春燕, 等.
基于前馈神经网络控制的球杆系统位置控制[J]. 控制工程, 2017, 24(6): 1186–1193.
ZHU Jian-min, XIE Ping, HUANG Chun-yan, et al. Ball and beam system position control based on feed forward neural network control[J]. Control Engineering of China, 2017, 24(6): 1186–1193. |
| [20] |
吕德刚, 都泽源, 张恒, 等.
无刷直流电动机PWM调制方式建模研究[J]. 微特电机, 2017, 45(9): 60–63.
LÜ De-gang, DU Ze-yuan, ZHANG Heng, et al. Study modeling of PWM modulation for permanent magnet brushless DC motor[J]. Small & Special Electrical Machines, 2017, 45(9): 60–63. |



