2. 云南电网有限责任公司 电力科学研究院, 云南 昆明 650217;
3. 南京丹迪克电力仪表有限公司, 江苏 南京 210049
2. Electric Power Research Institute, Yunnan Power Grid Limited Liability Corporation, Kunming 650217, China;
3. Nanjing Dandick Electric Instrument Company Limited, Nanjing 210049, China
目前市场上最常见的互感器校验仪检定装置在电源信号输出和信号处理等方面存在较大不足[1-2],在提取基波分量和计算校验仪比差和角差的过程中,也存在容易受到频率变化影响而导致误差偏大等问题。现有的大部分检定装置是利用硬件电路方式进行正交分解,得到正交分量和同相分量[3],或者是利用简单的基波提取算法[4-8],例如DFT算法和全波傅里叶变换算法。通过硬件电路进行正交分解得到的信号正交分量和同相分量的准确性在很大程度上取决于电路中电子器件的精准性,如果电路中某一个器件出现失准或失效状况,则会导致基波分量的提取结果出现较大误差,提取结果则不能被采用;在利用DFT算法或全波傅里叶变换算法得到信号正交分量和同相分量的过程中,需要对信号进行同步采样。由于我国实际电网的频率是在额定功率(50 Hz)上下波动(波动范围一般为49.5~50.5 Hz),标准源输出信号包含各种分量(各次谐波和白噪声等)的周期函数[9],因此这2种算法的基波提取效果会受到较明显的影响。目前在实际应用这2种算法时, 会进行相关算法改进和算法结合,最常见的有基于频谱的插值算法、DFT算法结合准同步算法等,进而抑制因无法进行信号同步采样而导致的频谱泄露和栅栏效应[10-13]。但在包含频率缓变、多谐波干扰等不利因素的实际电网信号中,基波提取仍会受到频谱泄露和栅栏效应的影响,导致改进算法的作用和效果不太显著。
为了解决以上提到的基波频率波动和非同步采样问题,本文提出在互感器校验仪自动检定系统中采用基于自适应频率跟踪的基波提取算法来提取基波分量。经过仿真验证及对自动检定系统测试实验结果的分析,可证明在互感器校验仪自动检定系统中采取基于自适应频率跟踪的基波提取算法具备一定的有效性和实用性。
1 基波分量提取方法 1.1 频谱泄露的原因设定离散信号的表达式为[14]:
| $ x\left( n \right) = \sum\limits_{h = 1}^H {{A_h}{{\rm{e}}^{\rm{j}}}^{(2{\rm{ \mathsf{ π} }}h{f_0}n/{f_{\rm{s}}} + {\varphi _h})}} $ | (1) |
式中:h代表谐波次数,h=1, 2, …, H;f0代表基波频率;Ah, φh分别代表第h次谐波的幅值和初相角;fs为采样频率;n代表采样信号长度,n=0, 1, …, N-1。
基波提取的信号在被离散化时相当于被一个矩形窗Wr(n)截短,信号经离散傅里叶变换后为:
| $ X\left( k \right) = \sum\limits_{h = 1}^H {{A_h}{{\rm{e}}^{{\rm{j}}{\varphi _h}}}} {W_{\rm{R}}}(\frac{{2{\rm{ \mathsf{ π} }}}}{N}(k - {k_0}h)) $ | (2) |
式中:k代表离散频谱线的序号,k=0, 1, …, N-1;k0=Nf0/fs, 为常数;WR(k)为Wr(n)的频谱函数,表达式:
| $ {W_{\rm{R}}}\left( k \right) = \frac{{{\rm{sin}}(k{\rm{ \mathsf{ π} }})}}{{{\rm{sin}}(k{\rm{ \mathsf{ π} }}/N)}}{{\rm{e}}^{{\rm{ - j}}\frac{{N - 1}}{N}k{\rm{ \mathsf{ π} }}}} $ | (3) |
同步采样时,k0为整数,即Nf0/fs为整数,表示在X(k)中基波及各次谐波的频率位置与信号的频率分辨率成整数倍关系,不会发生频谱泄露[15]。如果k0不是整数,表明X(k)中基波及各次谐波的频率位置与信号的频率分辨率不是整数倍关系,那么包括基波在内的各频率位置处的能量会向各自的临近频谱线靠近,则发生频谱泄露。
在对电网频率的实际测量中,采样时钟精度、信号频率变化等因素都会导致在采样过程做不到严格的同步采样,那么频谱泄露和栅栏效应现象的发生就不可避免了。
1.2 基于自适应频率跟踪的基波提取算法在互感器校验仪自动检定系统中涉及信号基波分量的提取,在提取过程中需要尽量避免非同步采样的发生,从而减小基波分量提取的误差。根据文献[16]的研究,基于自适应频率跟踪的基波提取算法可在提取基波分量的过程中避免发生非同步采样,提高基波分量提取的精度。
电网信号yp可表示为:
| $ {y_{\rm{p}}} = {z_{\rm{p}}} + {v_{\rm{p}}} $ | (4) |
式中:vp表示白噪声,它满足正态分布,vp~N(0, σv2);zp表示的是基波与信号中存在的各次谐波,表达式为:
| $ {z_{\rm{p}}} = \sum\limits_{h = 1}^M {{a_h}{\rm{sin}}({\omega _h}{t_h} + {\theta _h})} $ | (5) |
式中:ah,θh和ωh分别表示幅值、相位和角频率,th=hfs。
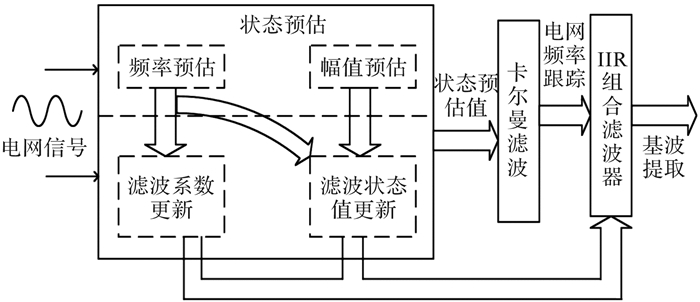
本文采用的基于自适应频率跟踪的基波提取算法原理如图 1所示,主要由状态预估、频率跟踪以及基波提取三部分构成。该算法可以对电网频率进行自适应跟踪,同时能够克服频率跟踪过程中的频率缓变、多次谐波干扰等缺点,从而实现精准基波信号分量的提取。算法主要分为以下3步:
|
| 图 1 基于自适应频率跟踪的基波提取算法原理 Fig.1 The principle of fundamental wave extraction algorithm based on adaptive frequency tracking |
1) 通过状态预估模块获得电网状态的预估值,并根据预估值完成对滤波系数和滤波状态值的更新;
2) 根据状态预估值,利用卡尔曼滤波算法实现频率的实时跟踪;
3) 基于IIR组合滤波器可根据实时跟踪到的电网基波频率完成基波提取,快速精确地得到基波分量。
由于篇幅限制,此三部分具体的算法理论可见文献[16]。
2 基波分量提取仿真实验 2.1 仿真实验条件设定电网频率在49.5~50.5 Hz之间,为了验证基波提取算法在这种情况下的提取效果,利用MATLAB 2017进行基波分量提取仿真实验。由于实际电网中的原始信号带有大量谐波和白噪声,根据式(4)表示的电网信号模型,设定基波分量提取仿真实验的测试信号为:
| $ y\left( t \right) = 0.5{\rm{sin}}(2{\rm{ \mathsf{ π} }}f{T_{\rm{s}}}t) + {v_{\rm{p}}} $ | (6) |
式中:f表示频率;Ts表示采样周期,Ts=0.1 ms;vp表示白噪声,且满足:
| $ {v_{\rm{p}}} \sim N(0, {0.001^2}) $ | (7) |
通过模拟电网实际变化情况,可对比出全波傅里叶变换算法、准同步DFT算法和基于自适应频率跟踪的基波提取算法这3种基波提取算法的基波提取效果。其中,全波傅里叶变换算法和准同步DFT算法原理分别在文献[17]和文献[13, 18]中有详细介绍,本文不再赘述。
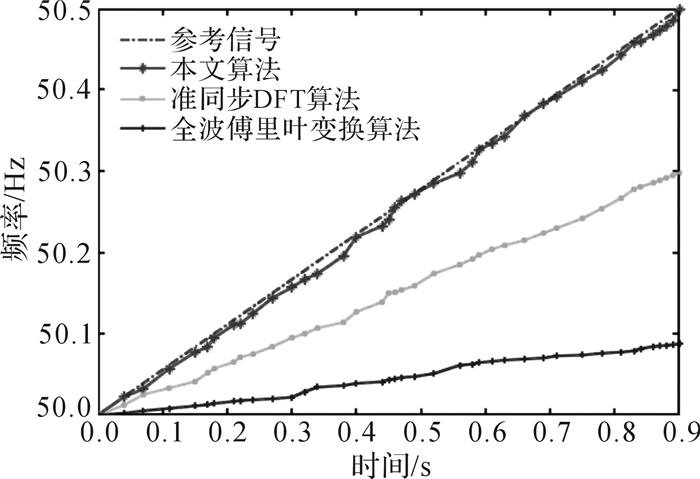
2.2 仿真实验结果为了验证互感器校验仪自动检定系统中采取的基于自适应频率跟踪的基波提取算法在发生频率缓变时的自适应跟踪特性,对比3种算法的频率跟踪特性。设置参考信号的基波频率在0-0.9 s内由50 Hz线性缓变到50.5 Hz,3种算法的频率跟踪效果对比情况如图 2所示。
|
| 图 2 基波频率缓变时3种算法的频率跟踪效果 Fig.2 Frequency tracking effect of three algorithms under the condition of fundamental frequency changing slowly |
由图 2可以看出,基于自适应频率跟踪的基波提取算法能够较为准确地跟踪基波频率变化,而当基波频率开始变化时,准同步DFT算法和全波傅里叶变换算法这2种算法就不能实现有效的频率跟踪,且跟踪曲线与参考信号曲线的偏离越来越大。此3种算法的频率跟踪整体误差值如表 1所示。
| Hz | |||
| 基波提取算法 | 本文算法 | 准同步DFT算法 | 全波傅里叶变换算法 |
| 跟踪整体误差 | 0~0.02 | 0.01~0.07 | >0.08 |
在频率跟踪过程中, 基于自适应频率跟踪的基波提取算法的频率跟踪曲线与参考信号的频率线性缓变曲线基本重合,整个跟踪过程的最大偏移量为0.02 Hz,即该算法的整体跟踪误差控制在0~0.02 Hz之间。另外2种算法的频率跟踪效果较差,跟踪的整体误差偏大,尤其是全波傅里叶变换算法,整体的跟踪误差大于0.08 Hz。对比这3种算法的频率跟踪效果和频率跟踪整体误差,表明在互感器校验仪自动检定系统中采用基于自适应频率跟踪的基波提取算法对频率的波动具有良好的适应能力,并且可以对波动的频率实现稳定的跟踪。
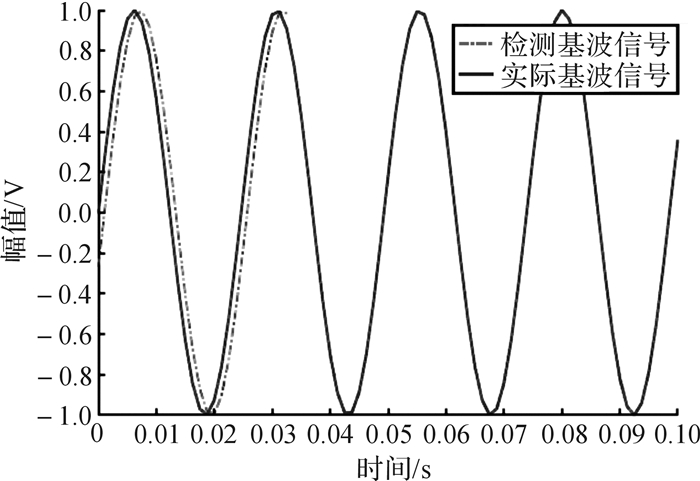
基于自适应频率跟踪的基波提取算法对实际基波信号的跟踪效果如图 3所示。
|
| 图 3 基于自适应频率跟踪的基波提取算法对实际基波信号的跟踪效果 Fig.3 The tracking effect of fundamental wave extraction algorithm based on adaptive frequency tracking to the actual fundamental wave signal |
从图 3中可以看出,在0-0.03 s期间,实际基波信号与利用基波提取算法检测到的基波信号之间存在微小间隔;在0.03 s后,2组基波信号完全重合。表明在互感器校验仪自动检定系统中应用基于自适应频率跟踪的基波提取算法能够满足基波信号跟踪的要求,在0.03 s时开始实现对实际基波信号的同步跟踪。
3 系统检定结果分析上述仿真实验已经证明了基于自适应频率跟踪的基波提取算法能够实现基波信号的同步跟踪,可以消除非同步采样带来的频谱泄露和栅栏效应缺陷,因此可以在互感器校验仪自动检定系统中利用该算法提取基波分量并计算角差、比差。为验证在实际检定过程中该算法计算比差值和角差值的精度,利用一台已被检定为稳定性、准确性良好的互感器校验仪作为测试对象,并设定自动检定系统采用电压互感器检定功能对该被试品进行检定。根据设定检定点分别测量50 Hz和50.5 Hz这2种标准源频率情况下的比差值和角差值,测试结果分别如表 2和表 3所示。
| 设定比差/ % | 测量比差/% | 比差偏差/% | ||||
| 50 Hz | 50.5 Hz | 50 Hz | 50.5 Hz | |||
| 0.000 0 | 0.014 0 | 0.013 9 | 0.014 0 | 0.013 9 | ||
| 0.100 0 | 0.091 0 | 0.091 2 | 0.009 0 | 0.008 8 | ||
| 0.010 0 | 0.002 0 | 0.002 0 | 0.008 0 | 0.008 0 | ||
| 0.001 0 | 0.015 1 | 0.015 0 | 0.014 1 | 0.014 0 | ||
| 0.000 1 | 0.011 3 | 0.011 3 | 0.011 2 | 0.011 2 | ||
| 设定角差 | 测量角差 | 角差偏差 | |||
| 50 Hz | 50.5 Hz | 50 Hz | 50.5 Hz | ||
| 0 | 0′04″ | 0′03″ | 0′04″ | 0′03″ | |
| 2′09″ | 2′07″ | 2′05″ | -0′02″ | -0′04″ | |
| 4′42″ | 4′39″ | 4′41″ | -0′03″ | -0′01″ | |
| 7′15″ | 7′20″ | 7′13″ | 0′05″ | -0′02″ | |
| 10′57″ | 11′02″ | 11′00″ | 0′05″ | 0′03″ | |
比差的标准偏差计算公式为:
| $ s\left( f \right) = \sqrt {\sum\limits_{i = 1}^n {\frac{{{{({f_i} - \bar f)}^2}}}{{n - 1}}} } $ | (8) |
式中
根据式(8)计算出比差的检测精度。当标准源频率设定为50 Hz时,利用基于频率自适应跟踪的基波提取算法计算得到的比差精度能够达到0.002 8%;当标准源频率设定为50.5 Hz时,利用该基波提取算法计算得到的比差精度能够达到0.002 78%。这远远小于互感器校验仪自动检定系统的设计误差要求。因此,在比差检测方面,采用基于自适应频率跟踪的基波提取算法的互感器校验仪自动检定系统符合检定误差要求,也满足检定系统达到0.05级检测精度的要求。
角差的标准偏差计算公式为:
| $ s\left( \delta \right) = \sqrt {\sum\limits_{i = 1}^n {\frac{{{{({\delta _i} - \bar \delta )}^2}}}{{n - 1}}} } $ | (9) |
式中
根据式(9)计算出角差的检测精度。当标准源频率设定为50 Hz时,利用基于频率自适应跟踪的基波提取算法计算得到的角差精度能够达到0.012%;当标准源频率设定为50.5 Hz时,利用该基波提取算法计算得到的角差精度能够达到0.019%。这2个精度值也是远远小于互感器校验仪自动检定系统的设计误差要求。因此,在角差检测方面,采用基于自适应频率跟踪的基波提取算法的互感器校验仪自动检定系统符合检定误差要求,也满足检定系统达到0.05级检测精度的要求。
互感器校验仪自动检定系统的检定结果表明该系统测试数据稳定可靠,比差值和角差值都能满足系统检定误差要求,具有很高精确性。互感器校验仪自动检定系统可满足0.05级的检定精度要求,可以作为互感器校验仪的检定及溯源标准使用。
4 结论在互感器校验仪自动检定系统中,为了消除基波提取过程中非同步采样引起的频谱泄露和栅栏效应缺陷,采取基于自适应频率跟踪的基波提取算法来完成基波提取。仿真实验结果和检定系统的检定测试结果验证了该算法的有效性和实用性。
针对在互感器校验仪自动检定系统研发过程中所存在的部分不足,拟开展下一步研究:
1) 在选用基波提取算法方面是直接采用他人提出的有效算法,虽然通过仿真实验验证了该算法的有效性,但在频率缓变时对频率的跟踪效果仍有改进的空间。计划继续搜寻或设计更有效的基波提取算法。
2) 在频率缓变设置阶段,可考虑在频率非线性变化过程中进行频率跟踪实验。
| [1] |
包玉树, 陈威, 李军, 等.
全自动互感器校验仪整体检定系统设计及应用[J]. 电测与仪表, 2012, 49(7): 41–44.
BAO Yu-shu, CHEN Wei, LI Jun, et al. The design and application of automatic transformer calibrator overall test system[J]. Electrical Masurement & Instrumentation, 2012, 49(7): 41–44. |
| [2] |
朱枫, 陈跃东, 舒圣焱, 等.
基于FPGA的高精度正弦波信号源设计[J]. 井冈山大学学报(自然科学版), 2015, 36(1): 56–60.
ZHU Feng, CHEN Yue-dong, SHU Sheng-yan, et al. Design of high-accuracy sine wave signal generator based on FPGA[J]. Journal of Jinggangshan University (Natural Science), 2015, 36(1): 56–60. |
| [3] |
刘庆余.
互感器校验仪整体检定的述评(上)[J]. 电测与仪表, 2003, 40(3): 12–17.
LIU Qing-yu. Evaluation of whole certification of transformer calibrator[J]. Electrical Measurement& Instrumentation, 2003, 40(3): 12–17. |
| [4] |
李一泉, 何奔腾.
一种基于傅氏算法的高精度测频方法[J]. 中国电机工程学报, 2005, 26(2): 78–81.
LI Yi-quan, HE Ben-teng. A high-accuracy algorithm for measuring frequency of power system based on Fourier filter[J]. Proceedings of the CSEE, 2005, 26(2): 78–81. |
| [5] | MING Z, KAICHENG L, YISHENG H, et al. A high efficient compression method for power quality applications[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1976–1985. DOI:10.1109/TIM.2011.2115590 |
| [6] |
海志华, 张旭飞, 钱辉敏, 等.
基于DSP的三相组合互感器校验仪的设计[J]. 自动化与仪器仪表, 2015(1): 97–99.
HAI Zhi-hua, ZHANG Xu-fei, QIAN Hui-min, et al. Design of three-phase combined transformer verifier based on DSP[J]. Automation and Instrumentation, 2015(1): 97–99. |
| [7] | KARIMI-GHARTEMANI M, IRAVANI M R. A nonlinear adaptive filter for online signal analysis in power systems:applications[J]. IEEE Power & Energy Society, 2002, 22(1): 72. |
| [8] |
孙旭霞, 郭永胜.
基于小波-卡尔曼滤波的基波分量提取[J]. 电力系统及其自动化学报, 2012, 24(4): 93–99.
SUN Xu-xia, GUO Yong-sheng. Wavelet-based Kalman filter for fundamental component[J]. Proceedings of the CSU-EPSA, 2012, 24(4): 93–99. |
| [9] |
刘江锋. 基于DSP的互感器校验仪设计及实现[D]. 武汉: 武汉理工大学自动化学院, 2004: 46-47.
LIU Jiang-feng. Design and realization of transformer calibrator based on DSP[D]. Wuhan: Wuhan University of Technology, School of Automation, 2004: 46-47. |
| [10] |
吕思颖, 裴旵, 秦昕, 等.
基于小波多尺度分析和Kalman滤波的微机保护算法[J]. 电力系统保护与控制, 2015, 43(21): 54–59.
LÜ Si-ying, PEI Chan, QIN Xin, et al. Microprocessor-based protection algorithm based on wavelet multi-scale analysis and Kalman filter[J]. Power System Protection and Control, 2015, 43(21): 54–59. |
| [11] |
梅永, 王柏林.
降阶快速傅里叶变换算法在电力系统谐波分析中的应用[J]. 电网技术, 2010, 34(11): 117–120.
MEI Yong, WANG Bo-lin. Application of order-reducing Fourier transform algorithm in power system harmonics analysis[J]. Power System Technology, 2010, 34(11): 117–120. |
| [12] | BELEGA D, DALLET D, PETRI D. Statistical description of the sine-wave frequency estimator provided by the interpolated DFT method[J]. Measurement, 2012, 45(1): 109–117. DOI:10.1016/j.measurement.2011.09.010 |
| [13] |
卢珞先, 任立志, 张蓬鹤, 等.
电子式互感器校验仪的算法研究[J]. 电力系统保护与控制, 2009, 37(2): 58–64.
LU Luo-xian, REN Li-zhi, ZHANG Peng-he, et al. Research of arithmetic in electronic transformer calibrator[J]. Power System Protection and Control, 2009, 37(2): 58–64. DOI:10.7667/j.issn.1674-3415.2009.02.013 |
| [14] |
温和, 滕召胜, 黎福海, 等.
改进加窗频谱峰值拟合算法及谐波分析应用[J]. 电工技术学报, 2011, 26(10): 8–16.
WEN He, TENG Zhao-sheng, LI Fu-hai, et al. Improved windowed spectral-peaks polynomial fitting algorithm and its application in power harmonic analysis[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 8–16. |
| [15] |
温和, 滕召胜, 王永, 等.
改进加窗插值FFT动态谐波分析算法及应用[J]. 电工技术学报, 2012, 27(12): 270–278.
WEN He, TENG Zhao-sheng, WANG Yong, et al. Improved windowed interpolation FFT algorithm and application for power harmonic analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 270–278. |
| [16] |
张斌, 张东来.
电力系统自适应基波提取与频率跟踪算法[J]. 中国电机工程学报, 2011, 31(25): 81–89.
ZHANG Bin, ZHANG Dong-lai. Adaptive fundamental component extraction and frequency tracking algorithm for power systems[J]. Proceedings of the CSEE, 2011, 31(25): 81–89. |
| [17] | YU Sun-li, GU Jyh-cherng. Removal of decaying DC incurrent and voltage signals using a modified Fourier filter algorithm[J]. IEEE Transactions on Power Delivery, 2001, 16(3): 372–379. DOI:10.1109/61.924813 |
| [18] |
傅中君, 周根元, 陈鉴富, 等.
基于准同步DFT的非整数谐波分析算法[J]. 仪器仪表学报, 2012, 33(1): 235–240.
FU Zhong-jun, ZHOU Gen-yuan, CHEN Jian-fu, et al. Non-integral harmonic analysis algorithm based on quasi-synchronous DFT[J]. Chinese Journal of Scientific Instrument, 2012, 33(1): 235–240. |



