精度是反映机器人综合性能的一个重要指标,主要包括绝对定位精度和重复定位精度。通常,工业机器人的重复定位精度普遍较高,而绝对定位精度普遍较低。绝对定位精度低无法满足现代制造业的需求,这就要求机器人具有高精度、高通用性和高可靠性。因此提高工业机器人的绝对定位精度成为现代机器人技术发展中的一个重要课题。
机器人误差建模与分析、误差标定等是机器人精度研究的重要内容。Waldron和Kuman较早开展操作机器人位置误差的研究[1],随后该领域的研究得到迅速发展,其研究对象包括串联机器人和并联机器人[2-8]。影响机器人定位精度的因素为结构参数误差和关节运动参数误差。这些参数均具有随机性,为此学者提出了基于概率的机器人误差建模与分析,并开展机器人运动精度可靠性研究。如:Liu和Wang提出了采用可靠性方法评估机器人的运动精度[9],Bhatti开展了工业机器人的概率建模研究并提出了机器人运动精度可靠性概念[10],Rao和Bhatti提出了工业机器人运动与动力学概率建模方法并采用抽样方法研究了机器人的运动与动力可靠性[11],Zhu和Ting研究了考虑运动副间隙的机器人运动学建模并给出机器人末端执行器位姿参考点的概率密度函数[12],Kim等建立了包含构件尺寸公差和运动副间隙的机器人运动不确定性模型, 并基于改进的一次二阶矩方法(advanced first order and second moment, AFOSM)和蒙特卡洛方法(Monte Carlo simulation,MCS)实现了机器人的运动可靠性求解[13]。
现有研究多数讨论机器人在某瞬时的位姿可靠性,即点可靠性[14], 而很少针对机器人在整条运动轨迹上的累积失效或在指定运动区间上的可靠性即区间(时变)可靠性[14]进行研究。机器人在指定时间区间上的可靠度反映机器人在运动区间上的全局信息,即机器人运动的系统可靠性。Pandey和Zhang采用最大熵原理获得机器人位置误差的极值分布及其概率密度函数[15],进而开展机器人运动的系统可靠性分析,但该方法存在求解效率与求解精度的匹配问题。针对机构运动精度的区间(时变)可靠性,Zhang和Du基于均值穿越算法(mean value first-passage method)[14]、包络算法[16],进行平面连杆机构的运动时变(区间)可靠性分析[17-18]。本文借鉴平面连杆机构运动时变可靠性研究成果,采用包络方法开展机器人运动时变可靠性研究,并重点关注机器人末端执行器的位置精度。
1 机器人位姿误差模型的建立 1.1 机器人位姿描述机器人位姿误差建模的方法有很多, 如矩阵方法和矢量方法,近年来学者们针对并联机器人又提出旋量方法。矩阵方法是建立工业机器人位姿误差模型较为常用的方法,它在机器人微分运动的基础上,基于机器人运动学模型导出机器人位姿误差模型。基于机器人各关节D-H参数,相邻两个关节的变换矩阵Ai可以表示为:
| $ {\mathit{\boldsymbol{A}}_i} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\theta _i}}&{ - {\rm{s}}{\theta _i}{\rm{c}}{\alpha _i}}&{{\rm{s}}{\theta _i}{\rm{s}}{\alpha _i}}&{{a_i}{\rm{c}}{\theta _i}}\\ {{\rm{s}}{\theta _i}}&{{\rm{c}}{\theta _i}{\rm{c}}{\alpha _i}}&{ - {\rm{c}}{\theta _i}{\rm{s}}{\alpha _i}}&{{a_i}{\rm{s}}{\theta _i}}\\ 0&{{\rm{s}}{\alpha _i}}&{{\rm{c}}{\alpha _i}}&{{d_i}}\\ 0&0&0&1 \end{array}} \right] $ | (1) |
式中c和s分别代表cos和sin。
根据坐标变换,由n个连杆组成的机器人系统,其末端执行器参考点在基础坐标系中的位姿矩阵为:
| $ {\mathit{\boldsymbol{T}}_n} = \prod\limits_{i = 1}^n {{\mathit{\boldsymbol{A}}_i}} = \left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right] $ | (2) |
式(2)中,第4列前3个元素表示机器人手部位置,即:
| $ \mathit{\boldsymbol{p}} = {\left[ {{p_x},{p_y},{p_z}} \right]^{\rm{T}}} $ | (3) |
矩阵Tn中前3行3列的元素表示机器人手部姿态。机器人手部姿态有多种表示方法,如采用滚动角、俯仰角、偏航角或欧拉角(α,β,γ)等。
1.2 机器人位姿误差模型根据微分理论,变换矩阵Ai的微分为:
| $ {\rm{d}}{\mathit{\boldsymbol{A}}_i} = {\mathit{\boldsymbol{A}}_i} \cdot {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{A}}_i} $ | (4) |
式中δAi为Ai的误差矩阵,即:
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{A}}_i} = {\mathit{\boldsymbol{H}}_{ai}}\Delta {a_i} + {\mathit{\boldsymbol{H}}_{\alpha i}}\Delta {\alpha _i} + {\mathit{\boldsymbol{H}}_{di}}\Delta {d_i} + {\mathit{\boldsymbol{H}}_{\theta i}}\Delta {\theta _i} $ | (5) |
式中
将dAi代入式(2),经简化可以推导得到机器人末端相对于基坐标的微分变换dTn,即:
| $ {\rm{d}}{\mathit{\boldsymbol{T}}_n} = {\mathit{\boldsymbol{T}}_n} \cdot {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{T}}_n} $ | (6) |
式中δTn为Tn的误差矩阵,即:
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{T}}_n} = {\left( {\mathit{\boldsymbol{T}}_i^n} \right)^{ - 1}} \cdot {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{A}}_i} \cdot \mathit{\boldsymbol{T}}_i^n $ | (7) |
由此可以导出机器人的末端执行器位姿误差模型:
| $ \Delta \mathit{\boldsymbol{p}} = {\mathit{\boldsymbol{J}}_p}\Delta \mathit{\boldsymbol{X}} $ | (8) |
| $ \Delta \delta = {\mathit{\boldsymbol{J}}_\delta }\Delta \mathit{\boldsymbol{X}} $ | (9) |
式中:Δp,Δδ分别表示机器人末端执行器位置误差和姿态误差向量,ΔX=(Δθ, Δd, Δa, Δα)T为机器人各关节参数的误差。
2 机器人的运动可靠性分析 2.1 运动可靠性模型机器人连杆的加工误差、温度变化以及机械传动误差等诸多因素会导致机器人各组成连杆的运动变量和结构参数产生误差,这些误差均具有随机性。假定机器人各关节D-H参数X服从正态分布,即X~(μX,σX2)。现根据式(8)讨论机器人末端执行器的运动可靠性。
假定在t时刻,机器人末端期望位置矢量为pd,实际到达位置为p,则机器人末端执行器运动的位置误差可表示为:
| $ \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right) = \mathit{\boldsymbol{p}} - {\mathit{\boldsymbol{p}}^{\rm{d}}} $ | (10) |
根据式(8),式(10)可表示为:
| $ \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right) = \Delta \mathit{\boldsymbol{p}} = {\mathit{\boldsymbol{J}}_p}\Delta \mathit{\boldsymbol{X}} $ | (11) |
考虑X为服从正态分布的随机变量,则有:
| $ \Delta \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{X}} - \mu = \sigma \mathit{\boldsymbol{U}} $ | (12) |
式中U=(U1, U2,…,Un),其中Ui~(0,12),n为机器人D-H参数的个数。
将式(12)代入式(11),得到:
| $ \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right) = {\mathit{\boldsymbol{J}}_p}\sigma \mathit{\boldsymbol{U}} $ | (13) |
设机器人末端执行器的位置允许误差限为ε,则有:
| $ \left| {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right)} \right| \le \varepsilon $ | (14) |
式中ε表示机器人末端执行器在三维坐标分量上的位置允许误差限矢量。
1) 点可靠性模型。
根据式(14),以机器人全部关节是转动关节为例,机器人末端执行器在t时刻的运动精度可靠性模型为:
| $ \mathit{\boldsymbol{R}}\left( t \right) = \Pr \left\{ {\left| {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right)} \right| \le \varepsilon } \right\} $ | (15) |
对应的失效概率为:
| $ {\mathit{\boldsymbol{p}}^{\rm{f}}}\left( t \right) = \Pr \left\{ {\left| {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right)} \right| > \varepsilon } \right\} $ | (16) |
式中R(t)=(Rx(t), Ry(t), Rz(t)),即在某指定位置处3个坐标分量上的运动精度可靠性。
2) 各坐标分量上的时变可靠性模型。
当机器人末端执行器参考点按连续轨迹运动时,若能获得机器人在整条轨迹上的运动可靠性则更具有价值。为此,需对式(15)给出的可靠性模型进行修正,假定机器人的运动时间区间为[ts, te], 则:
| $ \mathit{\boldsymbol{R}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \Pr \left\{ {\left| {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right)} \right| \le \varepsilon ,\forall t \in \left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right\} $ | (17) |
对应的失效概率为:
| $ {\mathit{\boldsymbol{p}}^{\rm{f}}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \Pr \left\{ {\left| {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}},t} \right)} \right| > \varepsilon ,\exists t \in \left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right\} $ | (18) |
式中:
| $ \mathit{\boldsymbol{R}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \left( {{R_x}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right),{R_y}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right),{R_z}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right) $ |
| $ {\mathit{\boldsymbol{p}}^{\rm{f}}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \left( {{p^{{\rm{f}}x}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right),{p^{{\rm{f}}y}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right),{p^{{\rm{f}}z}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right) $ |
3) 系统的运动时变可靠性模型。
式(17)和(18)描述了机器人在运动时间区间(ts, te)上的可靠性和失效概率,可称之为区间可靠性或者运动时变可靠性,该可靠性模型更能反映机器人跟踪一条轨迹的精度。而式(17)和(18)仅给出了机器人在各坐标分量上的运动时变可靠度。在上述分析的基础上,定义机器人在整条轨迹上运动的系统可靠性模型为:
| $ {R_{{\rm{sys}}}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \Pr \left\{ {\bigcap\limits_{k = 1}^3 {\left| {{g^k}\left( {\mathit{\boldsymbol{X}},t} \right)} \right|} \le {\varepsilon _k},\forall t \in \left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right\} $ | (19) |
对应的失效概率为:
| $ {p^{{\rm{f}},{\rm{sys}}}}\left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right) = \Pr \left\{ {\bigcup\limits_{k = 1}^3 {\left| {{g^k}\left( {\mathit{\boldsymbol{X}},t} \right)} \right|} > {\varepsilon _k},\exists t \in \left( {{t_{\rm{s}}},{t_{\rm{e}}}} \right)} \right\} $ | (20) |
由式(15)或(16)给出的可靠性模型,可以采用一次二阶矩方法(first order and second moment,FOSM)求解,即:
| $ R = 2\mathit{\Phi }\left( {\frac{{\varepsilon - {\mu _{\rm{g}}}\left( X \right)}}{{{\sigma _{\rm{g}}}\left( X \right)}}} \right) - 1 $ | (21) |
而由式(17)至(20)给出的可靠性模型,则需要应用随机过程理论进行处理。借鉴平面连杆机构运动时变可靠性的研究成果,采用包络方法完成机器人位置精度的时变可靠性分析。
包络方法的实质是将随机过程问题转化为随机变量问题求解[16],其核心在于求解随机过程的包络函数。一旦找到包络点,则与时间相关的可靠性问题就可转化为与时间无关的可靠性问题,具体方法详见文献[16]。包络方法的主要工作在于寻找生成包络函数的包络点ti(i=1, 2, …, p),获得ti后进一步求解这些包络点的联合概率分布密度,并采用多变量正态分布联合分布函数求解可靠度[16],即:
| $ \begin{array}{l} R = \int_0^\varepsilon {\frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{r/2}}{{\left| \Sigma \right|}^{1/2}}}}} \\ \;\;\;\;\;\;\exp \left[ { - \frac{1}{2}\left( {\mathit{\boldsymbol{L}} - {\mu _L}} \right)\sum {^{ - 1}{{\left( {\mathit{\boldsymbol{L}} - {\mu _L}} \right)}^{\rm{T}}}} } \right]{\rm{d}}\mathit{\boldsymbol{L}} \end{array} $ | (22) |
对应的失效概率为:
| $ {p_{\rm{f}}} = 2 \times \left[ {1 - R} \right] $ | (23) |
以斯坦福机器人为例,该机器人具有6个自由度,除第3个关节为移动关节外,其余关节均为旋转关节。现根据文献[3]给出的机器人关节运动规律来研究机器人的运动可靠性。各旋转关节θi的运动规律为:
| $ {\theta _i} = \left\{ \begin{array}{l} \frac{{\rm{ \mathsf{ π} }}}{6}\left[ {\frac{{2t}}{T} - \sin \left( {\frac{{4{\rm{ \mathsf{ π} }}t}}{T}} \right)/2{\rm{ \mathsf{ π} }}} \right],\;\;\;\;\;\;\;\;0 \le t \le \frac{T}{2}\\ \frac{{\rm{ \mathsf{ π} }}}{6}\left[ {2 - \frac{{2t}}{T} + \sin \left( {\frac{{4{\rm{ \mathsf{ π} }}t}}{T}} \right)/2{\rm{ \mathsf{ π} }}} \right],\;\;\;\frac{T}{2} < t \end{array} \right. $ | (24) |
移动关节d3的运动规律为:
| $ {d_3} = \left\{ \begin{array}{l} 50\left[ {1 - \cos \left( {\frac{{2{\rm{ \mathsf{ π} }}t}}{T}} \right)} \right]{\rm{mm}},\;\;\;\;\;\;0 \le t \le \frac{T}{2}\\ 100{\rm{mm}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{T}{2} < t \end{array} \right. $ | (25) |
在式(24)和(25)中,T为转动关节运动周期, 取2.5 s。机器人连杆为刚性杆,忽略其挠性变形对误差的影响。机器人各关节D-H参数X服从正态分布,其分布参数(均值和标准差)如表 1所示。取机器人末端执行器的位置允许误差限ε=(0.5,0.5,0.5)。
| n | 关节类型 | μθ/(°) | σθ/(°) | μd/mm | σd/mm | μa/mm | σa/mm | μα/(°) | σα/(°) |
| 1 | 旋转 | θ1 | 0.5 | 120 | 0.05 | 0 | 0.05 | -90 | 0.5 |
| 2 | 旋转 | θ2 | 0.5 | 162 | 0.05 | 0 | 0.05 | 90 | 0.5 |
| 3 | 移动 | -90 | 0.5 | d3 | 0.05 | 0 | 0.05 | 0 | 0.5 |
| 4 | 旋转 | θ4 | 0.5 | 0 | 0.05 | 0 | 0.05 | -90 | 0.5 |
| 5 | 旋转 | θ5 | 0.5 | 0 | 0.05 | 0 | 0.05 | 90 | 0.5 |
| 6 | 旋转 | θ6 | 0.5 | 247.6 | 0.05 | 0 | 0.05 | 0 | 0.5 |
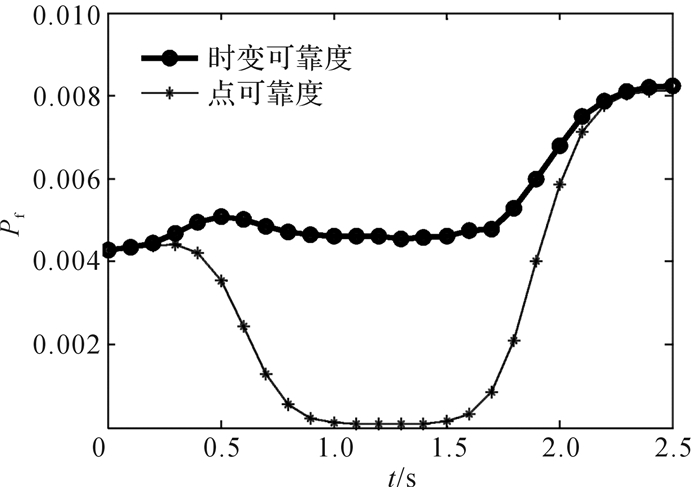
根据前述式(15)至(18),应用式(21)求解该机器人末端执行器参考点位置在x,y,z方向上的点失效概率,应用式(22),(23)求解该机器人末端执行器参考点位置在x,y,z方向上的时变失效概率,如图 1至图 3所示。
|
| 图 1 机器人x向的运动失效概率 Fig.1 Kinematic failure probability of robot manipulator in the x direction |
|
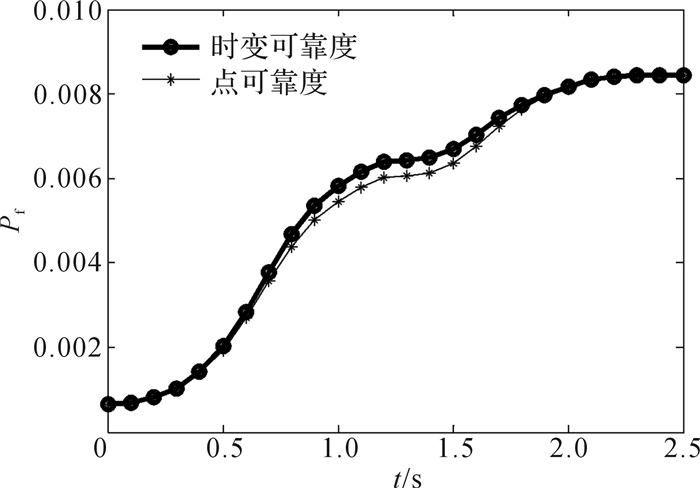
| 图 2 机器人y向的运动失效概率 Fig.2 Kinematic failure probability of robot manipulator in the y direction |
|
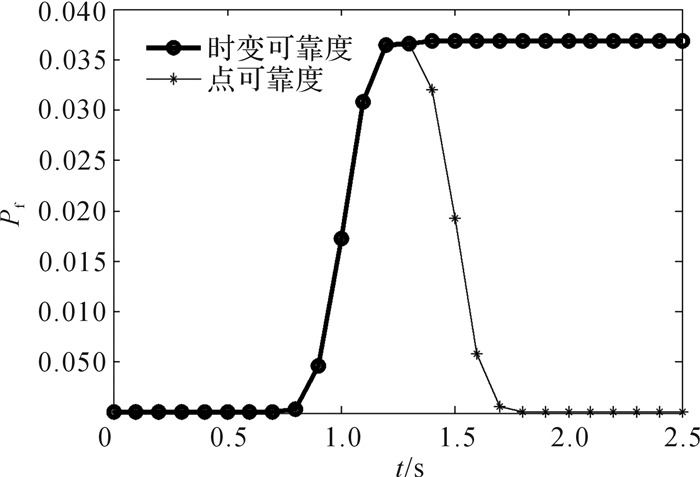
| 图 3 机器人z向的运动失效概率 Fig.3 Kinematic failure probability of robot manipulator in the z direction |
由图可以看出,机器人的点可靠度上下波动、有增有减,说明在不同时间点处,机器人的结构参数和运动参数对其运动精度影响程度不同。机器人的时变可靠度基本为不减函数(图 1中曲线出现波动是受所采用可靠度求解算法的精度和求解原理影响),在运动时间终点处最大,它反映了机器人在整个运动时间区间上的累积效应。比较机器人在x,y,z方向上的点失效概率可知,其在x,y方向的最大失效概率比z方向大;同时比较机器人在整个运动区间上的时变失效概率也可得到,其在x,y方向的时变失效概率比z方向大。由此可以得出结论,该机器人在前述假定关节运动规律下,其x,y方向的运动精度比z方向的低。
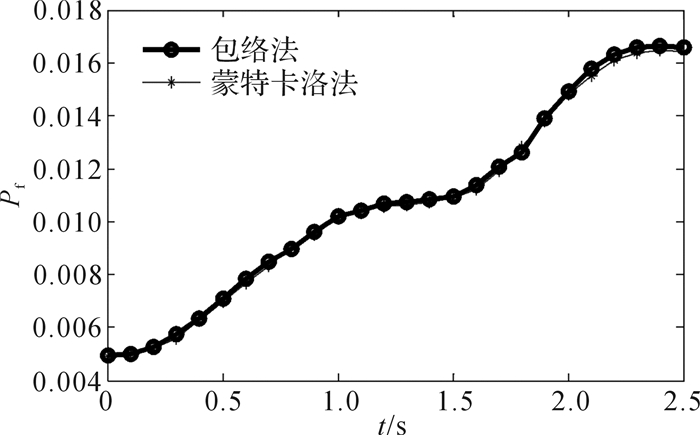
3.2 机器人系统可靠性分析为考察机器人在整个时间区间上的运动可靠度,根据式(19)和(20),应用式(22)和(23)求解该机器人系统可靠度即时变失效概率,如图 4所示。同时采用蒙特卡洛方法(MCS)验证方法的有效性,仿真次数N=106。从图 4中可以看出,采用文中提出的系统可靠性模型和求解算法得到的机器人系统可靠度与蒙特卡洛方法仿真结果非常接近,说明本文所提出方法具有较高的精度。采用包络方法求解系统可靠性模型避免了求解采用MCS仿真获得运动误差所用到的概率密度函数,因此与文献[15]相比,本文方法的计算量小。
|
| 图 4 机器人的系统失效概率 Fig.4 System failure probability of robot manipulator |
机器人在智能制造领域具有重要地位,高精度、高可靠性的智能机器人研发是一个重要课题。本文从提高机器人运动精度的角度出发,开展了机器人的运动不确定性建模、运动可靠性分析,提出了机器人时变(区间)运动可靠性模型及机器人运动的系统可靠性模型,在此基础上采用包络方法实现机器人时变(区间)可靠性求解和系统可靠性分析。
数值实例表明:1)时变(区间)可靠性能够反映机器人在整个运动时间区间内的累积效应,用时变(区间)可靠度衡量机器人绝对定位精度比用传统的点(静态)可靠度更为有效;2)基于时变(区间)可靠性模型而提出的机器人运动的系统可靠性模型及所采用的包络方法是有效的,该方法具有较高的求解精度,且由于所采用的求解算法避免了求解采用MCS仿真获得运动误差所用到的概率密度函数,因此该方法具有较小的计算量。
机器人系统中,影响其运动精度的不确定性因素众多,如制造公差、运动副间隙、构件弹性变形以及驱动器输入误差等。文中仅讨论了制造公差和驱动器输入误差的影响,而对于工业机器人而言,运动副间隙、构件弹性变形更是不可忽略因素,因此今后将重点研究,综合考虑前述不确定性作用下的机器人的运动可靠性。此外,本文仅考虑了机器人末端执行器的位置误差,今后还应将机器人的姿态误差和位置误差融为一体,开展机器人在不确定性下的轨迹规划研究。
| [1] | WALDRON K J, KUMAR A. Development of a theory of errors for manipulators[C]//Proceedings of the Fifth World Congress on the Theory of Machines and Mechanisms, Montreal, Canada: American Society of Mechanical Engineers, 1979: 821-826. |
| [2] |
徐卫良.
机器人机构误差建模的摄动法[J]. 机器人, 1989, 3(6): 39–44.
XU Wei-liang. A perturbation approach to error modeling of robot linkage[J]. Robot, 1989, 3(6): 39–44. |
| [3] |
焦国太. 机器人位姿误差的分析与综合[D]. 北京: 北京工业大学机械工程与应用电子技术学院, 2002: 7-12.
JIAO Guo-tai. Analysis and synthesis of robot pose errors[D]. Beijing: Beijing University of Technology, College of Mechanical Engineering and Applied Electronics Technology, 2002: 7-12. |
| [4] |
卫玉昆, 焦国太.
基于MATLAB的柔性机械臂动力学分析[J]. 机械工程与自动化, 2016(1): 33–36.
WEI Yu-kun, JIAO Guo-tai. Flexible robot arm dynamics analysis based on MATLAB[J]. Mechanical Engineering & Automation, 2016(1): 33–36. |
| [5] |
陈明哲, 张启先.
工业机器人误差分析[J]. 北京航空学院学报, 1984(2): 11–22.
CHEN Ming-zhe, ZHANG Qi-xian. Error analyses of the industrial robots[J]. Journal of Beijing Institute of Aeronautics and Astronautics, 1984(2): 11–22. |
| [6] | PEDRAMMEHR S, QAZANI M, ABDI H, et al. Mathematical modelling of linear motion error for Hexarot parallel manipulators[J]. Applied Mathematical Modelling, 2016, 40(2): 942–954. DOI:10.1016/j.apm.2015.07.004 |
| [7] | CHEN Gen-liang, WANG Hao, LIN Zhong-qin. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance[J]. Mechanism and Machine Theory, 2013, 64(6): 1–17. |
| [8] | FRISOLI A, SOLAZZI M, PELLEGRINETTI D, et al. A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances[J]. Mechanism and Machine Theory, 2011, 46(12): 1929–1949. DOI:10.1016/j.mechmachtheory.2011.07.004 |
| [9] | LIU T S, WANG J D. A reliability approach to evaluating robot accuracy performance[J]. Mechanism and Machine Theory, 1994, 29(1): 83–94. DOI:10.1016/0094-114X(94)90022-1 |
| [10] | BHATTI P K. Probabilistic modeling and optimal design of robotic manipulators[D]. West Lafayette: Purdue University, Department of Mechanical and Aerospace Engineering, 1989: 8-16. |
| [11] | RAO S S, BHATTI P K. Probabilistic approach to manipulator kinematics and dynamics[J]. Reliability Engineering and System Safety, 2001, 72(1): 47–58. DOI:10.1016/S0951-8320(00)00106-X |
| [12] | ZHU J, TING K L. Uncertainty analysis of planar and spatial robots with joint clearances[J]. Mechanism and Machine Theory, 2000, 35(9): 1239–1256. DOI:10.1016/S0094-114X(99)00076-2 |
| [13] | KIM J, SONG W J, KANG B S. Stochastic approach to kinematic reliability of open-loop mechanism with dimensional tolerance[J]. Applied Mathematical Modelling, 2010, 34(5): 1225–1237. DOI:10.1016/j.apm.2009.08.009 |
| [14] | ZHANG Jun-fu, DU Xiao-ping. Time-dependent reliability analysis for function generator mechanisms[J]. Journal of Mechanical Design, 2011, 133(3): 031005. DOI:10.1115/1.4003539 |
| [15] | PANDEY M D, ZHANG X. System reliability analysis of the robotic manipulator with random joint clearances[J]. Mechanism and Machine Theory, 2012, 58(3): 137–152. |
| [16] | DU Xiao-ping. Time-dependent mechanism reliability analysis with envelope functions and first-order approximation[J]. Journal of Mechanical Design, 2014, 136(8): 081010. DOI:10.1115/1.4027636 |
| [17] | ZHANG Jun-fu, WANG Jing-ge, DU Xiao-ping, et al. Time-dependent probabilistic synthesis for function generator mechanisms[J]. Mechanism & Machine Theory, 2011, 46(9): 1236–1250. |
| [18] | ZHANG Jun-fu, DU Xiao-ping. Time-dependent reliability analysis for function generation mechanisms with random joint clearances[J]. Mechanism and Machine Theory, 2015, 92: 184–199. DOI:10.1016/j.mechmachtheory.2015.04.020 |



