机械臂定位精度是衡量其工作性能的一个重要指标,目前,国内外厂家生产的机械臂由于制造和安装精度等限制,大多数的绝对定位精度不高,无法满足高精加工以及离线编程的需要。因此,需对引起机械臂定位误差的各种因素进行分析,最大可能地提高机械臂绝对定位精度已经成为机器人技术研究中的核心内容[1]。
Judd等的标定实验研究表明,运动学参数误差对机械臂定位精度的影响占90%左右[2]。目前,国内外常用的机械臂运动学标定方法通常需要借助外界先进的测量设备[3-9],成本高,且测量过程复杂,需要专业人员进行操作。为了降低成本,许多研究学者提出了闭环标定法(自标定),通过施加物理约束(如点、线、面等),限制机器人末端执行器的运行空间[10-15],从各个关节编码器中获得关节角度并通过正运动学得到末端位姿。为了提高标定精度,往往需要得到上百个约束点信息甚至更多,然而,在对这些物理约束进行接触式测量时,采用的是人工手动示教方式,因此测量过程费时费力,效率很低。
针对上述情况,本文在一般平面约束的基础上,提出一种基于双目视觉辅助定位约束平面的机械臂运动学参数辨识方法,以期在保证标定精度的基础上,实现数据的自动化测量。采用的方法是:将一对摄像头安装在机械臂末端法兰,分别对左右两相机采集到的图像进行处理,提取目标点信息并进行立体匹配,最终得到约束平面在机械臂基坐标系下的三维位置信息,并在平面上规划出按一定规律分布的约束点,机械臂对这些约束点依次自动进行接触式测量并记录对应的关节角数据,最终辨识出机械臂运动学参数误差。
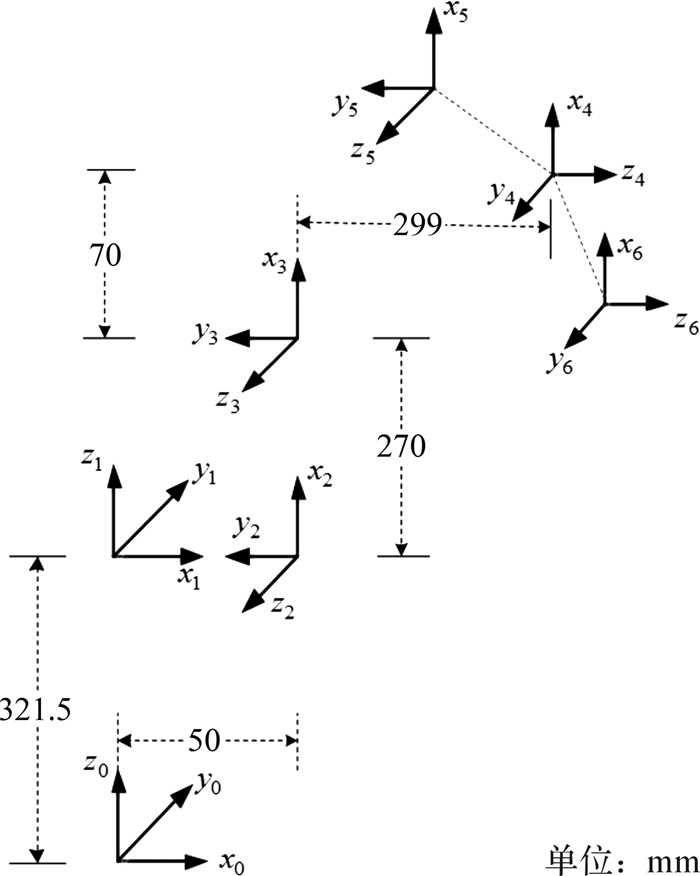
1 机械臂运动学 1.1 运动学模型要建立机械臂运动学模型,首先要确定连杆坐标系。目前,常用的连杆坐标系建立方法有2种[16]:Paul法(标准D-H)和Craig法(改进D-H),都是在Denavit和Hartenberg[17]提出的连杆参数基础上提出或改进的,前者将坐标系建立在连杆的首端,而后者建立在连杆末端。本文使用Craig法,建立的连杆坐标系如图 1,对象为6R型串联工业机械臂。
|
| 图 1 6R型串联工业机械臂连杆坐标系 Fig.1 Link coordinate frames of 6R serial industrial robot arm |
相邻两连杆坐标系{i-1}到{i}的齐次坐标变换矩阵Ai可由4个连杆参数描述,如公式(1):
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_i} = {\rm{Rot}}\left( {{x_{i - 1}},{\alpha _{i - 1}}} \right){\rm{Trans}}\left( {{a_{i - 1}},0,{d_i}} \right){\rm{Rot}}\left( {{z_{i - 1}},{\theta _i}} \right) = \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} {c{\theta _i}}&{ - s{\theta _i}}&0&{{a_{i - 1}}}\\ {s{\theta _i}c{\alpha _{i - 1}}}&{c{\theta _i}c{\alpha _{i - 1}}}&{ - s{\alpha _{i - 1}}}&{ - {d_i}s{\alpha _{i - 1}}}\\ {s{\theta _i}s{\alpha _{i - 1}}}&{c{\theta _i}s{\alpha _{i - 1}}}&{c{\alpha _{i - 1}}}&{{d_i}c{\alpha _{i - 1}}}\\ 0&0&0&1 \end{array}} \right] \end{array} $ | (1) |
式中:ai-1是zi-1沿xi-1方向平移至zi的距离,αi-1是zi-1绕xi-1轴旋转至zi的角度,di是xi-1沿zi或zi-1(此时zi与zi-1重合)平移至xi的距离,θi是xi-1绕zi或zi-1旋转至xi的角度,i=1,2,…,6,si表示sinθi,ci表示cosθi,后面公式一律采用此约定。
需要注意的是,由于矩阵乘法一般不满足交换律,当用Craig法建立坐标系时,必须先关于x轴变换,再关于z轴变换,与Paul法变换顺序相反。因此2种方法对应的中间转换矩阵是完全不同的,不能混用[16]。
对于机械臂标定研究,各连杆之间不能视作完全平行或垂直,因此相关名义参数值存在微小偏差,当相邻关节轴线近似平行(关节2, 3)时,微小的不平行度会引起参数突变,公式(1)所表示的四参数模型不再适用,需要增加绕y轴旋转的参数β才能准确描述Ai(i=3),基于上述Craig法所建立的连杆坐标系,改进后的D-H模型表示如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_i} = {\rm{Rot}}\left( {{x_{i - 1}},{\alpha _{i - 1}}} \right){\rm{Trans}}\left( {{a_{i - 1}},0,0} \right){\rm{Rot}}\left( {{y_{i - 1}},\beta } \right) \times \\ \;\;\;\;\;\;\;{\rm{Trans}}\left( {0,0,{d_i}} \right){\rm{Rot}}\left( {{z_{i - 1}},{\theta _i}} \right),i = 3 \end{array} $ | (2) |
末端工具坐标系相对于机械臂六轴坐标系的位姿矩阵A7为:
| $ {\mathit{\boldsymbol{A}}_7} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&\mathit{\boldsymbol{t}}\\ 0&1 \end{array}} \right] $ |
其中:I为单位阵, t=[tx ty tz]T。
那么,机械臂末端工具坐标系相对于基坐标系的位姿矩阵TT为:
| $ {\mathit{\boldsymbol{T}}_{\rm{T}}} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2} \cdots {\mathit{\boldsymbol{A}}_7} $ |
将各种因素的影响全都归结为机械臂运动学参数误差,建立末端位姿误差与各连杆几何参数误差之间的关系模型。由于θi, αi, di, ai, β均存在误差,那么Ai也存在误差,按照微分变换的思想对Ai进行全微分,得到由连杆几何参数误差造成的相邻坐标系间的微分摄动齐次矩阵dAi:
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{A}}_i} = \frac{{\partial {\mathit{\boldsymbol{A}}_i}}}{{\partial {\alpha _{i - 1}}}}\Delta {\alpha _{i - 1}} + \frac{{\partial {\mathit{\boldsymbol{A}}_i}}}{{\partial {\alpha _{i - 1}}}}\Delta {\alpha _{i - 1}} + \frac{{\partial {\mathit{\boldsymbol{A}}_i}}}{{\partial {\theta _i}}}\Delta {\theta _i} + \\ \;\;\;\;\;\;\;\;\frac{{\partial {\mathit{\boldsymbol{A}}_i}}}{{\partial {d_i}}}\Delta {d_i} + \frac{{\partial {\mathit{\boldsymbol{A}}_i}}}{{\partial \beta }}\Delta \beta \end{array} $ | (3) |
令
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{A}}_i} = {\mathit{\boldsymbol{A}}_i}\left( {{\mathit{\boldsymbol{B}}_{{\alpha _{i - 1}}}}\Delta {\alpha _{i - 1}} + {\mathit{\boldsymbol{B}}_{{\alpha _{i - 1}}}}\Delta {\alpha _{i - 1}} + {\mathit{\boldsymbol{B}}_{{\theta _i}}}\Delta {\theta _i} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{B}}_{{d_i}}}\Delta {d_i} + {\mathit{\boldsymbol{B}}_\beta }\Delta \beta } \right) = {\mathit{\boldsymbol{A}}_i}\delta {\mathit{\boldsymbol{A}}_i} \end{array} $ | (4) |
同理:
| $ {\rm{d}}{\mathit{\boldsymbol{A}}_7} = \frac{{\partial {\mathit{\boldsymbol{A}}_7}}}{{\partial {t_x}}}\Delta {t_x} + \frac{{\partial {\mathit{\boldsymbol{A}}_7}}}{{\partial {t_y}}}\Delta {t_y} + \frac{{\partial {\mathit{\boldsymbol{A}}_7}}}{{\partial {t_z}}}\Delta {t_z} = {\mathit{\boldsymbol{A}}_7}\delta {\mathit{\boldsymbol{A}}_7} $ |
那么机械臂末端工具坐标系相对于基坐标系的实际齐次变换矩阵TR为:
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_{\rm{R}}} = {\mathit{\boldsymbol{T}}_{\rm{T}}} + {\rm{d}}{\mathit{\boldsymbol{T}}_{\rm{T}}} = \prod\limits_{i = 1}^7 {\left( {{\mathit{\boldsymbol{A}}_i} + {\rm{d}}{\mathit{\boldsymbol{A}}_i}} \right)} = \prod\limits_{i = 1}^7 {\left( {{\mathit{\boldsymbol{A}}_i} + {\mathit{\boldsymbol{A}}_i}\delta {\mathit{\boldsymbol{A}}_i}} \right)} = \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{T}}_{\rm{T}}} + {\mathit{\boldsymbol{T}}_{\rm{T}}}\delta {\mathit{\boldsymbol{A}}_7} + \sum\limits_{i = 1}^6 {{\mathit{\boldsymbol{T}}_{\rm{T}}}{{\left( {{\mathit{\boldsymbol{A}}_{i + 1}} \cdots {\mathit{\boldsymbol{A}}_7}} \right)}^{ - 1}}} \\ \;\;\;\;\;\;\;\delta {\mathit{\boldsymbol{A}}_i}\left( {{\mathit{\boldsymbol{A}}_{i + 1}} \cdots {\mathit{\boldsymbol{A}}_7}} \right) \end{array} $ | (5) |
将式(5)展开,并略去高阶摄动项,化简后得到式(6),其中,ΔP=[dPx dPy dPz]T是机器人位置误差矩阵,J为3×28阶连杆参数的微分变换雅可比矩阵,ΔX=[Δα Δa Δθ Δd Δβ Δt]T为28×1阶连杆参数误差矩阵,即需要辨识的所有参数。
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{P = }}\left[ {\begin{array}{*{20}{c}} {{\rm{d}}{P_x}}\\ {{\rm{d}}{P_y}}\\ {{\rm{d}}{P_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{J_{{\alpha _x}}}}&{{J_{{a_x}}}}&{{J_{{\theta _x}}}}&{{J_{{d_x}}}}&{{J_{{\beta _x}}}}&{{J_{{t_x}}}}\\ {{J_{{\alpha _y}}}}&{{J_{{a_y}}}}&{{J_{{\theta _y}}}}&{{J_{{d_y}}}}&{{J_{{\beta _y}}}}&{{J_{{t_y}}}}\\ {{J_{{\alpha _z}}}}&{{J_{{a_z}}}}&{{J_{{\theta _z}}}}&{{J_{{d_z}}}}&{{J_{{\beta _z}}}}&{{J_{{t_z}}}} \end{array}} \right]\\ \;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\Delta \alpha }\\ {\Delta a}\\ {\Delta \theta }\\ {\Delta d}\\ {\Delta \beta }\\ {\Delta t} \end{array}} \right] = \mathit{\boldsymbol{J}}\Delta \mathit{\boldsymbol{X}} \end{array} $ | (6) |
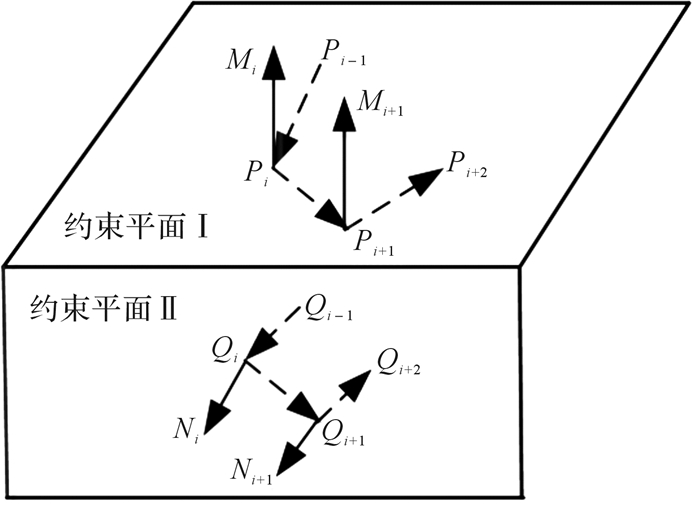
设Pi为约束平面Ⅰ上第i个接触点,Qi为约束平面Ⅱ上的第i个接触点,两约束平面相互垂直,如图 2所示。
|
| 图 2 双平面约束误差模型建立条件 Fig.2 Building conditions of two perpendicular planes constraint error model |
名义位置PiN=
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{P}}_i^{\rm{R}} = \mathit{\boldsymbol{P}}_i^{\rm{R}} - \mathit{\boldsymbol{P}}_{i - 1}^{\rm{R}} = {{\left[ {\begin{array}{*{20}{c}} {\Delta x_{pi}^{\rm{N}}}&{\Delta y_{pi}^{\rm{N}}}&{\Delta z_{pi}^{\rm{N}}} \end{array}} \right]}^{\rm{T}}} + }\\ {\Delta {\mathit{\boldsymbol{J}}_{pi}}\Delta \mathit{\boldsymbol{X}}} \end{array} $ | (7) |
其中:
同理可得:
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{P}}_{i + 1}^{\rm{R}} = \mathit{\boldsymbol{P}}_{i + 1}^{\rm{R}} - \mathit{\boldsymbol{P}}_i^{\rm{R}} = {{\left[ {\begin{array}{*{20}{c}} {\Delta x_{pi + 1}^{\rm{N}}}&{\Delta y_{pi + 1}^{\rm{N}}}&{\Delta z_{pi + 1}^{\rm{N}}} \end{array}} \right]}^{\rm{T}}} + }\\ {\Delta {\mathit{\boldsymbol{J}}_{pi + 1}}\Delta \mathit{\boldsymbol{X}}} \end{array} $ | (8) |
那么由相邻的2个偏差向量可构建一垂直于平面的名义法向量:
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_i} = \Delta \mathit{\boldsymbol{P}}_i^{\rm{R}} \times \Delta \mathit{\boldsymbol{P}}_{i + 1}^{\rm{R}} = {\left[ {\begin{array}{*{20}{c}} {n_{pi}^x}&{n_{pi}^y}&{n_{pi}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {J_{pi}^x}&{J_{pi}^y}&{J_{pi}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} \end{array} $ | (9) |
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_{i + 1}} = \Delta \mathit{\boldsymbol{P}}_{i + 1}^{\rm{R}} \times \Delta \mathit{\boldsymbol{P}}_{i + 2}^{\rm{R}} = {\left[ {\begin{array}{*{20}{c}} {n_{pi + 1}^x}&{n_{pi + 1}^y}&{n_{pi + 1}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {J_{pi}^x}&{J_{pi}^y}&{J_{pi}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} \end{array} $ | (10) |
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_i} \times {\mathit{\boldsymbol{M}}_{i + 1}} = {\left[ {\begin{array}{*{20}{c}} {s_{pi}^x}&{s_{pi}^y}&{s_{pi}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {h_{pi}^x}&{h_{pi}^y}&{h_{pi}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} = 0 \end{array} $ | (11) |
由式(11)辨识出的机械臂运动学参数误差ΔX,是根据单个约束平面Ⅰ上相关点之间的关系计算得到的,因此,若将它修正到控制器中,通过更新的正运动学模型得到的机械臂末端位置点所拟合得到的平面与实际约束平面的偏差较大[18]。
因此,增加一约束平面Ⅱ,与平面Ⅰ相垂直,两平面在保证自身平面度的同时,还需要满足互相垂直关系,相当于多了一个约束条件,减小了实际平面与理论拟合平面之间的偏差。
对于约束平面Ⅱ,QiN=
| $ \begin{array}{l} {\mathit{\boldsymbol{N}}_i} = \Delta \mathit{\boldsymbol{Q}}_i^{\rm{R}} \times \Delta \mathit{\boldsymbol{Q}}_{i + 1}^{\rm{R}} = {\left[ {\begin{array}{*{20}{c}} {n_{qi}^x}&{n_{qi}^y}&{n_{qi}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {J_{qi}^x}&{J_{qi}^y}&{J_{qi}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} \end{array} $ | (12) |
| $ \begin{array}{l} {\mathit{\boldsymbol{N}}_{i + 1}} = \Delta \mathit{\boldsymbol{Q}}_{i + 1}^{\rm{R}} \times \Delta \mathit{\boldsymbol{Q}}_{i + 2}^{\rm{R}} = {\left[ {\begin{array}{*{20}{c}} {n_{qi + 1}^x}&{n_{qi + 1}^y}&{n_{qi + 1}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {J_{qi + 1}^x}&{J_{qi + 1}^y}&{J_{qi + 1}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} \end{array} $ | (13) |
Ni和Ni+1都是垂直于平面Ⅱ的法向量,满足以下条件:
| $ \begin{array}{l} {\mathit{\boldsymbol{N}}_i} \times {\mathit{\boldsymbol{N}}_{i + 1}} = {\left[ {\begin{array}{*{20}{c}} {s_{qi}^x}&{s_{qi}^y}&{s_{qi}^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {h_{qi}^x}&{h_{qi}^y}&{h_{qi}^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} = 0 \end{array} $ | (14) |
对于满足垂直关系的约束平面Ⅰ和Ⅱ,各法向量满足以下条件:
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_i} \times {\mathit{\boldsymbol{N}}_i} = {\left[ {\begin{array}{*{20}{c}} {s_i^x}&{s_i^y}&{s_i^z} \end{array}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {h_i^x}&{h_i^y}&{h_i^z} \end{array}} \right]^{\rm{T}}}\Delta \mathit{\boldsymbol{X}} = 0 \end{array} $ | (15) |
若在两平面上各采集N+3个点,且连续相邻的3个点不能共线:P0, P1, …, PN+2,Q0, Q1, …, QN+2,联立式(11)、(14)和(15),得到最终的双平面约束误差模型如下:
| $ \mathit{\boldsymbol{H}}\Delta \mathit{\boldsymbol{X}} + \mathit{\boldsymbol{S}} = 0 $ | (16) |
其中:
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \left[ {h_{p1}^x\;\;h_{p1}^y\;\;h_{p1}^z\;\;h_{q1}^x\;\;h_{q1}^y\;\;h_{q1}^z\;\;h_1^x\;\;h_1^y\;\;h_1^z \cdots } \right.\\ \;\;\;\;\;\;\;{\left. {h_N^x\;\;h_N^y\;\;h_N^z\;\;h_{pN}^x\;\;h_{pN}^y\;\;h_{pN}^z\;\;h_{qN}^x\;\;h_{qN}^y\;\;h_{qN}^z} \right]^{\rm{T}}} \end{array} $ |
| $ \begin{array}{l} \mathit{\boldsymbol{S}} = \left[ {s_{p1}^x\;\;s_{p1}^y\;\;s_{p1}^z\;\;s_{q1}^x\;\;s_{q1}^y\;\;s_{q1}^z\;\;s_1^x\;\;s_1^y\;\;s_1^z \cdots } \right.\\ \;\;\;\;\;\;\;{\left. {s_{pN}^x\;\;s_{pN}^y\;\;s_{pN}^z\;\;s_{qN}^x\;\;s_{qN}^y\;\;s_{qN}^z\;\;s_N^x\;\;s_N^y\;\;s_N^z} \right]^{\rm{T}}} \end{array} $ |
则可产生9k个方程,其中k为测量点数量。
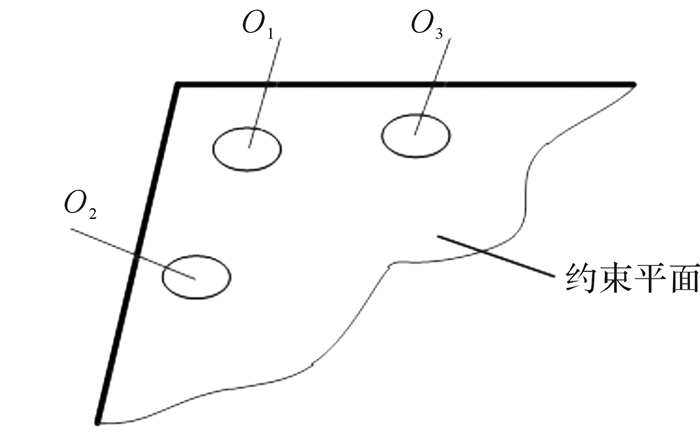
2 视觉辅助定位 2.1 靶点三维定位一般的平面约束标定方法,通过手动示教完成数据测量,本文应用双目视觉系统定位约束平面基准,实现自动化测量。由于双目视觉公共视场范围较小,在约束平面上粘贴3个靶点,如图 3所示,由此对约束平面的定位即可等效成对靶点的定位。
|
| 图 3 约束平面定位靶点图 Fig.3 Target spots for locating constraint plane |
对左右两个相机分别进行张正友内参标定,得到四参数内参矩阵:
| $ {\mathit{\boldsymbol{M}}_j} = \left[ {\begin{array}{*{20}{c}} {{f_{xj}}}&0&{{u_{j0}}}&0\\ 0&{{f_{yj}}}&{{v_{j0}}}&0\\ 0&0&1&0 \end{array}} \right] $ | (17) |
其中:fxj, fyj(j=1, 2)分别是x方向和y方向的尺度因子,(uj0, yj0)(j=1, 2)是左右两相机的主点坐标。
对左右两个相机分别进行手眼标定,即确定摄像机坐标系相对于机械臂末端六轴坐标系的齐次转换矩阵,利用传统手眼标定方法(AU=UB),至少使机械臂运动到3个不同的姿态,分别计算获得左右两个相机的手眼矩阵U1, U2[19]。
建立世界坐标系,使之与机械臂末端六轴坐标系重合,并令L=M1X1-1,R=M2X2-1,得到:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{l_{11}}}&{{l_{12}}}&{{l_{13}}}&{{l_{14}}}\\ {{l_{21}}}&{{l_{22}}}&{{l_{23}}}&{{l_{24}}}\\ {{l_{31}}}&{{l_{32}}}&{{l_{33}}}&{{l_{34}}} \end{array}} \right],\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}} \end{array}} \right] $ | (18) |
设目标点在末端六轴坐标系(世界坐标系)中的三维位置坐标为POi=[xi yi zi]T(i=1, 2, 3),可建立三维定位模型:
| $ {\mathit{\boldsymbol{Z}}_{li}}\left[ {\begin{array}{*{20}{c}} {{u_{li}}}\\ {{v_{li}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_{11}}}&{{l_{12}}}&{{l_{13}}}&{{l_{14}}}\\ {{l_{21}}}&{{l_{22}}}&{{l_{23}}}&{{l_{24}}}\\ {{l_{31}}}&{{l_{32}}}&{{l_{33}}}&{{l_{34}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}}\\ {{z_i}}\\ 1 \end{array}} \right] $ | (19) |
| $ {\mathit{\boldsymbol{Z}}_{ri}}\left[ {\begin{array}{*{20}{c}} {{u_{ri}}}\\ {{v_{ri}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}}\\ {{z_i}}\\ 1 \end{array}} \right] $ | (20) |
式中Zli, Zri分别是目标点在摄像机坐标系下的深度信息。
联立以上2个方程,可得:
| $ \left\{ \begin{array}{l} \left( {{u_{li}}{l_{31}} - {l_{11}}} \right){x_i} + \left( {{u_{li}}{l_{32}} - {l_{12}}} \right){y_i} + \left( {{u_{li}}{l_{33}} - {l_{13}}} \right){z_i} = {l_{14}} - {u_{li}}{l_{34}}\\ \left( {{v_{li}}{l_{31}} - {l_{21}}} \right){x_i} + \left( {{v_{li}}{l_{32}} - {l_{22}}} \right){y_i} + \left( {{v_{li}}{l_{33}} - {l_{23}}} \right){z_i} = {l_{24}} - {v_{li}}{l_{34}}\\ \left( {{u_{ri}}{r_{31}} - {r_{11}}} \right){x_i} + \left( {{u_{ri}}{r_{32}} - {r_{12}}} \right){y_i} + \left( {{u_{ri}}{r_{33}} - {r_{13}}} \right){z_i} = {r_{14}} - {u_{ri}}{r_{34}}\\ \left( {{v_{ri}}{r_{31}} - {r_{21}}} \right){x_i} + \left( {{v_{ri}}{r_{32}} - {r_{12}}} \right){y_i} + \left( {{v_{ri}}{r_{33}} - {r_{23}}} \right){z_i} = {r_{24}} - {v_{ri}}{r_{34}} \end{array} \right. $ |
其中,[uli vli]T, [uri vri]T分别是目标点在左右两像素坐标系中的位置值,由此,可计算得到[xi yi zi]T,即通过立体匹配定位得到O1, O2, O3在机械臂基坐标系下的三维位置信息。
2.2 构建靶点坐标系取靶点坐标系原点O1(x1, y1, z1),将O1O2单位化(记为X),作为X轴的单位矢量:
| $ \mathit{\boldsymbol{X}} = \frac{{\left( {{x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1}} \right)}}{{\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} }} $ | (21) |
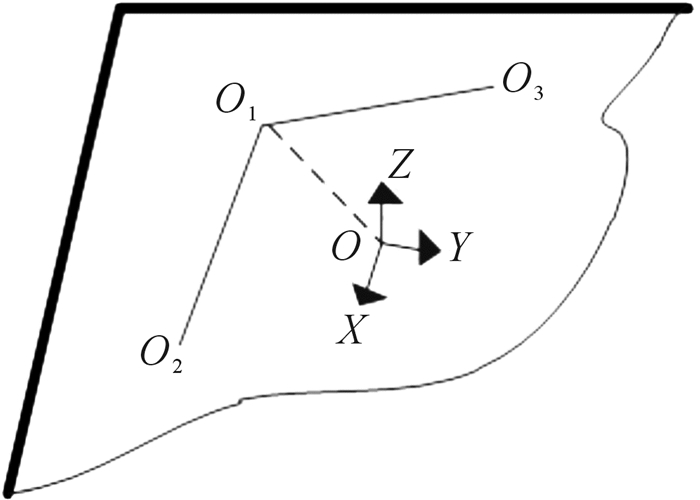
同理,将O1O2×O1O3单位化,作为Z轴的单位矢量,通过右手法则确定Y轴,得到最终的靶点坐标系O-XYZ,如图 4所示,坐标系参数均可通过O1, O2, O3位置信息计算得到。
|
| 图 4 约束平面定位靶点坐标系 Fig.4 Coordinate frame of target spots for locating constraint plane |
那么,平面上的所有点在机械臂基坐标系下的三维位置都可以通过靶点坐标系的原点以及X, Y轴方向矢量描述:
| $ \mathit{\boldsymbol{P}} = {\left[ {{x_1},{y_1},{z_1}} \right]^{\rm{T}}} + a\mathit{\boldsymbol{X}} + b\mathit{\boldsymbol{Y}} $ | (22) |
其中O点坐标及X, Y均已知,通过改变参数a, b,即可确定各约束点在基坐标系下的三维信息。
3 实验及结果分析 3.1 实验系统本文实验对象为埃夫特ER3C-C60本体,采用作者自主研发的6R型串联工业机械臂控制系统;双目摄像机选用德国Imaging工业相机;接触式测量头选用英国Renishaw公司生产的MCP型测量头,其在测量的5个方向上精度均达到0.75 μm;大理石各表面(除底面外)的平面度均为3.5 μm,满足标定所需要的约束要求。整个标定实验系统如图 5所示。

|
| 图 5 标定实验系统 Fig.5 Calibration experiment system |
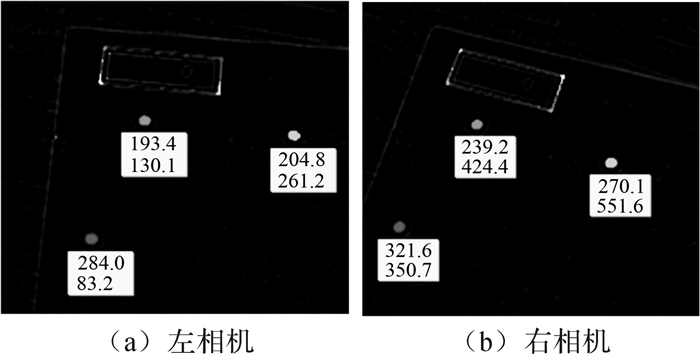
首先通过MATLAB相机标定工具箱,分别得到左右相机的4个内参数;其次通过传统手眼标定方法(AU=UB),得到相机与机械臂之间的手眼关系矩阵;最后分别对左右相机采集得到的靶点图像进行灰度化、图像增强、分割、填充、特征提取等操作以得到各靶点的圆心坐标。为了提高精度,采用亚像素值,考虑到篇幅,截取部分图像如图 6所示(实际采集的图像大小为640×480像素)。
|
| 图 6 各靶点圆心坐标 Fig.6 Circle center of each target spot |
图 6中各坐标分别是靶点圆心O1, O2, O3在左右两相机图像像素坐标系下的坐标值,分别代入公式(19)和(20),即可得到各靶点在世界坐标系(末端六轴坐标系)下的三维位置坐标。
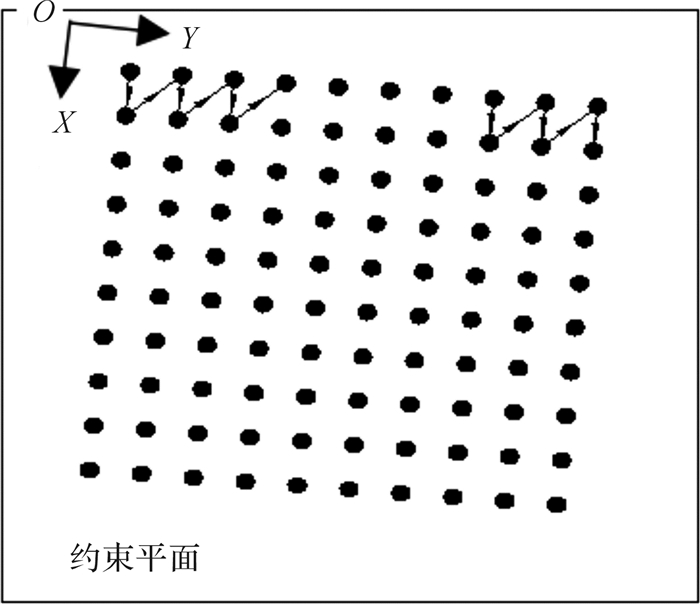
依次取a=10n, b=10n(n=1, 2, …),可得到约束平面上按矩形阵列分布的一系列约束点,在约束平面上的投影及测量路径如图 7所示, 满足任意连续的3个点不共线。
|
| 图 7 按矩形阵列分布的约束点 Fig.7 Constraint points distributed by rectangular array |
将约束点坐标导入机械臂控制器,从而控制测量头对约束平面实现接触式测量。
然而,由于双目视觉定位、机械臂等都存在一定的误差,在实际测量过程中,测量头不会理想地到达理论约束点,甚至会出现测量头已经接触约束平面,而控制器仍然控制其运动到理论约束点。因此,考虑实际因素,需要对公式(22)进行如下修正:
| $ \mathit{\boldsymbol{P}} = \left( {{x_1},{y_1},{z_1}} \right) + a\mathit{\boldsymbol{X}} + b\mathit{\boldsymbol{Y}} + c\mathit{\boldsymbol{Z}} $ | (23) |
其中c是约束平面的法向偏置参数,本文取20,从而保证了在实际测量过程中,在测量头达到理论约束点时,仍然没有接触约束平面。
之后控制器控制测量头在低速下沿约束平面法线方向逼近约束平面,当测量头有触发信号时,记录各关节角度值,并继续到达下一个约束点。为了进一步提高标定效率,本文为机械臂设定2个速度:快速到达理论约束点位置以及低速逼近约束平面。如此在4个平面上共测量120个点,得到120组关节角数据,通过机械臂正运动学计算名义位置值,将其代入公式(16)。
如果辨识雅可比矩阵H满秩,方程组存在唯一解,可利用普通最小二乘法对公式(16)进行求解:
| $ \Delta \mathit{\boldsymbol{X}} = - {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (24) |
若H不是满秩,可利用改进的最小二乘法对公式(16)进行求解:
| $ \Delta \mathit{\boldsymbol{X}} = - {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}} + \mu \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (25) |
其中μ为方程的组合系数,本文取0.001。
参数误差辨识最终结果如表 1所示, 其中工具参数误差分别为:Δtx=0.402 7 mm;Δty=-0.087 4 mm;Δtz=-1.169 3 mm。
| 连杆i | Δθi/(°) | Δαi-1/(°) | Δai-1/mm | Δdi/mm | Δβ/(°) |
| 1 | -0.079 6 | 0.098 8 | 0.210 8 | 1.705 3 | |
| 2 | -0.113 7 | 0.002 7 | -1.443 6 | 0.055 4 | |
| 3 | -0.126 1 | 0.003 6 | 2.548 1 | 0 | -0.059 5 |
| 4 | -0.229 8 | -0.027 8 | 2.237 5 | 0.564 1 | |
| 5 | -0.672 3 | -0.920 0 | -0.108 4 | 0.039 0 | |
| 6 | 0.197 8 | -0.797 9 | 0.020 4 | 0.009 6 |
由控制器使机械臂运动得到50个位形,通过加拿大Creoform公司的光学测量设备Vxtrack380(精度可达到22 μm),测量得到每个工位的实际位置数据,同时记录对应的关节角度值,通过理论运动学参数及修正后的运动学参数,分别计算得到机械臂末端对应的名义位置值及修正位置值,取前10组数据,比较分析基于一般平面约束误差模型的参数修正(记为修正1)与双平面约束误差模型的参数修正(记为修正2)前后机械臂在X, Y, Z方向的位置误差,如图 8所示。

|
| 图 8 运动学参数修正前后各位置误差比较 Fig.8 Comparison of position error before and after modifying the kinematic parameter |
由图 8可知,修正运动学参数后,机械臂的定位误差在X, Y, Z方向都明显减小。比较50组数据后发现,基于一般的平面约束误差模型,修正运动学参数后,机械臂绝对定位精度由1.234 mm提高至0.616 mm,而基于双平面约束误差模型,可将标定精度提高至0.453 mm,验证了此方法在大大提高标定效率的同时,也进一步提高了标定精度。
4 结论本文提出了一种基于视觉辅助定位的机械臂运动学参数辨识方法。首先通过Craig法确定机械臂坐标系,并建立运动学模型、末端位姿误差模型,在此基础上,为了进一步提高标定精度,提出双平面约束误差模型;然后应用双目视觉系统定位约束平面,实现了数据的自动化测量,大大提高了标定效率;最终通过改进的最小二乘法辨识出真实的运动学参数误差。实验结果表明,基于双平面约束误差模型修正运动学参数后,机械臂的绝对定位精度由1.234 mm提高到了0.453 mm。此外,双目视觉系统在提取靶点信息后构建了靶点坐标系,使得约束点按一定规律有序分布,为后期研究标定位形对参数辨识的影响奠定了基础。
| [1] |
苏萌. 高速SCARA工业机器人的静态误差和动态误差模型研究[D]. 杭州: 浙江大学机械工程学院, 2012: 1-4.
SU Meng. The static and dynamic error model analysis of high-speed SCARA industrial robot[D]. Hangzhou: Zhejiang University, College of Mechanical Engineering, 2012: 1-4. |
| [2] | JUDD R P, KNASINSKI A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE Transactions on Robotics and Automation, 1990, 6(1): 20–30. DOI:10.1109/70.88114 |
| [3] |
叶声华, 王一, 任永杰, 等.
基于激光跟踪仪的机器人运动学参数标定方法[J]. 天津大学学报, 2007, 40(2): 202–205.
YE Sheng-hua, WANG Yi, REN Yong-jie, et al. A robot kinematic calibration method based on laser tracker[J]. Journal of Tianjin University, 2007, 40(2): 202–205. |
| [4] |
王琨. 提高串联机械臂运动精度的关键技术研究[D]. 合肥: 中国科学技术大学自动化系, 2013: 66-74.
WANG Kun. Research on key technology in improvement of motion accuracy of serial manipulator[D]. Hefei: University of Science and Technology of China, Department of Automation, 2013: 66-74. |
| [5] |
周学才, 张启先, 郑时雄.
一种新的机器人机构距离误差模型及补偿算法[J]. 机器人, 1991, 13(1): 44–49.
ZHOU Xue-cai, ZHANG Qi-xian, ZHENG Shi-xiong. A new kind of range error model of robot mechanism and compensation algorithm[J]. Robotics, 1991, 13(1): 44–49. |
| [6] |
刘洁, 平雪良, 齐飞, 等.
基于视觉跟踪的机器人测量方法与实现[J]. 应用光学, 2016, 37(5): 686–692.
LIU Jie, PING Xue-liang, QI Fei, et al. A robot measurement method based on vision tracking[J]. Journal of Applied Optics, 2016, 37(5): 686–692. |
| [7] | SANTOLARIA J, CONTE J, GINÉS M. Laser tracker-based kinematic parameter calibration of industrial robots by improved CPA method and active retroreflector[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9/12): 2087–2106. |
| [8] | CONTE J, MAJARENA A C, ACERO R, et al. Performance evaluation of laser tracker kinematic models and parameter identification[J]. International Journal of Advanced Manufacturing Technology, 2015, 77(5/8): 1353–1364. |
| [9] | NAKAMURA H, ITAYA T, YAMAMOTO K, et al. Robot autonomous error calibration method for off line programming system[C]//IEEE International Conference on Robotics and Automation, Nagoya, May 21-27, 1995. |
| [10] | ZHONG X L, LEWIS J M. A new method for autonomous robot calibration[C]//Robotics and Automation, Nagoya, May 21-27, 1995. |
| [11] |
齐飞, 平雪良, 刘洁, 等.
考虑关节柔性误差的机器人参数辨识方法研究[J]. 机械科学与技术, 2017, 36(4): 512–518.
QI Fei, PING Xue-liang, LIU Jie, et al. A robot's parameter identification method with joint flexible errors taken into account[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(4): 512–518. |
| [12] | JOUBAIR A, BONEV I A. Non-kinematic calibration of a six-axis serial robot using planar constraints[J]. Precision Engineering, 2015(40): 325–333. |
| [13] | GATLA C S, LUMIA R, WOOD J, et al. An automated method to calibrate industrial robots using a virtual closed kinematic chain[J]. IEEE Transactions on Robotics, 2007, 23(6): 1105–1116. DOI:10.1109/TRO.2007.909765 |
| [14] |
夏天, 孙翰英, 范嘉桢, 等.
虚拟封闭运动链法提高机器人运动学标定精度[J]. 机械设计与研究, 2009, 25(2): 57–59.
XIA Tian, SUN Han-ying, FAN Jia-zhen. Research of industrial robot calibration based on virtual closed kinematic chain[J]. Machine Design and Research, 2009, 25(2): 57–59. |
| [15] | CHEN H, FUHLBRIGGE T, SANG C, et al. Practical industrial robot zero offset calibration[C]//IEEE International Conference on Automation Science and Engineering, Washington DC, Aug. 23-26, 2008. |
| [16] |
谭民, 徐德, 侯增广, 等.
先进机器人控制[M]. 北京: 高等教育出版社, 2007: 39-46.
TAN Min, XU De, HOU Zeng-guang, et al. Advanced robot control[M]. Beijing: Higher Education Press, 2007: 39-46. |
| [17] | DENAVIT J, HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1955, 22: 215–221. |
| [18] | IKITS M, HOLLERBACH J M. Kinematic calibration using a plane constraint[C]//IEEE International Conference on Robotics and Automation, New Mexico, Apr. 25, 1997. |
| [19] |
卢钰庭. 基于视觉的机器人标定的研究[D]. 广州: 华南理工大学计算机科学与工程学院, 2013: 30-37.
LU Yu-ting. Research on robot calibration based on vision[D]. Guangzhou: South China University of Technology, School of Computer Science and Engineering, 2013: 30-37. |



