2. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China
在制造业快速发展的初期,科技水平不高,社会财富较少,各大制造企业主要的目标是生产更多的产品,通过各种途径, 如标准化、流水线等生产模式,进行大批量的生产,因为生产批量大,加工数据非常多,此时对生产加工过程进行统计分析或质量控制是非常便利的。随着社会的发展和科技的进步,消费者对于产品的需求呈现多样化,各制造企业纷纷推出个性化定制产品,生产模式逐渐从以往的大批量转到多品种小批量,但在满足客户需求的同时也要保证产品质量,即需要进行生产过程的质量控制和工序能力分析,可是小批量模式下数据量不足给这项工作带来了巨大的不便,因此针对多品种小批量生产的质量控制和工序能力分析是亟需解决的问题。
目前,已有学者基于不同的理论从不同角度提出了自己的研究成果。针对工序成组问题:王丽颖[1]提出“虚拟工序”的概念,通过建立工序特征编码系统,实现了对虚拟工序质量控制和预测;张越迪[2]参考零件编码方法,对轴承加工过程进行相似性分析,并利用SPC技术对轴承生产过程进行了质量控制;贾学增等[3]利用多变异分析(multi-vari analysis,MVA)对成组工序进行质量分析;吴小勇[4]利用直觉模糊集理论对工序进行相似性分析,并开发出成组工序质量管理信息系统;Dovich[5]提出了基于重复性、零件族和工艺评价的小批量车间SPC技术;Statham等[6]提出了一种在小批量模式下评估工序特征的方法。针对质量控制技术:Steiner等[7]提出了利用分组数据对休哈特控制图进行绘制的方法;Roberts[8]提出了多品种小批量生产过程的EWMA图的绘制方法;Hillier[9]提出小批量控制图,按用途可分为2种,分别用来对过程进行分析和控制;Quesenberry[10-11]提出了针对小批量生产的Q控制图,并分析了样本大小对X控制图的影响;Vargas等[12]比较了CuSum和EWMA控制图的不同;牟永善等[13]以公差百分数控制图为工具建立了一个与成组加工相适应的质量控制系统。
在已有的研究成果中,对工序的成组技术研究不是非常多,分类成组分析也不是非常准确和全面。另外,针对多品种小批量生产模式的工序能力分析少之又少。对于小批量生产的质量控制技术,国内外学者提出了多种质量控制图和分析模型,但对于实际工程应用较为复杂。因此,本文提出了一种基于相似元的多品种小批量生产的工序能力分析方法。首先分析了影响工序质量的因素,然后基于工序的影响因素,利用相似元理论,分析各工序与目标工序的相似性程度,通过分析结果对工序进行成组,从而利用成组后工序的大量加工数据,对原始的目标工序进行工序能力分析,最后进行实例验证,以期解决多品种小批量生产模式下质量控制和过程分析中样本数量不足的问题。
1 相似元理论设因素ai属于系统A,因素bi属于系统B,P是因素ai和因素bi共有的特征,则称因素ai和因素bi为系统A和系统B间的相似因素。一个因素ai和一个因素bi组合起来,就成为一个相似单元,称作相似元,记为ui(ai, bi)。2个系统之间存在的相似性质,可以通过相似元结构化表现出来。另外,2个系统之间可以存在多个相似元,并且可以把相似系统分解到不同的层次来构造相似元,也就是说每一个相似元可以逐层分解出次级相似元,组成递阶性的结构[14-16]。
相似元可以清晰明了地描述2个系统之间的相似性关系。为了定量化分析系统间的相似性程度,引入相似元。假设相似因素ai, bi间存在m个共有特征,可以表示为P1, P2, …, Pm。设
| $ {{\tilde r}_{ij}} = \frac{{\min \left\{ {{{\tilde U}_j}\left( {{a_i}} \right),{{\tilde U}_j}\left( {{b_i}} \right)} \right\}}}{{\max \left\{ {{{\tilde U}_j}\left( {{a_i}} \right),{{\tilde U}_j}\left( {{b_i}} \right)} \right\}}} $ | (1) |
式中
求得2个因素对于每一个特征的比例系数之后,用加权求和的方法,得到2个因素间的相似性程度,即相似元ui(ai, bi)的相似性程度的表达式为:
| $ q\left( {{u_i}} \right) = \sum\limits_{j = 1}^m {{d_j}{{\tilde r}_{ij}}} $ | (2) |
式中dj为2个因素间共有的各项特征的权重。
系统A和系统B有n个相似元,可用U={u1, u2, …, un}来表示,那么两系统的相似性程度表达式为:
| $ Q = \sum\limits_{k = 1}^n {{w_k}q\left( {{u_k}} \right)} $ | (3) |
式中wk表示两系统间各相似元的权重。权重数值越大,表示该相似元对两系统相似程度的影响越大;反之,则影响越小。
2 多品种小批量生产模式下工序能力分析流程在多品种小批量生产模式下,进行工序能力分析的前提是选取目标工序。一般来讲,需要对目标工序进行定量评价,即对目标工序的各项指标进行测量或评分,以便进行相似性的定量计算。
为了扩充样本容量,需要随机选取目标工序之外的一些工序,可以是相同类型的工序,也可以是不同类型的工序。这些工序共同构建成备选工序集。
备选工序集中的工序并不能直接用于扩充目标工序的样本容量,还需要作进一步筛选和处理。筛选就是对备选工序集中所有工序与目标工序进行相似评判,将满足相似条件的工序挑选出来与目标工序生成相似工序组的过程。相似工序组中的工序与目标工序都是强相似关系,但可能存在尺寸要求不同的问题,这时需要用相对公差法对所有加工数据进行归一化处理,处理后的数据才可用于扩充目标工序的样本容量。
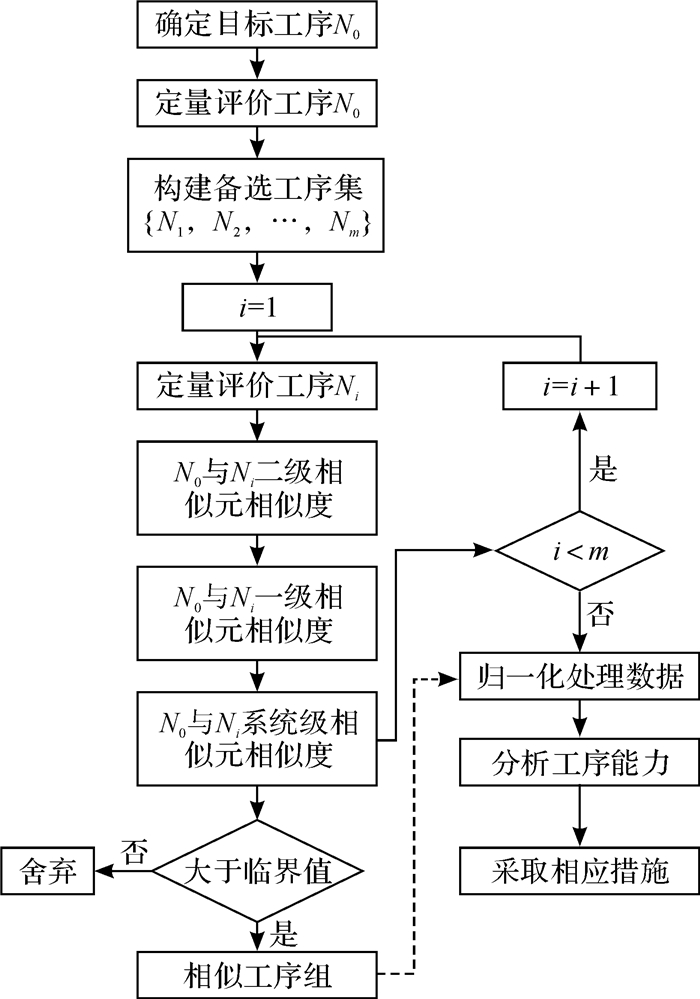
扩充样本容量之后,就可以利用质量控制和分析技术计算目标工序的工序能力指数,并采取相应措施提高该工序的能力。其具体分析流程如图 1所示。
|
| 图 1 多品种小批量生产模式下工序能力分析流程 Fig.1 Process capability analysis flow under the multiple-variety and small-batch |
为了对各道工序进行工序能力分析,需要收集各工序完成后的工件尺寸参数,但在多品种小批量生产模式下,如滚珠丝杠副螺母的生产加工,产品型号很多,生产方式为订单式生产,某一规格产品一次加工数量最多几十件,生产批量非常小,而工序能力分析需要大量的数据支持,因此需要扩充数据容量。通过工序特征分析评判出相似工序,再把相似工序的加工数据合并起来处理,构建相似工序组,这样目标工序就拥有足够多的加工数据,可解决工序能力分析时数据不足的问题。
3.1 相似性分析在制造业中存在很多彼此相似的工序,可以利用相似理论将这些相似的工序聚合成组。在相似理论中,现有的分组方法大多是针对零件的,主要有视检法、生产流程分析法和编码分类法等。根据相似理论中“相似的本质是系统间的各种属性或特征的相似”的观点,要判断各工序是否相似,首先应该判断影响工序加工质量的因素是否相似。工序间的相似性分析常用的有2种方法:计算相似度方法和编码法。编码法本质上也是计算相似度,只是作了一定的简化,即根据每个工序的各项特征对工序赋予唯一的编码,然后通过比较工序的编码即可判定工序是否相似,但编码法相对来说误差较大,为了提高工序能力分析的准确性,本文采用相似元理论对各工序之间的相似度进行定量分析。
3.1.1 影响因素分析判断2个工序是否相似,可以从分析影响工序质量的因素入手,如果两工序的影响因素差异很小,则可以判定两工序为相似工序。根据质量工程理论,影响工序的因素主要有人员、设备、材料、方法和环境这五大类,在这此因素综合作用下,不同工序有不同的能力。所以,可以把人员、设备、材料、方法和环境这五大类影响因素视作工序系统下的5个因素,通过分析工序的影响因素是否相似来判别两工序是否相似[17]。
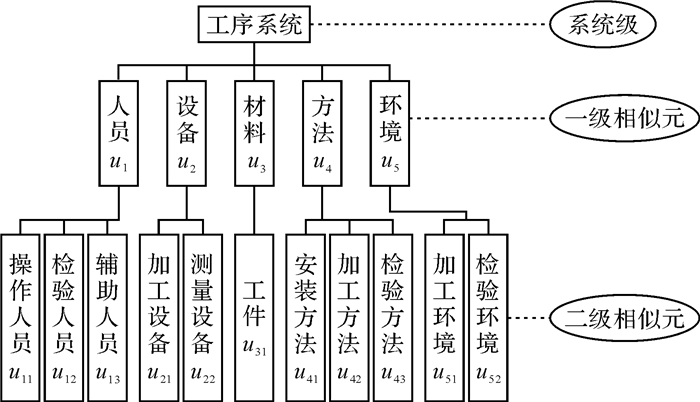
另外,人员、设备、材料、方法、环境这五大类因素还可以继续分解,比如人员因素可以分解为操作人员、检验人员和辅助人员。最后通过这些子因素间的相似性判别来判定2个工序系统间的相似性程度,如图 2所示。

|
| 图 2 工序影响因素分析图 Fig.2 Analysis graph of factors affecting process |
人员是每一道工序的发起点,它是五大影响因素中比较灵活且较难控制的一个因素。常规生产过程中的人员,主要分为操作人员、检验人员和辅助人员。不管是哪类人员,都有不同的技术水平、质量意识和工作状态,而这些都会影响人员工作的质量。
设备是工序的载体,所有工序都要在设备上进行,是影响因素中非常重要的一类。设备可以分为加工设备如车床、铣床和各类机床,以及测量设备如各类量具。可以用可靠性、精度、磨损、调整状态以及使用频度、重要等级等来评判设备水平。
材料是加工过程的对象,对于工序来讲,材料特指工件,工件从生命周期开始的毛坯,到半成品,到最后的成品,经过了一道道工序。材料的复杂程度、规格性能和加工性能等都是非常重要的特征。
方法也是非常重要的一个因素,生产过程的每一步都要依据一定的方法进行,比如工件安装方法、工件加工方法、设备的操作方法和工件尺寸参数的检验方法等。在评判方法的时候,需考虑工艺方案、加工参数、操作规程和测量误差等。
环境因素在产品生命周期的每一个阶段,都影响着产品的质量和可靠性。在其他因素都满足要求的情况下,只有在合适的环境下加工出的产品才能达到最好的质量,产品的寿命才能更长,也才能发挥出最好的产品效用。
3.1.2 相似元构造假设要判断工序系统A与工序系统B是否相似,可以把两者的因素集合分别记为A={a1, a2, …,an},B={b1, b2, …, bn}。对2个工序系统进行相似性分析之前,需要作2点简化:
1) 集合A={a1, a2, …,an}与B={b1, b2, …, bn}的因素项数相同;
2) 因素间的交互作用对于工序的相似性程度影响不大,可忽略不计。
第1层的相似元为ui(ai, bi),由于因素ai和因素bi还可以进一步分解,可表示为(ai, bi)=(ai1, bi1), (ai2, bi2), …(aik, bik),其中i=1, 2, …, n,n是第1层相似元的数目,k是各级相似元下的二级相似元的标号。因此,相似元的结构可以表示为:
| $ {u_i}\left\{ {{a_i},{b_i}} \right\} = \left\{ {{u_{i1}},{u_{i2}}, \cdots ,{u_{ik}}} \right\} $ |
其中uik={aik, bik}。
结合车间的实际情况和工程应用的便捷,只需要把相似元分解到第2层就可以满足需求。构造的两层相似元见图 3。
|
| 图 3 相似元结构图 Fig.3 Structure graph of similarity cell |
将相似系统分解为二级相似元后,需要选取一些典型特征来评判各相似元,从而可以利用特征值对相似系统进行定量分析。
五大影响因素中,人员因素的二级相似元有操作人员、检验人员、辅助人员,特征指标选取技术水平、质量意识和工作状态,人员因素下的每一个二级相似元都存在这3个特征。另外,因为这3个特征指标没有具体的度量方式,所以采用专家打分和自我评估的方式进行量化。
设备因素的二级相似元有加工设备和测量设备,选取6个特征指标,分别是加工设备定位精度、加工设备重复定位精度、加工设备平均故障间隔时间、测量设备使用频度、测量设备精度、测量设备最小分辨率,前三个特征指标属于加工设备,后三者属于测量设备。
材料因素的二级相似元只有工件,而工件的特征指标主要有复杂程度、规格性能和加工性能。这里选取4个特征指标,分别是工件精度等级、材料可加工性、材料力学性能和工件合格率。
方法因素的二级相似元分别是安装方法、加工方法和检验方法。选取4个特征指标,分别是等级要求、复杂程度、经济精度和方法正确度,这4个特征指标在方法因素下的每一个二级相似元中共有。其中复杂程度和方法正确度是定性指标,也需要通过专家打分的方式进行量化。
环境因素的二级相似元有加工环境和检验环境。选取2个特征指标,分别是稳定性和规范性,两者在加工环境和检验环境中共有,且皆为定性指标,需要通过专家打分的方式进行量化。
得到各二级相似元的特征指标,如表 1。
| 一级相似元 | 二级相似元 | 特征指标 |
| 人员u1 | 操作人员u11 | 技术水平P11 |
| 检验人员u12 | 质量意识P12 | |
| 辅助人员u13 | 工作状态P13 | |
| 设备u2 | 加工设备u21 | 加工设备定位精度P21 |
| 加工设备重复定位精度P22 | ||
| 加工设备平均故障间隔时间P23 | ||
| 测量设备u22 | 测量设备使用频率P24 | |
| 测量设备精度P25 | ||
| 测量设备最小分辨率P26 | ||
| 材料u3 | 工件u31 | 工件精度等级P31 |
| 材料可加工性P32 | ||
| 材料力学性能P33 | ||
| 工件合格率P34 | ||
| 方法u4 | 安装方法u41 加工方法u42 检验方法u43 |
等级要求P41 |
| 复杂程度P42 | ||
| 经济精度P43 | ||
| 方法正确度P44 | ||
| 环境u5 | 加工环境u51 | 稳定性P51 |
| 检验环境u52 | 规范性P52 |
在确定各特征指标数值之后和计算相似元相似度之前,需要确定各一级、二级相似元和各特征指标的权重,合理的权重分配可以提高相似性分析的准确性。本文采用主客观相结合的方法进行各一级、二级相似元和各特征指标权重的分配。
主观权重采用层次分析法,它是通过构造判断矩阵,针对判断矩阵准则,分别对元素两两比较,判断两者的重要性程度,重要性程度用数值1~9描述,具体含义见表 2。按照上述原则与方法,进行两两比较,分别赋值,形成判断矩阵[18]。
| 标度值 | 含义 |
| 1 | 2个元素相比,前者与后者同等重要 |
| 3 | 2个元素相比,前者比后者稍重要 |
| 5 | 2个元素相比,前者比后者明显重要 |
| 7 | 2个元素相比,前者比后者强烈重要 |
| 9 | 2个元素相比,前者比后者极端重要 |
| 2,4,6,8 | 重要性程度介于上述各含义之间 |
计算判断矩阵中每行数值的几何均数Ai:
| $ {A_i} = \sqrt[n]{{{k_1} \times {k_2} \times \cdots \times {k_n}}} = \sqrt[n]{{\prod\limits_{i = 1}^n {{k_i}} }} $ |
对Ai进行规范化处理即可得到各指标的权重值:
| $ {w_{{\rm{z}}i}} = \frac{{{A_i}}}{{\prod\limits_{i = 1}^n {{A_i}} }} $ | (4) |
由此可以得到主观权重向量Wz= (wz1, wz2, …, wzn)T。
客观权重采用熵值理论来确定。由信息论可知,第i个因素的熵为:
| $ {H_i} = - \frac{1}{{\ln m}}\sum\limits_{j = 1}^m {{f_{ij}} \cdot {f_{ij}}} ,i = 1,2, \cdots ,n $ |
式中:
那么第i个因素的权重为:
| $ {w_{{\rm{k}}i}} = \frac{{1 - {H_i}}}{{\sum\limits_{i = 1}^n {\left( {1 - {H_i}} \right)} }},i = 1,2, \cdots ,n $ | (5) |
由此可以得到客观权重向量Wk=(wk1, wk2, …, wkn)T。
假设综合主观权重和客观权重后得到的权重向量W=(w1, w2, …, wn)T,利用最小二乘法对综合权重进行计算。
| $ \begin{array}{l} \min H\left( w \right) = \sum\limits_{i = 1}^n {\left[ {{{\left( {{w_{{\rm{z}}i}} - {w_i}} \right)}^2} + {{\left( {{w_{{\rm{k}}i}} - {w_i}} \right)}^2}} \right]} \\ {\rm{s}}.\;{\rm{t}}.\sum\limits_{i = 1}^n {{w_i} = 1} ,{w_i} \ge 0,i = 1,2, \cdots ,n \end{array} $ |
构建拉格朗日函数,令它对wi和λ的偏导等于0,解方程后可得:
| $ \mathit{\boldsymbol{W}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left[ {\mathit{\boldsymbol{c}} + \frac{{1 - {\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{c}}}}{{{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{e}}}}\mathit{\boldsymbol{e}}} \right] $ | (6) |
式中:B=diag[1, 1, …, 1];e=(1, 1, …, 1)T;
| $ \begin{array}{l} \mathit{\boldsymbol{c}} = \left[ {\sum\limits_{j = 1}^m {\frac{1}{2}\left( {{w_{{\rm{z}}1}} + {w_{{\rm{k}}1}}} \right)} ,\sum\limits_{j = 1}^m {\frac{1}{2}\left( {{w_{{\rm{z}}2}} + {w_{{\rm{k}}2}}} \right)} , \cdots ,} \right.\\ \;\;\;\;\;{\left. {\sum\limits_{j = 1}^m {\frac{1}{2}\left( {{w_{{\rm{z}}n}} + {w_{{\rm{k}}n}}} \right)} } \right]^{\rm{T}}} \end{array} $ |
各一级、二级相似元和各特征指标的权重确定之后,就需要根据各特征值加权求和的方法,由公式(2)计算一级和二级相似元的相似性程度,再由公式(3)计算系统级的相似性程度。
求得系统级的相似性程度后,根据数值大小判断2个工序是否为相似工序。若Q>0.9,就可以判定两工序属于强相似关系,可以归类至同一个相似工序组。
4 工序能力分析 4.1 数据归一化处理因为一组相似工序中的各工序加工数据属于不同的工序,所以这些工序加工数据的尺寸要求不尽相同,因此要先对数据作归一化处理,也就是用相对公差法对数据进行转换,数据转换公式为:
| $ {{X'}_i} = \frac{{{X_i} - {M_i}}}{{{T_i}}} $ | (7) |
式中:Xi为第i个工件的原始数据;Ti=TUi-TLi, 是第i个数据对应的公差范围,TUi是尺寸上限,TLi, 是第i是尺寸下限;Mi=(TUi+TLi, 是第i)/2,为第i个数据对应的尺寸范围中心值;i=1, 2, …,n。
数据转换后的均值与方差为:
| $ \overline {X'} = \frac{1}{n}\sum\limits_{i = 1}^n {{{X'}_i}} $ | (8) |
| $ S' = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{{X'}_i} - \overline {X'} } \right)}^2}} } $ | (9) |
通过相似元理论将相似工序成组并进行数据归一化处理后,目标工序的数据量就得到了大幅度的提升,之后就可以利用成组后相似工序的样本数据,对目标工序进行过程能力分析。
关于工序能力指数的计算,已经有很多学者作了研究[19],普遍公认的工序能力指数计算公式主要有Juran提出的Cp指数和Kane提出的Cpk指数,分别如下:
| $ {C_{\rm{p}}} = \frac{T}{{6\sigma }} = \frac{{{T_{\rm{U}}} - {T_{\rm{L}}}}}{{6\sigma }} \approx \frac{{{T_{\rm{U}}} - {T_{\rm{L}}}}}{{6S}} $ | (10) |
| $ {C_{{\rm{pk}}}} = \left( {1 - K} \right){C_{\rm{p}}} = \frac{{T - 2\varepsilon }}{{6\sigma }} \approx \frac{{T - 2\varepsilon }}{{6S}} $ | (11) |
式中:Cp为无偏移工序能力指数;Cpk为有偏移工序能力指数;σ为总体标准差;TU为公差上限;TL为公差下限;S为样本标准差;K=2ε/T, 为偏移系数;
由于Cp法体现工序的输出中心和范围中心之间的位置关系,所以这里选用有偏移工序能力指数Cpk。通过以上分析可得,目标工序组的数据均值
| $ \begin{array}{l} {C_{{\rm{pk}}}} \approx \frac{{{T_x} - 2\left| {M - \bar x} \right|}}{{6S}} = \frac{{T - 2\left| {\overline {X'} \times T} \right|}}{{6S' \times T}} = \\ \;\;\;\;\;\;\;\frac{{1 - 2\overline {X'} }}{{6S'}} \end{array} $ | (12) |
计算出Cpk的具体数值后,就可以根据工序能力指数评价标准(表 3)对目标工序的能力进行分析。
| 等级 | Cpk值 | 工序能力判断 | 解决措施 |
| A++ | Cpk≥2.0 | 特优 | 工序能力过剩,可考虑降低成本 |
| A+ | 2.0>Cpk≥1.67 | 优 | 应该继续保持 |
| A | 1.67>Cpk≥1.33 | 良 | 可以适当提高工序能力 |
| B | 1.33>Cpk≥1.0 | 一般 | 应采取各种措施提升为A级 |
| C | 1.0>Cpk≥0.67 | 差 | 不合格品较多,必须提升工序能力 |
| D | 0.67>Cpk>0 | 不可接受 | 需要重新整改设计 |
传统意义上的相似工序特指工序类型相同的工序,比如车外圆是一类工序,与镗孔、钻孔等工序不能归为一组。但本文构造出的相似元结构不以工序类型为评判标准,而是通过工序影响因素的分层、量化和综合得到相似工序,这样就打破了传统工序分组的局限性。为了证明该方法的有效性,本文在滚珠丝杠副螺母加工工段采集了2组加工数据。
1) 工序类型都是车外圆的8种工序,它们的尺寸要求分别是:∅16-0.022+0.016 mm,∅25+0+0.188 mm,∅30-0.100+0.035 mm,∅40-0.127+0.102 mm,∅50-0.086+0.048 mm,∅60-0.173+0.056 mm,∅80-0+0.109 mm,∅120-0.201+0.010 mm;
2) 工序类型各不相同的8种工序,工序名称和尺寸要求分别是:车外圆∅16-0.022+0.016 mm,镗孔∅20-0.088+0 mm,钻孔∅25-0.018+0 mm,铣平面(侧端面高度)57+0+0.127 mm,铣键槽(底面高度)30-0.005+0.008 mm,铰孔∅5-0.010+0.002 mm,镗孔∅80-0.087+0 mm,钻孔∅10-0.050+0.050 mm。
所有工序的五大影响因素不相同,每一道工序都是小批量生产的,各有10个加工数据。这里进行工序能力指数分析的对象是车外圆∅16-0.022+0.016 mm,即2组工序的目标工序都是车外圆∅16-0.022+0.016 mm这一工序,分别对2组工序进行处理和对比,选出相似性程度最高的若干工序与目标工序组成相似工序组,即可对目标工序进行过程能力分析。
对于选取的16种工序,结合工序相似元结构分解,经过专家组的讨论和各种技术手段,得到了每一道工序各二级相似元对应的定性和定量的特征指标值。
2组数据中各有80道工序,记目标工序为N0,需要评判出与目标工序相似的工序,组成相似工序组,然后以相似工序组为基础对目标工序进行能力分析。为了确保最终结果的准确性,需要对定量数据和定性数据进行归一化处理,即通过专家打分(0~100)对定性指标赋值,通过技术人员分析讨论确定定量指标的百分制数值。通过公式(4)至(6)计算出各级相似元和各特征指标的权重,如表 4所示。
| 一级相似元 | 相似元权重 | 二级相似元 | 相似元权重 | 特征指标 | 特征指标权重 |
| 人员u1 | w1=0.167 8 | 操作人员u11 | w11=0.772 1 | 技术水平P11 | d11=0.552 8 |
| 检验人员u12 | w12=0.149 7 | 质量意识P12 | d12=0.291 7 | ||
| 辅助人员u13 | w13=0.078 2 | 工作状态P13 | d13=0.155 5 | ||
| 设备u2 | w2=0.411 8 | 加工设备u21 | w21=0.802 2 | 加工设备定位精度P21 | d21=0.384 7 |
| 加工设备重复定位精度P22 | d22=0.410 8 | ||||
| 加工设备MTBF P23 | d23=0.204 5 | ||||
| 测量设备u22 | w22=0.197 8 | 测量设备使用频率P24 | d24=0.180 1 | ||
| 测量设备精度P25 | d25=0.442 1 | ||||
| 测量设备最小分辨率P26 | d26=0.377 8 | ||||
| 材料u3 | w3=0.192 6 | 工件u31 | w31=1.000 | 工件精度等级P31 | d31=0.238 3 |
| 工件材料可加工性P32 | d32=0.275 1 | ||||
| 工件材料力学性能P33 | d33=0.221 4 | ||||
| 工件合格率P34 | d34=0.265 2 | ||||
| 方法u4 | w4=0.161 3 | 安装方法u41 加工方法u42 检验方法u43 |
w41=0.226 9 w42=0.570 1 w43=0.203 0 |
等级要求P41 | d41=0.254 7 |
| 复杂程度P42 | d42=0.285 7 | ||||
| 经济精度P43 | d43=0.103 5 | ||||
| 方法正确度P44 | d44=0.356 1 | ||||
| 环境u5 | w5=0.066 5 | 加工环境u51 | w51=0.789 1 | 稳定性P51 | d51=0.374 5 |
| 检验环境u52 | w52=0.210 9 | 规范性P52 | d52=0.625 5 |
在第1组数据中除掉目标工序外,随机选取2个待判定工序N1和N2,分别分析两工序与目标工序的相似性程度。
以第1个工序为例,通过公式(1),可求出该工序与目标工序在相似元u11(操作人员)下的3个特征指标(技术水平P11、质量意识P12、工作状态P13)的特征值比例系数分别是:
| $ q\left( {{u_{11}}} \right) = {d_{11}}{{\tilde r}_{11}} + {d_{12}}{{\tilde r}_{12}} + {d_{13}}{{\tilde r}_{13}} = 0.9466 $ |
同理,q(u12)=0.935 1,q(u13)=0.930 1。在得到u1(人员)下的3个二级相似元的相似性程度数值的情况下,就可以计算u1的数值,即:
| $ q\left( {{u_1}} \right) = {w_{11}}q\left( {{u_{11}}} \right) + {w_{12}}q\left( {{u_{12}}} \right) + {w_{13}}q\left( {{u_{13}}} \right) = 0.9436 $ |
同理可得,q(u2)=0.951 7,q(u3)=0.886 8,q(u4)=0.927 9,q(u5)=0.965 8。
根据公式(3),就可以求出工序N1与目标工序N0在系统层面的相似性程度:
| $ \begin{array}{l} {Q_1} = {w_1}q\left( {{u_1}} \right) + {w_2}q\left( {{u_2}} \right) + {w_3}q\left( {{u_3}} \right) + {w_4}q\left( {{u_4}} \right) + \\ \;\;\;\;\;\;\;{w_5}q\left( {{u_5}} \right) = 0.9349 \end{array} $ |
同理可得工序N2与目标工序N0的系统级相似性程度Q2=0.873 6。
根据判定准则,系统级的相似性程度大于0.9即可认为两系统相似, 则N1与N0相似,N2与N0不相似。对2组数据中所有的工序进行相似性分析,并在2组中找出与N0相似性程度最高的20个工序,分别与N0的10个数据组成2组相似工序组。
根据公式(7),对选出的30个工序的加工数据Xi进行归一化,得到X′i。
对相似工序组中所有工序的加工数据都进行归一化后计算移动极差:
| $ {R_{{\rm{s}}i}} = \left| {{{X'}_i} - {{X'}_{i - 1}}} \right|,i = 2,3, \cdots ,30 $ |
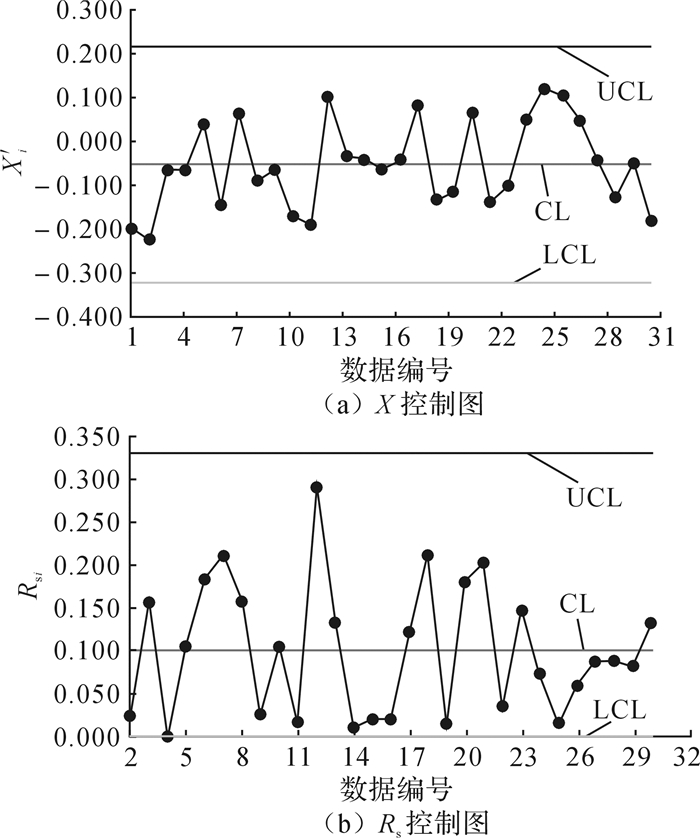
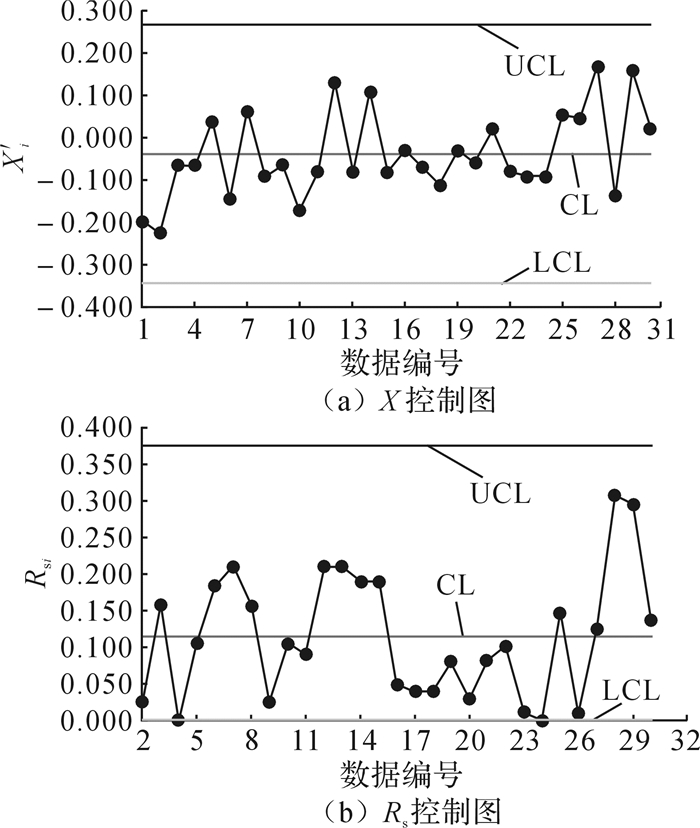
然后根据处理后的数据画出X-Rs控制图,第1组相似工序组的X-Rs控制图见图 4,第2组的见图 5。
|
| 图 4 第1组相似工序组的X-Rs控制图 Fig.4 X-Rs control chart of the first similar processes group |
|
| 图 5 第2组相似工序组X-Rs控制图 Fig.5 X-Rs control chart of the second similar processes group |
根据公式(8)和(9),计算得出:
| $ {\overline {X'} ^①} = - 0.054,{\overline {X'} ^②} = - 0.038 $ |
| $ {{S'}^①} = 0.099965,{{S'}^②} = 0.101005 $ |
则2个相似工序组的工序能力指数分别为:
| $ C_{{\rm{pk}}}^① \approx \frac{{1 - 2{{\left| {\overline {X'} } \right|}^①}}}{{6{{S'}^①}}} = \frac{{1 - 2 \times \left| { - 0.054} \right|}}{{6 \times 0.099965}} = 1.49 $ |
| $ C_{{\rm{pk}}}^② \approx \frac{{1 - 2{{\left| {\overline {X'} } \right|}^②}}}{{6{{S'}^②}}} = \frac{{1 - 2 \times \left| { - 0.038} \right|}}{{6 \times 0.101005}} = 1.52 $ |
| $ 1.67 > C_{{\rm{pk}}}^② > C_{{\rm{pk}}}^① \ge 1.33 $ |
对于目标工序车外圆∅16-0.022+0.016 mm,利用2个相似工序组计算出的工序能力指数相差很小,且都在[1.33, 1.67)的范围内,因此,由表 3可以判定目标工序的能力是A级,属于良好水平,状态比较稳定,不过还需要采用各种方法将工序能力提升一个等级。
6 结论针对多品种小批量生产模式,在分析影响工序质量与可靠性各因素的前提下,分解并构建了工序相似的两级相似元模型,该利用此模型判定出与目标工序相似的工序并组合成为相似工序组。采集了滚珠丝杠副螺母工段实际生产过程中来源不同的2组数据,对数据进行了归一化处理。对于目标工序,解除了多品种小批量生产模式下数据量不足的限制,分别计算了其两相似工序组的工序能力指数,给企业的过程分析工作带来了很多便捷。
| [1] |
王丽颖. 小批量工序质量控制方法及其若干关键技术的研究[D]. 大连: 大连交通大学机械工程学院, 2007: 42-45.
WANG Li-ying. Research on small batch procedure quality control method and their key techniques[D]. Dalian: Dalian Jiaotong University, School of Mechanical Engineering, 2007: 42-45. |
| [2] |
张越迪. 面向轴承制造过程的工序质量控制研究[D]. 重庆: 重庆大学机械工程学院, 2012: 16-17.
ZHANG Yue-di. Study on process quality control for manufacturing process of bearing[D]. Chongqing: Chongqing University, School of Mechanical Engineering, 2012: 16-17. |
| [3] |
贾学增, 吴小勇.
基于多变异分析的成组工序过程质量控制与分析[J]. 机械制造, 2012, 50(4): 73–76.
JIA Xue-zeng, WU Xiao-yong. Quality control and analysis of process group based on MVA[J]. Machinery, 2012, 50(4): 73–76. |
| [4] |
吴小勇. 多品种小批量环境下成组工序质量控制方法的研究及应用[D]. 重庆: 重庆大学机械工程学院, 2011: 14-15.
WU Xiao-yong. The study and application of quality control method for grouping of procedures in multi-varieties & small batch production[D]. Chongqing: Chongqing University, School of Mechanical Engineering, 2011: 14-15. |
| [5] | DOVICH R A. Statistics for the small-lot job shop[J]. Machine and Tool Blue Book, 1998, 83(1): 10–12. |
| [6] | STATHAM A, Al-SALTI M. The application of group technology concept for implementing SPC in small batch manufacture[J]. International Journal of Quality & Reliability Management, 1994, 11(4): 64–76. |
| [7] | STEINER S H, GEYER P L, WESOLOWSKY G O, et al. Shewhart control charts to detect mean and standard deviation shifts based on grouped data[J]. Quality and Reliability Engineering International, 1996, 12(5): 345–353. DOI:10.1002/(ISSN)1099-1638 |
| [8] | PAGE E S. Continuous inspection schemes[J]. Biometrika, 1954, 41(1/2): 100–115. DOI:10.2307/2333009 |
| [9] | HILLIER F S. Chart control limits based on a small number of subgroups[J]. Journal of Quality Technology, 1969, 1(1): 17–26. DOI:10.1080/00224065.1969.11980343 |
| [10] | QUESENBERRY C P. SPC q-charts for start-up and short or long runs[J]. Journal of Quality Technology, 1991, 23(3): 213–224. DOI:10.1080/00224065.1991.11979327 |
| [11] | QUESENBERRY C P. The effect of sample size on estimated limits for X control charts[J]. Journal of Quality Technology, 1993, 25(4): 237–247. DOI:10.1080/00224065.1993.11979470 |
| [12] | VARGAS V D C C D, LOPES L F D, SOUZA A M. Comparative study of the performance of the CuSum and EWMA control charts[J]. Computers & Industrial Engineering, 2004, 46(4): 707–724. |
| [13] |
牟永善, 赵文波.
成组加工质量控制中工序诊断调节法与公差百分数控制图的应用[J]. 工业工程与管理, 2005, 10(2): 81–85.
MOU Yong-shan, ZHAO Wen-bo. On control of process quality in group production cell with diagnosis and regulation method of operation and control diagram of tolerance percentage[J]. Industrial Engineering and Management, 2005, 10(2): 81–85. |
| [14] |
陈博, 孙薇.
SPC技术在多品种小批量数控车削中的应用[J]. 价值工程, 2014(28): 56–57.
CHEN Bo, SUN Wei. Application of SPC technology in multi-type & small batch CNC turning[J]. Value Engineering, 2014(28): 56–57. |
| [15] |
郎茂涛. 多品种小批量制造模式下工序质量控制研究[D]. 西安: 西安电子科技大学经济与管理学院, 2012: 24-25.
LANG Mao-tao. Study on the quality control of working procedure in multi-specification & small-batch manufacturing[D]. Xi'an: Xidian University, School of Economics and Management, 2012: 24-25. |
| [16] |
黄朝志, 伍建军, 刘飞飞, 等.
基于相似性原理的轴类零件小批量多品种生产的统计质量控制[J]. 组合机床与自动化加工技术, 2008(2): 110–112.
HUANG Chao-zhi, WU Jian-jun, LIU Fei-fei, et al. SQC of axis parts under multi-type and small batch condition based on analogical theory[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2008(2): 110–112. |
| [17] |
张根保.
现代质量工程[M]. 北京: 机械工业出版社, 2015: 54-82.
ZHANG Gen-bao. Advanced quality engineering[M]. Beijing: China Machine Press, 2015: 54-82. |
| [18] |
余进, 陈维进, 王弘, 等.
层次分析法在确定评估体系指标权重中的应用[J]. 中国医疗设备, 2013, 28(12): 44–47.
YU Jin, CHEN Wei-jin, WANG Hong, et al. Application of analytic hierarchy process in establishing the weight values of PACS score system[J]. China Medical Devices, 2013, 28(12): 44–47. |
| [19] |
汤淑明, 王飞跃.
过程能力指数综述[J]. 应用概率统计, 2004, 20(2): 207–216.
TANG Shu-ming, WANG Fei-yue. Recent development in process capability indices[J]. Chinese Journal of Applied Probability and Statistics, 2004, 20(2): 207–216. |



