引用本文
陈洪月, 李永红, 邓文浩, 袁智, 李恩东.
滚筒采煤机液压拉杆受力分析[J]. 工程设计学报, 2018, 25(1): 118-122.
CHEN Hong-yue, LI Yong-hong, DENG Wen-hao, YUAN Zhi, LI En-dong. Tension analysis of the drum shearer hydraulic pull rod[J]. Chinese Journal of Engineering Design, 2018, 25(1): 118-122.
滚筒采煤机液压拉杆受力分析
1.
辽宁工程技术大学 机械工程学院, 辽宁 阜新 123000;
2. 宾夕法尼亚大学 工程与应用科学学院, 宾夕法尼亚 19104;
3. 中国煤矿机械装备有限责任公司, 北京 100011
2. 宾夕法尼亚大学 工程与应用科学学院, 宾夕法尼亚 19104;
3. 中国煤矿机械装备有限责任公司, 北京 100011
摘要:
为了研究采煤机滚筒截割载荷对其机身上4根液压拉杆负载的影响，采用小位移变形协调原理和静力学平衡方程，建立了采煤机工况载荷下4根液压拉杆的受力模型，推导了拉杆的载荷公式，设定4根拉杆的初始预紧力均为500 kN，以滚筒和滑靴的实验测试载荷为输入，对拉杆受力模型进行了求解。结果表明：4根拉杆的变形量均值分别为3.164 2，1.934 8，2.353 8，2.248 8 mm；采煤机工作过程中4根拉杆载荷相差较大，其中煤壁区上侧拉杆的载荷最大，均值为536 578 N，采空区上侧拉杆的载荷最小，均值为449 991 N。最后通过实验对拉杆受力模型的准确性进行了验证，研究结果为采煤机液压拉杆的预紧力设定及寿命分析提供依据。
关键词:
采煤机
液压拉杆
预紧力
变形协调原理
基金项目: 国家自然科学基金青年科学基金资助项目（51404132）
Tension analysis of the drum shearer hydraulic pull rod
1. College of Mechanical Engineering, Liaoning Technical University, Fuxin 123000, China;
2. School of Engineering and Applied Science, University of Pennsylvania, Pennsylvania 19104, America;
3. China National Coal Mining Equipment Co., Ltd., Beijing 100011, China
2. School of Engineering and Applied Science, University of Pennsylvania, Pennsylvania 19104, America;
3. China National Coal Mining Equipment Co., Ltd., Beijing 100011, China
Abstract:
To study the effect of the shearer drum cutting load to the four hydraulic pull rods, the force model of the four hydraulic pull rods was established under the shearer working load by using the small displacement deformation coordination principal and the statics equilibrium equation, and the load formula was derived. Assuming the pre-tension load of four pull rods was 500 kN, the force model of the pull rod was solved by input the test loading of the drum and the sliding shoes. The test results showed that the deformation average of four pull rods were 3.164 2, 1.934 8, 2.353 8, 2.248 8 mm respectively. The loads of the four pull rods were different in the working process of the shearer, where the largest load of pull rods was on the upper coal wall, the average value was 536 578 N, the lowest load of pull rods was on the goaf, and the average value was 449 991 N. The accuracy of the pull rod force model was verified by the test. The research results provide the convenience to the setting of the pre-tension force of the shearer hydraulic pull rod and the lifetime analysis.
Key words:
shearer
hydraulic pull rod
pre-tension force
deformation coordinate principle
液压拉杆是联接采煤机机身与前后行走部的关键部件，采煤机截割过程中常因初始预紧力不合理而导致机身与行走部件的联接松动或拉杆疲劳断裂[1]。因大型螺栓预紧的联接方式能大大提高设备的承载能力，所以除了采煤机外，其还广泛应用于组合机架液压机等设备中[2-4]。针对设备部件间预紧联接：毛君等[5]研究了采煤机在斜切工况下液压拉杆受力随采煤机俯仰角的变化情况，并对液压拉杆进行了强度分析；单东生等[6]建立了全预紧组合框架液压机的预紧力受力数学模型，采用有限元法对拉杆的应力、应变进行了分析；吴生富等[7]采用有限元接触算法分析了锻造液压机全预紧机架的整体工作性能，较为准确地计算了各部件变形及接触内力分布；何敏等[8]利用接触力学和有限元法对精密压力机预紧力进行了研究；金淼等[9]建立了组合机架的预紧力模型及上限载荷模型，并通过试验进行分析验证；董晓传等[10-11]对偏心载荷下液压机临界预紧力进行了研究；郭宝峰等[12]对中心工况和扩孔工况下压力机的临界预紧力进行了研究；段志东等[13]研究了当前拉杆预紧力对已预紧拉杆残余应力的影响；唐景林等[14]通过力学分析得到拉杆端部施加拉力过程中拉杆相对拉力的变化规律，并借用物理模型试验验证所提出的非缓解测量原理的正确性以及测试了系统的可行性；李艳聪等[15-16]建立了考虑拉杆预紧力、耦合接触、液压载荷与成形载荷的主机整机模型，并利用有限元法对液压机主机结构性能进行分析，根据激光追踪法验证了分析的合理性。由以上文献可知，对采煤机液压拉杆预紧力的理论研究相对较少，而采煤机的结构又与压力机存在较大的区别，导致采煤机装配过程中只能凭借传统经验设定拉杆的初始预紧力，影响了采煤机整机的性能和可靠性。
本文首先采用变形协调原理和静力学平衡方程建立采煤机液压拉杆受力数学模型，再以采煤机滚筒载荷和滑靴支撑载荷为输入，对模型进行求解，并通过试验对求解结果进行验证，研究结果可为采煤机的设计、安装提供工程依据。
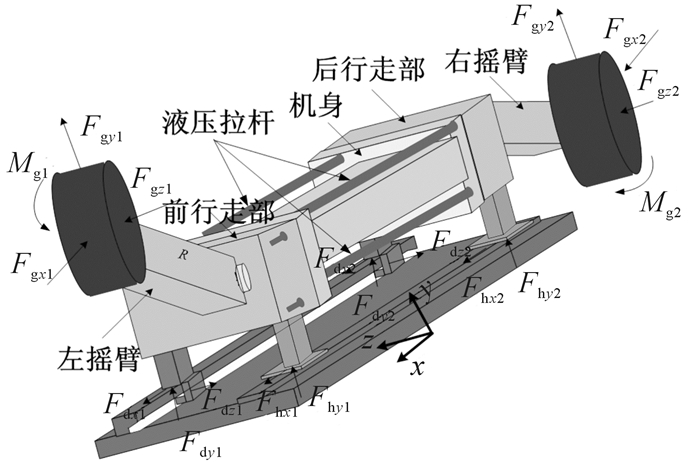
1 液压拉杆力学模型建立如图 1所示，采煤机的4根液压拉杆将机身与左、右行走部联接为一个整体。采煤机工作过程中主要承受：左滚筒的水平载荷Fgx1、竖直载荷Fgy1、轴向载荷Fgz1、扭矩Mg1；右滚筒的水平载荷Fgx2、竖直载荷Fgy2、轴向载荷Fgz2、扭矩Mg2；左、右平滑靴的水平摩擦阻力载荷Fhx1, Fhx2和竖直支撑载荷Fhy1, Fhy2；左、右导向滑靴水平牵引载荷Fdx1，Fdx2、竖直支撑载荷Fdy1，Fdy2和轴向支撑载荷Fdz1，Fdz2。
|
| 图 1 采煤机结构及受力分析简图 Fig.1 The diagram of shearer structure and force analysis |
为了保证采煤机在工况载荷下能够正常工作，采煤机安装时需对液压拉杆施加一定的初始预紧力，在初始预紧力的作用下，拉杆会产生拉伸变形，取采煤机的右侧摇臂、右侧行走部进行受力分析，忽略机身的弹性变形，令4根拉杆的初始预紧力为F′u1, F′u2, F′d1, F′d2，长度为Lu1, Lu2, Ld1, Ld2，液压拉杆的截面面积为A, 弹性模量为E，则4根液压拉杆的初始变形量分别为:
| $ \Delta {{l'}_{{\rm{u1}}}} = \frac{{{{F'}_{{\rm{u1}}}}}}{{EA}}{L_{{\rm{u1}}}} $ | (1) |
| $ \Delta {{l'}_{{\rm{u2}}}} = \frac{{{{F'}_{{\rm{u2}}}}}}{{EA}}{L_{{\rm{u2}}}} $ | (2) |
| $ \Delta {{l'}_{{\rm{d1}}}} = \frac{{{{F'}_{{\rm{d1}}}}}}{{EA}}{L_{{\rm{d1}}}} $ | (3) |
| $ \Delta {{l'}_{{\rm{d2}}}} = \frac{{{{F'}_{{\rm{d2}}}}}}{{EA}}{L_{{\rm{d2}}}} $ | (4) |
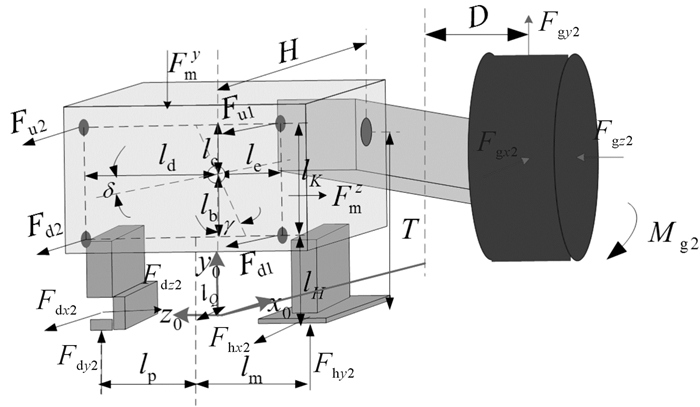
以右侧行走部和右摇臂为研究对象，建立初始预紧状态下的坐标系，原点为右侧行走部和右摇臂的重心，如图 2所示，主要结构参数大小如下：lb=380 mm, lc=460 mm, ld=584 mm，le=420 mm, lh=620 mm, lk=900 mm, lp=1 550 mm, lm=525 mm, H=1 080 mm, T=1 250 mm, R=2 500 mm, 摇臂摆角α2=10°。
|
| 图 2 液压拉杆受力分析 Fig.2 Hydraulic pull rod force analysis |
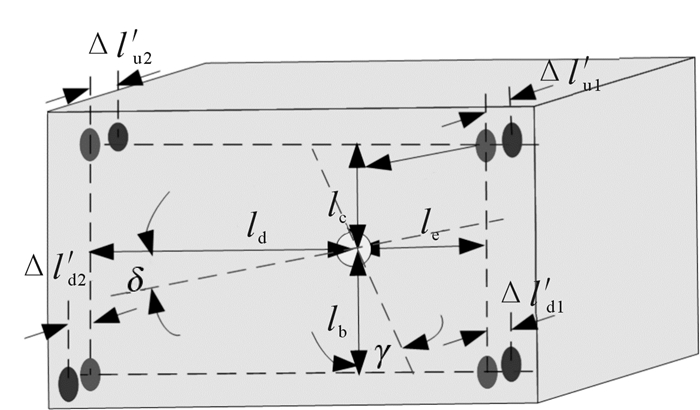
当采煤机工作时，受滚筒截割载荷和滑靴支撑载荷的影响，4根拉杆受力发生改变，导致伸长量发生变化，根据小位移变形协调原理[17-18]，令右侧行走部相对机身的位移为x，横向摆角为δ，纵向摆角为γ，如图 3所示，因δ和γ值相对较小，所以外部载荷引起的4根拉杆变形量可表示为：
| $ \Delta {l_{{\rm{u1}}}} = \left( {x + {l_{\rm{c}}}\delta + {l_{\rm{e}}}\gamma } \right) $ | (5) |
| $ \Delta {l_{{\rm{u2}}}} = \left( {x + {l_{\rm{c}}}\delta - {l_{\rm{d}}}\gamma } \right) $ | (6) |
| $ \Delta {l_{{\rm{d1}}}} = \left( {x - {l_{\rm{b}}}\delta + {l_{\rm{e}}}\gamma } \right) $ | (7) |
| $ \Delta {l_{{\rm{d2}}}} = \left( {x - {l_{\rm{b}}}\delta - {l_{\rm{d}}}\gamma } \right) $ | (8) |
|
| 图 3 液压拉杆受力变形协调原理 Fig.3 Hydraulic pull rod force deformation coordinate principle |
这时4根拉杆载荷变化量表示为：
| $ \Delta {F_{{\rm{u1}}}} = {K_{{\rm{u1}}}}\Delta {l_{{\rm{u1}}}} $ | (9) |
| $ \Delta {F_{{\rm{u2}}}} = {K_{{\rm{u2}}}}\Delta {l_{{\rm{u2}}}} $ | (10) |
| $ \Delta {F_{{\rm{d1}}}} = {K_{{\rm{d1}}}}\Delta {l_{{\rm{d1}}}} $ | (11) |
| $ \Delta {F_{{\rm{d2}}}} = {K_{{\rm{d2}}}}\Delta {l_{{\rm{d2}}}} $ | (12) |
式中：
| $ {K_{{\rm{u1}}}} = \frac{{EA}}{{{L_{{\rm{u1}}}}}},{K_{{\rm{u2}}}} = \frac{{EA}}{{{L_{{\rm{u2}}}}}},{K_{{\rm{d1}}}} = \frac{{EA}}{{{L_{{\rm{d1}}}}}},{K_{{\rm{d2}}}} = \frac{{EA}}{{{L_{{\rm{d2}}}}}} $ |
建立静力学平衡方程, 令∑Mx0=0，有：
| $ \begin{array}{l} \left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}} + {K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right)x + \left( {{l_{\rm{c}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right) - } \right.\\ \left. {{l_{\rm{b}}}\left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right)} \right)\delta + \left( {{l_{\rm{e}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}} + } \right.} \right.\\ \left. {\left. {{K_{{\rm{d2}}}}} \right)} \right)\gamma = {F_{{\rm{g}}x2}} - \left( {{{\left| {{F_{{\rm{d}}y2}}} \right|}_\mu } + {{\left| {{F_{{\rm{d}}z2}}} \right|}_\mu } + {{\left| {{F_{{\rm{h}}y2}}} \right|}_\mu }} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{F_{{\rm{d}}x2}} - {F_{{\rm{h}}x2}} \end{array} $ | (13) |
令∑My0=0，有：
| $ \begin{array}{l} \left( {{l_{\rm{e}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}} + {K_{{\rm{d2}}}}} \right)} \right)x + \left( {{l_{\rm{e}}}\left( {{K_{{\rm{u1}}}}{l_{\rm{c}}} - } \right.} \right.\\ \left. {\left. {{K_{{\rm{d1}}}}{l_{\rm{b}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}}{l_{\rm{c}}} + {K_{{\rm{d2}}}}{l_{\rm{b}}}} \right)} \right)\delta + \left( {l_{\rm{e}}^2\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) + } \right.\\ \;\;\left. {l_{\rm{d}}^2\left( {{K_{{\rm{u2}}}} + {K_{{\rm{d2}}}}} \right)} \right)\gamma - F_{\rm{m}}^z{l_{\rm{q}}} = {F_{{\rm{g}}x2}}D + {F_{{\rm{g}}z2}}\left( {H + } \right.\\ \;\;\;\left. {R\cos {\alpha _2}} \right) - \left| {{F_{{\rm{d}}y2}}} \right|\mu {l_{\rm{P}}} - \left| {{F_{{\rm{h}}y2}}} \right|\mu {l_{\rm{m}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{F_{{\rm{d}}z2}}} \right|{l_{\rm{q}}} - {F_{{\rm{d}}x2}}{l_{\rm{p}}} \end{array} $ | (14) |
令∑Mz0=0，有：
| $ \begin{array}{l} \left( {\left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right)\left( {{l_{\rm{k}}} + {l_{\rm{h}}}} \right) + \left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right){l_{\rm{h}}}} \right)x + \left( {\left( {{l_{\rm{k}}} + } \right.} \right.\\ \;\;\left. {\left. {{l_{\rm{h}}}} \right){l_{\rm{c}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right) - {l_{\rm{h}}}{l_{\rm{b}}}\left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right)} \right)\delta + \left( {\left( {{l_{\rm{k}}} + } \right.} \right.\\ \;\;\left. {\left. {{l_{\rm{h}}}} \right)\left( {{K_{{\rm{u1}}}}{l_{\rm{e}}} + {K_{{\rm{u2}}}}{l_{\rm{d}}}} \right) - {l_{\rm{h}}}\left( {{K_{{\rm{d1}}}}{l_{\rm{e}}} - {K_{{\rm{d2}}}}{l_{\rm{d}}}} \right)} \right)\gamma - F_{\rm{m}}^y{l_q} = \\ \;\;{F_{{\rm{g}}x2}}\left( {T + R\sin {\alpha _2}} \right) - {F_{{\rm{g}}y2}}\left( {H + R\cos {\alpha _2}} \right) + {M_{{\rm{g}}2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{F_{{\rm{d}}y2}} + {F_{{\rm{h}}y2}}} \right){l_{\rm{q}}} \end{array} $ | (15) |
再令
| $ \mathit{\boldsymbol{\tilde A\tilde X}} = \mathit{\boldsymbol{\tilde B}} $ | (16) |
其中:
| $ \mathit{\boldsymbol{\tilde A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}}&{{\mathit{\boldsymbol{A}}_{12}}}&{{\mathit{\boldsymbol{A}}_{13}}}\\ {{\mathit{\boldsymbol{A}}_{21}}}&{{\mathit{\boldsymbol{A}}_{22}}}&{{\mathit{\boldsymbol{A}}_{23}}}\\ {{\mathit{\boldsymbol{A}}_{31}}}&{{\mathit{\boldsymbol{A}}_{32}}}&{{\mathit{\boldsymbol{A}}_{33}}} \end{array}} \right] $ |
| $ {A_{11}} = \left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}} + {K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right) $ |
| $ {A_{12}} = \left( {{l_{\rm{e}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right) - {l_{\rm{b}}}\left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right)} \right) $ |
| $ {A_{13}} = {l_{\rm{e}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}} + {K_{{\rm{d2}}}}} \right) $ |
| $ {A_{21}} = {l_{\rm{e}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}} + {K_{{\rm{d2}}}}} \right) $ |
| $ {A_{22}} = {l_{\rm{e}}}\left( {{K_{{\rm{u1}}}}{l_{\rm{c}}} - {K_{{\rm{d1}}}}{l_{\rm{b}}}} \right) - {l_{\rm{d}}}\left( {{K_{{\rm{u2}}}}{l_{\rm{c}}} - {K_{{\rm{d2}}}}{l_{\rm{b}}}} \right) $ |
| $ {A_{23}} = l_{\rm{e}}^2\left( {{K_{{\rm{u1}}}} + {K_{{\rm{d1}}}}} \right) + l_{\rm{d}}^2\left( {{K_{{\rm{u2}}}} + {K_{{\rm{d2}}}}} \right) $ |
| $ {A_{31}} = \left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right)\left( {{l_{\rm{k}}} + {l_{\rm{h}}}} \right) + \left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right){l_{\rm{h}}} $ |
| $ {A_{32}} = \left( {{l_{\rm{k}}} + {l_{\rm{h}}}} \right){l_{\rm{c}}}\left( {{K_{{\rm{u1}}}} + {K_{{\rm{u2}}}}} \right) - {l_{\rm{h}}}{l_{\rm{b}}}\left( {{K_{{\rm{d1}}}} + {K_{{\rm{d2}}}}} \right) $ |
| $ {A_{33}} = \left( {{l_{\rm{k}}} + {l_{\rm{h}}}} \right)\left( {{K_{{\rm{u1}}}}{l_{\rm{e}}} + {K_{{\rm{u2}}}}{l_{\rm{d}}}} \right) - {l_{\rm{h}}}\left( {{K_{{\rm{d1}}}}{l_{\rm{e}}} - {K_{{\rm{d2}}}}{l_{\rm{d}}}} \right) $ |
| $ \mathit{\boldsymbol{\tilde A}} = \left[ {\begin{array}{*{20}{c}} {{F_{{\rm{g}}x2}} - \left( {\left| {{F_{{\rm{d}}y1}}} \right|\mu + \left| {{F_{{\rm{d}}z1}}} \right|\mu + \left| {{F_{{\rm{h}}y1}}} \right|\mu } \right)}\\ {\left( {{F_{{\rm{g}}x2}}D + {F_{{\rm{g}}z2}}\left( {T + R\cos {\alpha _2}} \right) - \left| {{F_{{\rm{d}}y2}}} \right|\mu {l_{\rm{p}}} - \left| {{F_{{\rm{h}}y2}}} \right|\mu {l_{\rm{m}}}} \right.}\\ {{F_{{\rm{g}}x2}}\left( {T + R\sin {\alpha _2}} \right) - {F_{{\rm{g}}y2}}\left( {T + R\cos {\alpha _2}} \right) - {M_{{\rm{g2}}}} + \left( {{F_{{\rm{d}}y2}} + {F_{{\rm{h}}y2}}} \right){l_{\rm{q}}}} \end{array}} \right] $ |
式中μ为滑靴与刮板机间的摩擦系数。
将式(16)的求解结果x, δ, γ代入式(5)至式(8)，可求得工况载荷下各拉杆的变形量，再将各变形量代入式(9)至式(12)，可得采煤机工作过程中4根拉杆载荷变化量，再将其与拉杆的初始预紧量求和，可得拉杆的实际载荷为：
| $ {F_{{\rm{u1}}}} = {{F'}_{{\rm{u1}}}} + \Delta {F_{{\rm{u1}}}} $ | (17) |
| $ {F_{{\rm{u2}}}} = {{F'}_{{\rm{u2}}}} + \Delta {F_{{\rm{u2}}}} $ | (18) |
| $ {F_{{\rm{d1}}}} = {{F'}_{{\rm{d1}}}} + \Delta {F_{{\rm{d1}}}} $ | (19) |
| $ {F_{{\rm{d2}}}} = {{F'}_{{\rm{d2}}}} + \Delta {F_{{\rm{d2}}}} $ | (20) |
采用实验方法测量采煤机截割过程中的滚筒载荷和滑靴支撑载荷，实验地点为中煤装备集团张家口煤矿机械有限公司“国家能源煤矿采掘机械装备研发(实验)中心”。实验中采用截齿三向力传感器和滑靴销轴传感器对滚筒和滑靴载荷进行测量，如图 4(a)、(b)所示；液压拉杆的拉力采用压力环传感器进行测量，如图 4(c)、(d)所示；现场实验如图 4(e)所示。实验中采煤机4根拉杆的初始预紧力均为500 kN，煤壁硬度f=3，抗拉强度为1.52 MPa，泊松比为0.32，煤层高度为3 000 mm，滚筒截割煤壁的厚度为400 mm，采煤机行走速度为1.5 m/min。为了保证实验过程的安全性和可靠性，实验数据采用无线传输方式传输，传感器的采用频率为200 Hz，信号采集系统采用北京必创科技有限公司的BeeData。
|
| 图 4 实验用传感器示意图和实验现场 Fig.4 Experimental sensor schematic diagram and experimental site |
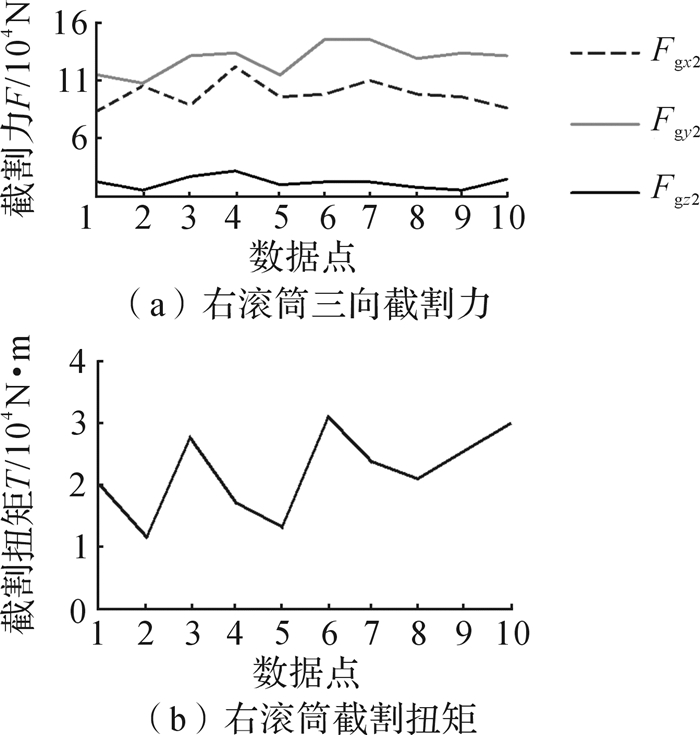
因系统采样频率较高，实验过程中采集的数据较多，为了更为清晰地观测采集数据的变化特点和规律，将滚筒每转所对应时间(2 s)内的滚筒载荷、滑靴载荷数据进行取均值处理，并记录滚筒连续工作10转时所对应的10组均值数据，如图 5和图 6所示。
|
| 图 5 右滚筒三向力截割力和截割扭矩 Fig.5 Three-direction cutting force and cutting torque of the right drum |
|
| 图 6 滑靴支撑力 Fig.6 Slipping shoe support force |
将图 5和图 6中的载荷代入式(16)进行求解，拉杆的总变形量ΔL为初始预紧变形量Δl′与外载荷引起的变形量Δl之和，由式(1)至式(8)可得工况载荷下4根拉杆的总变形量，如图 7所示：4根拉杆的变形量均值分别为3.164 2，1.934 8，2.353 8，2.248 8 mm。
|
| 图 7 拉杆的变形量 Fig.7 Pull rod deformation value |
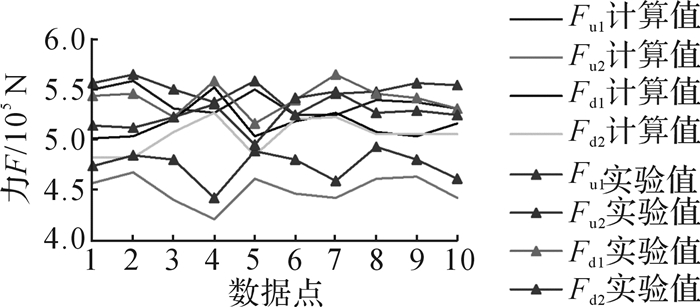
通过式(17)至式(20)可得采煤机截割工况下4根拉杆的实际载荷，再将其与实验值对比，如图 8所示：4根拉杆中，煤壁区上侧拉杆的载荷最大，其理论和实测均值分别为536 578，549 140 N；采空区上侧拉杆的载荷最小，其理论和实测均值分别为449 991，474 071 N；理论计算和实验测量值的变化曲线较为接近，但4根拉杆的实验载荷要稍大于理论计算载荷，其中采空区上侧拉杆的载荷误差相对较大，最大误差出现在第3个数据点处，为40 210 N，约为理论计算值的8%，煤壁区上侧拉杆的载荷误差相对较小，最小误差为690 N，仅为理论计算值的0.15%。
|
| 图 8 液压拉杆受力的计算值与实验值 Fig.8 The calculated and experimental force of the hydraulic pull rod |
采用小位移变形协调原理和静力学平衡方程建立了采煤机4根液压拉杆的受力模型，推导了液压拉杆载荷的理论计算公式；以采煤机滚筒和滑靴的实验测试载荷为输入，对拉杆的受力模型进行了求解，通过对比实验测试结果，验证了模型的准确性，研究结果对采煤机液压拉杆初始安装预紧力的设定具有较强的工程意义。
参考文献
| [1] |
宋泽锋, 王维发, 王培科.
采煤机液压拉杠断裂原因[J]. 煤矿机械, 2010, 31(11): 109–111.
SONG Ze-feng, WANG Wei-fa, WANG Pei-ke. Analysis on fracture reasons of shearer hydraulic rod[J]. Coal Mine Machinery, 2010, 31(11): 109–111. DOI:10.3969/j.issn.1003-0794.2010.11.046 |
| [2] |
刘显军, 洪军, 刘志刚.
不同载荷工况下机床主轴预紧力选取的数值分析方法[J]. 计算机辅助工程, 2011, 20(2): 90–94.
LIU Xian-jun, HONG Jun, LIU Zhi-gang. Numerical analysis method on preload selection for machine tool spindle under different load conditions[J]. Computer Aided Engineering, 2011, 20(2): 90–94. |
| [3] |
黄奎, 莫健华, 陈柏金, 等.
双柱上传动锻造水压机多根拉杆顺序加载预紧力分析[J]. 中国机械工程, 2008, 19(7): 865–871.
HUANG Kui, MO Jian-hua, CHEN Bai-jin, et al. Pretension analysis for sequence loaded tension-bolts of twin columns drive-up assembled frame hydraulic forging press[J]. China Mechanical Engineering, 2008, 19(7): 865–871. |
| [4] |
李玲, 蔡力钢, 郭铁能.
不同预紧力下栓接结合部法向等效特性[J]. 北京工业大学学报, 2013, 35(9): 660–666.
LI Ling, CAI Li-gang, GUO Tie-neng. Normal equivalent properpulls of the bolted joints in different reload[J]. Journal of Beijing University of Technology, 2013, 35(9): 660–666. |
| [5] |
毛君, 姜鹏, 谢苗.
斜切状态下滚筒采煤机液压拉杠力学分析与寿命预测[J]. 工程设计学报, 2015, 22(1): 95–100.
MAO Jun, JIANG Peng, XIE Miao. Force analysis and life prediction of hydraulic rod on drum shear under the condition of oblique cutting[J]. Chinese Journal of Engineering Design, 2015, 22(1): 95–100. |
| [6] |
单东生, 贾向东, 赵长财.
全预紧组合框架液压机的预紧力研究[J]. 机械工程学报, 2015, 51(14): 150–157.
SHAN Dong-sheng, JIA Xiang-dong, ZHAO Chang-cai. Research on pre-tension force of the preloaded composite frame hydraulic press[J]. Journal of Mechanical Engineering, 2015, 51(14): 150–157. |
| [7] |
吴生富, 聂绍珉, 金淼, 等.
大型锻造液压机全预紧机架的整体性分析[J]. 燕山大学学报, 2006, 30(2): 143–146.
WU Sheng-fu, NIE Shao-min, JIN Miao, et al. Overall working performance analysis of fully pretightened frame[J]. Journal of Yanshan University, 2006, 30(2): 143–146. |
| [8] |
何敏, 孙智.
基于接触理论的高速精密压力机预紧力研究[J]. 机械工程学报, 2010, 46(11): 165–172.
HE Min, SUN Zhi. Research on pre-tightened loads of the high-speed precision press with contact theory[J]. Journal of Mechanical Engineering, 2010, 46(11): 165–172. |
| [9] |
金淼, 董晓传, 邹宗园, 等.
给定预紧力下组合机架的上限载荷计算[J]. 中国机械工程, 2012, 23(20): 2476–2581.
JIN Miao, DONG Xiao-chuan, ZOU Zong-yan, et al. Calculation of upper limit load for assembled frame hydraulic press under given per-tightened force[J]. China Mechanical Engineering, 2012, 23(20): 2476–2581. DOI:10.3969/j.issn.1004-132X.2012.20.017 |
| [10] |
董晓传, 金淼, 姚阳, 等.
基于等效梁长法的组合深梁临界预紧力计算模型[J]. 机械工程学报, 2015, 51(15): 46–52.
DONG Xiao-chuan, JIN Miao, YAO Yang, et al. Calculation model of critical preload of prestressed composite deep beam based on the method of equivalent-beam-length[J]. Journal of Mechanical Engineering, 2015, 51(15): 46–52. |
| [11] |
董晓传, 金淼.
预紧组合结构液压机临界预紧力的研究[J]. 中国机械工程, 2014, 25(9): 1158–1163.
DONG Xiao-chuan, JIN Miao. Study on critical preload of prestressed composite structure hydraulic press[J]. China Mechanical Engineering, 2014, 25(9): 1158–1163. |
| [12] |
郭宝峰, 于琳琳, 金淼.
预应力组合下横梁临界预紧力影响因素研究[J]. 中国机械工程, 2013, 24(19): 2567–2572.
GUO Bao-feng, YU Lin-lin, JIN Miao. Research on influence factors of critical pretension force in prestressed assembled lower beam[J]. China Mechanical Engineering, 2013, 24(19): 2567–2572. DOI:10.3969/j.issn.1004-132X.2013.19.003 |
| [13] |
段志东, 苏铁明.
组合机架的刚度分析和拉杆预紧力研究[J]. 机械科学与技术, 2009, 28(4): 450–454.
DUAN Zhi-dong, SU Tie-ming. Analysis of the deformation of assembled frames and the pretension of tension bolts[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(4): 450–454. |
| [14] |
唐景林, 李志明, 马丽霞, 等.
预应力框架大型液压机拉杆预紧力非缓解测量研究[J]. 机械工程学报, 2010, 46(22): 70–74.
TANG Jing-lin, LI Zhi-ming, MA Li-xia, et al. Research on non-release measurement of pretension force of the tie rod in pre-stressed frame hydraulic press[J]. Journal of Mechanical Engineering, 2010, 46(22): 70–74. |
| [15] |
李艳聪, 张连洪, 刘占稳, 等.
刚度和质量驱动的预紧组合框架式液压机多目标优化设计[J]. 机械工程学报, 2010, 46(1): 140–146.
LI Yan-cong, ZHANG Lian-hong, LIU Zhan-wen, et al. Multi-objective optimization design of heavy forge framed hydraulic press driven by stiffness and mass[J]. Journal of Mechanical Engineering, 2010, 46(1): 140–146. |
| [16] |
李艳聪, 张连洪, 喻宏波, 等.
液压机主机有限元分析模型建立及实验验证[J]. 机械科学与技术, 2012, 31(2): 229–233.
LI Yan-cong, ZHANG Lian-hong, YU Hong-bo, et al. Finite element analysis of hydraulic press and experimental verification[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(2): 229–233. |
| [17] |
单祖辉.
材料力学[M]. 北京: 高等教育出版社, 2010: 35-38.
SHAN Zu-hui. Mechanics of Materials[M]. Beijing: Higher Education Press, 2010: 35-38. |
| [18] |
徐芝纶.
弹性力学[M]. 北京: 高等教育出版社, 2013: 15-19.
XU Zhi-lun. Elastic theory[M]. Beijing: Higher Education Press, 2013: 15-19. |