2. 许继电气股份有限公司, 河南 许昌 461000;
3. 国家电网河北省电力有限公司 沧州市渤海新区供电分公司, 河北 沧州 061000
2. Xuji Electric Co., Ltd., Xuchang 461000, China;
3. Bohai New Area Power Branch, Cangzhou City, State Grid Hebei Electric Power Co., Ltd., Cangzhou 061000, China
电连接器是一种基础机电元件,主要用于实现电信号的传输和控制以及电气设备间的电连接功能,广泛应用于航空航天、电子、通信等领域。电连接器可靠性水平的高低对系统的安全运行有重要的影响[1]。
动态环境是影响电连接器使用阶段接触性能最主要的环境因素之一[2-3],国内外学者关于动态环境(如振动与冲击)对电连接器接触性能影响的研究主要包括2个方面。1)试验或物理模型研究:陈文华等对电连接器在振动应力作用下的接触失效进行了物理分析,推导出航天电连接器的寿命服从威布尔分布,并根据试验方案预测了电连接器寿命[4];Seehas通过建立接触件的物理模型来研究振动对电连接器接触失效的影响,并进行了寿命预测[5];Sawchyn和Sproles研究了机械冲击对电连接器接触可靠性的影响[6]。2)仿真研究:龙慧娟利用有限元软件ANSYS求得插合状态下电连接器接触件间的接触压力,并通过LS-DYNA软件分析了振动应力作用下插针与插孔间的相对运动[7];Xie等利用有限元分析软件ABAQUS仿真分析了针式电连接器接触件间微动的相位、幅值与激振频率的对应关系[8]; Ishimaru等通过仿真发现电连接器在微动磨损状态下接触件接触电阻的变化规律与传统试验结果相似[9]。然而,并未见冲击条件下电连接器接触性能的仿真研究文献。
综上,本文提出了基于ANSYS的电连接器冲击试验仿真研究方法,以某型号电连接器为例,仿真研究冲击环境下该电连接器接触性能的变化规律。
1 冲击试验仿真研究方案本文选用某公司生产的典型的圆形三针电连接器进行冲击试验仿真研究,试验条件选择试验严酷等级、冲击方向和次数。根据GB/T 2423.5—1995中的规定,选用半正弦波脉冲作为冲击脉冲,选择沿插孔到插针的垂直轴向方向作为冲击方向,冲击次数设定为1次,并结合实际需要制定不同的冲击试验严酷等级,如表 1所示。冲击试验的严酷等级包括脉冲峰值加速度P和脉冲持续时间D,本文用(P, D)来表达。
| 脉冲峰值加速度/(m/s2) | 脉冲持续时间/ms | |||||
| 1 | 3 | 6 | 11 | 18 | 30 | |
| 50 | (50, 1) | (50, 3) | (50, 6) | (50, 11) | (50, 18) | (50, 30)* |
| 150 | (150, 1) | (150, 3) | (150, 6) | (150, 11)* | (150, 18) | (150, 30) |
| 300 | (300, 1) | (300, 3)* | (300, 6)* | (300, 11)* | (300, 18)* | (300, 30) |
| 500 | (500, 1) | (500, 3) | (500, 6) | (500, 11)* | (500, 18) | (500, 30) |
| 1 000 | (1 000, 1) | (1 000, 3) | (1 000, 6)* | (1 000, 11)* | (1 000, 18) | (1 000, 30) |
| 2 000 | (2 000, 1) | (2 000, 3)* | (2 000, 6) | (2 000, 11) | (2 000, 18) | (2 000, 30) |
| 5 000 | (5 000, 1)* | (5 000, 3) | (5 000, 6) | (5 000, 11) | (5 000, 18) | (5 000, 30) |
| 注:1)“*”为GB/T 2423.5—1995推荐的部分试验严酷等级。 | ||||||
本文通过分量的方式施加加速度载荷; 通过函数方式施加半正弦波脉冲,即设置关于时间的正弦函数Z×sin(A×t),通过改变参数Z来得到不同的脉冲峰值加速度P,通过参数t来设置相应的脉冲持续时间D,根据设置好的脉冲持续时间调整系数A来得到该正弦函数的前半周期,这个正弦函数的前半周期波形即为所需波形。
2 冲击试验的仿真及其结果分析本文选用ANSYS软件仿真研究冲击环境下电连接器接触性能参数的变化规律。
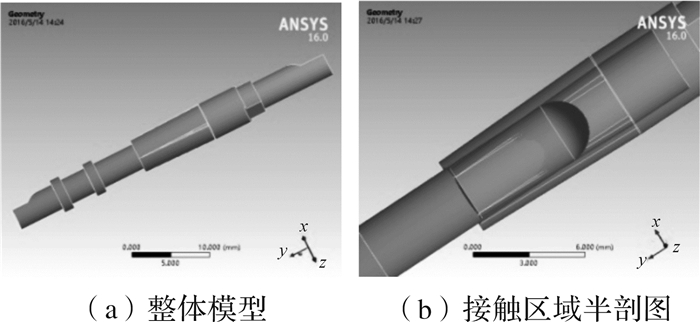
2.1 电连接器接触件建模某型号航空电连接器插合状态下的单个接触件模型如图 1所示。
|
| 图 1 插合状态下电连接器接触件的三维模型 Fig.1 Three dimensional model of electrical connector contact under the condition of pluge |
由图 1可知,插孔端部为缩口结构,插针与插孔为过盈配合,当插针插入时插孔簧片会发生一定程度的挤压变形,产生接触压力(即x方向的分力),以保障电连接器的可靠接触。
2.2 接触件静力学仿真分析本文依照表 2设置接触件材料属性, 接触类型设为摩擦接触, 接触行为设为非对称接触。采用自动网格划分方式,对各插孔簧片及接触棱线进行了细密划分,网格单元大小分别设定为1.5 mm和0.13 mm;将插针和插孔固定端分别施加固定约束后,接触件静力学仿真计算结果如图 2所示。
| 参数 | 材料类型 | 密度/kg·m-3 | 弹性模量/GPa | 泊松比 | 屈服强度/MPa | 切线模量/MPa | 抗拉强度/MPa | 弹性极限/MPa |
| 数值 | 黄铜(H62) | 8 400 | 100 | 0.324 | 240 | 1 150 | 600 | 420 |

|
| 图 2 接触件静力学仿真结果 Fig.2 Static simulation results of contact |
由图 2可知:1)接触件插合状态下,插孔簧片形变集中在簧片端部(最大形变量为0.155 46 mm),沿轴线方向呈递减趋势,距簧片根部2 mm处减小为零,随着离簧片端部距离的增加,形变变化梯度也呈递减趋势;2)插孔等效应力以“火焰状”集中分布在插孔与插针接触区域和簧片缝隙附近,其最大值为249.16 MPa,位于插孔簧片根部近缝隙处,该应力值超过了接触件材料的屈服强度,可能会产生局部塑性形变;3)接触件的受力中,主要是x方向的分力, 即垂直于接触件接触面的接触压力,为3.926 N,y方向的分力即摩擦力相对较小。
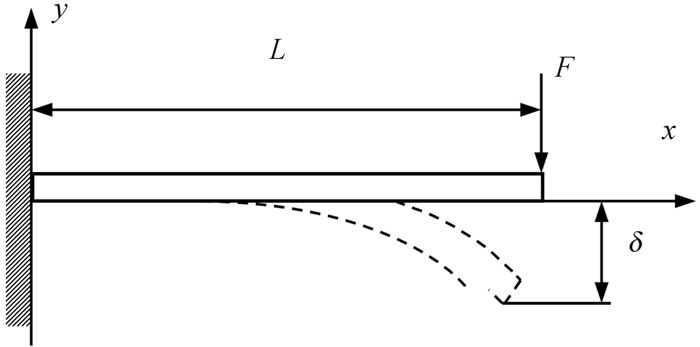
由材料力学相关理论可知,插孔中单个接触簧片可简化成悬臂梁模型,如图 3所示。
|
| 图 3 单个插孔簧片的悬臂梁简化模型 Fig.3 Simplified model of cantilever beam for single jack spring |
| $ F\text{=}\frac{3E{{I}_{x}}\delta }{{{L}^{3}}} $ |
式中:F为插孔发生变形后对插针产生的接触压力,N;E为插孔材料的弹性模量,MPa;δ为挠度(即插孔缩口处簧片的径向偏移),mm;Ix为插孔簧片截面关于中性层轴x的惯性矩,mm4;L为插孔簧片长度,mm。
依据插孔结构尺寸的测量数据,由公式(1)得接触压力的理论值为3.970 2 N。由此可知仿真结果误差约为1.1%,由此表明本文所建立的接触件模型可用于冲击试验仿真研究。
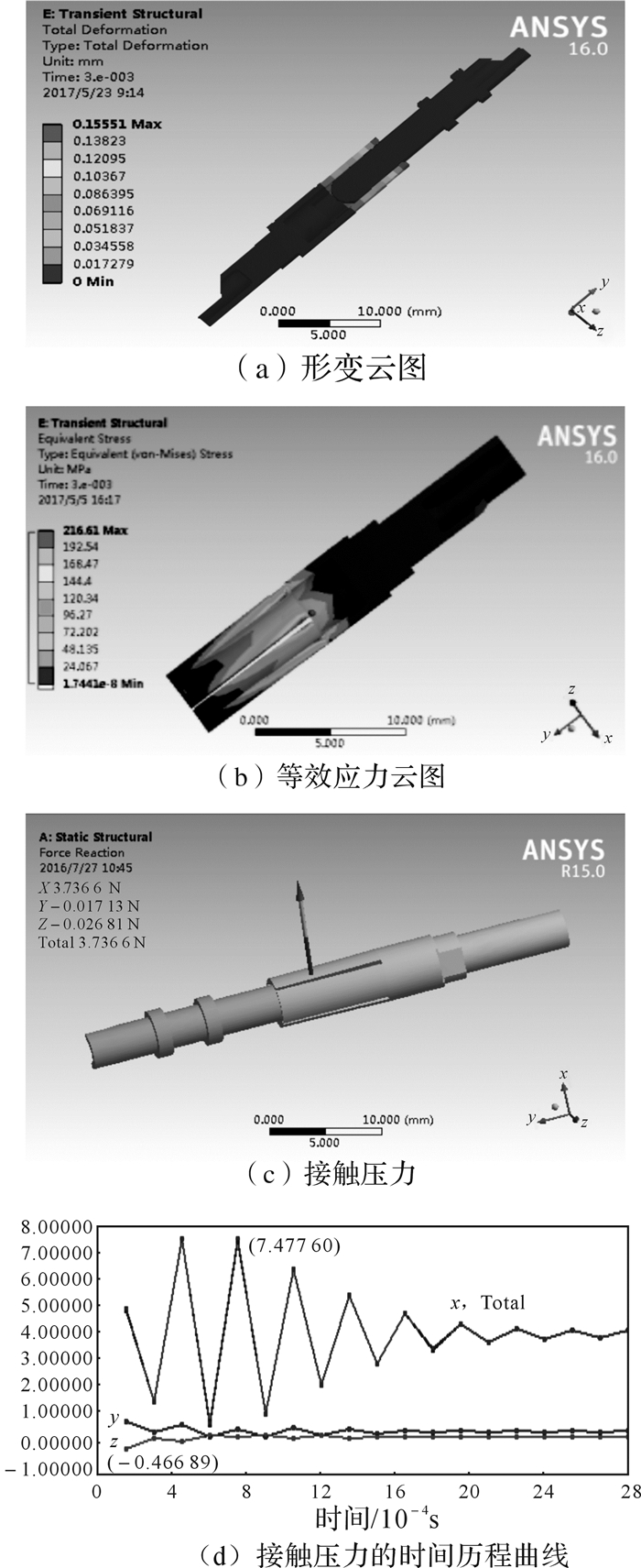
2.3 冲击试验仿真结果分析通过观察接触件的形变、应力和接触压力等参数的变化情况来研究冲击对电连接器接触性能的影响。图 4所示为严酷等级为(2 000, 3)时的接触件冲击试验仿真结果。
|
| 图 4 严酷等级为(2 000, 3)时的接触件冲击试验仿真结果 Fig.4 Simulation results of impact test for contacts at severity level (2 000, 3) |
由图 4(a)可知:1)在受到冲击作用后,插针形变微弱,插孔簧片形变规律近似于静力学仿真结果;2)相比于正常插合状态,插孔最大形变量(0.155 51 mm)略有增加,推测冲击作用使形变量增大。
由图 4(b)可知:1)受到冲击作用后,等效应力主要集中在插针与插孔接触区域和插孔簧片根部缝隙附近,与静力学分析一致,说明冲击作用未对等效应力分布产生影响;2)受到冲击作用后,接触件应力最大值略小于静力学仿真结果。
由图 4(c)、(d)可知:1)与静力学分析中接触压力(3.926 N)相比,冲击作用下接触压力(3.736 6 N)减小了约4.82%,且轴向方向(y方向)的摩擦力略微减小,这表明,冲击过程中,接触件会出现轴向位移微动现象;2)冲击初期,接触压力值有较大波动且最大值和最小值较静力学分析值有显著差异,随后其波动变小,直至趋于稳定。这是由于插针固装于针座中,而插孔嵌套于孔座中,在受到冲击作用的初始阶段,插针与针座可看作一个整体发生运动,而插孔与孔座的运动会有差异,因此插针与插孔可能会同时发生轴向和垂直于轴向的相对运动。
接触电阻是判断电连接器是否可靠工作的重要指标,与电连接器接触件间的接触压力成反比关系[11-12]:
| $ {{R}_{j}}=k{{\left( 0.102F \right)}^{-m}} $ |
式中:Rj为接触电阻,μΩ;F为接触压力,N;k是与接触材料密度、材料强度以及表面膜等相关的系数;m是与接触形式、压力范围以及实际接触点个数等因素有关的系数。本文选定接触件接触形式为[12]线接触(m=0.7)及黄铜-黄铜接触(k=670)。
若电连接器试品的接触电阻超过其阈值(5 mΩ),即被认为接触失效[13-16]。根据式(2),由接触电阻阈值可求出接触压力的最小临界值为0.555 N。
3 冲击对电连接器接触性能参数的影响进行电连接器冲击试验仿真研究,分析不同严酷等级、不同脉冲持续时间及不同峰值加速度下电连接器接触性能参数的变化规律。
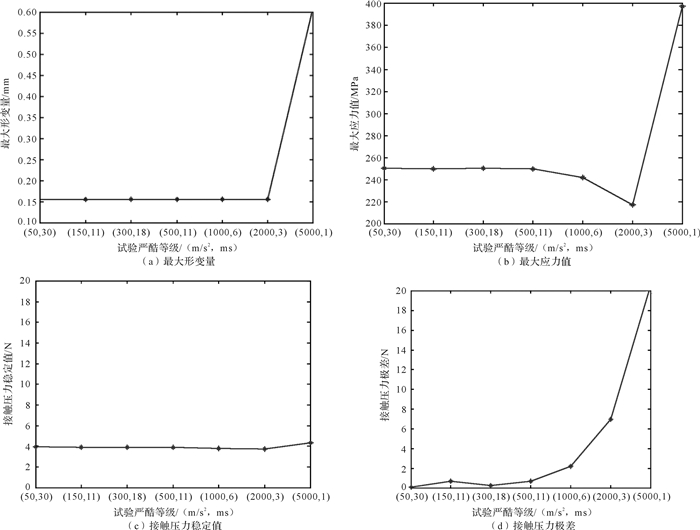
3.1 严酷等级的影响不同严酷等级下,电连接器接触件的最大形变量、最大应力值和接触压力变化曲线如图 5所示。
|
| 图 5 不同严酷等级下电连接器冲击试验仿真结果 Fig.5 Impact test simulation results of the electrical connector under different severity level |
由图 5可知:当试验严酷等级未超过(2 000, 3)时,随着试验严酷等级的不断提高,最大形变量保持稳定,最大应力值缓慢减小;超过(2 000, 3)时,最大形变量和最大应力值有大幅递增趋势。
接触压力的稳定值基本保持恒定,在严酷等级由(2 000, 3)增加到(5 000, 1)的过程中,有缓慢增大的趋势,但增幅不明显。除严酷等级(150, 11)外,随着试验严酷等级的不断提高,接触压力极差在整个冲击历程中呈指数性增大。从数值上看,严酷等级变化引起的最大形变量和接触压力稳定值变化远远低于最大应力值与压力极差的变化。
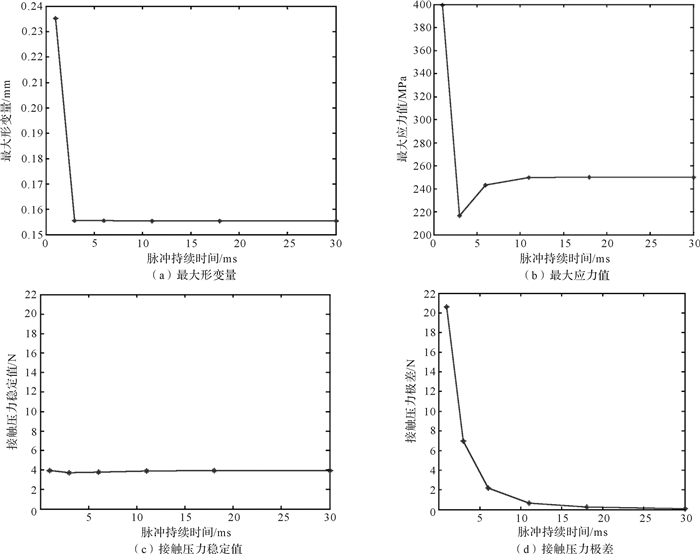
3.2 脉冲持续时间的影响图 6所示为峰值加速度为500 m/s2时,不同脉冲持续时间下接触件性能参数的变化规律;其他峰值加速度条件下,接触性能参数随脉冲持续时间的变化规律与图 6相似。
|
| 图 6 脉冲峰值加速度为500 m/s2、不同脉冲持续时间下电连接器冲击试验仿真结果 Fig.6 Impact test simulation results of the electrical connector under different pulse duration with peak acceleration of 500 m/s2 |
由图 6可知:随着脉冲持续时间的增加,最大形变量呈下降趋势,在1-3 ms时最大形变量变化幅度显著,减小了33.90%;当脉冲持续时间继续增加时,接触件的最大形变量小幅度减小。最大应力值呈先减小后增大趋势,在1-3 ms时最大应力值减小;在3-11 ms时应力值先逐渐增加,之后趋于稳定。接触压力的稳定值随脉冲持续时间的变化基本保持不变。而接触压力的极差随着脉冲持续时间的增大而减小,最后接近于零。对比图 6(a)、(b)、(c)和(d)可知,在1-6 ms时,除接触压力稳定值外各接触性能参数都出现较大波动,这表明在一定程度上较短的脉冲持续时间对电连接器接触件接触性能参数的影响更为显著。
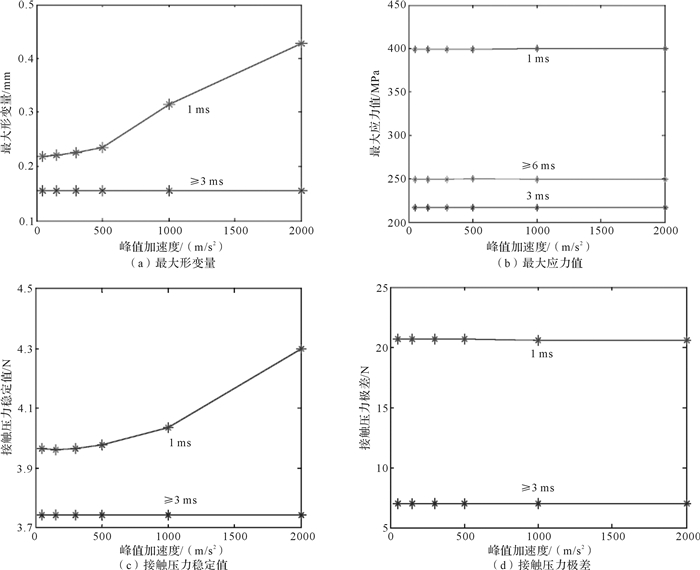
3.3 脉冲峰值加速度的影响图 7所示为不同脉冲峰值加速度下电连接器接触件接触性能参数的变化曲线。
|
| 图 7 不同脉冲峰值加速度下电连接器冲击试验仿真结果 Fig.7 Impact test simulation results of the electrical connector under different peak acceleration |
由图 7可见,当脉冲持续时间为1 ms时,随着峰值加速度的增大,接触件的最大形变量逐渐增大,且不同峰值加速度下其最大形变量均大于静力学分析下的最大形变值;而脉冲持续时间大于或等于3 ms时, 接触件的最大形变量恒为0.155 51 mm,与静力学分析结果(0.155 46 mm)基本一致。当脉冲持续时间为1,3 ms和大于或等于6 ms时,随着峰值加速度的增大,接触件的最大应力值均呈现微小波动,但脉冲持续时间为1 ms时最大应力值要高些,3 ms时最大应力值最小。当脉冲持续时间为1 ms时,接触压力稳定值逐渐增大,接触压力极差保持不变。脉冲持续时间大于或等于3 ms时,接触压力的稳定值和极差都基本恒定。
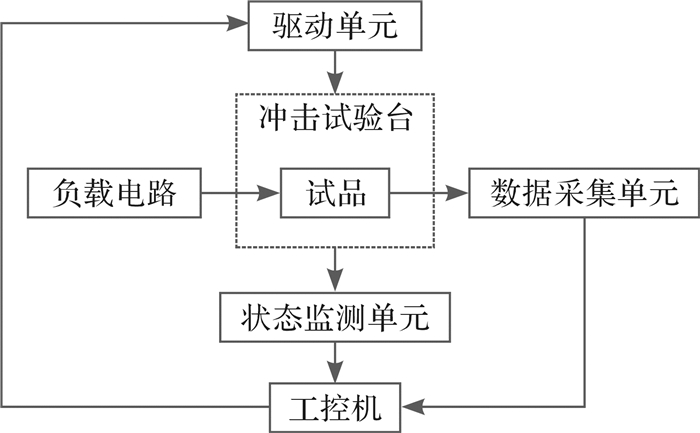
4 冲击试验验证 4.1 冲击试验装置的设计结合电连接器试品的结构特点,以应变传感技术为基础设计了冲击环境下电连接器接触压力的检测装置,其工作原理框图如图 8所示。
|
| 图 8 电连接器接触压力检测装置原理框图 Fig.8 Principle block diagram of contact force detection device for electrical connector |
由图 8所示,电连接器接触压力检测装置主要分为冲击驱动单元、状态监测单元、负载电路和数据采集单元四个部分。
数据采集单元选用电阻应变法来检测冲击环境下电连接器的接触压力,其测试原理如公式(3)[17]:
| $ F=\frac{{{W}_{i}}E{{\varepsilon }_{i}}}{l-i} $ | (3) |
式中:Wi表示接触簧片i处的抗弯模量,MPa; E为插孔材料弹性模量,MPa; εi为应变处的应变量; l为接触簧片长度, mm。
根据机械设计手册可知[10],接触簧片i处的抗弯模量为:
| $ {{W}_{i}}=\frac{{{I}_{x}}}{R-h} $ | (4) |
式中:Ix为插孔簧片截面关于中性层轴x的惯性矩,R为插孔外半径,h为中性层轴x与插孔外圆圆心的距离。
接触簧片截面在轴向上可认为是不变的,即截面对中性层轴Ix及i处的抗弯模量Wi都为常量,即不随i的位置改变而变化。由式(3)和(4)及接触件尺寸数据可得到简化式:
| $ F=\frac{19.126}{0.0958-i}{{\varepsilon }_{i}} $ | (5) |
测得应变量εi,就可根据式(5)得到接触压力值。
4.2 验证试验结果分析冲击试验仿真结果中的接触压力值与接触电阻值直接相关,最能直观体现电连接器接触性能的变化规律。因此,本文对接触压力进行了部分验证试验,并与其仿真结果进行比较,如表 4所示。
| 试验严酷等级/(m/s2, ms) | 接触压力/N | 误差/% | |
| 仿真试验结果 | 验证试验结果 | ||
| 50, 30 | 3.936 3 | 3.981 34 | 1.13 |
| 50, 18 | 3.922 7 | 3.975 90 | 1.34 |
| 50, 11 | 3.891 5 | 3.913 61 | 0.56 |
| 50, 6 | 3.789 5 | 3.847 18 | 1.50 |
| 150, 30 | 3.966 3 | 4.141 62 | 4.23 |
| 150, 18 | 3.922 6 | 4.151 71 | 5.55 |
| 150, 11 | 3.891 4 | 4.163 52 | 6.53 |
| 150, 6 | 3.789 4 | 4.118 26 | 3.12 |
| 150, 3 | 3.742 7 | 4.125 48 | 4.43 |
| 150, 1 | 3.963 2 | 4.139 87 | 4.26 |
由表 4可以看出,冲击作用下接触压力仿真结果与验证试验结果的误差最大值为6.53%,最小值为0.56%,说明仿真结果具有一定的可靠性。
5 结论本文以某型号航空电连接器为研究对象,采用仿真方法分析了冲击作用对电连接器接触性能参数的影响。结果表明:
1) 受到机械冲击作用后,接触件的最大形变量略有增加,最大应力值减小,接触压力有较为明显的变化且出现了轴向位移,可能会造成接触件的磨损。冲击初期接触压力值有较大的波动,由理论公式推算,某些时刻可能会出现瞬断故障。
2) 随着试验严酷等级的提高,接触件最大形变量缓慢增大,最大应力值缓慢减小,接触压力的稳定值缓慢减小;当试验严酷等级超过(2 000, 3)时,最大形变量增大幅度较大,最大应力值突然增大,接触压力的稳定值增大,接触压力的极差呈指数性增长,表明接触压力波动显著。
3) 相比于脉冲峰值加速度,机械冲击的脉冲持续时间对电连接器接触性能的影响更为显著。
4) 根据验证试验可知,接触压力仿真结果的误差介于6.53%和0.56%之间,表明仿真结果有一定的参考意义。
5) 在产品设计阶段,冲击试验仿真研究可有效便捷地为接触件结构设计的合理性验证提供一定的理论参考。
不同冲击条件引发的接触件性能参数变化的机理还有待于深入探索。
| [1] |
任国泰.
电连接器基本知识(1)[J]. 机电元件, 2004, 24(1): 42–45.
REN Guo-tai. Basic knowledge of electrical connector (1)[J]. Electromechanical Components, 2004, 24(1): 42–45. |
| [2] |
张菊华, 祝自强.
连接器在动态应力下电接触可靠性的研究[J]. 机电元件, 1991, 11(2): 15–19.
ZHANG Ju-hua, ZHU Zi-qiang. Research on electrical contact reliability of connectors under dynamic stress[J]. Electromechanical Components, 1991, 11(2): 15–19. |
| [3] |
储刘庆. 振动环境对开关电连接器的电接触影响的研究[D]. 北京: 北京邮电大学自动化学院, 2011: 16.
CHU Liu-qing. Research on reliability of switch connectors under dynamic environment[D]. Beijing: Beijing University of Posts and Telecommunications, School of Automation, 2011: 16. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1987190 |
| [4] |
陈文华, 崔杰, 潘骏, 等.
威布尔分布下失效率的Bayes验证试验方法[J]. 机械工程学报, 2005, 41(12): 118–121.
CHEN Wen-hua, CUI Jie, PAN Jun, et al. Bayesian demonstration test method for failure rate under Weibull distribution[J]. Journal of Mechanical Engineering, 2005, 41(12): 118–121. DOI:10.3321/j.issn:0577-6686.2005.12.023 |
| [5] | SEEHASE H. A reliability model for connector contact[J]. IEEE Transactions on Reliability, 1991, 40(5): 513-523. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=106766 |
| [6] | SAWCHYN I, SPROLES E. Optimizing force and geometry parameters in design of reduced insertion force connectors[C]//Proceedings of the 42nd Electronic Components & Technology Conference, San Diego, CA, May 18-20, 1992. http://www.ingentaconnect.com/content/iee/01486411/1992/00000015/00000006/art00014 |
| [7] |
龙慧娟. 振动对汽车电连接器可靠性的影响[D]. 北京: 北京邮电大学自动化学院, 2013: 15-48.
LONG Hui-juan. Effect of vibration on reliability of vehicle connector[D]. Beijing: Beijing University of Posts and Telecommunications, School of Automation, 2013: 15-48. http://cdmd.cnki.com.cn/Article/CDMD-10013-1013244082.htm |
| [8] | XIE Fei, FLOWERS G T, CHEN Chen. Analysis and prediction of vibration induced fretting motion in a blade/receptacle connector pair[J]. IEEE Transactions on Components and Packaging Technologies, 2009, 32(3): 585–592. DOI:10.1109/TCAPT.2009.2025776 |
| [9] | ISHIMARU Y, MASHIMO K, SUSAI K. Computational modeling for fretting simulation[C]//Proceedings of the 55th IEEE Holm Conference on Electrical Contacts, Vancouver, British Columbia, Sep. 14-16, 2009. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5284411 |
| [10] |
电机工程手册编辑委员会.
机械工程手册[M]. 2版. 北京: 机械工业出版社, 1997: 5-1-5-25.
Electrical Engineering Manual Editorial Board. Mechanical engineering manual[M]. 2th ed. Beijing: China Machine Press, 1997: 5-1-5-25. |
| [11] |
郭凤仪, 陈忠华.
电连接理论及其应用技术[M]. 北京: 中国电力出版社, 2008: 126.
GUO Feng-yi, CHEN Zhong-hua. Electric connection theory and its application technology[M]. Beijing: China Electric Power Press, 2008: 126. |
| [12] |
张冠生.
电器理论基础[M]. 北京: 机械工业出版社, 1989: 145-170.
ZHANG Guan-sheng. Electrical theory foundation[M]. Beijing: China Machine Press, 1989: 145-170. |
| [13] |
徐咏梅, 王树荣. 电工电子产品环境试验第2部分: 试验方法试验Ea和导则: 冲击: GB/T 2423. 5-1995[S]. 北京: 中国标准出版社, 1996: 3-5.
XU Yong-mei, WANG Shu-rong. Environmental testing for electric and electronic products Part 2: test methods test Ea and guidance: shock: GB/T 2423. 5-1995[S]. Beijing: China Standards Press, 1996: 3-5. |
| [14] |
国防科学技术工业委员会. 耐环境快速分离小圆形电连接器总规范: GJB 101A-1997[S]. 北京: 国防科学技术工业委员会, 1997: 10-16.
Commission of Science, Technology and Industry for National Defense. General specification for fast separation of small round electrical connectors for environmental protection: GJB 101A-1997[S]. Beijing: the Commission of Science, Technology and Industry for National Defense, 1997: 10-16. |
| [15] |
国防科学技术工业委员会. 电连接器接触件总规范: GJB 1216-1991[S]. 北京: 中国标准出版社, 1991: 10-16.
Commission of Science, Technology and Industry for National Defense. General specification for electrical connector contacts: GJB 1216-1991[S]. Beijing: China Standards Press, 1991: 10-16. |
| [16] |
任万滨, 王鹏, 马晓明, 等.
微动诱发的触点电接触间歇失效现象研究[J]. 摩擦学学报, 2013, 33(4): 382–387.
REN Wan-bin, WANG Peng, MA Xiao-ming, et al. Intermittency phenomenon of electrical contacts induced by fretting behavior[J]. Tribology, 2013, 33(4): 382–387. |
| [17] |
于长潮. 振动状态下电连接器接触压力测试技术研究[D]. 天津: 河北工业大学电气工程学院, 2015: 10-50.
YU Chang-chao. Study on testing technology of contact force for electric connectors underthe vibration state[D]. Tianjin: Hebei University of Technology, School of Electrical Engineering, 2015: 10-50. |


