2. 中南林业科技大学 物流与交通学院, 湖南 长沙 410004
2. College of Transportation and Logistics, Central South University of Forestry and Technology, Changsha 410004, China
与柴油锤、振动锤和压桩机等桩工机械相比,液压打桩锤的打击能量大,能量传递效率高,打击能可以调节,在施工中产生的噪声和污染小[1],而且锤击频率、锤击行程可控,它在桩基施工中发挥越来越重要的作用[2-3]。控制系统作为打桩锤的核心装置,其工作性能直接关系到打桩质量及打桩效率。
Patrick等[3]提出了一种利用电磁铁控制打桩机打击能和打击频率的方案。James[4]基于纯液压控制提出了水下打桩锤的控制方法,但是打桩锤的能量和频率无法调节。Iskander[5]详细地论述了单作用电液打桩锤的设计和控制。吕景忠等[6]提出了利用气液联合控制打桩锤工作的方法,但其打击能量只能通过行程阀进行有级调节。液压打桩锤的打桩频率高,则对换向的平稳性和快速性要求高[7-12],采用行程开关或接近开关控制电磁阀控制打桩锤工作产生的换向冲击大,导致系统故障率高,可靠性较差[12-18]。为此,本文设计了一种新型打桩锤的电液控制系统,使液压打桩锤的打桩过程更加平稳可靠,同时通过时间继电器控制换向阀的换向时间也使冲击能和冲击频率实现了无级调节,同时还能保证打击重复的精度,提高液压打桩锤的打桩质量和打桩效率。
1 新型打桩锤电液控制系统原理设计电液一体化打桩锤工作原理如图 1所示。首先,在上位机上设置打桩锤的桩的大小和类型,上位机从离线数据库中调取上升时间数据, 电磁阀16处于右位机得电状态,电磁阀的控制口和电磁阀的回油口相通,顺序阀18控制腔内的压力油流向电磁阀的控制口(即顺序阀18处于关闭状态),再流向电磁阀16的回油口,之后流回回油箱。第3插装阀14控制腔内的压力油流向电磁阀的控制口(即第3插装阀14处于打开状态),再流向电磁阀16的回油口,再流回回油箱。压力油装置中的压力油流向第1单向阀7后:一部分流向差动液压缸9的下液压腔,以促使打桩锤向上运动;另一部分流向第1插装阀12和第2插装阀13的控制腔,使得第1插装阀12和第2插装阀13处于关闭状态。由于第1插装阀12和第2插装阀13处于关闭状态,压力油只能流入第1插装阀12和第2插装阀13的下容腔内;由于顺序阀18处于关闭状态,一部分的压力油只能流到顺序阀18的第一油口处。差动液压缸9上液压腔内的压力油,一部分流向第1插装阀12的上容腔,另一部分流向第3插装阀14的下容腔。第1插装阀12上容腔的压力油流向第2插装阀13的上容腔后再流向第3插装阀14的下容腔。由于第3插装阀14处于打开状态,第3插装阀14下容腔内的压力油流向回油箱。通过控制电磁阀的得电时间可控制打桩锤的上升高度。
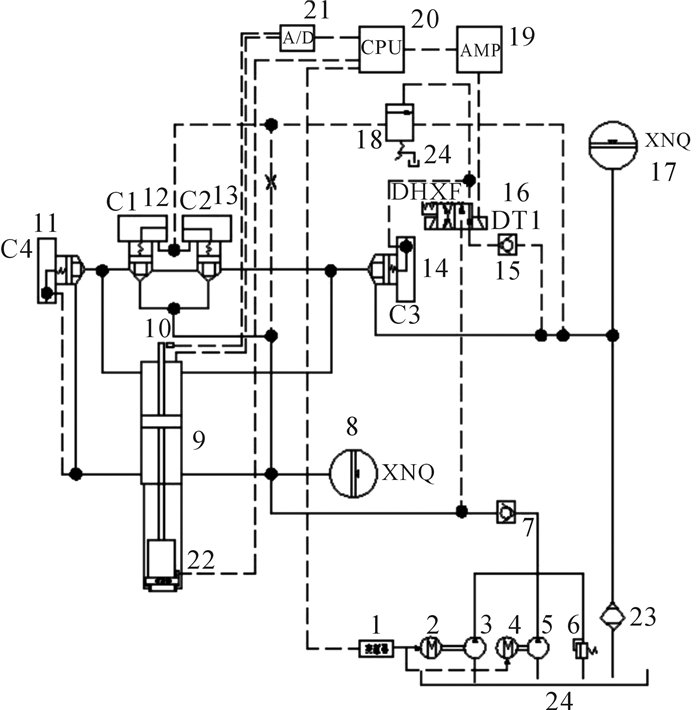
|
| 1—变频器;2,4—变频电机;3,5—定量泵;6—溢流阀;7,15—单向阀;8,17—蓄能器;9—差动液压缸;10—行程开关;11,12,13,14—插装阀;16—电磁阀;18—顺序阀;19—功率放大器;20—CPU;21—数/模转换器;22—脱桩保护开关;23—精滤油器;24—油箱 图 1 电液一体化打桩锤系统原理图 Fig.1 Schematic diagram of the electro-hydraulic pile hammer system |
当打桩锤进行落锤作业时,该液压控制系统的电磁阀16处于左位机得电状态,电磁阀的控制口和压力油口相通,压力油装置中的压力油流向第1单向阀7后:一部分经电磁阀后流向顺序阀18的控制腔内(即顺序阀18处于打开状态);另一部分经电磁阀后流向第3插装阀14的控制腔(即第3插装阀14处于关闭状态)。由于顺序阀处于打开状态,第1插装阀12和第2插装阀13控制腔内的压力油流过顺序阀18后再流回回油箱。然后压力油装置的压力油再次流向第1单向阀后,一部分压力油流向第1插装阀12和第2插装阀13的下容腔后(即第1插装阀12和第2插装阀13已处于打开状态),再流入差动液压缸9的上液压腔,以促使打桩锤向下运动。差动液压缸9下液压腔内的压力油流向第1插装阀12和第2插装阀13的下容腔,从而使得上液压腔和下液压腔相连通。数/模转换器21、行程开关10反馈的信号可以确定当前岩土的阻力,从而通过上位机的计算来优化上升和下降时间。
该液压控制系统处于中位缓冲过程时,打桩锤处于最低位置,第1插装阀12、第2插装阀13和第3插装阀14处于换向期间的关闭状态,顺序阀18处于关闭状态。当所打击的桩有反弹时,差动液压缸9的上液压腔的压力处于瞬时憋压状态,此时第4插装阀11会打开,从而使差动液压缸9的上液压腔和下液压腔相连通,起到缓冲作用;同时,第1蓄能器8可以吸收此时油路振动脉冲的能量,起到减振作用。
配备该控制系统的打桩锤具有如下独特的功能:
1) 采用在线监测和上位机处理数据,保证打桩所要求的能量和打击的重复精度高,同时使得打桩锤时间控制更加合理且打桩效率更高。
2) 插装阀和蓄能器的使用使得换向压力波动小、输油管晃动小。
3) 具有高的安全保护作用,上位机CPU能监测打桩过程中出现的危险情况,如预制桩的断裂或者桩帽的脱离等。脱桩保护开关22反馈信号使得液压系统通过自锁来制动锤头,从而很好地保护了桩锤,保证了操作安全。
4) 该系统采用高速开关阀和大流量插装阀组合,使得该系统与上位机系统连接方便,同时使该系统的响应速度和可靠性更好。蓄能器的使用也使得该系统的能量利用率增高。
5) 上位机CPU的闭环控制使得该系统能够通过传感器对打桩过程进行动态监测和反馈,从而很好地控制了油压和桩锤的上升及下降时间,提高了打桩效率。
2 打桩锤液压系统的数学模型及参数设计 2.1 提锤过程的数学模型建立打桩锤提锤过程中液压系统简化图如图 2所示。
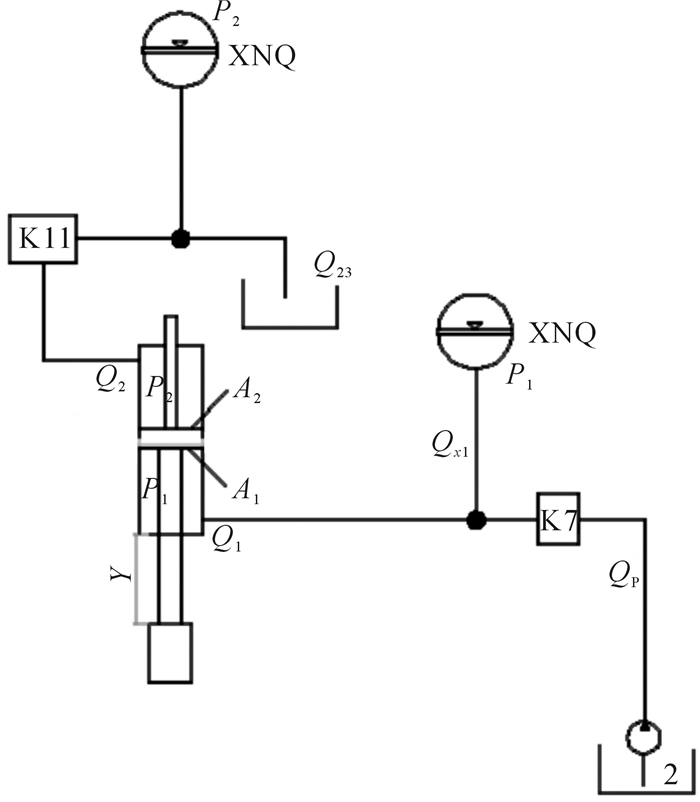
|
| 图 2 提锤过程中液压系统简化图 Fig.2 Schematic diagram of the hydraulic system in the process of hammer lifting |
打桩锤活塞杆受力平衡方程:
| $ \begin{array}{l} m{{\ddot Y}_1} + mg + {F_{{\rm{s1}}}}\left( {{{\dot Y}_1},\Delta P} \right) + {F_{{\rm{l1}}}}\left( {{P_1},{P_2}} \right) + \\ {F_{\rm{f}}} + {F_2}\left( {{P_2}} \right) = {F_1}\left( {{P_1}} \right) \end{array} $ | (1) |
| $ \begin{array}{l} {F_{{\rm{s1}}}} = \frac{{{\rm{ \mathsf{ π} }}u}}{{\sqrt {1 - {\xi ^2}} }}\left( {\frac{{d{l_1}}}{h} + \frac{{DL}}{h}} \right){{\dot Y}_1} + {\mathop{\rm sgn}} \left( {{{\dot Y}_1}} \right)\\ \;\;\;\;\;\;\;\left[ {\frac{{{\rm{ \mathsf{ π} }}dh}}{2}\left( {{P_1} - {P_0}} \right) + \frac{{{\rm{ \mathsf{ π} }}dh}}{2}\left( {{P_1} - {P_2}} \right)} \right] \end{array} $ | (2) |
| $ {F_{{\rm{l1}}}} = \tau lD\left( {{P_1} - {P_2}} \right) $ | (3) |
| $ {F_{\rm{f}}} = 3\mu {\rm{ \mathsf{ π} }}{P_1}d{l_1} $ | (4) |
| $ {F_1}\left( {{P_1}} \right) = {P_1}{A_1} $ | (5) |
| $ {F_2}\left( {{P_2}} \right) = {P_2}{A_2} $ | (6) |
式中:m为锤体和活塞杆的质量之和,kg;Y为活塞杆位移, m;Fs1为黏性摩擦阻力,N; Fl1为液压卡紧力,N; Ff为密封圈阻力,N; F1(P1),F2(P2)为轴向阻力,N; D为液压缸内径,m;h为活塞杆大径的厚度,m;P1为提锤过程中液压腔下腔工作压力,MPa;P2为提锤过程中液压腔上腔工作压力,MPa;A1为液压缸体下腔面积,m2;A2为液压缸体上腔面积,m2。
提锤油缸进油口流量方程:
| $ {Q_1} = {Q_{\rm{p}}} - {Q_{{\rm{x}}10}} $ | (7) |
阶段压力平衡方程:
| $ {P_1} = {P_{{\rm{x}}10}} - {C_1}{\left( {{A_1}v} \right)^2} $ | (8) |
| $ {P_2} = {P_{{\rm{x}}2}} + {C_2}{\left( {{A_2}v} \right)^2} $ | (9) |
提锤过程中蓄能器内气体体积为:
| $ {V_{{\rm{x}}10}} = {V_{{\rm{x}}11}} + {A_2} \cdot Y - {Q_{\rm{p}}} \cdot t $ | (10) |
第1蓄能器的气体状态方程:
| $ {P_{{\rm{x1}}}}V_{{\rm{x1}}}^{1.4} = {P_{{\rm{x10}}}}V_{{\rm{x10}}}^{1.4} = {C_{{\rm{x1}}}} $ | (11) |
第2蓄能器的气体状态方程:
| $ {P_{{\rm{x2}}}}V_{{\rm{x2}}}^{1.4} = {P_{{\rm{x20}}}}V_{{\rm{x20}}}^{1.4} = {C_{{\rm{x2}}}} $ | (12) |
油泵开启后,系统压力逐渐升高,达到与平衡桩锤重力相等时,假定此时临界压力为Px11,由锤体平衡条件得:
| $ {P_{{\rm{x11}}}}{A_1} = mg $ | (13) |
| $ {P_{{\rm{x11}}}}V_{{\rm{x11}}}^{1.4} = {C_{{\rm{x1}}}} $ | (14) |
结合式(7),(9),(12)和(13)可得:
| $ {P_1} = \frac{{{C_{{\rm{x1}}}}}}{{{{\left( {\sqrt[{1.4}]{{{C_{{\rm{x1}}}}{A_1}/mg}} + {A_1}Y - {Q_{\rm{p}}}{\rm{t}}} \right)}^{1.4}}}} - {C_1}{\left( {{A_1}v} \right)^2} $ | (15) |
将式(15)代入式(1)可得:
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{{\frac{{{C_{{\rm{x1}}}}{A_1}}}{{{{\left( {\sqrt[{1.4}]{{{C_{{\rm{x1}}}}{A_1}/mg}} + {A_1}Y - {Q_{\rm{p}}}{\rm{t}}} \right)}^{1.4}}}} - {C_1}{A_1}{{\left( {{A_1}v} \right)}^2}}}{m} - }\\ {\frac{{{F_{{\rm{s1}}}} - {F_{{\rm{l1}}}} - {F_{\rm{f}}} - {P_{{\rm{x2}}}}{A_2} - {C_2}{A_2}{{\left( {{A_2}v} \right)}^2}}}{m} - g} \end{array} $ | (16) |
式中:v为提锤过程中锤的速度,m/s;Qp为液压泵输出流量,m3/s;Qx10表示蓄能器进口管道流量,m3/s; Px0,Px11为第1蓄能器瞬时压力,MPa;C1为进油管道和阀体K7的液阻,N·s2/m8;C2为进油管道和阀体K7及K11的液阻,N·s2/m8,Cx1,Cx2为气体常数,J/mol·K。
2.2 下打过程的数学模型建立打桩锤下打过程中液压系统简化图如图 3所示。
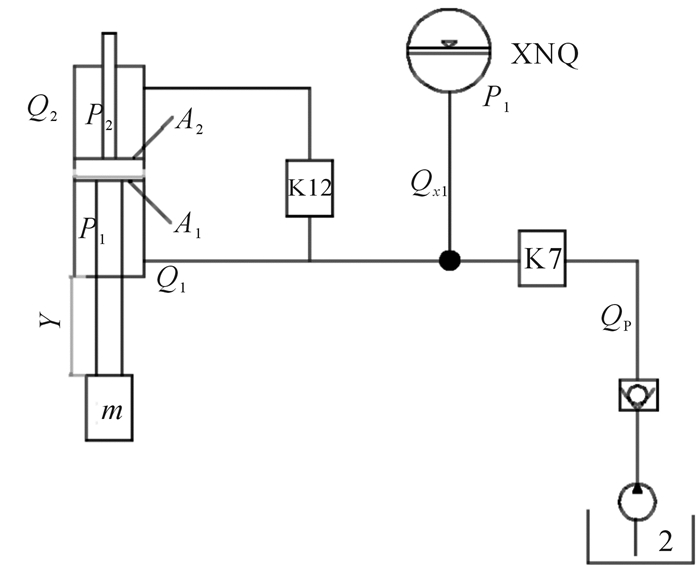
|
| 图 3 下打过程中液压系统简化图 Fig.3 Schematic diagram of the hydraulic system in the process of hammer hitting |
打桩锤活塞杆受力平衡方程:
| $ \begin{array}{*{20}{c}} {mg + {F_2}\left( {{P_2}} \right) = m{{\ddot Y}_1} + {F_1}\left( {{P_1}} \right) + {F_{{\rm{s1}}}}\left( {{{\dot Y}_1},\Delta P} \right) + }\\ {{F_{{\rm{l1}}}}\left( {{P_1},{P_2}} \right) + {F_{\rm{f}}}} \end{array} $ | (17) |
流量连续方程为:
| $ {Q_2} = {Q_1} + {Q_{\rm{p}}} + {Q_{{\rm{1x}}}} $ | (18) |
| $ {Q_2} = {A_2}v $ | (19) |
| $ {Q_1} = {A_1}v $ | (20) |
| $ v = \frac{1}{{{A_1} - {A_2}}}\left( {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right) $ | (21) |
其中单位时间蓄能器内氮气体积的变化量就是蓄能器的瞬时流量, 因此蓄能器瞬时流量的计算公式为:
| $ {Q_{{\rm{1x}}}} = \frac{{{\rm{d}}V}}{{{\rm{d}}t}} $ | (22) |
根据式(18)至(22)可得:
| $ {Q_2} = \frac{{{A_1}}}{{{A_2} - {A_1}}}\left( {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right) $ | (23) |
阶段压力平衡方程:
| $ {P_1} = {P_2} + {C_3}Q_2^2 $ | (24) |
式中C3为进油管道和阀体K7及K12的液阻,N·s2/m8。
将式(11)和(22)代入式(24)得:
| $ {P_1} = \frac{{{C_{{\rm{x1}}}}}}{{{V^{1.4}}}} - {\left( {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right)^2}\left[ {{C_1} - {C_3}{{\left( {\frac{{{A_2}}}{{{A_1} - {A_2}}}} \right)}^2}} \right] $ | (25) |
| $ {P_2} = P - {C_1}{\left( {{Q_2} + {Q_{\rm{p}}}} \right)^2} $ | (26) |
将式(11)和(21)代入式(26)得:
| $ {P_2} = \frac{{{C_{{\rm{x1}}}}}}{{{V^{1.4}}}} - {C_1}{\left( {\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right)^2} $ | (27) |
在t=0,y=0时, 蓄能器的容积V为:
| $ V = {V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t $ | (28) |
将式(26)、(27)、(28)和(21)代入式(17)得:
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{{\frac{{{C_{{\rm{x1}}}}A}}{{{{\left( {{V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t} \right)}^{1.4}}}} + mg - \left( {{C_1} \cdot {A^3} + {C_3} \cdot A_2^3} \right) \cdot {v^2}}}{m} - \frac{{mg + {F_{{\rm{s1}}}} - {F_{{\rm{l1}}}} - {F_{\rm{f}}}}}{m} $ | (29) |
将式(28)分别代入式(25)和(27)得:
| $ \begin{array}{l} {P_1} = \frac{{{C_{{\rm{x1}}}}}}{{{{\left( {{V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t} \right)}^{1.4}}}} - {\left[ {\frac{{{\rm{d}}\left( {{V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t} \right)}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right]^2} \cdot \\ \;\;\;\;\;\;\;\left[ {{C_1} - {C_3}{{\left( {\frac{{{A_2}}}{{{A_1} - {A_2}}}} \right)}^2}} \right] \end{array} $ | (30) |
| $ \begin{array}{l} {P_2} = \frac{{{C_{{\rm{x1}}}}}}{{{{\left( {{V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t} \right)}^{1.4}}}} - \\ \;\;\;\;\;\;\;{C_1}{\left[ {\frac{{{\rm{d}}\left( {{V_{{\rm{all}}}} + AY - {Q_{\rm{p}}}t} \right)}}{{{\rm{d}}t}} + {Q_{\rm{p}}}} \right]^2} \end{array} $ | (31) |
阀芯平衡方程为:
| $ \sum F = {P_{\rm{a}}}{A_{\rm{a}}} + {P_{\rm{b}}}{A_{\rm{b}}} - {P_{\rm{x}}}{A_{\rm{x}}} - {F_{\rm{x}}} $ | (32) |
式中:Aa为油口A处阀芯面积,m2;Ab为油口B处阀芯面积,m2;Ax为控制油口处阀芯面积,m2;Fx为弹簧力,N,Fx=k(x0+x), k为弹簧的刚度, x0为弹簧的预压缩量, mm, x为阀芯位移,mm;Pa为油口A处压力, MPa;Pb为油口B处压力, MPa;Px为油口X处压力, MPa。
当∑F>0时,阀芯开启,油路接通; 当∑F<0时,阀芯关闭,油路断开。
综上所述,设定打桩锤控制系统的关键参数:打桩锤液压系统压力为21 MPa, 流量为540 L/min; 打桩锤打击频率为36~90次/min; 打桩锤打击能量为50~210 kN·m; 锤头的最大行程为0.2~1.5 m; 锤头质量为14 000 kg; 油缸下腔有杆腔面积为0.007 8 m2; 高压蓄能器8的初始充气压力为18 MPa, 初始充气体积为25 L; 插装阀为11, 12, 13, 14的通径分别为100, 50, 50, 100 mm。
3 系统建模与仿真及实验结果分析 3.1 系统AMESim模型的建立AMESim是一款用于模拟控制对象真实建模环境的图形化仿真软件。本文建立的系统AMESim模型充分考虑到了液压油的物理特性和元件的非线性,例如油温,油的压缩性、库仑力等,同时能够实现机电液耦合动力学仿真。根据打桩锤液压系统的原理图搭建了仿真模型,如图 4所示。
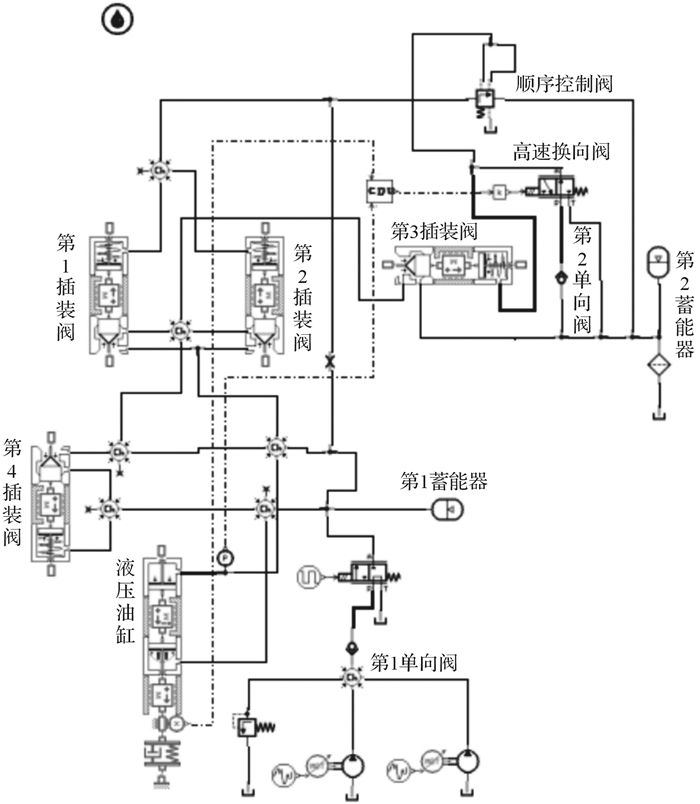
|
| 图 4 电液一体化打桩锤控制系统的AMESim模型 Fig.4 AMESim model of control system of electro-hydraulic pile hammer |
由于影响因素较多,本文主要对打桩锤电液控制系统的油腔压力、锤体速度和位移等几个重要的性能进行分析。图 5所示为打桩锤性能现场测试图。

|
| 图 5 打桩锤性能现场测试图 Fig.5 Performance field test of the pile hammer |
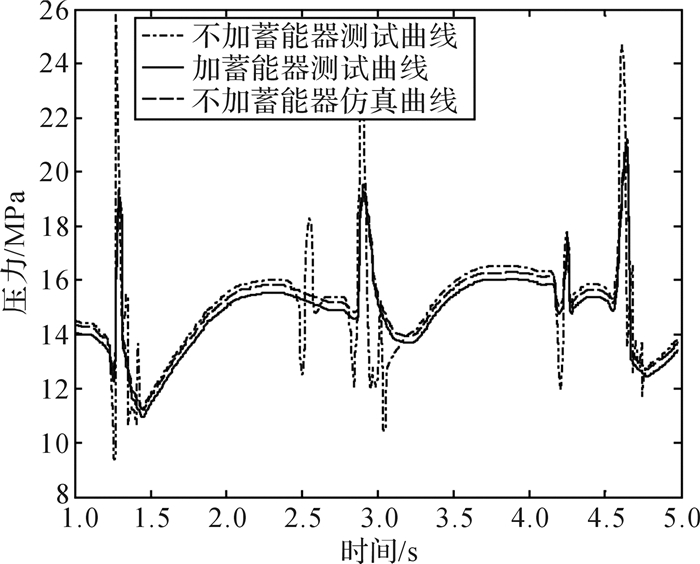
图 6所示为该电液控制系统在有无蓄能器时,打桩锤液压油缸上腔压力随时间变化曲线的对比。在没有蓄能器时,提锤过程中打桩锤液压油缸上腔在排油过程中,压力脉动剧烈从而引起液压油管的振动,该过程中最大油压力值达到18 MPa, 冲击压力最大值达到26 MPa。在该系统中加入蓄能器和大流量插装阀后,由于蓄能器的充压和插装阀的流量增大,在提锤过程中液压油缸上腔排油压力的峰值降至16 MPa,进油压力的峰值降为14 MPa,打击时产生的最大压力为20 MPa。同时在差动连接的时候,上下腔的压力差降至2 MPa。由上述仿真和实验对比可知,该仿真误差较小,同时插装阀和蓄能器的使用使得换向压力波动小、输油管波动小。
|
| 图 6 打桩锤液压油缸上腔压力仿真与实验结果对比 Fig.6 Comparison of the simulation and experimental results of the upper chamber pressure of the hydraulic cylinder of pile hammer |
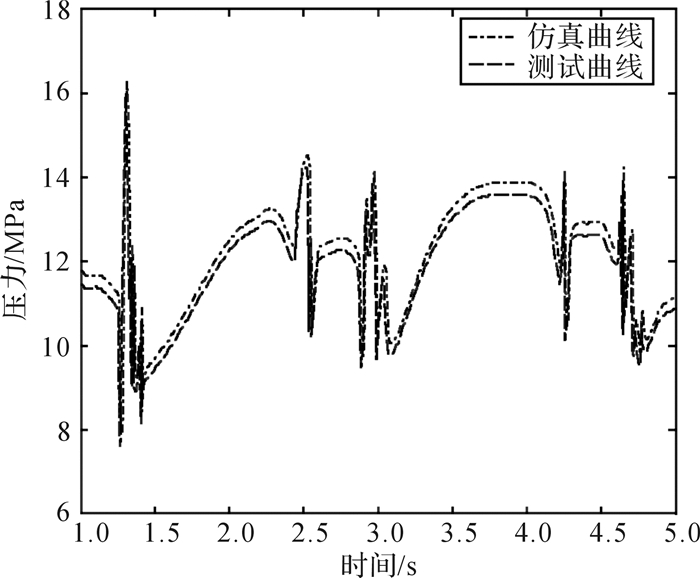
图 7所示为打桩锤液压油缸下腔压力随时间变化的曲线。一开始,蓄能器慢慢地冲压,当下腔压力达到一定值时,锤体在油压增大的过程中慢慢往上提锤,下腔压力最大值为14 MPa。当液压回路转变为差动油路的时候,下腔排油压力的最大值为13 MPa。查阅资料可知,相同规格的其他液压打桩锤的下腔压力峰值达到了25 MPa[18]。由此可见采用蓄能器和大通径插装阀组合的电液控制系统很好地控制了上、下腔油压峰值,由于油压峰值的减小,液压油的发热减少,且系统的能量损失也相应减小。因此该电液控制系统的能量利用率得到了提高,同时也使得系统的稳定性更好。
|
| 图 7 打桩锤液压油缸下腔压力仿真与实验结果对比 Fig.7 Comparison of the simulation and experimental results of the lower chamber pressure of the hydraulic cylinder of pile hammer |
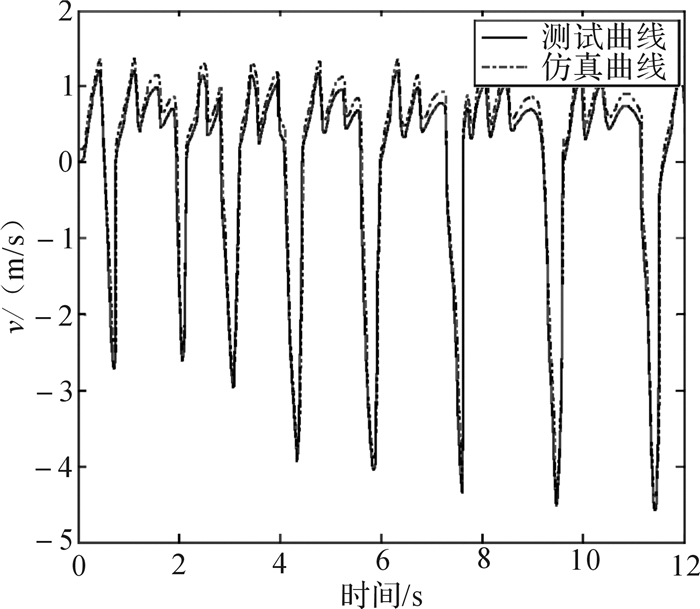
由图 8和图 9可知,锤体速度的仿真与实验结果的相对误差为5%,锤体位移速度的相对误差为3%。基于传感器反馈的桩下降的位移和油压的大小,上位机根据其反馈值调整电磁阀换向时间以调整打桩锤锤头的上升高度,进而调整打击能量。由锤体速度和位移曲线可知,采用闭环控制系统,打桩锤根据土壤土层的阻力不同来调整打桩的频率从而使得打桩效率高,可以方便且高效地实现对打桩过程打击能的自适应控制。
|
| 图 8 电液一体化打桩锤液压系统锤体速度仿真与实验结果对比 Fig.8 Comparison of the simulation and experimental results of the hammer velocity of hydraulic system for electro-hydraulic pile hammer |

|
| 图 9 电液一体化打桩锤液压系统锤体位移仿真与实验结果对比 Fig.9 Comparison of the simulation and experimental results of the hammer displacement of hydraulic system for electro-hydraulic pile hammer |
1) 通过对新型打桩锤结构组成和工作原理的分析,设计了新型打桩锤的电液控制系统,该系统具有换向压力波动小、油管振动小、打桩效率高等优点。
2) 根据该控制系统,本文建立了打桩锤提锤、下打及插装阀的数学模型,并搭建了AMESim控制模型,进行了动态仿真和实验,通过分析液压腔压力曲线、锤体速度曲线、锤体位移曲线,验证了该控制系统的能够使得打桩锤的油压峰值小和自适应调节频率。
3) 该仿真模型考虑了打桩锤油液回路和打桩过程中多种因素的影响,通过实验验证,该系统仿真结果的误差在5%以内,表明该仿真模型能够较好地描述打桩锤的实际工作情况,为今后的设计和研发提供了很好的依据。
| [1] |
胡均平, 郭勇, 张政华, 等.
液压打桩锤主控阀换向性能的动态特性分析[J]. 中南大学学报(自然科学版), 2012, 43(7): 2622–2628.
HU Jun-ping, GUO Yong, ZHANG Zheng-hua, et al. Dynamic analysis of main control valve reversing performance for hydraulic pile hammer[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2622–2628. |
| [2] |
胡均平, 李科军.
考虑打桩反弹的组合锤头冲击过程的动态特性分析[J]. 中南大学学报(自然科学版), 2017, 48(2): 348–354.
HU Jun-ping, LI Ke-jun. Dynamic characteristics analysis of impact model of composite hammer considering rebound in piling[J]. Journal of Central South University (Science and Technology), 2017, 48(2): 348–354. |
| [3] | PATRICK D B, MARK T, DAVID H. Pile driving control apparatus and pile driving system: US7404449B2[P]. 2008-07-29. |
| [4] | JAMES E A. Deep water pile driver: US 20100012336A1[P]. 2009-05-18. http://www.freepatentsonline.com/EP2940217.html |
| [5] | ISKANDER M. Behavior of pipe piles in sand[M]. Heidelberg: Springer, 2011: 127-176. |
| [6] |
吕景忠, 隋振, 杨永海, 等.
新型液压桩锤气液驱动系统[J]. 吉林大学学报(工学版), 2004, 34(4): 597–601.
LU Jing-zhong, SUI Zhen, YANG Yong-hai, et al. Hydropneumatic driving system of new type hydraulic pile hammer[J]. Journal of Jilin University (Engineering and Technology Edition), 2004, 34(4): 597–601. |
| [7] |
胡均平, 郭勇, 宋光伟, 等.
金属颗粒填充桩锤锤击模型的数值分析[J]. 中国公路学报, 2010, 23(2): 122–126.
HU Jun-ping, GUO Yong, SONG Guang-wei, et al. Numerical analysis for impact model of pile hammer filled with metal particles[J]. China Journal of Highway and Transport, 2010, 23(2): 122–126. |
| [8] |
杨永海, 王勋龙, 吕景忠, 等.
液压桩锤性能评价体系及其试验方法的研究[J]. 农业机械学报, 2005, 36(4): 597–601.
YANG Yong-hai, WANG Xun-long, LU Jing-zhong, et al. Study on performance evaluation system and testing methods of hydraulic pile hammer[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005, 36(4): 597–601. |
| [9] |
李廷, 何继善, 徐振华, 等.
特大型组合式高应变动力试桩重锤[J]. 中南大学学报(自然科学版), 2008, 39(5): 1112–1118.
LI Ting, HE Ji-shan, XU Zhen-hua, et al. Special large-scaled and knock-down hammer in high strain dynamic pile test[J]. Journal of Central South University (Science and Technology), 2008, 39(5): 1112–1118. |
| [10] | WILJK G. Rotary drilling prediction[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1991, 28(1): 35–42. |
| [11] | RAUSCHE F, GOBLE G G, LIKINS G E, et al. Dynamic determination of pile capacity[J]. Journal of Geotechnical Engineering, 1985, 111(3): 367–383. DOI:10.1061/(ASCE)0733-9410(1985)111:3(367) |
| [12] | JIAO S, WANG Y, ZHANG L, et al. Shock wave characteristics of a hydraulic damper for shock test machine[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1570–1578. DOI:10.1016/j.ymssp.2009.12.005 |
| [13] | MELAMED Y, KISELEY A, GELFGAT M, et al. Hydraulic hammer drilling technology:developments and capabilities[J]. Journal of Energy Resources Technology, 2000, 122(1): 1–7. DOI:10.1115/1.483154 |
| [14] |
刘德顺, 杨志高, 杨书仪, 等.
电锤冲击系统的波动力学研究[J]. 振动工程学报, 2013, 26(6): 864–870.
LIU De-shun, YANG Zhi-gao, YANG Shu-yi, et al. Wave mechanics for an electric hammer impact system[J]. Journal of Vibration Engineering, 2013, 26(6): 864–870. |
| [15] | KARNOPP D C, MARGOLIS D L, ROSENBERG R C. System dynamics:modeling, simulation, and control of mechatronic systems[M]. New York: John Wiley & Sons, 2012: 17-33. |
| [16] | MARIKAR A C, UMMLAND L. Modeling of switching systems in bond graphs using the concept of switched power junctions[J]. Journal of the Franklin Institute, 2005, 342(2): 131–147. DOI:10.1016/j.jfranklin.2004.08.005 |
| [17] | BORUTZKY W. Bond graph methodology:development and analysis of multidisciplinary dynamic system models[M]. Berlin: Springer, 2010: 305-349. |
| [18] | ZHANG Lei, GONG Xiao-nan, YANG Zhong-xuan, et al. Elastoplastic solutions for single piles under combined vertical and lateral loads[J]. Journal of Central South University of Technology, 2011, 18(1): 216–222. DOI:10.1007/s11771-011-0682-x |



