2. 天津职业技术师范大学 自动化与电气工程学院, 天津 300222
2. School of Automation and Electrical Engineering, Tianjin University of Technology and Education, Tianjin 300222, China
并联机构(parallel mechanisms, PMs)是指固定平台和运动平台通过至少2个独立开环运动链相连,具有2个或者2个以上自由度的机构[1]。
自Hunt[2]1983年提出3-RPS并联机构以来, 各国学者对这类机构的工作原理、性能优化及实际应用作了大量研究,并在并联机构的构型综合、运动学分析、动力学分析等方面取得了重要成果。谢志江等[3]采用蚁群算法,毛冰滟等[4]采用引导人工群算法,胡映光等[5]采用混合遗传算法,陈长忆等[6]应用粒子群算法,张伟等[7]采用改进粒子群算法,分别求解出3-RPS并联机构的正解。高峰等[8]提出一种坐标搜索法,蒲志新等[9]借助极限搜索法,张斌等[10]采用蒙特卡洛法,分别分析了3-RPS并联机构的工作空间。周斌、原政等[11-12]采用数值法对3-RPS并联机构进行了工作空间分析。朱大昌等[13]基于影响系数对3-RPS柔性并联机构运动学和动力学进行分析。方跃法等[14]通过建立约束方程组,简化了3-RPS并联机构的雅可比矩阵,进而对其运动学进行分析。齐大志等[15]采用解析法分析了运动副不同布局下的3-RPS并联机构的运动特性。彭中波等[16]采用螺旋理论求Jacobian的方法,Li等[17]基于几何代数的方法,分别分析了3-RPS并联机构的奇异情况。落海伟、郑魁敬等[18-19]研究了3-RPS并联机构的刚度。程刚、李新友等[20-21]对3-RPS并联机构的几何误差进行了分析。
现有的文献主要针对3-RPS并联机构的正解、反解、工作空间、奇异性、动力学、性能优化等方面进行研究。这些文献中机构的3个运动支链的驱动副R的回转轴线大多呈共面的三角形或者共面相交于一点,有的相互垂直且相交于一点。然而,较少有人关注能够改善机构综合性能的支链中间运动副结构的拓扑形式。
发明问题解决理论(TRIZ)提供的创新设计理论和方法,已成为各领域产品开发中解决技术难题的有效工具[22],它包括40条发明创新原理、76个标准解以及效应知识库。其中,曲面化(Spheroidality)原理是将直线、平面向曲线、球面化方向或功能转变,来改善产品的性能,如在建筑中采用拱形或圆屋顶来增加强度等等。
本文基于曲面化原理,将现有的3-RPS并联机构中的直线移动副改为弧形移动副,且改变各个运动支链中转动副的装配方式,构造出3种具有弧形移动副的3-RPS并联机构[23]。运用螺旋理论,对这3种机构的自由度、运动学进行分析,并得到各自的灵巧度工作空间。
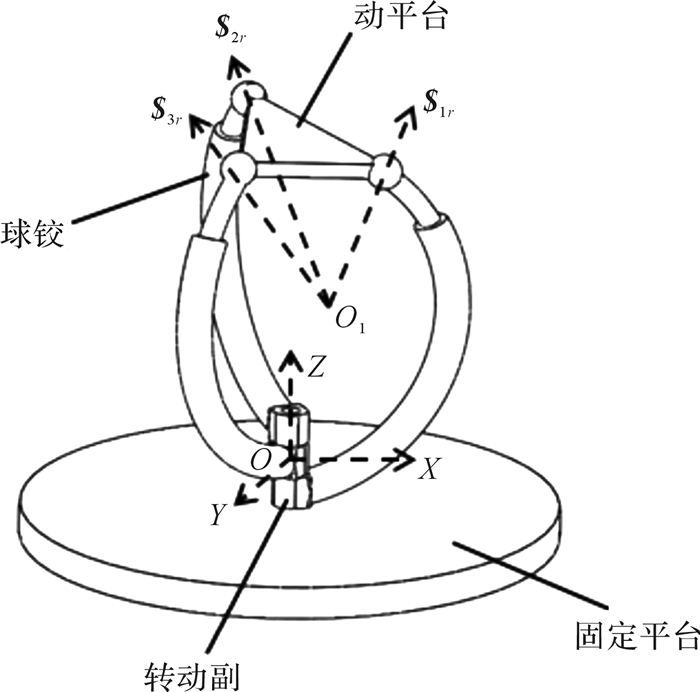
1 3-RPS并联机构运动学分析 1.1 第1种3-RPS并联机构第1种3-RPS并联机构如图 1所示,其动平台与固定平台之间采用3个圆周方向对称分布的运动支链连接。其中,每个支链由2段共弧心的弧形连杆组成,上段弧形连杆与动平台之间采用球铰的方式连接,并且上段弧形连杆安装在下段弧形连杆的空腔内,能够沿着此空腔圆弧的切线方向作往复移动。3个下段弧形连杆与固定平台之间均采用转动副连接,转动副的轴线相互重合,并垂直于固定平台,指向弧形连杆的弧心。通过驱动下段弧形连杆绕固定平台的转动,来实现动平台绕弧形连杆中心O1的3个方向的转动。
|
| 图 1 第1种3-RPS并联机构的结构 Fig.1 Structure of the first type 3-RPS parallel mechanism |
选取并联机构固定平台的中心点作为分支坐标系O-XYZ的原点,OXY平面平行于固定平台,Z轴和转动副轴线重合,X轴位于弧形连杆形成的平面内,Y轴由右手法则确定,如图 2所示,取其中一个运动支链进行分析,该支链的运动螺旋为:

|
| 图 2 第1种3-RPS并联机构的支链坐标系 Fig.2 Coordinate system of a chain of the first type 3-RPS parallel mechanism |
| $ \left\{ \begin{array}{l} {\mathit{\$ }_1} = \left[ {0\;0\;1;0\;0\;0} \right]\\ {\mathit{\$ }_2} = \left[ {0\;0\;0;\frac{{\sin {\alpha _1}}}{{\tan {\theta _1}}}\;\frac{{\cos {\alpha _1}}}{{\tan {\theta _1}}}\;1} \right]\\ {\mathit{\$ }_3} = \left[ {1\;0\;0;0\;{z_1}\; - {y_1}} \right]\\ {\mathit{\$ }_4} = \left[ {0\;1\;0; - {z_1}\;0\;{x_1}} \right]\\ {\mathit{\$ }_5} = \left[ {0\;0\;1;{y_1}\; - {x_1}\;0} \right] \end{array} \right. $ | (1) |
根据$i·$r=0,对式(1)求反螺旋可得支链的约束螺旋为:
| $ {\mathit{\$ }_{1r}} = \left[ {\begin{array}{*{20}{c}} {{l_1}}&{{m_1}}&{{n_1}; - {y_1}}&{{x_1}}&0 \end{array}} \right] $ | (2) |
| $ {l_1} = \frac{{{x_1}}}{{\sqrt {x_1^2 + y_1^2 + {{\left( {{z_1} - R} \right)}^2}} }} $ |
| $ {m_1} = \frac{{{y_1}}}{{\sqrt {x_1^2 + y_1^2 + {{\left( {{z_1} - R} \right)}^2}} }} $ |
| $ {n_1} = \frac{{{z_1} - R}}{{\sqrt {x_1^2 + y_1^2 + {{\left( {{z_1} - R} \right)}^2}} }} $ |
式中:$1r表示沿球铰中心与弧形连杆弧心的连线的力线矢;l1, m1, n1为$1r的方向余弦,θ1为上段弧形移动副的移动方向,球铰副的中心点坐标P1=(x1, y1, z1),α1为支链的驱动角,即转动副的输入角。
| $ \begin{array}{l} \tan {\theta _1} = \frac{{{y_1}}}{{{z_1} \times \cos ({\alpha _1})}}\\ \tan {\alpha _1} = \frac{{{x_1}}}{{{y_1}}} \end{array} $ | (3) |
其他2个运动支链的驱动角也可参照式(3)求得。因此,每个RPS支链都对动平台施加1个力线矢,它们都通过彼此球铰的中心,相交于弧形连杆所构成球面的中心处。3个约束力线矢相交于一点,导致机构不存在公共约束和虚约束,并且约束力线矢构成的机构约束螺旋系的标准基为:
| $ \left\{ \begin{array}{l} \mathit{\$ }_1^r = \left[ {1\;0\;0;0\;0\;0} \right]\\ \mathit{\$ }_2^r = \left[ {0\;1\;0;0\;0\;0} \right]\\ \mathit{\$ }_3^r = \left[ {0\;0\;1;0\;0\;0} \right] \end{array} \right. $ | (4) |
这3个约束力线矢限制了动平台3个方向的移动自由度,导致动平台只能够绕三维空间内的一固定点作3个方向的转动运动。由式(2)可知,此并联机构动平台在连续运动后,分支约束始终具有统一形式,即各力线矢通过彼此球铰的中心,相交于弧形连杆所构成球面的中心处。3个球铰副的中心不重合,导致该机构约束螺旋系的标准基始终与式(4)形式一致。因此,该机构不是瞬时机构[24-26],并且其绕Z轴的旋转运动相对于其他2个方向的旋转运动具有解耦性。
根据机构自由度计算的一般Gru·bler-Kutzbach公式为:
| $ M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i}} $ | (5) |
式中:M为机构的自由度;d为机构的阶;d=6-λ;λ为机构的公共约束数;n为机构的杆件数;g为运动副数。
从前面的分析可知,在3-RPS并联机构中不存在公共约束,即λ=0,由式(5)可得M=6×(8-9-1)+15=3。
设$A为动平台球铰中心的瞬时螺旋,其在固定坐标系O-XOYOZO中表示为:
| $ \begin{array}{l} {\mathit{\$ }_A} = {\omega _{1,i}}{\mathit{\$ }_{1,i}} + {d_{2,i}}{\mathit{\$ }_{2,i}} + {\omega _{3,i}}{\mathit{\$ }_{3,i}} + \\ \;\;\;\;\;\;\;{\omega _{4,i}}{\mathit{\$ }_{4,i}} + {\omega _{5,i}}{\mathit{\$ }_{5,i}},i = 1,2,3 \end{array} $ | (6) |
式中:ω1, i为第i条支链第1个运动副的转动速率;$1, i为第i条支链第1个运动副的瞬时运动螺旋;d2, i第i条支链移动副的瞬时移动速率。
将式(6)与式(2)联立作互易积,即可求得约束雅克比矩阵Jc:
| $ {\mathit{\boldsymbol{J}}_c} \cdot {\mathit{\$ }_A} = 0 $ | (7) |
锁定各支链中的驱动副(即转动副),则每条支链的反螺旋系维数比之前的增加1个。设$iT为i条支链的驱动力螺旋,由$i与$iT的互易积为零,在式(6)两端乘以$iT,可得:
| $ \tan {\theta _1} = \frac{{{y_1}}}{{{z_1} \times \cos \left( {{\alpha _1}} \right)}} $ |
可求出Jx:
| $ {\omega _{1,i}} = {\mathit{\boldsymbol{J}}_x}{\mathit{\$ }_A} $ | (8) |
式中Jx为驱动雅克比矩阵,是动平台速度与驱动关节速度之间的映射。
综合式(7)以及式(8),可得并联机构的全雅可比矩阵J:
| $ {\omega _{1,i}} = \mathit{\boldsymbol{J}}{\mathit{\$ }_A} $ | (9) |
其中
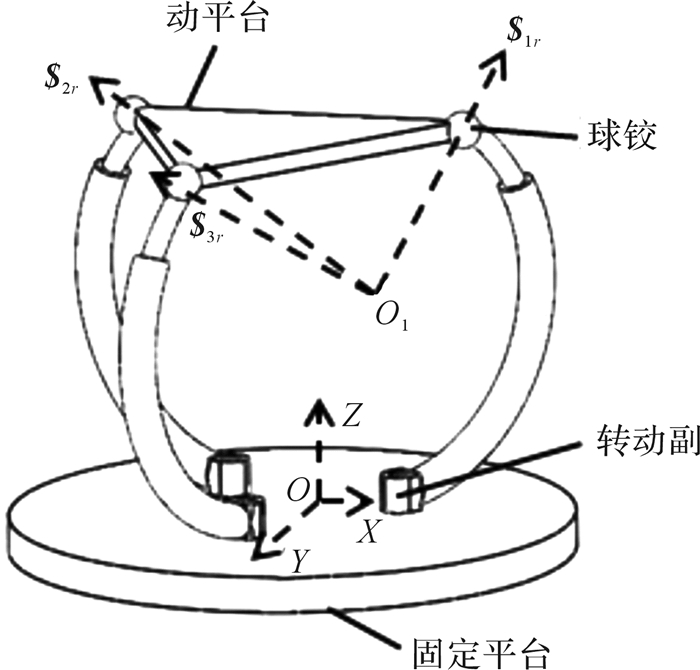
第2种3-RPS并联机构如图 3所示,动平台与固定平台之间采用3个圆周方向对称分布的运动支链连接。其中,每个支链由2段共弧心的弧形连杆组成,上段弧形连杆与动平台之间采用球铰的方式连接,并且上段弧形连杆还包含于下段弧形连杆的空腔内,能够沿着此空腔圆弧的切线方向作往复移动。下段弧形连杆与固定平台之间采用转动副连接,转动副的轴线方向垂直于固定平台,并指向弧形连杆的弧心。另外,3个转动副的轴线相互平行,且沿圆周方向均布于定平台上。通过驱动下段弧形连杆绕固定平台的转动,来实现动平台绕O1的3个方向的转动。
|
| 图 3 第2种3-RPS并联机构的结构 Fig.3 Structure of the second type 3-RPS parallel mechanism |
由于该3-RPS并联机构与第1种3-RPS并联机构的结构类似,故其支链运动螺旋形式和图 2所示一致。取其中一个支链进行分析,它的支链运动螺旋系如下:
| $ \left\{ \begin{array}{l} {\mathit{\$ }_1} = \left[ {0\;0\;1;0\; - r\;0} \right]\\ {\mathit{\$ }_2} = \left[ {0\;0\;0;\frac{{\sin {\alpha _1}}}{{\tan {\theta _1}}}\;\frac{{\cos {\alpha _1}}}{{\tan {\theta _1}}} \pm r\;1} \right]\\ {\mathit{\$ }_3} = \left[ {1\;0\;0;0\;{z_1}\; - {y_1}} \right]\\ {\mathit{\$ }_4} = \left[ {0\;1\;0; - {z_1}\;0\;{x_1}} \right]\\ {\mathit{\$ }_5} = \left[ {0\;0\;1;{y_1}\; - {x_1}\;0} \right] \end{array} \right. $ | (10) |
对式(10)求反螺旋,可得支链的约束螺旋为:
| $ \begin{array}{l} \mathit{\$ }_i^T{\mathit{\$ }_A} = \mathit{\$ }_i^T\left( {{\omega _{1,i}}{\mathit{\$ }_{1,i}} + {d_{2,i}}{\mathit{\$ }_{2,i}} + {\omega _{3,i}}{\mathit{\$ }_{3,i}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{\omega _{4,i}}{\mathit{\$ }_{4,i}} + {\omega _{5,i}}{\mathit{\$ }_{5,i}}} \right) \end{array} $ |
其中
式中:r为固定平台上的3个转动副所构成的外接圆半径,
| $ \tan {\alpha _1} = \frac{{{x_1}}}{{r \pm {y_1}}} $ | (11) |
其他2个支链的运动螺旋系与该运动支链类似,并且那2个运动支链的驱动角也可参照式(11)求出;另外,这3个支链对动平台施加3个过各自支链球铰中心点与弧形连杆弧心连心的约束线矢。这3个约束线矢汇交于空间内某一点,所构成的机构约束螺旋系的标准基与式(4)一致,其约束动平台的3个移动自由度,所以动平台具有在空间某一点(3个约束线矢的交汇点)处的3个转动自由度。
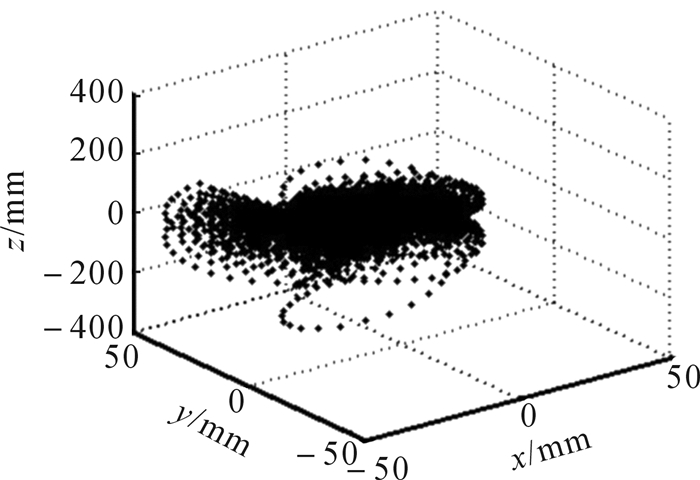
设弧形连杆的弧心坐标为(ai, bi, ci),球铰副的中心点坐标Pi=(xi, yi, zi),由式(12)可求得交汇点的坐标O1=(x, y, z),如图 4所示。
|
| 图 4 约束力矢量的交汇点空间 Fig.4 Meeting points space of constraint force vectors |
| $ \frac{{x - {a_i}}}{{{x_i} - {a_i}}} = \frac{{y - {b_i}}}{{{y_i} - {b_i}}} = \frac{{z - {c_i}}}{{{z_i} - {c_i}}} $ | (12) |
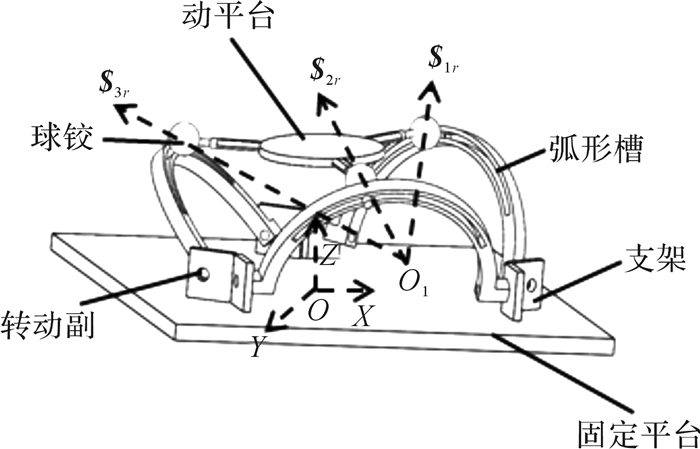
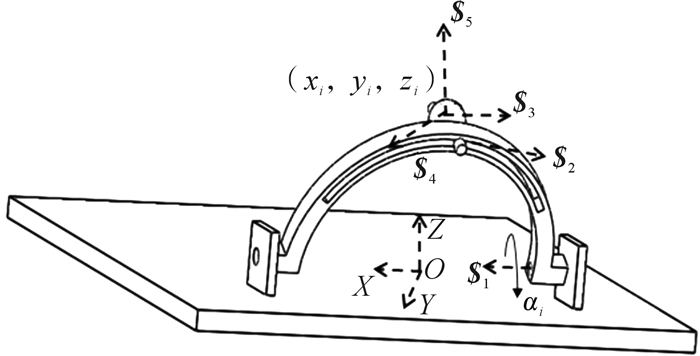
第3种3-RPS并联机构如图 5所示,动平台与固定平台之间采用3个圆周方向对称分布的运动支链连接。其中,每个支链都含有1个半圆弧形连杆,此半圆弧形连杆底端采用旋转副与固定平台上的支架连接,其上有一弧形长槽,球铰链的一端可沿弧形长槽方向移动,另一端与动平台固定连接。另外,3个转动副的轴线处于同一平面内,彼此相交。通过驱动下段弧形连杆绕机架的转动,来实现动平台绕弧形连杆中心O1的3个方向的转动。
|
| 图 5 第3种3-RPS并联机构的结构 Fig.5 Structure of the third type 3-RPS parallel mechanism |
由于该3-RPS并联机构与前2种3-RPS并联机构的结构形式不同,选取并联机构半圆弧形连杆的圆心坐标系O-XYZ的原点, 分支坐标系OXY平面平行于固定平台,X轴和转动副轴线重合,Z轴垂直于固定平台,如图 6所示,取其中一个支链进行分析,它的支链运动螺旋系如下:
|
| 图 6 第3种3-RPS并联机构的支链坐标系 Fig.6 Coordinate system of a chain of the third type 3-RPS parallel mechanism |
| $ \left\{ \begin{array}{l} {\mathit{\$ }_1} = \left[ {0\;1\;0;0\;0\;0} \right]\\ {\mathit{\$ }_2} = \left[ {\begin{array}{*{20}{c}} {0\;0\;0;\cos {\theta _1}\cos {\alpha _1}}&{ - \cos {\theta _1}\cot {\theta _1}} \end{array}} \right.\\ \;\;\;\;\;\;\;\left. {\cos {\theta _1}\sin {\alpha _1}} \right]\\ {\mathit{\$ }_3} = \left[ {1\;0\;0;0\;{z_1}\; - {y_1}} \right]\\ {\mathit{\$ }_4} = \left[ {0\;1\;0; - {z_1}\;0\;{x_1}} \right]\\ {\mathit{\$ }_5} = \left[ {0\;0\;1;{y_1}\; - {x_1}\;0} \right] \end{array} \right. $ | (13) |
对式(13)求反螺旋可得支链的约束螺旋为:
| $ {\mathit{\$ }_{1r}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{x_1} - r}}{{{y_1}}}}&{1c;c{y_1} - {z_1}}&{\frac{{{x_1} - r}}{{{y_1}}} \times {z_1} - c{x_1}r} \end{array}} \right] $ |
α1为支链1的驱动角,即转动副的输入角:
| $ \tan {\alpha _1} = \frac{{{z_1}}}{{{y_1}}} $ | (14) |
其他2个支链的运动螺旋系与该运动支链类似,并且那2个运动支链的驱动角也可参照式(14)求出;另外,这3个支链对动平台施加3个过各自支链球铰中心点与半圆弧形连杆弧心连心的约束线矢。这3个约束线矢汇交于空间内某一点,所构成的机构约束螺旋系的标准基与式(4)一致,其约束动平台的3个移动自由度,所以动平台具有在空间某一点处的3个转动自由度,该点为3个约束线矢的交汇点,可以根据式(11)求出交汇点的坐标。
2 并联机构灵巧度空间分析雅克比矩阵一般是指末端执行器的速度到关节速度的线性映射。当机构处于奇异位形时,雅克比矩阵至少存在1个为零或者无穷大的奇异值,其物理意义则为末端执行器增加了至少1个不可控自由度。机构的灵巧度可定义为[27]:
| $ \left\{ \begin{array}{l} {\mathit{\$ }_1} = \left[ {0\;1\;0;0\;0\;0} \right]\\ {\mathit{\$ }_2} = \left[ {\begin{array}{*{20}{c}} {0\;0\;0;\cos {\theta _1}\cos {\alpha _1}}&{ - \cos {\theta _1}\cot {\theta _1}} \end{array}} \right.\\ \;\;\;\;\;\;\;\left. {\cos {\theta _1}\sin {\alpha _1}} \right]\\ {\mathit{\$ }_3} = \left[ {1\;0\;0;0\;{z_1}\; - {y_1}} \right]\\ {\mathit{\$ }_4} = \left[ {0\;1\;0; - {z_1}\;0\;{x_1}} \right]\\ {\mathit{\$ }_5} = \left[ {0\;0\;1;{y_1}\; - {x_1}\;0} \right] \end{array} \right. $ | (13) |
由(13)可以直接判断机构的奇异性,当W=0时,机构处于奇异状态,W值越大,机构越灵活。给定3种3-RPS并联机构的基本参数:弧形连杆以及半圆弧形连杆的半径R=50 mm,固定平台上的3个转动副所构成的外接圆半径r=10 mm,第1种和第2种3-RPS并联机构的球铰沿弧形长槽移动的方向θi=60°,第2种并联机构动平台的3个球铰中心所构成的外接圆半径l=r+R×sin 60°,第1种与第3种并联机构的动平台外接圆半径为R×sin 60°,设动平台的姿态角为(ϕ, φ, γ),其取值范围为-60°~60°,利用MATLAB软件求解这3种并联机构的灵巧度空间,结果如图 7至图 9所示。

|
| 图 7 第1种3-RPS并联机构灵巧度空间 Fig.7 The dexterous workspace of the first type 3-RPS parallel mechanism |
|
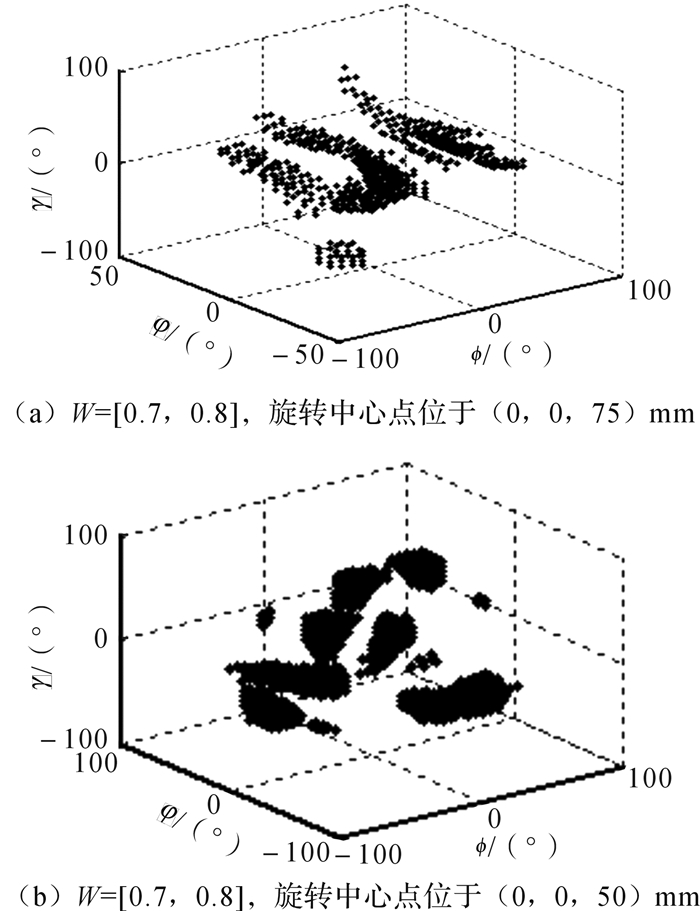
| 图 8 第2种3-RPS并联机构灵巧度空间 Fig.8 The dexterous workspace of the second type 3-RPS parallel mechanism |
|
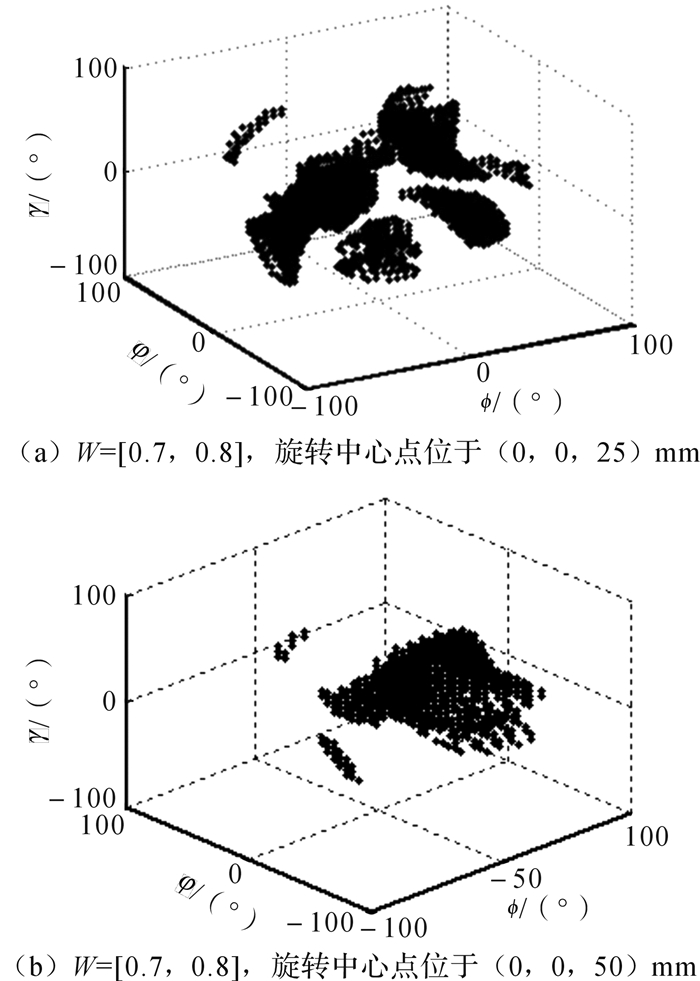
| 图 9 第3种3-RPS并联机构灵巧度空间 Fig.9 The dexterous workspace of the third type 3-RPS parallel mechanism |
由图 7可知,在动平台的姿态空间内,第1种并联机构的灵巧度主要集中在[0.7,1]内,反映该并联机构有较好的灵活性,而且动平台处于初始位置(即表示动平台平行于固定平台,弧形连杆圆周方向均匀布置)附近。由图 8和图 9可知,由于第2种并联机构的运动支链与第1种相同,只是动平台的半径不同。第3种并联机构的连杆弧形半径和第1种并联机构的相同,只是动平台的半径不同。第2种和第3种并联机构的旋转中心均与第1种并联机构的不同,它们的转动中心随着动平台的位姿变化而变化,且第2种和第3种机构的灵巧度处在[0.7,0.8]这个区间内,随着旋转中心点的上移,灵巧度空间逐渐聚集。另外,第1种并联机构的灵活度空间优于后2种并联机构,可以用于替代传统球面机构,而后2种并联机构的灵活度实质是一致的。
3 结论1) 提出3种含有弧形移动副的3-RPS并联机构。运用螺旋理论,对这3种并联机构的自由度进行分析。这3种并联机构本质上都属于3-US型并联机构。其中,第1种并联机构相对于现有球型并联机构而言,其分支链的转动中心在安装的过程中更容易对齐;第2、第3种并联机构,可根据具体实际需求来调整弧形连杆的半径以及弧形连杆的安装方式(如第2种并联机构的转动副轴线不均布于一个圆周上,第3种并联机构的转动副轴线之间不成60°)。
2) 对3种并联机构在特定转动点处的灵巧度空间进行了分析,为后续优化影响灵巧度工作空间的相关参数(动平台的外接圆半径、弧形连杆的半径、第1种和第2种3-RPS并联机构的球铰沿弧形长槽移动的方向等), 分析支链力传递效率、瞬时转轴奠定基础。另外,这3种并联机构有结构简单、安装性能较好等优点,故有望成为虚轴机床、航空模拟设备、医疗设备等的新型实用机型。
| [1] |
黄真, 孔令富, 方跃法.
并联机器人机构学理论及控制[M]. 北京: 机械工业出版社, 1997: 29-30.
HUANG Zhen, KONG Ling-fu, FANG Yue-fa. Theory and control of parallel robotic mechanisms manipulator[M]. Beijing: China Machine Press, 1997: 29-30. |
| [2] | HUNT K H. Kinematic geometry of mechanisms[M]. New York: Oxford University Press, 1978: 886-903. |
| [3] |
谢志江, 梁欢, 宋代平.
基于连续蚁群算法的3-RPS并联机构正解[J]. 中国机械工程, 2015, 26(6): 799–803.
XIE Zhi-jiang, LIANG Huan, SONG Dai-ping. Forward kinematics of 3-RPS parallel mechanism based on a continuous aut colony algorithm[J]. China Mechanical Engineering, 2015, 26(6): 799–803. |
| [4] |
毛冰滟, 谢志江, 吴小勇, 等.
基于引导人工蜂群算法的3-RPS并联机构正解优化[J]. 农业机械学报, 2017, 48(1): 339–345.
MAO Bing-yan, XIE Zhi-jiang, WU Xiao-yong, et al. Forward kinematics optimization of 3-RPS parallel manipulator based on global-best artificial bee colony algorithm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(1): 339–345. DOI:10.6041/j.issn.1000-1298.2017.01.045 |
| [5] |
胡映光, 胡明, 刘军红.
基于混合遗传算法的3-RPS并联机构正解[J]. 组合机床与自动化加工技术, 2017(6): 34–36.
HU Ying-guang, HU Ming, LIU Jun-hong. Forward kinematic for 3-RPS parallel mechanism based on hybrid genetic algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2017(6): 34–36. |
| [6] |
陈长忆, 车林仙.
应用粒子群算法的3-RPS并联机器人机构位置正解[J]. 现代制造工程, 2017(5): 77–79.
CHEN Chang-yi, CHE Lin-xian. Forward position analysis of 3-RPS in-parallel manipulators based on particle swarm optimization[J]. Modern Manufacturing Engineering, 2017(5): 77–79. |
| [7] |
张伟, 高洪, 陈玉, 等.
基于改进粒子群算法的3-RPS并联机构正解研究[J]. 井冈山大学学报(自然科学版), 2016, 37(4): 63–67.
ZHANG Wei, GAO Hong, CHEN Yu, et al. Forward kinematics study of 3-RPS parallel mechanism based on improved particle swarm optimization[J]. Journal of Jinggangshan University(Natural Science), 2016, 37(4): 63–67. |
| [8] |
高峰, 黄玉美, 史文浩, 等.
3-RPS并联机构工作空间分析的球坐标搜索法[J]. 西安理工大学学报, 2001, 17(3): 239–242.
GAO Feng, HUANG Yu-mei, SHI Wen-hao, et al. The sphere-coordinate searching method of the workspace analysis of the 3-RPS parallel mechanism[J]. Journal of Xi'an University of Technology, 2001, 17(3): 239–242. |
| [9] |
蒲志新, 李艳梅, 于英华.
3-RPS并联机器人工作空间分析及参数研究[J]. 机械传动, 2015, 39(1): 17–21.
PU Zhi-xin, LI Yan-mei, YU Ying-hua. Study on workspace and structural parameters of 3-RPS parallel robot[J]. Journal of Mechanical Transmission, 2015, 39(1): 17–21. |
| [10] |
张斌, 马春生, 郝亮亮, 等.
两种方法对比分析3-RPS机构的工作空间[J]. 煤矿机械, 2016, 37(1): 248–250.
ZHANG Bin, MA Chun-sheng, HAO Liang-liang, et al. Study on workspace of 3-RPS mechanism in two methods[J]. Coal Mine Machinery, 2016, 37(1): 248–250. |
| [11] |
周兵, 毛泰祥, 杨汝清.
3自由度RPS并联机构的工作空间分析[J]. 湖南大学学报(自然科学版), 2003, 30(1): 58–61.
ZHOU Bing, MAO Tai-xiang, YANG Ru-qing. Workspace analysis of 3-DOF RPS parallel mechanism[J]. Journal of Hunan University (Natural Sciences), 2003, 30(1): 58–61. |
| [12] |
原政.
3-RPS和3-SPR机构的工作空间差异分析[J]. 机械工程与自动化, 2015(6): 170–171.
YUAN Zheng. Analysis of workspace differences between 3-RPS and 3-SPR mechanisms[J]. Mechanical Engineering & Automation, 2015(6): 170–171. |
| [13] |
朱大昌, 冯文结, 刘运鸿.
基于影响系数3-RPS并联机构运动学分析与仿真[J]. 机械传动, 2014, 38(3): 76–79.
ZHU Da-chang, FENG Wen-jie, LIU Yun-hong. Kinematics analysis and simulation of 3-RPS parallel mechanism based on the influence coefficient[J]. Journal of Mechanical Transmission, 2014, 38(3): 76–79. |
| [14] |
方跃法, 黄真.
三自由度3-RPS并联机器人机构的运动分析[J]. 机械科学与技术, 1997, 16(1): 82–88.
FANG Yue-fa, HUANG Zhen. Kinematic analysis of 3-RPS parallel robot mechanism[J]. Mechanical Science and Technology for Aerospace Engineering, 1997, 16(1): 82–88. |
| [15] |
齐大志, 张彦婓, 宫金良.
转动轴线共面型3-RPS并联机构运动特性分析[J]. 机械设计与制造, 2014(9): 235–237.
QI Da-zhi, ZHANG Yan-fei, GONG Jin-liang. Kinetic characteristics analysis of 3-RPS parallel mechanism with coplanar rotation axes[J]. Machinery Design & Manufacture, 2014(9): 235–237. |
| [16] |
彭中波, 黄玉美, 马建辉, 等.
3-RPS并联机构奇异位形分析[J]. 组合机床与自动化加工技术, 2004(7): 31–32.
PENG Zhong-bo, HUANG Yu-mei, MA Jian-hui, et al. Singularity analysis of 3-RPS parallel manipulators[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2004(7): 31–32. |
| [17] | LI Qin-chuan, XIANG Ji-nan, CHAI Xin-xue, et al. Singularity analysis of a 3-RPS parallel manipulator using geometric algebra[J]. Chinese Journal of Mechanical Engineering, 2015, 28(6): 1204–1212. DOI:10.3901/CJME.2015.0728.103 |
| [18] |
落海伟, 张俊, 王辉, 等.
3-RPS并联机构静刚度建模方法[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(9): 797–803.
LUO Hai-wei, ZHANG Jun, WANG Hui, et al. Static stiffness modeling method of 3-RPS PKM[J]. Journal of Tianjin University(Science and Technology), 2015, 48(9): 797–803. |
| [19] |
郑魁敬, 崔培, 郭海军.
3-RPS并联机构运动与静力特性分析[J]. 机械设计, 2011, 28(9): 28–33.
ZHENG Kui-jing, CUI Pei, GUO Hai-jun. Kinematics and static characteristics analysis of 3-RPS parallel mechanism[J]. Journal of Machine Design, 2011, 28(9): 28–33. |
| [20] |
程刚, 葛世荣.
3-RPS对称并联式机械腿误差模型及分析[J]. 中国矿业大学学报, 2009, 38(1): 50–55.
CHENG Gang, GE Shi-Rong. Error model and analysis of 3-RPS symmetrical parallel robot leg with three degree-of-freedom[J]. Journal of China University of Mining & Technology, 2009, 38(1): 50–55. |
| [21] |
李新友, 陈五一, 韩先国.
基于正交设计的3-RPS并联机构精度分析与综合[J]. 北京航空航天大学学报, 2011, 37(8): 979–984.
LI Xin-you, CHEN Wu-yi, HAN Xian-guo. Accuracy analysis and synthesis of 3-RPS parallel machine based on orthogonal design[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8): 979–984. |
| [22] |
陆成松, 车建明.
TRIZ技术在自动化打孔装订机进给系统创新设计中的应用[J]. 机械设计, 2005, 22(11): 54–56.
LU Cheng-song, CHE Jian-ming. Application of TRIZ technique in the innovation design for feeding system of automatic hole punching and bookbinding machine[J]. Journal of Machine design, 2005, 22(11): 54–56. |
| [23] |
王永奉, 赵国如, 杨静, 等. 三支链三自由度并联机构: 201610902874. 5[P]. 2016-10-17.
WANG Yong-feng, ZHAO Guo-ru, YANG Jing, et al. Three-chain three-degree-of-freedom parallel mechanism:201610902874.5[P]. 2016-10-17. |
| [24] | PALPACELLI M C, CARBONARI L, PALMIERI G. Analysis and design of a reconfigurable 3-DOF parallel manipulator for multimodal tasks[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1975–1985. DOI:10.1109/TMECH.2014.2365616 |
| [25] | ZHANG Fan, YANG Jian-guo. Type synthesis of instantaneous motion-free 2R1T parallel mechanism by IMGA method[C]//2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, Jun. 26-28, 2010. |
| [26] |
李仕华, 李秦川, 黄真.
3-TPT并联机构的瞬时运动特性[J]. 机械科学与技术, 2003, 22(3): 456–463.
LI Shi-hua, LI Qin-chuan, HUANG Zhen. The instantaneous motion characteristics of 3-TPT parallel mechanism[J]. Mechanical Science and Technology, 2003, 22(3): 456–463. |
| [27] |
杨玉维, 赵新华.
3-RRRT并联机器人工作空间与灵巧度的分析[J]. 机械设计, 2005, 22(2): 11–13.
YANG Yu-wei, ZHAO Xin-hua. Analysis on working space and dexterousness of 3-RRRT parallel robots[J]. Journal of Machine Design, 2005, 22(2): 11–13. |



