2. 湖北省油气钻完井工具工程技术研究中心, 湖北 荆州 434023
2. Hubei Engineering Research Center for Oil & Gas Drilling and Completion Tools, Jingzhou 434023, China
随着油气资源的不断开采,石油钻井逐渐向大位移井、多分支水平井方向发展,井眼轨迹控制难度越来越大。传统的井眼轨迹控制方法是在钻柱上安装稳定器,但传统的稳定器因结构固定、通用性差而导致在钻井过程中需频繁更换,且更换只能在停钻、起钻条件下方可实现,这样不但易引起遇阻和“拔活塞”等现象,甚至还会引发井塌、井喷等事故[1-4]。
为了克服上述困难,国内外学者研制了可变径稳定器,通过其和螺杆钻具的配套使用来实现防斜打快和有效控制井眼轨迹[5-8]。可变径稳定器作为一种能有效控制井眼轨迹的工具,其已经得到广泛研究。为了给可变径稳定器的设计提供理论基础,文献[9]对可变径稳定器作了初步分析,并指出井下控制机构设计学是井眼轨道控制执行机构设计的理论基础。文献[10]介绍了一种井下闭环可变径稳定器的工作原理及其控制井眼轨迹的方法。文献[11]提出了一种井下闭环可变径稳定器结构并对其可调稳定块进行了静力学分析,推导出可调稳定块保持稳定平衡所需的钻井液驱动力的计算公式。文献[12]提出了一种遥控可变径稳定器结构并介绍了其工作原理,分析了遥控可变径稳定器存在状态信号不可靠的原因,其研究表明:该类稳定器内平衡活塞位于上限、下限位置时会导致状态信号减弱或无信号;利用前后两次开泵泵压差值确定其状态的方法可靠,可为地面遥控稳定器的研制提供依据。
上述稳定器主要通过信号控制,其可靠性差且控制困难。鉴于此,本文设计了一种新型多级可变径稳定器并申请了发明专利[13],该稳定器采用纯液压控制,可以通过调节稳定器外径来改变井眼斜率并能在单趟钻进时完成多种尺寸变化。因此,它相对于上述稳定器更加可靠;其次,考虑均布载荷及弯矩等因素的联合作用,基于纵横弯曲法理论,对使用该多级可变径稳定器的钻具组合的力学模型进行分析,参考文献[14-15]列出了其相应的三弯矩方程组,借助MATLAB软件并采用迭代法计算了不同支撑块伸出长度所需最小钻井液驱动力和钻头侧向力的值,结果表明该可变径稳定器具有增斜、降斜和稳斜功能。
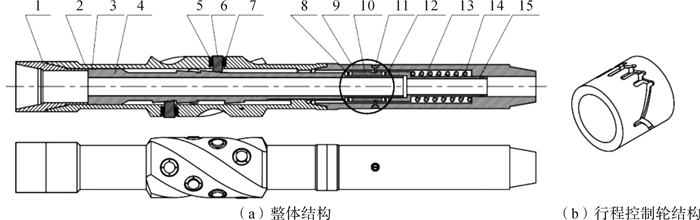
1 多级可变径稳定器结构及工作原理 1.1 多级可变径稳定器结构井下多级可变径稳定器结构如图 1(a)所示,该稳定器主要由变径短节和控制短节两部分组成,其中变径短节主要由上接头、本体、支撑块、弹簧、压盖和芯轴组成;控制短节主要由外壳、推力轴承、中心管、行程控制轮、销钉和复位弹簧组成。图 1(b)为行程控制轮结构的三维图形。
|
| 1—上接头;2—本体;3—O形密封圈组a;4—芯轴;5—压盖;6—支撑块;7—弹簧;8—推力轴承a;9—外壳;10—行程控制轮;11—销钉;12—推力轴承b;13—中心管;14—复位弹簧;15—O形密封圈组b 图 1 多级可变径稳定器整体结构及行程控制轮结构 Fig.1 Multistage variable diameter stabilizer overall structure and stroke control wheel structure |
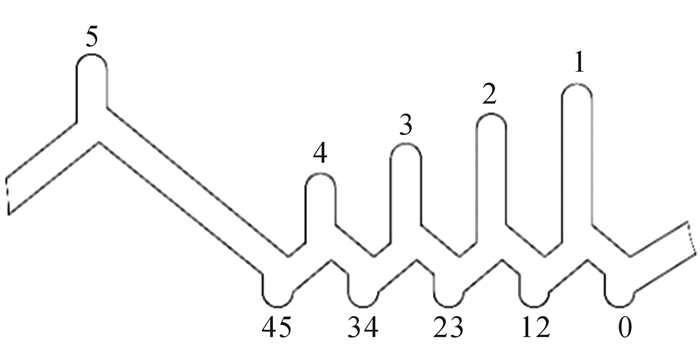
可变径稳定器的导向滑槽如图 2所示。初始状态时销钉位于0号导向滑槽下端,下钻时,泥浆泵正常开启,稳定器芯轴受泥浆压力向下运动,因销钉的限位作用,销钉最终位于1号导向滑槽的上端,此时稳定器的外径为r1;如果降低泥浆泵出口压力,此时在复位弹簧与导向滑槽特殊结构的共同作用下,芯轴将在向上移动的同时转动,最终沿着导向滑槽进入12号导向滑槽的下端;若增加泥浆泵出口压力,芯轴向下运动,销钉沿着导向滑槽进入2号槽的上端,此时稳定器的外径为r2。基于此,可实现销钉依次循环地进入1,2,3,4,5号导向滑槽的上端,即调整稳定器的外径分别为r1,r2,r3,r4,r5,而稳定器芯轴移动距离分别为h1,h2,h3,h4,h5,其中r5>r1>r2>r3>r4,h5>h1>h2>h3>h4。此外,轨道槽可根据实际工况进行设计,包括调整级数和行程差等。
|
| 图 2 导向滑槽示意图 Fig.2 Guide chute schematic |
本节首先分析了井下钻具力学模型,并根据芯轴与支撑块之间的几何关系得到了支撑块伸缩长度计算公式。
通过对支撑块伸出长度的分析可知,要想定量地分析支撑块伸出长度必须先要定量地分析芯轴位移,即弹簧压缩量。而根据对芯轴的受力分析可知,复位弹簧弹力与支撑块处所受井壁支撑力和钻井液驱动力有关,因此本文通过简化钻具组合并建立其数学模型,得到了钻井液驱动力与复位弹簧弹力和支撑块处所受井壁支撑力之间的关系式。在钻井过程中,一般为便于控制钻井液相关参数且可变径稳定器每档处的支撑块伸出长度为定值,于是将支撑块伸出长度作为自变量,而将钻井液驱动力作为因变量,这样就可以通过求出各个档位处所需最小钻井液驱动力来反求钻井液流量,并通过计算各个档位处钻头侧向力来控制水平井微调。
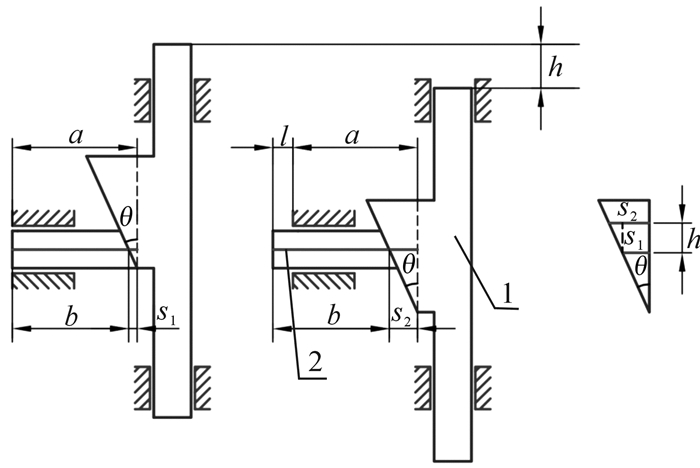
2.1 井下钻具力学模型的简化井下钻具在井下受到轴向载荷与横向均布载荷及弯矩的联合作用,其力学模型如图 3所示。
|
| 图 3 井下钻具力学模型 Fig.3 Mechanical model of the downhole drilling tool |
参考文献[16]可得其基本计算公式如下:
| $ {\theta _{\rm{L}}} = \frac{{q{L^3}}}{{24EI}}X\left( u \right) + \frac{{{M_{\rm{L}}}L}}{{3EI}}Y\left( u \right) + \frac{{{M_{\rm{R}}}L}}{{6EI}}Z\left( u \right) $ | (1) |
| $ {\theta _{\rm{R}}} = \frac{{q{L^3}}}{{24EI}}X\left( u \right) + \frac{{{M_{\rm{R}}}L}}{{3EI}}Y\left( u \right) + \frac{{{M_{\rm{L}}}L}}{{6EI}}Z\left( u \right) $ | (2) |
其中:
| $ X\left( u \right) = \frac{3}{{{u^3}}}\left( {{\rm{tg}}\;u - u} \right) $ |
| $ Y\left( u \right) = \frac{3}{{2u}}\left( {\frac{1}{{2u}} - \frac{1}{{{\rm{tg}}\;2u}}} \right) $ |
| $ Z\left( u \right) = \frac{3}{u}\left( {\frac{1}{{\sin 2u}} - \frac{1}{{2u}}} \right) $ |
| $ I = \frac{{\rm{ \mathsf{ π} }}}{{64}}\left( {{D^4} - {d^4}} \right) $ |
式中:q为横向均布载荷密度,kN/mm;L为梁柱长度,mm;E为材料的弹性模量,GPa;I为梁柱惯性矩,mm4;Np为轴向载荷,kN;ML为梁柱左端的内弯矩,kN·mm;MR为梁柱右端的内弯矩,kN·mm; θL为梁柱左端部转角,rad;θR为梁柱右端部转角,rad;d,D分别为轴的内外径,mm。
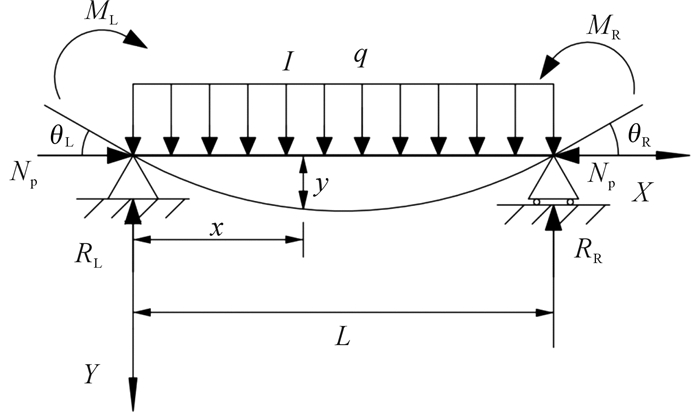
2.2 芯轴位移h与支撑块伸出长度l之间的关系芯轴位移与支撑块伸出长度之间的数学模型如图 4所示。假设芯轴向下移动距离为h,支撑块斜面与芯轴轴线的夹角为θ,则初始状态处,a=b+s1,末状态处,a=b+s2-l,又因s2-s1=htan θ,可得支撑块伸出长度l=s2-s1=htan θ。
|
| 1—芯轴;2—支撑块 图 4 芯轴位移与支撑块伸出长度的几何关系 Fig.4 Geometrical relationship between the displacement of the mandrel and the telescopic length of the support block |
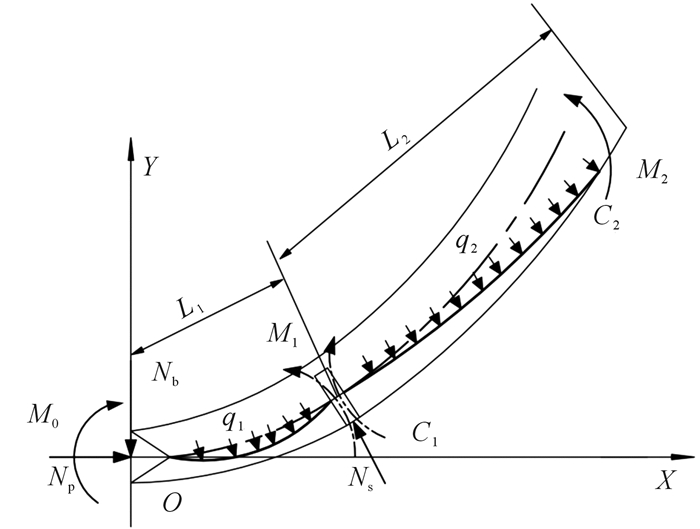
图 5所示为井下钻具组合的力学模型,其中单弯螺杆钻具安装在钻头与可变径稳定器之间,并用该可变径稳定器替代单弯螺杆钻具上的欠尺寸稳定器。假设支撑块伸出长度为l,考虑到均布载荷、等效横向集中载荷、弯矩、支座位移所引起的转角及螺杆弯角对梁柱端部转角的影响,将式(1)和式(2)代入连续性条件和上边界条件[17-18]可得:
|
| 图 5 井下钻具组合力学模型 Fig.5 Mechanical model of the downhole drilling tool assembly |
| $ \left\{ \begin{array}{l} \frac{{{q_1}L_1^3}}{{24E{I_1}}}X\left( {{u_1}} \right) + \frac{{{M_{\rm{1}}}{L_1}}}{{3E{I_1}}}Y\left( {{u_1}} \right) + \frac{{{M_{\rm{0}}}{L_1}}}{{6E{I_1}}}Z\left( {{u_1}} \right) - \\ \frac{{{e_1} - {e_0}}}{{{L_1}}} + \delta \theta _1^R = - \frac{{{q_2}L_2^3}}{{24E{I_2}}}X\left( {{u_2}} \right) - \frac{{{M_1}{L_2}}}{{3E{I_2}}}Y\left( {{u_2}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{M_2}{L_2}}}{{6E{I_2}}}Z\left( {{u_2}} \right) - \frac{{{e_2} - {e_1}}}{{{L_2}}}\\ \frac{{{q_2}L_2^3}}{{24E{I_2}}}X\left( {{u_2}} \right) + \frac{{{M_2}{L_2}}}{{3E{I_2}}}Y\left( {{u_2}} \right) + \frac{{{M_1}{L_2}}}{{6E{I_2}}}Z\left( {{u_2}} \right) - \\ \frac{{{e_2} - {e_1}}}{{{L_2}}} = K\left( {{L_1} + {L_2}} \right) \end{array} \right. $ | (3) |
整理得:
| $ \left\{ \begin{array}{l} {M_0}Z\left( {{u_1}} \right) + 2{M_1}\left[ {Y\left( {{u_1}} \right) + \frac{{{L_2}{I_1}}}{{{L_1}{I_2}}}Y\left( {{u_2}} \right)} \right] + \\ {M_2}\left[ {\frac{{{L_2}{I_1}}}{{{L_1}{I_2}}}Z\left( {{u_2}} \right)} \right] = - \frac{{{q_1}L_1^2}}{4}X\left( {{u_1}} \right) - \\ \frac{{{q_2}L_2^2}}{4}\left( {\frac{{{L_2}{I_1}}}{{{L_1}{I_2}}}} \right)X\left( {{u_2}} \right) + \frac{{6E{I_1}}}{{{L_1}}}\left[ {\frac{{{e_1} - {e_0}}}{{{L_1}}} - \frac{{{e_2} - {e_1}}}{{{L_2}}} - \delta \theta _1^R} \right]\\ {q_2}X\left( {{u_2}} \right)L_2^4 + 4\left[ {2{M_2}Y\left( {{u_2}} \right) + {M_1}Z\left( {{u_2}} \right)} \right] = L_2^2 = \\ 24E{I_2}\left[ {{L_2}\left( {{L_1} + {L_2}} \right)K + {e_2} - {e_1}} \right] \end{array} \right. $ | (4) |
其中:e0=0
| $ {e_1} = \frac{1}{2}\left[ {{D_0} - \left( {{D_{c1}} + 2l} \right)} \right] $ |
| $ {e_2} = \frac{1}{2}\left[ {{D_0} - {D_{c2}}} \right] $ |
| $ {\left( {{\alpha _i}} \right)_{\rm{m}}} = {\alpha _{\rm{b}}} - K\sum\limits_{j = 1}^{i - 1} {{L_j}} - \frac{{K{L_i}}}{2} $ |
| $ {N_1} = {N_{\rm{p}}}\cos \frac{{K{L_1}}}{2} - \frac{1}{2}{w_1}{L_1}\cos {\left( {{\alpha _1}} \right)_{\rm{m}}} $ |
| $ \begin{array}{l} {N_i} = {N_{i - 1}} - \frac{1}{2}{w_{i - 1}}{L_{i - 1}}\cos {\left( {{\alpha _{i - 1}}} \right)_{\rm{m}}} - \\ \;\;\;\;\;\;\;\;\frac{1}{2}{w_i}{L_i}\cos {\left( {{\alpha _i}} \right)_{\rm{m}}} \end{array} $ |
| $ {q_i} = {w_i}\sin {\left( {{\alpha _i}} \right)_{\rm{m}}} $ |
| $ {w_i} = \frac{{{\rm{ \mathsf{ π} }}d_i^2\rho g}}{4} \times {10^{ - 9}} $ |
由于三弯矩方程组共有2个方程,且只有2个未知数M1和L2,因而是定解的。
再参考文献[15],基于正弦定理可得
以上各式中:D0为井眼直径,mm;Dc1为可变径稳定器直径,mm;Dc2为上切点钻具直径,mm;Mi为第i个支座处的内弯矩值,kN·mm;qi为第i跨梁柱上的横向均布载荷密度,kN/mm;L1为钻头底面至可变径稳定器中点的距离,mm;L2为可变径稳定器中点至上切点钻具中点的距离,mm;Ni为第i跨梁柱上的轴向载荷,kN;Ii为第i跨梁柱的横向轴惯性矩,mm4;K为井身曲线的曲率,(°/30m);(αi)m表示第i跨梁柱中点的井斜角,rad;wi为每跨梁柱单位长度钻具在钻井液中的重量,kN/mm;αb为井斜角,(°);Np为井底钻压,kN;di为钻具内径,mm;ρ为钻井液密度,g/cm3;g为重力加速度,m/s2。
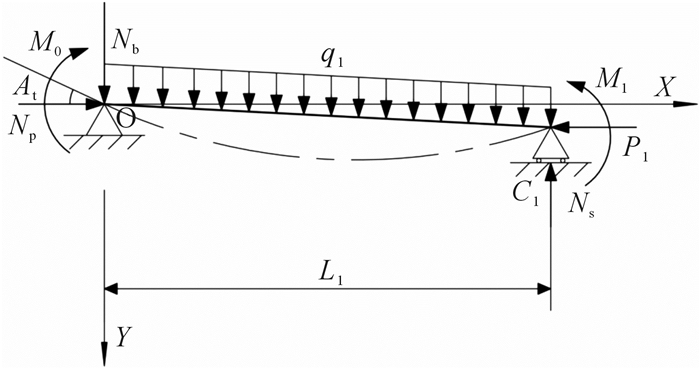
2.3.2 钻头侧向力、支撑块处所受井壁支撑力与钻井液驱动力的计算钻头侧向力与钻头倾角如图 6所示,则可求得钻头侧向力与支撑块处所受井壁支撑力,其计算公式如下:
|
| 图 6 钻头侧向力与钻头倾角 Fig.6 Drill side force and drill bit tilt angle |
| $ {N_{\rm{b}}} = \frac{1}{{{L_1}}}\left( {{N_{\rm{p}}}{e_1} - \frac{1}{2}{q_1}L_1^2 + {M_0} - {M_1}} \right) $ | (5) |
| $ {N_{\rm{s}}} = \frac{1}{{{L_1}}}\left( {{N_{\rm{p}}}{e_1} - \frac{1}{2}{q_1}L_1^2 + {M_0} - {M_1}} \right) $ | (6) |
式中:Nb为钻头侧向力,kN;Ns为支撑块处所受井壁支撑力,kN。
若Nb>0,则为造斜力; 若Nb < 0,则为降斜力。
又由文献[11]可得芯轴处钻井液驱动力的计算公式为:
| $ \begin{array}{*{20}{c}} {{F_{\rm{L}}} = \frac{{12\left( {{f_1} + \tan \theta } \right)}}{{\left( {1 - {f_1}{f_2}} \right) - \left( {{f_1} + {f_2}} \right)\tan \theta }}{N_{\rm{s}}} + T}\\ {T = {k_{\rm{r}}}\Delta x \times {{10}^{ - 3}}} \end{array} $ | (7) |
式中:f1为支撑块与导向体楔块间的静摩擦系数,无量纲;f2为支撑块与本体槽间的静摩擦系数,无量纲;θ为支撑块斜面倾角,(°);kr为复位弹簧的弹性模量,N/mm;Δx为复位弹簧压缩量,mm;T为复位弹簧弹力,kN;FL为钻井液驱动力,kN。
将式(6)代入式(7),可得可变径稳定器钻井液驱动力与芯轴位移之间的关系式为:
| $ \begin{array}{*{20}{c}} {{F_{\rm{L}}} = \frac{k}{{\tan \theta }}l \times {{10}^{ - 3}} + \frac{1}{{{L_1}}}\left( {{N_{\rm{p}}}{e_1} + \frac{1}{2}{q_1}L_1^2 + {M_0} - } \right.}\\ {\left. {{M_1}} \right) \times \frac{{12\left( {{f_1} + \tan \theta } \right)}}{{\left( {1 - {f_1}{f_2}} \right) - \left( {{f_1} + {f_2}} \right)\tan \theta }}} \end{array} $ | (8) |
本文所设计的多级可变径稳定器主要用于水平井井眼轨迹微调。现借助MATLAB软件采用迭代法对现场实际情形进行仿真。钻具组合为:∅215.9 mm PDC钻头+1.15°螺杆+∅130 mm可变径稳定器+无磁承压钻杆×1根+无磁悬挂+∅127 mm加重钻杆×3根+∅127 mm钻杆×54根+∅165 mm震击器+旁通阀+∅127 mm加重钻杆×48根+∅139.7 mm G105钻杆。钻具组合的基本尺寸参数如表 1。
| 参数 | 数值 |
| 梁柱材料的弹性模量E/GPa | 210 |
| 井身曲线的曲率K/(°/30m) | 0 |
| 钻井液密度ρ/(g/cm3) | 1.20 |
| 井眼直径D0/mm | 215.9 |
| 重力加速度g/(m/s2) | 9.8 |
| 井斜角αb/(°) | 90.64~90.69 |
| 井底钻压Np/kN | 50 |
| 螺杆弯角到钻头顶端的距离m1/mm | 1 137 |
| 螺杆弯角到螺杆顶端的距离m2/mm | 4 975 |
| 稳定器内径dc1/mm | 45 |
| 稳定器外径Dc1/mm | 130 |
| 无磁承压钻杆内径dc2/mm | 97 |
| 无磁承压钻杆外径Dc2/mm | 127 |
| 复位弹簧弹性模量kr/(N/mm) | 92 |
| 支撑块斜面倾角θ/(°) | 8.1 |
| 支撑块与导向体楔块间的静摩擦系数f1 | 0.11 |
| 支撑块与本体槽间的静摩擦系数f2 | 0.11 |
| 钻头底面到稳定器中点的距离L1/mm | 7 360 |
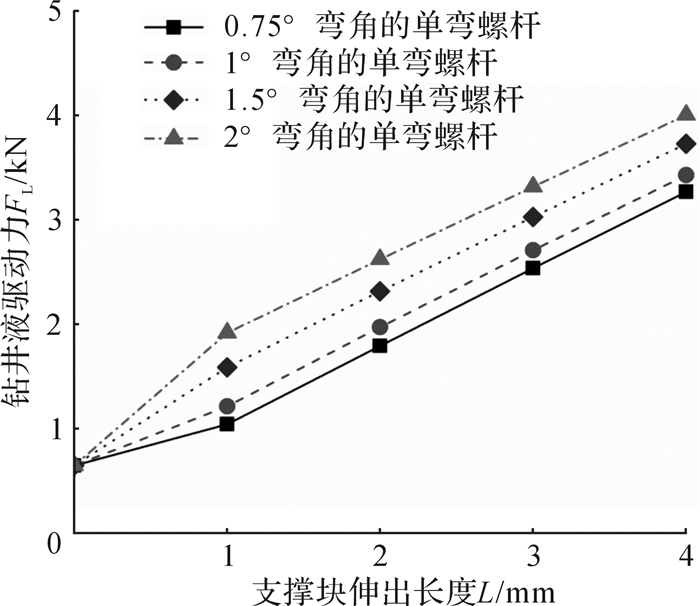
该钻具组合中,可变径稳定器支撑块每次伸出长度为1 mm且共有5个档位,单弯螺杆弯角分别采用0.75°,1°,1.5°,2°进行计算,代入数据可得弯角不同时单弯螺杆钻具处可变径稳定器在每个档位处支撑块伸出长度对应的钻井液驱动力和钻头侧向力, 结果如图 7和图 8。
|
| 图 7 支撑块伸出长度对钻井液驱动力的影响 Fig.7 The effect of the extension length of the support block on the driving force of the drilling fluid |
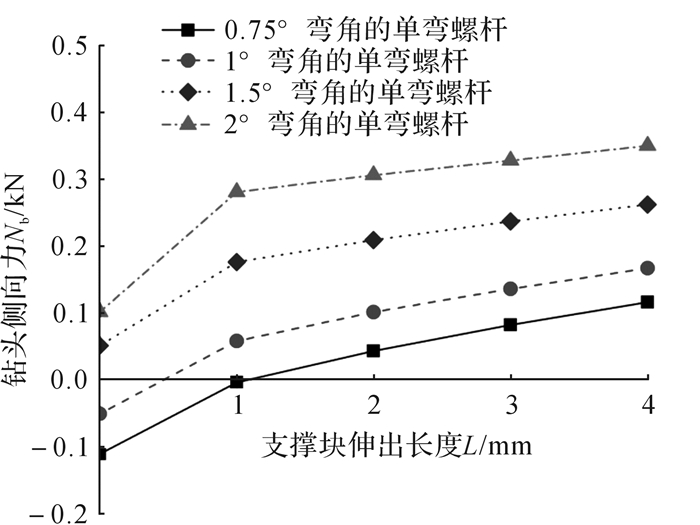
|
| 图 8 支撑块伸出长度对钻头侧向力的影响 Fig.8 The effect of the length of the support block on the lateral force of the drill bit |
由图 7和图 8可知:随着支撑块伸出长度的增加,钻井液驱动力和钻头侧向力增加;且在单弯螺杆钻具弯角为0.75°和1°时,钻头侧向力既有正值也有负值,表明可变径稳定器既有增斜能力也有降斜能力;当支撑块伸出长度为1 mm,单弯螺杆钻具弯角为0.75°时,钻头侧向力近似为零,则可变径稳定器此时起稳斜效果。这一结果表明,该可变径稳定器具有水平井井眼轨迹微调能力。
4 结论1) 设计了一种主要用于水平井井眼轨迹微调的新型多级可变径稳定器并介绍了其工作原理,该稳定器能在钻井液驱动力控制下通过改变销钉在行程控制轮导向滑槽中的状态来实现几级变径,且其采用纯液压控制时可靠性更好。
2) 考虑均布载荷、弯角等因素的联合作用, 基于纵横弯曲法理论,建立了使用多级可变径稳定器的钻具组合的力学模型,计算了不同支撑块伸出长度所需最小钻井液驱动力和钻头侧向力的值,结果表明该稳定器能实现增斜、降斜和稳斜功能,并能在单趟钻进时完成多种尺寸变化从而降低钻井成本。
| [1] | AL-BALUSHI H, AL-RASHDI M H, AL-SHANDOODI M H, et al. World longest expandable open hole clad & open hole liner with swelling elastomer deployed in Yibal horizontal well[C]//SPE Asia Pacific Drilling Technology Conference, Kuala Lumpur, Malaysia, Sep. 13-15, 2004. |
| [2] |
祝效华, 刘少胡, 聂荣国, 等.
KWQ-216型地面可控井下变径稳定器[J]. 石油钻采工艺, 2011, 33(1): 120–122.
ZHU Xiao-hua, LIU Shao-hu, NIE Rong-guo, et al. KWQ-216 surface controlled downhole variable diameter stabilizer[J]. Oil Drilling & Production Technology, 2011, 33(1): 120–122. |
| [3] |
肖仕红, 梁政.
旋转导向钻井技术发展现状及展望[J]. 石油机械, 2006, 34(4): 66–70.
XIAO Shi-hong, LIANG Zheng. Development status and prospect of the rotary steerable drilling technology[J]. China Petroleum Machinery, 2006, 34(4): 66–70. |
| [4] |
苏义脑, 窦修荣, 王家进.
变径稳定器及其应用[J]. 石油钻采工艺, 2003, 25(3): 4–8, 81.
SU Yi-nao, DOU Xiu-rong, WANG Jia-jin. Variable diameter stabilizer and its application[J]. Oil Drilling & Production Technology, 2003, 25(3): 4–8, 81. |
| [5] | MARLAND C, BUCHAN J, THAILAND C, et al. Understanding downhole vibration transmission and disruption in Gulf of Thailand[C]//SPE Asia Pacific Oil and Gas Conference, Perth, Australia, Oct. 18-20, 2004. |
| [6] |
苏义脑.
井下控制工程学研究进展[M]. 北京: 石油工业出版社, 2001: 18-22.
SU Yi-nao. Research progress of underground control engineering[M]. Beijing: Petroleum Industry Press, 2001: 18-22. |
| [7] | MCCORMICK J, OSORIO G, ANDACHI J, et al. Adjustable gauge stabilizer and torque and drag reduction tools reduce over-all drilling times by at least:a case study[C]//SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, Sep. 25-28, 2011. |
| [8] |
张玉英, 王永宏, 邹涌.
遥钻井遥控变径稳定器的研制及应用[J]. 石油矿场机械, 2008, 37(1): 87–89.
ZHANG Yu-ying, WANG Yong-hong, ZOU Yong. Development and application of remote control diameter stabilizer in drilling[J]. Oil Field Equipment, 2008, 37(1): 87–89. |
| [9] |
刘英辉, 苏义脑, 刘旭辉.
井眼轨道控制系统中可变径稳定器的发展概况[J]. 石油机械, 2000, 28(5): 52–53, 58.
LIU Ying-hui, SU Yi-nao, LIU Xu-hui. Development of variable diameter stabilizer in wellbore orbit control system[J]. China Petroleum Machinery, 2000, 28(5): 52–53, 58. |
| [10] |
余志清.
井下闭环可变径稳定器的工作原理及应用研究[J]. 石油学报, 2002, 23(3): 95–97, 9.
YU Zhi-qing. Mechanism of controlling borehole trajectory with close-loop adjustable stabilizer at downhole[J]. Acta Petrolei Sinica, 2002, 23(3): 95–97, 9. DOI:10.7623/syxb200203021 |
| [11] |
张光伟.
井下闭环可变径稳定器的设计计算[J]. 石油机械, 2004, 32(2): 23–25, 41.
ZHANG Guang-wei. Design and calculation of downhole close-loop adjustable stabilizers[J]. China Petroleum Machinery, 2004, 32(2): 23–25, 41. |
| [12] |
周志刚.
遥控变径稳定器变径动作分析及现场试验[J]. 石油钻探技术, 2015, 43(3): 120–124.
ZHOU Zhi-gang. Analysis and field testing by remote control of the action of a variable diameter stabilizer[J]. Petroleum Drilling Techniques, 2015, 43(3): 120–124. |
| [13] |
夏成宇, 王杰, 华勇. 一种多级可变径稳定器: CN106368621A[P]. 2017-02-01.
XIA Cheng-yu, WANG Jie, HUA Yong. A multi-stage variable diameter stabilizer:CN106368621A[P]. 2017-02-01. |
| [14] |
唐雪平.
变截面(变刚度)纵横弯曲梁[J]. 力学与实践, 1999, 12(4): 47–50.
TANG Xue-ping. Timoshenko beam of variable cross-section (variable stiffness)[J]. Mechanics in Engineering, 1999, 12(4): 47–50. |
| [15] |
唐雪平, 苏义脑, 陈祖锡.
求解中短半径弯螺杆钻具的纵横弯曲法[J]. 力学与实践, 2011, 33(3): 20–24.
TANG Xue-ping, SU Yi-nao, CHEN Zu-xi. Beam-column theory for bent housing pdm assemblies with medium-short radius of building capability[J]. Mechanics in Engineering, 2011, 33(3): 20–24. |
| [16] |
苏义脑, 白家祉.
用纵横弯曲法对弯接头——井下动力钻具组合的三维分析[J]. 石油学报, 1991, 12(3): 110–120.
SU Yi-nao, BAI Jia-zhi. Three-dimensional analysis of bending joint-downhole dynamic drilling tools by vertical and horizontal bending method[J]. Acta Petrolei Sinica, 1991, 12(3): 110–120. DOI:10.7623/syxb199103014 |
| [17] |
卫增杰. 中短半径水平井螺杆钻具力学性能分析[D]. 成都: 西南石油学院石油工程学院, 2005: 23-27.
WEI Zeng-jie. Mechanical performance analysis of screw drill with medium and short radial horizontal well[D]. Chengdu:Southwest Petroleum Institute, College of Petroleum Engineering, 2005:23-27. |
| [18] |
苏义脑, 唐雪平, 陈祖锡.
初弯曲纵横弯曲梁的等效载荷法及其应用[J]. 力学与实践, 2004, 26(1): 42–44.
SU Yi-nao, TANG Xue-ping, CHEN Zu-xi. Equivalent loading method for solving beam-column with initial bending and its application in drilling engineering[J]. Mechanics in Engineering, 2004, 26(1): 42–44. |



