2. 浙江大学 机械工程学院, 浙江 杭州 310027
2. College of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China
制动系统作为汽车的一个重要组成部分,直接影响汽车行驶的安全性能。随着电动汽车的发展[1],国内外相继兴起了对汽车线控制动技术的研究[2-4]。汽车线控制动(brake by wire, BBW)系统主要有电子机械制动(electromechanical brake, EMB)系统和电子液压制动(electrohydraulic brake, EHB)系统两种形式[5]。相比电子液压制动系统,电子机械制动系统有诸多优点:1)无需制动液,环境友好[6-7];2)控制响应快;3)制动力控制更加精确[8-9];4)易于融入ABS, TCS等控制技术[10-11]。一些国际著名的汽车零配件生产厂商如Bosch, Siemens, Delphi等陆续开展了对EMB的研究[12-13]。
现有的EMB存在一些不足:1)为了实现对制动系统输出电流、转速、制动力的三闭环控制,应用较多传感器,导致制动器结构庞大,无法达到安装要求[14];2)GB12676—2014中规定,制动系统应有磨损补偿装置,摩擦片磨损后能自动调节[15], 现有的EMB缺少国标规定的间隙自动调节功能[16-17]。
针对上述不足,本文设计了一种具有间隙自动调节功能的新型汽车电子机械制动系统,具有轴向、径向尺寸小的特点。在MATLAB/Simulink中建立系统模型,通过仿真与实验测试对比,验证所建模型的正确性,并分析制动性能参数间的关系,对比有/无间隙自动调节机构的系统制动效果。
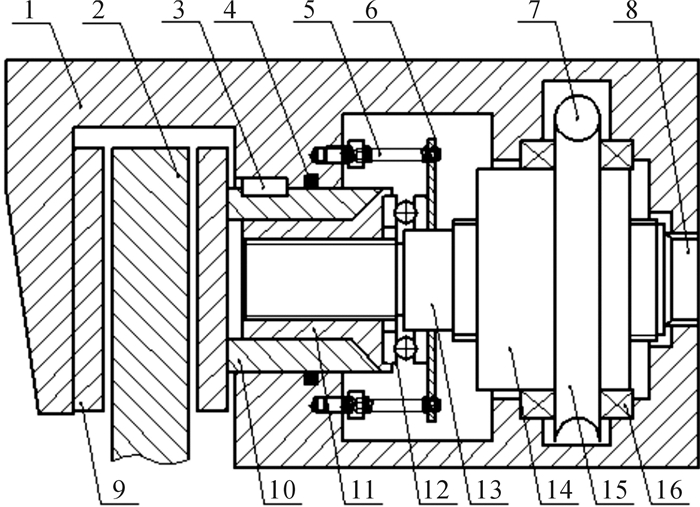
1 汽车电子机械制动系统总体设计 1.1 EMB设计方案抛弃传统制动器的液压管路,根据浮钳盘式制动器的行车制动、间隙自动调节功能进行组合设计,综合考虑空间布置、结构形式和原理配合等,得出如图 1的设计方案。所设计的汽车线控制动系统已获得国家发明专利[18]。
|
| 1—制动钳体;2—制动盘;3—平键;4—矩形密封圈;5—弹簧;6—挡板;7—蜗杆;8—花键;9—摩擦片;10—活塞;11—锥形螺母;12—推力轴承;13—丝杠;14—螺母;15—蜗轮;16—滚动轴承 图 1 电子机械制动系统设计方案 Fig.1 Design program of EMB system |
EMB工作原理如下:制动信号输入,电机旋转,电机输出轴(图中未显示)与蜗杆连接,驱动蜗轮蜗杆机构运动;蜗轮通过轴承安装在制动钳体上,并与螺母固定连接;螺母只能作旋转运动,不能作轴向移动,螺母驱动丝杠作轴向移动,丝杠右端设置有花键,仅作轴向移动,丝杠推动锥形螺母向左作直线移动,进而使摩擦片贴近制动盘,实现制动。电机反转,则解除制动。当摩擦片发生磨损时,活塞在矩形密封圈的作用下,其轴向移动距离在矩形密封圈的最大变形量之内。电机反转时,丝杠(在花键的作用下,只能轴向移动)将带动锥形螺母(非自锁螺纹)回位,锥形螺母与活塞分离。此时,锥形螺母在弹簧和推力轴承的作用下,相对丝杠发生旋转,实现轴向左移,与活塞再次贴合,移动距离等于摩擦片的磨损量。这样就实现了制动间隙的自动调节功能。
1.2 EMB设计目标参数本文选择某桑塔纳车型作为目标车型,参数如表 1所示。
| 参数 | 整备质量m/kg | 前后轮胎规格 | 制动盘外径C/mm | 制动盘有效半径R/mm | 轮胎滚动半径r/mm |
| 数值 | 1 120 | 185/60 R15 | 280 | 120 | 302 |
制动系统的最大制动正压力、制动间隙、间隙消除时间是其最主要的设计目标参数。传统液压盘式制动器制动管路内的最大液压力通常为10~12 MPa,活塞直径为20~50 mm。本文取压力p=12 MPa,活塞直径D=50 mm,估算制动系统输出的最大正压力Fmax。选定制动间隙为0.2 mm,间隙消除时间为0.1 s, 则:
| $ {F_{\max }} = p \times {\rm{ \mathsf{ π} }}{D^2}/4 = 23.55\;{\rm{kN}} \approx {\rm{24}}\;{\rm{kN}} $ | (1) |
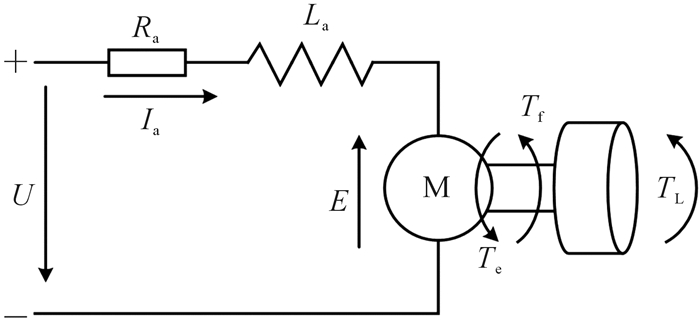
永磁直流力矩电机的工作原理如图 2所示。
|
| 图 2 永磁直流力矩电机工作原理 Fig.2 Working principle of permanent magnet DC torque motor |
电机的动态方程如下[19]:
| $ U = {I_{\rm{a}}}{R_{\rm{a}}} + {L_{\rm{a}}}{{\dot I}_{\rm{a}}} + E $ | (2) |
| $ E = {C_{\rm{e}}}\mathit{\Phi n} = {K_{\rm{t}}}{{\dot \theta }_{\rm{m}}} $ | (3) |
| $ {J_{\rm{m}}}{{\ddot \theta }_{\rm{m}}} = {T_{\rm{e}}} - {T_{\rm{f}}} - {T_{\rm{L}}} $ | (4) |
| $ {T_{\rm{e}}} = {C_{\rm{t}}}\mathit{\Phi }{I_{\rm{a}}} = {K_{\rm{t}}}{I_{\rm{a}}} $ | (5) |
式中:U为电枢电压;Ia为电枢电流;Ra为电枢电阻;La为电枢电感;E为反电动势;Te为电机电磁转矩;Tf为电机摩擦转矩;TL为负载转矩;Jm为电机转动惯量;Ce为电动势常数;Ct为转矩常数;Ф为每极气隙磁通;θm为电机转角;n为电机转速;Kt为转矩系数。
永磁直流力矩电机的参数如表 2所示。
| 参数 | 额定功率/W | 额定电压/V | 空转转速/(r/min) | 峰值电流/A | 峰值转速/(r/min) |
| 数值 | 120 | 12 | 2 000 | 25 | 1 050 |
根据制动系统的工作特性可知,直流力矩电机常处于堵转状态。堵转时电机转速为零,则反电动势E为零,电流为定值,即dIa/dt为零,可得电机在堵转状态下的电磁转矩关系:
| $ {T_{\rm{e}}} = {K_{\rm{t}}} \cdot {I_{\rm{a}}} = {K_{\rm{t}}} \cdot U/{R_{\rm{a}}} $ | (6) |
因此,电机堵转时转矩与电压成正比。根据这一特性,可以通过控制输入信号—电压,控制输出—力矩。
2.2 电机摩擦模型对EMB系统中的电机摩擦环节进行建模分析,并在控制器中进行有效补偿,可以减少摩擦环节对系统的影响,提高系统响应的实时性和控制精度。本文选择Stribeck摩擦模型,表达式如下[20]:
| $ {T_{\rm{f}}} = \left\{ \begin{array}{l} {T_{\rm{e}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _{\rm{m}}} = 0\;且\;\left| {{T_{\rm{e}}}} \right| < {T_{\rm{s}}}\\ {T_{\rm{s}}} \cdot {\mathop{\rm sgn}} \left( {{T_{\rm{e}}}} \right)\;\;\;\;\;\;\;\;\;\;\;{\omega _{\rm{m}}} = 0\;且\;\left| {{T_{\rm{e}}}} \right| \ge {T_{\rm{s}}}\\ {T_{\rm{c}}} + \left( {{T_{\rm{s}}} - {T_{\rm{c}}}} \right){{\rm{e}}^{ - \left( {{\omega _{\rm{m}}}/{\omega _{\rm{s}}}} \right)\delta }} + {B_{\rm{v}}}\omega \;\;\;\;\;{\omega _{\rm{m}}} \ne 0 \end{array} \right. $ | (7) |
式中:ωs为Stribeck速度;Bv为黏性摩擦系数;δ为经验常数,取0.5~1。
2.3 蜗轮蜗杆模型蜗轮蜗杆作为减速增矩机构,将电机输出力矩放大。蜗轮蜗杆传动系统的数学模型可描述如下:
| $ {J_{\rm{w}}}{{\ddot \theta }_{\rm{n}}} = {T_{\rm{w}}} - {T_{\rm{n}}} = i\eta {T_{\rm{L}}} - {F_{\rm{d}}}S/2{\rm{ \mathsf{ π} }} $ | (8) |
| $ {\theta _{\rm{n}}} = {\theta _{\rm{m}}}/i $ | (9) |
由式(4)、(8)可得:
| $ \left( {{J_{\rm{m}}} + \frac{1}{{{i^2}\eta }}{J_{\rm{w}}}} \right){{\ddot \theta }_{\rm{m}}} = {T_{\rm{e}}} - {T_{\rm{f}}} - \frac{1}{{i\eta }}{T_{\rm{n}}} $ | (10) |
| $ {x_{\rm{n}}} = \frac{S}{{2{\rm{ \mathsf{ π} }}}}{\theta _{\rm{n}}} = \frac{S}{{2{\rm{ \mathsf{ π} }}i}}{\theta _{\rm{m}}} $ | (11) |
式中:Jw为蜗轮转动惯量;θn为蜗轮转角;i为传动比;S为滚珠丝杠导程;η为蜗轮传动效率;Tw为蜗轮驱动转矩;Tn为蜗轮负载转矩;xn为由螺母转角换算所得的直线位移。
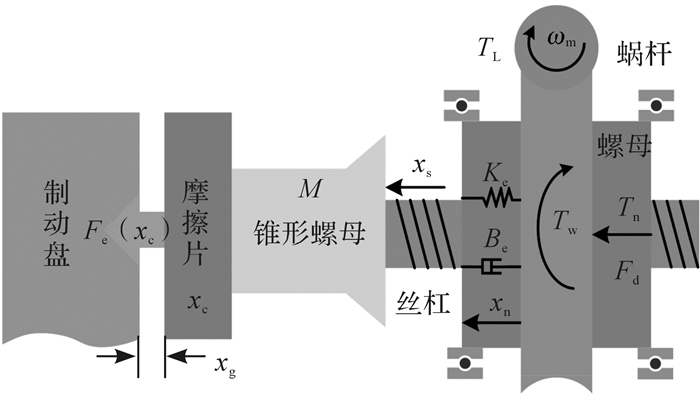
2.4 滚珠丝杠模型滚珠丝杠将旋转运动转换为直线运动,螺母通过滚动轴承安装在制动钳体上,驱动丝杠作直线移动。如图 3所示,滚珠丝杠简化为“质量块-弹簧-阻尼器”系统。
|
| 图 3 EMB系统模型原理图 Fig.3 Schematic diagram of EMB system model |
| $ \Delta x = {x_{\rm{n}}} - {x_{\rm{s}}} $ | (12) |
| $ {F_{\rm{d}}} = M\Delta \ddot x + {K_{\rm{e}}}\Delta x + {B_{\rm{e}}}\Delta \dot x $ | (13) |
式中:Fd为滚珠丝杠驱动力;M为摩擦片、锥形螺母、丝杠的等效质量;xs为丝杠的直线位移;Be为阻尼系数;Ke为等效轴向刚度。其中滚珠丝杠的轴向加速度很小,此处忽略。
滚珠丝杠系统的等效轴向刚度Ke由轴承刚度Kb与丝杠轴向刚度Ks确定,即:
| $ \frac{1}{{{K_{\rm{e}}}}} = \frac{1}{{{K_{\rm{b}}}}} + \frac{1}{{{K_{\rm{s}}}}} $ | (14) |
其中取Kb=6×107 N/m。丝杠轴向刚度Ks为:
| $ {K_{\rm{s}}} = \frac{{EA}}{l} = \frac{{E{\rm{ \mathsf{ π} }}d_{\rm{s}}^2}}{{4l}} $ | (15) |
式中:E为材料弹性模量;ds为丝杠直径,ds=20 mm;l为丝杠长度, l=180 mm。
丝杠的位移xs等于制动间隙xg(xg=0.2 mm)与摩擦片的变形量xc之和, 即:
| $ {x_{\rm{s}}} = {x_{\rm{g}}} + {x_{\rm{c}}} $ | (16) |
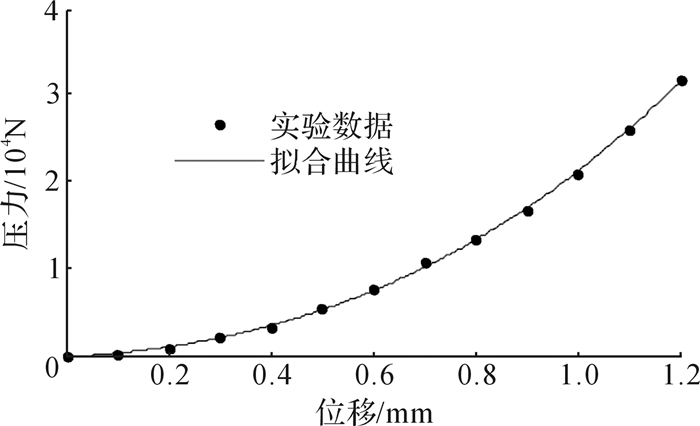
制动器零部件中摩擦片的刚度相对较低,制动器刚度主要由摩擦片的刚度决定,摩擦片变形与丝杠直线位移一致,可选取摩擦片的压力-变形关系作为制动正压力负载模型。利用5吨压力试验机,对摩擦片进行3次压力测试,求均值后在MATLAB中拟合曲线,如图 4所示。
|
| 图 4 摩擦片压力-变形拟合曲线 Fig.4 Friction plate Fc-xc fitted curve |
可得摩擦片压力-变形关系式如下:
| $ {F_{\rm{c}}} = 5715x_{\rm{c}}^3 + 12430x_{\rm{c}}^2 + 3218{x_{\rm{c}}} - 187.5 $ | (17) |
式中:Fc为摩擦片压力、制动正压力; xc为摩擦片的变形量。
摩擦片与制动盘间的正压力由滚珠丝杠推动产生,滚珠丝杠的驱动力矩与制动正压力有如下关系:
| $ {T_{\rm{n}}} = \frac{{{F_{\rm{c}}} \cdot S}}{{2{\rm{ \mathsf{ π} }}}} $ | (18) |
式中Tn为作用在滚珠丝杠上的驱动转矩、蜗轮负载转矩。
电机的负载转矩通过蜗轮蜗杆传给滚珠丝杠,因此电机的负载转矩为:
| $ {T_{\rm{L}}} = {T_{\rm{w}}}/i\eta $ | (19) |
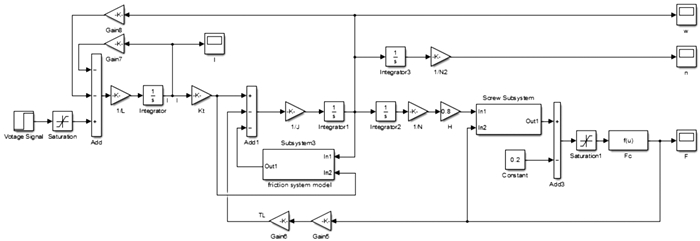
根据上述所建数学模型,在MATLAB/Simulink中建立仿真模型,如图 5所示。
|
| 图 5 EMB系统仿真模型 Fig.5 EMB system simulation model |
搭建实验台进行实测,并与仿真结果对比,分析所设计的EMB制动性能。EMB实验台由硬件和软件组成,主要包括电源、上位机(PC)、下位机(PLC)、电机驱动电路和EMB执行器等,如图 6所示。

|
| 1—直流稳压电源;2—PC;3—电流传感器;4—H桥电路;5—固态继电器;6—A/D模块;7—下位机;8—12V直流电源;9—24V直流电源;10—急停开关;11—放大器;12—编码器;13—EMB;14—直流电机;15—力传感器 图 6 EMB实验台 Fig.6 EMB bench |
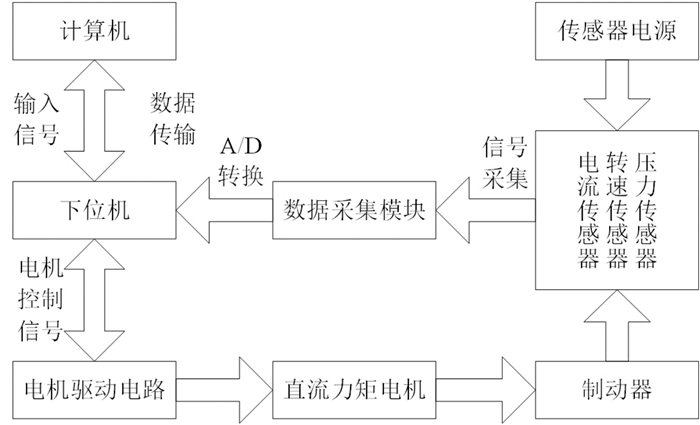
实验目的是测试EMB的性能参数和验证间隙自动调节功能,实验台系统框架如图 7所示。
|
| 图 7 EMB实验台系统框架 Fig.7 EMB bench system framework |
根据模型关系式,堵转状态时的制动正压力理论值为:
| $ {F_{\rm{c}}} = \frac{{2{\rm{ \mathsf{ π} }}i{K_{\rm{t}}}U}}{{S \cdot {R_{\rm{a}}}}} $ | (20) |
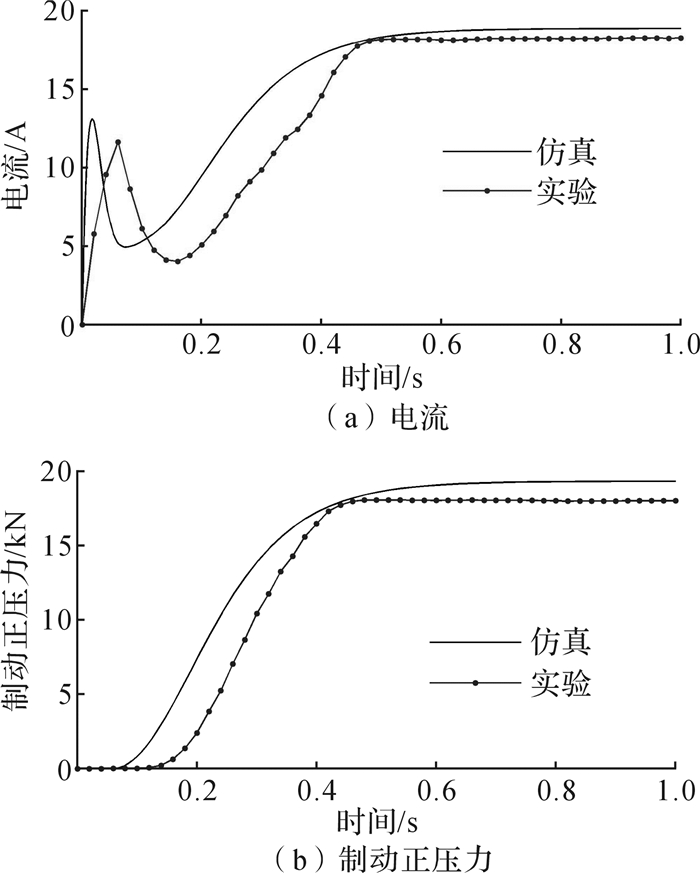
可得10 V电压对应的堵转电流理论值为20 A,制动正压力理论值为20 kN。输入阶跃信号用于模拟紧急制动,图 8为EMB系统在10 V阶跃电压信号下的电流、制动正压力响应曲线。仿真和实验中,在制动间隙消除前,电机都处于空载状态,电流迅速增加,接触到制动盘(负载)后电流迅速降低,呈现“尖峰”电流特性。此后,仿真电流从0.10 s时开始增加,0.45 s时趋于稳态值(18.75 A)。实验电流在0.12 s开始增加,滞后0.02 s,稳态值为18.17 A。制动正压力仿真值在0.08 s开始增加,稳态值为18.69 kN。制动正压力实验值滞后0.04 s开始增加,稳态值为18.08 kN。因此,仿真与实验所得的电流特性和制动正压力响应基本一致,实验中制动正压力的增加比仿真滞后0.04 s,这是由于Simulink仿真模型中均为理想传感器和理想控制器,而实验数据采集有一定延时,所以实验结果滞后0.02~0.04 s,属合理范围之内。
|
| 图 8 EMB系统在10 V阶跃电压信号下的响应曲线 Fig.8 Response curve of EMB system under 10 V step voltage signal |
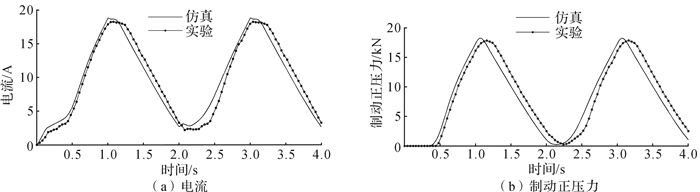
三角波信号用于模拟一次完整的制动过程,图 9为系统在10 V(0.5 Hz)三角波电压信号下的电流、制动正压力响应曲线。仿真的电流最大值为18.42 A,实验的电流最大值为18.22 A;仿真的制动正压力最大值为18.18 kN,实验的制动正压力最大值为18.15 kN。仿真制动正压力的启动时间为0.42 s,实验测得的滞后0.04 s。
|
| 图 9 EMB系统在10 V(0.5 Hz)三角波电压信号下的响应曲线 Fig.9 Response curve of EMB system under 10 V (0.5 Hz) triangular wave voltage signal |
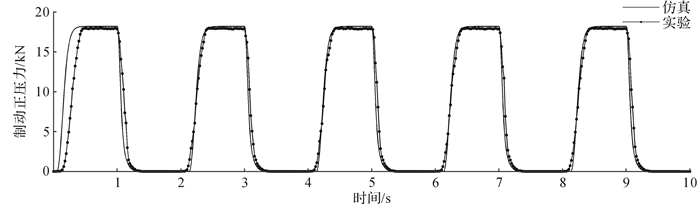
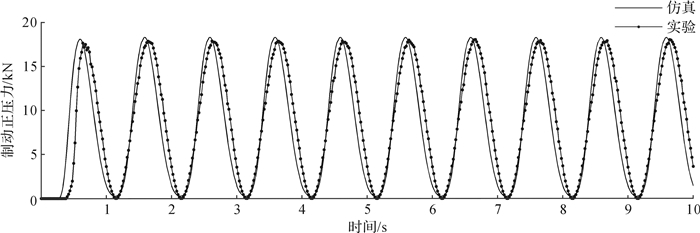
通过控制方波、正弦的高频输入信号,模拟多次连续制动的制动力响应,以进一步检测EMB的制动性能。图 10、图 11分别为EMB系统在方波(0.5 Hz)、正弦信号(1 Hz)下的制动正压力仿真和实验曲线。结果显示,系统在第1次启动时,实验滞后于仿真模型,但是后续的连续制动跟随性较好,系统响应速度快。
|
| 图 10 EMB系统在方波(0.5 Hz)信号下的制动正压力曲线 Fig.10 Brake positive pressure curve of EMB system under square wave signal (0.5 Hz) |
|
| 图 11 EMB系统在正弦信号(1 Hz)下的制动正压力曲线 Fig.11 Brake positive pressure curve of EMB system under sinusoidal signal (0.5 Hz) |
根据实验与仿真结果的对比分析可知,EMB具有首次启动的“尖峰”电流特性,系统的电流、制动正压力响应与仿真模型有较好的一致性,高频连续测试结果显示制动正压力反应灵敏,可以满足制动要求。因此,EMB具有响应速度快、跟随性好的特点。
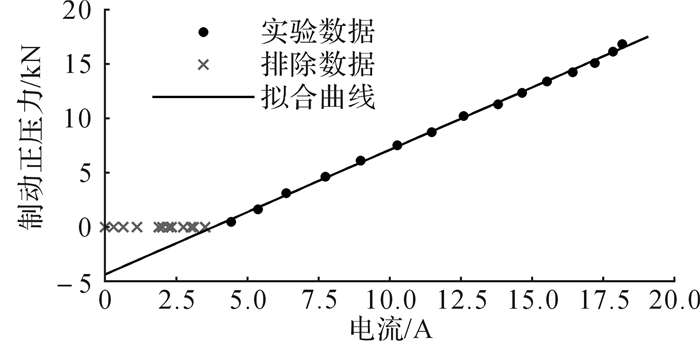
3.3 EMB参数关系分析 3.3.1 制动正压力与堵转电流的关系为了研究和寻找减少传感器数量的理论方法,需进一步分析各制动性能参数间的关系。由式(20)可知,电机在堵转状态下的制动正压力与电流成线性关系,根据实验数据进一步验证该特性。排除在消除间隙之前的数据(电机未堵转),拟合所得曲线如图 12所示。
|
| 图 12 制动正压力-电流关系 Fig.12 Fc-Ia relation |
制动正压力与堵转电流满足线性关系,线性回归方程为:
| $ {F_{\rm{c}}} = 1144{I_{\rm{a}}} - 4345 $ | (21) |
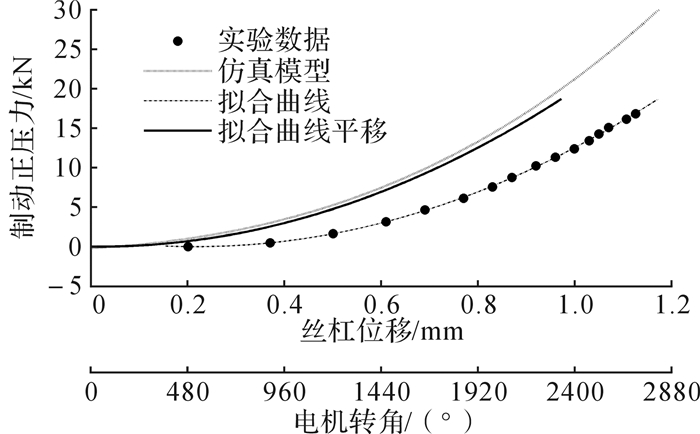
如图 13所示,根据实验数据,对Fc-xs进行拟合。得函数关系如下:
|
| 图 13 制动正压力-丝杠位移关系 Fig.13 Fc-xs relation |
| $ \begin{array}{*{20}{c}} {{F_{\rm{c}}} = 265.6{{\left( {{x_{\rm{s}}} - {x_{\rm{g}}}} \right)}^3} - 19960{{\left( {{x_{\rm{s}}} - {x_{\rm{g}}}} \right)}^2} - }\\ {8644\left( {{x_{\rm{s}}} - {x_{\rm{g}}}} \right) + 929\;\;\;\;\;\;\;\;\left( {{x_{\rm{s}}} \ge {x_{\rm{g}}}} \right)} \end{array} $ | (22) |
实验数据包含间隙未消除的数据,需将拟合曲线向左平移0.2 mm,所得制动正压力-丝杠位移的关系曲线与仿真负载模型(式(17))较好吻合,进一步验证由刚度最低的摩擦片代替系统负载的模型的正确性和有效性。
由于制动器的安装空间十分狭小,力传感器、编码器安装困难,根据所得的制动正压力-堵转电流关系、制动正压力-丝杠位移关系,可以预估输出的制动力,为后续在EMB中减少力传感器、编码器、位移传感器等提供理论基础。
3.4 EMB间隙自动调节功能实验分析GB12676—2014规定制动系统应有磨损补偿装置。制动间隙自动调节功能,即每一次制动完成之后,下次制动时应有效保证制动行程的一致性。通过对比有间隙自动调节功能与无间隙自动调节功能(磨损量为1 mm)的制动系统的性能差异,来检测所设计的制动间隙调节机构的性能。图 14为10 V(0.5 Hz)三角波电压信号下有/无间隙自动调节功能制动系统的电流对比曲线。
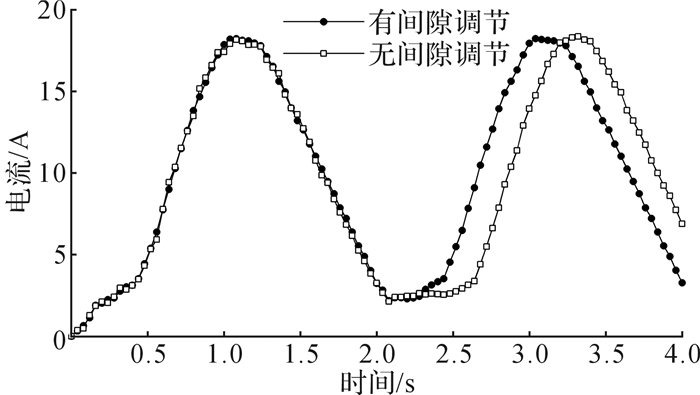
|
| 图 14 10 V(0.5 Hz)三角波电压信号下有/无间隙自动调节功能制动系统的电流对比曲线 Fig.14 Current contrast curve of EMB system with / without gap automatic adjustment function under 10 V (0.5 Hz) triangular wave voltage signal |
由图 14可知:第1次制动时,有/无间隙自动调节功能的电机电流基本一致,电流最大值分别为18.18 A和18.06 A;第2次制动(第2秒)时,无间隙自动调节功能的电机启动时间比具有间隙自动调节功能的启动时间滞后0.2 s。由此可知,如磨损未能及时补偿,系统启动时间、制动力响应将滞后,直接影响制动系统的安全性。
图 15为有/无间隙自动调节功能的制动正压力对比曲线。第1次制动时,有/无间隙自动调节功能的制动正压力启动时间均为0.44 s,制动正压力基本一致,制动正压力最大值分别为17.81 kN和17.88 kN。第2次制动时,无间隙自动调节功能的制动正压力启动时间比具有间隙自动调节功能的滞后0.24 s,制动正压力最大值分别为17.83 kN和17.87 kN。从实验对比可知,本文所设计的EMB间隙自动调节机构可以有效保障制动行程的一致性,以及电流和制动正压力响应速度的一致性,提高制动系统的安全性。
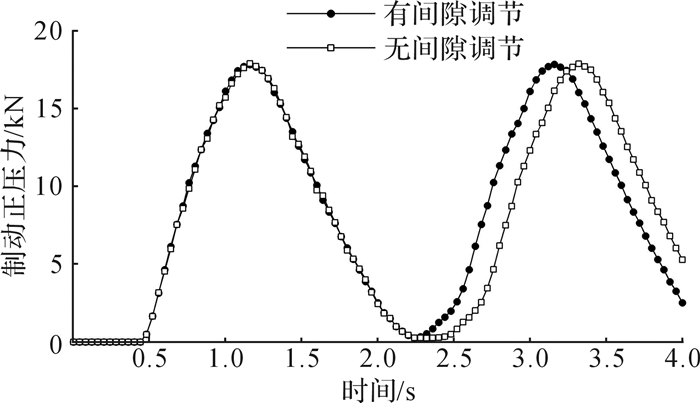
|
| 图 15 10 V(0.5 Hz)三角波电压信号下有/无间隙自动调节功能制动系统的制动正压力对比曲线 Fig.15 Brake positive pressure contrast curve of EMB system with / without gap automatic adjustment function under 10 V (0.5 Hz) triangular wave voltage signal |
1) 实验与仿真对比分析得出,所设计的EMB的启动电流具有“尖峰”特性,在阶跃信号下,可以满足间隙消除时间为0.1 s的要求。由于系统存在阻尼,三角波信号控制启动时响应存在滞后现象。所设计的EMB在方波、正弦高频控制信号下,系统具有反应灵敏、跟随性好的特点。在进一步的研究工作中,可在汽车电子控制单元中添加前置补偿环节,提高系统响应速度。
2) 实验结果与仿真结果吻合较好,验证了选取刚度最低的摩擦片代替系统负载模型的正确性和有效性。实验结果得出了制动正压力与堵转电流满足线性关系,制动正压力与丝杠位移满足三次多项式的非线性关系的结论,可以预估输出的制动力,为后续在EMB系统中减少力传感器等装置提供了理论基础,从而可减小EMB系统尺寸大小。
3) 通过对比分析有间隙自动调节功能与无间隙自动调节功能制动器的电流、制动正压力的响应性能,验证了所设计的EMB可以保障制动行程、响应速度的一致性,符合GB12676—2014的规定,从而提高制动系统的安全性。
| [1] | MICHELS K. Trends in the development of drive components for electric and hybrid vehicles[J]. ATZ Elektronik Worldwide, 2015, 10(4): 4–7. |
| [2] | YU L Y, ZHAO W Z, YI J B. Modeling and analysis of brake by wire system in electric vehicle[J]. Applied Mechanics and Materials, 2013, 249-250: 622–627. |
| [3] |
李顶根, 张绿原, 何保华.
基于滑移率的汽车电子机械制动系统的模糊控制[J]. 机械工程学报, 2012, 48(20): 121–126.
LI Ding-gen, ZHANG Lü-yuan, HE Bao-hua. Fuzzy control based on vehicle slip-ratio for electro-mechanical braking systems[J]. Journal of Mechanical Engineering, 2012, 48(20): 121–126. |
| [4] | LEE J. A study on braking system using fully electric brake system[C]//2014 IEEE International Conference on Industrial Technology (ICIT). Busan, Feb. 26-Mar. 1, 2014. |
| [5] | JEON K, PARK J I, CHOI S J, et al. Electronic brake safety index for evaluating fail-safe control of brake-by-wire systems for improvement in the straight braking stability[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2014, 228(8): 873–893. DOI:10.1177/0954407014522032 |
| [6] | LEE Y O, JANG M, LEE W, et al. Novel clamping force control for electric parking brake systems[J]. Mechatronics, 2011, 21(7): 1156–1162. DOI:10.1016/j.mechatronics.2011.07.006 |
| [7] | AHN J K, JUNG K H, KIM D H, et al. Analysis of a regenerative braking system for hybrid electric vehicles using an electro-mechanical brake[J]. International Journal of Automotive Technology, 2009, 10(2): 229–234. DOI:10.1007/s12239-009-0027-z |
| [8] | JEON K, HWANG H, CHOI S, et al. Development of a fail-safe control strategy based on evaluation scenarios for an FCEV electronic brake system[J]. International Journal of Automotive Technology, 2012, 13(7): 1067–1075. DOI:10.1007/s12239-012-0109-1 |
| [9] | SARIC S, BAB-HADIASHAR A, HOSEINNEZHAD R. Clamp-force estimation for a brake-by-wire system:a sensor-fusion approach[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 778–786. DOI:10.1109/TVT.2007.905251 |
| [10] |
张露, 王国业, 张延立, 等.
电动汽车再生摩擦集成制动系统ABS控制性能研究[J]. 农业机械学报, 2015, 46(10): 350–356.
ZHANG Lu, WANG Guo-ye, ZHANG Yan-li, et al. ABS control performance of integrated brake system with regenerative friction brake in electric vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(10): 350–356. DOI:10.6041/j.issn.1000-1298.2015.10.047 |
| [11] | HAGGAG S A, ABIDOU D. An approach to vehicle brake-by-wire optimal control tracking strategy[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2013, 6(1): 154–162. DOI:10.4271/2013-01-0686 |
| [12] | GMBH R B. Electromechanical braking device for a braking system and braking system for a vehicle:US20160107628A1[P]. 2016-04-21. |
| [13] | GOMBERT B, GUTTENBERG P. The electronic wedge brake[J]. ATZ Worldwide, 2006, 108(11): 2–5. DOI:10.1007/BF03224890 |
| [14] | JO C, HWANG S, KIM H. Clamping-force control for electromechanical brake[J]. IEEE Transactions on Vehicular Technology, 2010, 59(7): 3205–3212. DOI:10.1109/TVT.2010.2043696 |
| [15] |
刘地, 刘兆英, 金约夫, 等. 商用汽车和挂车制动系统技术要求及试验方法: GB12676-2014[S]. 北京: 中国标准出版社, 2014: 11-18.
LIU Di, LIU Zhao-ying, JIN Yue-fu, et al. Technical requirements and testing methods for commercial vehicle and trailer braking system:GB12676-2014[S]. Beijing:Standards Press of China, 2014:11-18. |
| [16] | GONG X X, CHANG S Q, JIANG L C, et al. A new brake-by-wire system based on direct-drive electro-hydraulic brake unit[J]. Applied Mechanics and Materials, 2014, 627: 231–235. DOI:10.4028/www.scientific.net/AMM.627 |
| [17] | FARRIS R J, GOLDFARB M. Design of a multidisc electromechanical brake[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(6): 985–993. DOI:10.1109/TMECH.2010.2064332 |
| [18] |
王维锐, 石浩然, 葛正, 等. 汽车线控制动器: 2012103407932[P]. 2014-07-09.
WANG Wei-rui, SHI Hao-ran, GE Zheng, et al.Automotive brake by wire actuator:2012103407932[P]. 2014-07-09. |
| [19] |
唐任远.
现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2000: 93-98.
TANG Ren-yuan. Modern permanent magnet motor-theory and design[M]. Beijing: China Machine Press, 2000: 93-98. |
| [20] | MÁRTON L, LANTOS B. Control of mechanical systems with Stribeck friction and backlash[J]. Systems & Control Letters, 2009, 58(2): 141–147. |


