非球面透镜对半导体激光器发出的激光具有准直和汇聚的功能,其对准精度是决定半导体激光封装器件性能的关键因素[1]。目前非球面透镜与半导体激光器的对准方式为人工操作,自动化程度低,且非球面透镜的长度不足5 mm, 与半导体激光器的相对位置只能通过人眼反复调节,器件的性能完全取决于操作工人的经验以及熟练程度。
近年来,机器视觉技术的应用迅速地从最初的电子半导体领域扩展到其他领域,越来越多的工业生产企业和设备制造商开始采用[2]。国外研发的基于机器视觉技术的激光机器视觉检测系统已经成功在机械加工、汽车制造、电子生产等领域发挥重要作用[3]。机器视觉技术在检测精度方面具有极大优势,配置高性能的相机和镜头进行图像采集,利用一系列图像处理算法,在检测精度上可达到亚微米级别[4]。相对于人工视觉,机器视觉具有连续工作不疲劳、对恶劣工作环境适应性强、速度快、效率高、容易实现整线的自动化、可方便地集成到现有生产设备中等优点[5]。将机器视觉系统应用到激光器的封装过程中,可以大大提高检测精度和自动化程度。
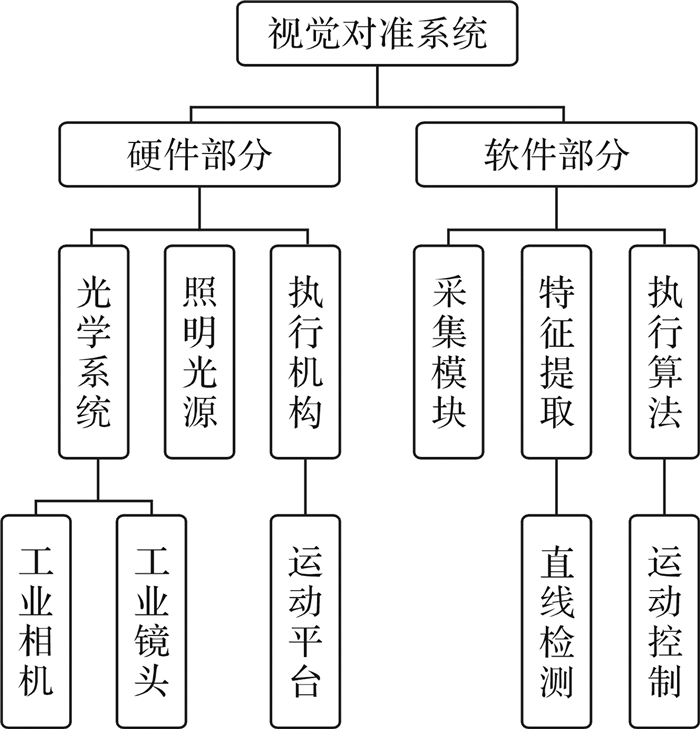
1 视觉对准系统基于机器视觉的对准系统分为硬件和软件两部分,如图 1所示。硬件部分包括光学系统、照明光源、运动执行平台;软件分为3个模块:图像采集模块、图像特征识别模块以及运动控制模块。而工业相机、工业镜头、光源三部分的选型是视觉对准系统成功搭建、实现高精度对准功能的关键。接下来重点介绍这3个核心器件的选型。
|
| 图 1 视觉对准系统组成 Fig.1 Composition of visual alignment system |
工业相机是视觉对准系统获取图像的必备器件,其作用是利用通过光学系统聚焦于成像平面的光线生成图像。相机的质量直接影响了采集图像的质量,具有高质量的相机是视觉对准系统准确提取图像特征的前提[7]。核心器件非球面透镜长度接近5 mm,预设定视野为5 mm×4 mm,精度要求为0.005 mm。此时相机分辨率要求至少为5/0.005×4/0.005=1 000×800 dpi(dots per inch)。因此,一般选用80万像素以上的相机即可。因非球面透镜与半导体激光器的对准精度要求比较高,为降低图形的畸变度,选取了200万像素(理论要求的2倍多)的德国Basler相机,型号为acA2500-14gm,分辨率为2 592×1 944 dpi。
1.2 镜头选型镜头是成像单元获取清晰图像的重要光学器件,其作用是将成像目标聚集在图像传感器的光敏感面上。
镜头的主要参数如图 2所示,其几何关系如公式(1)所示。参数之间计算关系有:

|
| 图 2 工业镜头的主要参数 Fig.2 Main parameters of industrial lens |
| $ {\rm{PMAG}} = \frac{{{\rm{SensorSize}}}}{{{\rm{FOV}}}} = \frac{{{H_{\rm{i}}}}}{{{H_{\rm{o}}}}} = \frac{{{D_2}}}{{{D_1}}} $ | (1) |
式中:Hi为相机有效成像面的高度(即相机芯片的大小);Ho为视野的高度;D1为物距;D2为像距;PMAG为镜头的放大倍率。
本系统选用日本奥提龙公司的镜头,型号为VS-TCH1-110;工作距离D=110 mm; 放大倍率为1。
已知相机芯片尺寸为5.76 mm×4.29 mm,根据公式(1)可以得到:
1) 对准工位实际视场为5.76 mm×4.29mm;
2) 图像精度为5.76/2 592 mm×4.29/1 944 mm=0.002 mm×0.002 mm。
由上可知,该系统采集的图像精度达到了0.002 mm(亚微米级别),可实现非球面透镜与半导体激光器的高精度定位与对准。
1.3 光源选型光源也是影响视觉对准系统采集图像质量的重要因素。通过适当的光源照明设计,使图像中的目标信息与背景信息得到最佳分离,可以大大降低图像处理算法分割、识别的难度,同时提高系统的定位、测量精度,使系统的可靠性和综合性能得到提高。根据半导体激光器的封装特点和具体工况,选择了日本CCS的平面光源和环形蓝色光源。
2 视觉对准系统算法为了实现非球面透镜与半导体激光器的高精度对准,必须分别对它们的边缘进行直线拟合,然后对2条直线进行平行对准。
传统边缘直线检测方法有Hough变换(hough transform, HT)算法和最小二乘直线拟合(least square, LS)算法[8]。Hough变换算法是图像处理中经典的特征提取技术,采用投票方法检测具有特定形状的物体,通过利用点线之间的对偶原理,在2个坐标空间之间,将一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。其基本原理如图 3所示,将参数空间量化为许多细小空间,并且将图像空间的每个像素点映射到参数空间,最后在参数空间进行累加和统计。其映射关系可由式(2)表示:

|
| 图 3 Hough变换原理 Fig.3 The principle of Hough transform |
| $ \rho = x\cos \theta + y\sin \theta \;\;\;\left( {0 \le \theta < {\rm{ \mathsf{ π} }}} \right) $ | (2) |
式中:ρ为原点到直线的距离;θ为直线法线与x轴正方向的夹角[9]。
由于采用穷尽式搜索方式,它运算速度慢、占用内存大,无法满足实时性要求。针对这些缺陷,已有相关学者提出了很多改进算法:Kiryati等提出了概率Hough变换(probabilistic Hough transform, PHT)算法,其可将图像数据映射到参数空间中具有更大概率的单元[10];Matas等提出了累计概率Hough变换(progressive probability Hough transform, PPHT)算法,其通过比较包含像素点的各个小区域的不同有效减少了检测直线所需的计算量[11],还对比了HT,PHT,PPHT三种算法,发现PPHT算法降低了算法的运算开销,其不但有Hough变换与概率Hough变换算法的优点,而且运行速度也最快。
迭代重复加权最小二乘法(iterative repeated weighted least square,IRLS)考虑了随机误差对线性检测精度的影响,该方法检测精度较高,可以很好弥补累计概率Hough算法精度不足的缺陷[12]。
设图像空间特征区域有n个像素点,记作U={(xi, yi), i=1, 2, …, n},通过这些像素点可以进行直线拟合;表达式y=ax+b是常用的直线表示形式,但是通过像素点拟合的直线可以是任何方向的,因此这种表示方法并不能满足要求[13]。本文采用黑塞范式直线进行拟合,假设U的线性估计方程为:
| $ \alpha r + \beta c + \gamma = 0 $ | (3) |
令α2+β2=1,以防止直线的过参数化。同时,点(ri, ci)到拟合直线的距离δi=|αri+βci+γ|。为了抑制离群值对拟合直线的影响,引入权重wi,对于较远距离的点应给予较小的权重[14]。因此,线性拟合准则为:
| $ {\varepsilon ^2} = \mathop {\min }\limits_{\left( {{x_i},{y_i}} \right) \in w} \left\{ {\sum\limits_{i = 1}^n {{w_i}{{\left( {\alpha {r_i} + \beta {c_i} + \gamma } \right)}^2}} } \right\} $ | (4) |
引入方程:
| $ {\mu _r} = \frac{1}{n}\sum\limits_{i = 1}^n {{r_i}} $ | (5) |
| $ {\mu _c} = \frac{1}{n}\sum\limits_{i = 1}^n {{c_i}} $ | (6) |
可得:
| $ \gamma = - \left( {\alpha {\mu _r} + \beta {\mu _c}} \right) $ | (7) |
将式(5)至式(7)代入式(4),有:
| $ {\varepsilon ^2} = \mathop {\min }\limits_{\left( {{x_i},{y_i}} \right) \in w} \left\{ {\sum\limits_{i = 1}^n {{w_i}{{\left[ {\alpha \left( {{r_i} - {\mu _r}} \right) + \beta \left( {{c_i} - {\mu _c}} \right)} \right]}^2}} } \right\} $ | (8) |
加入约束条件G(α, β)=α2+β2-1=0,引入Lagrange乘子λ,建立Lagrange函数:
| $ \begin{array}{l} L\left( {\alpha ,\beta } \right) = \sum\limits_{i = 1}^n {{w_i}{{\left[ {\alpha \left( {{r_i} - {\mu _r}} \right) + \beta \left( {{c_i} - {\mu _c}} \right)} \right]}^2}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {{\alpha ^2} + {\beta ^2} - 1} \right)n \end{array} $ | (9) |
图 4为视觉对准系统进行图像采集、图像识别、运动控制与高精度对准的核心部分。运动平台控制气嘴移动到料盘处吸取非球面透镜,然后移动非球面透镜至半导体激光器上方,视觉对准系统采集并处理图像,将运动参数传递给运动平台,实现非球面透镜与半导体激光器边缘高度平齐与贴合。

|
| 图 4 视觉对准核心工位 Fig.4 Core position of visual alignment |
将非球面透镜运动到半导体激光器上方,相机对非球面透镜与半导体器件上下相对位置进行实时采集,得到图 5所示垂直对准左视图。为了拟合非球面透镜与半导体激光器的边缘直线,首先对图像进行模糊去噪、膨胀腐蚀等操作,然后进行二值化分割得到二值图像[15]。图像的二值化处理是指将256个灰度等级的采集图像通过适当的阈值将图像上点的灰度值置为0或255,灰度值大于T的像素点置为255,反之,灰度值置为0。其原理可用公式(10)表示:

|
| 图 5 垂直对准左视图 Fig.5 Left view of vertical alignment |
| $ {f_{\rm{t}}}\left( {x,y} \right) = \left\{ \begin{array}{l} 255,\left( {x,y} \right) \ge T\\ 0,其他 \end{array} \right. $ | (10) |
ft(x, y)为图像像素点灰度值,T为图像分割阈值。对垂直对准左视图进行二值化之后得到图 6所示的二值化左视图。

|
| 图 6 二值化左视图(全局阈值T1) Fig.6 Left view of binaryzation (global threshold T1) |
图 7为视觉对准系统对非球面透镜运动到半导体激光器边缘进行直线拟合与垂直方向平行对准的具体过程。利用PPHT算法对非球面透镜的二值化图像进行直线检测(角度分辨率设定为0.1 rad),得到相应的线段集合Seq1(用PPHT算法采集出一条直线上分布分成的多条线段端点,再通过这些端点拟合出直线,具体原理请参照第2节);利用Canny算子对二值化图像进行边缘检测,然后与Seq1点集进行“与”运算得到特征点集Seq2;最后,使用基于Fair权重函数的IRLS算法对Seq2点集进行直线拟合[16],可得图 7(b)所示非球面透镜下边缘拟合直线。重复以上步骤,得出非球面透镜上边缘拟合直线,通过这2条边缘直线参数,拟合出图 7(d)所示的非球面透镜的中心拟合直线。重复以上步骤,利用PPHT算法和IRLS算法对半导体上边缘进行直线特征点提取与拟合,得到图 7(f)所示的半导体激光器上边缘拟合直线。

|
| 图 7 左视图直线拟合过程 Fig.7 Line-fitting process of left view |
如图 8所示,系统自动调整非球面透镜边的中心拟合直线和半导体激光器上边缘拟合直线的夹角,保证它们高精度平行;自动计算2条直线的距离d,气嘴向下移动距离为d, 使非球面透镜边与半导体激光器处于同一水平面高度。

|
| 图 8 左视图平行对准 Fig.8 The alignment of left view |
由于非球面透镜本身材质为玻璃,其不同角度对光的反射率和吸收率各不相同,导致视觉对准系统采集的水平对准俯视图成像不太清晰,尤其核心器件非球面透镜的边缘特征很模糊,对其边缘进行直线拟合有很大困难。PPHT算法对图像采用全局搜索方式,对图像所有边缘进行直线检测,面对非常模糊的边缘,采用PPHT算法并不能取得良好的效果。针对水平对准俯视图非球面透镜的边缘直线检测,本文提出了一种简单而快速的方法—求导寻点法。
从数学原理角度来说,图像边缘出现颜色、纹理不一样的区域时,比较合理的一种方式是将边缘定义为灰度剧烈变化的位置[17],从而对图像各个方向求导,寻找导数变化剧烈的点集作为边缘直线的候选点,然后再进行直线拟合。如果对图像每个像素点各方向求导,计算量将非常庞大,因而只选取非球面透镜附近的区域进行处理,对图像进行低对比度小目标分割可极大减少运算量[18]。
图 9为视觉对准系统采集的非球面透镜边与半导体激光器水平对准俯视图,图 10(a)、(b)是从被检测目标中选取的3个边缘直线特征明显的区域ROI1,ROI2和ROI3,然后在3个ROI内使用求导寻点法。

|
| 图 9 水平对准俯视图 Fig.9 Planform of horizontal alignment |

|
| 图 10 俯视图直线拟合过程 Fig.10 Line-fitting process of planform |
对图像进行模糊去噪、膨胀腐蚀等操作,然后对3个区域进行多阈值分割。用阈值T2对区域ROI1,ROI2进行分割,得到二值化图像(图 10(c)),分别对ROI1与ROI2区域内每个像素点的灰度值进行检测,寻找ROI1,ROI2区域中灰度值变化梯度大的点集(灰度值从0到255剧变的点),得到候选特征点集Seq3, Seq4,再通过迭代重加权最小二乘法将Seq3, Seq4的点集拟合出图 10(e)所示的半导体激光器的边缘直线。对区域ROI3采用与上相同的步骤,搜寻直线特征点集Seq5,通过Seq5拟合出图 10(f)所示的非球面透镜的边缘直线。
针对低对比度水平对准俯视图,分别用PPHT算法和本算法对非球面透镜边缘进行特征点提取与直线拟合,结果如表 1所示。用PPHT算法的边缘的特征点提取数目为0,该算法完全失效。通过求导寻点法在小区域ROI1,ROI2,ROI3找出大量的特征点并拟合出非球面透镜边缘直线。
| 算法 | 特征点提 取区域 |
特征点提 取数目 |
直线拟 合效果 |
| PPHT算法 | 全局 | 0 | - |
| 本算法 | ROI1和ROI2 | 260 | 好 |
| ROI3 | 1 000 | 好 |
自动调整两直线的夹角,保证半导体激光器与非球面透镜高精度平行,然后计算两直线距离d2, 根据半导体激光器已知参数d1,气嘴移动距离为d2—d1,如图 11所示。最后,通过点胶平台在透镜两端点上胶水,非球面透镜便成功封装到半导体激光器出光的右面边缘了。

|
| 图 11 俯视图平行对准 Fig.11 Parallel alignment of planform |
系统对5组透镜进行了对准测试,结果如表 2所示,可得平均对准时间为0.38~0.39 s,而目前一个熟练的操作工人手工对准一个器件至少需要10 s左右, 相对人工视觉,本系统的效率有大幅度提高。
| 组号 | 对准时间t/s |
| 1 | 0.384 |
| 2 | 0.385 |
| 3 | 0.391 |
| 4 | 0.391 |
| 5 | 0.382 |
相对于人工对准,本系统具有以下优点:
1) 高精度。由上文可知,系统所采集的图像的像素精度为亚微米级别,因此直线拟合精度也为亚微米级别,满足了对非球面透镜与半导体器件封装过程中的定位与自动对准的精度要求。
2) 速度快。系统自动进行直线拟合、角度计算和调整对准,一次性实现非球面透镜与半导体激光器定位和对准,且完成以上所有过程用时不到0.5 s,对目前自动化程度不高的半导体激光器件的封装过程来说大大提高了生产效率以及产品的成品率。
5 结论本文结合机器视觉与机械自动化的优点,开发了一套自动化对准系统来替代半导体激光器件封装的人工流水线作业,提高了激光器封装自动化程度,相关结论如下:
1) 正确选型。相机、镜头、光源是机器视觉的三大基本组成部分。相机决定了图像的分辨率和精度,镜头决定了放大倍率与工作距离,光源决定了采集图像的质量与明暗对比度。机器视觉系统作为机械自动化设备的“眼睛”,正确选择相机、镜头和光源的类型对提高整个对准系统的精度与效率具有重要意义。
2) 算法探究。作者在PPHT算法对灰度随机分布低对比度俯视图失效的情况下,根据图像处理的基本数学原理,提出了一种简单的方法—求导寻点法,成功提取了半导体激光器与非球面透镜的边缘直线特征点并实现直线的拟合。
3) 未来趋势。在很多因人工对准操作效率低、精度不高而难以满足要求的场合,用机器视觉替代人工视觉,可以大大提高生产效率和生产的自动化程度。机器视觉与机械自动化的结合是未来的必然趋势,工业4.0离不开智能制造,智能制造离不开机器视觉,将基于高精度检测技术的机器视觉系统引入机械自动化设备开发中,对提高工业自动化生产效率和精度将产生巨大的推动作用。
| [1] |
范增明, 李卓, 钱丽勋, 等.
非球面透镜组激光光束整形系统[J]. 红外与激光工程, 2012, 41(2): 353–357.
FAN Zeng-ming, LI Zhuo, QIAN Li-xun, et al. Aspherical lens laser beam shaping system[J]. Infrared and Laser Engineering, 2012, 41(2): 353–357. |
| [2] |
何永辉, 王康健, 石桂芬, 等.
基于机器视觉的高速带钢孔洞检测系统[J]. 应用光学, 2007, 28(3): 345–349.
HE Yong-hui, WANG Kang-jian, SHI Gui-fen, et al. High-speed hole inspection system for steel strips based on machine vision[J]. Journal of Applied Optics, 2007, 28(3): 345–349. |
| [3] |
何勇, 孙钊, 李华厦, 等.
机器视觉技术及其在机械制造自动化中的应用[J]. 黑龙江科技信息, 2016(24): 119.
HE Yong, SUN Zhao, LI Hua-sha, et al. Machine vision technology and its application in mechanical manufacturing automation[J]. Heilongjiang Science and Technology Information, 2016(24): 119. DOI:10.3969/j.issn.1673-1328.2016.24.114 |
| [4] |
赵伟杰, 高勇.
机器视觉在光纤端面缺陷检测中的应用[J]. 现代电子技术, 2011, 34(19): 136–139.
ZHAO Wei-jie, GAO Yong. Application of machine vision in defects inspection of optical fiber end surface[J]. Modern Electronic Technology, 2011, 34(19): 136–139. DOI:10.3969/j.issn.1004-373X.2011.19.044 |
| [5] |
桂卫华, 阳春华, 徐德刚, 等.
基于机器视觉的矿物浮选过程监控技术研究进展[J]. 自动化学报, 2013, 39(11): 1879–1888.
GUI Wei-hua, YANG Chun-hua, XU De-gang, et al. Machine-vision-based online measuring and controlling technologies for mineral flotation:a review[J]. Acta Automatica Sinica, 2013, 39(11): 1879–1888. |
| [6] |
王运哲, 白雁兵, 张博, 等.
机器视觉系统的设计方法[J]. 现代显示, 2011, 22(11): 24–27.
WANG Yun-zhe, BAI Yan-bing, ZHANG Bo, et al. Machine vision system design method[J]. Advanced Display, 2011, 22(11): 24–27. DOI:10.3969/j.issn.1006-6268.2011.11.007 |
| [7] |
杨丹, 刘亚威, 张小洪, 等.
高精度图像测量与对准系统的算法研究[J]. 计算机科学, 2003, 30(12): 132–135.
YANG Dan, LIU Ya-wei, ZHANG Xiao-hong, et al. Research on the algorithms of high accuracy image measurement and registration system[J]. Computer Science, 2003, 30(12): 132–135. DOI:10.3969/j.issn.1002-137X.2003.12.038 |
| [8] |
董晶, 杨夏, 于起峰.
基于边缘连接的快速直线段检测算法[J]. 光学学报, 2013, 33(3): 213–220.
DONG Jing, YANG Xia, YU Qi-feng. fast line segment detection based on edge connecting[J]. Acta Optica Sinica, 2013, 33(3): 213–220. |
| [9] |
BRADSKI Gary, KAEBLER Adrian. 学习OpenCV(中文版)[M]. 于仕琪, 刘瑞祯译. 北京: 清华大学出版社, 2009: 175-177.
BRADSKI Gary, KAEBLER Adrian. Learning OpenCV[M]. Translated by YU Shi-qi, LIU Rui-zhen. Beijing:Press of Tsinghua University, 2009:175-177. |
| [10] | KIRYATI N, ELDAR Y, BRUCKSTEIN A M, et al. A probabilistic Hough transform[J]. Pattern Recognition, 1991, 2(4): 303–316. |
| [11] | MATAS J, GALAMBOS C, KITTLER J, et al. Robust detection of line using the progressive probabilistic Hough transform[J]. Computer Vision and Image Understanding, 2000, 78(1): 119–137. DOI:10.1006/cviu.1999.0831 |
| [12] |
肖宿, 韩国强.
基于变量分离和加权最小二乘法的图像复原[J]. 计算机应用研究, 2012, 29(4): 1584–1587.
XIAO Su, HAN Guo-qiang. Image restoration based on variable splitting and weighted least squares[J]. Application Research of Computers, 2012, 29(4): 1584–1587. |
| [13] |
仲崇豪, 姚宜斌, 刘强, 等.
加权整体最小二乘的迭代解法[J]. 大地测量与地球动力学, 2014, 34(4): 153–156.
ZHONG Chong-hao, YAO Yi-bin, LIU Qiang, et al. Iterative method of weighted whole least squares[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 153–156. |
| [14] |
SZELISKI Richard. 计算机视觉: 算法与应用(中文版)[M]. 艾海舟, 兴军亮译. 北京: 清华大学出版社, 2012: 233-235.
SZELISKI Richard. Computer vision:algorithms and applications[M]. Translated by AI Hai-zhou, XING Jun-liang. Beijing:Press of Tsinghua University, 2012:233-235. |
| [15] |
王惠华, 游福成, 段怀锋, 等.
基于二值图像连通域提取的图像滤波方法[J]. 北京印刷学院学报, 2015, 23(6): 39–41.
WANG Hui-hua, YOU Fu-cheng, DUAN Huai-feng, et al. An image filtering method to extract connected domain in binary image[J]. Journal of Beijing Institute of Graphic Communication, 2015, 23(6): 39–41. |
| [16] |
熊波, 尹周平.
滑动平均和改进权重函数的快速非局部平均图像去噪算法[J]. 中国图象图形报, 2012, 17(5): 628–634.
XIONG Bo, YIN Zhou-ping. Fast non-localmeans for image de-noising on moving average and modified weight function[J]. Journal of Image & Graphics, 2012, 17(5): 628–634. |
| [17] |
徐阳, 曹杰.
一种基于对比度阈值的改进SIFT算法[J]. 电子设计工程, 2012, 20(19): 174–177.
XU Yang, CAO Jie. Improved SIFT algorithm based on the contrast threshold[J]. Electronic Design Engineering, 2012, 20(19): 174–177. DOI:10.3969/j.issn.1674-6236.2012.19.057 |
| [18] |
曾毅, 郭龙源, 赵娇燕.
基于邻域空间特征的低对比度小目标分割算法[J]. 激光与红外, 2017, 47(4): 507–512.
ZENG Yi, GUO Long-yuan, ZHAO Jiao-yan. Low contrast small target segmentation algorithm based on neighborhood space feature[J]. Laser & Infrared, 2017, 47(4): 507–512. |


