高速曲柄压力机作为一种高效率、高精度的锻压设备,广泛应用于工业生产中[1-2]。曲柄滑块机构是高速曲柄压力机主要的传动结构,用于传递运动和动力[3], 其中曲轴的受力最为复杂,其承受着巨大的周期性冲击载荷和惯性力载荷,且支承颈和曲柄颈的轴肩处截面尺寸变化剧烈,导致截面处出现应力集中,而应力集中往往是零件损坏的根源[4-5]。针对高速曲柄压力机的曲轴,衣锐对其进行了受力分析,根据相应载荷谱,用Workbench软件进行了静力学分析和疲劳分析[6]。牛瑞霞等建立了曲轴的数学模型,进行了理论计算,并对其进行静态和模态分析,得到了曲轴的固有频率[7]。张德峰等分析了曲轴在公称力冲击下的应力分布[8]。王磊等建立了压力机转子-轴承系统的振动模型并采用Newmark方法进行求解,通过模拟仿真分析了转子-轴承系统的振动响应[9]。
在目前对高速曲柄压力机曲轴的研究中,往往忽略了曲柄滑块机构高速运动时不平衡惯性力对曲轴的影响。经研究发现,随着曲柄转速的提高,惯性力所引起的附加转矩在一定速度下可超过由公称力产生的转矩[10]。因此,在对曲轴进行分析时,忽略不平衡惯性力对曲轴的影响,会导致分析结果不符合实际。
本文基于联立约束法和达朗贝尔原理建立了曲柄滑块机构的动力学模型。首先采用达朗贝尔原理建立机构的动力学方程,然后,根据机构的位移闭环矢量方程,建立各构件的运动学方程及加速度方程,最后通过联立约束法联立所建立的运动学方程与动力学方程。该方法可以准确地反映出速度、加速度和惯性载荷之间的关系[11]。将动力学方程组装成稀疏矩阵,并将其作为Function模块嵌入Simulink仿真模型中,通过模型对矩阵进行迭代求解。通过任意改变曲轴的转速和冲压力的大小,快速、准确地求出曲轴各个轴颈处载荷随时间的变化规律。根据仿真求得的载荷大小,用Workbench软件对压力机曲轴施加载荷,进行疲劳分析。由于考虑了惯性力对曲轴的影响,得到的分析结果更加接近实际,其为高速曲柄压力机曲柄和曲轴支撑结构的设计提供可靠的理论依据。
1 曲柄滑块机构动力学模型的建立高速曲柄压力机高速运转时,曲柄滑块机构自身会产生周期性变化的不平衡惯性力,不平衡惯性力超过一定范围时会导致滑块下死点的动态性能急剧恶化,引起机床的强烈振动和摆动。因此为了保证冲压性能和机身的稳定性,部分高速压力机采用反向配置平衡副滑块的方法以抵消冲压时所产生的不平衡惯性力,该方法是一种较理想的不完全动平衡方法[12-14]。
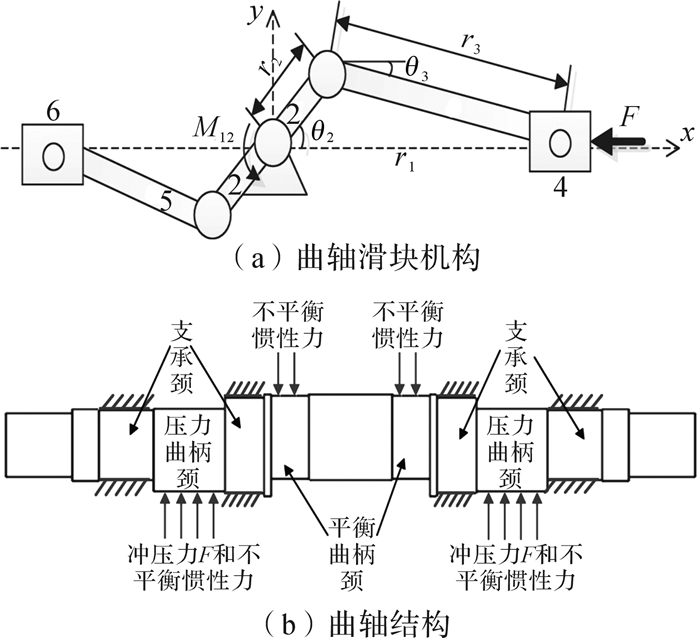
高速压力机中的曲柄滑块机构如图 1(a)所示放置,x方向为实际竖直方向, y方向为实际水平方向。其中连杆3和滑块4为压力机冲压部分,连杆5和副滑块6为平衡部分。曲轴的结构和其承受的载荷分布如图 1(b)所示:平衡曲柄颈驱动平衡副滑块,受到连杆5和滑块6产生的不平衡惯性力;压力曲柄颈驱动冲压滑块,承受冲压力和连杆3与滑块4产生的不平衡惯性力。
|
| 图 1 曲柄滑块机构及曲轴结构简图 Fig.1 Sketch of slider crank mechanism and crankshaft |
平衡部分和冲压部分均为曲柄滑块机构,由同一曲轴驱动。平衡曲柄颈和压力曲柄颈之间存在支承颈,忽略运动副之间的间隙,根据刚化原理,分析曲柄颈时,将支承颈视为刚体,其平衡状态不变。因此只需对一侧曲柄滑块机构进行受力分析,然后在相同的仿真条件下,通过改变曲柄连杆的参数分别求得两侧曲柄滑块机构动力学仿真结果。
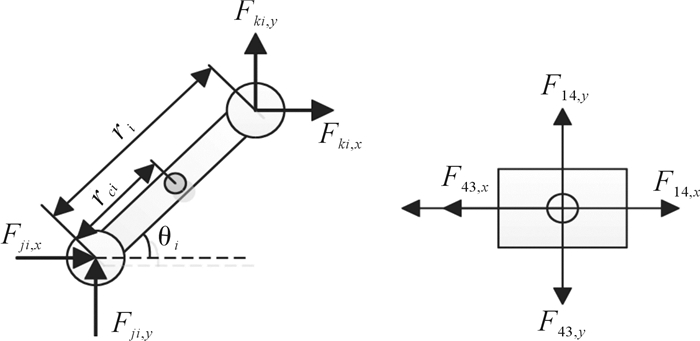
图 2为各连杆和滑块的受力简图。
|
| 图 2 连杆和滑块的受力分析 Fig.2 Force analysis of linkage and slider |
根据图 2所示的受力图,基于达朗贝尔原理建立机构动力学方程:
| $ {F_{ji,x}} + {F_{ki,x}} = {m_i}{a_{{\rm{c}}i,x}} $ | (1) |
| $ {F_{ji,y}} + {F_{ki,y}} = {m_i}{a_{{\rm{c}}i,y}} $ | (2) |
| $ \begin{array}{*{20}{c}} { - {F_{ki,x}}\left( {{r_i} - {r_{{\rm{c}}i}}} \right)\sin {\theta _i} + {F_{ki,y}}\left( {{r_i} - {r_{{\rm{c}}i}}} \right)\cos {\theta _i} + }\\ {{F_{ij,x}}{r_{{\rm{c}}i}}\sin {\theta _i} - {F_{ij,y}}{r_{{\rm{c}}i}}\cos {\theta _i} = {I_i}{\alpha _i}} \end{array} $ | (3) |
| $ {F_{34,x}} + F = {m_4}{{\ddot r}_1} $ | (4) |
| $ {F_{43,y}} + {F_{14,y}} = 0 $ | (5) |
式中:Fji, x,Fki, x为x方向上连杆j和k对连杆i的作用力;Fji, y,Fki, y为y方向上连杆j和k对连杆i的作用力;aci, x,aci, y为连杆i在x和y方向上的加速度;ri为连杆i的长度; rci为第i个连杆质心到连杆旋转中心的距离;
为了建立连杆的力和加速度关系,对闭环矢量方程进行二阶求导并建立质心加速度方程,即方程(6)至(11)。然后将运动学方程与动力学方程组装成稀疏矩阵,编入MATLAB的程序文件中,稀疏矩阵如(12)所示。
| $ {{\ddot r}_1} + {r_3}{\alpha _3}\sin {\theta _3} + {r_2}{\alpha _2}\sin {\theta _2} = - {r_2}\omega _2^2\cos {\theta _2} - {r_3}\omega _3^2\cos {\theta _3} $ | (6) |
| $ - {r_3}{\alpha _3}\cos {\theta _3} + {r_2}{\alpha _2}\cos {\theta _2} = - {r_2}\omega _2^2\sin {\theta _2} - {r_3}\omega _3^2\sin {\theta _3} $ | (7) |
| $ {a_{{\rm{c}}2,x}} = - {r_{{\rm{c}}2}}{\alpha _2}\sin {\theta _2} - {r_{{\rm{c}}2}}\omega _2^2\cos {\theta _2} $ | (8) |
| $ {a_{{\rm{c}}2,y}} = {r_{{\rm{c}}2}}{\alpha _2}{\rm{con}}{\theta _2} - {r_{{\rm{c}}2}}\omega _2^2\sin {\theta _2} $ | (9) |
| $ \begin{array}{l} {a_{{\rm{c}}3,x}} = - {r_2}{a_2}\sin {\theta _2} - {r_2}\omega _2^2\cos {\theta _2} - \\ \;\;\;\;\;\;\;\;\;{r_{{\rm{c3}}}}{\alpha _3}\sin {\theta _3} - {r_{{\rm{c3}}}}\omega _3^2\cos {\theta _3} \end{array} $ | (10) |
| $ \begin{array}{l} {a_{{\rm{c}}3,y}} = - {r_2}{a_2}{\rm{con}}{\theta _2} - {r_2}\omega _2^2\sin {\theta _2} + \\ \;\;\;\;\;\;\;\;\;{r_{{\rm{c3}}}}{\alpha _3}{\rm{con}}{\theta _3} - {r_{{\rm{c3}}}}\omega _3^2\sin {\theta _3} \end{array} $ | (11) |
| $ \left[ {\begin{array}{*{20}{c}} 1&0&1&0&0&0&0&0&0&0&{ - {m_2}}&0&0&0\\ 0&1&0&1&0&0&0&0&0&0&0&{ - {m_2}}&0&0\\ 0&0&{ - {r_2}{S_2}}&{{r_2}{C_2}}&0&0&0&1&0&0&0&0&0&0\\ 0&0&{ - 1}&0&1&0&0&0&0&0&0&0&{ - {m_3}}&0\\ 0&0&0&{ - 1}&0&1&0&0&0&0&0&0&0&{ - {m_3}}\\ 0&0&{ - {r_{{\rm{c}}3}}{C_3}}&{{r_3}{S_3}}&{\left( {{r_{{\rm{c}}3}} - {r_3}} \right){S_3}}&{\left( {{r_3} - {r_{{\rm{c}}3}}} \right){C_3}}&0&0&0&{ - {I_3}}&0&0&0&0\\ 0&0&0&0&1&0&0&0&{ - {m_4}}&0&0&0&0&0\\ 0&0&0&0&0&1&1&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&1&{{r_3}{S_3}}&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&{ - {r_3}{C_3}}&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&1&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0&0&{{r_{{\rm{c3}}}}{S_3}}&0&0&1&0\\ 0&0&0&0&0&0&0&0&0&{ - {r_{{\rm{c3}}}}{C_3}}&0&0&0&1 \end{array}} \right] \\ \left[ {\begin{array}{*{20}{c}} {{F_{12,x}}}\\ {{F_{12,y}}}\\ {{F_{32,x}}}\\ {{F_{32,y}}}\\ {{F_{43,x}}}\\ {{F_{43,y}}}\\ {{F_{14,y}}}\\ {{M_{12}}}\\ {\ddot r}\\ {{\alpha _3}}\\ {{a_{{\rm{c2}},x}}}\\ {{a_{{\rm{c2}},y}}}\\ {{a_{{\rm{c3}},x}}}\\ {{a_{{\rm{c3}},y}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ F\\ 0\\ { - {r_2}{C_2}\omega _2^2 - {r_3}{C_3}\omega _3^2}\\ { - {r_2}{S_2}\omega _2^2 - {r_3}{S_3}\omega _3^2}\\ { - {r_{{\rm{c2}}}}{C_2}\omega _2^2}\\ { - {r_{{\rm{c2}}}}{S_2}\omega _2^2}\\ { - {r_2}{C_2}\omega _2^2 - {r_{{\rm{c3}}}}{C_3}\omega _3^2}\\ { - {r_2}{S_2}\omega _2^2 - {r_{{\rm{c3}}}}{S_3}\omega _3^2} \end{array}} \right] $ | (12) |
式中:ω2,ω3为连杆2和连杆3的角速度;C2=cos θ2,S2=sin θ2,C3=cos θ3,S3=sin θ3。
2 曲柄滑块机构仿真模型及仿真结果 2.1 仿真初始条件某型号压力机曲柄滑块构件参数如表 1所示。
| 滑块构件 | r/mm | m/kg | I/kg·m2 | rc/mm |
| 压力曲柄 | 25 | 132 | 0 | 0 |
| 平衡曲柄 | 5 | 40 | 0 | 0 |
| 连杆3 | 318 | 136 | 1.8 | 76 |
| 连杆5 | 50 | 65 | 1.5 | 135 |
| 滑块4 | 64 | |||
| 滑块6 | 92 |
压力机的公称力F=800 kN,滑块行程为30 mm,行程次数为1 250次/min。仿真起始位置为压力机的下死点位置,即θ2=θ3=0。曲柄滑块共线时的速度方程为:
| $ \left\{ \begin{array}{l} - {r_2}{\omega _2}\sin {\theta _2} - {r_3}{\omega _3}\sin {\theta _3} = {{\dot r}_1}\\ {r_2}{\omega _2}\cos {\theta _2} + {r_3}{\omega _3}\cos {\theta _3} = 0 \end{array} \right. $ | (13) |
根据式(13),求出行程次数为1 250次/min时,ω3=-1.03 rad/s。仿真的初始条件为:ω2=130.83 rad/s,ω3=-1.03 rad/s,θ2=θ3=0。
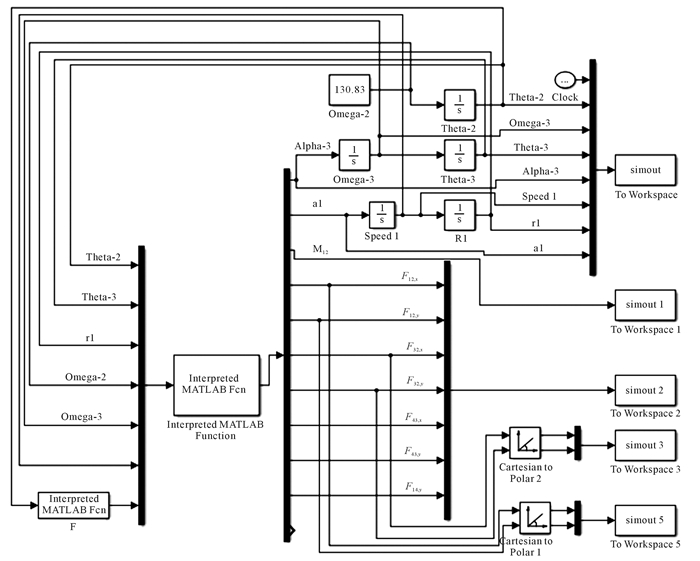
2.2 Simulink仿真模型曲柄滑块机构Simulink仿真模型如图 3所示。选择ode45变步长求解器,相对误差设为10-3。
|
| 图 3 曲柄滑块机构Simulink仿真模型 Fig.3 Simulink simulation model of slider crank mechanism |
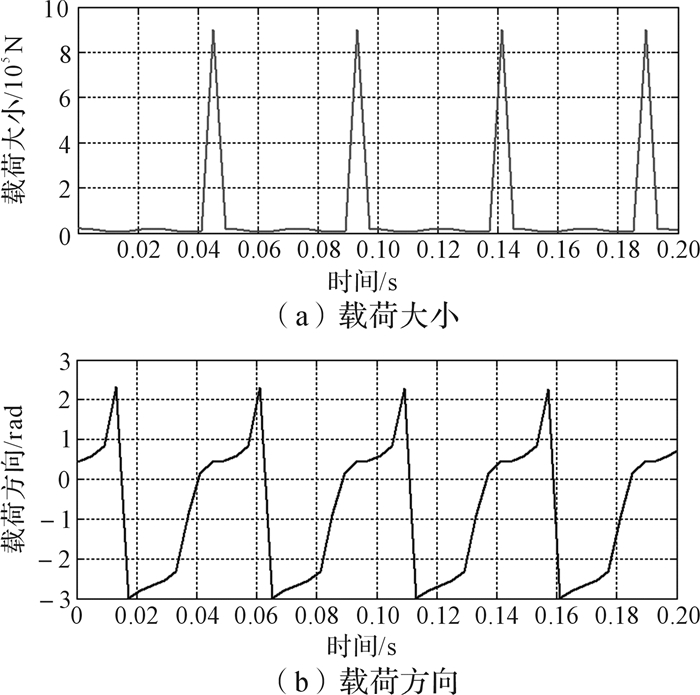
根据建立的Simulink仿真模型进行动力学仿真,取仿真时间为0.2 s,冲压力为800 kN。得到压力曲柄颈处载荷随时间的变化规律,如图 4所示。
|
| 图 4 压力曲柄颈处载荷变化 Fig.4 Load variation of pressure crank journal |
图 4(a)为压力曲柄颈处载荷大小的变化。1个行程周期为0.048 s。其中0-0.04 s为空载阶段,压力曲柄受到连杆和滑块的不平衡惯性力,最大为25 kN; 0.04-0.048 s为冲压阶段,受到连杆和滑块的不平衡惯性力和冲压力, 最大为825 kN。图 4(b)为以x轴正方向为基准的压力曲柄颈处载荷方向的变化。
通过改变曲柄连杆参数及冲压力,在同样的仿真条件下得到平衡曲柄颈处载荷随时间的变化规律, 如图(5)。
|
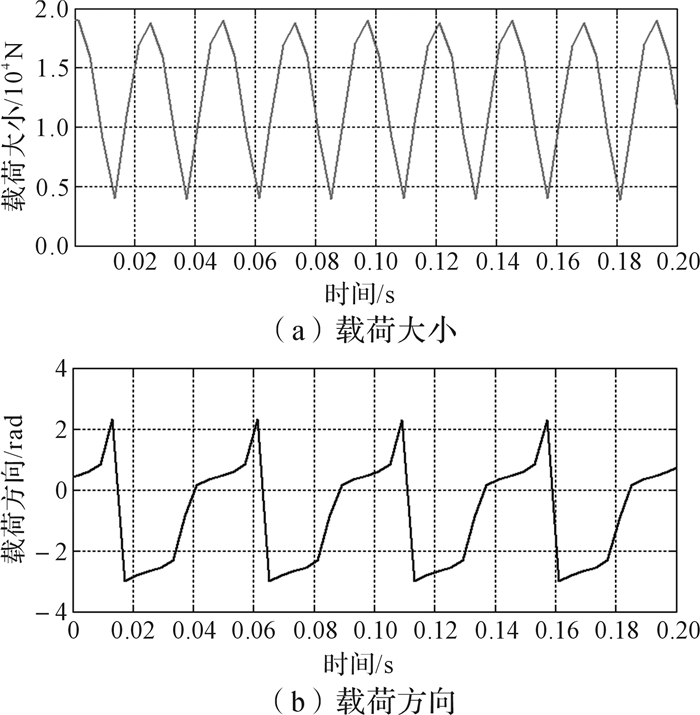
| 图 5 平衡曲柄颈处载荷变化 Fig.5 Load variation of balance crank journal |
图 5(a)为平衡曲柄处载荷大小的变化。1个行程周期为0.048 s,在第0秒和第0.048秒时, 滑块处于右极限位置,第0.024秒时滑块处于左极限位置。由图可以看出滑块处于极限位置时,平衡曲柄颈处的载荷最大,滑块位于行程中间位置时,平衡曲柄颈处的载荷最小。图 5(b)为以x轴正方向为基准的平衡曲柄颈处载荷方向的变化。
由于压力机反置了平衡副滑块,抵消了机构绝大部分的不平衡惯性力,所以支承颈处的不平衡惯性力相比于冲压力可以忽略不计。根据刚化原理,视曲柄颈为刚体, 在同样的仿真条件下得到支承颈处载荷随时间的变化规律, 如图 6所示。
|
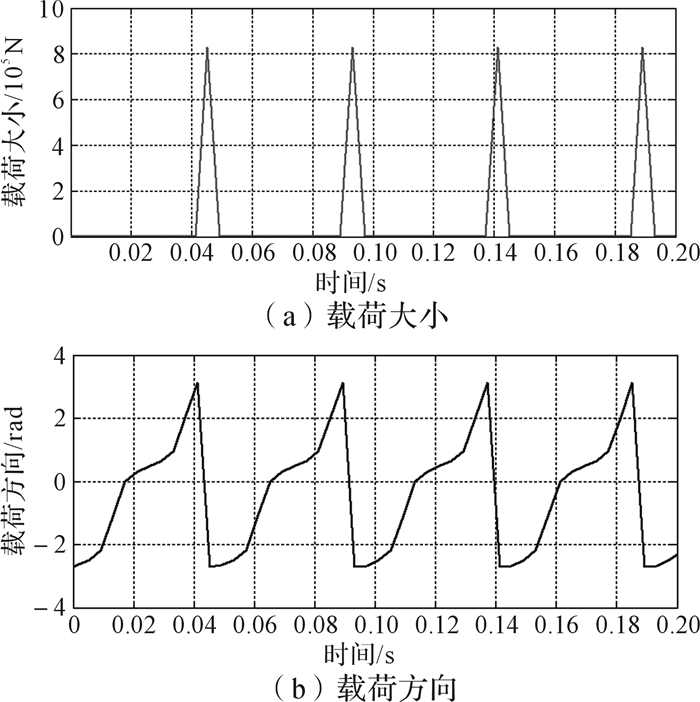
| 图 6 支承颈处载荷变化 Fig.6 Load variation of supporting journal |
由图 6(a)可以看出,曲轴支承颈处的惯性力载荷经平衡副滑块抵消后,最大的不平衡惯性力为6 kN,远远小于冲压力。所以曲轴支承颈主要承受冲压力的作用,承受的最大载荷为806 kN。
4 曲轴疲劳分析根据现有研究得知,利用有限元分析法分析曲轴时,按照均布载荷形式对其加载, 得到的分析结果才更可靠, 更接近曲轴变形的真实情况[15]。曲轴滑块的受力情况如图 1(a)所示,根据Simulink仿真求得的曲轴支承颈处和曲柄颈处载荷谱,采用Workbench软件对其加载,并进行静态分析和疲劳寿命分析[16-19]。
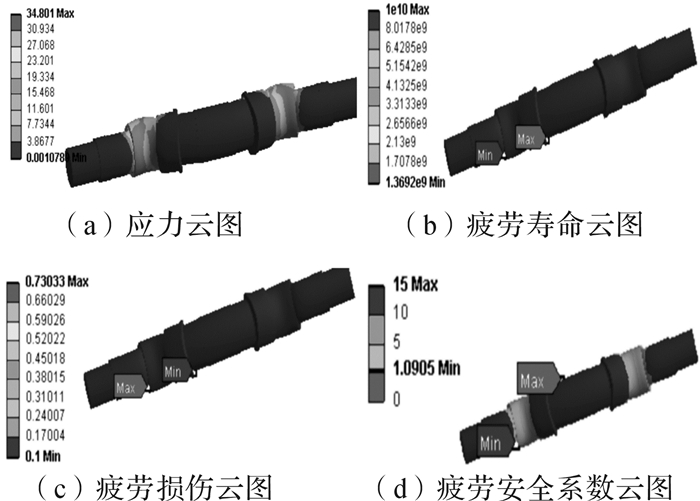
图 7为曲轴的疲劳寿命分析结果。图 7(a)为曲轴的应力云图,最大应力为34.8 MPa,位于压力曲柄颈和支承颈的轴肩处,这是因为轴肩处截面尺寸发生突变,导致应力集中严重。图 7(b)为曲轴的疲劳寿命云图,最小疲劳寿命达到1.36×109次,根据工程设计中的规定:对于应力疲劳曲线有水平渐近线的材料,若经历107次应力循环后不损坏,即认为其可承受无穷多次应力循环,因此认为该曲轴已达到无限寿命。图 7(c)为曲轴的疲劳损伤云图,可知曲轴的损伤最大值为0.73,损伤数值小于1,即达到无限寿命时没有出现明显损伤。图 7(d)为曲轴的疲劳安全系数云图,曲轴的最低安全系数为1.09,安全系数大于1,因此,曲轴的安全系数满足设计要求。
|
| 图 7 曲轴疲劳寿命分析 Fig.7 Fatigue life analysis of crankshaft |
1) 采用联立约束法建立了曲柄滑块机构动力学模型,并用MATLAB中的Simulink模块进行了仿真分析, 快速、准确地求出了曲轴各个轴颈处载荷随时间的变化规律。
2) 仿真得到的各曲柄颈和支承颈处载荷的变化规律是根据运动学参数求得的,可以真实地反映出速度、加速度和惯性载荷之间的关系,为压力机曲轴、曲轴支撑结构和动平衡结构设计及压力机下死点精度的研究提供重要的理论依据。
3) 根据Simulink仿真求得的曲轴支承颈处和曲柄颈处载荷谱,采用Workbench软件对其进行加载,并进行静态分析和疲劳寿命分析。疲劳分析结果验证了曲轴的疲劳寿命符合设计要求,分析结果更加接近实际,为压力机曲轴的实际应用提供参考。
| [1] |
邓明, 胡根铭, 吕琳, 等.
精冲压力机的现状及发展趋势[J]. 锻压技术, 2016, 41(8): 1–6.
DENG Ming, HU Gen-ming, LÜ Lin, et al. Present situation and development trend of fine blanking press[J]. Forging & Stamping Technology, 2016, 41(8): 1–6. |
| [2] |
何亚银, 李志峰, 陈纯.
由串联四杆机构组成的多连杆压力机运动特性研究[J]. 机械设计, 2015, 32(5): 87–90.
HE Ya-yin, LI Zhi-feng, CHEN Chun. Study on motion characteristics of multi-link press made up of series four-bar linkage[J]. Journal of Machine Design, 2015, 32(5): 87–90. |
| [3] |
彭玉海, 何亚银, 李志峰.
由串联四杆机构组成的多连杆压力机下死点精度的研究[J]. 机械设计, 2016, 33(5): 97–100.
PENG Yu-hai, HE Ya-yin, LI Zhi-feng. Study on the bottom dead center accuracy of multi-link press machine composed of series four-bar linkage[J]. Journal of Machine Design, 2016, 33(5): 97–100. |
| [4] |
刘鸿文.
材料力学[M]. 北京: 高等教育出版社, 2011: 48-49.
LIU Hong-wen. Mechanics of materials[M]. Beijing: Higher Education Press, 2011: 48-49. |
| [5] |
李烨健, 孙宇, 胡峰峰, 等.
高速机械压力机综合动平衡优化研究[J]. 华中科技大学学报(自然科学版), 2016, 44(6): 25–28.
LI Ye-jian, SUN Yu, HU Feng-feng, et al. Research on synthetic optimum dynamic balancing of high-speed press machine[J]. Huazhong University of Science & Technology(Natural Science Edition), 2016, 44(6): 25–28. |
| [6] |
衣锐.
基于Workbench的高速压力机曲轴疲劳分析[J]. 锻压装备与制造技术, 2014(6): 16–18.
YI Rui. Fatigue analysis of crankshaft for high speed press on the basis of Workbench software[J]. China Metalforming Equipment & Manufacturing Technology, 2014(6): 16–18. |
| [7] |
牛瑞霞, 詹俊勇, 仲太生.
高速闭式压力机曲轴的动、静态有限元分析[J]. 锻压装备与制造技术, 2015(1): 29–31.
NIU Rui-xia, ZHAN Jun-yong, ZHONG Tai-sheng. Static and dynamic analysis of crankshaft in high-speed press based on the FEM[J]. China Metalforming Equipment & Manufacturing Technology, 2015(1): 29–31. |
| [8] |
张德峰, 贾方, 胡金龙.
基于有限元子模型技术的高速压力机曲轴应力集中分析[J]. 锻压装备与制造技术, 2008, 43(4): 27–29.
ZHANG De-feng, JIA Fang, HU Jin-long. Stress-concentration analysis on high-speed press crank based on fem sub-modeling technology[J]. China Metalforming Equipment & Manufacturing Technology, 2008, 43(4): 27–29. |
| [9] |
王磊, 贾方, 陈树新, 等.
高速压力机转子-轴承系统的动力学研究[J]. 振动工程学报, 2012, 25(4): 460–466.
WANG Lei, JIA Fang, CHEN Shu-xin. Dynamics of rotor-bearing system in high speed press[J]. Journal of Vibration Engineering, 2012, 25(4): 460–466. |
| [10] |
鹿新建, 朱思洪, 何光军, 等.
高速精密压力机理想驱动转矩研究[J]. 机械设计, 2011, 28(9): 38–41.
LU Xin-jian, ZHU Si-hong, HE Guang-jun, et al. Research on ideal driving torque of high-speed precision press[J]. Journal of Machine, 2011, 28(9): 38–41. |
| [11] |
GARDNER John F. 机构动态仿真: 使用MATLAB和Simulink[M]. 周进雄, 张陵, 译. 西安: 西安交通大学出版社, 2002: 49-73.
GARDNER John F. Simulations of machines using MATLAB and Simulink[M]. Translated by ZHOU Jin-xiong, ZHANG Ling. Xi'an:Xi'an Jiaotong University Press, 2002:49-73. |
| [12] |
阮卫平, 刘强, 吴殿军.
高速曲柄压力机的动平衡机构探讨[J]. 锻压装备与制造技术, 2008(6): 34–36.
RUAN Wei-ping, LIU Qiang, WU Dian-jun. Dynamic balance structure discuss of high speed crank press[J]. China Metalforming Equipment & Manufacturing Technology, 2008(6): 34–36. |
| [13] |
胡战胜, 欧汝康, 欧建业, 等.
高速压力机对称动平衡机构设计与实例分析[J]. 锻压装备与制造技术, 2015(2): 30–31.
HU Zhan-sheng, OU Ru-kang, OU Jian-ye, et al. Design and instance analysis about dynamic balance mechanism on high speed press[J]. China Metalforming Equipment & Manufacturing Technology, 2015(2): 30–31. |
| [14] |
付求涯, 柯尊芒, 钟涛生.
高速压力机下死点动态精度的影响因素及其提高措施[J]. 机床与液压, 2016, 44(16): 165–168.
FU Qiu-ya, KE Zun-mang, ZHONG Tao-sheng. Influencing factors of dynamic precision of lower dead center of high speed press and improving measures[J]. Machine Tool & Hydraulics, 2016, 44(16): 165–168. DOI:10.3969/j.issn.1001-3881.2016.16.048 |
| [15] |
周志鸿, 李晓, 孙常盛.
基于ANSYS的曲柄压力机曲轴刚度分析[J]. 锻压技术, 2007, 32(5): 114–117.
ZHOU Zhi-hong, LI Xiao, SUN Chang-sheng. Crankshaft flexibility analysis of the crank press based on ANSYS[J]. Forging & Stamping Technology, 2007, 32(5): 114–117. |
| [16] |
张强, 王海舰, 胡南.
起升载荷下门式起重机主梁损伤与疲劳寿命预测研究[J]. 工程设计学报, 2015, 22(5): 461–468.
ZHANG Qiang, WANG Hai-jian, HU Nan. Study on injury and fatigue life forecast of gantry crane's girder under rising load[J]. Chinese Journal of Engineering Design, 2015, 22(5): 461–468. |
| [17] |
董超群, 梁政, 唐伟, 等.
天然气压缩机活塞杆失效机理及疲劳寿命分析[J]. 机械设计, 2015, 32(11): 74–78.
DONG Chao-qun, LIANG Zheng, TANG Wei, et al. Failure mechanism and fatigue life analysis of piston rod from natural gas compressors[J]. Journal of Machine Design, 2015, 32(11): 74–78. |
| [18] |
邹梦麒, 刘初升, 武继达.
单边驱动式摇摆筛偏心轴的应力与疲劳分析[J]. 工矿自动化, 2017, 43(5): 58–61.
ZOU Meng-qi, LIU Chu-sheng, WU Ji-da. Analysis of stress and fatigue of eccentric shaft of unilateral driven swing screen[J]. Industry and Mine Automation, 2017, 43(5): 58–61. |
| [19] |
王国丽, 黄小海, 刘树辉, 等.
汽车悬架稳定杆连杆支架的疲劳仿真分析及结构优化[J]. 工程设计学报, 2013, 20(1): 18–21.
WANG Guo-li, HUANG Xiao-hai, LIU Shu-hui, et al. Fatigue simulation and structure optimization of suspension stabilizer link bracket[J]. Chinese Journal of Engineering Design, 2013, 20(1): 18–21. |


