工程中的滚动摩擦主要有驱动滚动和自由滚动两种形式。驱动滚动时的摩擦阻力实质是支撑表面对滚动体的切向反力,其大小由驱动机构传递至滚动体的转动力矩所决定,同时又受制于接触表面间的摩擦系数。自由滚动时的摩擦阻力是一种阻碍滚动发生的力。驱动滚动和自由滚动的摩擦机理、磨损形式均不相同。目前人们对驱动滚动的关注较多,而关于自由滚动方面的研究,无论在理论模型上还是在实验上都比较少[1-4]。
自由滚动中的摩擦阻抗主要来源于微观滑移、弹性滞后、黏附效应及塑性变形等[5-6]。聚合物的黏弹性质使其弹性滞后效应比其它材料显著得多,因此其滚动摩擦行为受材料的蠕变柔量、松驰模量等因素影响较大[7-8]。然而,库伦古典滚动摩擦定律的表达式过于理想化,没有将对滚物体的机械、力学性质及接触性质的影响反映出来,在描述聚合物滚动摩擦行为时与实验数据及工程实际偏差较大[1, 3, 9],如:Akama[10]和Ringsberg等[11]利用有限元法和库伦定律相结合的方式分析了轮-轨滚动接触应力,并以此为理论基础讨论了轮-轨疲劳损伤机理;也有学者采用有限元法进行轮-轨滚动接触的弹塑性分析[12-13],并据此考察了列车高速运行时的轮轨接触特性[14];Liu等[15]模拟了轮-轨滚动过程中接触表面裂纹的扩展情况,并对比分析了仿真结果和现场观测数据。上述研究多是针对坚硬接触面间的滚动行为,把对滚物体看作纯弹性体,且采用常系数库伦摩擦定律来定义接触面之间的关系,因此计算结果难以真实反映具有高黏弹特性的聚合物的滚动摩擦行为[16-18]。
本文利用电磁加载的新型斜面法考察了聚四氟乙烯(PTFE)、聚甲基丙烯酸甲酯(PMMA)、聚醚型聚氨酯(PEUR)等工程中常用的聚合物材料与淬火45#钢配副时的滚动摩擦阻力,以及这3种工程塑料的蠕变、松驰特性,并从弹性滞后效应的角度探讨聚合物黏弹性质对滚动摩擦阻力的影响机理。
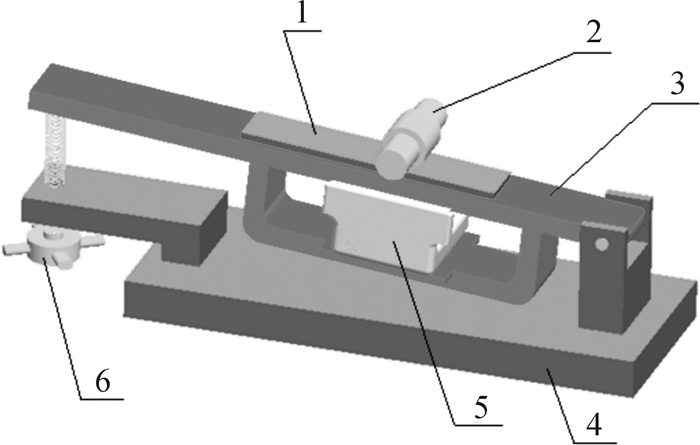
1 基于新型斜面法的滚动摩擦实验自由滚动时摩擦阻力的精密测量一直是摩擦学研究中的重要部分。目前试验中常用的M-2000滚动摩擦试验机、小车法等不可避免会受到轴承误差的影响。自由滚动时摩擦阻力较小,与轴承转动阻力基本处于同一数量级,有时甚至小于轴承阻力,因此实验仪器中轴承传动误差是摩擦阻力测量误差的重要来源。为消除轴承转动阻力的影响,本文采用电磁加载的斜面法测量滚动摩擦阻力,具体试验台如图 1所示。实验全程在封闭的环境里进行,滚动体材料为45#钢,淬火处理后硬度为HRC57,外圆直径为30 mm,宽为90 mm,其表面经磨削后粗糙度为0.2 μm。PTFE,PMMA,PEUR试件均加工成200 mm×100 mm×8 mm的长方形板,表面粗糙度为0.4 μm。综合调节电磁铁线圈中的电流强度及滚动体重量,设定实验载荷为10 N。以约1°/s的速度缓慢调节丝杠改变斜面倾角使45#钢试件开始滚动,通过千分表读出升起高度并换算成倾角θ。相同实验重复5次,实验结果取5次实验的平均值。
|
| 1—聚合物试件;2—45#钢试件;3—斜面板;4—支座;5—电磁铁;6—调节丝杠 图 1 滚动摩擦试验台示意图 Fig.1 Schematics of the rolling friction test system |
蠕变、松驰实验在CETR UMT-2型多功能试验机上进行。实验用PTFE,PMMA,PEUR车削加工成10 mm×10 mm的圆柱体,试件表面粗糙度均为0.4 μm。实验温度为18 ℃,湿度为53%。蠕变实验载荷为50 N,加载后在1 h内持续测量试件的压缩变形量。松弛实验中,在试件上施加50 N载荷后,保持试件的压缩变形量不变,在1 h内持续测量试件内部的压应力。
2 实验结果与分析表 1示出了45#钢与PTFE,PMMA和PEUR接触滚动时的实验结果。根据tan θ可以计算出滚动摩擦阻力。由表 1可见,PEUR的滚动摩擦阻力最大,PTFE次之,PMMA最小,三者的比值约为1:0.51:0.28。
| 聚合物 | 升起高度/mm | tan θ | 滚动摩擦阻力/N | |
| 平均值 | 方差 | |||
| PTFE | 3.87 | 0.101 | 0.003 9 | 0.026 |
| PMMA | 2.05 | 0.511 | 0.002 1 | 0.014 |
| PEUR | 7.63 | 0.428 | 0.007 6 | 0.051 |
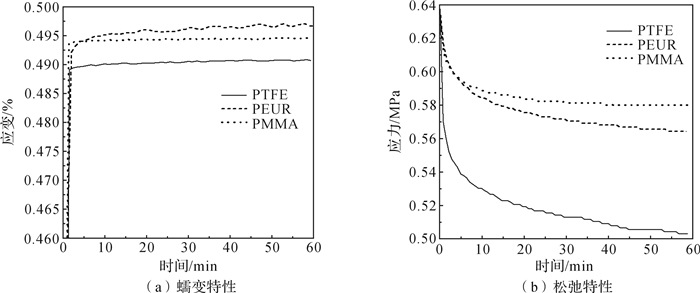
PTFE, PMMA和PEUR的蠕变、松驰特性如图 2所示。
|
| 图 2 PTFE, PMMA和PEUR的蠕变、松驰特性 Fig.2 Creep and relaxation characteristics of PTFE, PMMA, and PEUR |
由图 2可见,蠕变实验中在加载载荷的瞬间,PTFE, PMMA和PEUR均发生了较大的应变,其后载荷保持恒定,但随时间推移,应变呈继续增加的趋势。松驰实验中,3种聚合物材料的内部应力均随着时间的推移而逐渐减小。实验结果表明:PMMA, PTFE和PEUR均具有比较显著的黏弹特性。用标准线性固体模型对3种材料的实验结果进行模拟,得各参数如表 2所示。
| 聚合物 | 标准线性固体模型参数 | ||
| E1 | E2 | η1 | |
| PTFE | 1.202×106 | 7.791×106 | 3.586×109 |
| PMMA | 1.258×106 | 1.842×107 | 6.328×109 |
| PEUR | 1.261×106 | 1.346×107 | 8.168×109 |
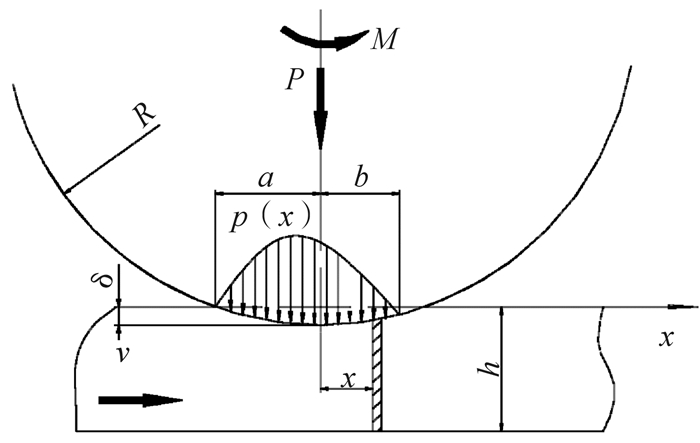
滚动体在法向载荷P及力矩M作用下向前滚动时的受力情况如图 3所示[19]。
|
| 图 3 滚动摩擦时力偶平衡示意图 Fig.3 Couple stress balance in rolling friction |
设滚动体的滚动速度为v,且假设在x=-a处与基础作第1次接触。如果a≪R,则支撑基体在x=-a处的应变可表示为:
| $ \varepsilon {\rm{ = }}-\frac{{(\delta-\frac{{{x^2}}}{{2R}})}}{h}, -a \le x \le b $ | (1) |
式中δ为最大变形深度。
对于理想弹性体,其弹性模量为E,则接触将是对称的,即a=b,此时接触压力分布可表示为:
| $ p\left( x \right) = \frac{E}{{2Rh}}({a^2}-{x^2}) $ | (2) |
对于黏弹性材料,其弹性模量E可用松驰函数Ψ(t)代替,因此在x处,黏弹性单元的应力可表达为:
| $ p\left( {x, t} \right) =-\sigma =-{\smallint ^t}_0\psi \left( {t-t\prime } \right)\frac{{\partial \varepsilon \left( {t\prime } \right)}}{{\partial t\prime }}{\rm{d}}t\prime $ | (3) |
在稳定滚动过程中,
| $ p\left( {x, t} \right) =-\frac{1}{{Rh}}\int_{-x}^x {x'\psi (x-x'){\rm{d}}x'} $ | (4) |
标准线性固体模型的松驰函数可写为:
| $ \psi (t) = \frac{{{E_1}{E_2}}}{{{E_1} + {E_2}}}\left( {1 + \frac{{{E_1}}}{{{E_2}}}{{\rm{e}}^{-\frac{{{E_1} + {E_2}}}{{{\eta _1}}}t}}} \right) $ |
将该松驰函数代入式(3),则得应力分布的表达式为:
| $ \begin{array}{l} p(x) =- \frac{{{E_1}{E_2}}}{{Rh({E_1} + {E_2})}}\left\{ {\frac{{{{(x')}^2}}}{2} + \frac{{v{E_1}{\eta _1}}}{{{E_2}({E_1} + {E_2})}}} \right.\\ \left. {\left. {\left[{\left( {x'-\frac{{v{\eta _1}}}{{{E_1} + {E_2}}}} \right){{\rm{e}}^{-\frac{{{E_1} + {E_2}}}{{v{\eta _1}}}(x-x' )}}} \right]} \right\}} \right|_{ -a}^x \end{array} $ | (5) |
对压力分布函数进行积分,则可求得圆柱滚动时所受到的阻力为:
| $ F = \frac{M}{R} = \frac{{\int_{-a}^b {xp(x){\rm{d}}x} }}{R} $ | (6) |
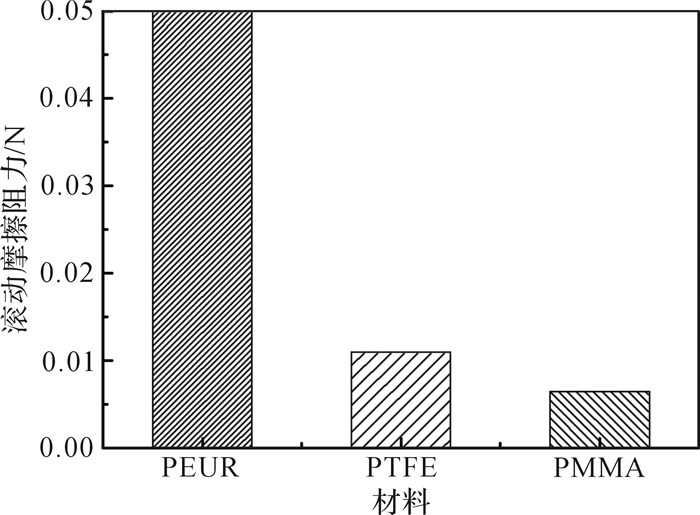
将表 2中各聚合物的拟合参数代入式(5)和式(6),可求得PTFE,PMMA,PEUR三种材料滚动摩擦阻力的相对关系,如图 4所示。
|
| 图 4 不同聚合物的滚动摩擦阻力模拟计算结果 Fig.4 The simulation results of rolling friction force of different polymers |
图 4所示结果表明,在相同实验条件下,PEUR的滚动摩擦阻力最高,PTFE次之,PMMA最低,这与实验结果完全一致。PEUR,PTFE,PMMA三种材料滚动摩擦阻力的比值为1:0.22:0.13, 这与实验结果有所不同。一般认为,滚动过程中的摩擦阻抗是微观滑移、弹性滞后、黏附及塑性变形等行为综合作用的结果,PMMA,PTFE和PEUR的高黏弹性使得弹性滞后效应在摩擦阻抗中发挥重要作用,但摩擦阻抗中其它组分的存在以及实验中存在的误差,造成了基于弹性滞后效应的模拟计算结果与实验数据不完全相同。但模拟计算结果基本上与实验数据还是吻合的,因此可以认为弹性滞后效应是聚合物滚动过程中摩擦阻抗的主要来源。
4 结论1) PMMA,PTFE,PEUR与淬火45#钢配副滚动时,PEUR的滚动摩擦阻力最大,PTFE次之,PMMA最小,三者的比值约为1:0.51:0.28。
2) 基于标准线性固体模型,从弹性滞后效应的角度推导了滚动摩擦阻力与聚合物黏弹特性之间的耦合关系,模拟计算结果与实验数据基本吻合,可以说明弹性滞后效应是聚合物滚动过程中摩擦阻抗的主要来源。
3) 采用电磁加载的新型斜面法研究滚动摩擦行为,为滚动摩擦阻力的测量提供了新的方法,并为聚合物滚动摩擦的工程设计提供新的参考依据,这对于从黏弹性角度研究聚合物滚动摩擦行为具有一定的意义。
| [1] |
黄传辉. 聚合物复合材料滚动摩擦行为研究[D]. 徐州: 中国矿业大学机电工程学院, 2007: 2-19.
HUANG Chuan-hui. Study about rolling friction behavior of polymers and composites[D]. Xuzhou:China University of Mining and Technology, School of Mechanical Engineering, 2007:2-19. |
| [2] | THIEL K H, RUEHMER T, KIESEKAMP J. Novel functionalized synthetic rubbers for tire applications[J]. Kautschuk Gummi Kunststoffe, 2013, 66(3): 38–44. |
| [3] | MIEGE A J P, POPOV A. Truck tyre modelling for rolling resistance calculations under a dynamic vertical load[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2005, 219(4): 441–456. DOI:10.1243/095440705X11176 |
| [4] |
王文健, 郭俊, 刘启跃.
接触应力对轮轨材料滚动摩擦磨损性能影响[J]. 摩擦学学报, 2011, 31(4): 352–356.
WANG Wen-jian, GUO Jun, LIU Qi-yue. Effect of contact stress on rolling friction and wear behavior of wheel-rail materials[J]. Tribology, 2011, 31(4): 352–356. |
| [5] |
王少锋, 许玉德, 周宇, 等.
基于临界平面法的钢轨裂纹萌生寿命预测模型研究[J]. 华东交通大学学报, 2011, 28(5): 77–82.
WANG Shao-feng, XU Yu-de, ZHOU Yu, et al. A research on rail crack initiation life prediction models based on critical plane method[J]. Journal of East China Jiaotong University, 2011, 28(5): 77–82. |
| [6] |
黄传辉, 王前.
PV值对尼龙PA66滚动摩擦阻力的影响[J]. 机械设计, 2016, 33(7): 82–84.
HUANG Chuan-hui, WANG Qian. Investigation on the effect of PV on rolling friction resistance of PA66 nylon[J]. Journal of Machine Design, 2016, 33(7): 82–84. |
| [7] | YIN H S, HU Y S, ZHANG H, et al. Truck tire thermal-mechanical FEA and DMA with application to endurance evaluation[J]. Tire Science and Technology, 2006, 34(4): 220–236. DOI:10.2346/1.2345651 |
| [8] | SHIMIZU S. Fatigue limit concept and life prediction model for rolling contact machine elements[J]. Tribology Transactions, 2002, 45(1): 39–46. DOI:10.1080/10402000208982519 |
| [9] |
龚科家, 危银涛, 叶进雄.
基于热力学有限元分析的轮胎滚动阻力仿真[J]. 中国机械工程, 2009, 20(5): 626–629.
GONG Ke-jia, WEI Yin-tao, YE Jin-xiong. Simulation techniques of tire rolling resistance based on thermal-mechanical FEA[J]. China Mechanical Engineering, 2009, 20(5): 626–629. |
| [10] | AKAMA M. Development of finite element model for analysis of rolling contact fatigue cracks in wheel/rail systems[J]. Railway Technical Research Institute Quarterly Reports, 2007, 48(1): 8–14. |
| [11] | RINGSBERG J W, LOO-MORREY M, JOSEFSON B L, et al. Prediction of fatigue crack initiation for rolling contact fatigue[J]. International Journal of Fatigue, 2000, 22(3): 205–215. DOI:10.1016/S0142-1123(99)00125-5 |
| [12] | EKH M, JOHANSSON A, THORBERNTSSON H, et al. Models for cyclic ratcheting plasticity-integration and calibration[J]. Journal of Engineering Materials and Technology, 2000, 122(1): 49–55. DOI:10.1115/1.482764 |
| [13] |
温泽峰, 金学松, 肖新标.
多步非稳态载荷下钢轨滚动接触应力和弹塑性变形分析[J]. 工程力学, 2007, 24(12): 158–168.
WEN Ze-feng, JIN Xue-song, XIAO Xin-biao. Elastic-plastic analysis for rolling contact stresses and deformations of rail under multiple-step non-steady state loading[J]. Engineering Mechanics, 2007, 24(12): 158–168. DOI:10.3969/j.issn.1000-4750.2007.12.027 |
| [14] | JIANG Xiao-yu, JIN Xue-song. Numerical simulation of wheel rolling over rail at high-speeds[J]. Wear, 2007, 262(5/6): 666–671. |
| [15] | LIU Yong-ming, LIU Li-ming, SANKARAN M. Analysis of subsurface crack propagation under rolling contact loading in railroad wheels using FEM[J]. Engineering Fracture Mechanics, 2007, 74(17): 2659–2674. DOI:10.1016/j.engfracmech.2007.02.012 |
| [16] |
顾少杰, 杨新文, 练松良.
基于非Hertz滚动接触理论的轮轨滑动摩擦生热分析[J]. 内蒙古科技大学学报, 2015, 34(1): 67–71.
GU Shao-jie, YANG Xin-wen, LIAN Song-linag. Analysis of the wheel-rail friction heating during wheel sliding based on non-Hertz rolling contact theory[J]. Journal of Inner Mongolia University of Science and Technology, 2015, 34(1): 67–71. |
| [17] | BRUNEL J F, CHARKALUK E, DUFRÉNOY. Rolling contact fatigue of railways wheels:influence of steel grade and sliding conditions[J]. Procedia Engineering, 2010, 2(1): 2161–2169. DOI:10.1016/j.proeng.2010.03.232 |
| [18] |
肖乾, 方骏, 王磊.
摩擦系数对高速列车车轮瞬时滚动接触疲劳的影响[J]. 中国铁道科学, 2016, 37(3): 68–74.
XIAO Qian, FANG Jun, WANG Lei. Influence of friction coefficient on wheel transient rolling contact fatigue of high speed train[J]. China Railway Science, 2016, 37(3): 68–74. |
| [19] |
JOHNSON K L. 接触力学[M]. 徐秉业, 译. 北京: 高等教育出版社, 1992: 343-348.
JOHNSON K L. Contact mechanics[M]. Translated by XU Bing-ye. Beijing:Higher Education Press, 1992:343-348. |


