TRIP780高强钢是一种兼具高强度和高塑性的汽车用钢,在其冷变形过程中会发生残余奥氏体向马氏体的相变,导致材料塑性提高及回弹增大,引起的尺寸精度下降对回弹的控制一直是一个难点,扭曲回弹尤其难以控制。
国内外学者在扭曲回弹方面作了很多的研究。Pham等[1]对超薄金属板U形梁进行了扭曲回弹分析,发现当试件的2个端部偏移量较大时,扭转程度较高。Abdullah等[2]研究了AA6061螺旋桨叶片,发现扭曲回弹随着扭曲角度和变形率的增大而增大。Xue等[3]研究了双相钢C形梁在非轴对称拉伸成形过程中的扭曲回弹特性,提出了通过改变模具圆角半径减小回弹的方法。谢延敏等[4]研究了高强钢弯曲梁的扭曲回弹,提出了将回弹前后两个截面测量点构成直线夹角的变化量作为扭曲回弹的评价指标。
为了有效控制回弹,获得准确的本构模型参数是关键。近年来,基于优化思想反求材料本构参数的方法成为研究热点。李振友等[5]利用遗传算法,结合鸟撞铝板试验数据,获得了适用于中等冲击的鸟体本构模型参数。Qu等[6]研究了基于遗传算法的超塑性本构模型参数反求。高晖等[7]结合响应面模型,提出了一种在冲压成形过程中反求材料参数的方法。Malakizadi等[8]基于响应面模型,对金属切削过程中Johnson-Cook本构模型参数进行反求。
TRIP780高强钢扭曲回弹方面的研究相对较少,并且利用遗传算法与响应面模型能够获得较为准确的模型参数,基于此,本文以TRIP780高强钢双C梁为研究对象,建立混合硬化模型,通过试验并结合响应面模型与遗传算法的方法反求硬化模型参数。基于反求参数,结合确定的有限元模型与极差分析方法,确定影响扭曲回弹的关键因素,为扭曲回弹的有效控制提供一种综合分析方法。
1 混合硬化模型金属薄板冲压成形中常用的硬化模型有各向同性硬化、随动硬化和混合硬化三类[9]。在塑性变形中,多数材料的屈服面既有大小的变化也有位置的变化。Voce非线性各向同性硬化模型能够描述屈服面大小的变化,含2项背应力的Chaboche非线性随动硬化模型能够描述屈服面位置的变化。为了能够更好地描述金属材料的真实硬化行为,本文采用上述两种硬化模型组成的混合硬化模型。
考虑混合硬化的屈服准则通用表达式如式(1)所示[10]:
| $ f\left( {\sigma - \alpha ,R} \right) = {\sigma _{{\rm{eq}}}}\left( {\sigma - \alpha } \right) - \left( {{\sigma _0} + R} \right) = 0 $ | (1) |
式中:f为塑性势,σeq为等效应力,σ为流动应力,α为随动硬化水平的背应力,σ0为初始屈服应力,R为各向同性硬化应力。
且塑性流动方程满足:
| $ {\rm{d}}{\varepsilon _{\rm{p}}} = {\rm{d}}\lambda \frac{{\partial f}}{{\partial \sigma }} $ | (2) |
式中:dεp为塑性应变增量,dλ为待定比例系数。
Voce非线性各向同性硬化模型[11]如式(3)和式(4)所示:
| $ R = {R_1} + {R_2} $ | (3) |
| $ {\rm{d}}{R_i} = {b_i}\left( {{Q_i} - {R_i}} \right){\rm{d}}\lambda $ | (4) |
式中:R和Ri分别是各向同性硬化应力及分量,bi和Qi是待定系数。
| $ {R_i} = {Q_i}\left[ {1 - \exp \left( { - {b_i}{\varepsilon _{\rm{p}}}} \right)} \right],i = 1,2 $ | (5) |
含2项背应力的Chaboche非线性随动硬化模型[12],其背应力如式(6)和式(7)所示:
| $ \alpha = {\alpha _1} + {\alpha _2} $ | (6) |
| $ {\rm{d}}{\alpha _i} = \frac{2}{3}{c_i}{\rm{d}}{\varepsilon _{\rm{p}}} - {\gamma _i}{\alpha _i}{\rm{d}}p,i = 1,2 $ | (7) |
式中:α和αi分别是随动硬化应力及分量;ci和γi是待定系数;dp是等效塑性应变率,对于单向拉伸,
| $ {\rm{d}}p = \left\langle {\frac{2}{3}{\rm{d}}{\varepsilon _{\rm{p}}},{\rm{d}}{\varepsilon _{\rm{p}}}} \right\rangle 1/2 = {\rm{d}}{\varepsilon _{\rm{p}}} $ | (8) |
联立式(7)和式(8),并进行积分,得到:
| $ {\alpha _i} = \frac{2}{3}\frac{{{c_i}}}{{{\gamma _i}}}\left[ {1 - \exp \left( { - {\gamma _i}{\varepsilon _{\rm{p}}}} \right)} \right] $ | (9) |
在单向拉伸变形中,有约束条件[13]:
| $ {b_i} = {\gamma _i},i = 1,2 $ | (10) |
由式(1)(5)(9)(10)可知,混合硬化模型的待定系数为6个,即b1,b2,c1,c2,Q1和Q2,这些参数的反求将在第6节详细说明。
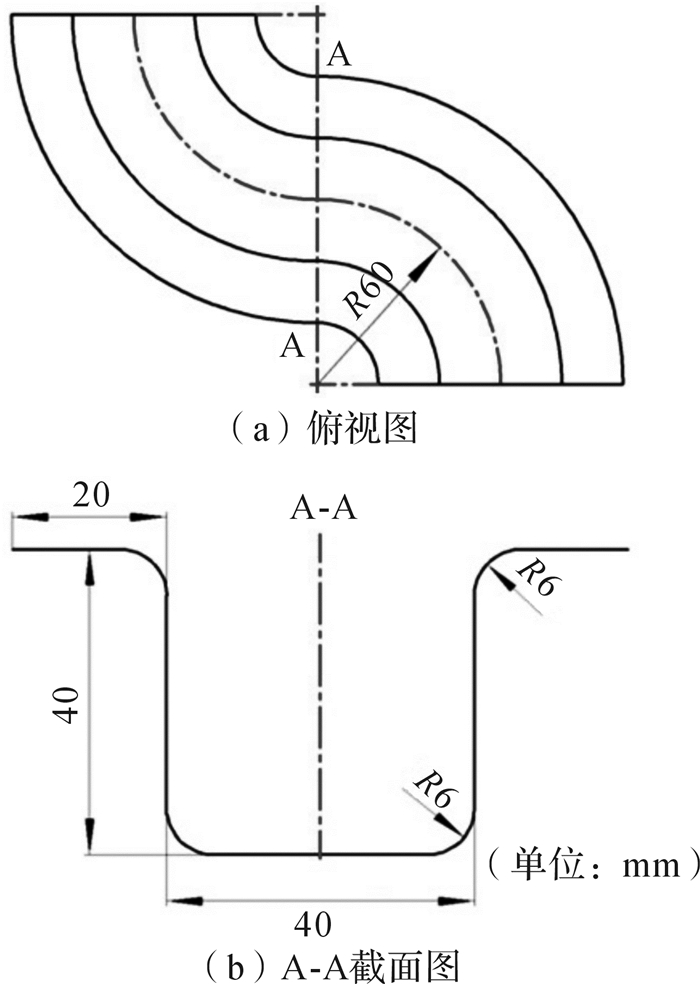
2 双C梁几何尺寸由于S梁类零件结构和形状的特殊性,当梁的两侧拉延很充分时,梁的底端才刚刚进入塑性变形阶段,拉延不够充分,造成零件的各个部位拉延程度不均匀,很容易出现扭曲回弹现象。基于此,设计了双C梁零件,板料厚度为1 mm,具体尺寸如图 1所示。
|
| 图 1 双C梁几何尺寸 Fig.1 The geometric dimensions of the double C rail |
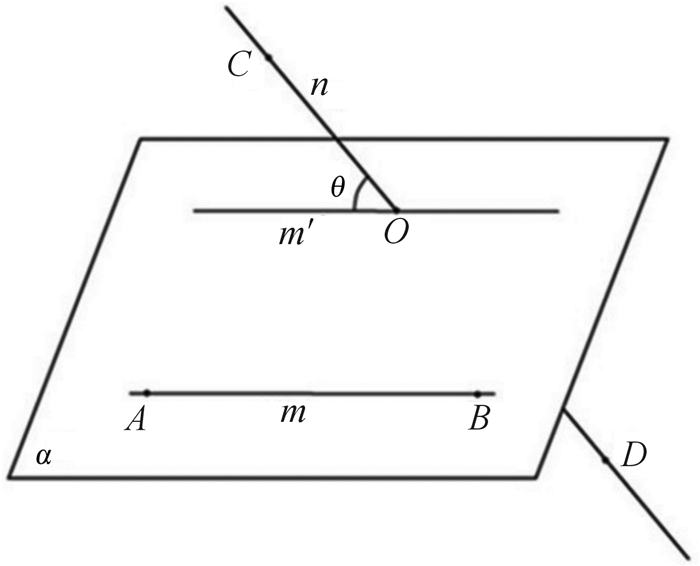
为了对扭曲回弹进行定量分析,需要确定扭曲回弹的评价指标。基于扭曲回弹是三维空间中的变换,提出了三维空间两异面直线夹角作为扭曲回弹的评价指标。如图 2所示,m和n为两异面直线,m′是m的平行线,与n相交于点O,所成夹角θ即为扭曲回弹角。若已知A(x1, y1, z1),B(x2, y2, z2),C(x3, y3, z3),D(x4, y4, z4),则:
|
| 图 2 三维空间两异面直线所成夹角 Fig.2 The angle between two lines in different planes in the three-dimensional space |
| $ \theta = \arccos \left( {\frac{{\mathit{\boldsymbol{AB}} \cdot \mathit{\boldsymbol{CD}}}}{{\left| {\mathit{\boldsymbol{AB}}} \right| \cdot \left| {\mathit{\boldsymbol{CD}}} \right|}}} \right) $ | (11) |
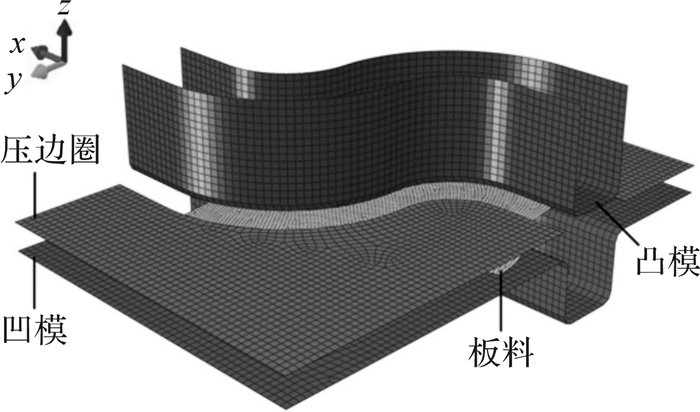
基于双C梁,运用ABAQUS-Explicit (VUMAT)和ABAQUS-Standard (UMAT)对冲压成形和扭曲回弹过程进行仿真模拟。冲压成形过程采用动力显示求解器,扭曲回弹过程采用静力隐式求解器。凸模、凹模和压边圈设置为刚体,板料设置为变形体。所有部件的单元均为壳单元,凸模、凹模和压边圈的单元类型为四结点双线性四边形,板料的单元类型为四节点曲面薄壳。冲压行程为40 mm,压边力为200 kN,摩擦系数为0.2,双C梁有限元模型如图 3所示。
|
| 图 3 双C梁有限元模型 Fig.3 Finite element model of the double C rail |
试验材料为宝山钢铁股份有限公司生产的冷轧TRIP780高强钢板,材料厚度为1 mm,其化学成分由厂家提供,见表 1,材料参数见表 2[14-15]。
| 化学成分 | C | Mn | P | S | Si |
| 质量分数/% | 0.16 | 1.78 | 0.015 | 0.002 | 1.31 |
| 参数 | E/GPa | υ | ρ/(kg/m3) | σs/MPa | σb/MPa |
| 数值 | 207 | 0.3 | 7890 | 442.44 | 786.33 |
试验装置有:YJ32-100A四柱液压机,其公称力为1 000 kN,如图 4(a)所示;Micro 575三坐标测量仪,其规格为X=500 mm,Y= 700 mm,Z=500 mm, 如图 4(b)所示。

|
| 图 4 双C梁扭曲回弹试验装置 Fig.4 The experimental devices of twist springback for the double C rail |
采用线切割方式加工零件坯料,冲压完成后的双C梁零件如图 5所示。

|
| 图 5 冲压成形后的双C梁零件 Fig.5 The double C rail parts after stamping |
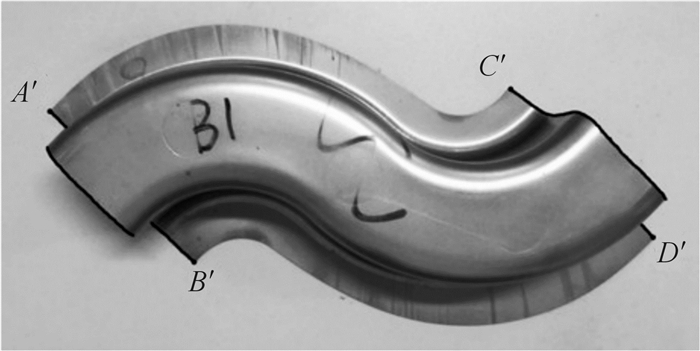
双C梁回弹后,两端扭转程度最大,故采用两端截面线构成的空间夹角作为扭曲回弹评价指标。双C梁测量点位置如图 6所示,A′,B′和C′,D′分别代表双C梁两端截面端点,截面线A′B′与C′D′之间所成空间夹角即为扭曲回弹角。
|
| 图 6 双C梁测量点位置 Fig.6 The position of measuring points for the double C rail |
将冲压成形后的零件按图 6所示划分截面线,采用Micro 575三坐标测量仪测量测量点坐标值,每次试验值测量3次,取其平均值,以减小测量误差。采用式(11)计算扭曲回弹角θ,将9个零件的平均值作为试验结果。9个零件扭曲回弹角的测量值分别为1.685°,1.673°, 1.625°, 1.604°, 1.692°, 1.611°, 1.634°, 1.628°和1.619°,平均测量值为1.641°。
6 混合硬化模型参数反求以混合硬化模型参数b1,b2,c1,c2,Q1,Q2为设计变量,以扭曲回弹角θ作为响应值来表征回弹量的大小,回弹后双C梁应力图如图 7所示。采用Box-Behnken试验设计方法进行六因素三水平模拟试验,共进行54次试验,部分数值模拟试验方案及回弹角如表 3所示。

|
| 图 7 回弹后双C梁应力图 Fig.7 The stress diagram of the double C rail after springback |
| 序号 | 设计变量 | 回弹角 | ||||||
| b1 | b2 | c1/MPa | c2/MPa | Q1/MPa | Q2/MPa | θ/(°) | ||
| 1 | 199 | 4.0 | 21 474 | 591.5 | 393.9 | 315 | 1.742 4 | |
| 2 | 199 | 5.5 | 25 769 | 710.0 | 209.4 | 473 | 1.739 1 | |
| 3 | 199 | 7.0 | 21 474 | 591.5 | 24.9 | 473 | 1.501 3 | |
| 4 | 199 | 4.0 | 17 179 | 591.5 | 393.9 | 394 | 1.749 2 | |
| 5 | 159 | 4.0 | 21 474 | 710.0 | 209.4 | 394 | 1.680 9 | |
| 6 | 159 | 7.0 | 21 474 | 710.0 | 209.4 | 394 | 1.708 7 | |
| 7 | 239 | 7.0 | 21 474 | 473.0 | 209.4 | 394 | 1.576 3 | |
| 8 | 199 | 7.0 | 17 179 | 591.5 | 24.9 | 394 | 1.474 7 | |
| 9 | 239 | 5.5 | 25 769 | 591.5 | 209.4 | 315 | 1.698 4 | |
| 10 | 199 | 7.0 | 21 474 | 591.5 | 393.9 | 315 | 1.748 9 | |
| 11 | 199 | 7.0 | 17 179 | 591.5 | 393.9 | 394 | 1.742 4 | |
| 12 | 239 | 4.0 | 21 474 | 710.0 | 209.4 | 394 | 1.715 6 | |
| 13 | 159 | 5.5 | 21 474 | 710.0 | 393.9 | 394 | 1.762 1 | |
| 14 | 239 | 5.5 | 21 474 | 473.0 | 393.9 | 394 | 1.758 8 | |
| 15 | 199 | 5.5 | 25 769 | 710.0 | 209.4 | 315 | 1.739 1 | |
| 16 | 199 | 5.5 | 25 769 | 473.0 | 209.4 | 315 | 1.670 3 | |
| 17 | 159 | 4.0 | 21 474 | 473.0 | 209.4 | 394 | 1.684 5 | |
| 18 | 199 | 5.5 | 21 474 | 591.5 | 209.4 | 394 | 1.708 8 | |
| 19 | 159 | 7.0 | 21 474 | 473.0 | 209.4 | 394 | 1.698 5 | |
| 20 | 199 | 5.5 | 17 179 | 710.0 | 209.4 | 473 | 1.659 6 | |
| 21 | 239 | 5.5 | 25 769 | 591.5 | 209.4 | 473 | 1.698 4 | |
| 22 | 199 | 7.0 | 25 769 | 591.5 | 24.9 | 394 | 1.501 6 | |
| 23 | 239 | 7.0 | 21 474 | 710.0 | 209.4 | 394 | 1.681 1 | |
| 24 | 159 | 5.5 | 17 179 | 591.5 | 209.4 | 473 | 1.691 6 | |
| 25 | 199 | 5.5 | 17 179 | 473.0 | 209.4 | 473 | 1.663 2 | |
| 26 | 199 | 5.5 | 214 74 | 591.5 | 209.4 | 394 | 1.703 1 | |
| 27 | 239 | 5.5 | 21 474 | 710.0 | 393.9 | 394 | 1.794 0 | |
基于所得样本,建立的响应面模型为:
| $ \begin{array}{l} \theta = 1.941 - 1.005{{\rm{e}}^{ - 3}}{b_1} + 0.029{b_2} - 5.751{{\rm{e}}^{ - 5}}{c_1} - \\ \;\;\;\;\;\;4.348{{\rm{e}}^{ - 4}}{c_2} + 2.691{{\rm{e}}^{ - 4}}{Q_1} + 2.031{{\rm{e}}^{ - 3}}{Q_2} - \\ \;\;\;\;\;\;3.548{{\rm{e}}^{ - 4}}{b_1}{b_2} + 5.155{{\rm{e}}^{ - 5}}{b_2}{c_2} + \\ \;\;\;\;\;\;3.130{{\rm{e}}^{ - 5}}{b_2}{Q_2} - 3.766{{\rm{e}}^{ - 3}}b_2^2 \end{array} $ | (12) |
为了评价响应面模型的可信度,利用决定系数R2和调整系数Radj2对响应面模型进行评估, 其公式如下:
| $ {R^2} = 1 - \left[ {\frac{{{S_{\rm{r}}}}}{{\left( {{S_{\rm{r}}} + {S_{\rm{m}}}} \right)}}} \right] $ | (13) |
| $ R_{{\rm{adj}}}^2 = 1 - \left[ {\left( {\frac{{{S_{\rm{r}}}}}{{{D_{\rm{r}}}}}} \right)/\left( {\frac{{{S_{\rm{r}}} + {S_{\rm{m}}}}}{{{D_{\rm{r}}} + {D_{\rm{m}}}}}} \right)} \right] $ | (14) |
式中:Sr为残差误差平方和,Sm为模型误差平方和,Dr为残差自由度,Dm为模型自由度。
经过计算,决定系数R2=0.982 9,调整系数Radj2=0.965 2,说明预测值与实测值之间具有高度相关性,即上述响应面模型具有较高的可信度。
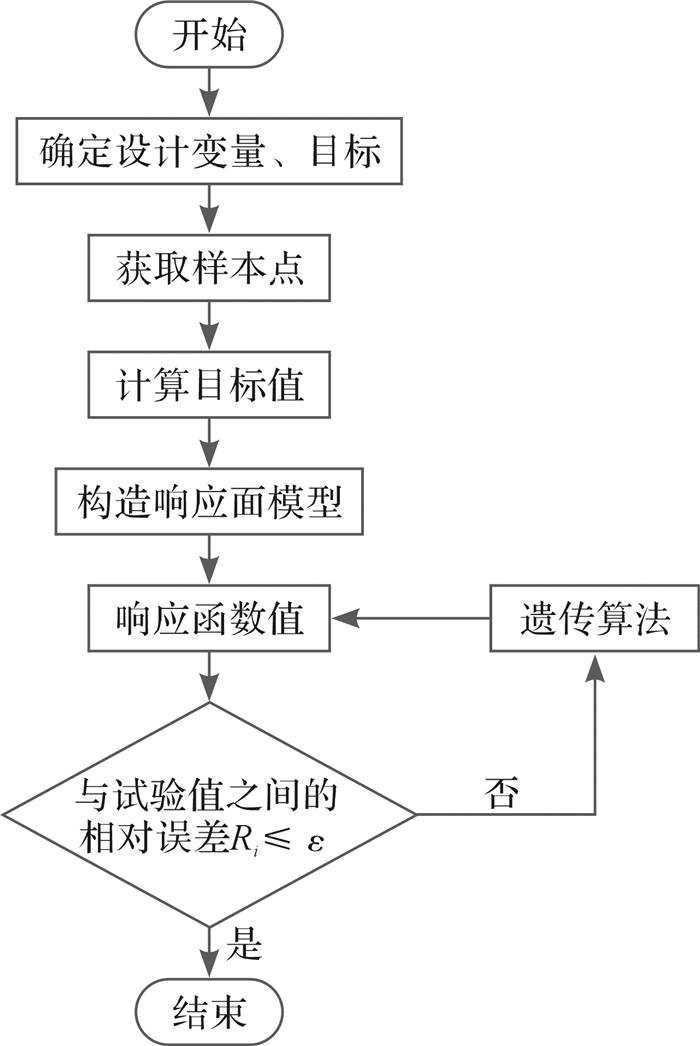
基于上述试验结果,结合响应面模型与遗传算法进行混合硬化模型参数反求,求解过程如图 8所示,硬化模型参数范围如表 4所示,反求所得参数如表 5所示。
|
| 图 8 混合硬化模型参数反求过程 Fig.8 The parameter inversion process of mixed hardening model |
| 参数 | b1 | b2 | c1/MPa | c2/MPa | Q1/MPa | Q2/MPa |
| 数值范围 | 159~239 | 4~7 | 17 179~25 769 | 473~710 | 19~30 | 315~473 |
| 参数 | b1 | b2 | γ1 | γ2 | c1/MPa | c2/MPa | Q1/MPa | Q2/MPa |
| 数值 | 205.63 | 5.196 5 | 205.63 | 5.196 5 | 21 832.3 | 601.46 | 26.145 | 387.34 |
其中,ε为期望误差值(本文取ε=2%),Re是响应值与测量值之间的相对误差,定义如下:
| $ {R_{\rm{e}}} = \frac{{\left| {{u_i} - {u_{\rm{e}}}} \right|}}{{{u_{\rm{e}}}}} \cdot 100\% $ | (15) |
式中:ui表示第i组试验的响应值,ue表示试验平均值。
基于反求所得混合硬化模型参数,结合双C梁有限元模型,利用式(11)计算的扭曲回弹角为1.615°,与试验平均值1.641°的相对误差为1.6%。利用该混合硬化模型参数初始设置[10]建立有限元模型,获得的扭曲回弹角为1.416°,与试验平均值的相对误差为13.7%,表明了有限元模型的准确性。基于反求参数获得的扭曲回弹角更接近于试验测得的扭曲回弹角,证明了反求方法的有效性。
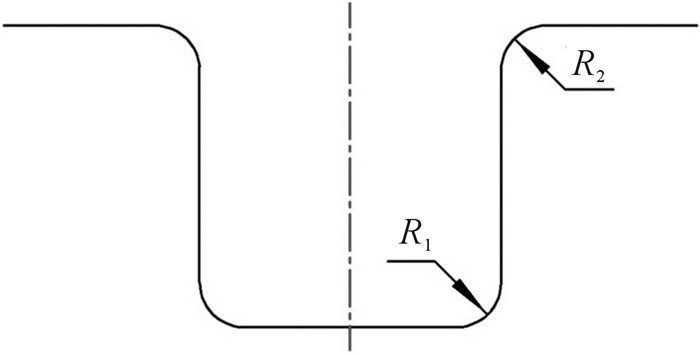
7 扭曲回弹参数分析为了减少试验次数,剔除对扭曲回弹影响较小的因素,基于已验证的双C梁有限元模型,利用正交试验设计方法进行参数分析。选取如图 9所示的凹模圆角半径R1和R2、摩擦系数μ、凸凹模间隙Z、冲压速度v和压边力FN为试验因素,以扭曲回弹角θ作为目标值。试验选用L18(37)正交表,试验因素和水平值如表 6所示,对于各影响因素水平所建立的正交表如表 7所示。
|
| 图 9 凹模圆角半径示意图 Fig.9 The diagrammatic sketch of die radius |
| 因素 | R1/mm | R2/mm | μ | Z/mm | ν/(mm/s) | FN/kN |
| 水平1 | 6 | 6 | 0.1 | 1.1 | 4 | 100 |
| 水平2 | 8 | 8 | 0.2 | 1.2 | 5 | 200 |
| 水平3 | 10 | 10 | 0.3 | 1.3 | 8 | 300 |
| 试验序号 | 试验因子 | 回弹角 | ||||||
| R1/ mm |
R2/ mm |
μ | Z/ mm |
ν/ (mm/s) |
FN/ kN |
θ/ (°) |
||
| 1 | 6 | 6 | 0.1 | 1.1 | 4 | 100 | 1.290 | |
| 2 | 6 | 8 | 0.2 | 1.2 | 5 | 200 | 2.768 | |
| 3 | 6 | 10 | 0.3 | 1.3 | 8 | 300 | 1.003 | |
| 4 | 8 | 6 | 0.1 | 1.2 | 5 | 300 | 1.983 | |
| 5 | 8 | 8 | 0.2 | 1.3 | 8 | 100 | 2.912 | |
| 6 | 8 | 10 | 0.3 | 1.1 | 4 | 200 | 3.220 | |
| 7 | 10 | 6 | 0.2 | 1.1 | 8 | 200 | 1.670 | |
| 8 | 10 | 8 | 0.3 | 1.2 | 4 | 300 | 1.350 | |
| 9 | 10 | 10 | 0.1 | 1.3 | 5 | 100 | 1.850 | |
| 10 | 6 | 6 | 0.3 | 1.3 | 5 | 200 | 2.181 | |
| 11 | 6 | 8 | 0.1 | 1.1 | 8 | 300 | 2.322 | |
| 12 | 6 | 10 | 0.2 | 1.2 | 4 | 100 | 2.433 | |
| 13 | 8 | 6 | 0.2 | 1.3 | 4 | 300 | 2.631 | |
| 14 | 8 | 8 | 0.3 | 1.1 | 5 | 100 | 2.070 | |
| 15 | 8 | 10 | 0.1 | 1.3 | 4 | 200 | 2.862 | |
| 16 | 10 | 6 | 0.3 | 1.2 | 8 | 100 | 1.082 | |
| 17 | 10 | 8 | 0.1 | 1.3 | 4 | 200 | 3.070 | |
| 18 | 10 | 10 | 0.2 | 1.1 | 5 | 300 | 3.183 | |
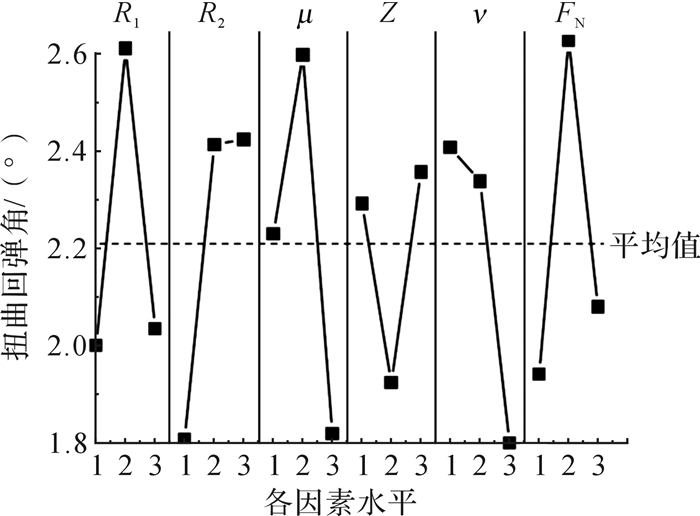
采用极差分析方法对试验结果进行分析,双C梁因素水平对扭曲回弹角的影响如图 10所示。经过计算,R1的极差为0.613,R2的极差为0.619,μ的极差为0.782,Z的极差为0.435,ν的极差为0.610,FN的极差为0.689,对双C梁扭曲回弹影响程度从大到小依次是μ,FN,R2,R1,ν,Z,即对回弹影响较大的因素依次为摩擦系数μ、压边力FN、凹模圆角半径R1和R2。
|
| 图 10 双C梁因素水平对扭曲回弹角的影响 Fig.10 Effect of double C rail factor levels on twistspringback angle |
为了准确反映TRIP780高强钢的变形行为,基于混合硬化模型对双C梁扭曲回弹进行了仿真和试验,得到如下结论:
1) TRIP780高强钢双C梁试验结果表明,冲压成形后会产生明显的扭曲回弹现象。
2) 对双C梁扭曲回弹角进行了测量,利用响应面法结合遗传算法,反求获得了混合硬化模型的参数,分别为:b1=γ1=205.63,b2=γ2=5.196 5,c1=21 832.3 MPa,c2=601.46 MPa, Q1=26.145 MPa,Q2=387.34 MPa。
3) 基于提出的扭曲回弹评价指标,运用极差分析方法对影响扭曲回弹的相关因素进行分析。研究结果表明,对扭曲回弹影响较大的因素依次为:摩擦系数μ、压边力FN、凹模圆角半径R1和R2,为双C梁扭曲回弹的有效控制提供一定的理论依据。
| [1] | PHAM C H, THUILLIER S, MANACH P Y. Twisting analysis of ultra-thin metallic sheets[J]. Journal of Materials Processing Technology, 2014, 214(4): 844–855. DOI:10.1016/j.jmatprotec.2013.12.006 |
| [2] | ABDULLAH A B, SALIT M S, SAMAD Z, et al. Twist springback measurement of autonomous underwater vehicle propeller blade based on profile deviation[J]. American Journal of Applied Sciences, 2013, 10(5): 515–524. DOI:10.3844/ajassp.2013.515.524 |
| [3] | XUE X, LIAO J, VINCZE G, et al. Twist springback characteristics of dual-phase steel sheet after non-axisymmetric deep drawing[J]. International Journal of Material Forming, 2015, 10(2): 267–278. |
| [4] |
谢延敏, 孙新强, 田银, 等.
基于改进粒子群算法和小波神经网络的高强钢扭曲回弹工艺参数优化[J]. 机械工程学报, 2016, 52(19): 162–167.
XIE Yan-min, SUN Xin-qiang, TIAN Yin, et al. Optimization of parameters in twist springback process for high-strength sheets based on improved particle swarm optimization algorithm and neural network[J]. Journal of Mechanical Engineering, 2016, 52(19): 162–167. |
| [5] |
李振友, 朱书华, 周华闯, 等.
基于遗传算法的鸟体本构参数优化研究[J]. 航空计算技术, 2017, 47(1): 47–50.
LI Zhen-you, ZHU Shu-hua, ZHOU Hua-chuang, et al. Parameters optimization on constitutive model of bird based on genetic algorithm[J]. Aeronautical Computing Technique, 2017, 47(1): 47–50. |
| [6] | QU J, JIN Q, XU B. Parameter identification of superplastic constitutive model by GA-based global optimization method[J]. Journal of Mechanical Engineering, 2009, 197(1): 212–220. |
| [7] |
高晖, 郑刚, 李光耀.
基于响应面方法的材料参数反求[J]. 机械工程学报, 2008, 44(8): 102–105.
GAO Hui, ZHENG Gang, LI Guang-yao. Identification of material parameters based on the response surface method[J]. Journal of Mechanical Engineering, 2008, 44(8): 102–105. |
| [8] | MALAKIZADI A, CEDERGREN S, SADIK I, et al. Inverse identification of flow stress in metal cutting process using response surface methodology[J]. Simulation Modelling Practice & Theory, 2016, 60(3): 40–53. |
| [9] | ZHU Y X, LIU Y L, YANG H, et al. Development and application of the material constitutive model in springback prediction of cold-bending[J]. Materials & Design, 2012, 42: 245–258. |
| [10] |
余海燕, 王友.
一种基于Chaboche理论的混合硬化模型及其在回弹仿真中的应用[J]. 机械工程学报, 2015, 51(16): 127–134.
YU Hai-yan, WANG You. A combined hardening model based on Chaboche theory and its application in the springback simulation[J]. Journal of Mechanical Engineering, 2015, 51(16): 127–134. |
| [11] | VOCE E. The relationship between stress and strain for homogeneous deformation[J]. Journal of the Institute Metals, 1948, 74: 537–562. |
| [12] |
姜金朋, 陈涛, 金平, 等.
Chaboche随动硬化模型参数确定及棘轮效应[J]. 北京航空航天大学学报, 2014, 40(10): 1430–1435.
JIANG Jin-peng, CHEN Tao, JIN Ping, et al. Parameter determination of Chaboche kinematic hardening models and ratcheting simulation[J]. Journal of Beijing University of Aeronautice and Astronautics, 2014, 40(10): 1430–1435. |
| [13] | TARIGOPULA V, HOPPERSTAD O S, LANGSETH M, et al. Elastic-plastic behaviour of dual-phase, high-strength steel under strain-path changes[J]. European Journal of Mechanics, 2008, 27(5): 764–782. DOI:10.1016/j.euromechsol.2008.01.002 |
| [14] |
张卿卿, 李大永, 彭颖红, 等.
TRIP780高强度钢板动态力学特性的研究[J]. 塑性工程学报, 2009, 16(6): 6–10.
ZHANG Qing-qing, LI Da-yong, PENG Ying-hong, et al. Research on the dynamic mechanical characteristics of TRIP780 high strength steel sheets[J]. Journal of Plasticity Engineering, 2009, 16(6): 6–10. |
| [15] | GHAEI A, GREEN D E, ARYANPOUR A. Springback simulation of advanced high strength steels considering nonlinear elastic unloading-reloading behavior[J]. Materials & Design, 2015, 88(1): 461–470. |



