2. 武夷学院 生态与资源工程学院, 福建 武夷山 354300
2. College of Ecological and Resources Engineering, Wuyi University, Wuyishan 354300, China
注塑成型是塑料产品批量生产的重要方法,而模具结构是获得高质量塑料产品的关键因素,但即使拥有较高模具制造精度,注塑产品的实际形状、尺寸也会因注塑成型缺陷而出现差异,尤其是外观要求高、内部结构复杂且设置筋板的塑件,筋板成型收缩引起的注塑缺陷常常难以控制,因此如何合理地进行注塑成型工艺设计,在注塑技术中就显得十分重要[1-3]。本文以汽车前立柱饰盖(下文简称“饰盖”)塑件为例,进行筋板结构成型CAE分析及工艺多目标优化,获取多筋板塑件成型特性,期望对类似产品的注塑成型工艺及模具设计提供参考。
1 汽车饰盖塑件筋板设计要点为了满足生产或者结构上的需要,筋板设计需要注意以下几点:1)筋板两边必须加上拔模斜度,以降低脱模推出产品时的摩擦力,但随着拔模斜度不断增加而筋板底部宽度不变时,产品的刚性与强度降低,可顶出面积也会随之减少;2)筋板与产品接触部位必须合理设计圆角,减缓或消除应力集中;3)筋板高度一般不高于产品壁厚的3倍,筋板宽度必须比相接零件的外壁厚度小,通常不超过其相接零件壁厚的80%,因为此处极易产生收缩,导致缩痕、变形翘曲及夹水纹等缺陷的出现。如何将筋板设计准则有效地应用于实际,获得合理的筋板结构参数与模具结构,使塑件在成型过程中,不但可以控制流动收缩,而且能提高塑件刚性,一直是业内学者研究热点。相对于其他注塑成型件,汽车前立柱饰盖塑件装配位置在前排正、副座上方,驾驶者及乘客头部能直接接触到,其不仅外观要求高且性能要求严格,因此前立柱饰盖内侧结构复杂,多为空间曲面,加强筋板多。如果筋板设计太厚,产品就容易出现凹陷痕迹,或导致大收缩率;反之,筋板设计太薄,则必须增加筋板高度以增强刚性,且成型时容易发生翘曲变形,薄筋板还存在模具活动镶件设计加工困难、不利于塑料熔体充填等问题。因此,以汽车前立柱饰盖塑件为例,进行筋板结构及工艺优化设计探讨,具有显著代表性。
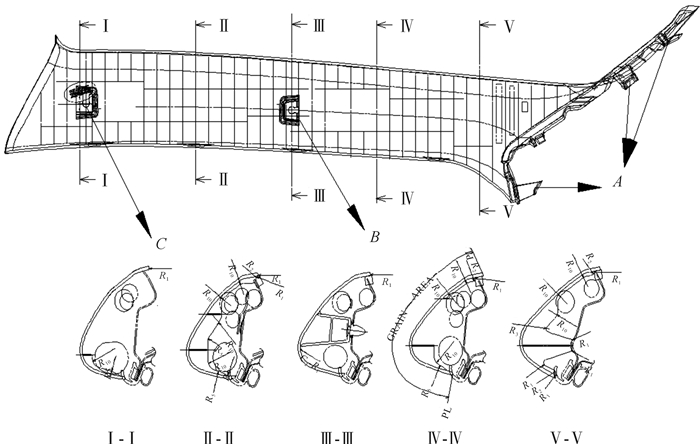
2 饰盖零件结构与工艺图 1为汽车饰盖二维零件图,该零件为弧形曲面长条壳体状,厚度分布均匀,平均壁厚T=2.5 mm,长×宽×高=869 mm×228 mm× 86 mm,根据饰盖使用环境,饰盖设计有合理的筋板结构,要求产品最大翘曲变形量不超过5 mm,表面缩痕不超过0.1 mm,满足饰盖机械性、装配性、美观度等需求。
|
| 图 1 汽车饰盖二维零件图及其特征截面 Fig.1 Two-dimensional parts diagram and characteristic section of automobile trim cover |
从图 1可知饰盖零件有如下工艺特点:1)塑件A处有倒扣,用以连接汽车仪表面板,塑件B与C处设计有2个固定安装支撑柱,且开口方向相反,这些独特结构给模具设计带来了一定的困难;2)为了保证汽车饰盖的结构强度,图中塑件内表面从头到尾平行布置大量筋板,但筋板的存在又极易造成产品的注塑缺陷;3)截面图Ⅰ-Ⅰ, Ⅱ-Ⅱ,Ⅲ-Ⅲ,Ⅳ-Ⅳ,Ⅴ-Ⅴ分别表示Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ处筋板结构形状,图中R1, R2, R5, R10表示筋板各连接处的倒圆角半径,分别为1,2,5,10 mm,另外为了便于产品脱模,筋板的拔模角约为1°。从零件图可以看出该筋板结构复杂,不但不利于冷却水路的排布,而且进一步加剧了塑件的缩痕及翘曲倾向,所以在注塑成型与模具结构设计中,如何调整优化筋板结构及工艺显得特别重要。
饰盖注塑原料为汽车工业常用工程塑料:丙烯腈-丁二烯-苯乙烯共聚合物(ABS),型号为Polylace PA-765B。ABS聚合物每种单体都有不同的特性:丙烯腈具有高强度、热稳定性及化学稳定性;丁二烯具有坚韧性、抗冲击特性;苯乙烯具有易加工、高光洁度及高强度等特性,非常适用于汽车内饰板、仪表板、车轮盖、反光镜等塑件成型[4-5],但ABS材料具有吸湿性,在加工之前必须进行干燥处理,干燥条件:干燥温度为80~90 ℃,干燥时间为2 h。
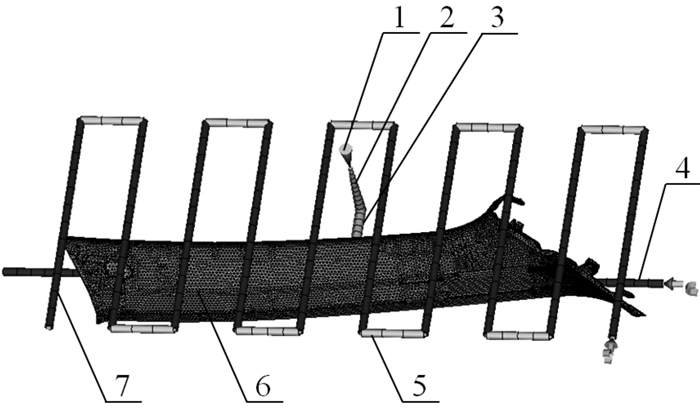
3 汽车饰盖模流分析与优化设计 3.1 有限元模型建立运用UGNX8.0建立汽车饰盖塑件三维模型,并以STL格式导入Moldflow中,通过内建指令对塑件进行表面网格化[6]。为了保证熔体在模具型腔内合理流动,浇口位置的选择尤为重要,其不仅影响塑件的熔接线位置、翘曲变形量等,而且对模具结构设计也有重大影响[7-8]。以往浇口位置设计依赖经验,而Moldflow可以通过有限元分析技术,对每个合适的单元进行分析,极易获取最佳浇口设置区域,汽车饰盖数值模拟分析系统如图 2所示,模拟时采用侧浇口边缘进料方式。由于饰盖塑件内部存在筋板、倒扣以及支撑柱,为了降低模具设计制造的成本,选用一模两腔的布局,同时为了提高模流分析效率,只构建一个塑件的有限元分析系统,但MPI(moldflow plastics insight)分析时出现次数设置为2。
|
| 1—注射口;2—主流道;3—分流道;4—动模水路;5—水路连接管;6—塑件;7—定模水路 图 2 汽车饰盖数值模拟分析系统 Fig.2 Numerical simulation analysis system of automobile cover |
成型工艺条件的选择不仅影响产品的生产率,而且对产品成型质量起关键作用,本文根据模流软件推荐与实际经验相结合的办法,选用熔体温度为230 ℃,模具温度为60 ℃,采用恒定保压方式,保压压力取最大注射压力值的80%,保压冷却后产品顶出温度为90 ℃,冷却时间为30 s,在填充体积达98%时切换速度和压力。
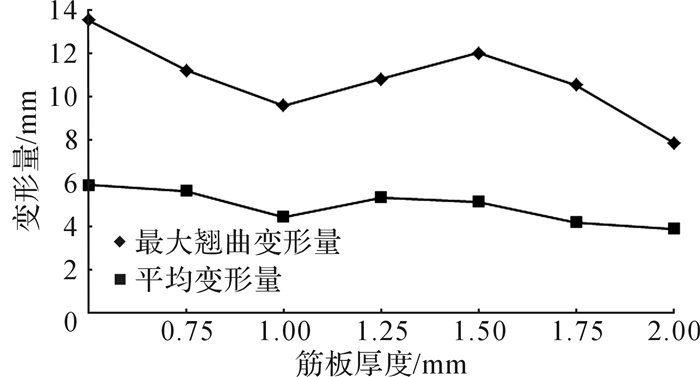
3.2 筋板厚度优化设计图 3为筋板壁厚变化对饰盖翘曲变形的影响,由于筋板厚度不允许超过产品自身壁厚,在此筋板厚度t取值范围为0~2 mm。图 3中, 不同筋板厚度所对应的产品最大翘曲变形量分别为13.55,11.22,9.609,10.84,12.02,10.55和7.888 mm,平均变形量分别为5.927,5.648,4.457,5.356,5.164,4.198和3.904 mm。由图 3可知饰盖的最大翘曲变形量随着筋板厚度变化而变化的幅度较大,而平均变形量曲线明显平缓许多,此外饰盖的翘曲变形量并不与筋板厚度变化呈正相关。当饰盖不设计筋板时,即t=0 mm,饰盖最大变形量为13.55 mm,为曲线最高点;当饰盖设计筋板时,即t=2 mm时,饰盖最大变形量获得最小值,为7.888 mm,但是筋板厚度太大势必引起较大的缩痕。
|
| 图 3 筋板厚度变化对饰盖翘曲变形影响 Fig.3 Effect of the stiffener panels thickness variation on the warpage distortion of decorative cover |
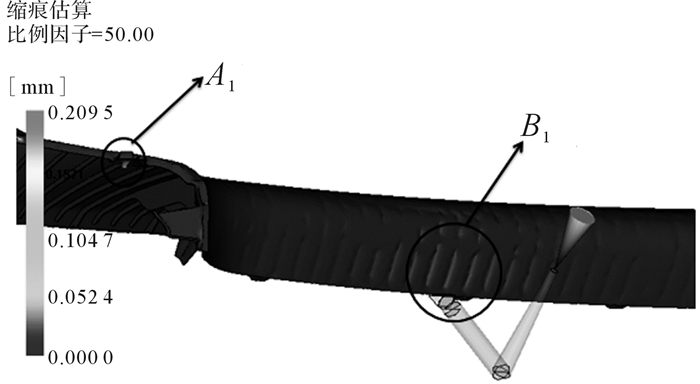
图 4为筋板厚度为2 mm时放大50倍后的饰盖缩痕估算模拟分析结果。图 4中A1处为饰盖装配卡扣部分,最大卡扣壁厚达到4 mm,因此A1处存在最大块状缩痕,深度约为0.2 mm,但卡扣为装配部分,其并不影响外观;图 4中B1处存在较大的条状缩痕,深度约为0.1 mm,对于存在0.1 mm深度缩痕的车内外观塑件,在阳光反射作用下有非常明显的缺陷,必须采取一定的措施进行改善。
|
| 图 4 筋板厚度t=2 mm时饰盖缩痕估算模拟分析结果(放大50倍) Fig.4 Sink mark estimation simulation result of trim cover when thickness of rib plate t=2 mm (enlarge 50 times) |
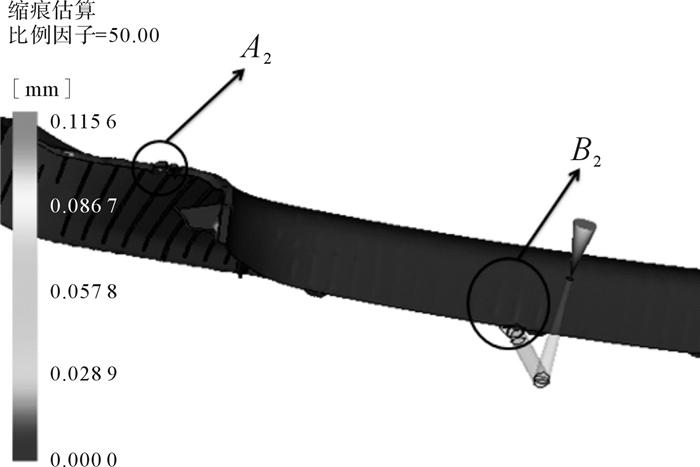
图 5为筋板厚度为1 mm时放大50倍后的饰盖缩痕估算模拟分析结果。图 5中A2处同样为最大缩痕所在区域,深度约为0.11 mm,较图 4有明显好转,更重要的是饰盖表面的条状缩痕有了很大的改善,即B2处的深度由0.2 mm下降为0.02 mm,若对塑件表面进行适当处理,则难以发觉饰盖缩痕,因此饰盖零件筋板厚度应优选为1 mm,此时饰盖最大翘曲变形量为9.609 mm,平均变形量为4.457 mm,虽然产品缩痕满足要求,但其翘曲变形量仍较大。
|
| 图 5 筋板厚度t=1 mm时饰盖缩痕估算模拟分析结果(放大50倍) Fig.5 Sink mark estimation simulation result of trim cover when thickness of rib plate t=1 mm (enlarge 50 times) |
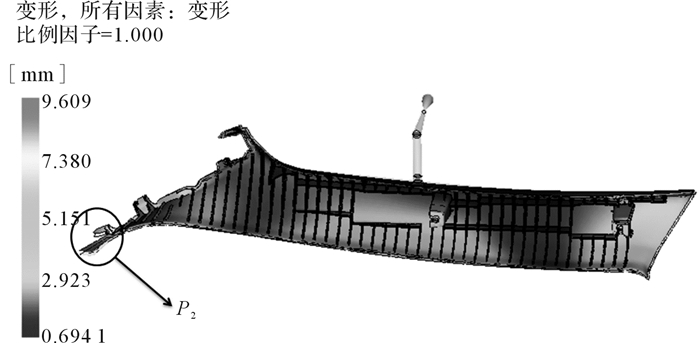
图 6为无筋板饰盖翘曲变形量分布图,图 7为筋板厚度t=1 mm的饰盖翘曲变形量分布图。比较图 6与图 7不难发现,增加筋板后饰盖的变形量整体下降不少,最大翘曲变形量由13.55 mm下降至9.609 mm,下降幅度约为30%,另外从图中颜色深浅变化也可察觉到,图 7低变形量的区域明显高于图 6,且图 7中饰盖大部分变形量都在5 mm以下,符合产品变形量不高于5 mm的要求,但是饰盖安装末端长条尖角处,即图 6的P1处和图 7的P2处,无论是否增加筋板,且无论筋板厚度如何选择,此处总是产品的薄弱环节,存在的变形量超出了技术要求。由文献[9-10]可知,成型工艺参数的优化对改善注塑件产品的翘曲变形有帮助,尤其是保压方式的选择,因此需要进一步探讨成型条件变化对饰盖成型质量的影响。

|
| 图 6 无筋板饰盖翘曲变形量分布图(t=0 mm) Fig.6 Warping deformation distribution of decorative cover without stifferer panel(t=0 mm) |
|
| 图 7 有筋板饰盖翘曲变形量分布图(t=1 mm) Fig.7 Warping deformation distribution of decorative cover with stifferer panel(t=1 mm) |
参考综合平衡法[11],以饰盖翘曲变形量和模具内壁面温度分布均匀性为优化目标,以熔体温度、模具温度、保压压力、冷却时间为控制因子,前两因子水平值在材料库推荐范围内均匀选取,后两因子水平值由流动、保压及冷却模拟分析确定,进行四因素三水平的正交试验,选用的正交表为L9(34),最后确定控制因子水平如下:熔体温度为230,240和250 ℃;模具温度为45,60和75 ℃;保压压力(定义为注射压力的百分比)为75%,80%,85%,注射压力为108 MPa;冷却时间为20,25和30 s。
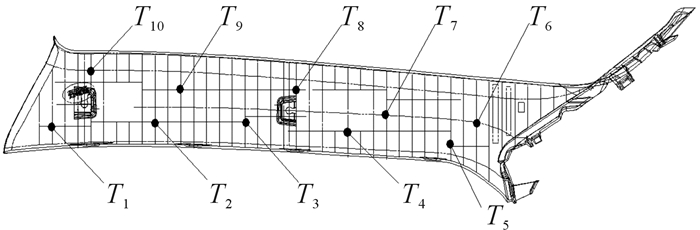
优化目标中的模壁温度分布均匀性,以标准偏差的方式,作为评估控制因子对模具型腔壁面温度分布均匀性的影响,首先定义T1, T2, T3, …,Tn表示模具型腔壁面温度样本点,如图 8中T1, …,T10所示,则其样本偏差定义如下:
| $ {S^2} = \frac{{\sum\limits_{i = 1}^n {{{\left( {{T_i} - \bar T} \right)}^2}} }}{n} $ | (1) |
|
| 图 8 型腔壁面温度样本点 Fig.8 Temperature sample point of cavity wall |
式中:S表示样本标准偏差;T表示样本平均值,
| $ \bar T = \frac{{\sum\limits_{i = 1}^n {{T_i}} }}{n} $ | (2) |
由式(1)、式(2)可知,所求得的标准偏差较小时,代表成型得到的型腔壁面温度分布比较接近型腔壁面温度的平均温度值;相反地,标准偏差较大时,代表成型得到的型腔壁面温度偏离型腔壁面的平均温度。换句话说,标准偏差较大的成型工艺设计,容易导致型腔壁面温度变化较大,甚至会导致产品不能均匀冷却,或者无法达到成型冷却模具目标温度,而标准偏差较小的成型工艺设计,能够使型腔壁面温度变化幅度小,使产品能够以均匀化的温度冷却,降低注塑缺陷的发生概率,达到优化设计目标。
如果正交实验结果为多指标,各指标之间可能存在一定的矛盾,这时需要兼顾各个指标,寻找使得每个指标都尽可能达到最优的生产工艺条件[11]。针对汽车饰盖成型工艺特点,运用多指标处理方法中的综合平衡法,通过对正交实验中极差和方差结果的分析,获知当筋板厚度t=1 mm,熔体温度为240 ℃,模具温度为60 ℃,保压压力取注射压力值的80%,冷却时间为25 s时,饰盖模具壁面温度整体上分布均匀,温度集中于55~59 ℃之间,并且饰盖的翘曲变形量较小, 为7.158 mm,相较于9.609 mm减小约25%,有了较大改善,但仍未满足最大翘曲变形量小于5 mm的要求。
3.3.2 基于Fibonacci保压优化通过参考文献[12-13]获悉,在注塑机上设定的保压阶段参数,通常采用单一恒定保压方式,此种做法虽然简单但是保压后的产品效果不佳,造成能源消耗高,同时又无法降低不均匀收缩率,不利于改善塑件翘曲变形。因为模具型腔内的压力变化很大程度上受保压时间与保压压力的作用,保压方式的优化以及保压时间的调整会直接影响最终成型品的收缩率及其分布。常见保压参数优化方法有响应曲面法、遗传算法、BP神经网络算法等[14-17],这些方法一般是将设计变量代入相关方程后,自动迭代计算出最终的结果数据,但是其必须依靠大量数学方程式进行计算,而斐波那契法(Fibonacci)不需要过多的数学方程式,每一次迭代的结果可以通过模流软件进行分析计算,在优化方向架构不变的前提下,简化了方程式设计和实验过程,更加接近实际工程应用。本文运用斐波那契法对饰盖保压过程进行分段压降调整,获取较理想的保压曲线,寻找合适的保压相关参数,从而降低饰盖翘曲变形量。
Fibonacci数列在当代许多工业领域都得到了应用[18],运用斐波那契法可以搜寻出函数的最小值,此法同其他许多方法一样,有如下条件限制:1)一开始不确定的初始迭代必须是已知的;2)使用单峰描述函数的优化迭代;3)只有在得知最终迭代函数后,才可以得到最优解,在不确定最终迭代区间间距时,若能使迭代间距越小则越接近优化值,则需要计算次数越多。目前注塑机只能设置4段保压压降,第1阶段保压压力保持不变,仍为注射压力的80%,后面三阶段运用斐波那契法进行优化调整,各阶段的压降幅度为:
| $ {p_n} = 80 - \left( {80 - 2} \right)\frac{{n \times {x_i}}}{{100}}, n = 0, 1, 2, 3 $ | (3) |
式中:xi表示切割点的位置;pn表示压降幅度;n为压力分段数。
斐波那契优化实验基于计算以及模流分析,先取一组原始保压参数作为实验的原始数据,优化过程中计算每一个阶段所取得的2组实验数据,模流分析比较饰盖的翘曲变形量,保留理想组别,并设定为新的边界,再取另一组实验数据,依照选择搜寻范围,重复计算分析。
以综合平衡法获取的工艺参数进行模流初分析,获知饰盖注射充填时间为2.20 s,产品末端冷却凝固时间约为4.20 s,近浇口冷却凝固时间约为16.20 s,所需注射压力值为108.5 MPa,保压压力为注射压力的80%,保压时间为14.00 s。优化实验仅对保压压力及时间进行调整,所以将其他几个关键的模流参数设置为定值。现将保压过程分为2个部分:第1部分设定为恒压,保压压力为注射压力的80%,保压时间为2.20~4.20 s;第2部分设定为三段阶梯式降压,保压时间为4.20~16.20 s,各阶段分配时间分别为4.20~8.20,8.20~12.20和12.20~16.20 s,以饰盖最大翘曲变形量为优化目标,通过斐波那契优化方法,寻找压降最优组合。
已知注塑机压力分段数为4,实验目标为求出9个切割点xi,所以取斐波那契数列第10项开始优化计算,根据Fibonacci数列[19]取Fn=89,Fn-2=34,数列边界条件设计如下:
| $ {W_0} = {L_0} \times \left( {{F_{n - 2}}/{F_n}} \right) $ | (4) |
式中:W0为初始迭代,并以a≤x≤b为限制条件,a,b为边界范围值;L0为搜寻范围长度。
因为压力不能为负,所以当n=3时,需要限制式(4)中L0的搜寻长度,令L0≤33.33,可以求出第1次迭代时的x1=12.73,以及x2=20.60。再将x1和x2分别代入公式(3)求出2组压力组合值,并舍去变形量较大的一组,重新根据公式(4)定义边界进行下一次迭代分析。第1次迭代获得2组压降组合如下:
| $ \begin{array}{l} {P_{x1}} = \left( {{P_0}, {P_1}, {P_2}, {P_3}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {80.00\%, 70.06\%, 60.14\%, 50.21\% } \right)\\ {P_{x2}} = \left( {{P_0}, {P_1}, {P_2}, {P_3}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {80.00\%, 63.93\%, 47.87\%, 31.80\% } \right) \end{array} $ |
然后将百分比转化为压力值,用Pn′表示保压压力值,用yn表示翘曲变形值,如下:
| $ \begin{array}{l} {P_{x1}}^\prime = \left( {{P_0}^\prime, {P_1}^\prime, {P_2}^\prime, {P_3}^\prime } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {86.60, 76.01, 65.25, 54.48} \right){\rm{ MPa}}, \\ {y_1} = 7.888\ {\rm{ mm}}\\ {P_{x2}}^\prime = \left( {{P_0}^\prime, {P_1}^\prime, {P_2}^\prime, {P_3}^\prime } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {86.60, 69.36, 51.93, 34.50} \right){\rm{ MPa}}, \\ {y_2} = 7.145\ {\rm{ mm}} \end{array} $ |
保留翘曲变形量较小的压力组合Px2′。
以此类推重复计算,共进行8次迭代,第8次优化迭代计算结果如下:
| $ \begin{array}{l} {P_{x9}}^\prime = \left( {{P_0}^\prime, {P_1}^\prime, {P_2}^\prime, {P_3}^\prime } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {86.60, 81.41, 76.02, 70.63} \right){\rm{MPa}}, \\ {y_9} = 4.482\ {\rm{ mm}}\\ {P_{x7}}^\prime = \left( {{P_0}^\prime, {P_1}^\prime, {P_2}^\prime, {P_3}^\prime } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left( {86.60, 81.09, 75.37, 69.66} \right){\rm{ MPa}}, \\ {y_7} = 4.502\ {\rm{ mm}} \end{array} $ |
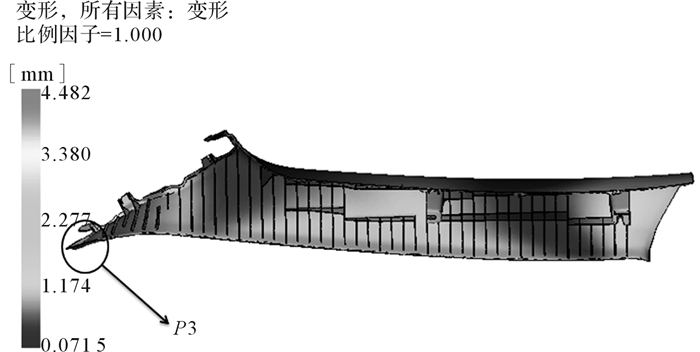
优化演算到第8次迭代时,发现演算结果已经收敛,保留获得最小翘曲变形量的压力组合Px9′,可得保压压力的最优组合为86.60,81.41,76.02和70.63 MPa,此时平均收缩率可以控制得最为理想,获得的饰盖最大翘曲变形量为4.482 mm。虽然两分割点中间还有一段间距,但其变形量变化已经很微小,约为0.02 mm,再切割的效益不大。图 9为优化后饰盖翘曲变形量分布图,P3处变形量仍为最大,但与保压优化前比较,变形量下降幅度高达37%,已经限制在产品要求范围内,且其他表面平均变形量不到2 mm,完全满足汽车饰盖外观以及装配性能需求。将优化结果应用于实际生产,发现确实可以降低产品变形量。
|
| 图 9 优化后饰盖翘曲变形量分布图(t=1 mm) Fig.9 Warpage deformation of the optimized decorative cover(t=1 mm) |
汽车饰盖塑件外观质量要求高且含内部筋板等结构复杂,导致缩痕、翘曲变形等注塑缺陷难以控制,本研究基于CAD/CAE技术,运用多目标成型工艺参数优化方法,开展饰盖成型工艺优化的分析探讨,获得如下结论:
1) 利用Moldflow模流分析软件,模拟筋板壁厚尺寸变化对成型质量的影响,获知筋板厚度的选择对饰盖翘曲变形量影响显著,但不呈正相关,其中较大的筋板厚度引起饰盖外表面的缩痕明显,当筋板厚度取1 mm时,饰盖表面缩痕达到最小值(0.02 mm),但饰盖最大翘曲变形量仍欠佳。
2) 运用综合平衡法对饰盖注塑成型参数进行多目标优化,发现当熔体温度为240 ℃、模具温度为60 ℃、保压压力取注射压力值的80%、冷却时间为25 s时,饰盖最大翘曲变形量下降约25%,饰盖的翘曲变形量为7.158 mm,进一步运用斐波那契法进行分段保压优化,通过8次迭代演算符合收敛,获取了理想的保压参数,最大变形量继续下降约37%,最终饰盖翘曲变形量为4.482 mm,满足产品技术要求。
| [1] | HAKIMIAN E, SULONG A B. Analysis of warpage and shrinkage properties of injection-molded micro gears polymer composites using numerical simulations assisted by the Taguchi method[J]. Materials and Design, 2012, 42: 22–24. |
| [2] |
冯刚, 张朝阁, 江平, 等.
我国注塑模具关键技术的研究与应用进展[J]. 塑料工业, 2014, 42(4): 16–19.
FENG Gang, ZHANG Chao-ge, JIANG Ping, et al. Progress in research and application of key technology of injection mold in China[J]. China Plastics Industry, 2014, 42(4): 16–19. |
| [3] |
钱欣, 金杨福.
塑料注射制品缺陷与CAE分析[M]. 北京: 化学工业出版社, 2010: 6-8.
QIAN Xin, JIN Yang-fu. Defects and CAE analysis of plastic injection products[M]. Beijing: Chemical Industry Press, 2010: 6-8. |
| [4] |
王金水, 魏爱思, 杨大成, 等.
基于Moldflow的汽车外饰件成型缺陷分析与优化设计[J]. 中国塑料, 2016, 30(4): 102–108.
WANG Jin-shui, WEI Ai-si, YANG Da-cheng, et al. Analysis of molding defects and optimization design for automotive exterior parts based on Moldflow[J]. China Plastics, 2016, 30(4): 102–108. |
| [5] |
樊新民, 车剑飞.
工程塑料及其应用[M]. 北京: 机械工业出版社, 2016: 78-80.
FAN Xin-min, CHE Jian-fei. Engineering plastics and application[M]. Beijing: China Machine Press, 2016: 78-80. |
| [6] |
张建卿.
汽车暖风机下壳体CAE优化与模具设计[J]. 工程塑料应用, 2016, 44(5): 65–69.
ZHANG Jian-qing. Mould design and CAE optimization for automobile heater under-shell[J]. Engineering Plastics Application, 2016, 44(5): 65–69. |
| [7] |
段贤勇, 韩忠冠, 张新建, 等.
仪表前壳注塑模具设计[J]. 塑料工业, 2016, 44(10): 46–49.
DUAN Xian-yong, HAN Zhong-guan, ZHANG Xin-jian, et al. Design of injection mold for the front case of the instrument[J]. China Plastics Industry, 2016, 44(10): 46–49. DOI:10.3969/j.issn.1005-5770.2016.10.012 |
| [8] |
程美.
基于Moldflow的汽车盒体件注塑模具设计[J]. 中国塑料, 2016, 30(2): 104–108.
CHENG Mei. Injection mold design of auto parts based on Moldflow[J]. China Plastics, 2016, 30(2): 104–108. |
| [9] | CELLERE A, LUCCHETTA G. Identification of trims model parameters for warpage prediction in injection moulding simulation[J]. International Journal of Material Forming, 2010, 3(1): 37–40. |
| [10] |
孙健华, 顾海, 张捷, 等.
基于CAE和DOE技术的薄壁塑件翘曲变形分析及优化[J]. 计算机辅助工程, 2017, 26(3): 40–43.
SUN Jian-hua, GU Hai, ZHANG Jie, et al. Analysis and optimization of warpage of thin-wall plastic parts based on CAE and DOE technology[J]. Computer Aided Engineering, 2017, 26(3): 40–43. |
| [11] |
林权.
基于综合平衡法的注塑工艺参数多目标优化设计[J]. 塑料科技, 2011, 39(1): 84–88.
LIN Quan. Optimized design of injection molding processing parameters for multi-object based on integral balance method[J]. Plastics Science and Technology, 2011, 39(1): 84–88. |
| [12] |
张德强, 张琰, 孟小鑫, 等.
基于Moldflow的保压曲线优化方法研究[J]. 辽宁工业大学学报(自然科学版), 2015, 35(1): 37–40.
ZHANG De-qiang, ZHANG Yan, MENG Xiao-xin, et al. Packing curve optimization methods based on Moldflow[J]. Journal of Liaoning University of Technology (Natural Science Edition), 2015, 35(1): 37–40. |
| [13] | SHOKRI Parvin, BHATNAGAR Naresh. Effect of packing pressure on fiber orientation in injection molding of fiber-reinforced thermoplastics[J]. Polymer Composites, 2007, 28(2): 214–223. DOI:10.1002/(ISSN)1548-0569 |
| [14] |
符宇, 孙玲.
基于响应面法的汽车轮眉注塑工艺优化[J]. 塑料, 2015, 44(5): 43–46.
FU Yu, SUN Ling. Process optimization for car wheel trims based on response surface method[J]. Plastics, 2015, 44(5): 43–46. |
| [15] |
孙宝寿, 吴真繁, 陈哲, 等.
响应面法与遗传算法相结合的注塑工艺优化[J]. 中国机械工程, 2010, 21(9): 1115–1118.
SUN Bao-shou, WU Zhen-fan, CHEN Zhe, et al. Process parameter optimization of injection molding by combining RSM/GA method[J]. China Mechanical Engineering, 2010, 21(9): 1115–1118. |
| [16] |
李瑞娟, 黄力.
基于BP神经网络的汽车内饰面板注塑成型工艺参数优化[J]. 塑料, 2016, 45(3): 81–85.
LI Rui-juan, HUANG Li. Optimization of injection molding process for automotive interior panel based on BP neural network[J]. Plastics, 2016, 45(3): 81–85. |
| [17] |
李昆, 赵刚.
基于神经网络与遗传算法的短纤维复合材料注塑成型参数优化研究[J]. 南昌航空大学学报(自然科学版), 2017, 31(2): 39–43.
LI Kun, ZHAO Gang. Parameters optimization of short fiber-reinforced composites injection molding by the combining neural network and genetic algorithm[J]. Journal of Nanchang Hangkong University(Natural Sciences), 2017, 31(2): 39–43. |
| [18] |
张广华, 于洲春.
斐波那契数列与电路分析[J]. 电气电子教学学报, 2013, 35(6): 30–33.
ZHANG Guang-hua, YU Zhou-chun. Fibonacci series and circuit analysis[J]. Journal of Electrical & Electronic Education, 2013, 35(6): 30–33. |
| [19] |
吴振奎.
斐波那契数列欣赏[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012: 14-18.
WU Zhen-kui. Fibonacci appreciation[M]. Harbin: Harbin Institute of Technology Press, 2012: 14-18. |


