作为一种非爆炸性震源,可控震源克服了传统爆炸震源的诸多缺点,具有可控性强、环保经济、安全高效等优点, 其已经成为地震勘探的主要装备,在地震勘探中被广泛运用[1-2]。随着地震勘探精度要求的提高,对可控震源激发频率宽度和输出信号精度的要求越来越高,而可控震源振动器平板作为能量传递的媒介,其性能决定着可控震源输出信号的品质,因此受到了国内外学者和工程技术人员的广泛关注。Hall通过试验发现提高振动器平板的刚度可以改善可控震源在中高频段输出信号的品质[3]。Wei等建立了振动器平板与大地耦合的有限元模型,研究了平板与大地耦合性质对可控震源性能的影响[4-5]。丁志淦对比分析了不同结构振动器平板的特点和性能,为平板的结构设计提出了建议[6]。庄娟等推导了高频可控震源动力学方程,分析了平板面积、平板质量和土介质密度对可控震源输出信号幅频特性的影响[7]。马磊等应用矩阵束法对振动器平板模态进行了分析并探讨了平板结构改进的方法[8-9]。上述文献主要研究了平板的宏观特性及其与输出信号之间的关系,而缺乏微观及定量的分析。
此外,目前国内外学者对平板性能的研究主要集中在单一频率下,然而可控震源的激发信号是一段频率随时间线性增加的正弦扫描信号,在实际工作中,平板在不同扫描频率下的响应性能存在差异。平板响应差异的存在影响了振动器在全频段响应性能的稳定性,制约了可控震源向宽频和高精度的发展。因此,为了掌握平板在不同扫描频率下的响应变化规律,并找到响应差异产生的原因,为平板的结构设计提供指导,有必要开展平板多频响应分析。
以KZ-28型可控震源振动器平板为研究对象,基于有限元法的基本理论研究了振动器平板在不同扫描频率下的响应性能,同时通过分析平板加速度、变形和接触力三者间的关系,揭示平板在不同频率下存在响应差异的根本原因。
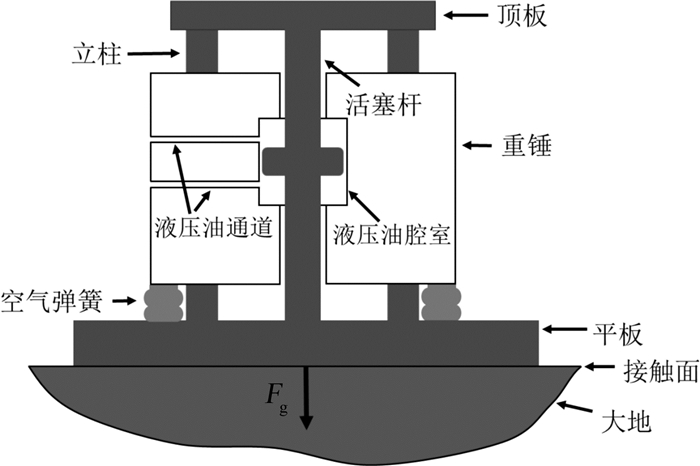
1 可控震源振动器输出力模型如图 1所示,KZ-28型可控震源振动器主要由顶板、重锤、活塞杆、立柱以及平板组成。可控震源在工作过程中,振动器平板与大地紧密贴合传递振动输出力。同时震源系统利用输出力作为反馈控制系统的输入信号,振动器的实际输出力不能直接测量,通常利用加权和法计算得到[10]。
|
| 图 1 KZ-28型可控震源振动器结构示意图 Fig.1 The structure schematic of KZ-28 vibroseis vibrator |
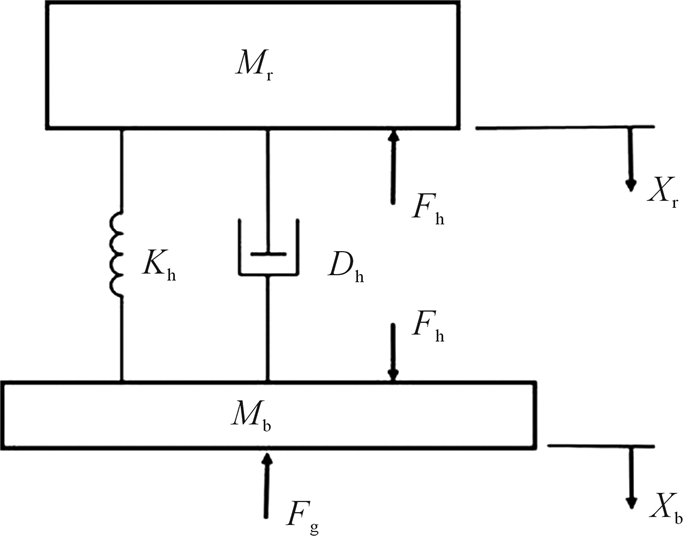
图 2所示为振动器输出力模型,振动器被简化为质量-弹簧-阻尼系统,假设重锤和平板为刚体,平板与大地紧密耦合,由力平衡方程得:
| $ - {F_{\rm{h}}} = {M_{\rm{r}}}{\ddot X_{\rm{r}}} + {D_{\rm{h}}}\left( {{{\dot X}_{\rm{r}}} - {{\dot X}_{\rm{b}}}} \right) + {K_{\rm{h}}}\left( {{X_{\rm{r}}} - {X_{\rm{b}}}} \right) $ | (1) |
| $ - {F_{\rm{h}}} - {F_{\rm{g}}} = {M_{\rm{b}}}{{\ddot X}_{\rm{b}}} + {D_{\rm{h}}}\left( {{{\dot X}_{\rm{r}}} - {{\dot X}_{\rm{b}}}} \right) + {K_{\rm{h}}}\left( {{X_{\rm{r}}} - {X_{\rm{b}}}} \right) $ | (2) |
|
| 图 2 振动器输出力模型 Fig.2 The output force model of vibrator |
联立式(1)和式(2)得:
| $ - {F_{\rm{g}}} = {M_{\rm{r}}}{{\ddot X}_{\rm{r}}} + {M_{\rm{b}}}{{\ddot X}_{\rm{b}}} $ | (3) |
式中:Xr为重锤的位移;Xb为平板的位移;Fh为液压油产生的液压力;Fg为振动器输出力;Mr为重锤的质量;Mb为平板的质量;Kh为液压油的弹性系数;Dh为液压油的阻尼。
由式(3)可以看出,振动器的输出力可以通过测量重锤和平板的加速度后计算得到。然而在实际工作中,平板的响应随着频率的变化而改变,平板的加速度往往难以准确测量,从而造成输出力控制失准,影响可控震源输出信号的精度。因此掌握平板在不同频率下的响应规律,是提高平板加速度测量准确性、实现可控震源输出力准确控制的关键。
2 基于有限元法的平板多频响应仿真分析 2.1 有限元仿真模型的建立根据KZ-28型可控震源振动器的实际结构建立比例为1:1的有限元仿真模型。为了真实地模拟振动器的工作状态,同时尽可能缩短求解时间,对振动器结构作相应的简化[11-12]:1)简化振动器重锤,将重锤的重量作为静态载荷加载到平板上,同时将液压力直接加载到活塞杆上;2)在网格划分时,振动器的倒角和倒圆可能导致网格单元过小或翘曲度过高,故省略倒角和倒圆。为了模拟振动器平板与大地之间的相互作用,建立合理的大地模型,并利用LS-DYNA软件的无反射边界条件模拟大地无限大的效果[13-15]。平板与大地之间的接触定义为面面自动接触。由于在振动器工作过程中,振动器和大地的变形均处于弹性变形阶段,故将大地与振动器模型材料设置为弹性材料。振动器平板用16Mn钢,振动器其余部分材料为45钢,大地模型材料选用混凝土,具体材料参数如表 1所示。
| 材料 | 密度/(kg/m3) | 弹性模量/Pa | 泊松比 |
| 16Mn | 7 850 | 2.12×1011 | 0.310 |
| 45钢 | 7 890 | 2.09×1011 | 0.269 |
| 混凝土 | 2 600 | 5.50×1010 | 0.270 |
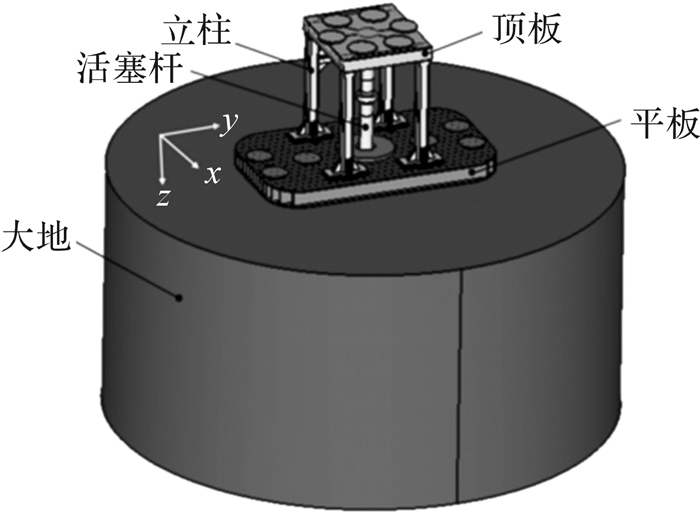
振动器在工作过程中同时受到静态载荷和动态载荷的作用,其中静态载荷为震源车身和简化后重锤的重量,动态载荷为周期性的液压力,如图 3所示。静态载荷作为压重使平板与大地紧密贴合,动态载荷为振动器的激振力,有限元分析过程中通过改变动态载荷的频率来实现多个频率下平板动力学特性的分析。为了获得稳定的响应,动态载荷加载时间为5个周期,动态载荷曲线如图 4所示。图 5为完整的振动器有限元仿真模型。

|
| 图 3 振动器工作过程中载荷加载位置示意图 Fig.3 Schematic of loading position of vibrator in working process |

|
| 图 4 振动器动态载荷曲线 Fig.4 The dynamic loading curve of vibrator |
|
| 图 5 振动器有限元仿真模型 Fig.5 The finite element simulation model of vibrator |
KZ-28型可控震源的扫描频率范围为5~120 Hz,为了分析平板在低频、中频、高频三个频段中的动力学响应,选取5,20,40,50,80,100,120 Hz等频率进行分析。由于载荷加载初期系统不稳定,截取系统稳定后(3个周期)各个频率下的数据进行分析。
2.2.1 平板加速度从振动器输出力计算公式可以看出,振动器的输出力与平板加速度密切相关,而输出力计算的准确性是震源系统反馈控制的关键,直接影响系统的控制精度,因此有必要分析不同频率下平板加速度变化规律。不同频率下平板的加速度曲线如图 6所示。

|
| 图 6 不同频率下振动器平板的加速度曲线 Fig.6 The acceleration curve of vibrator baseplate under different frequencies |
对比分析不同频率下平板的加速度曲线可知,平板的加速度随着动态载荷频率的增加而增大。在低频段,平板的加速度变化具有周期性。进入中高频段后,平板的加速度曲线变得无序,不利于平板加速度的准确测量。因此,随着频率的增加,正确计算振动输出力的难度增大,可控震源的可控性减弱,震源输出信号的品质降低。这就是导致可控震源随着频率升高控制精度降低的直接原因。
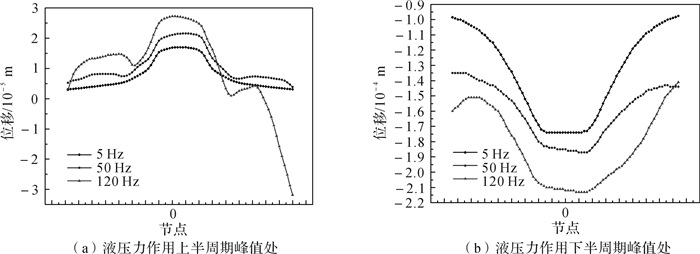
2.2.2 平板变形由于平板并非刚体,其在振动器工作过程中会产生变形,造成平板与大地之间脱耦,降低振动器能量传递效率,从而影响振动器性能,因此需要分析不同频率下平板的变形情况。提取不同频率下平板底部变形云图,如图 7所示。通过分析平板底部变形云图可以看出,随着频率的增加,平板底部中心的变形与四周的变形差异越来越明显,平板变形趋于不均匀,尤其是沿X轴方向,平板的变形随着频率的增加出现明显的不对称。为了进一步分析平板底部沿X轴方向变形的不对称程度,提取平板底部中心沿X轴方向各节点在液压力作用上半周期和下半周期峰值处的位移,并绘出节点-位移曲线,如图 8所示。

|
| 图 7 不同频率下振动器平板底部变形云图 Fig.7 The deformation contour of vibrator baseplate under different frequencies |
|
| 图 8 平板底部沿X轴方向各节点位移曲线 Fig.8 The displacement curve of the nodes at the bottom of the baseplate along the X-axis direction |
从图 8可以看出:1)随着频率的增加,平板底部沿X轴方向变形的不对称程度增大。5 Hz时平板底部沿X轴方向的位移曲线基本对称,50 Hz时平板位移曲线出现不对称,120 Hz时曲线明显不对称。2)平板底部沿X轴方向变形的不对称程度在液压力作用上半周期比液压力作用下半周期严重,而平板在液压力作用上半周期向大地传递振动输出力,平板变形的不对称会降低平板与大地接触的均匀性,降低振动器能量传递效率。
图 8中节点0代表平板底部中心点,从图中可以看出,随着频率的增加,平板底部中心的变形增大。在液压力作用上半周期,平板底部中心是平板与大地接触的主要部分,平板底部中心部分变形过大将导致平板四周的翘曲,引起平板四周与大地的脱耦,影响振动输出和能量传递。在液压力作用下半周期,平板中心部分变形过大会加剧平板底部中心与大地的脱耦,会造成平板与大地间的冲击,引起信号干扰,影响振动器输出信号的品质。
2.2.3 平板与大地的接触力平板与大地之间的接触力即是平板向大地的输出力,反映了振动器实际输出力的情况。提取不同频率下平板与大地的接触力,如图 9所示。

|
| 图 9 不同频率下平板与大地的接触力曲线 Fig.9 The curve of contact force between the baseplate and ground under different frequencies |
对比分析不同频率下平板与大地的接触力曲线可知,随着频率的增加,平板与大地的接触力峰值增大,即平板的输出力增大。同时,通过不同频率下平板接触力曲线波形的变化可知:随着频率的增加,输出力信号的畸变越来越严重,尤其在高频段,输出力波形几乎不再具有正弦波的形态。为了更加直观地分析输出力波形的畸变,利用傅里叶变换,得到接触力曲线的频谱图,如图 10所示。

|
| 图 10 平板与大地的接触力曲线频谱图 Fig.10 The curve spectrum of contact force between the baseplate and ground |
由图 10可知,接触力在5 Hz时频域响应仅在激振频率处有峰值,50 Hz时频域响应在激振频率的整数倍频率处也有峰值,但峰值均比较低,说明输出信号存在畸变,但畸变并不算严重。而120 Hz时频域响应不仅在激振频率的整数倍频率处有较大的峰值,在非整数倍频率处也有较低的峰值,说明此时输出信号的畸变严重且导致畸变信号的成分也比较复杂。产生畸变的原因在于:随着频率的增加,平板的低刚度导致的平板与大地接触的非线性对振动输出力的影响越来越明显,使得输出力波形中出现了明显的谐波成分。因此,在高频段,振动器输出力信号精度低,这是制约可控震源向宽频发展的重要原因。
综上所述,通过分析不同频率下平板加速度、变形以及接触力的变化规律可以看出,随着频率的增加,平板的响应性能越来越不稳定,准确测量加速度的难度增大,平板与大地接触非线性对输出信号品质的影响越来越显著,导致可控震源输出信号不可控。同时,在中高频段平板变形较低频段急剧增大,这必将影响振动器的输出力,而现有的振动器输出力模型是在假设平板为刚体的情况下推导出的,因此其只适用于低频段。
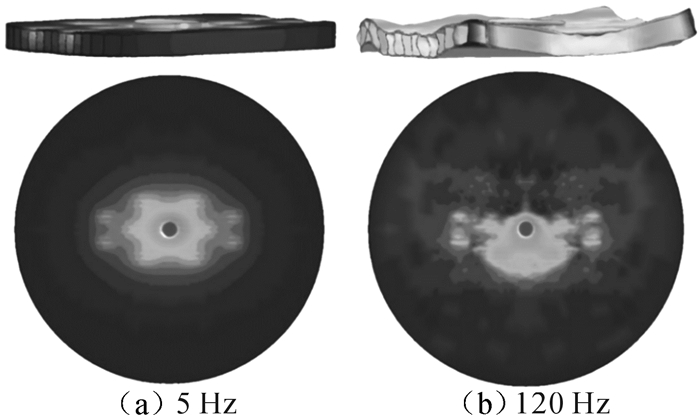
3 平板响应差异原因分析通过上述分析可知,平板的加速度、变形以及接触力随着扫描信号频率的改变而表现出明显的差异性。同时,这三者的动态响应性能是相互影响。平板与大地之间接触力的改变会影响平板的加速度,而平板变形的差异又是影响平板与大地之间接触力的关键因素。如图 11所示,在相同的放大倍数下观察平板和大地在液压力作用上半周期时的最大变形可知,在低频段,平板的变形比较均匀,变形后平板与大地的接触也相对均匀。而到了高频段,平板的变形不再均匀,造成了平板与大地接触的非线性,导致了载荷集中,从而影响了平板与大地之间的接触力。
|
| 图 11 平板和大地变形图(放大4 000倍) Fig.11 The deformation of baseplate and ground (enlarge 4 000 times) |
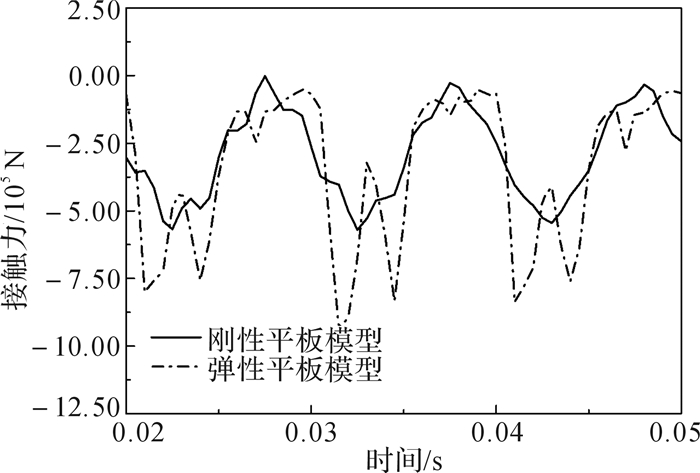
为了验证上述推测,建立刚体平板模型,提取其在120 Hz频率下的接触力曲线, 与弹性模型平板接触力曲线进行对比,如图 12所示。由图可知,频率为120 Hz时,平板与大地之间接触力曲线基本维持了正弦波形的形态,畸变明显减小,与弹性平板模型接触力曲线相比其接触力峰值也有所减小。这说明平板的刚度不足是造成平板在不同频率下响应性能产生差异的根本原因。因此,设计高刚度平板是提高平板响应稳定性,提高振动器在高频段输出信号精度,拓宽可控震源激发频率宽度的有效措施。
|
| 图 12 刚性平板模型与弹性平板模型接触力曲线对比 Fig.12 Comparison of contact force curve between rigid pad model and original pad model |
本文以KZ-28型可控震源振动器平板为研究对象,利用有限元法的基本理论研究了振动器平板在不同频率下的动力学特性和响应性能,揭示了平板在不同频率下产生响应差异的根本原因,得到如下结论:
1) 平板的加速度随着扫描频率的增加而增大,高频段平板加速度曲线混乱无序,导致平板加速度测量准确性降低,影响可控震源系统输出信号控制精度。
2) 随着扫描频率的增加,平板的变形增大。在液压力作用上半周期,平板变形增大会引起平板与大地脱耦,降低平板与大地接触均匀性,影响振动输出力。在液压力作用下半周期,平板变形增大将造成平板底部中心与大地脱耦加剧,引起平板与大地间的冲击,影响输出信号的品质。
3) 随着扫描频率的增加,平板与大地接触力峰值增大,输出力信号的畸变越来越严重,振动器输出信号的精度降低,同时震源系统的控制难度增加。
4) 通过分析可知,由于振动器输出力计算公式在推导过程中未考虑平板变形对输出力的影响,其存在局限性,只适用于低频段。
5) 通过分析平板加速度、变形及接触力之间的关系,找到了产生平板响应差异的根本原因在于平板的刚度不足,并建立刚性平板模型验证了结论的正确性。因此在设计平板时,应尽量提高平板的刚度,减小平板的响应差异对输出信号品质的影响。
| [1] |
刘金中, 马铁荣.
可控震源的发展状况[J]. 石油科技论坛, 2008, 27(5): 38–42.
LIU Jin-zhong, MA Tie-rong. Development of the vibroseis[J]. Oil Forum, 2008, 27(5): 38–42. |
| [2] |
佟训乾, 林君, 姜弢, 等.
陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912–1921.
TONG Xun-qian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Progress in Geophysics, 2012, 27(5): 1912–1921. DOI:10.6038/j.issn.1004-2903.2012.05.011 |
| [3] | HALL M. Analysis of field tests with an improved hydraulic vibrator[C]//SEG Technical Program Expanded Abstracts 2009. Katras:Society of Exploration Geophysicists, 2009:104-108. |
| [4] | WEI Z, PHILLIPS T F, HALL M A. Fundamental discussions on seismic vibrators[J]. Geophysics, 2010, 75(6): W13–W25. DOI:10.1190/1.3509162 |
| [5] | WEI Z. How good is the weighted-sum estimate of the vibrator ground force?[J]. Leading Edge, 2009, 28(8): 960. DOI:10.1190/1.3192844 |
| [6] |
丁志淦.
可控震源振动平板的探讨[J]. 物探装备, 1998(4): 36–38.
DING Zhi-gan. Discussion on seismic vibration vibrator[J]. Equipment for Geophysical Prospecting, 1998(4): 36–38. |
| [7] |
庄娟, 林君, 吴东江, 等.
高频可控震源与大地振动耦合过程幅频特性分析[J]. 吉林大学学报(地球科学版), 1999, 29(2): 184–187.
ZHUANG Juan, LIN Jun, WU Dong-jiang, et al. Analyzing coupling process of the earth-high frequency vibrator[J]. Journal of Jilin University (Earth Science Edition), 1999, 29(2): 184–187. |
| [8] |
马磊, 赵永林, 王洪涛.
矩阵束方法在可控震源振动平板模态分析中的应用[J]. 物探装备, 2011, 21(5): 285–288.
MA Lei, ZHAO Yong-lin, WANG Hong-tao. Application of matrix pencil method for modal analysis on seismic vibrator[J]. Equipment for Geophysical Prospecting, 2011, 21(5): 285–288. |
| [9] |
马磊, 季颖, 夏鹏翎.
可控震源振动平板设计的研究探讨[J]. 物探装备, 2015, 25(5): 297–301.
MA Lei, JI Ying, XIA Peng-ling. Discussion for vibration baseplate of seismic vibroseis[J]. Equipment for Geophysical Prospecting, 2015, 25(5): 297–301. |
| [10] | SALLAS J J. Seismic vibrator control and the downgoing P-wave[J]. SEG Technical Program Expanded Abstracts, 1984, 1(1): 732–740. |
| [11] |
杜平安.
有限元网格划分的基本原则[J]. 机械设计与制造, 2000(1): 34–36.
DU Ping-an. Fundamental principles of finite element meshing[J]. Machinery Design & Manufacture, 2000(1): 34–36. |
| [12] |
熊珍兵, 罗会信.
基于HyperMesh的有限元前处理技术[J]. 排灌机械工程学报, 2006, 24(3): 35–38.
XIONG Zhen-bing, LUO Hui-xin. Preprocessing technology of FEA based on HyperMesh software[J]. Drainage and Irrigation Machinery, 2006, 24(3): 35–38. |
| [13] | WEI Z H, PHILLIPS T F. Characterizing the vibrator captured ground mass system using finite element analyses[C]//SEG Technical Program Expanded Abstracts 2013, Katras:Society of Exploration Geophysicists, 2013:126-130. |
| [14] |
白金泽.
LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005: 37-47.
BAI Jin-ze. LS-DYNA3D theory foundation and the example analysis[M]. Beijing: Science Press, 2005: 37-47. |
| [15] |
李裕春, 时党勇, 赵远.
ANSYS 11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008: 20-29.
LI Yu-chun, SHI Dang-yong, ZHAO Yuan. Basic theory and engineering practice of ANSYS 11.0/LS-DYNA[M]. Beijing: China Water & Power Press, 2008: 20-29. |


