结构的损伤通常首先表现为结构裂纹的出现,进而在外荷载的长期作用下发生扩展,裂纹的扩展往往会导致重大灾难事故的发生。为保证结构的安全性和可靠性,国内外学者提出了许多结构损伤检测方法[1-4],如声发射、射线检测、漏磁检测等。结构上出现的裂纹会引起结构局部柔度的变化,局部柔度可以用裂纹柔度来描述。裂纹柔度随着裂纹的发生和扩展而发生变化,其能有效地反映结构损伤的程度,在结构损伤检测方面具有重要的理论和工程意义。
目前,常用的裂纹模拟模型有基于等效降截面法的裂纹模型[5]、基于一致裂纹梁原理的裂纹模型[6-7]与基于局部柔度的裂纹模型[8-15]。其中,基于局部柔度的裂纹模型采用断裂力学的应变能理论分析裂纹柔度变化的机理,因其理论性强、物理意义明确而被广泛应用。Zheng等[8]使用高斯积分法计算了在纯弯矩作用下含横向裂纹的矩形截面梁结构的局部柔度系数。Chasalevris等[9]研究了含裂纹方向角的圆形截面轴的局部柔度计算方法。胡家顺等[10]通过研究裂纹管结构在轴力、剪力和弯矩耦合作用下的局部柔度理论,建立了管类结构的裂纹分析模型,并进行了裂纹管的振动特性分析。Lee[11]基于局部柔度法建立了多裂纹悬臂梁结构的有限元计算模型并且讨论了多裂纹的识别方法。Han等[12]给出了椭圆裂纹圆轴受拉伸、弯曲作用时的裂纹结构局部柔度。刘文光等[13]利用建立裂纹结构局部柔度模型来探讨裂纹界面接触对弹性梁振动特性的影响。Attar等[14]结合局部柔度法分析了处于弹性地基上含裂纹的Timoshenko梁的自由振动特性。Liu等[15]建立了含有水平内埋裂纹的悬臂梁模型,分析了裂纹柔度对结构前3阶固有频率和振型的影响。这些研究大多集中在裂纹柔度的求解问题上。由于结构的复杂性,通过计算所得的裂纹柔度往往与实际工况存在一定误差,因此,对更准确的裂纹柔度测量方法的研究具有重要意义。针对矩形截面梁结构的裂纹柔度问题,本文讨论了一种基于固有频率的测量方法。该方法适用于矩形梁中不同类型和形状裂纹的柔度测量,可以有效地提高测量的准确性。
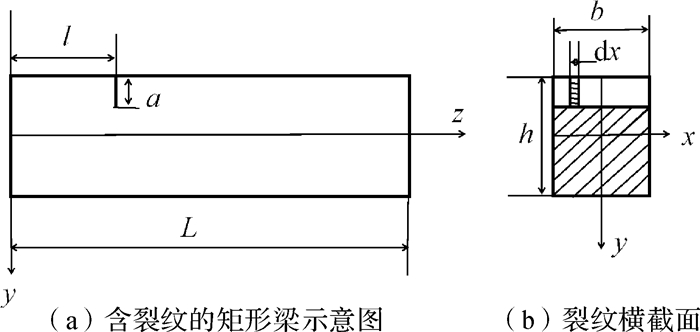
1 矩形梁裂纹动力学模型的建立如图 1所示,梁的总长为L,以梁的左端为坐标原点,裂纹位于l处且深度为a。
|
| 图 1 矩形梁裂纹模型 Fig.1 Crack model of the rectangular beam |
无裂纹梁的横向自由振动方程为[16]:
| $ {q^2}\frac{{{\partial ^4}w\left( {z,t} \right)}}{{\partial {z^4}}} + \frac{{{\partial ^2}w\left( {z,t} \right)}}{{\partial {t^2}}} = 0 $ | (1) |
式中:
裂纹梁的横向自由振动方程为:
| $ {q^2}\frac{{{\partial ^4}{w_1}\left( {z,t} \right)}}{{\partial {z^4}}} + \frac{{{\partial ^2}{w_1}\left( {z,t} \right)}}{{\partial {t^2}}} = 0,0 \le z \le l $ | (2) |
| $ {q^2}\frac{{{\partial ^4}{w_2}\left( {z,t} \right)}}{{\partial {z^4}}} + \frac{{{\partial ^2}{w_2}\left( {z,t} \right)}}{{\partial {t^2}}} = 0,l \le z \le L $ | (3) |
式中:w1(z, t)表示裂纹左侧梁的挠度,z∈[0, l];w2(z, t)表示裂纹右侧梁的挠度,z∈[l, L]。
设裂纹梁的横向自由振动方程的解为:
| $ {w_1}\left( {z,t} \right) = {W_1}\left( z \right)\sin \left( {\omega t + \varphi } \right),0 \le z \le l $ | (4) |
| $ {w_2}\left( {z,t} \right) = {W_2}\left( z \right)\sin \left( {\omega t + \varphi } \right),l \le z \le L $ | (5) |
式中:W1(z)为裂纹左侧梁的固有振型函数;W2(z)为裂纹右侧梁的固有振型函数;ω为结构的固有频率;φ为初相位。
裂纹连接处的边界条件为[17]:
| $ \left\{ \begin{array}{l} {W_1}\left( z \right) = {W_2}\left( z \right)\\ \frac{{{{\rm{d}}^2}{W_1}\left( z \right)}}{{{\rm{d}}{z^2}}} = \frac{{{{\rm{d}}^2}{W_2}\left( z \right)}}{{{\rm{d}}{z^2}}}\\ \frac{{{{\rm{d}}^3}{W_1}\left( z \right)}}{{{\rm{d}}{z^3}}} = \frac{{{{\rm{d}}^3}{W_2}\left( z \right)}}{{{\rm{d}}{z^3}}}\\ \frac{{{\rm{d}}{W_1}\left( z \right)}}{{{\rm{d}}z}} + cEI\frac{{{{\rm{d}}^2}{W_1}\left( z \right)}}{{{\rm{d}}{z^2}}} - \frac{{{\rm{d}}{W_2}\left( z \right)}}{{{\rm{d}}z}} = 0\\ z = l \end{array} \right. $ | (6) |
式中c为裂纹柔度。
假设含横向裂纹的梁结构两端受到弯矩M作用,裂纹横截面如图 1(b)所示,则裂纹结构的应变能为[18]:
| $ U = \iint\limits_\mathit{\Omega } {J{\rm{d}}y{\rm{d}}x} $ | (7) |
式中J指应变能密度函数。
| $ J = \frac{{1 - {v^2}}}{E}K_{\rm{I}}^2 $ | (8) |
式中:v为泊松比;E为杨氏弹性模量;KI为Ⅰ型裂纹应力强度因子[19]。
| $ {K_{\rm{I}}} = \sigma \sqrt {{\rm{ \mathsf{ π} }}y} {F_2}\left( {y/h} \right) $ | (9) |
式中:
根据卡氏第二定理,U对于某一载荷的变化率就等于该载荷相应的位移,故有:
| $ \delta = \partial U/\partial M $ | (10) |
式中δ为与M相应的位移。
δ对M进行求导,可得到裂纹柔度c:
| $ c = \frac{{{\partial ^2}U}}{{{\partial ^2}M}} = \frac{{72{\rm{ \mathsf{ π} }}}}{{E'{b^2}{h^4}}}\iint\limits_\mathit{\Omega } {yF_2^2\left( {y/h} \right){\rm{d}}y{\rm{d}}x} $ | (11) |
其中E′=E/(1-v2)。
2 固有频率与裂纹柔度的关系如图 2所示,为了描述由裂纹引起的结构局部柔度的变化,将裂纹等效为无质量的扭转线弹簧,扭转线弹簧的柔度可以表示裂纹柔度。根据裂纹处的连接条件,弹簧两侧的挠度值相等,转角可以通过裂纹单元的刚度矩阵Ke相连接。在利用有限元方法建立模型时,裂纹单元质量矩阵为零,裂纹单元刚度矩阵Ke可以由裂纹柔度求得:
| $ {\mathit{\boldsymbol{K}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {1/c}&{ - 1/c}\\ { - 1/c}&{1/c} \end{array}} \right] $ | (12) |

|
| 图 2 Crack model of the rectangular beam Fig.2 The model of torsion line spring of the cracked beam |
将裂纹梁无裂纹部分的单元刚度矩阵、质量矩阵以及裂纹部分的单元刚度矩阵进行组装,从而获得系统的总刚度阵K和总质量阵M。梁的振动特征方程为:
| $ \left| {\mathit{\boldsymbol{K}}\left( {c,\beta } \right) - \omega _i^2\mathit{\boldsymbol{M}}} \right| = 0 $ | (13) |
式中:ωi为结构固有频率;β为裂纹相对位置。
式(13)也可以表示为以下形式:
| $ {\omega _i} = F\left( {c,\beta } \right),i = 1,2,3 $ | (14) |
式(14)可看作是在函数关系式F已知情况下,通过裂纹参数c和β求解结构的固有频率ωi。
在获得对应于裂纹柔度和位置的结构固有频率之后,可以建立根据梁的固有频率来求解裂纹柔度以及裂纹位置的关系式,该关系式可以表示如下:
| $ \left( {c,\beta } \right) = {F^{ - 1}}\left( {{\omega _i}} \right),i = 1,2,3 $ | (15) |
因此,在函数关系F-1(ωi)已知的条件下,可以求解出任意一个固有频率值所对应的裂纹位置和裂纹柔度。由于一个固有频率值对应着多个裂纹位置和裂纹柔度,为了准确确定裂纹位置和裂纹柔度,常常使用多个振动固有频率。又因为结构的前几阶固有频率测量方便且精度较高,因此在实际工程中,通常选用结构的前3阶固有频率。
根据式(13)至式(15),能够建立一种基于固有频率的矩形梁裂纹柔度测量方法,步骤如下:
1) 在裂纹位置和裂纹柔度的取值范围内分别选取一系列的样本点;
2) 步骤1)中获得的样本点作为式(13)的输入参数,求解对应于不同裂纹位置和裂纹柔度的固有频率数据库;
3) 将固有频率数据库拟合成以裂纹位置和裂纹柔度作为自变量的固有频率影响曲面;
4) 对结构进行振动测试,获得前3阶固有频率;
5) 采用获得的结构前3阶固有频率去截取固有频率影响曲面,绘制出对应于裂纹柔度和裂纹位置的前3阶频率影响曲线,根据3条影响曲线的交点(或3个交点所形成的三角形的形心)可以得到裂纹柔度以及相应的裂纹位置。
从测量过程看到,求解固有频率数据库的输入参数是一系列包含裂纹位置和裂纹柔度的样本点,并没有涉及裂纹的类型、形状以及裂纹柔度的计算公式。因此,这种方法适用于矩形截面梁中不同类型和形状裂纹的柔度测量。
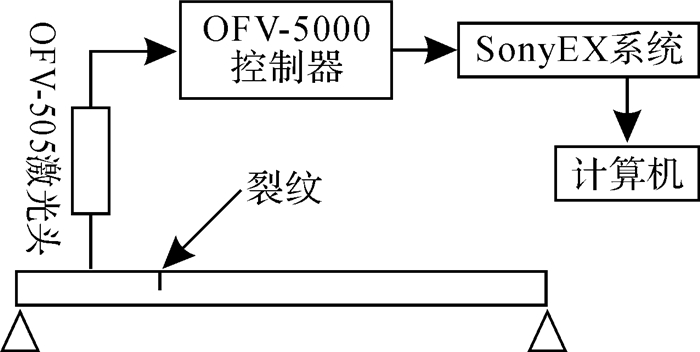
3 实验研究为了验证算法的有效性,搭建了测量裂纹柔度的试验台,测量原理如图 3所示。梁两端简支,长度L=0.4 m,宽度b=0.012 m,高度h=0.02 m,裂纹位于l处且深度为a,相对位置β=l/L,相对深度α=a/h,杨氏弹性模量E=1.738 1×1011N/m2,泊松比v=0.3,材料密度ρ=7 348.9 kg/m3。裂纹采用数控线切割机加工而成,切缝宽度为0.02 mm。裂纹类型和形状如图 1(b)所示。
|
| 图 3 裂纹柔度试验台测试原理图 Fig.3 Measuring principle chart of crack flexibility test-bed |
不同工况下裂纹的位置、深度及柔度如表 1所示,表中的c为根据式(11)计算的裂纹柔度值。
| 工况 | β | α | c/(10-5rad/Nm) |
| Ⅰ | 0.2 | 0.3 | 1.23 |
| Ⅱ | 0.2 | 0.4 | 2.40 |
| Ⅲ | 0.3 | 0.3 | 1.23 |
| Ⅳ | 0.3 | 0.4 | 2.40 |
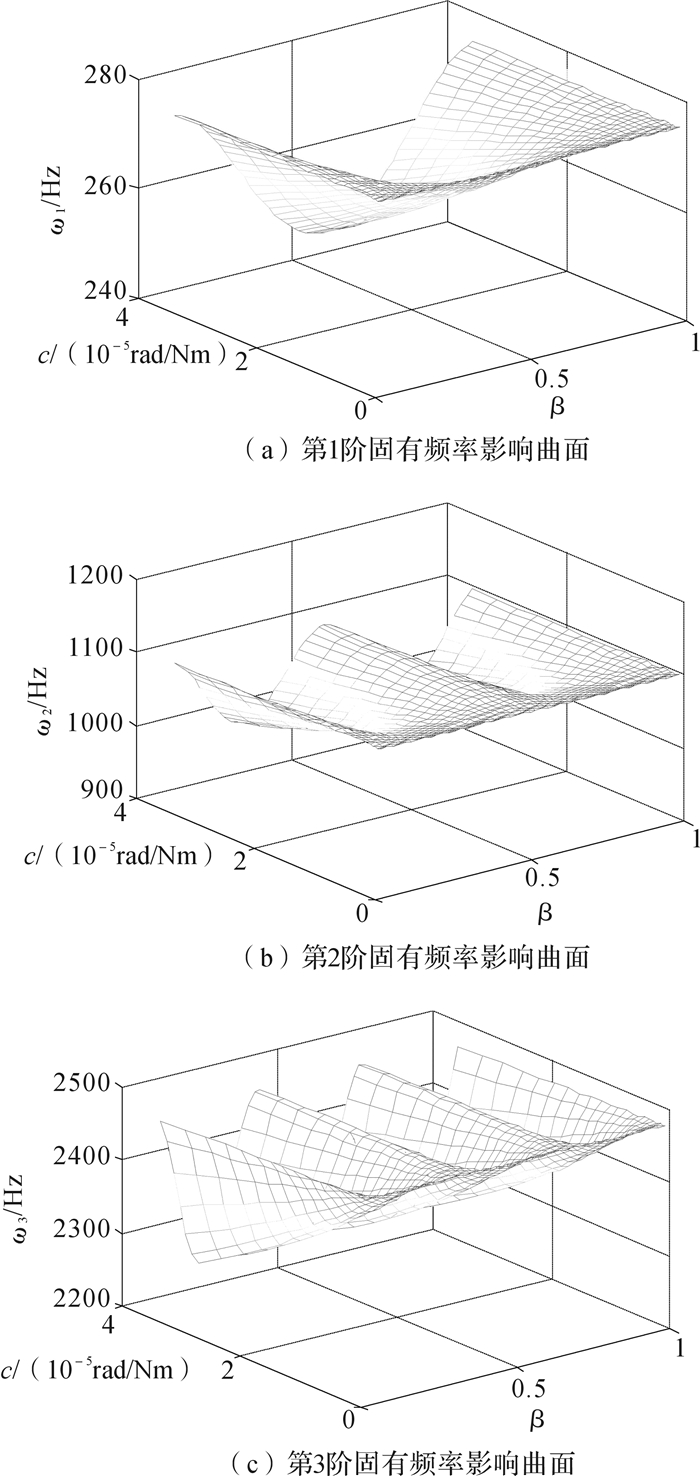
根据裂纹柔度测量方法的步骤1)至3),绘制前3阶固有频率影响曲面,如图 4所示。在采用式(13)求解对应于不同裂纹位置和裂纹柔度的固有频率数据库时,由于数值模型和实际结构之间不完全一致,如阻尼、支撑条件等,需要对数值模型进行修正。考虑到数值模型和实际结构的误差对结构不同模态的影响,采用模态修正系数ki(i=1, 2, 3)对数值模型的前3阶模态分别进行修正。式(14)、式(15)建立了结构固有频率与裂纹柔度和裂纹位置的关系,修正后如下所示:
| $ {{\omega '}_i} = {k_i}F\left( {c,\beta } \right),i = 1,2,3 $ | (16) |
| $ \left( {c,\beta } \right) = {\left( {{k_i}F} \right)^{ - 1}}\left( {{{\omega '}_i}} \right),i = 1,2,3 $ | (17) |
|
| 图 4 不同裂纹位置和裂纹柔度的结构前3阶固有频率影响曲面 Fig.4 The first three order natural frequency influence surfaces of structures with different crack locations and flexibilities |
式中:ω′i为采用修正模型计算的第i阶固有频率;ki为第i阶模态修正系数,可以通过比较固有频率的测量值与采用数值模型的计算值来确定。
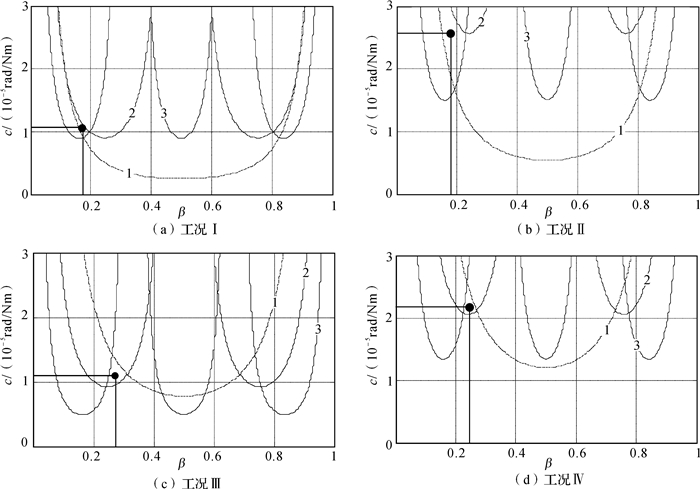
获得固有频率影响曲面后,对结构进行振动测试。将实测的前3阶固有频率作为输入,截取前3阶固有频率影响曲面,获得固有频率影响曲线,利用其交点测量出裂纹柔度及对应的裂纹位置。测量结果见图 5和表 2。εβ,εc为裂纹位置和裂纹柔度测量误差。
| $ {\varepsilon _\beta } = \left| {\beta ' - \beta } \right| \times 100\% $ | (18) |
| $ {\varepsilon _c} = \frac{{\left| {c' - c} \right|}}{c} \times 100\% $ | (19) |
|
| 1—1阶固有频率影响曲线; 2—2阶固有频率影响曲线; 3—3阶固有频率影响曲线 图 5 不同工况下结构的前3阶固有频率影响曲线 Fig.5 The first three order natural frequency influence curves of structures under different conditions |
| 工况 | ω1/Hz | ω2/Hz | ω3/Hz | β′ | c′/(10-5rad/Nm) | 相对误差/% | |
| εβ | εc | ||||||
| Ⅰ | 273.3 | 1 070.3 | 2 410.5 | 0.18 | 1.13 | 2.0 | 8.1 |
| Ⅱ | 270.6 | 1 020.5 | 2 369.0 | 0.19 | 2.60 | 1.0 | 8.3 |
| Ⅲ | 268.5 | 1 069.7 | 2 440.9 | 0.28 | 1.15 | 2.0 | 6.5 |
| Ⅳ | 264.8 | 1 034.6 | 2 380.0 | 0.24 | 2.25 | 6.0 | 6.3 |
式中:β′为裂纹相对位置测量值,c′为裂纹柔度测量值。
通过图 5和表 2可以看出,裂纹相对位置误差不超过6.0%,裂纹柔度的误差不超过8.3%,因此这种方法可以有效地测量出裂纹柔度及对应的裂纹位置。实验结果验证了该方法的可行性和正确性。实验中利用裂纹柔度的计算值对测量精度进行了估计,在求解裂纹柔度的计算值时用到了矩形截面中的Ⅰ型裂纹的应力强度因子。因此,这种方法的精度与裂纹应力强度因子有关。对于含其它类型裂纹的柔度测量问题,在进行测量精度估计时,则需要采用相应类型裂纹的应力强度因子去计算裂纹柔度。
4 结论本文通过将结构动力学分析和振动测试相结合,讨论了一种基于固有频率的裂纹柔度测量方法。该方法操作简便,可用于矩形截面梁结构中不同类型和形状裂纹的柔度测量。
| [1] |
唐力伟, 张晓涛, 王平.
管状金属构件裂纹电磁声发射激发特性试验研究[J]. 振动与冲击, 2014, 33(19): 48–58.
TANG Li-wei, ZHANG Xiao-tao, WANG Ping. Tests for exciting features of electromagnetic acoustic emission of tubular metal parts' crack[J]. Journal of Vibration and Shock, 2014, 33(19): 48–58. |
| [2] | SHARMA A, KIM H S, KIM D W, et al. A carbon nanotube field emission X-ray tube with a stationary anode target[J]. Microelectronic Engineering, 2015, 15(2): 35–40. |
| [3] |
焦敬品, 常予, 李光海, 等.
铁磁构件内外表面裂纹低频漏磁检测技术研究[J]. 仪器仪表学报, 2016, 37(8): 1808–1817.
JIAO Jing-pin, CHANG Yu, LI Guang-hai, et al. Study on low frequency AC magnetic flux leakage detection for internal and external cracks of ferromagnetic structures[J]. Chinese Journa1 of Scientific Instrument, 2016, 37(8): 1808–1817. |
| [4] | REHMAN S K U, IBRAHIM Z, MEMON S A, et al. Nondestructive test methods for concrete bridges:a review[J]. Construction and Building Materials, 2016, 107: 58–86. DOI:10.1016/j.conbuildmat.2015.12.011 |
| [5] | SINOU J J. Effects of a crack on the stability of a non-linear rotor system[J]. International Journal of Non-Linear Mechanics, 2007, 42(7): 959–972. DOI:10.1016/j.ijnonlinmec.2007.04.002 |
| [6] | CHONDROS T G, DIMAROGONAS A D, YAO J. Vibration of a beam with a breathing crack[J]. Journal of Sound and Vibration, 2001, 239(1): 57–67. DOI:10.1006/jsvi.2000.3156 |
| [7] | DIMAROGONAS A D, PAIPETIS S A, CHONDROS T G. Analytical methods in rotor dynamics[M]. 2th ed. Berlin: Springer Netherlands, 2013: 55-95. |
| [8] | ZHENG D Y, KESSISSOGLOU N J. Free vibration analysis of a cracked beam by finite element method[J]. Journal of Sound and Vibration, 2004, 273(3): 457–475. DOI:10.1016/S0022-460X(03)00504-2 |
| [9] | CHASALEVRIS A C, PAPADOPOULOS C A. Identification of multiple cracks in beams under bending[J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1631–1673. DOI:10.1016/j.ymssp.2006.03.008 |
| [10] |
胡家顺, 冯新, 李昕, 等.
裂纹梁振动分析与裂纹识别方法研究进展[J]. 振动与冲击, 2007, 26(11): 146–151.
HU Jia-shun, FENG Xin, LI Xin, et al. State-of-art of vibration analysis and crack identification of cracked beams[J]. Journal of Vibration and Shock, 2007, 26(11): 146–151. DOI:10.3969/j.issn.1000-3835.2007.11.033 |
| [11] | LEE J. Identification of multiple cracks in a beam using natural frequencies[J]. Journal of Sound and Vibration, 2009, 320(3): 482–490. DOI:10.1016/j.jsv.2008.10.033 |
| [12] | HAN Qin-kai, CHU Fu-lei. Local flexibility of an elliptical cracked shaft under bending and tension[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 3198–3203. DOI:10.1016/j.ymssp.2011.04.015 |
| [13] |
刘文光, 严铖, 贺红林.
结构裂纹对弹性梁振动特性的影响[J]. 失效分析与预防, 2013, 8(5): 259–263.
LIU Wen-guang, YAN Cheng, HE Hong-lin. Impacts of structure crack on vibration characteristic of an elastic beam[J]. Failure Analysis and Prevention, 2013, 8(5): 259–263. |
| [14] | ATTAR M, KARRECH A, REGENAUER-LIEB K. Free vibration analysis of a cracked shear deformable beam on a two-parameter elastic foundation using a lattice spring model[J]. Journal of Sound and Vibration, 2014, 333(11): 2359–2377. DOI:10.1016/j.jsv.2013.11.013 |
| [15] | LIU J, ZHU W D, CHARALAMBIDES P G, et al. A dynamic model of a cantilever beam with a closed, embedded horizontal crack including local flexibilities at crack tips[J]. Journal of Sound and Vibration, 2016, 382: 274–290. DOI:10.1016/j.jsv.2016.04.036 |
| [16] |
李欣业, 张明路.
机械振动[M]. 4版. 北京: 清华大学出版社, 2009: 439-442.
LI Xin-ye, ZHANG Ming-lu. Mechanical vibration[M]. 4th ed. Beijing: Tsinghua University Press, 2009: 439-442. |
| [17] | NANDWADA B P, MAITI S K. Detection of the location and size of a crack in stepped cantilever beams based on measurements of natural frequencies[J]. Journal of Sound and Vibration, 1997, 203(3): 435–446. DOI:10.1006/jsvi.1996.0856 |
| [18] | DIMAROGONAS A D. Vibration of cracked shafts in bending[J]. Engineering Fracture Mechanics, 1983, 91(4): 583–593. |
| [19] | TATA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[M]. 3th ed. New York: ASME Press, 2000: 11-13. |


