在可靠性评估中,一些复杂系统往往缺少能够直接使用的可靠性数据,呈现小子样特性。但是,在其研发和试验阶段或不同环境、相似产品中却存在很多有用的可靠性数据。因此,可靠性数据具有多源性,能否综合、合理地利用这些可靠性信息,就显得尤为重要[1]。基于布尔逻辑和概率论的传统故障树分析方法要求有清楚的事件关系和精确的部件可靠性信息,然而,目前国内缺乏相关部件的失效信息数据库,并且在实际系统中,故障机理常常不确定[2]。所以零部件正常或失效的二态假设与实际故障程度差距较大,传统故障树在实际应用中有很大的局限性。
本文引入t检验对样本数据和验前信息进行相容性检验,防止样本数据和验前信息不相容。通过引入基于相关函数的多源信息融合法对不同来源的可靠性数据进行信息融合,根据融合后数据确定底事件可靠度。将T-S模糊故障树引入小子样系统可靠性评估中,该方法所使用的模糊概率数据的精度要求低,且多态模糊数可以较好地描述起升机构零部件的故障程度。最后以铸造起重机主起升机构可靠性评估为例验证本文所提方法的可行性。
1 底事件信息的分析与处理在系统级可靠性试验数据极少的情况下进行可靠性评估时,必须收集专家的可靠性意见和分系统、相似系统及不同环境下系统的可靠性数据等信息,采用信息融合技术中的定性-定量融合方法来得出可信结论[3]。信息融合技术能合理协调多源数据,充分利用有用信息,可获得关于系统可靠性的更完整和更准确的判断信息,提高在多变环境中正确决策的能力,从而进一步形成对系统可靠性的有效预测[4]。
不同来源的样本数据和验前数据的信息融合,必须建立在样本数据和验前信息相容的基础上,可靠性信息是否相容的问题即为多源信息是否来自同一总体,也就是其是否服从相同分布的问题。因此在进行多源信息融合前,需对多源数据进行相容性检验。机械系统零部件可靠度总体服从正态分布,所以采用单总体t检验较为合理。
1.1 单总体t检验方法单总体t检验方法是检验样本与已知的总体分布的差异是否显著。当总体分布是正态分布时,若总体标准差σ未知,且样本容量n<30,则样本与总体分布的离差统计量呈t分布。检验统计量为:
| $ t = \frac{{\bar X - \mu }}{{\left( {\frac{{{\sigma _X}}}{{\sqrt {n - 1} }}} \right)}} $ | (1) |
式中:t为样本与总体分布的离差统计量;X为样本平均数;μ为总体平均数;σX为样本标准差;n为样本容量。
选取显著性水平值α,一般以α=0.05为显著水平。通过查t值表,得到临界值t(n-1)α,比较样本离差t与临界值t(n-1)α:若t<t(n-1)α,则差异不显著,即接受原假设;若t>t(n-1)α,则差异显著,即原假设不被接受。
1.2 基于相关函数的多源信息融合 1.2.1 相关函数一切会对实验结果造成影响的因素,称为实验因素(简称因素)。这些因素用Z表示, 看作系统的输入;实验结果用Y来表示, 看作系统的输出。如果Y的数学期望Y0,取决于诸重要因素Z=(Z1, Z2, …, Zn)的数学期望Z0=(Z10, Z20, …, Zn0),则Z和Y为相关的。
设系统有n个输入, 即z=(z1, z2, …, zn),1个输出Y。设yi为第i次实验的输出结果,i=1, 2, …, h,y为全因素试验的输出结果,由回归分析求得yi和y的解析式:
| $ {y_i} = {{b'}_0} + {{b'}_1}{{z'}_1} + \cdots + {{b'}_k}{{z'}_k} $ | (2) |
| $ y = {b_0} + {b_1}{z_1} + \cdots + {b_k}{z_k} + \cdots + {b_n}{z_n} $ | (3) |
式中:z′j为影响yj的因素,1≤j≤k,与每次的试验安排有关;b′j, bi为回归系数,1≤j≤k,i=1, 2, …, h。
定义个体相关函数为:
| $ {\eta _{{y_i}y}} = \frac{{{{b'}_1}{b_1}\sigma _{{z_1}}^2 + \cdots + {{b'}_k}{b_k}\sigma _{{z_k}}^2}}{{\sqrt {{{\left( {{{b'}_1}} \right)}^2}\sigma _{{z_1}}^2 + \cdots + {{\left( {{{b'}_k}} \right)}^2}\sigma _{{z_k}}^2} \cdot \sqrt {b_1^2\sigma _{{z_1}}^2 + \cdots + b_n^2\sigma _{{z_n}}^2} }} $ | (4) |
式中σzi2为随机变量zi的方差[5]。
1.2.2 基于相关函数的多源信息融合方法设复杂系统的可靠性指标随机变量为E(如系统寿命),概率密度函数为f(e|θ),其中θ为待估分布参数。设m个信息源为x1(e), x2(e), …, xm(e);n个现场子样为x1, x2,…, xn,xi~f(e|θ),xi(i=1, …, n)为独立同分布样本。
记πi(θ)为通过验前数据x1(i), x2(i), …, xn(i)求得的验前分布,i=1, 2, …, m,融后分布记为π(θ),则:
| $ {\rm{ \mathsf{ π} }}\left( \theta \right) = \sum\limits_{i = 1}^m {{\varepsilon _i}{{\rm{ \mathsf{ π} }}_i}\left( \theta \right)} $ | (5) |
| $ \sum\limits_{i = 1}^m {{\varepsilon _i}} = 1 $ | (6) |
式中:0≤εi≤1,是依赖于单一验前信息与验后分布的相关性所确定的权系数。
以m=2为例说明该融合方法。
| $ {\rm{ \mathsf{ π} }}\left( \theta \right) = {\varepsilon _1}{{\rm{ \mathsf{ π} }}_1}\left( \theta \right) + {\varepsilon _2}{{\rm{ \mathsf{ π} }}_2}\left( \theta \right) $ | (7) |
设π1(θ)的期望为μ1,π2(θ)的期望为μ2。根据贝叶斯理论,由θ的先验分布π(θ),结合现场样本X=(x1, x2, …, xn),可得到θ的后验分布π(θ|X),即
| $ {\rm{ \mathsf{ π} }}\left( {\theta \left| X \right.} \right) = \frac{{{\rm{ \mathsf{ π} }}\left( \theta \right)f\left( {e\left| \theta \right.} \right)}}{{\int_\mathit{\Theta } {{\rm{ \mathsf{ π} }}\left( \theta \right)f\left( {e\left| \theta \right.} \right){\rm{d}}\theta } }} $ | (8) |
式中Θ为参数θ的取值空间。
由验前分布π1(θ)结合现场子样X=(x1, x2, …, xn),通过贝叶斯公式,得到验后分布为π1(θ|X),期望为μ′1,方差为ν12;由验前分布π2(θ)结合现场子样X=(x1, x2, …, xn),得到验后分布为π2(θ|X),期望为μ′2,方差为ν22;由验前分布π(θ)得到的验后分布π(θ|X)的期望为μ,方差为ν2。令:
| $ {{\mu '}_i} = {{b'}_{0i}} + {{b'}_{1i}}{\mu _1} + {{b'}_{2i}}{\mu _2},i = 1,2 $ | (9) |
| $ \mu = {b_0} + {b_1}{\mu _1} + {b_2}{\mu _2} $ | (10) |
式(9)、式(10)中均有3个未知数,因此需要通过π1(θ),π2(θ),π1(θ|X),π2(θ|X)采用抽样技术,分别产生3组随机样本,用每一组样本的均值分别替代式(9)和(10)中各自的总体均值μ′i,μi,然后求解该方程,得到明确的解析表达式。
为确定πi(θ|X)与π(θ|X)的相关程度,定义相关函数:
| $ {\eta _{{{\rm{ \mathsf{ π} }}_i}{\rm{ \mathsf{ π} }}}} = \frac{{{{b'}_{1i}}{b_1}\sigma _{{{\rm{ \mathsf{ π} }}_1}}^2 + {{b'}_{2i}}{b_2}\sigma _{{{\rm{ \mathsf{ π} }}_2}}^2}}{{\sqrt {{{\left( {{{b'}_{1i}}} \right)}^2}\sigma _{{{\rm{ \mathsf{ π} }}_1}}^2 + {{\left( {{{b'}_{2i}}} \right)}^2}\sigma _{{{\rm{ \mathsf{ π} }}_2}}^2} \cdot \sqrt {b_1^2\sigma _{{{\rm{ \mathsf{ π} }}_1}}^2 + b_2^2\sigma _{{{\rm{ \mathsf{ π} }}_2}}^2} }} $ | (11) |
式中σπi2为πi(θ|X)的方差,σπi2=νi2,i=1, 2。
由式(11)易知0≤ηπiπ≤1,显然,ηπiπ越大,表示πi(θ|X)与π(θ|X)的相关程度越大,即关系越密切,则验前分布πi(θ)在融后分布中所占的权重应该越大。于是,令:
| $ {\varepsilon _i} = \frac{{{\eta _{{{\rm{ \mathsf{ π} }}_i}{\rm{ \mathsf{ π} }}}}}}{{{\eta _{{{\rm{ \mathsf{ π} }}_1}{\rm{ \mathsf{ π} }}}} + {\eta _{{{\rm{ \mathsf{ π} }}_2}{\rm{ \mathsf{ π} }}}}}},i = 1,2 $ | (12) |
通过求解式(12),即可以得到验前分布的融合权重。
一般情况下,m≥3,类似地,可利用上述方法求得具有多种验前信息源之下的融后分布:
| $ {\rm{ \mathsf{ π} }}\left( \theta \right) = \sum\limits_{i = 1}^m {{\varepsilon _i}{{\rm{ \mathsf{ π} }}_i}\left( \theta \right)} $ | (13) |
θ的验后分布为:
| $ {\rm{ \mathsf{ π} }}\left( {\theta \left| X \right.} \right) = \frac{1}{{m\left( {X\left| {\rm{ \mathsf{ π} }} \right.} \right)}}\sum\limits_{i = 1}^m {{\varepsilon _i}{{\rm{ \mathsf{ π} }}_i}\left( \theta \right)m\left( {X\left| {{{\rm{ \mathsf{ π} }}_i}} \right.} \right)} $ | (14) |
| $ {\lambda _i} = \frac{{{\varepsilon _i}m\left( {X\left| {{{\rm{ \mathsf{ π} }}_i}} \right.} \right)}}{{m\left( {X\left| {\rm{ \mathsf{ π} }} \right.} \right)}} $ | (15) |
式中
联立式(12)至式(15)可得:
| $ {\rm{ \mathsf{ π} }}\left( {\theta \left| X \right.} \right) = {\lambda _1}{{\rm{ \mathsf{ π} }}_1}\left( {\theta \left| X \right.} \right) + \cdots + {\lambda _m}{{\rm{ \mathsf{ π} }}_m}\left( {\theta \left| X \right.} \right) $ | (16) |
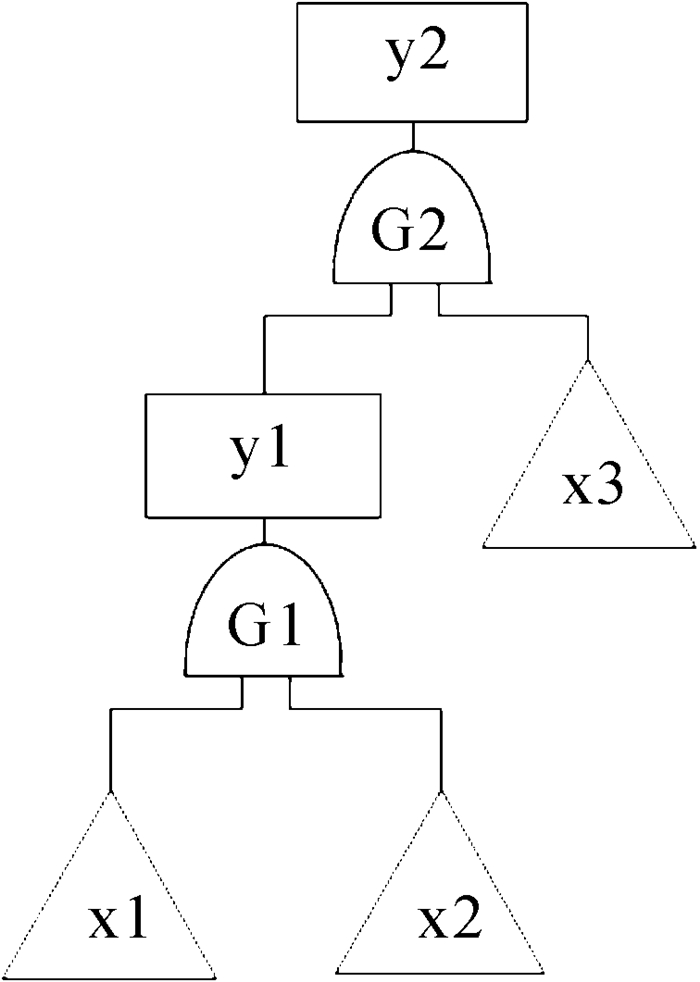
T-S模糊故障树分析方法一般以所分析的系统为顶事件,分系统为中间事件,零部件为底事件建立故障树。该方法建立故障树简单,可以有效避免重叠并且符合人类对客观世界的认识。其基本步骤是:首先对故障树各底事件进行模糊评价,得出它们在当前工况下的故障程度,然后利用T-S模糊门规则和历史数据进行计算,得出顶事件的模糊故障概率值[6]。图 1所示为一个简单的T-S模糊故障树,其中,x1,x2,x3为底事件,y1为中间事件,y2为顶事件,G1,G2为T-S模糊门。
|
| 图 1 简单的T-S模糊故障树 Fig.1 A simple T-S fuzzy fault tree |
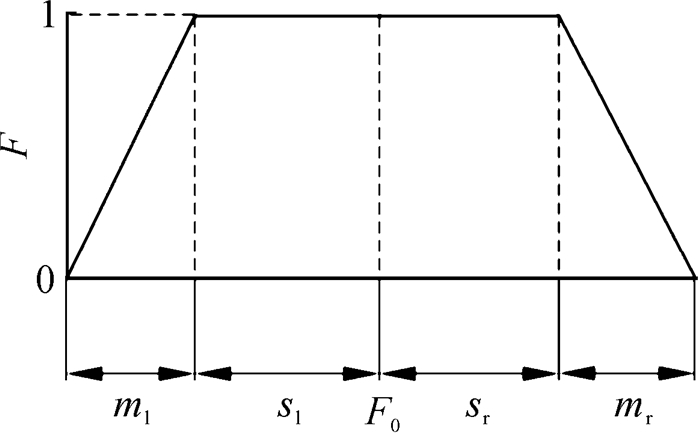
T-S模糊故障树中,用分布在[0, 1]上的模糊数来描述零部件的故障程度, 例如,可以用0, 0.5, 1来描述部件状态为完好、半故障、全故障。本文采用梯形隶属函数F作为模糊数的隶属函数,F=(F0, sl, ml, sr, mr),如图 2所示。
|
| 图 2 梯形隶属函数 Fig.2 Trapezoidal membership function |
隶属函数表述如下:
| $ F = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le x \le {F_0} - {s_1} - {m_1}\\ \frac{{x - \left( {{F_0} - {s_1} - {m_1}} \right)}}{{{m_1}}},{F_0} - {s_1} - {m_1} < x \le {F_0} - {s_1}\\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{F_0} - {s_1} < x < {F_0} + {s_{\rm{r}}}\\ \frac{{{F_0} + {s_{\rm{r}}} + {m_{\rm{r}}} - x}}{{{m_{\rm{r}}}}},\;\;\;\;{F_0} + {s_{\rm{r}}} \le x \le {F_0} + {s_{\rm{r}}} + {m_{\rm{r}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{F_0} + {s_{\rm{r}}} + {m_{\rm{r}}} < x \end{array} \right. $ | (17) |
式中:F0为模糊数支撑集的中心,sl为模糊数支撑集的支撑左半径,sr为模糊数支撑集的支撑右半径,ml为左模糊区,mr为右模糊区。
当sl=sr时,梯形隶属函数转换为三角形隶属函数[7];当ml=mr=0时,梯形隶属函数转换为常数。
2.2 T-S模糊门T-S模糊模型由一套IF-THEN模糊规则组成,并且可以用来描述事件之间的关系,故根据模糊规则可以构造出对应的模糊门。规定T-S模型的第l条规则(l=1, 2, …, m):若z1为sl1,z2为sl2,…,则Y为Yl。其中,z =[z1, z2, …]T为前提变量,{slj}是一个模糊集,用Fslj表示模糊集的隶属函数。则T-S模型的输出由式(18)决定:
| $ Y = \sum\limits_{l = 1}^m {\beta _l^ * \left( \mathit{\boldsymbol{z}} \right){Y_l}} $ | (18) |
式中βl*是模糊规则l的执行度。
假设基本事件的故障大小g1, g2, …, gn和顶事件Y分别表示为(g11, g12, …, g1k1),(g21, g22, …, g2k2),…,(gn1, gn2, …, gnkn)和(Y1, Y2, …, Yky),且满足式(19):
| $ \left\{ {\begin{array}{*{20}{c}} {0 \le g_1^1 < g_1^2 < \cdots < g_1^{{k_1}} \le 1}\\ {0 \le g_2^1 < g_2^2 < \cdots < g_2^{{k_2}} \le 1}\\ { \cdots \cdots }\\ {0 \le g_n^1 < g_{n1}^2 < \cdots < g_n^{{k_n}} \le 1}\\ {0 \le {Y^1} < {Y^2} < \cdots < {Y^{{k_y}}} \le 1} \end{array}} \right. $ | (19) |
T-S门可以表示为如下的模糊规则:
对规则l(l=1, 2, …, m),若
| $ \left\{ {\begin{array}{*{20}{c}} {{g_1} = g_1^{{i_1}},{i_1} = 1,2, \cdots ,{k_1}}\\ {{g_2} = g_2^{{i_2}},{i_2} = 1,2, \cdots ,{k_2}}\\ { \cdots \cdots }\\ {{g_n} = g_n^{{i_n}},{i_n} = 1,2, \cdots ,{k_n}} \end{array}} \right. $ |
则:在Y里,Y1,Y2,……,Yky的发生概率依次用Pl(Y1),Pl(Y2),…,Pl(Yky)表示,m是模糊规则的数量,且m=k1k2…kn[8]。
传统故障树分析中的“与”门和“或”门可以由T-S门实现。“与”门可以由以下模糊规则表示:若g1=g2=…=gn=1,则对于Y,Y1=Y2=…=Yky-1=0,Yky=1的隶属度为1。“或”门可以由以下规则表示:规则l(l=1, 2, …, n),若gi=1,对于Y来说,故障状态Y1,Y2,…,Yky-1的隶属度均为0,则Yky=1的隶属度为1[9]。如果模糊集变成确定值的集合,则T-S门就变成传统的“与”门和“或”门。因此,T-S门比传统的门更有普遍性。
假设已知基本事件的故障大小g=(g1, g2, …, gn),顶事件的模糊故障概率可以由T-S模糊门获得:
| $ \left\{ {\begin{array}{*{20}{c}} {P\left( {{Y^1}} \right) = \sum\limits_{l = 1}^m {\beta _l^ * \left( {g'} \right){P^l}\left( {{Y^1}} \right)} }\\ {P\left( {{Y^2}} \right) = \sum\limits_{l = 1}^m {\beta _l^ * \left( {g'} \right){P^l}\left( {{Y^2}} \right)} }\\ { \cdots \cdots }\\ {P\left( {{Y^n}} \right) = \sum\limits_{l = 1}^m {\beta _l^ * \left( {g'} \right){P^l}\left( {{Y^n}} \right)} } \end{array}} \right. $ | (20) |
式中:
在基本事件中,假设模糊失效概率的大小是P(g1i1)(i1=1, 2, …, k1),P(g2i2)(i2=1, 2, …, k2),…,P(gnin)(in=1, 2, …, kn),则执行规则l的概率为:
| $ {P^l} = P\left( {g_1^{{i_1}}} \right)P\left( {g_2^{{i_2}}} \right) \cdots P\left( {g_n^{{i_n}}} \right),l = 1, \cdots ,m $ | (21) |
顶事件的模糊概率为:
| $ \left\{ {\begin{array}{*{20}{c}} {P\left( {{Y^1}} \right) = \sum\limits_{l = 1}^m {{P^l} \times {P^l}\left( {{Y^1}} \right)} }\\ {P\left( {{Y^2}} \right) = \sum\limits_{l = 1}^m {{P^l} \times {P^l}\left( {{Y^2}} \right)} }\\ { \cdots \cdots }\\ {P\left( {{Y^n}} \right) = \sum\limits_{l = 1}^m {{P^l} \times {P^l}\left( {{Y^n}} \right)} } \end{array}} \right. $ | (22) |
因此,顶事件的模糊概率可基于基本事件的模糊概率即通过式(22)获得,也可以根据基本事件的当前状态,从式(20)得知。[11]
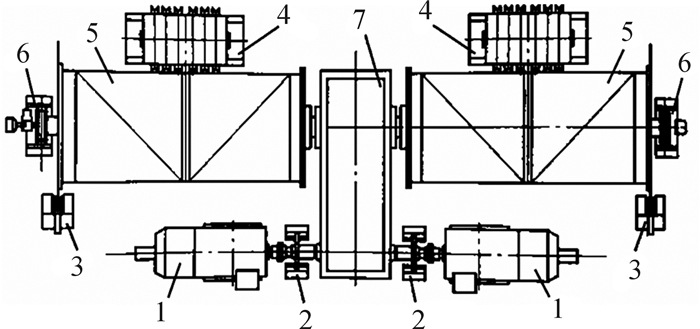
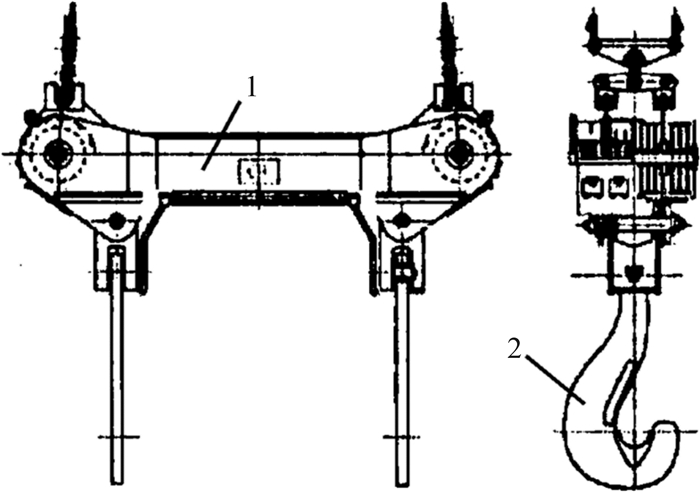
3 铸造起重机主起升机构可靠性分析以某企业2012年生产的75/30 t、跨度为28.5 m的铸造起重机主起升机构为评估对象,其主要技术参数如下:工作级别为A6,设计寿命为20 a,起升高度为14 m,起升速度为1~9 m/min,小车速度为20 m/min,轨道型号为UQ80,轨道接头高低差满足公差要求,环境温度为30 ℃,维护、保养良好。该铸造起重机主起升机构采用如图 3所示的单减速机双卷筒布置,图 4为所用起重横梁吊具[12]。其由2台电动机同时驱动1台行星减速器,行星减速器在1台电机或1套电控系统发生故障时,仍可以1/2的额定速度连续长时间正常运行,因此具有可靠性高的优点[13]。卷筒上装有安全制动器[14],以防止传动链失效时卷筒失控,从而保证主起升机构安全工作。旋转限位及编码装置位于卷筒轴外端,可监控所吊重物的上极限和下极限位置以及卷筒转速,当旋转限位及编码装置监测到重物超过极限位置或卷筒转速异常时,制动器抱闸[15]。该机构具有可靠性高、制造难度小、安装维护检修方便的优点,现对其进行可靠性分析。
|
| 1—电机; 2—工作制动器; 3—安全制动器; 4—定滑轮组; 5—卷筒; 6—旋转限位及编码装置; 7—行星减速器 图 3 铸造起重机主起升机构 Fig.3 Main hoisting mechanism of ladle crane |
|
| 1—横梁;2—吊钩 图 4 铸造用起重横梁吊具 Fig.4 Hoisting crossbeam spreader for casting |
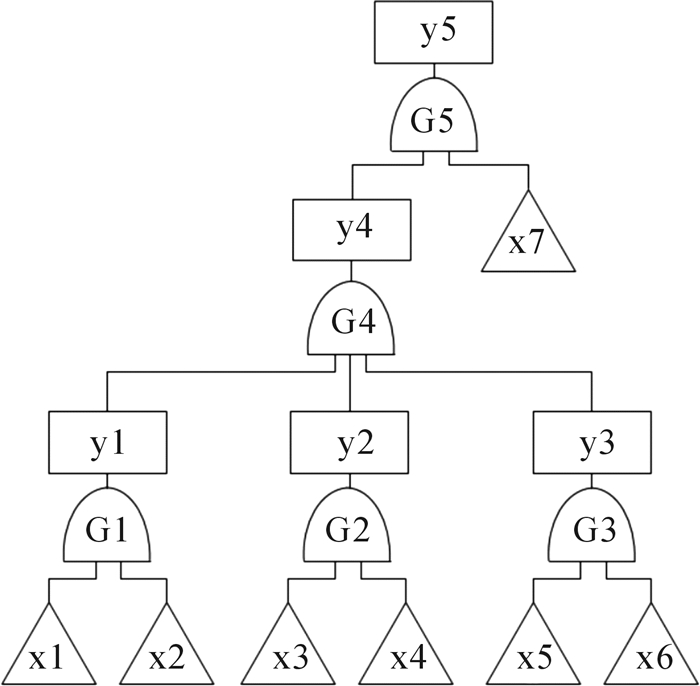
根据历史数据,建立以主起升机构为顶事件的T-S模糊故障树,如图 5所示。各符号所代表的系统、部件含义如表 1所示, 底事件门规则如表 2所示,中间事件门规则如表 3所示。一些故障概率较小的部件不列入故障树中,如联轴器、卷筒、滑轮组、横梁和限位及编码装置。
|
| 图 5 主起升机构T-S模糊故障树 Fig.5 T-S fuzzy fault tree of main hoisting mechanism |
| 符号 | 底事件 | 中间事件 | 顶事件 | |||||||||||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | y1 | y2 | y3 | y4 | y5 | |||
| 含义 | 电机1 | 电机2 | 减速器 | 工作制动器 | 钢丝绳 | 吊钩 | 安全制动器 | 驱动系统 | 传动制动系统 | 卷绕取物系统 | 工作系统 | 起升机构 | ||
| T-S门1 | T-S门2 | T-S门3 | |||||||||||||||||
| 规则 | x1 | x2 | y1 | 规则 | x3 | x4 | y2 | 规则 | x5 | x6 | y3 | ||||||||
| 0 | 0.5 | 1 | 0 | 0.5 | 1 | 0 | 0.5 | 1 | |||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | ||
| 2 | 0 | 0.5 | 0.9 | 0.1 | 0 | 2 | 0 | 0.5 | 0.3 | 0.4 | 0.3 | 2 | 0 | 0.5 | 0.3 | 0.4 | 0.3 | ||
| 3 | 0.5 | 0 | 0.9 | 0.1 | 0 | 3 | 0.5 | 0 | 0.3 | 0.4 | 0.3 | 3 | 0.5 | 0 | 0.3 | 0.4 | 0.3 | ||
| 4 | 0.5 | 0.5 | 0.7 | 0.2 | 0.1 | 4 | 0.5 | 0.5 | 0.1 | 0.5 | 0.4 | 4 | 0.5 | 0.5 | 0.1 | 0.5 | 0.4 | ||
| 5 | 0 | 1 | 0.8 | 0.2 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 5 | 0 | 1 | 0 | 0 | 1 | ||
| 6 | 1 | 0 | 0.8 | 0.2 | 0 | 6 | 1 | 0 | 0 | 0 | 1 | 6 | 1 | 0 | 0 | 0 | 1 | ||
| 7 | 0.5 | 1 | 0.2 | 0.4 | 0.4 | 7 | 0.5 | 1 | 0 | 0 | 1 | 7 | 0.5 | 1 | 0 | 0 | 1 | ||
| 8 | 1 | 0.5 | 0.2 | 0.4 | 0.4 | 8 | 1 | 0.5 | 0 | 0 | 1 | 8 | 1 | 0.5 | 0 | 0 | 1 | ||
| 9 | 1 | 1 | 0 | 0 | 1 | 9 | 1 | 1 | 0 | 0 | 1 | 9 | 1 | 1 | 0 | 0 | 1 | ||
| T-S门4 | T-S门5 | |||||||||||||
| 规则 | y1 | y2 | y3 | y4 | 规则 | y4 | x7 | y5 | ||||||
| 0 | 0.5 | 1 | 0 | 0.5 | 1 | |||||||||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | ||
| 2 | 0 | 0 | 0.5 | 0.2 | 0.7 | 0.1 | 2 | 0 | 0.5 | 0.9 | 0.1 | 0 | ||
| 3 | 0 | 0 | 1 | 0 | 0 | 1 | 3 | 0.5 | 0 | 0.8 | 0.2 | 0 | ||
| 4 | 0 | 0.5 | 0 | 0.2 | 0.7 | 0.1 | 4 | 0.5 | 0.5 | 0.1 | 0.4 | 0.5 | ||
| 5 | 0 | 0.5 | 0.5 | 0.3 | 0.4 | 0.3 | 5 | 0 | 1 | 0 | 0 | 1 | ||
| 6 | 0 | 0.5 | 1 | 0 | 0 | 1 | 6 | 1 | 0 | 0 | 0 | 1 | ||
| 7 | 0 | 1 | 0 | 0 | 0 | 1 | 7 | 0.5 | 1 | 0 | 0 | 1 | ||
| … | … | … | … | … | … | … | 8 | 1 | 0.5 | 0 | 0 | 1 | ||
| 27 | 1 | 1 | 1 | 0 | 0 | 1 | 9 | 1 | 1 | 0 | 0 | 1 | ||
现对铸造起重机主起升机构中减速器可靠度进行专家打分,得到的验前信息分别为π1(θ)=N(0.98, 0.006)和π2(θ)=N(0.97, 0.006)。收集到历史数据和相似产品的数据组成的样本数据为X=(0.986 2, 0.986 7, 0.979 6, 0.937 7, 0.968 7),设样本试验数据为x1,x2, …,x5服从正态分布N(θ, 0.000 3)。在样本数据的基础上,通过相关函数法融合多源验前信息,得到参数θ即铸造起重机主起升机构可靠度的贝叶斯估计。
3.2.1 相容性检验样本平均数:
| $ \begin{array}{l} \bar X = \frac{{{x_1} + {x_2} + {x_3} + {x_4} + {x_5}}}{5} = \\ \;\;\;\;\;\;\;\frac{{0.9862 + 0.9867 + 0.9796 + 0.9377 + 0.9687}}{5} = \\ \;\;\;\;\;\;\;0.97178 \end{array} $ |
检验样本数据X与验前信息π1(θ)的相容性, 计算t值:
| $ t = \frac{{\bar X - \mu }}{{\left( {\frac{{{\sigma _X}}}{{\sqrt {n - 1} }}} \right)}} = \frac{{0.97178 - 0.98}}{{\left( {\frac{{0.006}}{{\sqrt {5 - 1} }}} \right)}} = - 2.74 $ |
取正值即为2.74。以0.05为显著性水平,df=n-1=4,查t值表,临界值t(4)0.05=2.776,样本离差t=2.74,小于临界值2.776。所以,接受原假设,即样本数据与验前信息相容。
检验样本数据X与验前信息π2(θ)的相容性, 计算t值:
| $ t = \frac{{\bar X - \mu }}{{\left( {\frac{{{\sigma _X}}}{{\sqrt {n - 1} }}} \right)}} = \frac{{0.97178 - 0.97}}{{\left( {\frac{{0.006}}{{\sqrt {5 - 1} }}} \right)}} = 0.593\ 3 $ |
以0.05为显著水平,df=n-1=4,查t值表,临界值t(4)0.05=2.776,样本离差t=0.593 3,小于临界值2.776。同上结论,接受原假设,即样本数据与验前信息相容。
3.2.2 信息融合θ的融后分布为:
| $ {\rm{ \mathsf{ π} }}\left( \theta \right) = \varepsilon {{\rm{ \mathsf{ π} }}_1}\left( \theta \right) + \left( {1 - \varepsilon } \right){{\rm{ \mathsf{ π} }}_2}\left( \theta \right) $ |
由π1(θ)产生3组样本,得到θ的样本均值分别为0.980 478,0.982 761,0.977 913;由π2(θ)产生3组样本,得到θ的样本均值分别为0.969 575,0.963 451,0.971 788。根据贝叶斯公式,由π1(θ)结合现场样本X,得到后验分布π1(θ|X)=N(0.971 86, 0.000 059 4);由π2(θ)结合现场样本X,得到后验分布π2(θ|X)=N(0.971 76, 0.000 059 4)。
再由π1(θ|X)产生3组样本,得到θ的样本均值分别为0.971 78,0.971 90,0.971 95;由π2(θ|X)产生3组样本,得到θ的样本均值分别为0.971 80,0.971 84,0.971 80。
根据π(θ)=ε π1(θ)+(1-ε)π2(θ),结合现场子样X,得到后验分布π(θ|X)=N(0.971 76+0.000 1ε, 0.000 059 4)。由π(θ|X)产生3组样本,得到θ的样本均值分别为0.971 63+0.000 099 987× ε,0.971 75+0.000 099 996 4ε,0.971 01+0.000 099 993ε。
根据式(9)和θ的3组样本均值可得:
| $ \left\{ \begin{array}{l} 0.97178 = {{b'}_{01}} + {{b'}_{11}} \cdot 0.980\ 478 + {{b'}_{21}} \cdot 0.969\ 575\\ 0.97190 = {{b'}_{01}} + {{b'}_{11}} \cdot 0.982\ 761 + {{b'}_{21}} \cdot 0.963\ 451\\ 0.97195 = {{b'}_{01}} + {{b'}_{11}} \cdot 0.977\ 913 + {{b'}_{21}} \cdot 0.971\ 788 \end{array} \right. $ |
解得:
| $ \left\{ \begin{array}{l} {{b'}_{01}} = 0.971\ 94\\ {{b'}_{11}} = - 0.126\ 34\\ {{b'}_{21}} = - 0.066\ 992 \end{array} \right. $ |
同理可解得:
| $ \left\{ \begin{array}{l} {{b'}_{02}} = 0.898\ 84\\ {{b'}_{12}} = - 0.005\ 65\\ {{b'}_{22}} = - 0.007\ 72 \end{array} \right. $ |
于是:
| $ \left\{ \begin{array}{l} {b_1} = - 0.063\ 80 - 0.000\ 006\ 5\varepsilon \\ {b_2} = - 0.043\ 69 - 0.000\ 004\ 5\varepsilon \end{array} \right. $ |
将b1, b2代入相关函数表达式,得到关于ε的方程为:
| $ \varepsilon = \frac{{{\eta _{{{\rm{ \mathsf{ π} }}_1}{\rm{ \mathsf{ π} }}}}}}{{{\eta _{{{\rm{ \mathsf{ π} }}_2}{\rm{ \mathsf{ π} }}}} + {\eta _{{{\rm{ \mathsf{ π} }}_1}{\rm{ \mathsf{ π} }}}}}} $ |
解得:
| $ {\varepsilon _1} = 0.050\ 520,{\varepsilon _2} = - 9717.6 $ |
舍去值不在[0, 1]之间的解,即ε=0.050 520,则可得θ的融后分布为:
| $ \begin{array}{*{20}{c}} {{\rm{ \mathsf{ π} }}\left( \theta \right)0.050\ 552{{\rm{ \mathsf{ π} }}_1}\left( \theta \right) + 0.949\ 548{{\rm{ \mathsf{ π} }}_2}\left( \theta \right) = }\\ {N\left( {0.971\ 5765,0.005\ 542} \right)} \end{array} $ |
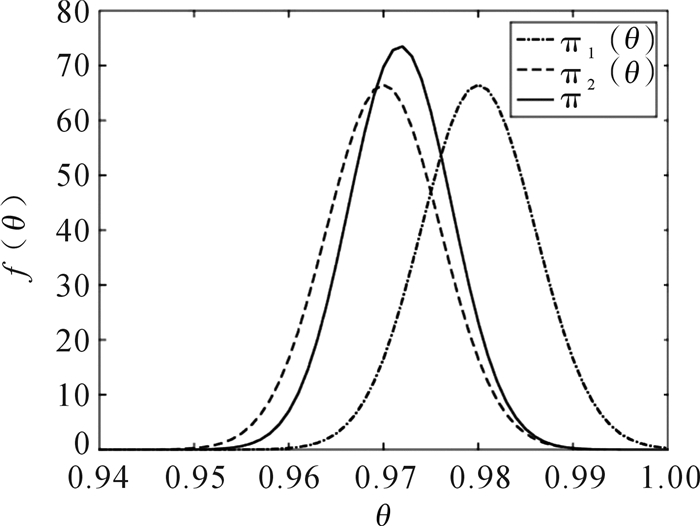
图 6为融合前的验前分布π1(θ),π2(θ)和融后分布π(θ)比较图。从图中可看出,在融后分布π(θ)中,对干扰数据形成的区间的信度分配较低,增大了评估结果的可靠性及准确度。
|
| 图 6 先验信息曲线与融合后的曲线 Fig.6 Prior information curve and the fused curve |
由上述可知,经多源信息融合得到的起重机减速器可靠度为0.971 765。同理可得主起升机构其他部件可靠度,如表 4所示。
| 部件 | 电机1 | 电机2 | 减速器 | 工作制动器 | 钢丝绳 | 吊钩 | 安全制动器 |
| 失效概率 | 0.001 2 | 0.001 2 | 0.014 1 | 0.010 3 | 0.002 3 | 0.008 8 | 0.001 5 |
表 4中的数据为各部件完全故障即故障程度为1时的模糊概率。假设各部件半故障即故障程度为0.5的概率与完全故障的概率相同,则可以根据表 2至表 4得到驱动系统、传动制动系统、卷绕取物系统、工作系统和起升机构的模糊可靠性。
3.3 系统可靠性评估与计算由表 2以及表 4中的数据可以计算得到驱动系统的故障模糊可靠性:
| $ \begin{array}{l} P\left( {{y_1} = 0.5} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_1} = 0.5} \right)} = \\ \;\;\;\;\;\;\;\;\;\;P_0^2{P^2}\left( {{y_1} = 0.5} \right) + P_0^3{P^3}\left( {{y_1} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y_1} = 0.5} \right) + P_0^5{P^5}\left( {{y_1} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;P_0^6{P^6}\left( {{y_1} = 0.5} \right) + P_0^7{P^7}\left( {{y_1} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;P_0^8{P^8}\left( {{y_1} = 0.5} \right) = 7.197 \times {10^{ - 4}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_1} = 1} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_1} = 1} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y_1} = 1} \right) + P_0^7{P^7}\left( {{y_1} = 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;P_0^8{P^8}\left( {{y_1} = 1} \right) + P_0^9{P^9}\left( {{y_1} = 1} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;0.1{P^4}\left( {{y_1} = 1} \right) + 0.4{P^7}\left( {{y_1} = 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;0.4{P^8}\left( {{y_1} = 1} \right) + {P^9}\left( {{y_1} = 1} \right) = 2.28 \times {10^{ - 6}} \end{array} $ |
| $ P\left( {{y_1} = 0} \right) = 1 - P\left( {{y_1} = 0.5} \right) - P\left( {{y_1} = 1} \right) = 0.999\ 278 $ |
| $ \begin{array}{l} P\left( {{y_2} = 0.5} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_2} = 0.5} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^2{P^2}\left( {{y_2} = 0.5} \right) + P_0^3{P^3}\left( {{y_2} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y_2} = 0.5} \right) = 9.6 \times {10^{ - 3}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_2} = 0} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_2} = 0} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^1{P^1}\left( {{y_2} = 0} \right) + P_0^2{P^2}\left( {{y_2} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^3{P^3}\left( {{y_2} = 0} \right) + P_0^4{P^4}\left( {{y_2} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.958\ 9 \end{array} $ |
| $ \begin{array}{l} P\left( {{y_2} = 1} \right) = 1 - P\left( {{y_2} = 0.5} \right) - P\left( {{y_2} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3.15 \times {10^{ - 2}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_3} = 0} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_3} = 0} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^1{P^1}\left( {{y_3} = 0} \right) + P_0^2{P^2}\left( {{y_3} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^3{P^3}\left( {{y_3} = 0} \right) + P_0^4{P^4}\left( {{y_3} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P^1}\left( {{y_3} = 0} \right) + 0.3{P^2}\left( {{y_3} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.3{P^3}\left( {{y_3} = 0} \right) + 0.1{P^4}\left( {{y_3} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.981\ 2 \end{array} $ |
| $ \begin{array}{l} P\left( {{y_3} = 0.5} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_3} = 0.5} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^2{P^2}\left( {{y_3} = 0.5} \right) + P_0^3{P^3}\left( {{y_3} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y_3} = 0.5} \right) = 4.42 \times {10^{ - 3}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_3} = 1} \right) = 1 - P\left( {{y_3} = 0.5} \right) - P\left( {{y_3} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1.439 \times {10^{ - 2}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_4} = 0} \right) = \sum\limits_{l = 1}^{27} {P_0^l{P^l}\left( {{y_4} = 0} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^1{P^1}\left( {{y_4} = 0} \right) + P_0^2{P^2}\left( {{y_4} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y_4} = 0} \right) + P_0^5{P^5}\left( {{y_4} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^{10}{P^{10}}\left( {{y_4} = 0} \right) + P_0^{11}{P^{11}}\left( {{y_4} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^{13}{P^{13}}\left( {{y_4} = 0} \right) + P_0^{14}{P^{14}}\left( {{y_4} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.943\ 2 \end{array} $ |
| $ \begin{array}{l} P\left( {{y_4} = 0.5} \right) = \sum\limits_{l = 1}^{27} {P_0^l{P^l}\left( {{y_4} = 0.5} \right) = } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^2{P^2}\left( {{y_4} = 0.5} \right) + P_0^4{P^4}\left( {{y_4} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^5{P^5}\left( {{y_4} = 0.5} \right) + P_0^{10}{P^{10}}\left( {{y_4} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^{11}{P^{11}}\left( {{y_4} = 0.5} \right) + P_0^{13}{P^{13}}\left( {{y_4} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^{14}{P^{14}}\left( {{y_4} = 0.5} \right) = 9.979 \times {10^{ - 3}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_4} = 1} \right) = 1 - P\left( {{y_4} = 0.5} \right) - P\left( {{y_4} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4.685 \times {10^{ - 2}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y_5} = 0} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_5} = 0} \right) = } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^1{P^1}\left( {{y^5} = 0} \right) + P_0^2{P^2}\left( {{y^5} = 0} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_0^3{P^3}\left( {{y^5} = 0} \right) + P_0^4{P^4}\left( {{y^5} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.949\ 6 \end{array} $ |
| $ \begin{array}{l} P\left( {{y_5} = 0.5} \right) = \sum\limits_{l = 1}^9 {P_0^l{P^l}\left( {{y_5} = 0.5} \right) = } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^2{P^2}\left( {{y^5} = 0.5} \right) + P_0^3{P^3}\left( {{y^5} = 0.5} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;P_0^4{P^4}\left( {{y^5} = 0.5} \right) = 2.137 \times {10^{ - 3}} \end{array} $ |
| $ \begin{array}{l} P\left( {{y^5} = 1} \right) = 1 - P\left( {{y_5} = 0.5} \right) - P\left( {{y^5} = 0} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4.829 \times {10^{ - 2}} \end{array} $ |
计算结果表明,所求得主起升机构在此状态下的完好可靠度约为0.949 6,半故障可靠度约为0.002 137,完全故障概率约为0.048 29。由此得知,当多个部件同时出现轻微故障时,起升机构发生故障的概率会增加。因此多个部件出现复合故障对整个系统具有一定影响,应当引起重视。
由结果可见,系统发生故障的模糊概率大于底事件发生故障的概率,这与实际情况相符,验证了T-S模糊故障树在可靠性分析中的正确性与可行性。
4 结论1) 将t检验引入机械系统可靠性数据相容性检验。相比目前普遍采用的检验方法,t检验具有计算方便、临界值易于查询的优点。
2) 将相关函数多源信息融合法引入可靠性数据融合的应用中,解决了故障树需要大量可靠性数据、专家信息不易融入可靠性计算、相似系统数据使用困难的问题。
3) 将T-S模糊故障树可靠性评估方法引入机械系统可靠性评估中,解决了传统故障树、布尔逻辑门无法精确描述部件之间关系、二态故障状态无法描述部件多种故障程度的问题。
4) 建立了基于多源信息融合和T-S故障树的模糊可靠性评估方法。事件之间的关系结合了专家经验与历史数据,使得分析更符合工程实际,结论更为准确。最后以铸造起重机主起升机构为例进行分析,结果说明该方法简便易行,在可靠性评估等工程实践领域中的可操作性强,具有良好的应用前景。
| [1] |
何江. 基于信息融合的民用飞机可靠性数据分析方法研究[D]. 南京: 南京航空航天大学民航学院, 2012: 8-20.
HE Jiang. Study on analysis methods for reliability data of civil airplane based on information fusion[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, College of Civil Aviation, 2012:8-20. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012042231.htm |
| [2] | LI Yan-feng, MI Jin-hua, LIU Yu, et al. Dynamic fault tree analysis based on continuous-time Bayesian networks under fuzzy numbers[J]. Proceedings of the Institution of Mechanical Engineers, Part O:Journal of Risk and Reliability, 2015, 229(6): 530–541. DOI:10.1177/1748006X15588446 |
| [3] |
姜晨, 徐廷学, 刘勇, 等.
维修性小子样验证中先验信息的融合方法[J]. 科学技术与工程, 2014, 14(22): 129–133.
JIANG Chen, XU Ting-xue, LIU Yong, et al. Priorinformation fusion method in maintainability small sample test[J]. Science Technology and Engineering, 2014, 14(22): 129–133. DOI:10.3969/j.issn.1671-1815.2014.22.023 |
| [4] |
陈浩, 张洋, 郭波, 等.
可靠性信息融合中继承因子的确定方法[J]. 机械科学与技术, 2016, 35(7): 1139–1143.
CHEN Hao, ZHANG Yang, GUO Bo, et al. Determining similarity factor in reliability information fusion[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(7): 1139–1143. |
| [5] |
冯静, 潘正强, 孙权, 等.
科学出版社[M]. 北京: 科学出版社, 2015: 26-30.
FENG Jing, PAN Zheng-qiang, SUN Quan, et al. Research on methods and applications of reliability information fusion for complex system with small sample test[M]. Beijing: Science Press, 2015: 26-30. |
| [6] |
黄亮亮, 姚安林, 杨鲁明, 等.
基于T-S模糊故障树的输气站场设备失效可能性研究[J]. 中国安全生产科学技术, 2014, 10(8): 144–149.
HUANG Liang-liang, YAO An-lin, YANG Lu-ming, et al. Study on failure possibility of facilities in gas transmission station based on T-S fuzzy FTA[J]. Journal of Safety Science and Technology, 2014, 10(8): 144–149. |
| [7] | LI Yan-feng, HONG Zhong-huang, LIU Yu, et al. A new fault tree analysis method:fuzzy dynamic fault tree analysis[J]. Eksploatacja i Niezawodnosc-Maintenance and Reliability, 2012, 14(3): 208–214. |
| [8] |
孙利娜, 黄宁, 仵伟强, 等.
基于T-S模糊故障树的多态系统性能可靠性[J]. 机械工程学报, 2016, 52(10): 197–204.
SUN Li-na, HUANG Ning, WU Wei-qiang, et al. Performance reliability of polymorphic systems by fuzzy fault tree based on T-S model[J]. Journal of Mechanical Engineering, 2016, 52(10): 197–204. |
| [9] |
姚成玉, 赵静一.
基于T-S模型的液压系统模糊故障树分析方法研究[J]. 中国机械工程, 2009, 20(16): 27–31.
YAO Cheng-yu, ZHAO Jing-yi. Research on fuzzy fault tree analysis method for hydraulic system based on T-S model[J]. China Mechanical Engineering, 2009, 20(16): 27–31. |
| [10] |
姚成玉, 陈东宁, 王斌.
基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J]. 机械工程学报, 2014, 50(2): 193–201.
YAO Cheng-yu, CHEN Dong-ning, WANG Bin. Fuzzy reliability assessment method based on T-S fault tree and Bayesian network[J]. Journal of Mechanical Engineering, 2014, 50(2): 193–201. |
| [11] |
陈东宁, 姚成玉, 党振.
基于T-S模糊故障树和贝叶斯网络的多态液压系统可靠性分析[J]. 中国机械工程, 2013, 24(7): 899–905.
CHEN Dong-ning, YAO Cheng-yu, DANG Zhen. Reliability analysis of multi-state hydraulic system based on T-S fuzzy fault tree and Bayesian network[J]. China Mechanical Engineering, 2013, 24(7): 899–905. |
| [12] |
文豪.
起重机械[M]. 北京: 机械工业出版社, 2013: 108-316.
WEN Hao. Lifting machinery[M]. Beijing: China Machine Press, 2013: 108-316. |
| [13] |
赵燚, 林振胜.
应用于冶金起重机中的行星减速器[J]. 重工与起重技术, 2011, 30(2): 1–4.
ZHAO Yi, LIN Zhen-sheng. Planetary reducer applied to metallurgical crane[J]. Heavy Industrial and Hoisting Machinery, 2011, 30(2): 1–4. |
| [14] | ZHAO Jing-yun, CHENG Xue-li, LI Qiang, et al. Design and simulation for the brake of crane lifting device[J]. Hydromechatronics Engineering, 2015, 43(12): 120–124. |
| [15] |
李会勤.
紧急制动器在铸造起重机主起升机构上的应用[J]. 起重运输技术, 2009(12): 1–5.
LI Hui-qin. Application of emergency brake in main hoisting mechanism of ladle crane[J]. Hoisting and Conveying Machinery, 2009(12): 1–5. |


