2. 滨州学院 电气工程学院, 山东 滨州 256600
2. College of Electrical Engineering, Binzhou University, Binzhou 256600, China
生物疫苗制造业主要采用“鸡胚法”生产,即将病毒注入鸡胚中,让病毒伴随鸡胚的发育自然繁殖,鸡胚发育3 d左右后,每枚鸡胚含有8~12 mL的半成品抗原[1-2]。在注射病毒前需要对鸡胚进行孵化培养,接种前需要对鸡胚进行2次照蛋,接种后需要1次照蛋,将弱胚、死胚蛋剔除,避免其污染正常蛋胚。照蛋过程是将蛋盘从蛋车上取下,进行胚胎发育情况检测,检测完成将蛋盘放回蛋车继续孵化。蛋胚放在一个尺寸为1 660 mm×570 mm×2 100 mm的箱式孵化蛋车上,一个蛋车装载32个蛋盘,每个蛋盘装载150枚鸡蛋。一个中型疫苗生产厂每天照蛋约10万枚,每天有600多盘鸡蛋需要装卸。
1 蛋车装卸机械臂的结构设计 1.1 装卸机械臂的功能需求现有的蛋车装卸机械臂是针对42枚蛋盘的装卸,42枚蛋盘下方设有4根支撑柱,距蛋车的支撑轨道有一定的间隙,装卸机械臂可以深入蛋车将蛋盘取出。目前针对42枚蛋盘装的卸机械臂一般采用多自由度机械臂,前端挂载伸缩臂,深入蛋车,将蛋盘取出[3-9],如美国的关节型装卸机械臂、中国电子科技集团41所的直角坐标型机械臂[10-13]。
本论文设计的装卸机械臂是针对150枚型箱式孵化蛋车(如图 1所示),共有16层,每层2个蛋盘。150枚蛋盘为10行×15列的长方形(720 mm×500 mm)大蛋盘,承载之后重量大,支撑柱容易变形。

|
| 图 1 150枚型箱式孵化蛋车 Fig.1 150 pieces box-type hatching egg vehicle |
如图 2所示,150枚蛋盘平铺在双导轨支撑板上,两端设有防蛋盘脱离钩,防脱钩的高度为6 mm。支撑板长约1.5 m,为防止支撑板中间变形而导致蛋盘落下,在2根平行支撑板之间设有3根联筋。大型支撑式装卸装置的伸缩臂虽能深入蛋盘之间空隙,但由于联筋的阻碍,无法取出蛋盘,目前均是依靠人工装卸,蛋车对装卸机械臂的限制条件如表 1所示。

|
| 图 2 150枚型箱式孵化蛋车结构 Fig.2 The structure of the 150 pieces box-type hatching egg vehicle |
| 参数 | 数值 |
| 蛋车层间隙/mm | 108 |
| 装载鸡蛋后剩余间隙/mm | 40 |
| 防脱钩高度/mm | 6 |
| 蛋车支撑边框联筋距蛋车端面最小距离/mm | 170 |
| 每盘鸡蛋约重(含盘)/kg | 10 |
| 蛋盘的长×宽/mm×mm | 720×500 |
受蛋盘之间小间隙和联筋的阻碍作用,关节型和直角坐标型的机械臂无法完成蛋盘的装卸工作。针对该问题,本文设计组合式机构,以此构成装卸机械臂,使伸缩臂未过蛋盘重心点也能托起蛋盘,同时将蛋盘绕过防脱钩,从蛋车上拖下。采用多自由度机械臂进行蛋盘装卸,主要受限于支撑边框的联筋,机械臂的伸缩臂伸入蛋车大于1/2蛋盘长度时,受联筋影响将无法拖出蛋盘,因为此时联筋介于伸缩臂和蛋盘之间。若机械臂的伸缩臂伸入蛋车小于1/2蛋盘长度时,伸缩臂将无法支起蛋盘将其拖出蛋车。伸缩臂托住蛋盘,需要抬起到一个大于防脱钩的高度,然后拖出蛋盘,以避免防脱钩的影响。
为了解决上述受限问题,装卸机械臂由2个机构组成,一个是升降机构,另一个是具有高度差的剪叉式装卸机构。升降架提供上下移动副,导轨和同步带组合的伸缩臂以及传送带机构各实现1个移动副和1个转动副,共计3个自由度。升降机构主要实现不同层位蛋盘的定位,以及蛋盘的上下传送。具有高度差的装卸机构,实现蛋盘的装卸功能。卸蛋盘时,伸缩臂勾住蛋盘,沿水平导轨拖动,传送带将蛋盘送至检测工作台。装蛋盘时,蛋盘在传送带的拖动下由检测工作台输送至蛋车的层位上,然后伸缩臂再推动蛋盘的边框,将蛋盘卡进防脱钩内。
1.3 升降机构的结构设计如图 3所示,升降机构主要由驱动电机、4组平行导轨、4组同步带传动模组、双链传动机构、掉电报闸模组以及升降平台组成。升降机构采用4组平行导轨,便于约束升降平台在上下运动时不会出现前后和左右摆动,保证剪叉式装卸机构与蛋车的等距定位。4组同步带传动模组实现升降平台在受力不均时,仍保证升降平台水平。

|
| 1—机架;2—垂直导轨;3—驱动电机;4—传动链;5—掉电报闸 图 3 升降机构 Fig.3 Lifting mechanism |
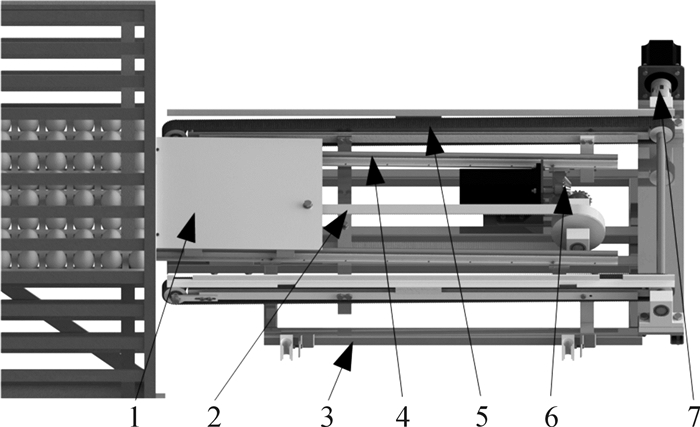
蛋车装卸机械臂需实现将蛋盘搬运至检测工作台,完成检测后,将蛋盘送回原蛋层位置。采用刚性的传递机构,如导轨同步带模组、导轨丝杆模组,能够实现蛋盘的拖出,但无法实现将蛋盘再传送给检测工作台,因为刚性传递机构的有效行程小于传动机构的总长。采用柔性的传递机构,如周向传送带,能够实现蛋盘的传递,但是实现不了从蛋车上取出蛋盘。为了实现既能取出蛋盘,又能传送蛋盘,采用刚性传递机构和柔性传递机构相结合的方案,将导轨同步带模组和传送带模组结合,组成类似剪叉式的组合机构。伸缩臂在同步带的带动下伸入蛋车将蛋盘拖出,并拖动蛋盘行至剪叉机构中心处,蛋盘的支撑点由伸缩臂落到传送带模组上。伸缩臂继续前移,伸缩臂上的挂钩将低于传送的高度。传送带带动蛋盘继续前移,将蛋盘送至检测工作台。剪叉式装卸机构的结构如图 4所示。
|
| 1—伸缩臂;2—同步带;3—升降平台;4—导轨;5—传送带;6—同步带机构驱动电机;7—传送带机构驱动电机 图 4 剪叉式装卸机构 Fig.4 Scissor type combination mechanism |
采用的胚蛋绝大多数为白皮蛋,白皮胚蛋自由落体至蛋盘后破损的平均高度为100 mm,转换为胚蛋自由落体至蛋盘的最大速度为1.4 m/s,这表明在蛋盘的装卸以及传送过程中突变速度不能超过1.4 m/s。
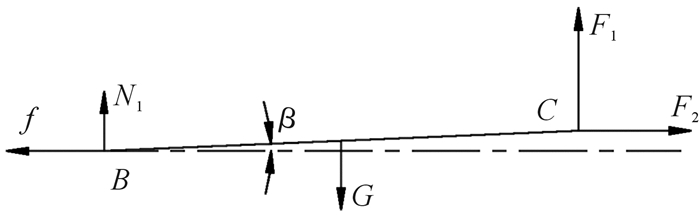
2.1 升降机构静力学分析在卸盘的过程中,升降平台带动蛋盘上升运动瞬间,蛋盘的一端受到升降平台给予的向上的支撑力F1。蛋盘在升降平台的带动下,发生平移而产生水平拉力F2。蛋盘受力分析如图 5所示,其中:BC为受到机械臂给予支撑力后倾斜的蛋盘,β为蛋盘与水平的夹角。
|
| 图 5 蛋盘受力图 Fig.5 Egg plate force diagram |
蛋盘受力平衡方程:
| $ \left\{ \begin{align} &\sum{{{F}_{x}}=0={{F}_{1}}-f} \\ &\sum{{{F}_{y}}=0=G-{{N}_{1}}-F} \\ &\sum{{{M}_{B}}=0=\frac{1}{2}}G{{l}_{BC\cos \beta }}-F{{l}_{BC\cos \beta }} \\ \end{align} \right. $ | (1) |
式中:F1为升降平台给予蛋盘的支撑力,N;F2为升降平台给予蛋盘的水平拉力,N;N1为蛋车给予蛋盘的支撑力,N;MB为蛋盘绕B点的力矩,Nm;f为蛋车对蛋盘的摩擦力,N。
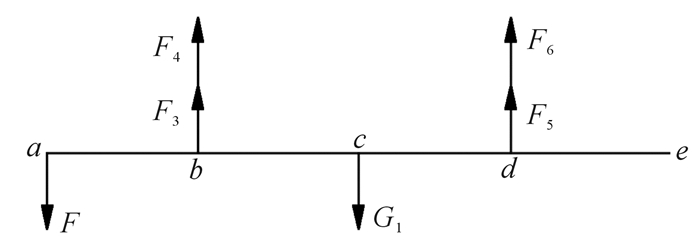
卸盘时升降平台受到蛋盘一端给予的反作用力F,4根同步带给予的拉力F3=F4,F5=F6,自身重力为G1。假设升降平台和4根导轨垂直,升降平台上下运动时不存在卡轴,同时忽略导轨滑块间的摩擦力,升降平台受力如图 6所示,其中:a, e为升降平台的左、右端面;b, d为4组同步带模组与升降平台的连接点;c为升降平台的中心。
|
| 图 6 升降平台受力分析 Fig.6 Lifting platform force analysis |
升降平台受力平衡方程:
| $ \left\{ \begin{align} &F={{F}_{1}}=\frac{1}{2}G \\ &{{F}_{3}}={{F}_{4}} \\ &{{F}_{5}}={{F}_{6}} \\ &\sum{{{F}_{x}}=0={{F}_{1}}+{{G}_{1}}-2{{F}_{3}}-2{{F}_{5}}} \\ &\sum{{{M}_{e}}=0={{F}_{1}}{{L}_{ae}}+{{G}_{1}}{{L}_{ce}}-2{{F}_{5}}{{L}_{de}}-2{{F}_{3}}{{L}_{be}}} \\ \end{align} \right. $ | (2) |
式中:F3,F4为前端同步带对蛋盘的拉力,N; F5, F6为后端同步带对蛋盘的拉力,N; G1为升降平台的重力,N; Me为升降平台对e点的平衡力矩,Nm。
2.2 升降机构动力学分析蛋盘装卸过程中,不能出现大的颠簸和振动。为了防止蛋胚受损,机械臂运行中不能出现动能的突变,因此在机械臂稳定运转状态下需对周期性的速度波动进行有效优化。蛋盘受到升降平台瞬时冲击时,蛋盘和升降平台的接触点速度一致。将蛋盘、升降平台构建成一个机构,蛋盘简化为右端绕着左端旋转的均质摇杆,蛋盘右端的速度为υ1,蛋盘的角速度为ω1,升降平台简化为平动的滑块,速度为υ2。简化的机构在dt瞬时的动能增量为:
| $ \text{d}E=\text{d}\left( {{J}_{1}}\frac{\omega _{1}^{2}}{2}+{{m}_{1}}\frac{\upsilon _{1}^{2}}{2}+{{m}_{2}}\frac{\upsilon _{2}^{2}}{2} \right) $ | (3) |
式中:ω1为蛋盘的角速度, rad/s;υ1为蛋盘右端的速度, m/s;υ2为升降平台的速度, m/s;m1为蛋盘(含胚蛋)的质量, kg;m2为升降平台的质量, kg。
电机作用驱动升降平台,忽略系统工作阻力,只计算蛋盘自重G所作的功,在dt瞬间所做的功为:
| $ \text{d}W=\left( 2{{F}_{3}}{{\upsilon }_{2}}+2{{F}_{5}}{{\upsilon }_{2}}-G{{\upsilon }_{2}} \right)\text{d}t $ | (4) |
根据动能定理,机械系统在某一瞬间其总动能的增量等于在该瞬间作用于机械系统的各外力所做的元功之和[14-18]。
该简化机构的运动方程为:
| $ \begin{align} &\text{d}\left( {{J}_{1}}\frac{\omega _{1}^{2}}{2}+{{m}_{1}}\frac{\upsilon _{1}^{2}}{2}+{{m}_{2}}\frac{\upsilon _{2}^{2}}{2} \right)= \\ &\left[ {{\upsilon }_{2}}\left( 2{{F}_{3}}+2{{F}_{5}}-G \right)-{{M}_{1}}{{\omega }_{1}} \right]\text{d}t \\ \end{align} $ | (5) |
如图 5所示,蛋盘绕B点转动,则式(5) 可转化为:
| $ \begin{align} &\text{d}\left\{ \frac{\omega _{1}^{2}}{2}\left[ {{J}_{1}}+{{m}_{1}}{{\left( \frac{{{\upsilon }_{1}}}{{{\omega }_{1}}} \right)}^{2}}+{{m}_{2}}{{\left( \frac{{{\upsilon }_{2}}}{{{\omega }_{1}}} \right)}^{2}} \right] \right\}= \\ &\ \ \ \ {{\omega }_{1}}\left[ \frac{{{\upsilon }_{2}}\left( 2{{F}_{3}}+2{{F}_{5}}-G \right)}{{{\omega }_{1}}}-{{M}_{1}} \right]\text{d}t \\ \end{align} $ | (6) |
式中M1为蛋盘受到的驱动力矩。
则等效转动惯量为:
| $ {{J}_{\text{e}}}={{J}_{1}}+{{m}_{1}}{{\left( \frac{{{\upsilon }_{1}}}{{{\omega }_{1}}} \right)}^{2}}+{{m}_{2}}{{\left( \frac{{{\upsilon }_{2}}}{{{\omega }_{1}}} \right)}^{2}} $ | (7) |
则等效力矩为:
| $ {{M}_{\text{e}}}=\frac{{{\upsilon }_{2}}\left( 2{{F}_{3}}+2{{F}_{5}}-G \right)}{{{\omega }_{1}}}-{{M}_{1}} $ | (8) |
则将蛋盘简化为摇杆后的等效角加速度为:
| $ a=\frac{\text{d}\omega }{\text{d}t}=\frac{{{M}_{\text{e}}}}{{{J}_{\text{e}}}} $ | (9) |
驱动电机的输出功率取决于负载的势能和动能的变化,机械臂的惯性冲击大小取决于机械臂的等效转动惯量和能量的变化率。升降驱动伺服电机的峰值输出功率为1.2 kW,升降平台的质量约为35 kg,蛋盘(含胚蛋)质量为10 kg。依据上述公式计算,蛋盘装卸过程中末端(D点)受到的峰值加速度为9.36 m/s2。
2.3 缷盘过程中蛋盘受冲击分析蛋盘装卸过程中,蛋盘任一位置的加速度不能过大以防止蛋胚受损,影响蛋胚的再孵化。装盘和卸盘过程中均存在速度突变点,即蛋盘受到的冲击力最大点。卸盘过程是将伸缩臂伸入距蛋盘下沿约5 mm处,后抬升臂座,将蛋盘的一端抬升30 mm,使蛋盘下沿脱离蛋车的蛋盘防脱钩,该过程称为脱钩过程。在伸缩臂的牵引下,蛋盘在脱钩位置进入升降平台的传送带,该过程称为取盘过程。以上2个过程构成卸盘动作,在卸盘过程中分析蛋盘受到的加速度峰值。
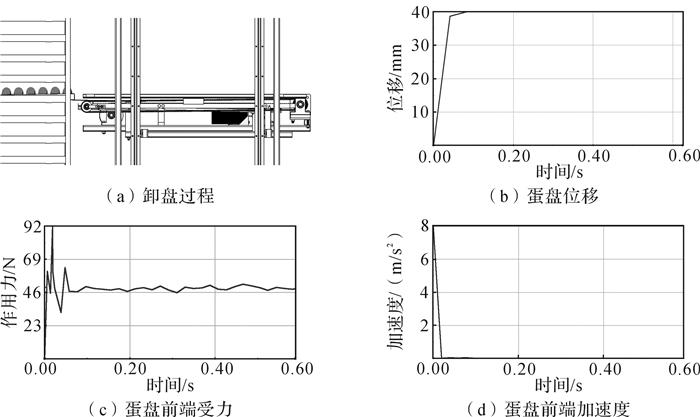
为了避免升降机提升的速度过快,给蛋盘造成过大的冲击,在蛋盘提升40 mm的行程中,采用匀加速、匀速控制方式,先以加速度为5 m/s2抬升5 mm,到达蛋盘的底面,后与蛋盘一起匀速抬升35 mm。则蛋盘所受的瞬时冲击速度的计算式为:
|
| 图 7 卸盘力学特性 Fig.7 Mechanical properties of plate unloading |
伸缩臂伸入蛋车后,在升降机的带动下,给予蛋盘瞬时冲量,受力仿真如图 7,表明蛋盘位移为300 mm的行程内,蛋盘一端受到的瞬时最大拉力约为90 N。达到稳定状态时,蛋盘受到46 N的拉力,约为蛋盘重力的一半,受到的瞬时最大加速度为10 m/s2。
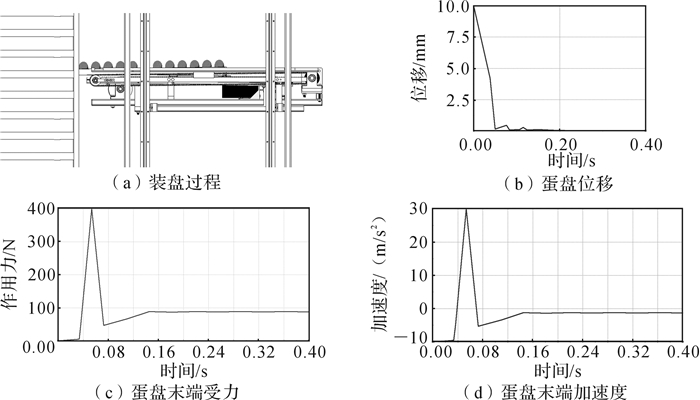
2.4 装盘过程中蛋盘受冲击分析装盘过程,机械臂升降平台将蛋盘送至蛋车层架上沿处,传送带先将蛋盘推入蛋车的蛋层架上,由于传送的推送距离限制,蛋盘末端还没能完全进入蛋车。此时,伸缩臂伸出,顶住蛋盘的边沿,将蛋盘继续推入蛋车。整个过程中蛋盘受到的最大冲击力是伸缩臂将蛋盘推出机械臂自由落体10 mm后所受的冲击。分析装盘过程中,蛋盘受到的加速度峰值。
蛋盘自由落体0.01 m,即
|
| 图 8 装盘力学特性 Fig.8 Mechanical properties of plate loading |
蛋盘在装载过程中受到的峰值冲击,如图 9仿真所示,蛋盘自由落体10 mm后,落在蛋车上受到的峰值力约为400 N,蛋盘稳定后受到蛋车约为100 N的支撑力。
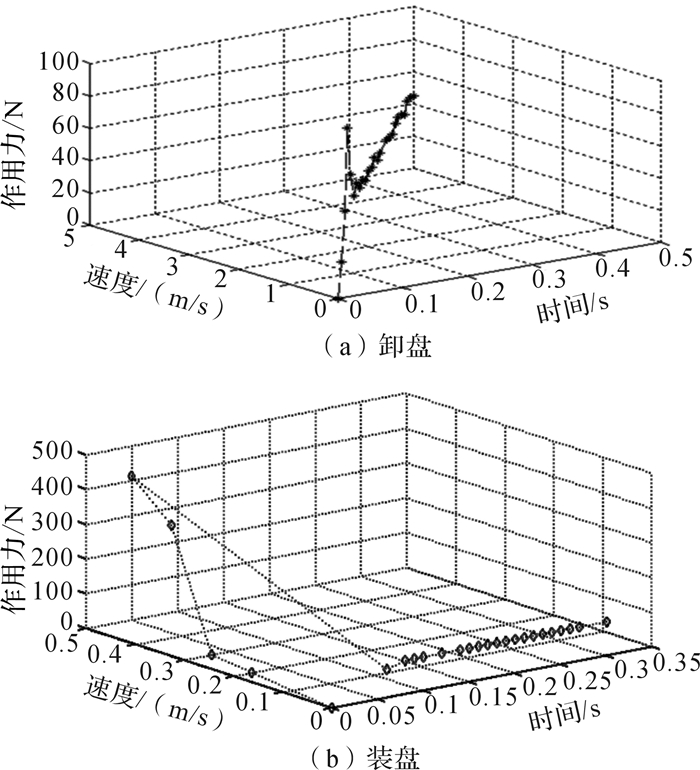
|
| 图 9 装缷盘过程蛋盘受力、速度与时间的关系 Fig.9 The relationship between force, velocity and time in the process of loading and unloading plate |
同时按照装卸仿真的条件,对不同日龄的胚蛋进行100次的装卸试验,未见有胚蛋发生裂纹和破损现象,表明控制系统采用的控制参数满足胚蛋的安全装卸要求。
3 蛋车定位精度和升降平台受力试验验证蛋车装卸机械臂的稳定可靠运行,主要取决于装卸机械臂对蛋车每层蛋托的定位精度,以及装卸机械臂给予蛋盘的最大冲击力。装卸机械臂的定位精度影响蛋盘的装卸成功率,装卸机械臂的最大冲击力应不致胚蛋破损。
3.1 装卸机械臂定位精度的测试应用箱式孵化蛋车装卸机械臂样机(如图 10所示)对蛋车每层蛋托定位精度进行试验验证,试验在某生物疫苗制造公司照蛋间内进行。试验箱式蛋车长为1 700 mm,高为2 100 mm,宽为560 mm,每层间距为108±2 mm,共计16层,每层放置2个蛋盘,第1层距地面高度为340 mm。150枚蛋盘的尺寸为720 mm×500 mm,载蛋后蛋盘总高为55 mm,重约10 kg。装卸机械臂将卸载的蛋盘送至绝对高度为900 mm的检测平台上。

|
| 1—箱式蛋车;2—蛋盘;3—蛋车下定位;4—剪叉式装卸机构;5—升降架;6—蛋车上定位;7—蛋盘水平纠正机构 图 10 样机结构 Fig.10 Prototype structure |
装卸机械臂对箱式蛋车分别进行16层连续装卸测试,结果如表 2所示。试验结果表明样机定位精度高、结构稳定可靠,执行节拍紧凑高效,能够顺利完成蛋盘的装卸工作。机械臂升降平台定位精度高,能够准确定位至蛋盘的支撑轨道处,运行中各部件动作协调,无干涉、卡死、摩擦力突变现象。蛋盘装卸的垂直定位误差为1.6 mm,水平定位误差为0.5 mm,装卸成功率为100%。不计蛋车更换时间,装卸效率达450盘/h,其中完成取盘动作仅为2 s。
| 取盘顺序 | 装卸盘方式 | 误差/mm | 层数 | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 自下而上 | 取本盘送前一盘 | 取盘定位误差 | 0 | 0.2 | 0.2 | 0.3 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.1 | 1.2 | 1.2 | 1.3 | 1.4 | 1.6 | 1.6 |
| 装盘定位误差 | 0.1 | 0.2 | 0.3 | 0.3 | 0.5 | 0.6 | 0.8 | 0.8 | 0.9 | 1.1 | 1.2 | 1.2 | 1.3 | 1.4 | 1.6 | 1.6 | ||
| 取本盘送本盘 | 取盘定位误差 | 0 | 0.2 | 0.2 | 0.3 | 0.6 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | |
| 装盘定位误差 | 0.1 | 0.2 | 0.2 | 0.4 | 0.6 | 0.7 | 0.7 | 0.9 | 0.9 | 1.1 | 1.2 | 1.2 | 1.3 | 1.4 | 1.6 | 1.6 | ||
| 自上而下 | 取本盘送前一盘 | 取盘定位误差 | 1.6 | 1.5 | 1.5 | 1.4 | 1.3 | 1.3 | 1.2 | 1.0 | 0.9 | 0.7 | 0.6 | 0.5 | 0.5 | 0.3 | 0.2 | 0 |
| 装盘定位误差 | 1.5 | 1.4 | 1.4 | 1.3 | 1.2 | 1.2 | 1.1 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.1 | ||
| 取本盘送本盘 | 取盘定位误差 | 1.6 | 1.5 | 1.5 | 1.4 | 1.3 | 1.3 | 1.2 | 1.0 | 0.9 | 0.7 | 0.6 | 0.5 | 0.4 | 0.2 | 0.2 | 0 | |
| 装盘定位误差 | 1.6 | 1.5 | 1.4 | 1.4 | 1.3 | 1.2 | 1.1 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.1 | ||
装卸过程中,蛋盘靠近装卸机械臂一端的胚蛋最容易破损,因此测试该端的受力并进行试验验证。蛋盘的受力与升降平台的左端受力是一对作用力,因而测试蛋盘的受力后转化为测试升降平台左端的受力。在装卸机械臂的4根同步带与升降平台连接处安装拉力传感器,拉力传感器随升降平台上下运动。采用HF-200型拉力传感器,其最大负荷值为200 N,负荷分度值为0.1 N。采用倍加福的多圈绝对编码RHI58N-0AAK1R61N-01024,测量升降平台的瞬时速度。采样频率为50 Hz,采集25个样本数据,记录蛋盘受到的瞬时冲击载荷,评估蛋盘装卸的安全性。
通过装卸机械臂的蛋层位置定位试验,对蛋盘装卸过程中受力测试数据可知:卸盘过程,蛋盘的最大受力为402 N;装盘过程,蛋盘的最大受力为94 N, 与理论分析数据近似。通过蛋盘装卸试验,发现无胚蛋损坏现象。
4 结论1) 设计了针对150枚蛋盘的箱式孵化蛋车装卸机械臂的升降机构,采用双链四平行同步带传动机构,有效解决了升降平台的动态高精度定位产生的平台倾斜问题。在多个平行导轨约束的情况下,未出现升降卡死、脉冲振动、劳损式摩擦,为蛋盘的精确定位提供位置基础。
2) 采用刚性伸缩臂与柔性传送带组合成具有高度差的剪叉式取送盘机构,有效解决了蛋盘支撑导轨间连杆障碍及支撑导轨两端防脱钩的影响。在有限空间下,通过蛋盘的抓取、牵引、传送、推送动作实现了蛋盘的取送功能,解决了箱式孵化蛋车的自动取送盘的关键问题。
3) 通过对蛋盘装卸过程中蛋盘受力的理论分析和仿真,确定胚蛋安全装卸条件。在理论分析的条件下,控制装卸机械臂进行装卸试验。通过样机为期2个月的测试,未出现胚蛋破损现象,试验结果证明,理论分析和仿真确定的装卸条件即为安全装卸条件。
4) 蛋盘装卸的垂直定位误差为1.6 mm,水平定位误差为0.5 mm,装卸成功率为100%。不计蛋车更换时间,装卸效率达450盘/h,其中完成取盘动作仅为2 s。蛋盘在装卸过程中,最大加速度为9.03 m/s2,装卸蛋盘测试中,未出现蛋胚损坏和裂纹现象。装卸机械臂提高了生物制药行业及孵化行业的自动化程度,降低了劳动强度,提高蛋胚检测效率,缩短了胚蛋离开孵化器时间,提高孵化成活率。
| [1] |
闫峰, 张辉.
孵化温湿度对鸡胚尿囊液的影响[J]. 中国兽医杂志, 2011, 47(1): 28–30.
YAN Feng, ZHANG Hui. The incubation temperature and humidity effects on chicken embryo allantoic fluid[J]. Chinese Journal of Veterinary Medicine, 2011, 47(1): 28–30. |
| [2] |
张彦杰, 贾玲霞, 李爱芬, 等.
禽流感H9亚型SD696株疫苗生产工艺改进试验[J]. 中国兽药杂志, 2011, 45(1): 45–48.
ZHANG Yan-jie, JIA Ling-xia, LI Ai-fen, et al. Experiment of improve technological process on avian influenza virus(H9) srain SD696 vaccine production[J]. Chinese Journal of Veterinary Drug, 2011, 45(1): 45–48. |
| [3] |
王红旗, 王庆林.
移动机械手鲁棒自适应模糊控制[J]. 控制与决策, 2010, 25(3): 461–465.
WANG Hong-qi, WANG Qing-lin. Robust and adaptive fuzzy control for mobile manipulator[J]. Control and Decision, 2010, 25(3): 461–465. |
| [4] |
金波, 林龙贤.
果蔬采摘欠驱动机械手爪设计及其力控制[J]. 机械工程学报, 2014, 50(19): 1–8.
JIN Bo, LIN Long-xian. Design and force control of an underactuated robotic hand for fruit and vegetable picking[J]. Journal of Mechanical Engineering, 2014, 50(19): 1–8. |
| [5] | WANG Hai-feng, LI Bin, LIU Guang-yu, et al. Design and test of pineapple harvesting manipulator[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(Supplement 2): 42–46, 5. |
| [6] |
姬伟, 程风仪, 赵德安, 等.
基于改进人工势场的苹果采摘机器人机械手避障方法[J]. 农业机械学报, 2013, 44(11): 253–259.
JI Wei, CHENG Feng-yi, ZHAO De-an, et al. Obstacle avoidance method of apple harvesting robot manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 253–259. DOI:10.6041/j.issn.1000-1298.2013.11.043 |
| [7] |
熊俊涛, 叶敏.
多类型水果采摘机器人系统设计与性能分析[J]. 农业机械学报, 2013, 44(1): 230–235.
XIONG Jun-tao, YE Min. System design and performance analysis on multi-type fruit harvesting robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 230–235. DOI:10.6041/j.issn.1000-1298.2013.01.043 |
| [8] |
刘继展, 刘炜.
面向立柱栽培的移栽机器人设计与协调运动仿真[J]. 农业机械学报, 2014, 45(7): 48–53.
LIU Ji-zhan, LIU Wei. Design and coordinated motion simulation of transplanting robot for column cultivation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7): 48–53. DOI:10.6041/j.issn.1000-1298.2014.07.008 |
| [9] |
王田苗, 陶永.
我国工业机器人技术现状与产业化发展战略[J]. 机械工程学报, 2014, 50(9): 1–13.
WANG Tian-miao, TAO Yong. Research status and industrialization development strategy of chinese industrial[J]. Journal of Mechanical Engineering, 2014, 50(9): 1–13. |
| [10] | KORAYEM M H, NIKOOBIN A, AZIMIRAD V. Maximum load carrying capacity of mobile manipulators optimal control approach[J]. Robotica, 2008, 27(1): 147–159. |
| [11] | GHASEMI M H, KASHIRI N, DARDEL M, et al. Analytical design of optimal trajectory with dynamicload-carrying capacity for cable-suspended manipulator[J]. International Journal of Advanced Manufacturing Technology, 2012, 60(1/4): 317–327. |
| [12] | GASPARETTO A, ZANOTTO V. Optimal trajectory planning for industrial robots[J]. Advances in Engineering Software, 2010, 41(4): 548–556. DOI:10.1016/j.advengsoft.2009.11.001 |
| [13] |
王明顺, 关守平.
一种分类机械手的研制与开发[J]. 东北大学学报(自然科学版), 2006, 27(9): 957–960.
WANG Ming-shun, GUAN Shou-ping. Research and development of a sorting manipulator[J]. Journal of Northeastern University(Natural Science), 2006, 27(9): 957–960. |
| [14] |
付铁, 李金泉.
一种新型高速码垛机械手的设计与实现[J]. 北京理工大学学报, 2007, 27(1): 17–20.
FU Tie, LI Jin-quan. Novel design and implementation of a high-speed palletizing manipulator[J]. Transactions of Beijing Institute of Technology, 2007, 27(1): 17–20. |
| [15] |
李玉航, 梅江平.
一种新型4自由度高速并联机械手动力尺度综合[J]. 机械工程学报, 2014, 50(19): 32–40.
LI Yu-hang, MEI Jiang-ping. Dynamic dimensional synthesis of a 4-DOF high-speed parallel manipulator[J]. Journal of Mechanical Engineering, 2014, 50(19): 32–40. |
| [16] |
杨玉维, 赵新华.
基于多体动力学特性的机械手时间最优轨迹规划[J]. 机械工程学报, 2014, 50(7): 8–13.
YANG Yu-wei, ZHAO Xin-hua. Trajectory optimization of manipulator for minimum working time based on multi-body dynamic characters[J]. Journal of Mechanical Engineering, 2014, 50(7): 8–13. |
| [17] |
陶莎, 胡志华.
单元化三级装卸搬运作业链集成优化的三层进化算法[J]. 系统工程理论与实践, 2014, 34(8): 17–20.
TAO Sha, HU Zhi-hua. A three-stage evolutionary algorithm for three-stage unit material handing operations[J]. Systems Engineering Theory & Practice, 2014, 34(8): 17–20. |
| [18] | HAYASHI S, SHIGEMATSU K, YAMAMOTO S, et al. Evaluation of a strawberry-harvesting robot in a field test[J]. Biosystems Engineering, 2010, 105(2): 160–171. DOI:10.1016/j.biosystemseng.2009.09.011 |



