热熔胶机已在包装、汽车、家具、电子、医疗卫生等民用行业得到广泛的应用[1]。在加热过程中,热熔胶机易受到各种干扰因素的影响,从而会使加热温度出现惯性大、滞后性强和非线性等动态特性,这使得热熔胶机在实际应用中无法很好地由常规PID控制温度[2-3]。
BP神经网络是一种通过不断反向调整网络权值和阈值的多层前馈型网络,具备良好的自适应能力、大规模数据处理能力及分布式存储能力,且具有原理简单、易于实现、能够逼近任意非线性曲线等优点[4-5],已被广泛应用于温度控制系统中的PID参数调整。然而,BP神经网络也存在着众多不可避免的问题[6-7],如对初始值敏感、收敛速度慢等。针对这些问题,国内外诸多学者基于BP神经网络提出了优化改进算法,混沌粒子群优化(chaos particle swarm optimization, CPSO)算法就是其中之一[8-9]。
结合某电子产品组装企业使用的热熔胶机温度控制要求,本文利用CPSO算法在全局搜索上的良好性能[10-11],提出了一种基于CPSO-BP神经网络的自整定PID控制器参数自适应调整算法,该算法可以在线调整PID参数。本文设计的自整定PID控制器作为嵌入式系统的一个温控单元,已投入实际使用。MATLAB仿真结果及实验测试表明,与传统的BP神经网络-PID控制器相比,本文设计的基于CPSO-BP神经网络的自整定PID控制器在温控方面效果更为显著。
1 热熔胶机加热工艺要求根据热熔胶机加热温度的一般特性,如惯性大、滞后性强、严重的时变性和非线性等,合理地调节热熔胶机的燃烧量,快速准确地控制加热温度,对于降低能源消耗,提高加热质量,从而进一步提高熔胶生产的经济效益,具有重要的意义。
根据某电子生产企业的要求,设计的热熔胶机加热温度控制指标如下:1) 温控精度为±4 ℃;2) 最大升温速度≥30 ℃/min;3) 系统最大超调量≤15%;4) 加热温度范围为0~155 ℃。
2 基于BP神经网络的PID控制算法PID控制器参数是决定系统静动态特性的关键因素[12-13],基于BP神经网络的PID控制系统结构如图 1所示。

|
| 图 1 基于BP神经网络的PID控制系统结构 Fig.1 PID control system structure based on BP neural network |
常规数字式PID控制表达式为:
| $ \begin{align} &u\left( k \right)={{K}_{\rm{p}}}e\left( k \right)+{{K}_{\rm{i}}}\sum\limits_{j=1}^{k}{e\left( j \right)T}+ \\ &\ \ \ \ \ \ \ \ \ \ \ {{K}_{\rm{d}}}\frac{e\left( k \right)-e\left( k-1 \right)}{T} \\ \end{align} $ | (1) |
式中:k为采样序号;u(k)为控制器在第k次采样时的输出;Kp,Ki,Kd分别为PID控制器的比例、积分、微分系数,可通过BP神经网络的学习得到最佳组合;T为采样周期;e(k)为第k次采样时的期望输出与实际输出的偏差,即e(k)=x(k)-y(k)。
增量式PID控制算法为:
| $ \begin{align} &\Delta u\left( k \right)={{K}_{\rm{p}}}[e\left( k \right)-e\left( k-1 \right)]+{{K}_{\rm{i}}}e\left( k \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ {{K}_{\rm{d}}}[e\left( k \right)-2e\left( k-1 \right)]+e\left( k-2 \right) \\ \end{align} $ | (2) |
式中Δu(k)为第k次采样时的增量输出。
根据式(2),可以将控制器的输出u(k)描述为与Kp,Ki,Kd,e(k),e(k-1),e(k-2) 等参数有关的非线性函数,即:
| $ \begin{align} &u\left( k \right)=f[u\left( k-1 \right),{{K}_{\rm{p}}},{{K}_{\rm{i}}},{{K}_{\rm{d}}}, \\ &\ \ \ \ \ \ \ \ \ \ e\left( k \right),e\left( k-1 \right),e\left( k-2 \right)] \\ \end{align} $ | (3) |
BP神经网络-PID的网络结构如图 2所示,本文采用的是一个4-5-3的三层前向网络,即4个输入层节点、5个隐含层节点和3个输出层节点。
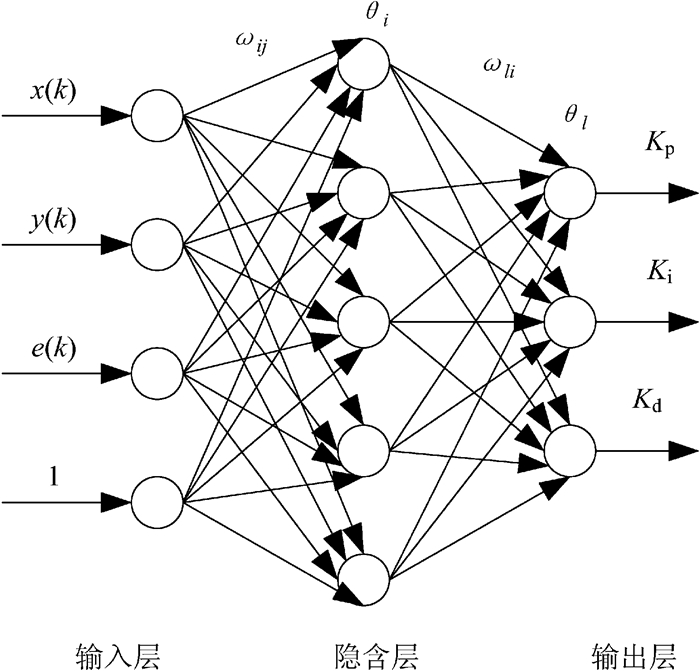
|
| 图 2 BP神经网络-PID的网络结构 Fig.2 Network structure of BP neural network-PID |
网络输入层节点对应于系统运行的状态量,并作归一化处理,可得输入层各节点的状态为:
| $ \left\{ \begin{align} &O_{1}^{\left( 1 \right)}\left( k \right)=x\left( k \right) \\ &O_{2}^{\left( 1 \right)}\left( k \right)=y\left( k \right) \\ &O_{3}^{\left( 1 \right)}\left( k \right)=e\left( k \right) \\ &O_{4}^{\left( 1 \right)}\left( k \right)\equiv x\left( k \right) \\ \end{align} \right. $ | (4) |
式中:x(k)为热熔胶机的理想加热温度值;y(k)为热熔胶机的实际加热温度值;e(k)为k时刻热熔胶机的温度偏差。
网络隐含层的输入-输出关系为:
| $ \left\{ \begin{align} &\text{net}_{i}^{\left( 2 \right)}\left( k \right)=\sum\limits_{j=1}^{4}{\omega _{ij}^{\left( 2 \right)}O_{j}^{\left( 1 \right)}\left( k \right)-\theta _{i}^{\left( 2 \right)}} \\ &O_{i}^{\left( 2 \right)}\left( k \right)=f\left[ \text{net}_{i}^{\left( 2 \right)}\left( k \right) \right] \\ &i=1,2,\cdots 5 \\ \end{align} \right. $ | (5) |
式中:ωij(2)为隐含层权值;θi(2)为隐含层阈值;f[·]为隐含层神经元的激励函数,一般来说,激励函数取正、负对称的Sigmoid函数,即
网络输出层节点分别对应PID控制器的3个可调参数Kp,Ki,Kd,输出层的神经单元激励函数选取非负的Sigmoid函数。网络输出层节点关系为:
| $ \left\{ \begin{align} &\text{net}_{l}^{\left( 3 \right)}\left( k \right)=\sum\limits_{i=1}^{5}{\omega _{li}^{\left( 3 \right)}O_{i}^{\left( 2 \right)}\left( k \right)-\theta _{i}^{\left( 3 \right)}} \\ &O_{l}^{\left( 3 \right)}\left( k \right)=g\left[ \text{net}_{l}^{\left( 3 \right)}\left( k \right) \right] \\ &l=1,2,3 \\ \end{align} \right. $ | (6) |
式中:ωli(3)为输出层权值系数;θl(3)为输出层阈值;g[·]为输出层神经元的激励函数,即g(x)=0.5[1+tanh x]。
公式(4) 至(6) 中的上角标(1),(2),(3) 分别对应输入层、隐含层和输出层。根据式(4) 至(6),可得:
| $ \left\{ \begin{align} &O_{1}^{\left( 3 \right)}\left( k \right)={{K}_{\rm{p}}} \\ &O_{2}^{\left( 3 \right)}\left( k \right)={{K}_{\rm{i}}} \\ &O_{3}^{\left( 3 \right)}\left( k \right)={{K}_{\rm{d}}} \\ \end{align} \right. $ | (7) |
选取性能指标函数为:
| $ E\left( k \right)=\frac{1}{2}{{[x\left( k \right)-y\left( k \right)]}^{2}}=\frac{1}{2}{{e}^{2}}\left( k \right) $ | (8) |
粒子群优化(particle swarm optimization, PSO)算法是由Kennedy和Eberhart等提出的[14-16],其基本原理是:假设该算法中的每个粒子以一定的速度在n维搜索空间中飞行,Xi=[xi1, xi2, …,xin]T为粒子i的当前位置,Vi= [vi1, vi2, …,vin]T为粒子i的当前飞行速度,Pi= [pi1, pi2, …,pin]T为粒子i所经历的最优位置,亦称作Pbesti。
设最小的目标函数为f(X),则粒子i当前的最优位置可更新为:
| $ {{p}_{i}}\left( t+1 \right)=\left\{ \begin{align} &{{p}_{i}}\left( t \right),\ \ \ \ \ f\left( {{X}_{i}}\left( t+1 \right) \right)\geqslant f\left( {{p}_{i}}\left( t \right) \right) \\ &{{X}_{i}}\left( t+1 \right),f\left( {{X}_{i}}\left( t+1 \right) \right) < f\left( {{p}_{i}}\left( t \right) \right) \\ \end{align} \right. $ | (9) |
设N个粒子经过的最优位置Gbest为全局最优位置:
| $ {{G}_{\rm{best}}}\left( t \right)=\min \left\{ f\left( {{p}_{1}}\left( t \right) \right),f\left( {{p}_{2}}\left( t \right) \right)\cdots f\left( {{p}_{N}}\left( t \right) \right) \right\} $ | (10) |
根据个体的飞行经验和群体的飞行经验分别对粒子的飞行速度和位置进行动态调整,更新方程为:
| $ \left\{ \begin{align} &{{v}_{ij}}\left( t+1 \right)=\omega {{v}_{ij}}+{{c}_{1}}{{r}_{1}}[{{p}_{ij}}\left( t \right)-{{x}_{ij}}\left( t \right)]+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{c}_{2}}{{r}_{2}}[{{G}_{\text{best}j}}\left( t \right)-{{x}_{ij}}\left( t \right)] \\ &{{x}_{ij}}\left( t+1 \right)={{x}_{ij}}\left( t \right)+{{v}_{ij}}\left( t+1 \right) \\ \end{align} \right. $ | (11) |
式中:i表示第i个粒子;j表示粒子的第j维;vij(t)表示粒子i在进化到t代时的第j维飞行速度;ω为惯性权系数,由Shi等提出[16],用来平衡全局搜局和局部搜索性能;c1,c2为加速度因子,取c1= c2=2;r1,r2为[0, 1]内的随机数;pij(t)表示粒子i在进化到t代时的第j维个体最优位置;xij(t)为粒子i在进化到t代时的第j维位置坐标;Gbestj(t)为进化到t代时整个粒子群中最优位置的第j维坐标。
实验表明,在算法迭代过程中,线性减小惯性权系数ω,能改善算法的收敛性能[16]。通常ω按式(12) 进行调节:
| $ \omega =\left( {{\omega }_{1}}-{{\omega }_{2}} \right)\times \frac{{{t}_{\rm{m}}}-t}{{{t}_{\rm{m}}}}+{{\omega }_{2}} $ | (12) |
式中:ω1和ω2分别为惯性权系数的初始值和最终值;t和tm分别为当前进化代数和最大进化代数。
混沌算法具有不重复地遍历整个搜索空间的优良特性,当PSO算法陷入局部最优而停滞不前时,可以在规定的解空间范围内进行混沌迭代,使PSO算法跳出局部极值点[17-18]。本文采用以Gbest为中心、R为半径的邻域内进行混沌搜索[19],即:
| $ R=\psi {{G}_{\rm{best}}} $ | (13) |
式中ψ为混沌搜索系数,取1.5。
本文采用最典型的Logistic映射方法对粒子群参数进行优化,即:
| $ {{z}_{n+1}}=\mu {{z}_{n}}\left( 1-{{z}_{n}} \right) $ | (14) |
式中:zn为[0, 1]内的随机数;μ=4。
混沌粒子群优化算法的流程如图 3所示。

|
| 图 3 CPSO算法流程 Fig.3 Flow of CPSO algorithm |
本文采用CPSO算法优化BP神经网络的权值和阈值,并将其看作粒子的位置矢量,将均方差能量函数作为粒子群的适应度函数,则粒子群中第k个粒子的维数为:
| $ {{X}_{k}}=[{{\omega }_{ij}},{{\omega }_{jt}},{{\theta }_{j}},{{\theta }_{t}}] $ | (15) |
式中:i=1, 2, …, 4;j=1, 2, …, 5;t=1, 2, 3;ωij为隐含层权值系数;ωjt为输出层权值系数;θj为隐含层阈值;θt为输出层阈值。
粒子群的适用度函数为:
| $ J\left( t \right)=\frac{1}{N}\sum\limits_{j=1}^{N}{\left( {{y}_{j}}\left( t \right)-\widehat{{{y}_{j}}}\left( t \right) \right)} $ | (16) |
式中:N为群体中的粒子数;
基于CPSO-BP神经网络的PID控制算法归纳如下:
1) 确定BP神经网络的结构:采用4-5-3结构。
2) 设置CPSO算法的参数:初始化粒子群位置x(t)、每个粒子的速度v(t)及每个粒子的个体最优位置pbest和全局最优位置Gbest;根据式(15) 确定粒子的维数,即BP神经网络中的权值和阈值之和,D=4×5+5×3+5+3=43;确定群体中粒子群个数N;根据BP神经网络结构特点,确定初始权系数ω1和结束权系数ω2,惯性权系数ω采用线性递减权值策略,按照式(12) 计算,提高了寻优效果和收敛速度。
3) 按照式(16) 计算每个粒子的适应度。
4) 根据CPSO算法流程确定BP神经网络权值。
5) 采样得到x(k)和y(k),计算第k次采样时的误差e(k)=x(k) -y(k)。
6) 根据式(4) 至(7),可得PID控制器的3个可调参数Kp,Ki,Kd。
7) 根据式(3) 计算PID控制器的输出信号u(k)。
8) CPSO-BP神经网络自适应学习,实时调整权值系数ωij(2)(k),ωli(3)(k),实现PID控制参数的自适应调整。
9) 置k=k+1,返回至3),直至式(8) 的性能指标E(k)满足要求。
4 仿真及实验分析 4.1 仿真分析本文设计的算法用于控制热熔胶机的加热温度,由于热熔胶机的加热温度具有大惯性和强滞后性,因此,热熔胶机加热温度的传递函数为一阶惯性环节加滞后环节,即:
| $ G\left( s \right)=\frac{K{{\rm{e}}^{-\tau s}}}{Ms+1} $ | (17) |
式中:K为比例系数;M为一阶系统的时间常数;τ为滞后时间。
4.1.1 系统在无干扰时的阶跃响应根据热熔胶机的胶箱体积及所需达到的加热温度,式(17) 的M=360 s,K=15,τ=10 s,选取采样周期为τ。仿真时,使用Ziegler-Nichols整定法[20]算出Kp0,Ki0,Kd0作为混沌算法的初始值,之后都用前一轮的Kp,Ki,Kd来进行实时优化控制。阶跃值设为150, 以模拟目标温度为150 ℃。为了验证本算法的优越性,使用MATLAB将本算法与BP神经网络-PID控制进行仿真对比,仿真得到的阶跃曲线如图 4所示,仿真结果对比如表 1所示。
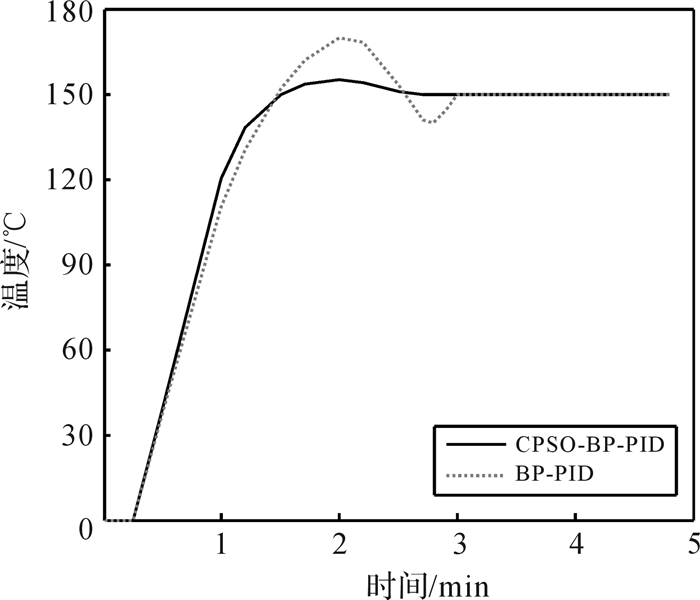
|
| 图 4 系统无干扰时的阶跃响应曲线 Fig.4 Step response curve of system with no disturbance |
| 控制算法 | 超调量/% | 调节时间/min |
| CPSO-BP-PID控制 | 3.98 | 1.5 |
| BP-PID控制 | 11.63 | 2.8 |
从图 4及表 1可知,在相同条件下,本文设计的温控系统算法与传统的BP神经网络-PID控制算法相比,超调量、调节时间明显减小,抗干扰能力增强,稳定速度加快,控制系统的动静态性能均得到改善,温控精度明显提高,很好地解决了热熔胶机加热温度控制强滞后性和大惯性的问题。
4.1.2 系统在受干扰时的响应能力系统进入稳态工作点后,为了观察2种不同控制器的抗干扰特性,在4 min时,给系统加入一定的扰动信号,得到的响应曲线如图 5所示。
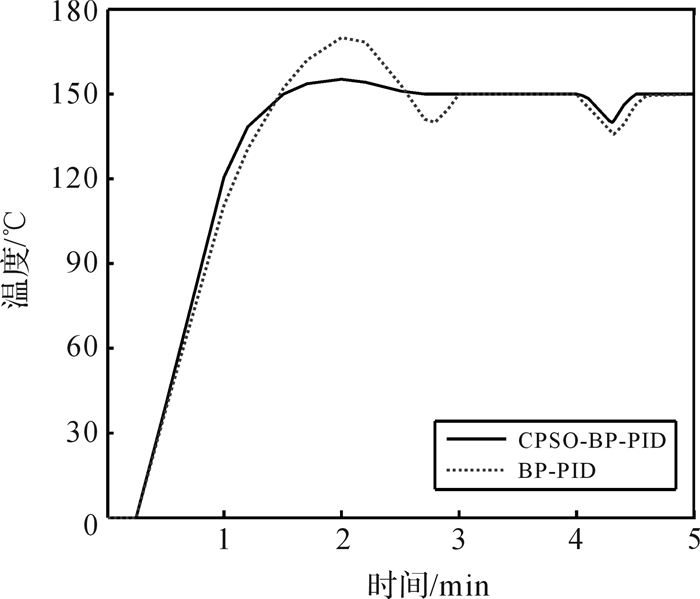
|
| 图 5 抗干扰特性响应曲线 Fig.5 Response curve of anti-jamming characteristics |
由图 5可知,当系统遇到干扰因素时,CPSO-BP神经网络-PID控制器能够及时调整控制参数,有效抑制了外界的随机干扰,而且能够以更快的速度和更小的偏差重新到达预先设定的稳态温度值,其抗干扰性能优于BP-PID控制器。
4.1.3 系统的鲁棒性实际工业生产过程中,生产对象常具有时变性,为验证系统的鲁棒能力,K和τ的值保持不变,M值由360 s变为400 s,得到的系统响应曲线如图 6所示。
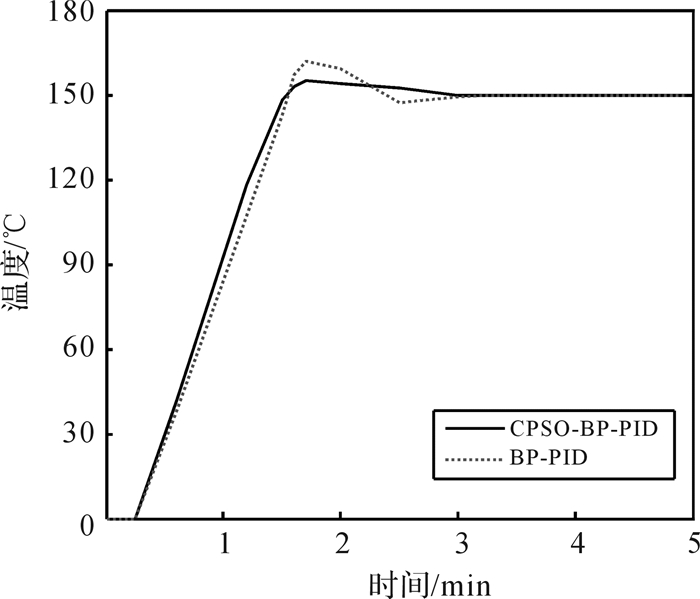
|
| 图 6 时间常数M=400 s时的系统响应曲线 Fig.6 System response curve with time constant of 400 s |
从图 6可以看出,CPSO-BP神经网络-PID控制器使得热熔胶机温控系统具备更高的适应能力和鲁棒性。
4.2 实验分析对采用本文算法控制的热熔胶机进行实际加热温度测量。当热熔胶机加热温度达到恒定温度并稳定后,用标准测温系统进行温度测试。根据记录的数据,进行相应的处理,得到了实测参数值,并与设计参数值进行比较,如表 2所示。
| 参数 | 设计值 | 实测值 |
| 加热温度范围/℃ | 0~155 | 0~160 |
| 达到设定温度时间/min | 5 | 3.5 |
| 温度控制精度/℃ | ±4 | ±2.5 |
由表 2可知,所测得的热熔胶机的加热温度范围、达到设定温度时间和温控精度等参数均优于设计参数,能满足温控系统的加热要求。
5 结论1) 针对热熔胶机加热温度存在惯性大、滞后性强、非线性、易受外界因素干扰等不足,且常规PID控制器难以满足温度控制要求,本文利用CPSO算法在全局搜索上的良好性能,提出了一种基于CPSO-BP神经网络的PID控制器参数自适应调整算法;
2) 采用MTALAB对设计的CPSO-BP神经网络-PID控制器进行了温控系统的仿真分析,仿真结果显示该控制器可实现对热熔胶机温度的精确控制,具有良好的自适应性和鲁棒性;实验测得采用该算法的温控系统能够在3.5 min内达到设定温度,温控精度为±2.5 ℃;
3) 设计的CPSO-BP神经网络-PID控制器作为嵌入式系统的一个控制单元,已投入热熔胶机温控系统实际应用,使用效果表明:温控系统性能稳定,温控精度高,有效实现了热熔胶机加热温度的自动控制,具有良好的实际应用及推广价值。
| [1] |
陆敏智, 许平平.
一种双轴伺服热熔机的研制[J]. 机电工程技术, 2016, 45(8): 125–128.
LU Min-zhi, XU Ping-ping. The research of a biaxial servo fuse machine[J]. Mechanical & Electrical Engineering Technology, 2016, 45(8): 125–128. |
| [2] |
孙灵芳, 邵萌萌, 刘旭颖.
基于改进BP算法的过热汽温建模[J]. 自动化技术与应用, 2010, 29(4): 1–3.
SUN Ling-fang, SHAO Meng-meng, LIU Xu-ying. Superheated steam temperature modeling based on improving BP algorithm[J]. Techniques of Automation and Applications, 2010, 29(4): 1–3. |
| [3] |
王秋平, 马春林, 肖玲玲, 等.
基于蚁群算法-BP神经网络的主蒸汽温度控制系统仿真研究[J]. 热力发电, 2013, 42(11): 64–68.
WANG Qiu-ping, MA Chun-lin, XIAO Ling-ling, et al. Main steam temperature control based on ant colony optimization algorithm and BP neural network[J]. Thermal Power Generation, 2013, 42(11): 64–68. DOI:10.3969/j.issn.1002-3364.2013.11.064 |
| [4] | LI J K, GUO B, SHEN Y, et al. A modeling approach for energy saving based on GA-BP neural network[J]. Journal of Electrical Engineering & Technology, 2016, 11(5): 1289–1298. |
| [5] |
刘国斌, 龚国芳, 朱北斗, 等.
基于BP神经网络的盾构推进速度自适应PID控制[J]. 工程设计学报, 2010, 17(6): 454–458.
LIU Guo-bin, GONG Guo-fang, ZHU Bei-dou, et al. Adaptive PID control for thrust speed of the shield based on BP neural networks[J]. Chinese Journal of Engineering Design, 2010, 17(6): 454–458. |
| [6] | WANG F, ZHU H, LI Y P, et al. Combined transmission laser spectrum of core-offset fiber and BP neural network for temperature sensing research[J]. Spectroscopy and Spectral Analysis, 2016, 36(11): 3732–3736. |
| [7] |
李东洁, 李君祥, 张越, 等.
基于PSO改进的BP神经网络数据手套手势识别[J]. 电机与控制学报, 2014, 18(8): 87–93.
LI Dong-jie, LI Jun-xiang, ZHANG Yue, et al. Gesture recognition of data glove based on PSO-improved BP neural network[J]. Electric Machines and Control, 2014, 18(8): 87–93. |
| [8] |
田东平.
混沌粒子群优化算法研究[J]. 计算机工程与应用, 2013, 49(17): 43–47.
TIAN Dong-ping. Research of chaos particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2013, 49(17): 43–47. DOI:10.3778/j.issn.1002-8331.1204-0599 |
| [9] |
胥小波, 郑康锋, 李丹, 等.
新的混沌粒子群优化算法[J]. 通信学报, 2012, 33(1): 24–30.
XU Xiao-bo, ZHENG Kang-feng, LI Dan, et al. New chaos-particle swarm optimization algorithm[J]. Journal on Communications, 2012, 33(1): 24–30. |
| [10] | PETROVIC M, VUKOVIC N, MITIC M, et al. Integration of process planning and scheduling using chaotic particle swarm optimization algorithm[J]. Expert Systems with Applications, 2016, 64(12): 569–588. |
| [11] | KIM J, JIN M L. Synchronization of chaotic systems using particle swarm optimization and time-delay estimation[J]. Nonlinear Dynamics, 2016, 86(3): 2003–2015. DOI:10.1007/s11071-016-3010-z |
| [12] | ANG K H, CHONG G, LI Y. PID control system analysis, design, and technology[J]. IEEE Transactions on Control Systems Technology, 2005, 13(4): 559–576. DOI:10.1109/TCST.2005.847331 |
| [13] | REN T, LIU S, YAN G C, et al. Temperature prediction of the molten salt collector tube using BP neural network[J]. IET Renewable Power Generation, 2016, 10(2): 212–220. DOI:10.1049/iet-rpg.2015.0065 |
| [14] | KENNEDY J, EBERHART C. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks, Washington, Nov.27-Dec.1, 1995. |
| [15] |
辛儒, 赵永杰, 何俊.
远邻粒子群算法及在Delta机器人优化设计中的应用[J]. 工程设计学报, 2014, 21(4): 334–339.
XIN Ru, ZHAO Yong-jie, HE Jun. Distant neighborhood PSO algorithm and its application on the optimization design of Delta robot[J]. Chinese Journal of Engineering Design, 2014, 21(4): 334–339. |
| [16] | SHI Y H, EBERHART R C. A modified particle swarm optimizer[C]//Proceedings of the IEEE International Conference on Evolutionary Computation. Piscataway, New Jersey:IEEE Press, 1998:69-73. |
| [17] |
陈如清, 俞金寿.
混沌粒子群混合优化算法的研究与应用[J]. 系统仿真学报, 2008, 20(3): 685–688.
CHEN Ru-qing, YU Jin-shou. Study and application of chaos-particle swarm optimization-based hybrid optimization algorithm[J]. Journal of System Simulation, 2008, 20(3): 685–688. |
| [18] |
段艳明.
基于PSO算法和BP神经网络的PID控制研究[J]. 计算机技术与发展, 2014, 24(8): 238–241.
DUAN Yan-ming. Research of PID control based on BP neural network and PSO algorithm[J]. Computer Technology and Development, 2014, 24(8): 238–241. |
| [19] |
廖振兴, 钟伟民, 钱锋.
基于高斯白噪声扰动变异的粒子群优化算法[J]. 华东理工大学学报(自然科学版), 2008, 34(6): 859–863.
LIAO Zhen-xing, ZHONG Wei-min, QIAN Feng. Particle swarm optimization algorithm based on mutation of Gaussian white noise disturbance[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2008, 34(6): 859–863. |
| [20] |
何克忠, 李伟.
计算机控制系统[M]. 北京: 清华大学出社, 1998: 110-120.
HE Ke-zhong, LI Wei. Computer control system[M]. Beijing: Tsinghua University Press, 1998: 110-120. |



