2. 江苏泰隆减速机股份有限公司, 江苏 泰兴 225400
2. Jiangsu Tailong Decelerator Machinery Co., Ltd., Taixing 225400, China
随着科技的进步,齿轮传动正朝着大功率、轻量化、低振动方向发展。对于三支点桥式起重机,由于其支承点少、起重量大、启动频繁,振动问题已成为制约其发展的重要因素,JB/T 8905.1—1999更是将振动作为起重机型式检验的项目之一[1]。国内外学者在齿轮系统的振动特性和减振方面做了大量研究,并取得了许多成果。Parker, Sun及陈洪月等通过建立系统的非线性动力学模型,对系统的振动特性进行了研究[2-4]。Wu, Theodossiades及王连生等运用多体动力学和牛顿力学方法分析了齿轮系统的振动特性,并通过试验加以验证[5-7]。Lin等考虑系统的内部动态激励,运用有限元法计算了齿轮系统的动态响应,并通过试验验证了分析的准确性[8]。陆波等考虑传动系统内部激励和外部激励的影响,对系统振动特性和结构噪声进行了数值仿真[9]。周建星等采用FEM/BEM方法研究了转速和负载对减速器振动噪声的影响[10]。Tuma通过优化齿轮参数和箱体刚度来减小齿轮箱振动[11]。Bruyère, Ghosh, 唐进元及王峰等以传动误差、啮入冲击力等为优化目标,确定了轮齿的最优修形方式和修形量,成功减小了系统的振动[12-15]。综上所述,前人的工作主要集中于系统的振动特性分析,并通过轮齿修形来达到减振的目的,针对齿轮系统相关参数对振动特性的影响规律还缺乏研究。
本文综合考虑轮齿啮合关系、轴承支承关系及齿轮系统内部动态激励,建立三支点桥式起重机整体有限元分析模型,采用模态叠加法实现动态响应和结构噪声的准确预估,并分别研究了模数、螺旋角、轴承支承刚度等对系统振动特性和结构噪声的影响规律,为起重机减振降噪设计提供理论依据。
1 三支点桥式起重机有限元模型 1.1 齿轮系统内部动态激励模拟桥式起重机减速器采用四级平行轴斜齿轮的传动形式,各级齿轮副的主要参数如表 1所示,其额定工况:输入转速为980 r/min,输入功率为30 kW。
| 参数 | 输入级 | 中间级Ⅰ | 中间级Ⅱ | 输出级 |
| 齿数z1, z2 | 18, 71 | 19, 67 | 20, 70 | 17, 69 |
| 模数mn/mm | 3 | 4.5 | 6 | 9 |
| 螺旋角β/(°) | 13 | 13 | 13 | 13 |
| 齿宽B/mm | 50 | 70 | 100 | 140 |
| 中心距a/mm | 140 | 200 | 280 | 400 |
| 变位系数x1, x2 | 0.5, 0.568 8 | 0.321 2, 0 | 0.5, 0.000 5 | 0.321 2, 0 |
齿轮系统内部动态激励是齿轮系统产生振动的重要原因。各级齿轮副的内部动态激励计算式为[8]:
| $ F\left( t \right)=\Delta k\left( t \right)\centerdot e\left( t \right)+S\left( t \right) $ | (1) |
式中:F(t)为内部载荷激励,Δk(t)为时变啮合刚度,e(t)为齿面综合误差,S(t)为冲击激励。
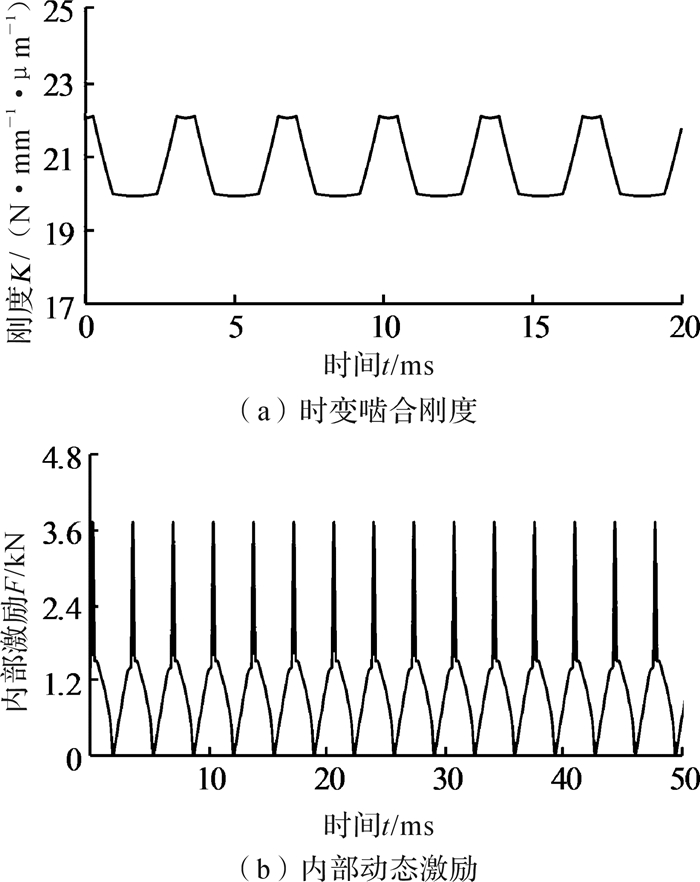
采用有限元法计算各级齿轮副的啮合刚度和冲击激励,同时根据轮齿加工精度,拟合得到齿轮传动误差,按照式(1) 并考虑各级齿轮副重合度,可得内部动态激励。输入级齿轮副的啮合刚度和内部动态激励如图 1所示。
|
| 图 1 输入级齿轮副的啮合刚度和内部动态激励 Fig.1 Meshing stiffness and internal dynamic excitation of input-stage gear pair |
根据齿轮系统结构及传动参数,利用ANSYS软件构建了包括箱体、齿轮、传动轴、轴承、卷筒和电机等的齿轮系统实体模型,采用Solid185单元结合自由网格和映射网格的划分方法对桥式起重机进行网格划分,其中齿轮、轴、轴承等采用六面体单元,箱体、端盖等采用四面体单元,划分时应尽量保证整体网格的均匀性,并时刻检查网格质量,防止网格的突变和畸变。
在啮合轮齿间添加啮合刚度模拟轮齿啮合,在轴和轴承座间建立弹簧单元模拟轴承支承,弹簧刚度是通过计算各零件的受力和变形,结合轴承刚度计算公式确定[16],各轴承支承刚度kij (i=1, 2…10; j=x, y, z)如表 2所示。最终桥式起重机有限元模型如图 2所示,共计节点为129 587个,单元为296 487个。
| (N·m-1) | ||||
| 轴承编号 | 轴承型号 | kx | ky | kz |
| 1 | 22210C | 3.59×108 | 3.21×108 | 1.74×107 |
| 2 | 22210C | 6.18×108 | 6.18×108 | 3.34×107 |
| 3 | 32314 | 3.79×108 | 9.68×108 | 7.33×107 |
| 4 | 32314 | 6.39×108 | 5.34×108 | 6.35×107 |
| 5 | 22318C | 5.20×108 | 1.22×109 | 9.17×107 |
| 6 | 22318C | 7.36×108 | 1.17×109 | 1.03×108 |
| 7 | 22324C | 9.29×108 | 1.99×109 | 1.45×108 |
| 8 | 22324C | 9.13×108 | 1.59×109 | 1.30×108 |
| 9 | 23048C | 1.60×109 | 2.69×109 | 9.97×107 |
| 10 | 23048C | 3.04×108 | 1.97×109 | 5.44×107 |

|
| 图 2 桥式起重机有限元模型 Fig.2 Finite element model of bridge crane |
在桥式起重机有限元模型基础上,对电机旁螺纹孔和卷筒两端支承架底部施加零位移约束,采用分块Lanczos法对齿轮系统进行约束模态分析,表 3给出了齿轮系统的前15阶固有频率。
| 模态阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 固有频率f/Hz | 9.61 | 20.59 | 53.57 | 66.39 | 88.34 | 94.23 | 107.6 | 143.2 | 180.73 | 213.3 | 240.9 | 255.6 | 317.4 | 340.5 | 362.1 |
根据输入转速和齿轮参数计算可得各传动轴转频及各级齿轮副啮合频率,如表 4所示。可以看出,最大激励频率为294 Hz,当系统的高阶固有频率远大于该频率时,模态能量占比较低,对系统振动影响较小。同时,各级转频或啮合频率与齿轮系统低阶固有频率相差较大,因而激起桥式起重机共振的可能性不大。
| 传动轴 | 输入轴 | 中间轴Ⅰ | 中间轴Ⅱ | 中间轴Ⅲ | 输出轴 |
| 转频fz/Hz | 16.33 | 4.14 | 1.17 | 0.34 | 0.08 |
| 齿轮副 | 输入级 | 中间级Ⅰ | 中间级Ⅱ | 输出级 | |
| 啮合频率fc/Hz | 294 | 78.68 | 23.49 | 5.70 | |
将齿轮系统内部动态激励分解为轴向、径向和周向三个方向的力,按时间步自动加载到各级齿轮副接触线上,并对电机旁螺纹孔和卷筒两端支承架底部施加零位移约束,采用模态叠加法对桥式起重机进行动态响应分析,求解时取前200阶模态进行叠加,截止频率为2 567 Hz,取时间步长Δt=0.17 ms,求解总时间t=650 ms,结构阻尼比为0.04。
为验证仿真结果的准确性,在江苏泰隆减速机股份有限公司的协助下,搭建了如图 3所示的桥式起重机试验平台,2个齿轮箱采用背靠背的方式连接,被测齿轮箱接驱动电机,陪试齿轮箱接水力测功机,测试工况与仿真分析一致。

|
| 图 3 桥式起重机试验平台 Fig.3 Test platform of bridge crane |
取箱体轴承座处6个不同位置的点作为动态响应测点,如图 4所示。各测点3个方向的振动加速度有效值如表 5所示,对比可知,仿真值与测试值比较吻合,最大相对误差为12.6%。

|
| 图 4 桥式起重机动态响应测点 Fig.4 Dynamic responsefor test points of bridge crane |
| 方向 | 对比项 | 测点1 | 测点2 | 测点3 | 测点4 | 测点5 | 测点6 |
| x向 | 仿真值/(m·s-2) | 3.13 | 1.46 | 1.56 | 4.34 | 3.02 | 4.15 |
| 测试值/(m·s-2) | 3.45 | 1.63 | 1.74 | 4.81 | 3.44 | 4.57 | |
| 误差/% | 9.28 | 10.4 | 10.3 | 9.77 | 12.2 | 9.19 | |
| y向 | 仿真值/(m·s-2) | 4.51 | 4.13 | 2.07 | 7.18 | 6.29 | 5.56 |
| 测试值/(m·s-2) | 4.87 | 4.52 | 2.32 | 7.61 | 7.11 | 6.02 | |
| 误差/% | 7.39 | 8.62 | 10.8 | 5.65 | 11.5 | 7.64 | |
| z向 | 仿真值/(m·s-2) | 7.18 | 4.40 | 1.95 | 5.31 | 6.98 | 6.18 |
| 测试值/(m·s-2) | 7.65 | 4.81 | 2.23 | 5.84 | 7.54 | 6.65 | |
| 误差/% | 6.14 | 8.52 | 12.6 | 9.08 | 7.43 | 7.07 |
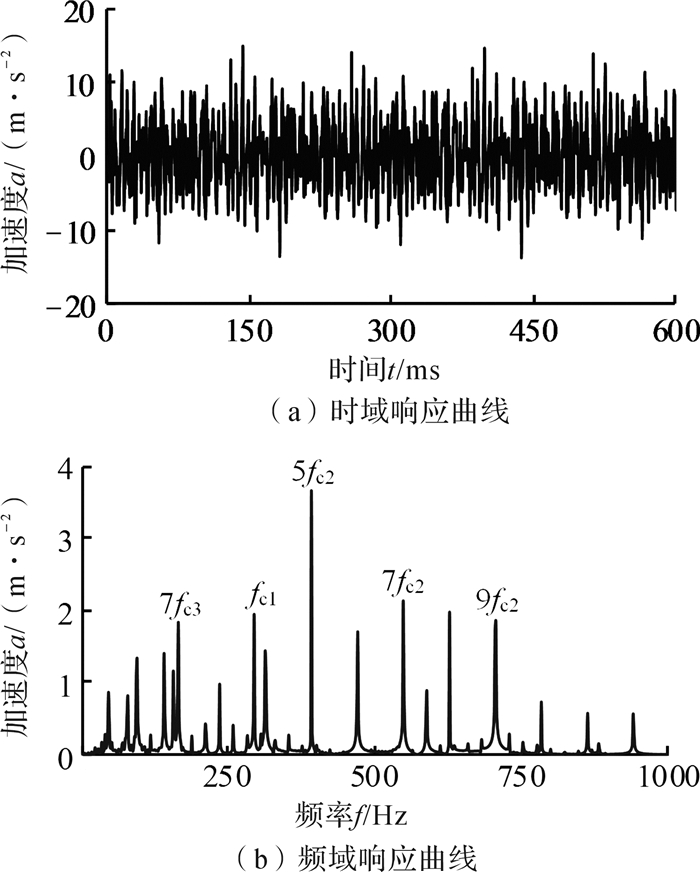
图 5和图 6分别给出了测点4的垂向(y向)振动加速度仿真及测试曲线。可以看出,两者变化规律较为接近,在仿真的频域响应曲线中,垂向振动加速度在中间级I齿轮副啮合频率的五倍频5fc2处最高,而测试的频域响应曲线中,垂向振动加速度在输入级齿轮副啮合频率的二倍频2fc1处最高,对比仿真与测试频域响应曲线发现其主要峰值均出现于各级齿轮副啮合频率及其倍频处,可见啮合频率对齿轮系统振动有较大影响。
|
| 图 5 测点4的垂向振动加速度仿真曲线 Fig.5 Simulation curve of vertical vibration acceleration at test point 4 |

|
| 图 6 测点4的垂向振动加速度测试曲线 Fig.6 Test curve of vertical vibration acceleration at test point 4 |
结构噪声指由于结构振动引起的噪声,它是评价齿轮系统振动性能的重要指标,其中振动加速度级结构噪声广泛应用于齿轮系统的分析和测试中。振动加速度级结构噪声定义为[9, 17-19]:
| $ {{L}_{a}}=20\log \frac{a}{{{a}_{0}}} $ | (2) |
式中:La为加速度级1/3倍频程结构噪声,dB;a为以某一频率为中心频率的频率段的加速度有效值,m/s2;a0为基准加速度,a0=1×10-6m/s2。
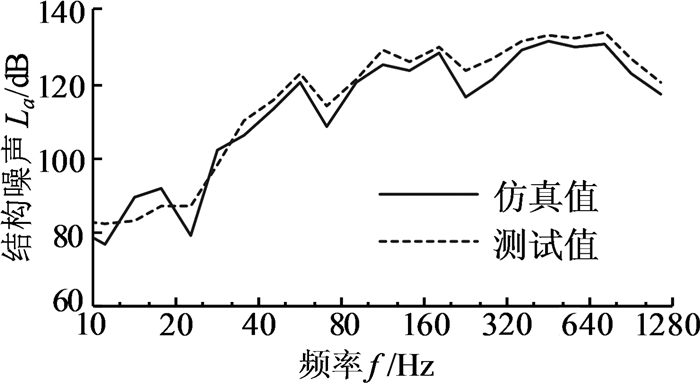
图 7给出了测点4的垂向振动加速度级结构噪声仿真及测试对比曲线。由图可知,结构噪声仿真最大值为131.4 dB,出现在400 Hz处,测试最大值为133.8 dB,出现在630 Hz处,与频域响应相符。同时,结构噪声还在各级齿轮副啮合频率倍频附近出现峰值,可以看出,箱体结构噪声主要是由齿轮啮合振动引起的。
|
| 图 7 测点4结构噪声的仿真与测试曲线对比 Fig.7 Comparison of simulation and test curves of structural noise at test point 4 |
由于桥式起重机减速器体积的限制,因此为保证各级齿轮副中心距不变及总传动比相近,通过调整齿数和变位系数来达到该条件,每级齿轮副分别选取5个模数,从小到大依次组成5组模数系列,如表 6所示。其中输入级齿轮副不同模数时的齿数、变位系数和重合度如表 7所示。
| 模数系列 | 模数mn/mm | 总传动比 | |||
| 输入级 | 中间级Ⅰ | 中间级Ⅱ | 输出级 | ||
| M1 | 2.5 | 3.75 | 5 | 7 | 197.12 |
| M2 | 2.75 | 4 | 5.5 | 8 | 197.43 |
| M3 | 3 | 4.5 | 6 | 9 | 197.59 |
| M4 | 3.25 | 5 | 6.5 | 10 | 198.13 |
| M5 | 3.5 | 5.5 | 7 | 11 | 198.59 |
| 模数mn/mm | 齿数 | 变位系数 | 轴向重合度 | 总重合度 |
| 2.5 | 22,86 | 0.3,0.300 6 | 1.432 | 2.952 |
| 2.75 | 20,79 | 0.05,0.057 8 | 1.302 | 2.909 |
| 3 | 18,71 | 0.5,0.568 8 | 1.193 | 2.565 |
| 3.25 | 17,66 | 0.35,0.154 4 | 1.102 | 2.560 |
| 3.5 | 16,61 | 0.25,0.258 0 | 1.023 | 2.485 |
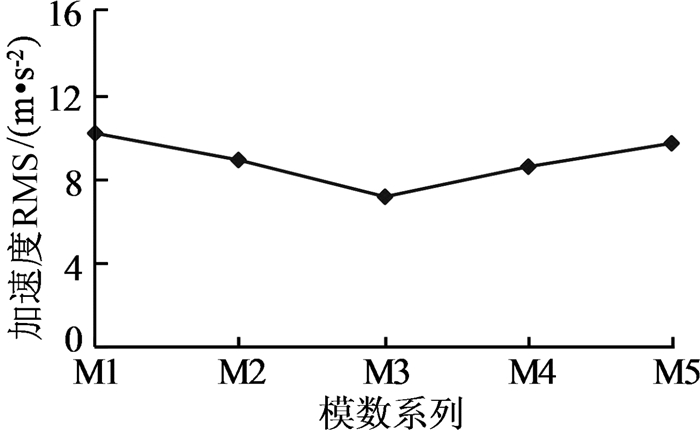
图 8给出了不同模数系列时测点4的垂向振动加速度有效值,随着模数的增大,振动加速度呈现先减小后增大的趋势。由表 7可知,模数增大使轴向重合度减小且逐渐接近于整数,进而啮合刚度峰值减小,刚度激励减小;但模数增大,总重合度减小,冲击激励增大;叠加之后总激励呈现先减小后增大的趋势,这正是振动随模数增大先减小后增大的原因。其它各级齿轮副也有类似规律。
|
| 图 8 不同模数系列时测点4的垂向振动加速度有效值 Fig.8 The RMS value of vertical vibration acceleration with different module series at test point 4 |
与振动变化规律一致,随着模数的增大,结构噪声最大值呈现先减小后增大的趋势。其中模数系列M1时最大,为136.21 dB;模数系列M3时最小,为131.37 dB。不同模数系列时结构噪声峰值均出现在齿轮副啮合频率及其倍频附近。因此模数对振动噪声的影响比较复杂,需根据具体情况确定。
3.2 螺旋角对结构噪声的影响在保证各级齿轮副中心距不变的条件下,通过调整变位系数,研究了各级齿轮副螺旋角分别为9°,10°,11°,12°和13°时齿轮系统振动特性和结构噪声的变化[1]。表 8给出了输入级齿轮副不同螺旋角时的变位系数和重合度,与仅仅增大螺旋角不同的是,调整变位系数并增大螺旋角使端面重合度和轴向重合度均增大。
| 螺旋角 | 变位系数 | 端面重合度 | 轴向重合度 | 总重合度 |
| 9° | 0.9,0.902 4 | 1.212 | 0.830 | 2.042 |
| 10° | 0.8,0.840 7 | 1.251 | 0.921 | 2.172 |
| 11° | 0.7,0.764 1 | 1.290 | 1.012 | 2.303 |
| 12° | 0.6,0.673 2 | 1.331 | 1.103 | 2.434 |
| 13° | 0.5,0.568 8 | 1.371 | 1.193 | 2.565 |
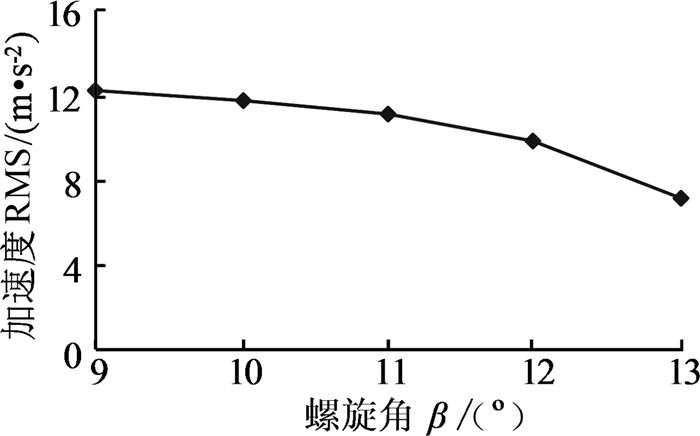
图 9给出了不同螺旋角时测点4的垂向振动加速度有效值,随着螺旋角的增大,振动加速度呈现减小趋势。原因是螺旋角增大使轴向重合度接近整数后又远离整数,则刚度激励先减小后增大;而螺旋角增大使总重合度增大,则冲击激励减小,叠加之后总激励减小。其它各级齿轮副也有类似规律。
|
| 图 9 不同螺旋角时测点4的垂向振动加速度有效值 Fig.9 The RMS value of vertical vibration acceleration with different helix angle at test point 4 |
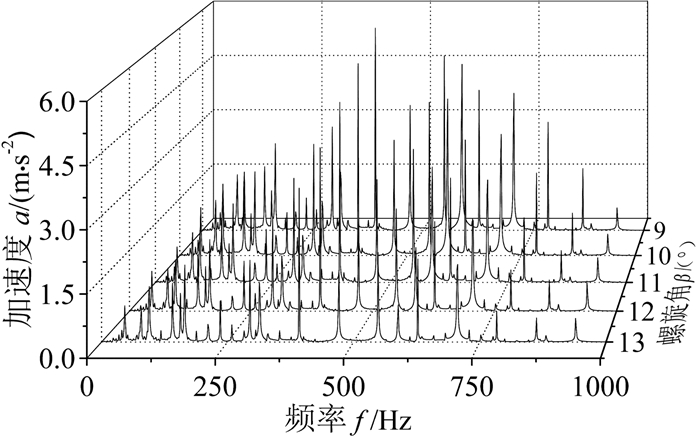
图 10给出了不同螺旋角时测点4的垂向振动加速度频谱图。可以看出:螺旋角增大使频域响应最大值降低,与振动变化规律一致;同时频域响应高频成分减小,尤其是在2fc1处,β=9°时加速度峰值为4.52 m/s2,而β=13°时加速度峰值仅为0.89 m/s2。
|
| 图 10 不同螺旋角时测点4的垂向加速度频谱图 Fig.10 Spectrum of vertical vibration acceleration with different helix angle at test point 4 |
图 11给出了不同螺旋角时测点4的垂向振动加速度级结构噪声。螺旋角增大使结构噪声最大值减小,与振动变化规律一致,其中β=9°时最大,为137.75 dB,β=13°时最小,为131.37 dB;同时螺旋角增大使最大值频率降低,当β=9°和β=11°时,结构噪声的最大值出现在630 Hz处。但不同螺旋角时的结构噪声规律基本相同,其峰值均出现在齿轮副啮合频率及其倍频附近。因此在保证中心距不变的情况下,适当增大螺旋角可以降低齿轮系统的振动噪声。

|
| 图 11 不同螺旋角时测点4的垂向振动加速度级结构噪声 Fig.11 Structural noise of vertical vibration acceleration level with different helix angle at test point 4 |
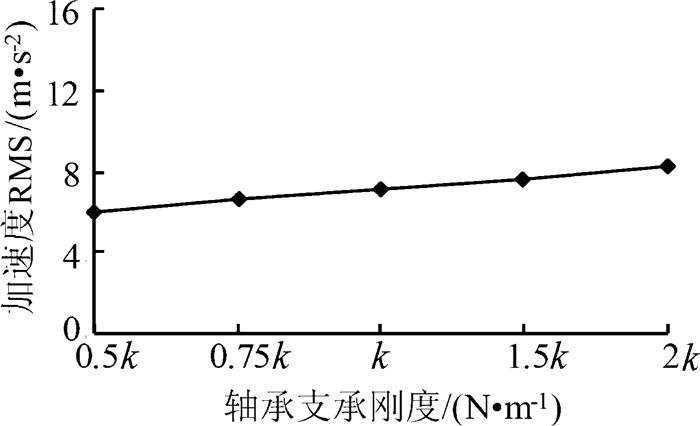
轴承对传动系统起支承作用,不仅影响传动系统的固有频率,还关系着整个系统的运转稳定性。图 12给出了5种支承刚度(0.5k,0.75k,k, 1.5k和2k, k为初始支承刚度)时测点4的垂向振动加速度有效值。可以看出,随着轴承支承刚度的增大,振动加速度呈现增大的趋势。
|
| 图 12 不同支承刚度时测点4的垂向振动加速度有效值 Fig.12 The RMS value of vertical vibration acceleration with different bearing stiffness at test point 4 |
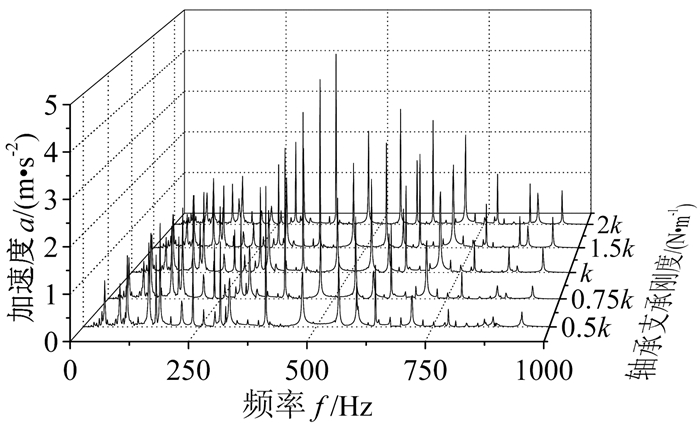
图 13给出了不同支承刚度时测点4的垂向振动加速度频谱图。可以看出:随着支承刚度的增大,频域响应最大值增大,与振动变化规律一致;同时频域响应低频率成分减小,高频率成分增大。
|
| 图 13 不同支承刚度时测点4的垂向振动加速度频谱图 Fig.13 Spectrum of vertical vibration acceleration with different bearing stiffness at test point 4 |
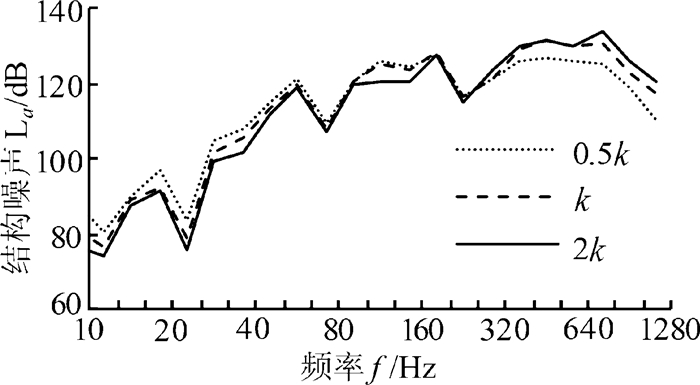
图 14给出了不同轴承支承刚度时测点4的垂向振动加速度级结构噪声。支承刚度增大使结构噪声最大值增大,其中刚度为0.5k时最小,为127.9 dB,刚度为2k时最大,为134.1 dB;同时结构噪声低频幅值降低,高频幅值增大。不同支承刚度时结构噪声各频带分布规律基本相同,其峰值均出现在齿轮副啮合频率及其倍频附近。
|
| 图 14 不同支承刚度时测点4的垂向振动加速度级结构噪声 Fig.14 Structural noise of vertical vibration acceleration level with different bearing stiffness at test point 4 |
阻尼比用于表达结构阻尼的大小,是结构的动力特性之一,是描述结构在振动过程中能量耗散的因素。图 15给出了结构阻尼比分别为0.03,0.04,0.05和0.06时测点4的垂向振动加速度有效值。随着结构阻尼比的增大,振动加速度呈现减小的趋势,因为结构阻尼比越大,其衰减作用也越大。

|
| 图 15 不同阻尼比时测点4的垂向振动加速度有效值 Fig.15 The RMS value of vertical vibration acceleration with different damping ratio at test point 4 |
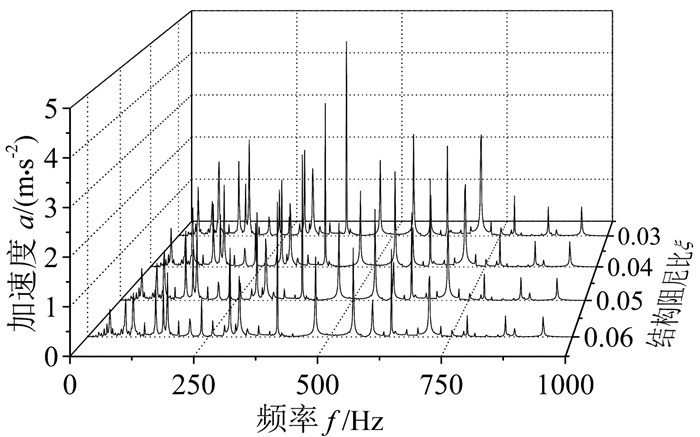
图 16给出了不同结构阻尼比时测点4的垂向振动加速度频谱图。可以看出:结构阻尼比不影响振动加速度的频率成分,随着结构阻尼比的增大,振动加速度各频率幅值依次减小;同时频域响应最大值减小,与振动变化规律一致。
|
| 图 16 不同阻尼比时测点4的垂向振动加速度频谱图 Fig.16 Spectrum of vertical vibration acceleration with different damping ratio at test point 4 |
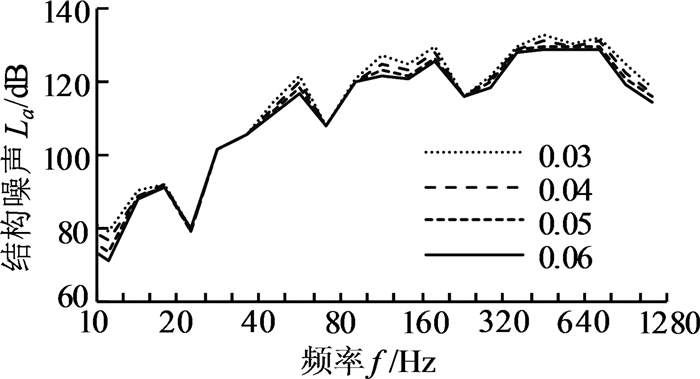
图 17给出了不同结构阻尼比时测点4的垂向振动加速度级结构噪声。阻尼比增大使结构噪声各频段幅值均减小,其中阻尼比为0.03时最大,为133.21 dB;阻尼比为0.06时最小,为129.19 dB。结构噪声峰值均出现在齿轮副啮合频率及其倍频附近。
|
| 图 17 不同阻尼比时测点4的垂向振动加速度级结构噪声 Fig.17 Structural noise of vertical vibration acceleration level with different damping ratio at test point 4 |
分别计算了5种载荷(0.5F,0.75F,F,1.5F和2F,F为额定工况载荷)作用下的齿轮系统振动噪声。图 18给出了不同负载时测点4的垂向振动加速度频谱图。可以看出:负载不影响振动加速度频率成分,随着载荷的增大,振动加速度各频率幅值均增大。

|
| 图 18 不同载荷时测点4的垂向振动加速度频谱图 Fig.18 Spectrum of vertical vibration acceleration with different loads at test point 4 |
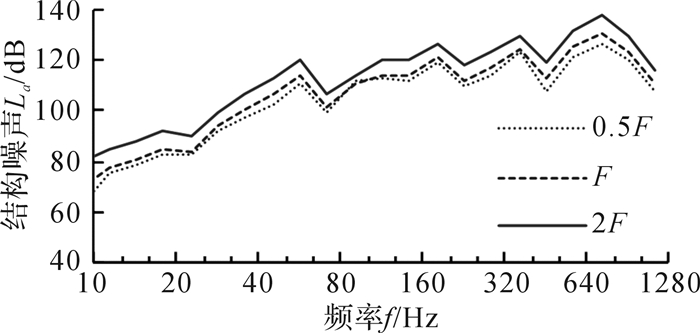
图 19给出了不同载荷时测点4的垂向振动加速度级结构噪声。由图可知结构噪声随载荷的增大而增大,其中载荷为0.5F时结构噪声的最大值为126.76 dB,载荷为F时为131.12 dB,载荷为2F时为138.18 dB;不同载荷时结构噪声各频带分布规律基本相同,其峰值均出现在齿轮副啮合频率及其倍频附近。
|
| 图 19 不同载荷时测点4的垂向振动加速度级结构噪声 Fig.19 Structural noise of vertical vibration acceleration level with different loads at test point 4 |
1) 利用ANSYS软件建立了三支点桥式起重机整体有限元分析模型,采用模态叠加法计算了齿轮系统的振动特性和结构噪声,通过与试验结果对比(以测点4为例)可知,两者吻合良好,验证了建模和仿真分析方法的可行性。
2) 随着模数的增大,齿轮副重合度改变,齿轮系统振动加速度有效值和结构噪声最大值先减小后增大,影响规律较为复杂;螺旋角增大使振动加速度高频成分、结构噪声最大值及最大值所对应频率降低,因此适当增大螺旋角可降低齿轮系统的振动和噪声。
3) 轴承支承刚度增大使振动加速度和结构噪声低频成分减小,高频成分增大,同时结构噪声最大值增大;结构阻尼比和负载的改变不影响振动加速度的频率成分,适当增大结构阻尼比或减小负载可减小系统的振动和噪声。
| [1] |
赵光德, 李鹏. 起重机用三支点减速器: JB/T 8905. 1-1999[S]. 北京: 机械工业出版社, 2000: 6-25.
ZHAO Guang-de, LI Peng. Three-point support gearboxes for cranes:JB/T 8905.1-1999[S]. Beijing:China Machine Press, 2000:6-25. |
| [2] | PARKER R G, VIJAYAKAR S M, IMAJO T. Non-linear dynamic response of a spur gear pair:modeling and experimental comparisons[J]. Journal of Sound and Vibration, 2000, 237(3): 435–455. DOI:10.1006/jsvi.2000.3067 |
| [3] | SUN Tao, HU Hai-yan. Nonlinear dynamics of a planetary gear system with multiple clearances[J]. Mechanism and Machine Theory, 2003, 38(12): 1371–1390. DOI:10.1016/S0094-114X(03)00093-4 |
| [4] |
陈洪月, 刘烈北, 毛君, 等.
激励与滚筒振动耦合下采煤机动力学特性分析[J]. 工程设计学报, 2016, 23(3): 228–234.
CHEN Hong-yue, LIU Lie-bei, MAO Jun, et al. The analysis of the shearer dynamic feature in the coupling relation between the motivation and the drum vibration[J]. Chinese Journal of Engineering Design, 2016, 23(3): 228–234. |
| [5] | WU Y R, TRAN V T. Dynamic response prediction of a twin-screw compressor with gas-induced cyclic loads based on multi-body dynamics[J]. International Journal of Refrigeration, 2016, 65: 111–128. DOI:10.1016/j.ijrefrig.2015.12.002 |
| [6] | THEODOSSIADES S, De la CRUZ M, RAHNEJAT H. Prediction of airborne radiated noise from lightly loaded lubricated meshing gear teeth[J]. Applied Acoustics, 2015, 100: 79–86. DOI:10.1016/j.apacoust.2015.06.014 |
| [7] |
王连生, 郝志勇, 郑康, 等.
考虑齿轮阻滞力矩的变速箱敲击噪声仿真与试验[J]. 浙江大学学报(工学版), 2014, 48(5): 911–916.
WANG Lian-sheng, HAO Zhi-yong, ZHENG Kang, et al. Simulation and experiment on transmission gear rattle considering drag torque[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(5): 911–916. |
| [8] | LIN Teng-jiao, HE Ze-yin, GENG Fei-yu, et al. Prediction and experimental study on structure and radiation noise of subway gearbox[J]. Journal of Vibroengineering, 2013, 15(4): 1838–1846. |
| [9] |
陆波, 朱才朝, 宋朝省, 等.
大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J]. 振动与冲击, 2009, 28(4): 76–80.
LU Bo, ZHU Cai-chao, SONG Chao-sheng, et al. Coupled nonlinear dynamic characteristics analysis and noise estimation of a large burden marine gearbox[J]. Journal of Vibration and Shock, 2009, 28(4): 76–80. |
| [10] |
周建星, 刘更, 吴立言.
转速与负载对减速器振动噪声的影响研究[J]. 振动与冲击, 2013, 32(8): 193–198.
ZHOU Jian-xing, LIU Geng, WU Li-yan. Effect of operating conditions on vibration and noise radiation of a gear reducer[J]. Journal of Vibration and Shock, 2013, 32(8): 193–198. |
| [11] | TUMA J. Gearbox noise and vibration prediction and control[J]. International Journal of Acoustics and Vibration, 2009, 14(2): 99–108. |
| [12] | BRUYERE J, VELEX P. A simplified multi-objective analysis of optimum profile modifications in spur and helical gears[J]. Mechanism and Machine Theory, 2014, 80: 70–83. DOI:10.1016/j.mechmachtheory.2014.04.015 |
| [13] | GHOSH S S, CHAKRABORTY G. On optimal tooth profile modification for reduction of vibration and noise in spur gear pairs[J]. Mechanism and Machine Theory, 2016, 105: 145–163. DOI:10.1016/j.mechmachtheory.2016.06.008 |
| [14] |
唐进元, 刘继凯, 雷敦财.
基于Romax与Kisssoft软件的齿形优化设计与分析[J]. 机械传动, 2011, 35(2): 1–3.
TANG Jin-yuan, LIU Ji-kai, LEI Dun-cai. Optimization design and analysis of tooth profile based on Romax and Kisssoft software[J]. Journal of Mechanical Transmission, 2011, 35(2): 1–3. |
| [15] |
王峰, 方宗德, 李声晋, 等.
齿面三维修形对人字齿轮振动特性影响分析与试验研究[J]. 振动工程学报, 2016, 29(2): 220–230.
WANG Feng, FANG Zong-de, LI Sheng-jin, et al. A theoretical and experimental investigation on effect of three dimensional modification on vibration characteristics of herringbone gear system[J]. Journal of Vibration Engineering, 2016, 29(2): 220–230. |
| [16] |
林腾蛟, 郭进, 刘波, 等.
风电增速箱结合部刚度分析及振动噪声预估[J]. 重庆大学学报(自然科学版), 2015, 38(1): 87–94.
LIN Teng-jiao, GUO Jin, LIU Bo, et al. Junction stiffness analysis and vibration noise prediction of wind power speed-increase gearbox[J]. Journal of Chongqing University(Natural Science Edition), 2015, 38(1): 87–94. |
| [17] | ISO Technical Committees. Mechanical vibration, shock and condition monitoring-vocabulary:ISO 2041-2009[S]. Switzerland:ISO Copyright Office, 2009:1-14. |
| [18] | ISO Technical Committees. Acoustics-preferred reference values for acoustical and vibratory levels:ISO 1683-2008[S]. Switzerland:ISO Copyright Office, 2015:1-3. |
| [19] |
马大猷.
现代声学理论基础[M]. 北京: 科学出版社, 2004: 33-34.
MA Da-you. Basic theory of modern acoustics[M]. Beijing: Science Press, 2004: 33-34. |


