2. 中南大学 机电工程学院, 湖南 长沙 410083
2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
周向拉杆转子是重型(发电)燃气轮机、部分航空发动机、船舶用发动机以及汽轮机等重大装备的核心部件,它通过多根拉杆将多级轮盘压紧组合而成,非连续的结构使其远比整体转子结构复杂。由于机组长期在高温、强载荷等复杂环境下服役,其性能将逐步退化,据不完全统计,燃气轮机等发生的各类型故障或事故中约58%是周向拉杆转子损伤所引起的[1]。因此,对周向拉杆转子进行损伤研究并掌握损伤对致裂寿命的影响,对保障燃气轮机长期安全运行有非常重要的意义。
在高温、复杂应力工况下,损伤作用易使周向拉杆转子产生裂纹,最终导致其断裂。在导致周向拉杆转子寿命损耗的因素中,一般蠕变约占20%,而疲劳则占80%[2],因此,对周向拉杆转子整体疲劳损伤的研究势在必行。目前国内外学者利用损伤力学对疲劳损伤进行的研究较多,如:Jing等[3]利用损伤力学对汽轮机转子的低周疲劳进行了研究,考虑了多轴应力的影响,得到了损伤非线性累计模型,其分析结果更加接近实际;Nayebi等[4]利用Lemaitre连续介质损伤模型建立了汽轮机转子的疲劳-蠕变损伤模型,得出了转子应力应变的演化关系;Kumar等[5]采用有限元技术建立了汽轮机叶片模型,并结合连续介质损伤方法评估了低周疲劳损伤的演化过程,给出了损伤指标;Mashayekhi等[6]建立了描述多轴应力损伤非线性发展的低周循环热疲劳模型,考虑了随温度变化的材料参数、载荷施加时非等温条件以及载荷施加顺序等,并且用工业应用实例验证了该模型的可行性;刘宁波[7]利用损伤力学建立了航空发动机轮盘损伤演化模型和寿命预测模型,为航空发动机寿命预测提供了理论依据;李雅武等[8]对30Cr1Mo1V转子钢低周疲劳性能及损伤演变规律进行了研究;高鹏[9]对涡轮盘蠕变及低周疲劳寿命可靠性进行了分析。
然而,以上利用损伤力学对疲劳损伤进行研究的对象均是单个元件,因此研究中所使用的解析模型也仅适用于单个元件。但周向拉杆转子是由多个元件构成,由单个元件的损伤预测其整体损伤的机理还不明确,也就无法根据单个元件的损伤计算整体损伤的大小。因此,建立周向拉杆转子整体疲劳损伤的解析模型,揭示元件损伤与整体损伤的关系,对提高转子运行安全,防止重大事故的发生具有重要意义。本文建立了考虑轮盘间接触效应的周向拉杆转子模型,通过理论分析得出其各组成部分刚度及整体的等效刚度,运用损伤力学对周向拉杆转子燃烧室、透平端拉杆和周向拉杆转子整体进行疲劳损伤分析,揭示周向拉杆转子的整体疲劳损伤与元件损伤以及致裂寿命的关系,为周向拉杆转子的结构设计和寿命预测提供理论依据。
1 考虑界面接触效应的周向拉杆转子建模 1.1 虚拟材料法燃气轮机周向拉杆转子由均布拉杆将轮盘、轴头等结构预紧成一个整体,轮盘之间存在接触效应,使得转子存在边界非线性的问题,因此难以用一个简单的力学模型来描述,这加大了转子动态特性分析的难度[10]。为了提高转子动力学分析的精度和效率,利用虚拟材料法解决周向拉杆转子轮盘间接触效应问题。
虚拟材料法是将固定结合部的2个接触面的微观接触部分假设为一种虚拟的各向同性材料,通过该材料的弹性模量、泊松比、厚度、密度等参数的数学模型来模拟接触面的接触效应[11]。
虚拟材料的弹性模量、泊松比、厚度和密度的数学模型分别为[12]:
| $ E = E\left( {{E_1},{E_2},{\mu _1},{\mu _2},{R_{{\rm{a}}1}},{R_{{\rm{a}}2}},P} \right) $ | (1) |
| $ \nu = \nu \left( {{E_1},{E_2},{\mu _1},{\mu _2},{R_{{\rm{a}}1}},{R_{{\rm{a}}2}},P} \right) $ | (2) |
| $ h = h\left( {{\sigma _{\rm{p}}},d} \right) $ | (3) |
| $ \rho = \rho \left( {{\rho _1},{\rho _2},{h_1},{h_2}} \right) $ | (4) |
虚拟材料各参数的理论计算公式如下:
| $ {E_{\rm{c}}} = \frac{{{2^{0.5D}}D{\psi ^{1 - 0.5D}}}}{{3{\rm{ \mathit{ π} }}\sqrt {\rm{ \mathit{ π} }} }}E'{G^{1 - D}}a_1^{0.5D}\left( {a_{\rm{c}}^{ - 0.5} - a_{\rm{1}}^{ - 0.5}} \right) $ | (5) |
| $ {\nu _{\rm{c}}} = \frac{{\left( {1 + \mu '} \right){E^ * }}}{{G_{\rm{x}}^ * }} - 1 $ | (6) |
| $ {h_{\rm{c}}} = {h_{\rm{1}}} + {h_{\rm{2}}} $ | (7) |
| $ {\rho _{\rm{c}}} = \frac{{{\rho _1}{h_{\rm{1}}} + {\rho _2}{h_{\rm{2}}}}}{{{h_{\rm{1}}} + {h_{\rm{2}}}}} $ | (8) |
式中:D为分形维数;ψ为由分形维数D决定的参数;E′为当量弹性模量;G为分形特征长度尺度;al为最大接触面积;ac为临界接触面积;μ′为当量泊松比;E*为无量纲的虚拟材料弹性模量;Gx*为无量纲的虚拟材料剪切模量;ρ1,ρ2为2个接触体材料密度;h1,h2为结合部2个接触材料微凸体层的厚度。
1.2 周向拉杆转子轮盘结合面接触模型以东方汽轮机有限公司某型燃气轮机周向拉杆转子为对象展开研究。根据工程实际,选取的周向拉杆转子材质为GH4169,该材料密度为7 850 kg/m3,弹性模量为205 GPa,屈服应力为950 MPa,泊松比为0.3,轮盘接触面粗糙度为0.8 μm。压气机端与透平端单根拉杆预紧力F=1.0×106 N,故12根拉杆总预紧力大小为1.2×107 N。
表面粗糙度为0.8 μm时,结合部2个接触材料微凸体层的厚度h1=h2≈0.5 mm[13],由式(7) 可得:
| $ h = {h_1} + {h_2} = 1{\rm{mm}} $ |
即轮盘间虚拟材料层的厚度为1 mm。
图 1为虚拟材料层等效接触界面示意图。

|
| 图 1 虚拟材料层等效接触界面示意图 Fig.1 Schematic of virtual material layer equivalent to contact interface |
根据式(5) 至式(8) 可计算出不同预紧力下虚拟材料层的性能参数值,如表 1所示。
| 预紧力/kN | 性能参数 | ||
| 弹性模量/GPa | 泊松比 | 密度/(kg/m3) | |
| 100 | 10.835 | 0.258 | 7 800 |
| 500 | 42.694 | 0.263 | 7 800 |
| 1 000 | 93.792 | 0.270 | 7 800 |
| 1 500 | 117.355 | 0.276 | 7 800 |
| 2 000 | 147.653 | 0.284 | 7 800 |
由表 1可知,将周向拉杆转子轮盘接触界面等效为虚拟材料层后,随着拉杆预紧力的增加,虚拟材料的弹性模量和泊松比均增大,而密度不变,所以拉杆预紧力的变化可通过改变虚拟材料的弹性模量和泊松比来体现。
1.3 周向拉杆转子等效刚度研究参考某300 MW型燃气轮机周向拉杆转子尺寸参数,利用虚拟材料层等效周向拉杆转子轮盘间的接触界面,建立了周向拉杆转子三维实体模型,如图 2所示,各尺寸参数如表 2所示。周向拉杆转子主要包括压气机端、透平端和燃烧室三部分,其中压气机端和透平端均由多级轮盘通过拉杆预紧在一起。

|
| 图 2 周向拉杆转子三维实体模型 Fig.2 Three-dimensional solid model of circumferential rod fastening rotor |
| 参数 | 量值/mm |
| 转子总长 | 11 582 |
| 压气机端拉杆长度 | 3 802 |
| 透平端拉杆长度 | 1 611 |
| 拉杆直径 | 80 |
| 燃烧室长度 | 1 905 |
| 压气机端4至7级轮盘厚度 | 310 |
| 压气机端8至11级轮盘厚度 | 300 |
| 压气机端12至14级轮盘厚度 | 190 |
| 压气机端15至17级轮盘厚度 | 150 |
| 透平端1,2级轮盘厚度 | 304 |
| 透平端3,4级轮盘厚度 | 205 |
| 轮盘直径 | 1 424 |
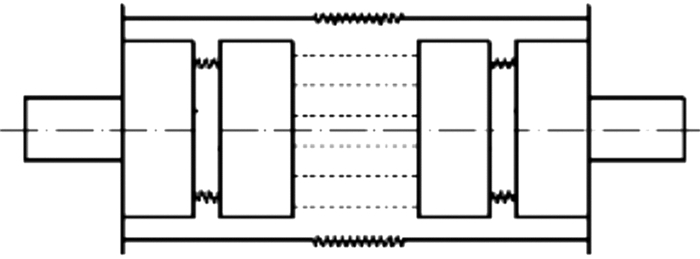
周向拉杆转子的物理模型如图 3所示,其总弯曲刚度可由压气机端弯曲刚度、透平端弯曲刚度和燃烧室弯曲刚度串联求得:
| $ {K_{{\rm{rot}}}} = {\left( {\frac{1}{{{K_{{\rm{com}}}}}} + \frac{1}{{{K_{{\rm{tur}}}}}} + \frac{1}{{{K_{{\rm{axl}}}}}}} \right)^{ - 1}} $ | (9) |
式中:Krot, Kcom, Ktur, Kaxl分别为周向拉杆转子、压气机端、透平端和燃烧室的弯曲刚度。
|
| 图 3 周向拉杆转子物理模型 Fig.3 Physical model of circumferential rod fastening rotor |
压气机端和透平端弯曲刚度由各级轮盘、虚拟材料层和拉杆的弯曲刚度组成,轮盘和虚拟材料层串联后与拉杆并联。因此压气机端和透平端弯曲刚度计算公式可表达如下:
| $ {K_{{\rm{com}}}}\left( {{K_{{\rm{tur}}}}} \right) = {\left( {\frac{{{n_{\rm{d}}}}}{{{K_{\rm{d}}}}} + \frac{{{n_{\rm{c}}}}}{{{K_{\rm{c}}}}}} \right)^{ - 1}} + {K_{\rm{r}}} $ | (10) |
式中:Kd,Kc,Kr为压气机端和透平端轮盘、虚拟材料层及拉杆的弯曲刚度;nd,nc为轮盘数和虚拟材料层数。
因周向拉杆转子在弯曲情况下的受力相对扭转和拉伸情况下复杂,故本文仅对弯曲情况进行研究。下面求轮盘、虚拟材料层、拉杆以及燃烧室弯曲刚度[14]。
1) 轮盘弯曲刚度。
设轮盘在弯矩M作用下的应变能为Ud,则轮盘弯曲刚度可表示为:
| $ {K_{\rm{d}}} = \frac{{{M^2}}}{{2{U_{\rm{d}}}}} $ | (11) |
其中应变能和轮盘惯性矩分别表示为:
| $ {U_{\rm{d}}} = \frac{{{M^2}{l_{\rm{d}}}}}{{2E{I_{{\rm{zd}}}}}} $ | (12) |
| $ {I_{{\rm{zd}}}} = \frac{{{\rm{ \mathit{ π} }}\left( {D_{\rm{d}}^4 - 12d_{\rm{r}}^4} \right)}}{{64}} $ | (13) |
式中:ld为轮盘厚度;Dd为轮盘直径;dr为拉杆直径。
2) 虚拟材料层弯曲刚度。
虚拟材料层弯曲刚度可表示为:
| $ {K_{\rm{c}}} = \frac{{{E_{\rm{c}}}{I_{{\rm{zc}}}}}}{{{l_{\rm{c}}}}} $ | (14) |
其中虚拟材料层惯性矩表示为:
| $ {I_{{\rm{zc}}}} = \frac{{{\rm{ \mathit{ π} }}\left( {D_{\rm{c}}^4 - d_{\rm{c}}^4} \right)}}{{64}} $ | (15) |
式中:lc为虚拟材料层厚度;Dc为虚拟材料层外径;dc为虚拟材料层内径。
3) 拉杆弯曲刚度。
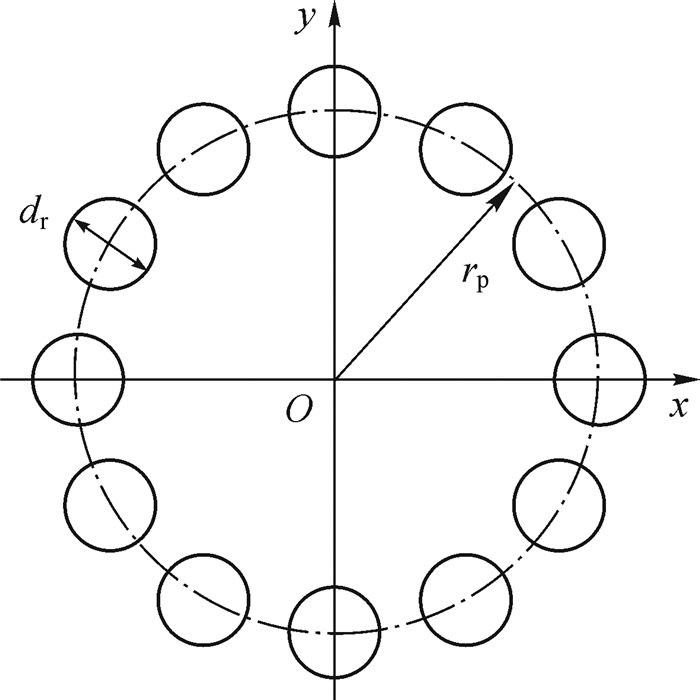
周向拉杆分布如图 4所示,其弯曲刚度可表示为:
| $ {K_{{\rm{rb}}}} = \frac{{{n_{\rm{r}}}{K_{{\rm{ral}}}}r_{\rm{p}}^2}}{2} + {n_{\rm{r}}}{K_{{\rm{rbl}}}} $ | (16) |
|
| 图 4 周向拉杆分布示意图 Fig.4 Schematic of circumferential rod distribution |
其中单根拉杆的轴向刚度Kra1和单根拉杆绕其中心轴的弯曲刚度Krb1可表示为:
| $ {K_{{\rm{ral}}}} = \frac{{AE}}{{{l_{\rm{r}}}}} = \frac{{{\rm{ \mathit{ π} }}d_{\rm{r}}^2E}}{{4{l_{\rm{r}}}}} $ | (17) |
| $ {K_{{\rm{rbl}}}} = \frac{{E{I_{{\rm{zr}}}}}}{{{l_{\rm{r}}}}} = \frac{{{\rm{ \mathit{ π} }}d_{\rm{r}}^2E}}{{64{l_{\rm{r}}}}} $ | (18) |
式中:nr为拉杆数目;rp为拉杆处圆周分布半径。
4) 燃烧室弯曲刚度。
燃烧室弯曲刚度可表示为:
| $ {K_{{\rm{axl}}}} = \frac{{E{I_{{\rm{zaxl}}}}}}{{{l_{{\rm{axl}}}}}} $ | (19) |
其中燃烧室惯性矩可表示为:
| $ {I_{{\rm{zaxl}}}} = \frac{{{\rm{ \mathit{ π} }}\left( {D_{{\rm{axl}}}^4 - d_{{\rm{axl}}}^4 - 12d_{\rm{r}}^4} \right)}}{{64}} $ | (20) |
式中:laxl为燃烧室厚度;Daxl为燃烧室外径;daxl为燃烧室内径。
根据公式(9) 至(20) 求得周向拉杆转子各元件弯曲刚度,如表 3。
| 元件 | 弯曲刚度/(N/m) |
| 轮盘 | 2.16×1011 |
| 拉杆(透平端) | 1.33×109 |
| 拉杆(压气机端) | 5.64×108 |
| 虚拟材料层 | 5.20×1012 |
| 燃烧室 | 2.91×1010 |
| 透平端 | 5.37×1010 |
| 压气机端 | 1.44×1010 |
| 周向拉杆转子 | 8.17×109 |
塑性应变是金属疲劳损伤的主要原因之一,各向同性材料的损伤耗散势一般为[15]:
| $ {\psi ^ * } = \frac{1}{2}\frac{{{Y^2}}}{{{s_0}}}\frac{{\dot p}}{{{{\left( {1 - {D_{\rm{f}}}} \right)}^{{\alpha _0}}}}} $ | (21) |
式中:ψ*为损伤耗散势;
损伤变量为[16]:
| $ {{\dot D}_{\rm{f}}} = \frac{{\partial {\psi ^ * }}}{{\partial Y}} $ | (22) |
损伤能量释放率为[16]:
| $ Y = \frac{{\sigma _{{\rm{eq}}}^2}}{{2E{{\left( {1 - {D_{\rm{f}}}} \right)}^2}}}{R_{\rm{v}}} $ | (23) |
其中三轴因子可表示为:
| $ {R_{\rm{v}}} = \frac{2}{3}\left( {1 + \nu } \right) + 3\left( {1 - 2\nu } \right){\left( {\frac{{{\sigma _{\rm{H}}}}}{{{\sigma _{{\rm{eq}}}}}}} \right)^2} $ | (24) |
式中:Rv为三轴因子;σH为静水压力;σeq为等效应力;ν为泊松比。
将式(21) 和(23) 代入(22) 可得单个循环的损伤变化:
| $ \frac{{{\rm{d}}{D_{\rm{f}}}}}{{{\rm{d}}N}} = \frac{{\sigma _{{\rm{eq}}}^2{R_{\rm{v}}}}}{{2E{s_0}{{\left( {1 - {D_{\rm{f}}}} \right)}^2}}} \cdot \frac{{\dot p}}{{{{\left( {1 - {D_{\rm{f}}}} \right)}^{{\alpha _0}}}}} $ | (25) |
在周期比例加载下,Rv为常数。无损伤时,N=0,Df=0;完全破坏时,N=Nf,Df=1,积分式(25) 得:
| $ {N_{\rm{f}}} = n'\frac{1}{{\left( {3 + {\alpha _0}} \right){R_{\rm{v}}}}} \cdot \frac{{2k'E{s_0}}}{{\sigma _{\rm{a}}^2}}{\left( {\frac{{2k'}}{{{\sigma _{\rm{a}}}}}} \right)^{\frac{1}{{n' - 1}}}} $ | (26) |
| $ {D_{\rm{f}}} = 1 - {\left( {1 - \frac{N}{{{N_{\rm{f}}}}}} \right)^{\frac{1}{{{\alpha _0} + 3}}}} $ | (27) |
式中:n′为循环硬化指数;k′为循环强度指数。
令
| $ {N_{\rm{f}}} = n'\frac{\beta }{{{R_{\rm{v}}}}} \cdot \frac{{2k'E{s_0}}}{{\sigma _{\rm{a}}^2}}{\left( {\frac{{2k'}}{{{\sigma _{\rm{a}}}}}} \right)^{\frac{1}{{n' - 1}}}} $ | (28) |
| $ {D_{\rm{f}}} = 1 - {\left( {1 - \frac{N}{{{N_{\rm{f}}}}}} \right)^\beta } $ | (29) |
以上非线性连续损伤模型考虑了平均应力对低周疲劳损伤的影响,可以用该模型处理多轴复杂应力下的疲劳损伤问题。
2.2 元件并联及串联时疲劳损伤组合模型| $ \sigma = E\left( {1 - {D_{\rm{f}}}} \right)\varepsilon $ |
利用上述定义,可得损伤变量的另一定义[19]:
| $ {D_{\rm{f}}} = 1 - \frac{{K'}}{K} $ | (30) |
1) 元件并联时的疲劳损伤。
总位移:
| $ {L_{\rm{p}}} = {l_1} = \cdots = {l_i} $ | (31) |
总弯曲刚度:
| $ {K_{\rm{p}}} = \sum\limits_{i = 1}^n {{k_i}} $ | (32) |
总受力:
| $ {F_{\rm{p}}} = \sum\limits_{i = 1}^n {{F_i}} = \sum\limits_{i = 1}^n {{k_i}\left( {1 - {d_i}} \right)l} $ | (33) |
式中di为单个元件的损伤值。
由以上并联关系并结合式(30) 可得出元件并联时总损伤为:
| $ {D_{{\rm{fp}}}} = \frac{{\sum\limits_{i = 1}^n {{k_i}{d_i}} }}{{{K_{\rm{p}}}}} $ | (34) |
2) 元件串联时的疲劳损伤。
总位移:
| $ {L_{\rm{s}}} = \sum\limits_{i = 1}^n {{l_i}} $ | (35) |
总弯曲刚度:
| $ \frac{1}{{{K_{\rm{s}}}}} = \sum\limits_{i = 1}^n {\frac{1}{{{k_i}}}} $ | (36) |
总受力:
| $ {F_{\rm{s}}} = {F_1} = \cdots {F_i} = K\left( {1 - D} \right)L = {k_i}\left( {1 - {d_i}} \right)l $ | (37) |
由以上串联关系并结合式(30) 可得出元件串联时总损伤为:
| $ {D_{{\rm{fs}}}} = 1 - \frac{1}{{{K_{\rm{s}}}\sum\limits_{i = 1}^n {\frac{1}{{{k_i}\left( {1 - {d_i}} \right)}}} }} $ | (38) |
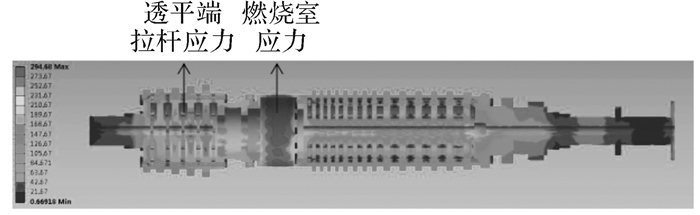
对周向拉杆转子进行有限元分析可知,燃烧室和透平端拉杆处应力最大(如图 5所示),因此这2处最容易发生疲劳损伤。故本文仅考虑燃烧室和透平端拉杆对周向拉杆转子损伤的影响。
|
| 图 5 周向拉杆转子等效应力分布 Fig.5 Equivalent stress distribution of circumferential rod fastening rotor |
由公式(34) 计算得出透平端损伤:
| $ {D_{{\rm{tur}}}} = {D_{{\rm{turr}}}} = \frac{{\sum\limits_{i = 1}^n {{k_{{\rm{turr}}i}}{d_{{\rm{turr}}i}}} }}{{{K_{{\rm{tur}}}}}} $ | (39) |
式中:Dturr为透平端拉杆损伤,kturri为透平端单根拉杆弯曲刚度,dturri为透平端单根拉杆损伤,其中i=1, 2,…,12。
透平端与燃烧室段串联,由公式(38) 最终计算得出周向拉杆转子整体损伤:
| $ {D_{{\rm{rot}}}} = 1 - \frac{1}{{{K_{{\rm{rot}}}}\left[ {1/{K_{{\rm{tur}}}}\left( {1 - {D_{{\rm{tur}}}}} \right) + 1/{K_{{\rm{axl}}}}\left( {1 - {D_{{\rm{axl}}}}} \right)} \right]}} $ | (40) |
公式(40) 考虑了周向拉杆转子元件损伤对整体损伤的影响,可解决由元件损伤预测整体损伤的问题。且该方法在周向拉杆转子拉伸、扭转情况下同样适用,因篇幅有限,本文不作叙述。
2.3.1 周向拉杆转子元件疲劳损伤分析根据有限元分析得出的周向拉杆转子等效应变,如图 6所示,从材料手册[20]查得k′=1 481 MPa,n′=0.098,s0通常为0.40~0.45[21],本文取0.42。

|
| 图 6 周向拉杆转子等效应变分布 Fig.6 Equivalent creep strain distribution of circumferential rod fastening rotor |
通过公式(24)、(28) 和(29) 可计算出燃烧室损伤和透平端单根拉杆损伤。
1) 燃烧室损伤。
| $ {R_{{\rm{v}},{\rm{axl}}}} = 1.425 $ | (41) |
| $ {N_{{\rm{axlf}}}} = \frac{{4.1825}}{{{R_{{\rm{v}},{\rm{axl}}}}}}\Delta \varepsilon _{\rm{P}}^{ - 1.1086} $ | (42) |
| $ {D_{{\rm{axl}}}} = 1 - {\left( {1 - \frac{N}{{{N_{\rm{f}}}}}} \right)^{0.4022}} $ | (43) |
2) 透平端单根拉杆损伤。
| $ {R_{{\rm{v}},{\rm{tur}}}} = 1.509 $ | (44) |
| $ {N_{{\rm{turf}}}} = \frac{{6.8721}}{{{R_{{\rm{v}},{\rm{tur}}}}}}\Delta \varepsilon _{\rm{P}}^{ - 1.1086} $ | (45) |
| $ {d_{{\rm{turr}}i}} = 1 - {\left( {1 - \frac{N}{{{N_{\rm{f}}}}}} \right)^{0.5512}} $ | (46) |
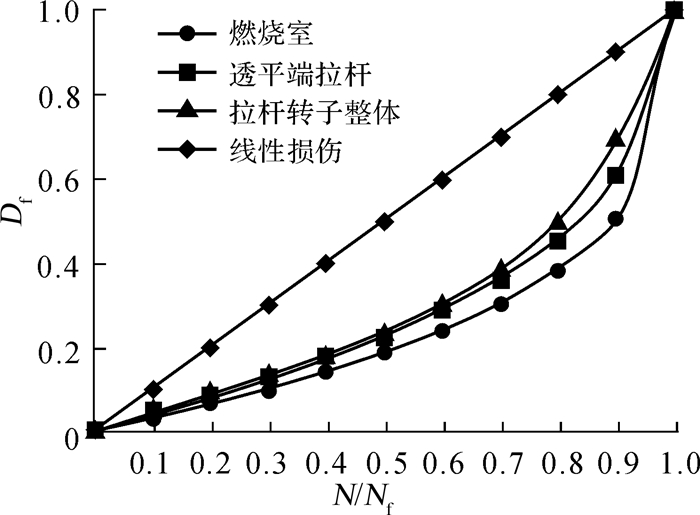
透平端拉杆均匀损伤时,由公式(39)、(40) 和(43) 可计算得出燃烧室、透平端拉杆和周向拉杆转子损伤结果。对比Miner线性损伤累积理论[22],结合本文所得三轴损伤值可得出损伤曲线,如图 7。
|
| 图 7 线性损伤与非线性损伤曲线对比 Fig.7 Comparison of linear and nonlinear damage curves |
由图 7可知:
1) 利用非线性疲劳损伤模型分析周向拉杆转子元件及整体损伤时,损伤和致裂寿命是一个复杂的、非线性的关系,而非简单的线性关系。
2) 在N/Nf≤0.9,损伤随着N/Nf的增加而均匀增加;在N/Nf≥0.9后,损伤急剧增加;当N/Nf=1时,损伤值达到1,表明周向拉杆转子彻底断裂。
3) 周向拉杆转子整体损伤大小由燃烧室和透平端拉杆损伤决定,整体损伤的值大于燃烧室和透平端拉杆损伤。
2.3.3 透平端拉杆非均匀损伤时转子整体损伤分析1) 透平端拉杆中仅有部分拉杆存在损伤。
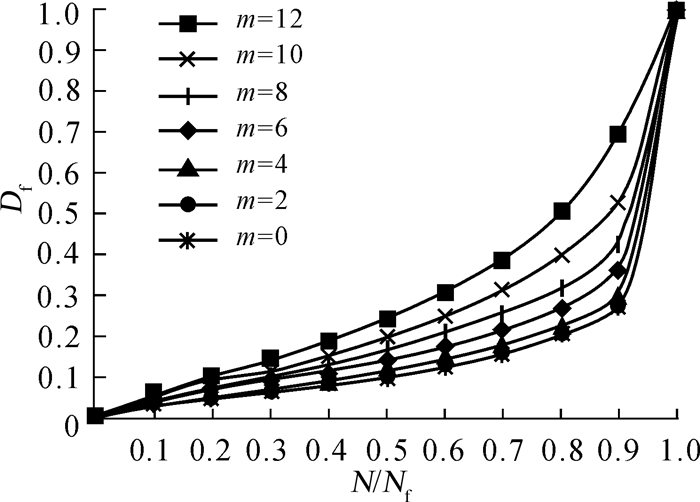
周向拉杆转子在运转的过程中,假设透平端拉杆存在非均匀损伤,即12根拉杆中有m根存在损伤dturri,而其余拉杆不存在损伤,则周向拉杆转子整体损伤结果如图 8所示。
|
| 图 8 部分拉杆损伤时周向拉杆转子整体损伤 Fig.8 The whole fatigue damage of circumferential rod fastening rotor with part rods damaged |
2) 透平端拉杆有不同损伤量。
周向拉杆转子在运转的过程中,假设12根拉杆中有m根的损伤为dturri,而其中12-m根的损伤是2dturri,周向拉杆转子整体损伤如图 9所示。

|
| 图 9 拉杆有不同损伤量时周向拉杆转子整体损伤 Fig.9 The whole fatigue damage of circumferential rod fastening rotor under rods with inhomogeneous damage |
当透平端拉杆受非均匀损伤时,转子整体损伤与致裂寿命依旧是非线性关系;拉杆的非均匀损伤会导致拉杆失谐,从而加剧周向拉杆转子的整体损伤;仅有1根拉杆损伤为2dturri时,转子的整体损伤只有微小的增加,随着损伤为2dturri的拉杆数目的增加,转子整体损伤加剧。
3 结论针对单个元件的损伤无法预测周向拉杆转子整体损伤的问题,本文考虑周向拉杆转子燃烧室损伤和透平端拉杆损伤对周向拉杆转子整体损伤的影响,建立了周向拉杆转子整体疲劳损伤的解析模型,揭示了周向拉杆转子整体疲劳损伤与周向拉杆转子元件及致裂寿命的非线性关系,并分析了透平端拉杆非均匀损伤情况对周向拉杆转子整体损伤的影响。研究结果可为单个及多个元件损伤预测周向拉杆转子整体损伤提供理论依据。
| [1] | HALL D K. Performance limits of turbomachines[D]. Cambridge, MA:Massachusetts Institute of Technology, Department of Aeronautics and Astronautics, 2010:102-113. |
| [2] |
荆建平, 孟光.
汽轮机转子疲劳-蠕变损伤的非线性损伤力学分析[J]. 中国电机工程学报, 2003, 23(9): 167–172.
JING Jian-ping, MENG Guang. On the fatigue-creep damage analysis of a steam turbine rotor by a nonlinear continuum damage mechanics model[J]. Proceedings of the CSEE, 2003, 23(9): 167–172. |
| [3] | JING Jian-ping, SUN Yi, XIA Song-bo, et al. A continuum damage mechanics model on low cycle fatigue life assessment of steam turbine rotor[J]. International Journal of Pressure Vessels and Piping, 2001, 78(1): 59–64. DOI:10.1016/S0308-0161(01)00005-9 |
| [4] | NAYEBI Ali, RANJBAR Hamid, ROKHGIREH Hojatollah. Analysis of unified continuum damage mechanics model of gas turbine rotor steel:life assessment[J]. Proceedings of the Institution of Mechanical Engineers Part L:Journal of Materials Design & Applications, 2012, 227(3): 216–225. |
| [5] | KUMAR Sandeep, ROY Niranjan, GANGULI Ranjan. Monitoring low cycle fatigue damage in turbine blade using vibration characteristics[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 480–501. DOI:10.1016/j.ymssp.2005.02.011 |
| [6] | MASHAYEKHI M, TAGHIPOUR A, ASKARI A, et al. Continuum damage mechanics application in low-cycle thermal fatigue[J]. International Journal of Damage Mechanics, 2012, 22(2): 285–300. |
| [7] |
刘宁波. 基于损伤力学的轮盘结构疲劳-蠕变损伤分析及寿命预测[D]. 成都: 电子科技大学机械电子工程学院, 2013: 10-25.
LIU Ning-bo. Life prediction and analysis of damage under fatigue-creep condition for disk based on damage mechanics[D]. Chengdu:University of Electronic Science and Technology of China, School of Mechanical and Electronic Engineering, 2013:10-25. |
| [8] |
李雅武, 李长宝, 王梅英, 等.
30Cr1Mo1V转子钢低周疲劳性能及损伤演变规律研究[J]. 汽轮机技术, 1998, 3: 58–61.
LI Ya-wu, LI Chang-bao, WANG Mei-ying, et al. Research on low cycle fatigue performance and damage evolution of 30Cr1Mo1V rotor steel[J]. Turbine Technology, 1998, 3: 58–61. |
| [9] |
高鹏. 涡轮盘蠕变及低周疲劳寿命可靠性分析方法[D]. 西安: 西北工业大学动力与能源学院, 2007: 5-32.
GAO Peng. Analysis for creep-fatigue damage life prediction of turbine discs[D]. Xi'an:Northwestern Polytechnical University, School of Power and Energy, 2007:5-32. |
| [10] |
张青雷, 陈堰芳, 赵佰余.
燃气轮机拉杆转子的轮盘结合面接触模型研究[J]. 热能动力工程, 2014, 29(5): 492–593.
ZHANG Qing-lei, CHEN Yan-fang, ZHAO Bai-yu. Research on contact model between discs of rod fastening gas turbine rotor[J]. Journal of Engineering for Thermal Energy and Power, 2014, 29(5): 492–593. |
| [11] | TIAN Hong-liang, LI Bin, LIU Hong-qi, et al. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J]. Elsevier International Journal of Machine Tools & Manufacture, 2011, 51(3): 239–249. |
| [12] |
田红亮. 机械结构固定结合部虚拟材料的动力学建模[D]. 武汉: 华中科技大学机械科学与工程学院, 2011: 8-41.
TIAN Hong-liang. Dynamic modeling on fixed joint interface virtual material in mechanical structure[D]. Wuhan:Huazhong University of Science and Technology, School of Mechanical Science and Engineering, 2011:8-41. |
| [13] | FISHKIS M, LIN J C. Formation and evolution of a subsurface layer in a metalworking process[J]. Wear, 1997, 206(1/2): 156–170. |
| [14] |
李浦, 袁奇, 高进, 等.
轮盘端面齿连接的周向拉杆转子刚度研究[J]. 航空动力学报, 2013, 28(7): 1618–1623.
LI Pu, YUAN Qi, GAO Jin, et al. Investigation on stiffness of circumferential distributed tie-rod rotor with curvic couplings of trochal disk[J]. Journal of Aerospace Power, 2013, 28(7): 1618–1623. |
| [15] | DEGUANG S, WEIXING Y. Study on nonlinear continuous damage cumulative model for multiaxial fatigue[J]. Acta Aeronautica Et Astronautica Sinica, 1998, 19(6): 647–656. |
| [16] | LEMAITRE J. Evaluation of dissipation and damage in metals submitted to dynamic loading[J]. Mechanical Behavior of Materials, 1972, 76(6): 540–549. |
| [17] |
初金阳, 胡殿印, 毛建兴, 等.
基于损伤力学的GH4169合金低循环裂纹萌生寿命预测[J]. 航空发动机, 2016, 42(2): 88–92.
CHU Jin-yang, HU Dian-yin, MAO Jian-xing, et al. Prediction of GH4169 low cycle crack initiation life based on damage mechanics[J]. Aeroengine, 2016, 42(2): 88–92. |
| [18] |
余天庆, 钱济成.
损伤理论及其应用[M]. 北京: 国防工业出版社, 1993: 34-51.
YU Tian-qing, QIAN Ji-cheng. Damage theory and application[M]. Beijing: National Defend Industry Press, 1993: 34-51. |
| [19] |
吴波, 李惠, 李玉华.
结构损伤分析的力学方法[J]. 地震工程与工程振动, 1997, 17(1): 14–22.
WU Bo, LI Hui, LI Yu-hua. The mechanic method for damage analysis of structures[J]. Earthquake Engineering and Engineering Dynamics, 1997, 17(1): 14–22. |
| [20] |
中国航空材料手册编辑委员会.
中国航空材料手册[M]. 北京: 中国标准出版社, 1988: 323-359.
China Aeronautical Materials Handbook Editorial Board. China aeronautical materials handbook[M]. Beijing: Standards Press of China, 1988: 323-359. |
| [21] | LIU N, GONG Z, TANG Y, et al. A study on fatigue damage accumulation:based on continuum damage mechanics[C]//Quality, Reliability, Risk, Maintenance, and Safety Engineering (ICQR2MSE). Chengdu:IEEE, 2012:867-870. |
| [22] |
荆建平, 孙毅, 夏松波, 等.
非线性连续损伤模型在汽轮机转子低周疲劳分析中的应用[J]. 中国电机工程学报, 2001, 21(10): 29–33.
JING Jian-ping, SUN Yi, XIA Song-bo, et al. Application of nonlinear continuous damage model on low cycle fatigue analysis of steam turbine rotor[J]. Proceedings of the CSEE, 2001, 21(10): 29–33. |



