2. 湖北省油气钻完井工具工程技术研究中心, 湖北 荆州 434023;
3. 非常规油气湖北省协同创新中心, 湖北 武汉 430100
2. Hubei Engineering Research Center for Oil & Gas Drilling and Completion Tools, Jinzhou 434023, China;
3. Hubei Cooperative Innovation Center of Unconventional Oil and Gas, Wuhan 430100, China
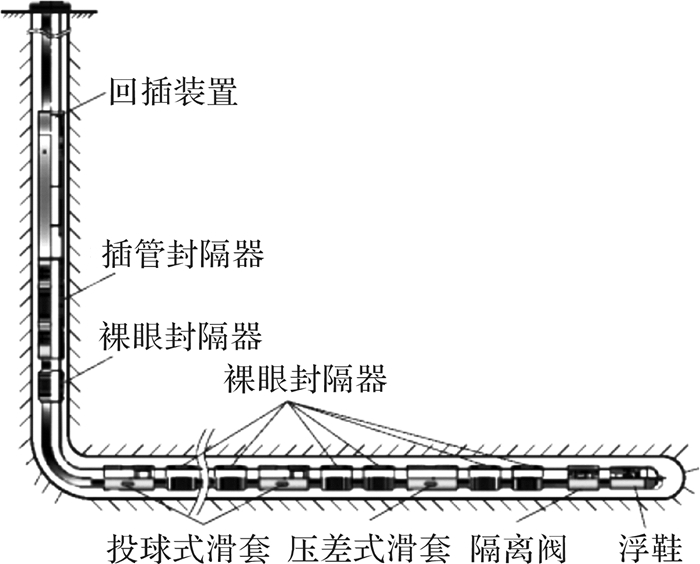
随着全球对油气资源需求的不断增长,常规油气资源开采难度逐渐增大且油气资源也相对匮乏,使得非常规油气藏成为了开发的热点。非常规油气资源的探明储量非常巨大,具有很好的开发前景[1-3]。对于非常规油气藏的生产,水平井投球滑套分段压裂技术能够实现油气井的增产和成本降低,在各大油田使用广泛[4]。如图 1所示[5],该技术的优点在于:通过投放不同直径的压裂球来打开不同层段的滑套,进而打开压裂地层的通道;压裂施工完成后,进行钻铣球座操作可实现油气通道全通径,有利于后期井下施工[6-7]。然而固体颗粒含量高、流速大、压力高的压裂液流经球座,并随着球座流道的急剧收缩,压裂液中的固体颗粒支撑剂和球座壁面的摩擦和撞击严重,将会造成球座的冲蚀磨损。球座的冲蚀磨损,会造成密封失效和压力泄漏,严重的将直接导致滑套不能正常开启,从而使压裂施工无法进行,影响油气井的生产[8-9]。因此对于球座冲蚀磨损的研究非常有必要。
|
| 图 1 水平井多级滑套分段压裂示意图 Fig.1 Schematic diagram of multistage sliding sleeve fracturing in horizontal wells |
冲蚀是一个复杂的现象,受到诸多因素的影响。国内外已有不少学者对冲蚀现象进行了研究,Liu和Das等[10-11]通过数值分析和实验研究了冲蚀现象和工具材料的关系;Zhu等[12]研究了流体冲蚀对钻杆的影响;董刚等[13]研究了固体粒子的冲蚀磨损导致的材料破坏;艾志久等[14]简单研究了压裂液的压力、砂流量和锥角对球座冲蚀的影响。本文选择了鄂尔多斯盆地失效最为严重的一组球座,并根据现场实际施工情况,结合理论详细分析了球座失效的原因,全面具体地分析了压裂液排量、颗粒浓度、颗粒直径和黏度对球座冲蚀磨损的影响;为降低球座冲蚀磨损及优化球座结构,研究了锥角对球座冲蚀磨损的影响;同时提出了凹面、凸面和双角度不同锥段结构,根据计算结果对比分析了不同锥段结构的冲蚀磨损。后期将结合实验对不同锥段结构进行更为详细的研究,以期对水平井投球滑套分段压裂技术的改进和现场压裂施工提供指导意义。
1 球座数学模型的建立 1.1 湍流模型水平井分段压裂时,由于压裂液含有支撑剂颗粒,球座内部流体是复杂的液-固两相三维流场;施工排量最高可达到8 m3/min,支撑剂体积分数可高达40%,湍流模型采用了适用性最强的标准k-ε模型,方程如下所示:
| $ \begin{array}{l} \rho {u_j}\frac{{\partial k}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\eta_t \frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon \end{array} $ | (1) |
| $ \begin{array}{*{35}{l}} \rho {{u}_{k}}\frac{\partial \varepsilon }{\partial {{x}_{k}}}=\frac{\partial }{\partial {{x}_{k}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{k}}} \right]+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{{C}_{1}}\varepsilon }{k}{{\eta }_{t}}\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)-{{C}_{2}}\rho \frac{{{\varepsilon }^{2}}}{k} \\ \end{array} $ | (2) |
| $ {\mu _t} = {C_\mu }\rho {k^2}/\varepsilon $ | (3) |
式中:ρ为流体密度,kg/m3;μ为湍流黏性系数,kg/(m·s);k为湍动能,m2/s2;u为流体速度,m/s;ε为耗散率,m2/s3;C1,C2, Cμ为经验常数,C1=0.09,C2=1.44,Cμ=1.92;σk为湍动能普朗特数,σk=1.0;σε为湍动能耗散率普朗特数,σε=1.3。
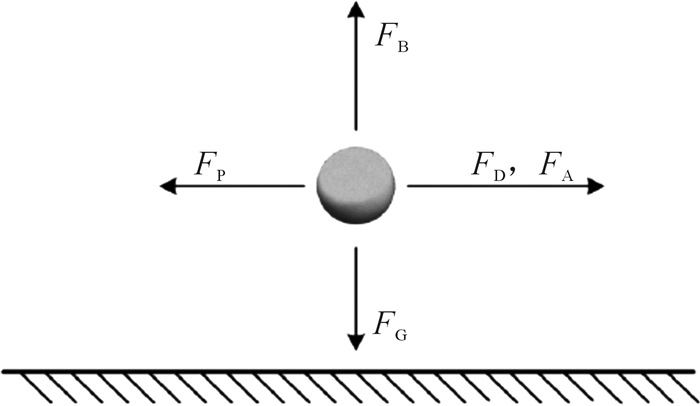
1.2 控制方程在压裂过程中,固体颗粒随压裂液流动,其状态受多种因素影响,故非常有必要分析固体颗粒的受力情况,如图 2所示。根据牛顿第二定律,颗粒的受力方程如下所示:
| $ {m_{\rm{p}}}\frac{{{\rm{d}}{v_{\rm{p}}}}}{{{\rm{d}}t}} = \sum {F = {F_{\rm{G}}} + {F_{\rm{D}}} + {F_{\rm{P}}} + {F_{\rm{B}}} + {F_{\rm{A}}}} $ | (4) |
|
| 图 2 压裂液固体颗粒受力示意图 Fig.2 Schematic diagram of force of solid particles in fracturing fluid |
式中:重力FG=mpg;
流体黏性阻力
压力梯度力
浮力
附加质量力
式中:mp为颗粒质量,kg;g为重力加速度,m/s2;CD为阻力系数,无量纲;ρf为流体密度,kg/m3;ρp为固体颗粒密度,kg/m3;dp为颗粒直径,m;vf为流体速度,m/s;vp为颗粒速度,m/s;▍p为压力梯度,MPa/m。
1.3 冲蚀模型| $ {E_{\rm{n}}} = \left\{ \begin{array}{l} \frac{{Mv_{\rm{p}}^2}}{{{\sigma _y}\psi l}}\sin 2\alpha - \frac{6}{l}\sin \alpha \;\;\;\;\alpha < {\alpha _0}\\ \frac{{Mv_{\rm{p}}^2}}{{{\sigma _y}\psi l}}\frac{6}{l}{\cos ^2}\alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \geqslant {\alpha _0} \end{array} \right. $ | (5) |
式中:En为材料体积耗散率,m3/s;M为颗粒总质量,kg;vp为颗粒速度,m/s;α为冲蚀角度,rad;σy为材料屈服应力,Pa;l为颗粒所承受的垂直分量与水平分量的比值,无量纲;ψ为颗粒切削深度与接触高度的比值,无量纲。
式(5) 是Finnie提出的经典切削理论模型;对于压裂液固体颗粒对球座壁面的冲蚀磨损,通过式(6) 可得到n个支撑剂颗粒对球座的冲蚀速率。
| $ {{E}_{\text{R}}}=\sum\limits_{n=1}^{{{N}_{\text{p}}}}{\frac{{{m}_{\text{q}}}C({{d}_{p}})f\left( \alpha \right)v_{\text{p}}^{'b}(v_{\text{p}}^{'})}{{{A}_{\text{f}}}}} $ | (6) |
式中:ER为冲蚀速率,kg/(m3·s);n为颗粒数;mq为颗粒质量流量,kg/s;C(dp)为颗粒粒径函数;f(α)为冲蚀攻角函数;Np为发生碰撞的颗粒数量,无因次;vp′为颗粒相对管壁的碰撞速度,m/s;b(vp')为颗粒相对速度函数;Af为冲蚀计算单元面积,m2。
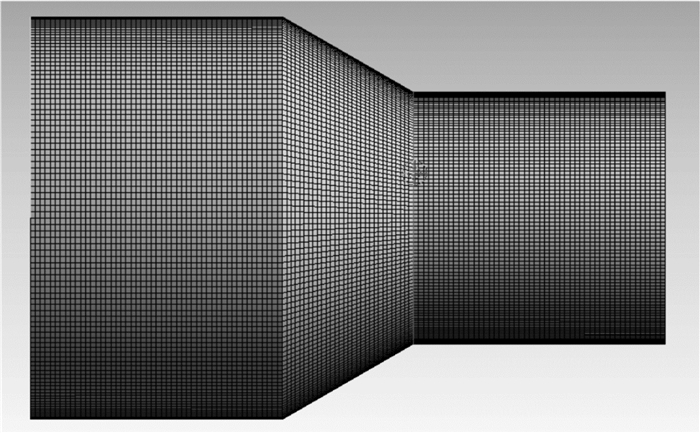
2 球座计算模型的确定 2.1 几何模型根据现场实际情况,本文选用现场失效频率较高的球座滑套作为研究对象,现以鄂尔多斯盆地一井所使用的滑套球座为研究对象,其1号投球滑套球座大柱段直径为80 mm,小柱段直径为50 mm,锥角为30°;后续球座仅改变小柱段直径即可。根据该井1号投球滑套球座建立流道模型,模型网格如图 3所示。
|
| 图 3 球座流道几何体网格划分 Fig.3 Flow geometry mesh of the ball seat |
假设压裂液为不可压缩流体,考虑到压裂液流速较高(最高可达8~10 m3/min),排量大,因此本文采用速度入口;在压裂过程中泵的压力为40 MPa或者更高,为保证球座出口压力,不影响后续压裂施工,本文采用压力出口;壁面采用无滑移壁面边界;球座材料采用QT5-A型球墨铸铁球。
现场压裂施工中,压裂液的密度为1 000~1 400 kg/m3,黏度为50~400 MPa·s,颗粒密度为2 000 kg/m3,粒径为200~600 μm,入口排量为4~8 m3/min,颗粒浓度为5%~40%,泵压为30~70 MPa。
3 数值模拟为研究冲蚀磨损,本文采用一组常规的现场压裂施工技术参数(如表 1所示),进行数值模拟。
| 参数 | 数值 |
| 压裂液密度ρ1/(kg/m3) | 1 400 |
| 压裂液黏度μ/(MPa·s) | 100 |
| 固体颗粒密度ρ2/(kg/m3) | 2 000 |
| 粒径D/μm | 400 |
| 压裂液排量V/(m3/min) | 4 |
| 固体颗粒浓度C/% | 20 |
| 泵压p/MPa | 42 |
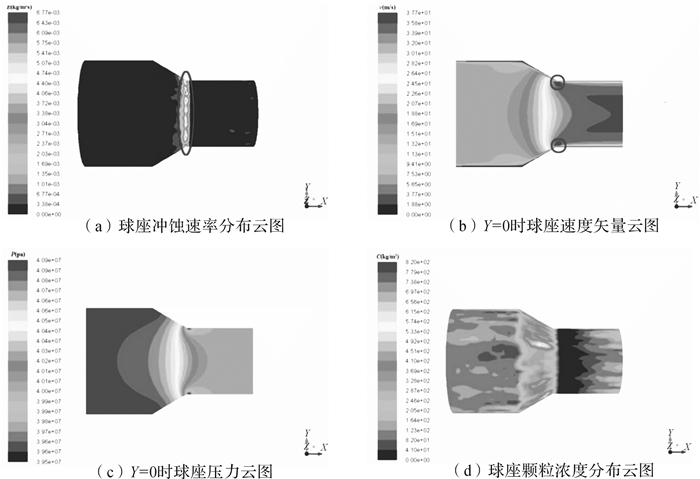
由于压裂液携带大量的固体颗粒,颗粒在连续相流体的携带作用下,在流动过程中以一定的速度和角度冲击球座的壁面,造成了球座壁面的冲蚀磨损。图 4(a)中给出了冲蚀速率分布云图,球座冲蚀速率最大的地方在锥段和小柱段相接处,且冲蚀磨损呈现片状分布,冲蚀速率最高可达到6.77×10-3kg/(m2·s)。图 4(b)中给出了Y=0平面的流场速度矢量云图,流体入口速度约为10 m/s,出口高达40 m/s,锥段处流道面积缩小,速度梯度大,导致颗粒脱离主流流线冲击球座锥面趋势增加;在锥段和小柱段相接处(即图 4(b)中圆圈标记处)壁面流体速度高,冲蚀速率高, 与冲蚀速度云图相吻合。图 4(c)为Y=0平面的压力分布云图,入口压力约为41 MPa,出口为40 MPa,进出口压差约为1 MPa。图 4(d)为颗粒浓度分布云图,锥段处浓度要高于其他地方且呈现片状分布,流道收缩,颗粒与壁面碰撞增加,导致壁面处的颗粒浓度高。锥段处流道内径减小,流体流线向内收缩,固体颗粒受惯性力作用继续沿之前方向运动,从而不断撞击球座锥段表面,导致锥段处冲蚀磨损严重。
|
| 图 4 球座流场特性图 Fig.4 Characteristics of flow field of the ball seat |
在实际应用中,若局部磨损率过高,将会显著影响球座的密封性能。现通过控制变量法,研究压裂液排量、颗粒浓度、颗粒直径和黏度对球座冲蚀磨损的影响。
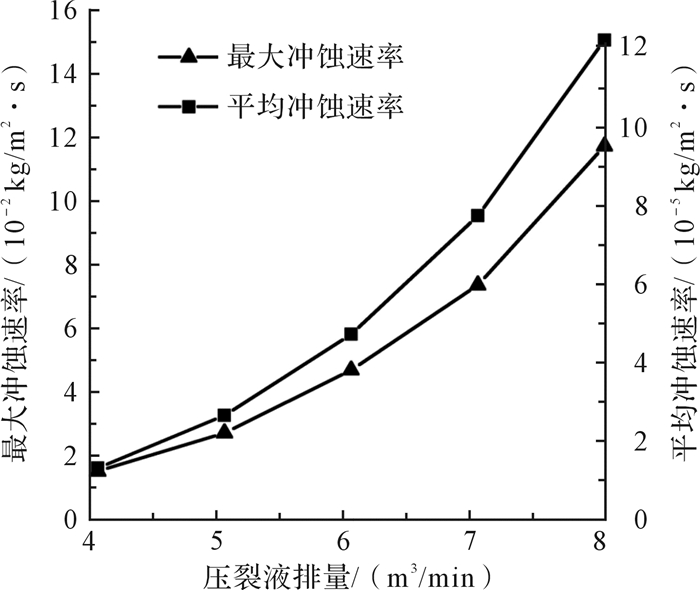
4.1 压裂液排量对冲蚀磨损的影响通过理论分析可知,压裂液的流速是影响球座冲蚀磨损的关键因素之一。为研究流体流速和球座冲蚀磨损之间的关系,改变压裂液排量,依次为4,5,6,7,8 m3/min,不改变其他施工参数。
由图 5可得,随着排量的增大,球座的冲蚀速率也逐渐增大。随着排量的增大,压裂液流速随之变大,导致颗粒动能也相应增加,因此,固体颗粒撞击壁面时,损失的动能也增大,对壁面的破坏程度加剧,造成了球座冲蚀磨损加剧。
|
| 图 5 压裂液排量对球座冲蚀磨损的影响 Fig.5 Effect of displacement of fracturing fluid on the erosion of the ball seat |
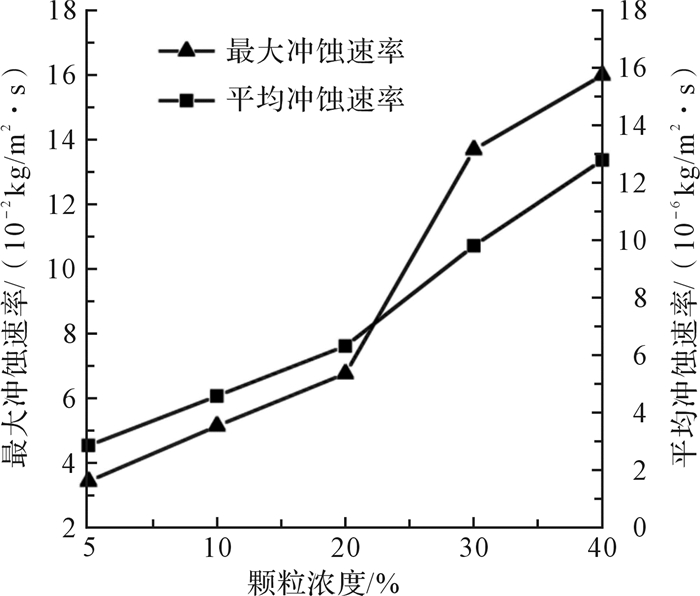
压裂液对球座的冲蚀磨损,除了流体流动时的冲蚀磨损,其中最为主要的是压裂液中的固体颗粒对壁面的冲击破坏作用造成的冲蚀磨损。因此,压裂液中的支撑剂固体颗粒含量也是导致球座冲蚀磨损的重要因素之一,在其他施工条件不变的情况下,改变压裂液中支撑剂的浓度,分别为5%,10%,20%,30%,40%。
由图 6可得,随着支撑剂浓度增加,球座的冲蚀速率将会随之增大。分析其原因,在其他工况不变的情况下,支撑剂浓度的增加意味着压裂液中固体颗粒数增多,将会增大固体颗粒与球座壁面发生碰撞的几率,从而导致球座冲蚀磨损加剧。
|
| 图 6 压裂液固体颗粒浓度对球座冲蚀磨损的影响 Fig.6 Effect of solid particle concentration of fracturing fluid on the erosion of the ball seat |
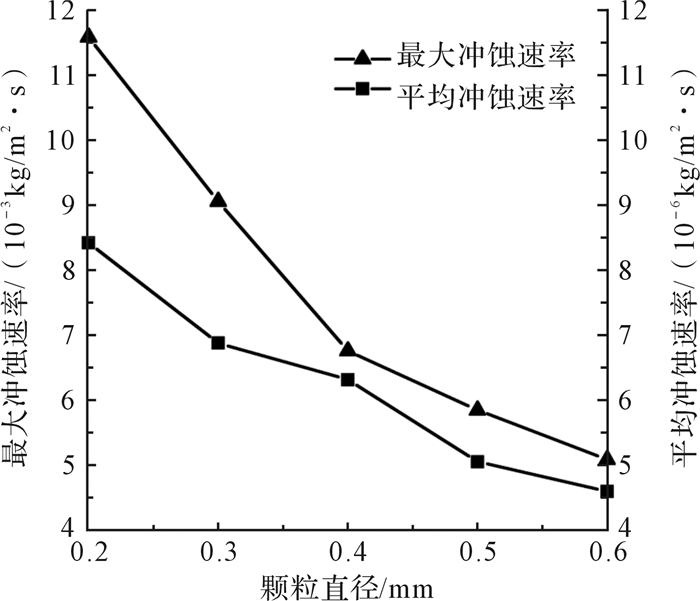
压裂液中固体颗粒直径的大小对球座冲蚀磨损也有一定的影响。为研究颗粒直径和球座冲蚀磨损之间的关系,在其他施工参数不变的前提下,选用不同直径的支撑剂颗粒,依次为0.2,0.3,0.4,0.5,0.6 mm。
由图 7可知,在其他施工参数一定的情况下,随着压裂液支撑剂颗粒直径的增大,球座冲蚀磨损速率呈现减小趋势。Finnie切削理论认为冲蚀磨损量与颗粒质量成正比,即质量大颗粒动能也相对较大,对球座的破坏也严重。但在实际施工中,流量和颗粒浓度一定,颗粒直径小,则单位体积数目大,颗粒更容易脱离主流流线,与壁面碰撞几率增加,加剧了球座锥段的冲蚀磨损;颗粒直径大,则单位体积数目小,颗粒与锥段壁面的碰撞几率小,则球座的冲蚀磨损反而减少。
|
| 图 7 压裂液中固体颗粒直径对球座冲蚀磨损的影响 Fig.7 Effect of solid particle diameter of fracturing fluid on the erosion of the ball seat |
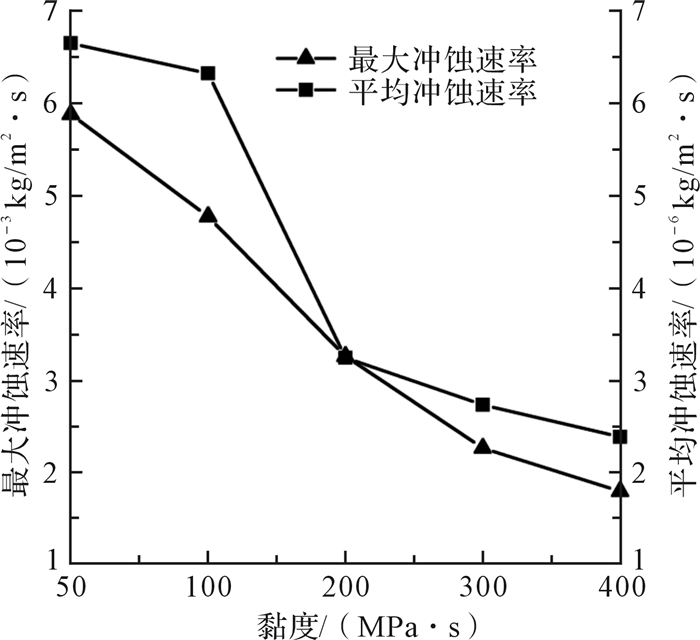
黏度对固体颗粒运动,以及整个球座流道内流体的运动状态和形态有着关键性的作用,现研究压裂液黏度和球座冲蚀磨损之间的关系。在不改变其他施工参数的前提下,选取不同黏度的压裂液,分别为50,100,200,300,400 MPa·s。
由图 8可知,压裂液黏度对球座的冲蚀磨损影响显著;随着压裂液黏度的增加,球座冲蚀速率逐渐减小。分析其原因,颗粒在高黏度下,对流体的追随性好,砂粒脱离主流流线与球座锥段壁面碰撞的剧烈程度降低;同时颗粒所受流体黏滞阻力增大,降低了颗粒撞击球座锥段壁面几率,降低了颗粒与壁面撞击的剧烈程度,从而减小了球座锥段冲蚀磨损速率。
|
| 图 8 压裂液黏度对球座冲蚀磨损的影响 Fig.8 Effect of viscosity of fracturing fluid on the erosion of the ball seat |
分析了不同锥角和结构形式的球座模型,希望通过优化球座结构,减少冲蚀磨损。
5.1 球座锥角对冲蚀磨损的影响球座锥角(即锥角)对两相流动状态以及锥段的冲蚀磨损存在显著的影响。改变球座锥角,分别为15°,30°,45°,60°,研究球座锥角对球座冲蚀磨损的影响。
由图 9可知:大柱段和小柱段颗粒浓度分布都相对非常均匀,锥段壁面颗粒浓度分布呈现片状;随着角度的增大,球座锥段的颗粒浓度也依次递增。说明随着角度的增大,颗粒与壁面的碰撞加剧。颗粒与壁面间的碰撞,导致了颗粒浓度分布不均。

|
| 图 9 不同锥角下球座颗粒浓度分布云图 Fig.9 Nephogram of particle concentration distribution of the ball seat under different cone angles |
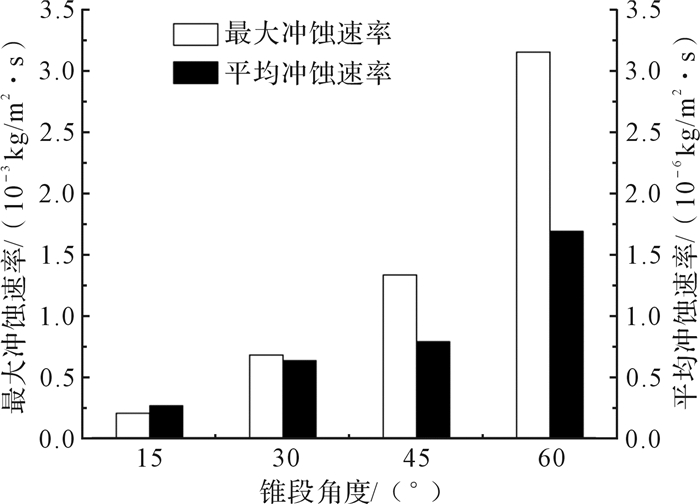
通过图 10可以发现,随着锥角的增大,球座的冲蚀磨损加剧。当锥角小于30°时,冲蚀速率较小,当锥角大于30°,冲蚀磨损速率急剧增大;当锥角为60°时,最大冲蚀速率达到3.15×10-2kg/(m2·s),为锥角为45°时的2倍,为锥角为30°时的5倍,为锥角为15°时的15倍。同时为了不让工具整体长度过大而影响安装,球座锥角应该在20°~30°范围内较为合理。
|
| 图 10 不同锥角下球座平均冲蚀速率和最大冲蚀速率 Fig.10 Average erosion rate and maximum erosion rate of the ball seat under different cone angles |
除球座锥角之外,球座锥段结构形式对两相流动状态以及锥段的冲蚀磨损也存在显著影响。在锥角一定的前提下(锥角为30°),通过改变球座锥段的结构形式:凹面、凸面、直面和双角度结构形式(第一锥面为30°,第二锥面小于30°),在同等条件下,对不同结构形式的球座冲蚀磨损进行研究。
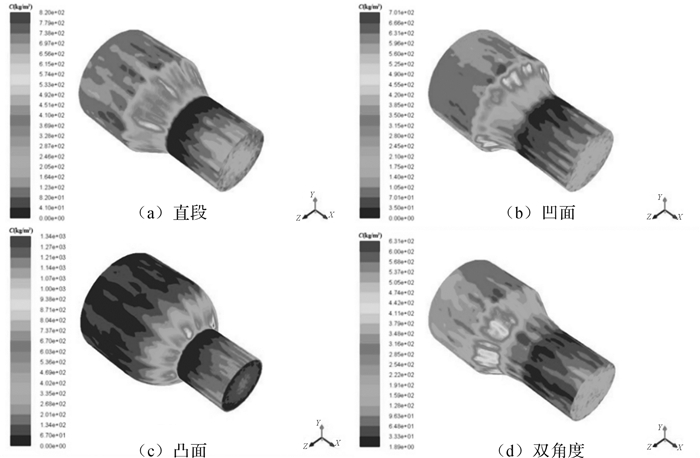
图 11分别给出了不同结构形式球座的颗粒浓度分布图。从图中可以发现,双角度结构形式的球座锥段壁面的颗粒浓度是最小的,凸面结构形式的球座锥段壁面颗粒浓度最大。在双角度的球座锥段颗粒浓度分布图中,球座由直段结构变成了2个锥角不同的锥段,颗粒大部分都集中在和大圆柱相连的锥面处,而在和小圆柱相连的锥段处颗粒聚集程度较低。颗粒浓度的大小直接反映了颗粒与壁面的撞击剧烈程度,也揭示了冲蚀磨损程度。从而说明双角度球座锥段冲蚀磨损集中在和大圆柱相连的锥段处,并较30°角度锥段冲蚀磨损小。
|
| 图 11 不同结构形式下球座固体颗粒分布云图 Fig.11 Nephogram of solid particle concentration distribution of the ball seat under different structural forms |
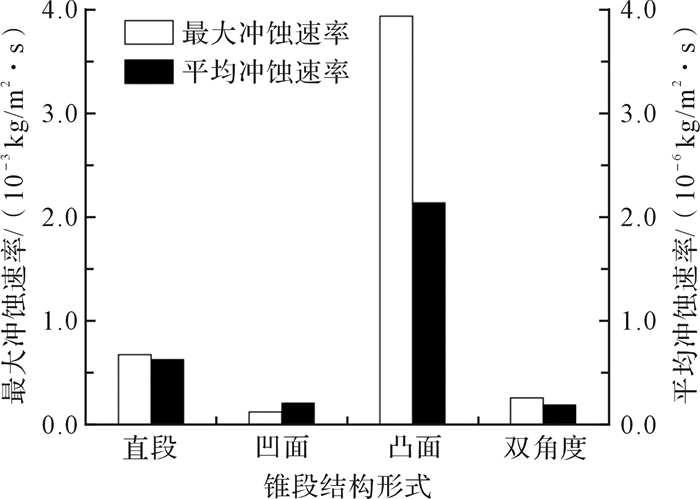
从图 12可知,凹面锥段最大冲蚀磨损速率最小,仅为1.27×10-3kg/(m2·s),因其较为合理的流线型的结构,降低了颗粒与壁面碰撞的几率;双角度锥段结构与凹面锥段的最大冲蚀磨损速率相近,但是其平均磨损速率最小。分析可知,双角度锥段结构在其与大圆柱相连锥面处,阻挡和减慢了颗粒运动,使得在和小圆柱相连锥段处固体颗粒的碰撞减弱,冲蚀磨损程度降低,这样可以从一定程度上减小球座的冲蚀磨损。凸面结构球座的壁面最大冲蚀速率达到3.94×10-2kg/(m2·s),为凹面结构最大冲蚀速率的31倍,为双角度结构的16倍,因其流道结构的急剧变化,颗粒运动极为复杂,导致了该结构球座的冲蚀磨损最为严重。通过分析可得,可以通过改变球座的结构形式,来减少球座的冲蚀磨损。
|
| 图 12 不同结构形式下球座平均冲蚀速率和最大冲蚀速率 Fig.12 Average erosion rate and maximum erosion of the ball seat under different structural forms |
1) 通过分析得,锥段处流道内径减小,流体流线向内收缩,固体颗粒受惯性力作用继续沿之前方向运动,从而不断撞击球座锥段表面,导致球座锥段处冲蚀磨损严重。
2) 随着压裂液排量和颗粒浓度的增加,球座冲蚀速率增加;随着压裂液颗粒直径和黏度的增加,球座冲蚀速率减小。
3) 经研究得,可以通过改变锥角和结构,降低球座冲蚀速率。球座冲蚀速率随着锥角的增加而增加,在20°~30°之间最为合理;球座锥段为双角度和凹面结构时,最大冲蚀速率都比较小。
| [1] |
胡文瑞, 鲍敬伟, 胡滨.
全球油气勘探进展与趋势[J]. 石油勘探与开发, 2013, 40(4): 409–413.
HU Wen-rui, BAO Jin-wei, HU Bin. Advances and trends in global oil and gas exploration[J]. Petroleum Exploration and Development, 2013, 40(4): 409–413. DOI:10.11698/PED.2013.04.03 |
| [2] |
贾承造, 郑民, 张永峰.
中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129–136.
JIA Cheng-zao, ZHENG Min, ZHANG Yong-feng. Unconventional oil and gas resources and exploration and development prospects in China[J]. Petroleum Exploration and Development, 2012, 39(2): 129–136. |
| [3] |
黄鑫, 董秀成, 肖春跃, 等.
非常规油气勘探开发现状及发展前景[J]. 天然气与石油, 2012, 30(6): 38–41, 4.
HUANG Xin, DONG Xiu-cheng, XIAO Chun-yue, et al. Present situation and development prospect of unconventional oil and gas exploration and development[J]. Natural Gas and Oil, 2012, 30(6): 38–41, 4. |
| [4] | BRUCE R, LUCAS W, ROBERT H, et al. Optimization of multiple transverse hydraulic fractures in horizontal wellbores[C]//SPE Unconventional Gas Conference, Pittsburgh, Pennsylvania, USA, Feb. 23-25, 2010. |
| [5] |
秦金立, 陈作, 杨同玉, 等.
鄂尔多斯盆地水平井多级滑套分段压裂技术[J]. 石油钻探技术, 2015, 43(1): 7–12.
QIN Jin-li, CHEN Zuo, YANG Tong-yu, et al. Multistage sliding sleeve fracturing technology for horizontal wells in Ordos Basin[J]. Petroleum Drilling Techniques, 2015, 43(1): 7–12. |
| [6] |
曹阳, 陈琛, 史雪枝, 等.
川西致密气藏裸眼水平井分段压裂技术[J]. 石油钻探技术, 2012, 40(3): 13–17.
CAO Yang, CHEN Chen, SHI Xue-zhi, et al. Staged fracturing technology for open hole horizontal wells in tight gas reservoirs in Western Sichuan[J]. Petroleum Drilling Techniques, 2012, 40(3): 13–17. |
| [7] |
邢景宝.
大牛地气田水平井分段压裂技术研究与应用[J]. 钻采工艺, 2011, 34(2): 25–114.
XING Jing-bao. Research and application of horizontal fracturing technology for horizontal wells in Daniudi gas field[J]. Drilling and Production Technology, 2011, 34(2): 25–114. |
| [8] | KHALAF A M, SEIBI A C. Failure analysis of lube oil feed tube of a gas turbine operating in oil fields[J]. Engineering Failure Analysis, 2011, 18(5): 1341–1350. DOI:10.1016/j.engfailanal.2011.03.023 |
| [9] | RODRÍGUEZ E S, ALÜAREZ V A, MONTEMARTINI P E. Failure analysis of a GFRP pipe for oil transport[J]. Engineering Failure Analysis, 2013, 28(28): 16–24. |
| [10] | LIU Z G, WAN S, NGUYEN V B, et al. A numerical study on the effect of particle shape on the erosion of ductile materials[J]. Wear, 2014, 313(1/2): 135–142. |
| [11] | DAS S K, MUNDA P, CHOWDHURY S G, et al. Effect of microstructures on corrosion and erosion of an alloy steel gear pump[J]. Engineering Failure Analysis, 2014, 40(2): 89–96. |
| [12] | ZHU H, LIN Y, ZENG D, et al. Numerical analysis of flow erosion on drill pipe in gas drilling[J]. Engineering Failure Analysis, 2012, 22(1): 83–91. |
| [13] |
董刚, 张九渊.
固体粒子冲蚀磨损研究进展[J]. 材料科学与工程学报, 2003, 21(2): 307–312.
DONG Gang, ZHANG Jiu-yuan. Research progress of solid particle erosion[J]. Journal of Materials Science and Engineering, 2003, 21(2): 307–312. |
| [14] |
艾志久, 王琴, 李永革, 等.
水平井分段压裂投球滑套球座冲蚀分析[J]. 石油机械, 2011, 39(10): 61–63.
AI Zhi-jiu, WANG Qin, LI Yong-ge, et al. Horizontal well fracturing pitching sliding sleeve ball erosion analysis[J]. China Petroleum Machinery, 2011, 39(10): 61–63. |
| [15] | FINNIE I. The mechanism of erosion of ductile metals. Proceedings of the Third National Congress on Applied Mechanics[C]//Proceedings of the Third National Congress on Applied Mechanics. Providence, Jun. 11-14, 1958. |
| [16] | FINNE I. Some observations on the erosion of ductile metals[J]. Wear, 1972, 19(1): 81–90. DOI:10.1016/0043-1648(72)90444-9 |



