2. 四川川庆石油钻采科技有限公司, 四川 广汉 618300
2. Sichuan Chuanqing Oil Drilling Technology Co., Ltd., Guanghan 618300, China
聚晶金刚石复合片钻头简称为PDC (polycrystalline diamond compact)钻头,其具有机械钻速高、钻井效率高的特点,是软到中硬地层油气井的主力钻头。PDC钻头依靠聚晶金刚石复合片剪切岩石的方式破碎岩石,其切削结构被称为切削齿。PDC钻头设计灵活性大,对适用地层与条件敏感性强。切削齿的设计参数也称为布齿参数,布齿设计是钻头设计的核心。PDC钻头的布齿参数较多,总体上可以分为切削齿型号、布齿密度(数量)、空间位置参数和空间方向参数。
反求设计参数是逆向工程中的关键环节,逆向工程不是对实物产品进行简单的复制,而是在学习优秀设计思想的基础上进行优化设计或创新性设计。目前,在逆向工程中研究的主要内容包括数据的处理与CAD模型的重构[1-3],重点在于复杂CAD模型的重构,如曲面重构。针对如何反求多自由度设计参数的研究较少,且常规PDC切削齿的几何模型单一,基本为圆柱型,故研究的重点应该是如何准确反求复杂的设计参数。已有的研究中主要存在两大问题:
1) 无法准确求解PDC钻头的全部布齿参数,可完成的仅仅是CAD模型的重构。然而布齿参数是还原原始设计思想与二次优化设计的前提。
2) 忽略了加工精度、扫描设备精度以及切削齿磨损对重构CAD模型以及反求设计参数的影响,误差导致无法准确还原原始设计,在一定程度上违背了原始设计的初衷。
因此,本文提出一种PDC钻头布齿参数逆向设计与优化的方法,以提高布齿设计的科学性与效率。根据钻头的切削参数理论与设计准则以及实际使用情况,高效并准确地求解布齿参数,并对布齿参数进行合理优化设计,缩短设计与生产的周期。
1 布齿参数逆向设计基本原理随着非接触式光学三维扫描技术的不断发展,测量精度不断提高,在逆向工程中光学扫描技术以其独特的测量方式和高效的工作效率而被广泛应用。虽然它的精度还达不到三坐标测量机(coordinate measuring machine,CMM)的等级,但其工作效率与实用性要远远强于CMM。此外,CMM所测量的观测点数量有限,由于PDC钻头加工精度与表面钎焊层及其使用后产生的磨损的影响,通过有限测量点还原的模型往往达不到预期的精度要求。因此,对于实体钻头模型的数据采集宜采用光学三维扫描设备。
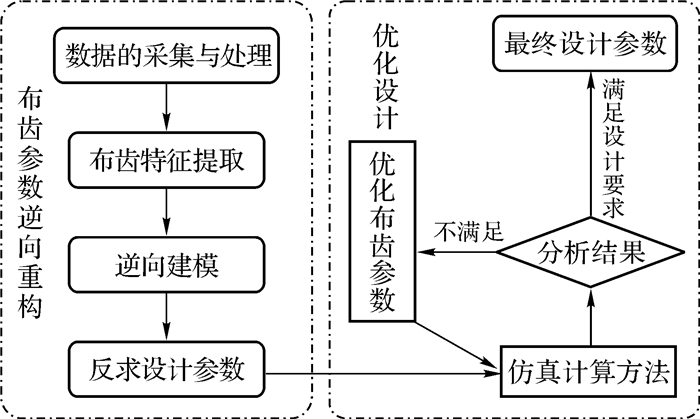
PDC钻头布齿参数的逆向设计与优化方法主要分为3个环节:逆向建模、反求设计参数与优化设计。逆向建模的实质是传统逆向工程中的CAD模型重构。反求设计参数是在逆向建模的基础上通过空间几何学原理来准确求解布齿参数。优化设计是基于反求的布齿参数,使用仿真计算模型进行分析,根据分析结果与钻头实际使用情况在设计准则的指导下对布齿参数进行调整。反求设计参数与优化设计区别于传统逆向工程(“抄数”)的本质。PDC钻头布齿参数的逆向设计与优化的流程如图 1所示。
|
| 图 1 PDC钻头布齿参数的逆向设计与优化的流程 Fig.1 The process of reverse design and optimization of PDC bit cutter parameters |
针对非接触式光学扫描设备的测量方法,其输出数据是非常庞大的点数据(点云),如何处理点云是提取切削齿几何特征的关键。本文在点云处理及几何特征提取上采取基于点云处理软件和正逆向功能软件协同的方案[3]。点云数据的处理通过常用的点云处理软件实现,将处理后的点云封装成三角网格文件(STL)。STL文件可以导入常用的正逆向设计软件,在STL模型中提取切削齿的几何特征。首先,建立钻头的全局坐标系。通过逆向设计软件Geomagic根据钻头接头处的圆柱特征拟合出钻头的中心轴线,按照右手法则建立空间直角坐标系,以钻头中心轴线为Z轴,建立全局坐标系O-XYZ。其次,在坐标系下提取布齿特征。在齿面上提取出工作平面(切削平面),在平面中拟合出齿刃的轮廓曲线,圆形PDC齿即为圆形。通过轮廓曲线拉伸圆柱,根据圆柱的半径与高度以及PDC的型号,匹配出最佳的齿型。最后,将各PDC齿的齿刃轮廓曲线作为布齿特征模型输出。以六刀翼A型PDC钻头为例,使用Creaform HandySCAN 3D进行测量,在STL模型中提取的布齿特征模型如图 2所示。

|
| 图 2 PDC钻头布齿特征模型 Fig.2 The characteristic model of PDC bit cutter |
逆向建模的实质是重构CAD模型。将布齿特征模型导入UG中,根据PDC齿切削面是圆形的几何特征,通过UG的二次开发功能直接获取圆弧或样条曲线的数量、半径与圆心坐标,即得到切削齿数量(布齿密度)、切削齿尺寸(齿型)与位置参数。通过齿面轮廓曲线建立工作平面,根据平面上不共线的三点可以确定2个向量,求其向量积,从而计算出工作平面的外法向量α0。
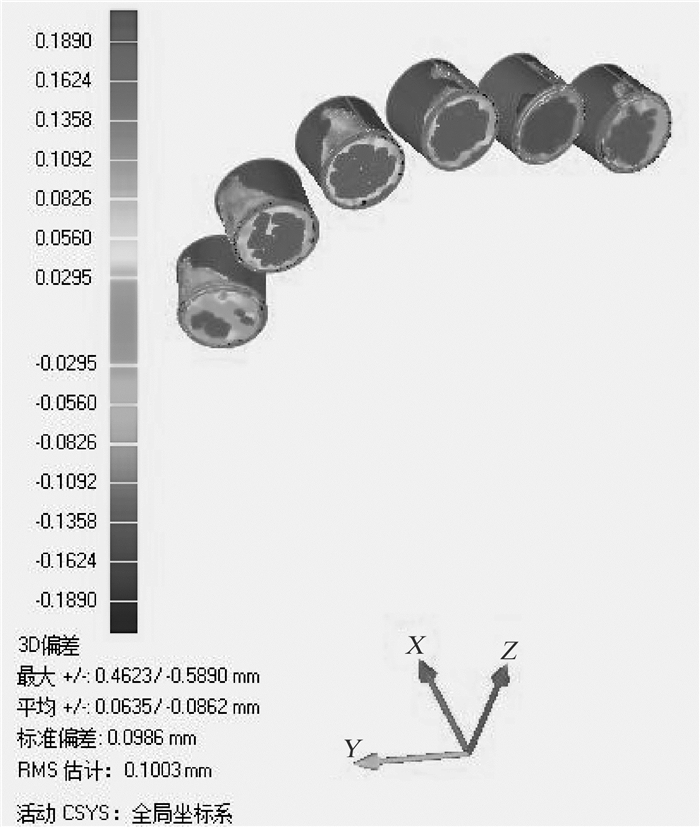
至此,通过布齿密度、齿型、切削齿中心坐标与工作平面的外法向量便可以建立所有切削齿的CAD模型。在UG中完成逆向建模后,通过校核检测软件Qualify将重构的CAD模型与原始STL模型进行对比[4],如某一PDC钻头刀翼上的6颗主切削齿的三维偏差分析如图 3所示,6颗主切削齿的平均偏差为+0.063 5 mm,-0.086 2 mm。考虑到原型钻头表面存在焊接层与磨损,逆向建模需符合逆向工程中重构实物的精度要求[1-2]。
|
| 图 3 重构切削齿模型的三维偏差分析结果 Fig.3 Three-dimensional deviation analysis of the reconstructed cutting cutter model |
将PDC钻头切削齿模型的直角坐标系转换为圆柱坐标系[5],工作平面圆心坐标的Rc,θ,Z即为切削齿的定位半径、周向方位角、轴向高度。
2.3 布齿参数的求解逆向建模中获取了布齿密度、齿型、齿心坐标、周向方位角与工作平面的外法向量。如何准确反求出切削角度是反求布齿设计参数的关键。切削齿的空间方向参数包括后倾角、侧倾角和法向角[5]。后倾角与侧倾角是对岩石进行剪切的切削角度。计算切削角度的前提是确定法向角,法向角由钻头的冠部轮廓曲线决定。
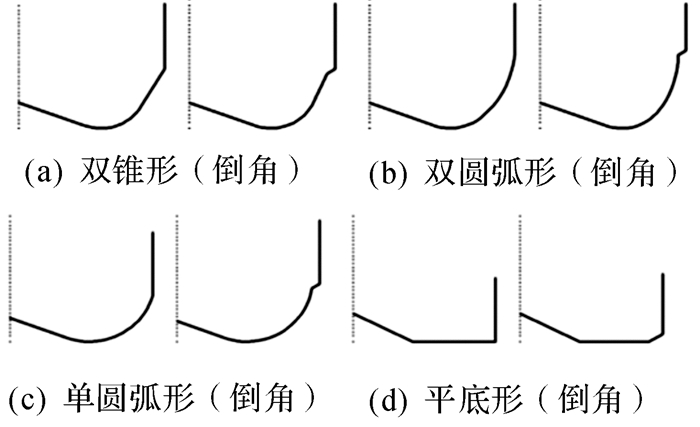
2.3.1 冠部曲线重构方法PDC钻头冠部曲线是指井底覆盖图[5]中各切削齿轴面轮廓线的包络线,由内锥、外锥和鼻部组成。当钻进速度为零时,将钻头绕中心轴线(Z轴)旋转1周,各切削齿的切削平面依次与XOZ平面相交,所有交线(轴面轮廓线)在XOZ平面上组成了井底覆盖图。在井底覆盖图中作出一条与各齿轴面轮廓线相切的包络曲线即为冠部曲线。常规PDC钻头的外锥弧线均采用圆弧形[6],冠部曲线的主要类型可以简化为双锥形(直线—圆弧—直线)、双圆弧形(直线—圆弧—圆弧)、单圆弧形(直线—圆弧)和平底形(直线—直线)四大类,如图 4所示,有些设计中冠部曲线与钻头保径处还存在倒角。通常将圆形PDC齿的轴面轮廓线视为圆形,冠部曲线可以通过对井底覆盖图中各切削齿的轴面轮廓线的圆心进行拟合得到。
|
| 图 4 PDC钻头冠部曲线类型 Fig.4 The type of PDC bit profile |
因为加工精度、数据采集精度以及切削磨损的影响,重构的CAD模型中的冠部曲线并不是光滑连续的,不能准确反映原始的设计参数。本文基于冠部曲线的几何特征约束,将冠部曲线进行重构,可以有效修正误差的影响。在XOZ平面的井底覆盖图中,将各主切削齿按照定位半径升序排列,齿心即为轴面轮廓线的圆心,齿心坐标为Ai。冠部曲线的重构分3个步骤:
1) 假定冠部曲线类型,对齿心点集合使用最小二乘法初步确定直线段、圆弧段;
2) 设定直线段与圆弧段的分段点在一定范围内前后浮动,寻找最优分段点与圆弧的半径;
3) 在冠部曲线拟合的不同类型方案中优选出最佳的冠部曲线类型。
确定了钻头的最优冠部曲线L后,将井底覆盖图中的齿心坐标以某种映射关系匹配到重构的冠部曲线上,即在钻头的圆柱坐标系中改变PDC齿的定位半径与轴向高度,映射准则为:
| $ {{A}_{i}}'=\min \ d_{i}^{2}({{A}_{i}}) $ | (1) |
式中:Ai为原始齿心坐标,A′i为修正后在冠部曲线上的齿心坐标,di为齿心修正前后A′iAi之间的距离, i表示切削齿的序号。显然,A′iAi沿A′i处冠部曲线法线方向。
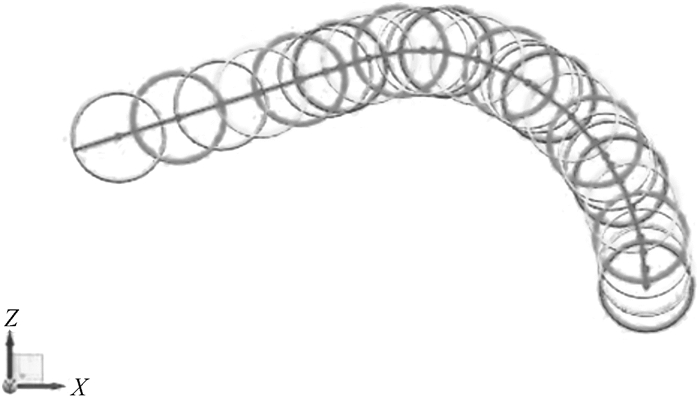
重构的冠部曲线与井底覆盖图如图 5所示。
|
| 图 5 重构的PDC钻头冠部曲线与井底覆盖图 Fig.5 The reconstructed PDC bit profile and bottom cover graph |
在重构冠部曲线的基础上可以计算各切削齿的法向角θ1。法向角为井底覆盖图上各切削齿过齿心的冠部曲线法线与钻头中心轴线的夹角。
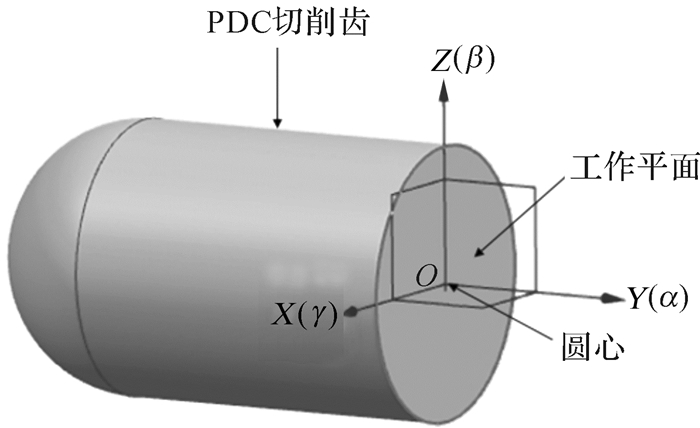
其次,基于PDC钻头的几何学原理建立数学方程,求解后倾角与侧倾角。将各切削齿的工作平面视为从特定的初始位置进行刚体运动的结果,各切削齿具有相同的初始工作平面,经过不同的正交变换后最终生成实际工作平面。将各切削齿初始工作平面的圆心设为坐标原点,法向角、后倾角、侧倾角都设为0°,在此基础上建立3个方向角的旋转轴线:法向轴、后倾轴与侧倾轴。初始工作平面的基本参数为:外法向量α0=(0,1,0);法向轴方向向量α=(0,1,0);侧倾轴方向向量γ=(1,0,0);后倾轴方向向量β=(0,0,1);圆心坐标O(0,0,0)。初始工作平面及其参数如图 6所表示。
|
| 图 6 切削齿初始工作平面及其参数 Fig.6 The initial working plane and its parameters of cutter tooth |
采用齐次坐标表示,三维几何变换矩阵是一个四阶方阵,其表现形式如下:
| $ \left\{ \begin{align} &\left[x'\ y'\ z'\ 1 \right]=\left[x\ y\ z\ 1 \right]\centerdot {{\mathit{\boldsymbol{T}}}_{3D}} \\ &{{\mathit{\boldsymbol{T}}}_{3\rm{D}}}=\left[\begin{matrix} a&b&c&p \\ d&e&f&q \\ g&h&i&r \\ l&m&n&s \\ \end{matrix} \right] \\ \end{align} \right. $ | (2) |
式中:
具体的求解过程如下:
1) 初始工作平面绕法向轴(Y轴)旋转,旋转角度为θ1(法向角),变换后平面的外法向量可以用线性变换表示为α1=T1α,侧倾轴线γ1=T1γ;其中线性变换可以采用矩阵的运算表示:
| $ \left\{ \begin{align} &\left[x'\ y'\ z'\ 1 \right]=\left[x\ y\ z\ 1 \right]\centerdot {{\mathit{\boldsymbol{T}}}_{3D}} \\ &{{\mathit{\boldsymbol{T}}}_{3\rm{D}}}=\left[\begin{matrix} \cos {{\theta }_{1}}&0 &-\sin {{\theta }_{1}}&0 \\ 0&1&0&0 \\ \sin {{\theta }_{1}}&0&\cos {{\theta }_{1}}&0 \\ 0&0&0&1 \\ \end{matrix} \right] \\ \end{align} \right. $ | (3) |
其中(x,y,z)为初始工作平面外法向量,同理可以进行绕X轴与Z轴的旋转变换。进行绕任意轴线旋转的计算时,先将任意轴线通过平移变换、绕坐标轴线旋转变换后与某一坐标轴线重合,将绕任意轴线的旋转变换转换为绕某一坐标轴线的旋转变换,最后进行旋转变换与平移变换的逆变换,将旋转轴变换到原始位置。
2) 绕侧倾轴线旋转,旋转角度为侧倾角θ2,此时工作平面的外法向量为α2,后倾轴线方向向量为β2,则:
| $ {\mathit{\alpha }_2}{\rm{ = }}{\mathit{\boldsymbol{T}}_2}{\mathit{\boldsymbol{T}}_1}\mathit{\alpha }, {\mathit{\beta }_2} = {\mathit{\boldsymbol{T}}_2}{\mathit{\boldsymbol{T}}_1}\mathit{\beta } $ | (4) |
3) 绕后倾轴线旋转,旋转角度为后倾角θ3,此时工作平面的外法向量可以表示为:
| $ {\mathit{\alpha }_3}{\rm{ = }}{\mathit{\boldsymbol{T}}_3}{\mathit{\boldsymbol{T}}_2}{\mathit{\boldsymbol{T}}_1}\mathit{\alpha } $ | (5) |
4) 绕钻头中心轴线(Z轴)旋转,角度为周向方位角θ,此时工作平面的外法向量可以表示为:
| $ {\mathit{\alpha }_4}{\rm{ = }}{\mathit{\boldsymbol{T}}_4}{\mathit{\boldsymbol{T}}_3}{\mathit{\boldsymbol{T}}_2}{\mathit{\boldsymbol{T}}_1}\mathit{\alpha } $ | (6) |
5) 实际工作平面圆心为O′,此时将工作平面沿着OO′平移至O′,便得到实际的工作平面,平移变换后其外法向量为α4,向量α4与逆向建模中获取的工作平面的外法向量α0相等:
| $ \alpha 4{\rm{ = }}\alpha 0 $ | (7) |
通过求解方程组解得最优侧倾角与后倾角。本文通过MATLAB软件编程实现求解的过程,同时基于UG/Open进行二次开发以实现切削齿三维模型的可视化与交互性。
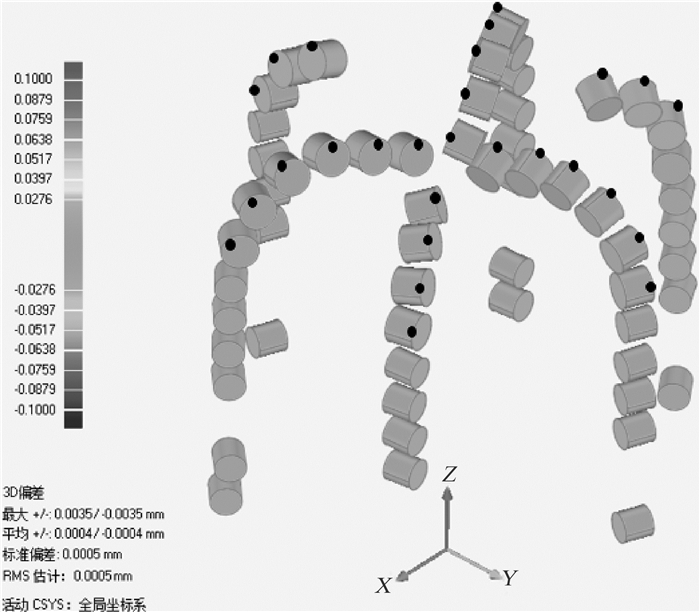
通过求解的法向角、后倾角、侧倾角以及在逆向建模时的获取齿中心坐标、切削齿型号、周向方位角,在UG中重新建立模型,通过检测软件与2.2节中重构的CAD模型进行对比[4],图 7为通过空间角度参数所建立的模型与重构CAD模型之间的3D偏差,平均偏差为0.000 4 mm,在各主切削齿的切削刃附近增加注释点(黑点表示),注释点与模型整体的偏差情况如表 1所示。结果表明获取的切削角度精度高,反求的设计参数符合精度要求。
|
| 图 7 基于空间角度参数所建立模型的三维偏差分析结果 Fig.7 Three-dimensional deviation analysis of the model determined based on the spatial angle parameters |
| 偏差类型 | 偏差值/mm |
| 注释点最大偏差 | 0.001 5 |
| 注释点最小偏差 | 0.000 1 |
| 注释点平均偏差 | 0.000 2 |
| 切削齿模型整体的偏差 | 0.000 4 |
对PDC钻头的布齿参数进行优化设计的目的是提高钻头破岩的效率,即提高钻头的钻进速度。影响钻头破岩效率的主要因素是切削齿的磨损,随着磨损加剧,其剪切岩石的能力下降[5],导致机械钻速不断下降,当钻速下降到一定程度时,钻头就处于失效状态,需要及时更换钻头。因为切削齿的尺寸(直径)、密度(数量)与冠部形状是决定钻头所适用地层与岩性的主要因素[6, 8],所以在优化设计时不改变切削齿尺寸、密度与冠部形状,而是通过合理调整其余布齿参数,来提高钻头在相似地层使用时的破岩效率。
PDC钻头的主要设计原则为经典三原则布齿和力平衡布齿[9]。经典三原则的设计出发点是PDC各切削齿的磨损与寿命均衡,而力平衡布齿是为了提高钻头的稳定性。本文采用等磨损原则与侧向力平衡布齿原则对布齿参数进行优化。
3.1 磨损速度优化在有关研究中已经提出PDC钻头切削齿磨损速度的预测模型,并且得到了试验验证[10-12]。切削齿磨损速度预测模型如下:
| $ {v_\text{t}} = \frac{{{F_\text{a}}}}{{l'}}\pi l(l + 2R{\rm{c}})C{\rm{p}}\tau \mu N\exp (\frac{h}{{D\cos {\theta _3}}}) $ | (8) |
式中:vt为切削齿体积磨损速度,mm3/h;l为切削齿的有效切削刃长(弧长),mm;l′为切削岩石的等效宽度,mm;Rc为切削距离(定位半径),等于切削齿至钻头中心轴线的距离,mm;Cp为水力系数;μ为切削齿与岩石之间的摩擦系数;τ为切削齿磨损强度;N为钻头转速,r/h;D为切削齿直径,mm;h为每一转所切削的深度,mm/r;θ3为切削齿后倾角;Fa为切削齿所受的轴向力,N。
同一钻头上各切削齿具有相似的硬度与物理属性,而磨损速度预测模型的目的是分析同一钻头上不同切削齿之间磨损速度的差异,磨损速度预测模型中忽略了材料硬度的影响。切削齿的有效切削刃长是由切削齿切削角度、定位半径、轴向高度与切削深度决定。
根据切削齿载荷测试与分析实验,轴向力可以表示为[13]:
| $ {F_\text{a}} = {F_1}\exp (K{\theta _3}) $ | (9) |
式中:F1是后倾角为零时的轴向力,由岩石性质、切削齿直径与切削深度决定;K是体现轴向载荷变化趋势的常数,主要由岩石性质决定。
在相同的地层岩性、切削深度、切削齿直径与水力参数条件下,磨损速度是关于切削齿切削距离(定位半径)、轴向高度与切削角度的函数。所以优化设计时,磨损速度方程可以表示为如下形式:
| $ {v_\text{t}} = f(R{\text{c}}, Z, {\theta _2}, {\theta _3}) $ | (10) |
式中Z为轴向高度。
钻头在旋转剪切岩石的过程中,各切削齿具有相同的角速度,切削齿至钻头中心的距离越远,则其线速度、力臂、破岩体积越大。根据磨损速度预测模型,在钻头设计中,切削齿切削距离的差异导致钻头外部切削齿的磨损速度高于内部切削齿。这就说明,按照等磨损原则的优化并不能保证全部切削齿的磨损速度一致,而是力求随着定位半径的增加,磨损速度变化趋于均衡,相邻切削齿之间磨损速度差异不大,避免切削齿与相邻齿的磨损速度相差过大,造成个别切削齿的磨损特别严重,提前失效,从而导致钻头整体钻进速度降低,破岩效率下降。
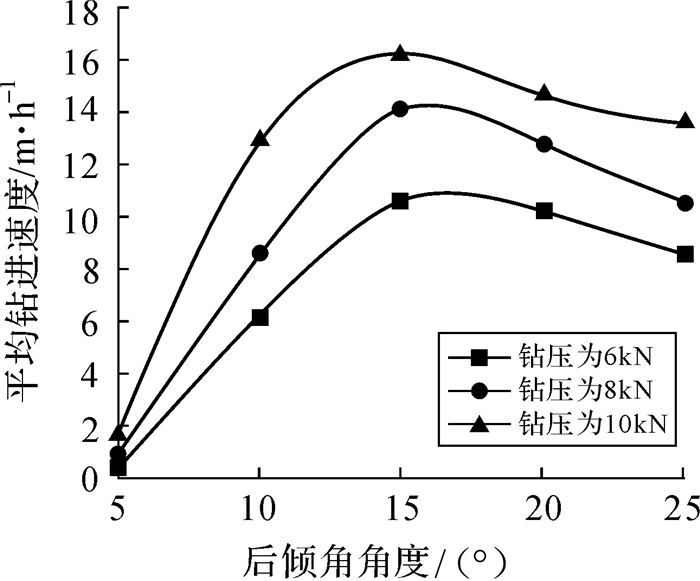
3.1.1 后倾角优选根据已有的后倾角优选实验,针对不同的岩样与切削齿直径分析后倾角对PDC钻头破岩效率的影响规律[14]。以某一六刀翼A型PDC钻头为例,其切削齿直径为16 mm,使用地层岩性为砂岩及泥岩,属于软至中软地层。根据相同岩性的岩样实验,在不同钻压的条件下,直径为16 mm的切削齿的后倾角与钻头钻进速度的关系如图 8所示[14]。
|
| 图 8 直径为16 mm的切削齿的后倾角与钻头平均钻速的关系 Fig.8 The relationship between back rake angle and average ROP (rate of penetration) of cutter with diameter of 16 mm |
从图 8可以发现,切削齿后倾角为15°时的PDC钻头钻进速度最高。12°~18°时钻速差异不大,所以对于A型PDC钻头,其最优切削齿后倾角为15°。
切削齿的侧倾角一般较小,主要作用是使切削齿在切削时对齿前切削产生侧向推力,使岩屑向钻头外缘移动,以利于排出岩屑,防止钻头泥包。研究和现场经验表明,随着水力清洗效果的提高,切削齿的侧倾角对PDC钻头性能的影响很小[14]。因此,在钻头的优化设计中可不更改原始钻头的侧倾角。
3.1.2 磨损速度优化模型在获得优选的后倾角之后,基于反求的布齿参数与磨损速度预测模型建立优化模型。对各切削齿的后倾角与井底覆盖图中位置参数(定位半径与轴向高度)进行优化。
通过文献[15]中的方法,可以在给定切削深度与布齿参数的条件下,计算各切削齿的有效切削弧长、轴向力与切向力。
设钻头有n颗切削齿,按照切削距离(定位半径)升序排列并依次编号,将约束条件设置为钻头冠部曲线不变,鼻部齿(轴向高度最大齿,编号为h)、定位半径最大齿(编号为n)与最小齿(编号为1) 的位置参数不变,并保证同一刀翼上相邻两齿不发生干涉,决策变量是各切削齿的定位半径与后倾角。相邻两齿之间的磨损速度之差的平方和表示为:
| $ E = \sum\limits_{i = 1}^{n - 1} {{{({v_{i + 1}} - {v_i})}^2}} $ | (11) |
式中vi表示第i颗切削齿的磨损速度。
磨损速度的优化模型如下:
| $ \begin{array}{l} \min {E_{\rm{m}}} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {{{({v_{i + 1}} - {v_i})}^2}} \\ {\rm{s}}.{\rm{t}}.\;\;\;\;L({R_i}, {Z_i}) = 0, {R_i} < {R_{i + 1}}\\ {R_i} < R_{_i}^0\;\;(i = 1, h, n)\\ {\theta _3} \in ({\theta _0} - \varepsilon, {\theta _0} + \varepsilon )\\ {d_{kj}} > \frac{1}{2}({D_{kj}} + {D_{k(j + 1)}})\\ k = 1, 2, 3, \cdots, m\\ j = 1, 2, 3, \cdots, {n_k} - 1 \end{array} $ |
其中:Ri为切削齿的定位半径; Ri0为原始钻头切削齿的定位半径; dkj为同一刀翼上相邻两齿的空间距离; k为刀翼号,刀翼数为m; j为k号刀翼上的齿号, k号刀翼的切削齿数量为nk; Dkj为k号刀翼上j号切削齿的直径; L为各切削齿在井底覆盖图中的位置函数; θ0为根据地层与相关实验数据优选后的后倾角; ε为后倾角变化值。
通过MATLAB软件使用内点法对布齿参数进行最优化求解,输出优化后的切削齿定位半径、轴向高度与后倾角。
3.2 侧向力平衡优化钻头瞬时旋转中心不断改变的现象称为钻头不规则偏心涡动,简称涡动。理论和实验研究表明,钻头涡动产生的冲击载荷是导致PDC钻头过早失效的主要原因之一[16-18]。钻头在井底受到侧向不平衡力是造成涡动的主要原因。在侧向不平衡力的作用下,钻头侧向上的一些点或面接触井壁,产生摩擦力与刮削力,在钻头上产生一个反扭矩,使钻头的旋转中心和运动状态发生变化,从而形成涡动。涡动造成钻头井下运动失稳,使切削刃及复合片部位受到剧烈、不规则的载荷冲击,造成切削齿崩齿(碎裂、断裂),最终导致PDC钻头过早失效。
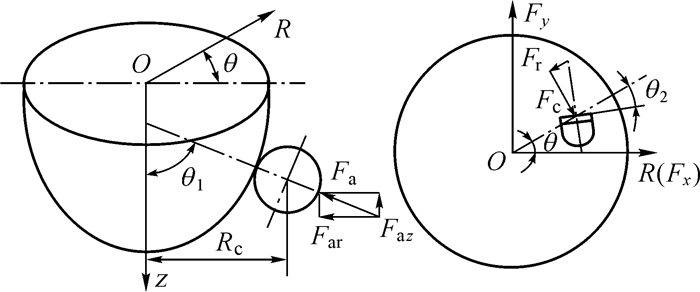
3.2.1 侧向力计算模型PDC钻头受力分析如图 9所示。
|
| 图 9 PDC钻头受力分析 Fig.9 The force analysis for PDC bit |
钻头上切削齿的径向分力由下式表示[12]:
| $ {F_{{\rm{ar}}}} = {F_{\rm{a}}}\cos {\theta _1} $ | (12) |
| $ {F_{\rm{r}}} = {F_{\rm{c}}}\tan {\theta _2} $ | (13) |
式中:Far与Fr是切削齿的径向分力; θ1与θ2是切削齿的法向角与侧倾角; Fa与Fc是单个切削齿所受的轴向力与切向力。
将各切削齿的切向力和径向分力向x,y坐标轴分解并求和,可求得2个坐标方向的分力,从而计算出钻头的总侧向力Fs及方向[16]。切削齿的周向方位角为θ,设切削齿数量为n,则坐标轴分力与总侧向力可表示如下:
| $ {F_x} = \sum\limits_{i = 1}^n {{{[{F_{\rm{c}}}\sin \theta-({F_{\rm{r}}} + {F_{{\rm{ar}}}})\cos \theta]}_i}} $ | (14) |
| $ {F_y} = \sum\limits_{i = 1}^n {{{[{F_{\rm{c}}}\cos \theta-({F_{\rm{r}}} + {F_{{\rm{ar}}}})\sin \theta]}_i}} $ | (15) |
| $ {F_\text{s}} = \sqrt {F_x^2 + F_y^2} $ | (16) |
由式(16) 可知,PDC钻头的总侧向力Fs取决于各切削齿的受力和周向方位角。当切削齿受力一定时,总侧向力仅与各切削齿的周向方位角有关[16]。对于螺旋型刀翼与直刀翼的PDC钻头,各刀翼的周向位置决定了切削齿的周向方位角。通过优化各刀翼的周向位置,可以整体优化刀翼上每颗切削齿的周向方位角,从而有效地控制总侧向力的大小。
3.2.2 侧向力优化模型设钻头共有n颗切削齿,分布在m个刀翼上,将每个刀翼上第1颗切削齿的周向方位角代表刀翼的方位角,升序排列并依次编号。第k号刀翼的周向方位角为φk,k号刀翼上第j颗齿的周向方位角为θkj,k号刀翼的切削齿数量为nk,则有如下关系:
| $ \left\{ \begin{array}{l} n = \sum\limits_{k = 1}^m {{n_k}} \\ {\varphi _k} = {\theta _{k1}}\\ k = 1, 2, 3, \cdots m \end{array} \right. $ |
设θkj0为优化前每个切削齿的周向方位角,通过反求设计参数得到。φk0为优化前每个刀翼的周向方位角,等于每个刀翼上第1颗切削齿的方位角。钻头侧向力平衡优化的数学模型为:
| $ \begin{array}{l} \min {F_{\rm{s}}} = \sqrt {F_x^2 + F_y^2} \\ {\rm{s}}.{\rm{t}}.\;\;\;\;{\varphi _k}(\varphi _k^0 - \varepsilon ', \varphi _k^0 + \varepsilon ')\\ {\theta _{kj}} = \theta _{kj}^0 + ({\varphi _k} - \varphi _k^0)\\ k = 1, 2, 3, \cdots, m\\ j = 1, 2, 3, \cdots, {n_k} \end{array} $ |
其中ε′为刀翼周向方位角优化调整值,ε′的取值根据实际刀翼数目与经验决定,在保证刀翼之间不发生干涉的同时提高计算效率。衡量不平衡力适当与否的标准为侧向不平衡力与钻压的比值,一般控制在5%以内[16-18]。
4 应用实例针对某一直径为215.9 mm的六刀翼A型PDC钻头,将其应用于水平井斜井段。该井段地层为:石千峰组,为棕红色、紫红色泥岩夹砂岩;石盒子组,为浅灰色块状砂岩与泥岩互层;山西组,为深灰、灰色泥岩,浅灰色砂岩。地层均属于软至中软地层。使用情况:鼻部与肩部之间磨损较严重,肩部附近切削齿存在崩齿现象,平均机械钻速为5.34 m/h,起钻原因为钻速较低。对其布齿参数进行逆向设计,并进行磨损速度优化与侧向力平衡优化。
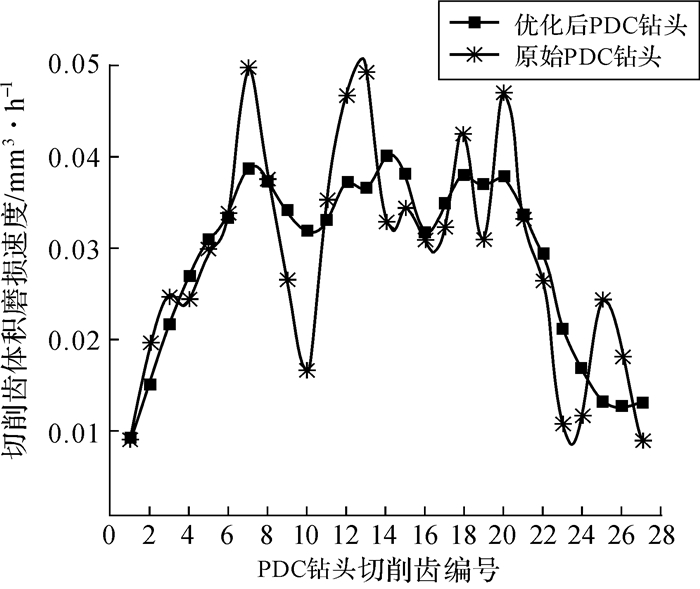
根据相似岩性的实验数据,将优选后的后倾角确定为15°,变化值为3°。通过文献[15]中方法计算有效弧长与各切削齿受力情况。使用磨损速度优化模型,计算分析中的参数如表 2所示。优化前后各切削齿磨损速度如图 10所示。各切削齿按照切削距离大小升序编号。
| 参数 | 数值 |
| 切削齿磨损强度τ /(N/mm2) | 70 |
| 水力系数Cp | 1.4×10-12 |
| 切削齿与岩石之间摩擦系数μ | 0.35 |
| 切削齿直径D /mm | 16 |
| 切削齿数量/颗 | 27 |
|
| 图 10 PDC钻头各切削齿的磨损速度 Fig.10 The wear rate of each cutter on PDC bit |
从图 10中可以看出原始钻头各齿的磨损速度分布不均衡,肩部与鼻部之间的数颗切削齿(7至21号齿)的磨损速度过大。这与钻头的实际磨损情况较一致,第7至第21颗齿位于钻头的鼻部与肩部之间,处于钻头磨损较严重的区域。优化后钻头与原始钻头的第7至第21颗齿磨损速度分析结果如表 3所示。优化后钻头的各切削齿尤其是鼻部与肩部之间的磨损速度更加均衡(磨损速度变化幅度不超过12%),这就保证了切削齿具有相近的磨损速度,防止某几颗切削齿的磨损速度异常大而导致磨损严重,从而保证了钻头整体切削岩石的效率。
| 钻头类型 | 每一转切削深度/mm·r-1 | 转速/r·h-1 | 最大磨损速度/mm3·h-1 | 最小磨损速度/mm3·h-1 | 平均磨损速度/mm3·h-1 | 标准差/mm3·h-1 |
| 原始A型钻头 | 1 | 7 200 | 0.050 5 | 0.009 0 | 0.036 4 | 0.009 3 |
| 优化后A型钻头 | 1 | 7 200 | 0.040 1 | 0.009 3 | 0.035 9 | 0.002 5 |
在进行磨损速度优化后,对钻头刀翼的周向方位角进行侧向力平衡优化。以原始刀翼的周向方位角作为初始值,将优化范围设置为-15°~+15°。对于1至6号刀翼,原始钻头的周向角度为0°,50.4°,123.5°,173.3°,233.1°,292°;优化后的周向方位角为0°,60.2°,126.9°,172.5°,243.1°,286.7°。优化后钻头与原始钻头的受力分析结果见表 4。优化后钻头的侧向力与钻压的比值由5.3%降至3.1%。
| 钻头类型 | 地层岩性 | 地层可钻性级值Kd | 钻压/kN | 扭矩/kN·m | 侧向力/kN | 侧向力方向角/(°) | 侧向力与钻压比值/% |
| 原始A型钻头 | 软至中软 | 3.5 | 8.63 | 0.71 | 0.46 | -16 | 5.3 |
| 优化后A型钻头 | 软至中软 | 3.5 | 8.63 | 0.71 | 0.27 | -33 | 3.1 |
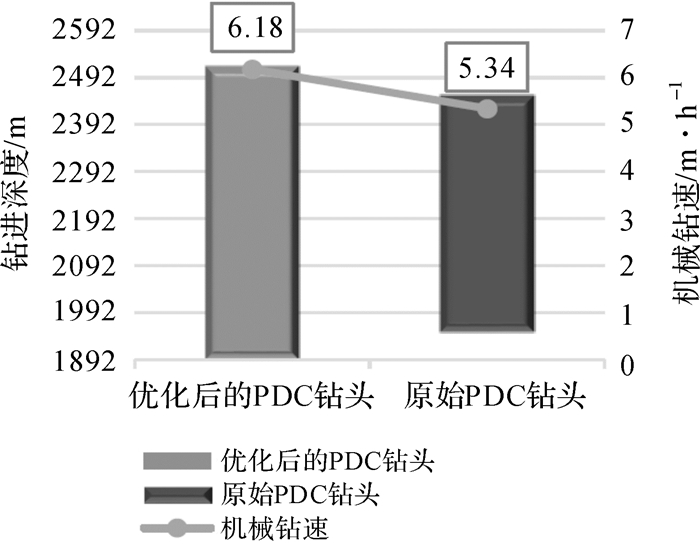
经过优化设计并制造的A型PDC钻头与原始钻头相比,切削齿的型号相同。优化后的钻头在邻井使用,与原始钻头的使用地层岩性相似(砂岩及泥岩,属于软至中软地层)。两者钻井数据如表 5所示,性能比较如图 11所示,图 12为原始钻头使用情况,图 13为优化后钻头的使用情况。
| 钻头类型 | 井段/m | 钻进时间/h | 螺杆型号 | 平均机械钻速/m·h-1 | IADC磨损分级 | |
| 复合钻进 | 滑动钻进 | |||||
| 原始A型钻头 | 195 1~245 3 | 94 | 165 1.5° | 6.92 | 2.26 | 1-2-BT-S-X-IN-WT-PR |
| 优化后A型钻头 | 189 2~251 6 | 101 | 165 1.5° | 7.34 | 2.74 | 1-2-WT-S-X-IN-BT-PR |
|
| 图 11 优化前后PDC钻头性能的比较 Fig.11 Comparison of PDC bit performance before and after optimization |

|
| 图 12 原始PDC钻头实际使用情况 Fig.12 The partial usage situation of original PDC bit |

|
| 图 13 优化后的PDC钻头实际使用情况 Fig.13 The partial usage situation of optimized PDC bit |
使用效果评价:邻井的斜井段需两趟钻,相比原井斜井段减少一趟钻;优化后的PDC钻头平均机械钻速相比原始钻头提高了16%,钻进深度提高了24%。经过磨损速度优化,使切削齿具有最佳切削角度的同时其磨损速度分布更加均衡,避免了个别切削齿磨损严重的现象,提高了钻头的整体破岩效率与钻进速度。优化后钻头各切削齿属于正常磨损,虽然鼻部与肩部的切削齿磨损仍相对严重,但不存在崩齿现象,主要是因为侧向力的平衡优化提高了钻头的稳定性,有效避免切削齿的崩齿现象,在提高钻进速度的同时保证了钻头的寿命(钻进时间),使钻进深度有效提高。
5 总结分析了PDC钻头布齿参数的逆向设计与优化方法,并以某一PDC钻头为实例,得出以下结论:
1) 结合逆向软件Geomagic与UG的二次开发功能快速实现了切削齿结构的逆向建模,重构模型的平均误差在0.086 mm以内。在此基础上高效并准确地实现钻头布齿参数的反求,求解出的布齿参数整体的误差控制在0.000 4 mm以内。
2) 基于反求的钻头布齿参数,使用磨损速度优化模型与侧向力平衡优化模型进行优化。优化后的PDC钻头在邻井的相似地层使用,具有更高的钻进速度与更大的钻进深度,机械钻速提高16%,钻进深度提高24%。
3) 逆向设计中的检测技术,可以有效检测重构模型与原始设计模型之间的误差,其技术方法可以应用于钢体钻头与胎体钻头制造加工中的误差分析。对误差实现量化处理与趋势分析,从而对原始设计模型进行修正或者改进制造工艺。
PDC钻头布齿参数的逆向设计与优化的方法为PDC钻头的个性化设计提供一种全新的设计思路,对布齿参数优化设计以及创新设计提供了理论依据,其设计思路与模式可以应用于其他钻头及机械产品的设计与研究当中。
| [1] | TSAI Y C, HUANG C Y, LIN K Y, et al. Development of automatic surface reconstruction technique in reverse engineering[J]. International Journal of Advanced Manufacturing Technology, 2008, 42(1): 152–167. |
| [2] |
王春香, 孟凡娟.
具有复杂内腔和外形的斗齿快速逆向设计[J]. 工程设计学报, 2012, 19(6): 460–464.
WANG Chun-xiang, MENG Fan-juan. The rapid reverse design of excavator bucket teeth with both complex inner cavity and outer shapes[J]. Chinese Journal of Engineering Design, 2012, 19(6): 460–464. |
| [3] |
胡双喜, 钟鼎.
复杂模型的快速参数化逆向建模研究[J]. 机械设计, 2015, 32(4): 91–95.
HU Shuang-xi, ZHONG Ding. Study on rapid parametric reverse for complex models[J]. Journal of Mechanical Design, 2015, 32(4): 91–95. |
| [4] |
李丽娟, 高姗, 林雪竹.
基于Geomagic Qualify的工件偏差检测技术[J]. 制造业自动化, 2014, 36(10): 35–38.
LI Li-juan, GAO Shan, LIN Xue-zhu. Workpiece deviation detection techniques based on Geomagic Qualify[J]. Manufacturing Automation, 2014, 36(10): 35–38. DOI:10.3969/j.issn.1009-0134.2014.10.010 |
| [5] |
杨迎新. PDC钻头切削力学研究[D]. 成都: 西南石油大学机电工程学院, 2003: 16-19.
YANG Ying-xin. PDC bit cutting mechanics research[D]. Chengdu:Southwest Petroleum University, School of Mechatronic Engineering, 2003:16-19. |
| [6] |
代大良, 王镇全, 潘起峰, 等.
肯吉亚克油田非盐丘井PDC钻头设计及实验研究[J]. 石油钻采工艺, 2009, 31(3): 5–9.
DAI Da-liang, WANG Zhen-quan, PAN Qi-feng, et al. Design of PDC bit and its laboratory test for non saline dome wells in Kenkiyak Oilfield[J]. Oil Drilling & Production Technology, 2009, 31(3): 5–9. |
| [7] |
张义宽.
计算机图形学[M]. 西安: 西安电子科技大学出版社, 2004: 128-137.
ZHANG Yi-kuan. Computer graphics[M]. Xi'an: Xi'an University of Electronic Science and Technology Press, 2004: 128-137. |
| [8] |
肖国益, 胡大梁, 廖忠会, 等.
川西须家河组地层PDC钻头结构参数优化及选型[J]. 石油钻探技术, 2012, 40(3): 28–32.
XIAO Guo-yi, HU Da-liang, LIAO Zhong-hui, et al. Parameter optimization and selection of PDC bits for Xujiahe formation in western Sichuan[J]. Petroleum Drilling Techniques, 2012, 40(3): 28–32. |
| [9] |
牛世伟, 杨迎新, 牛永超.
PDC钻头布齿计算方法的研究现状及发展[J]. 石油机械, 2015, 43(9): 6–9.
NIU Shi-wei, YANG Ying-xin, NIU Yong-chao. Research status and development of calculation method for PDC bit tooth arrangement[J]. China Petroleum Machinery, 2015, 43(9): 6–9. |
| [10] |
曲冠政, 曲大伟, 郭瑞, 等.
PDC钻头复合片磨损速度模型研究[J]. 复杂油气藏, 2013, 6(1): 62–64, 71.
QU Guan-zheng, QU Da-wei, GUO Rui, et al. Study on a swear rate model of PDC composite cutters[J]. Complex Hydrocarbon Reservoirs, 2013, 6(1): 62–64, 71. |
| [11] |
田家林, 付传红, 杨琳, 等.
基于扭转振动的PDC钻头布齿角度对复合片磨损规律的影响研究[J]. 固体力学学报, 2014, 35(6): 574–582.
TIAN Jia-lin, FU Chuan-hong, YANG Lin, et al. Influence of the tooth-distributing angle of PDC bit on wear of composite plate under torsion vibration[J]. Chinese Journal of Solid Mechanics, 2014, 35(6): 574–582. |
| [12] |
梁尔国, 李子丰, 邹德永.
PDC钻头综合受力模型的试验研究[J]. 岩土力学, 2009, 30(4): 938–942.
LIANG Er-guo, LI Zi-feng, ZOU De-yong. Experimental research on integrated mechanical model of PDC bit[J]. Rock and Soil Mechanics, 2009, 30(4): 938–942. |
| [13] |
石志明. PDC齿切削载荷的测试与分析[D]. 成都: 西南石油大学机电工程学院, 2006: 39-51.
SHI Zhi-ming. Testing and analysis cutting force of PDC cutters[D]. Chengdu:Southwest Petroleum University, School of Mechatronic Engineering, 2006:39-51. |
| [14] |
蔡环. PDC钻头关键设计参数优化研究[D]. 青岛: 中国石油大学(华东)石油工程学院, 2008: 54-61.
CAI Huan. Optimization of key parameters for PDC bit's design[D]. Qingdao:China University of Petroleum, (EastChina), School of Petroleum Engineering, 2008:54-61. |
| [15] |
陈玉中. 基于UG的PDC钻头钻进仿真方法研究[D]. 成都: 西南石油大学机电工程学院, 2015: 17-37.
CHEN Yu-zhong. Research on the PDC bit drill simulation method based on UG software[D]. Chengdu:Southwest Petroleum University, School of Mechatronic Engineering, 2015:17-37. |
| [16] |
邹德永, 王瑞和.
刀翼式PDC钻头的侧向力平衡设计[J]. 石油大学学报(自然科学版), 2005, 29(2): 42–44.
ZOU De-yong, WANG Rui-he. Lateral force balancing design of blade PDC bits[J]. Journal of the University of Petroleum(Edition of Nature Science), 2005, 29(2): 42–44. |
| [17] |
陈洪涛, 黄继庆, 滕惠婷, 等.
防涡PDC钻头的研究与应用[J]. 钻采工艺, 2010, 33(2): 76–78, 140.
CHEN Hong-tao, HUANG Ji-qing, TENG Hui-ting, et al. Research on anti-whirl technique for PDC bit[J]. Drilling and Production Technology, 2010, 33(2): 76–78, 140. |
| [18] | COOLEY C H, PASTUSEK P E, HUGHES C. The design and testing of anti-whirl bits[C]//SPE Annual Technical Conference and Exhibition, Washington D.C, Oct. 4-7, 1992. |



