镁合金综合性能优良,在工业领域具有广阔的应用前景,温成形技术在镁合金成形中的应用也越来越受到关注,与等温、常温成形工艺相比,差温成形更有利于提高成形件质量。
数值仿真方法能有效预测成形件的缺陷[1],而准确的本构参数是保证数值仿真结果可靠的前提。直接通过准静态实验获得的材料参数,由于没有考虑复杂加载情况和温度的影响而会引入较大误差[2]。采用分离式Hopkinson压杆装置能够大幅提高获取的材料本构参数的精度,但昂贵、复杂的实验设备使得这类方法并不能广泛地应用[3]。Clausen等[4]将数值模拟与实验结合,在优化迭代过程中不断调用有限元模型从而反求出材料参数,但是耗时很长,效率低下。乔良等[5]采用RBF近似模型代替有限元模型,结合粒子群算法对本构参数实现了反求。李恩颖等[6]利用支持向量机结合试验直接进行本构参数反求,其结果表明支持向量机在小样本非线性问题中具有良好的拟合精度。Wang等[7-8]对利用近似模型反求参数及相关不确定性因素等问题进行了研究,提高了反求方法的稳健性。Goel等[9]通过实验论述了多个近似模型组合使用解决实际问题的优势。Han等[10]将量子计算与传统遗传算法相结合并引入量子旋转门,通过对组合优化问题求解,取得了比传统遗传算法更好的效果。本文选取NUMISHEET2011标准考题中的十字杯形件作为研究对象,采用基于有限元思想的数值方法,通过建立以本构参数为设计变量,目标温度为响应的混合近似模型,利用改进的量子遗传优化算法寻求仿真结果与试验数据之间误差函数的最小解[11-12],从而更准确地获取适用于差温成形过程的AZ31B镁合金的本构参数。
1 基于SVR-ELM混合近似模型的反求模型 1.1 改进的量子遗传算法量子遗传算法是量子通信与遗传算法相结合的一种进化算法。它采用量子比特来表达一个基因,因此比经典遗传算法具有更好的特征多样性与收敛性。采用多量子比特编码p个参数的基因如下:
| $ q_{^\mathit{j}}^\mathit{t} = \left( \begin{array}{l} \left| \begin{array}{l} \alpha _{11}^t\\ \beta _{11}^t \end{array} \right.\left| \begin{array}{l} \alpha _{12}^t\\ \beta _{12}^t \end{array} \right.\left| \begin{array}{l} \cdots \\ \cdots \end{array} \right.\left| \begin{array}{l} \alpha _{1\mathit{k}}^\mathit{t}\\ \beta _{1\mathit{k}}^\mathit{t} \end{array} \right.\left| \begin{array}{l} \alpha _{21}^t\\ \beta _{21}^t \end{array} \right.\left| \begin{array}{l} \alpha _{22}^t\\ \beta _{22}^t \end{array} \right.\left| \begin{array}{l} \cdots \\ \cdots \end{array} \right.\\ \left| \begin{array}{l} \alpha _{{\rm{2}}\mathit{k}}^\mathit{t}\\ \beta _{{\rm{2}}\mathit{k}}^\mathit{t} \end{array} \right.\left| \begin{array}{l} \cdots \\ \cdots \end{array} \right.\left| \begin{array}{l} \alpha _{p1}^t\\ \beta _{p1}^t \end{array} \right.\left| \begin{array}{l} \alpha _{p{\rm{2}}}^t\\ \beta _{p{\rm{2}}}^t \end{array} \right.\left| \begin{array}{l} \cdots \\ \cdots \end{array} \right.\left| \begin{array}{l} \alpha _{pk}^t\\ \beta _{pk}^t \end{array} \right. \end{array} \right) $ | (1) |
式中:qjt指第t代中第j个个体的染色体编码,α和β表示量子比特编码,p为染色体基因个数,k为编码基因的量子比特数。
量子遗传算法的迭代更新通过量子旋转门实现:
| $ \left[\begin{array}{l} \alpha _i^*\\ \beta _i^* \end{array} \right] = \mathit{\boldsymbol{G}}\left( {{\theta _i}} \right)\left[\begin{array}{l} {\alpha _i}\\ {\beta _i} \end{array} \right] $ | (2) |
| $ \mathit{\boldsymbol{G}}\left( {{\theta _i}} \right) = \left[\begin{array}{l} {\rm{cos}}{\theta _i}\;\;-{\rm{sin}}{\theta _i}\\ {\rm{sin}}{\theta _i}\;\;\;{\rm{cos}}{\theta _i} \end{array} \right] $ | (3) |
式中:(αi, βi)T, (αi*, βi*)T分别表示编码染色体第i个量子比特旋转门更新前后的概率幅; θi为量子旋转门旋转角。
利用动态量子门代替固定旋转角量子门,对量子遗传算法进行改进。根据进化进程实时调整量子旋转门旋转角θi的大小,迭代过程中将通过测量染色体所得的二进制解与当前最优解进行逐位比较,根据比较结果以及进化程度,调整个体中相应位量子比特,使个体更快速地向最优解方向进化[13]。
设通过测量染色体得到的某二进制解为:
| $ d = {\lambda _1}{\lambda _2} \ldots {\lambda _s} $ | (4) |
式中:λ1λ2…λs表示长度为s的二进制串,λi(i=1, 2, …,s)表示染色体上第i位编码。
为方便与最优解比较,通过反正弦函数将λi向角度映射,则更新后染色体第i位对应的旋转角可表示为:
| $ {\theta _i} = \left( {\frac{{{\rm{arc}}\;{\rm{sin}}{\lambda _i} - \theta _i^*}}{g} + \delta } \right)\theta _i^* $ | (5) |
式中:θi*是当前第i位编码对应的旋转角; g为当前进化代数; δ为平衡参数,避免随进化代数增加而使更新后旋转角过小导致收敛速度减慢。
1.2 SVR-ELM混合模型建立不同近似模型针对不同工程问题的预测能力表现各异,精度高的近似模型不一定预测能力强,精度低的近似模型也可能得到更合适的最优解,选择某一种近似模型可能会存在一定的不足,而由多个近似模型组合而成的混合模型对高维度非线性问题的预测精度更高更稳定。
| $ {y_{avg}} = \sum\limits_{\mathit{i} = 1}^\mathit{N} {{\phi _\mathit{i}}\left( x \right){y_i}\left( x \right)} $ | (6) |
| $ \sum\limits_{\mathit{i} = 1}^\mathit{N} {{\phi _\mathit{i}}\left( x \right)} = 1 $ | (7) |
式中:yavg为混合模型的输出响应,ϕi(x)为第i个模型的权系数,yi(x)为第i模型的输出响应,N为近似模型的个数。
构造混合模型的关键是权系数的计算,根据各模型的预测精度来分配权系数。考虑到不同模型的精度有较大差别,采用启发式计算方法来计算各自的权系数。
| $ {E_{avg}} = \frac{1}{N}\sum\limits_{\mathit{i} = 1}^\mathit{N} {{E_i}} $ | (8) |
| $ \phi _i^* = {\left( {{E_i} + {\gamma _1} \cdot {E_{{\rm{avg}}}}} \right)^{{\gamma _2}}},{\gamma _1} < 1,{\gamma _2} < {\rm{ }}0 $ | (9) |
| $ {\phi _\mathit{i}} = \phi _i^*/\sum\limits_{\mathit{j} = 1}^\mathit{N} {\phi _j^*} $ | (10) |
式中:Ei为第i模型的均方误差; Eavg为系统平均均方误差; γ1, γ2为权重控制系数, 为保证混合模型的稳定性,此处取γ1=0.05, γ2=-1。
基于支持向量回归机(support vector regression,SVR)与极限学习机(extreme learning machine,ELM)两种回归近似模型,提出一种SVR-ELM混合近似模型用于反求镁合金本构参数。
1) 支持向量回归机。
支持向量机是以结构风险最小化原则为基础的一种基于统计学理论的新型机器学习方法,回归型支持向量机的基本思想是寻找一个最优分类超平面, 使得所有样本到该超平面的距离最小,即超平面回归函数与样本之间的误差最小。
利用对应约束条件以及Largrange函数,通过求解其对偶形式,得到回归方程:
| $ \begin{array}{l} f\left( \mathit{\boldsymbol{x}} \right) = {\mathit{\Psi }^*}\varphi \left( \mathit{\boldsymbol{x}} \right) + {\mathit{\boldsymbol{b}}^*} = \\ \sum\limits_{\mathit{i} = 1}^\mathit{l} {\left( {{\tau _i} - \tau _i^*} \right)} K({\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}) + {\mathit{\boldsymbol{b}}^*} \end{array} $ | (11) |
式中:τ=[τ1, τ2, …, τl], τ*=[τ1*, τ2*, …, τl*]为最优解;K(xi, x)=φ(xi)φ(x)为核函数;xi为输入响应; l为训练样本数量;b*为包含支持向量的待定参数。
2) 极限学习机回归模型。
极限学习机是由单隐含层前馈神经网络(single-hidden layer feed forward neural network,SLFN)发展而来[14],相比传统神经网络, 其学习速度更快,收敛效果更好。
设有Q个不同样本(xi, yi),i=1, 2, …, Q, 其中xi=[xi1, xi2, …, xin]T∈Rn, yi=[yi1, yi2, …, yim]T∈Rm; Rn, Rm分别为与xi,yi维数对应的实数空间。
对具有n个输入变量,m个输出变量及η个隐含层节点的单隐含层神经网络可表示为:
| $ {\mathit{\boldsymbol{y}}_\mathit{j}} = \sum\limits_{i = 1}^\eta {{\beta _\mathit{i}}\mathit{g}({\omega _\mathit{i}}\cdot{\mathit{\boldsymbol{x}}_\mathit{j}} + {\mathit{\boldsymbol{b}}_\mathit{i}}), \mathit{j} = 1, 2, \cdots, Q} $ | (12) |
式中:βi, ωi,bi分别为输出权值、输入权值和隐含层阈值;g(ωi·xj+bi)为激活函数。
为训练SLFN,需要确定ωi, bi, β,使得:
| $ \xi = \mathop {{\rm{min}}}\limits_{{\omega _\mathit{i}}, {\mathit{\boldsymbol{b}}_i}, \beta } \left\| {\mathit{\boldsymbol{H}}\left( {{\omega _1}, {\omega _2}, \cdots, {\omega _\eta }, {\mathit{b}_1}, {\mathit{b}_2}, \cdots, {\mathit{b}_\eta }} \right)\beta - \mathit{\boldsymbol{Y}}} \right\| $ | (13) |
式中:H为g(ωi·xj+bi)构成的隐含层输出矩阵;Y=[y1, y2, …, yQ]m×Q为神经网络的期望输出。
ELM训练时随机产生输入层与隐含层间的连接权值ω及隐含层神经元的阈值b,且整个训练过程中无需调整,只需要设置隐含层神经元的个数,便可以获得唯一的最优解。由ω与b可唯一确定出隐含层输出矩阵H,进而更快速获得构建神经网络所需的ω, b, β三个参数。通过对式(13) 的转化,神经网络可简述为线性系统。
| $ \mathit{\boldsymbol{H}}\beta = \mathit{\boldsymbol{Y}} $ | (14) |
求解该方程可得隐含层与输出层连接权值的最小二乘解β=H+Y,其中H+是H的Moore-Penrose广义逆。
1.3 SVR-ELM混合近似模型的自适应更新近似模型训练时,样本空间的大小与多样性直接制约着近似模型的拟合精度。采用量子遗传算法对混合近似模型求解域寻优并通过自适应方法将产生的局部最优解选择性地加入各模型初始样本库,重新拟合相应的近似模型并再次组合新的混合模型,通过不断地更新样本库,使得混合近似模型的求解域更快速地逼近目标最优解。具体操作如下:
1) 通过初始样本库分别训练SVR, ELM两模型并计算各自的均方误差Esvr, Eelm作为模型精度的判断依据。
2) 建立SVR-ELM混合近似模型,并利用量子遗传算法寻优,将迭代寻优得到的局部最优样本与初始样本库暂时组合成新样本库,用于重新训练SVR与ELM,并再次计算各自的均方误差E′svr, E′elm以及ΔEsvr=E′svr-Esvr, ΔEelm=E′elm-Eelm。
3) 若ΔEsvr<0, ΔEelm<0,将寻优得到的样本加入初始样本库用于后续的SVR, ELM训练;若ΔEsvr≥0, ΔEelm<0,将该样本只加入ELM的初始样本库;若ΔEsvr<0, ΔEelm≥0,将该样本只加入SVR的初始样本库;否则舍弃该样本并返回至步骤2)。
1.4 基于SVR-ELM混合近似模型的算法流程1) 使用拉丁超立方试验设计方法进行抽样并组成初始样本库,对样本点进行仿真计算出响应值。利用初始样本库分别训练SVR和ELM模型。
2) 建立SVR-ELM混合近似模型并利用启发式算法计算SVR和ELM的权系数。
3) 采用量子遗传算法对初始种群测量寻优,记录当前代最优个体。
4) 通过自适应方法将获得的个体选择性地加入对应的样本库。
5) 利用更新的样本库重新拟合两模型并建立混合模型,利用量子遗传算法迭代寻优,判断是否达到收敛条件,满足条件就结束,否则返回至步骤4)。
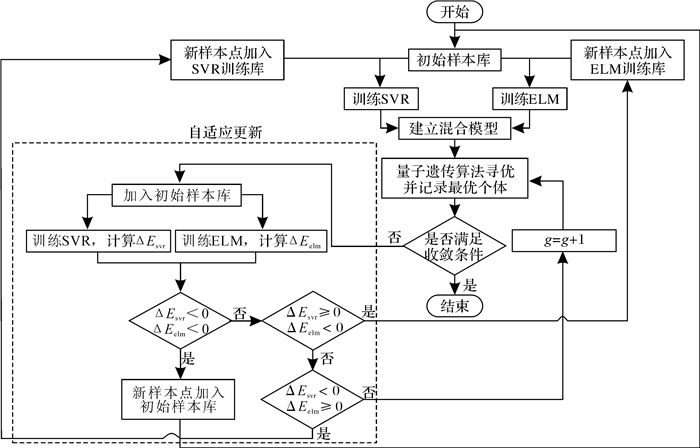
该算法流程如图 1。
|
| 图 1 基于自适应SVR-ELM混合近似模型的算法流程 Fig.1 Algorithm flow based on adaptive SVR-ELM mixture surrogate model |
为了验证SVR-ELM混合模型的效果,选取非线性函数对其测试,并与单一SVR模型以及ELM模型对比。此处采用的测试函数为:
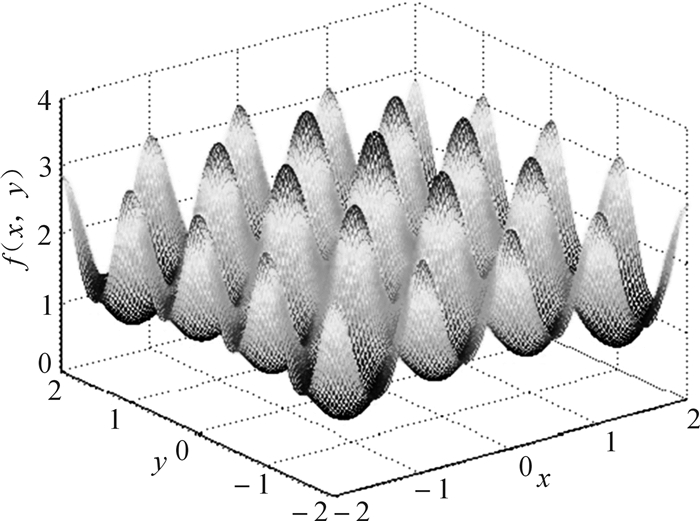
| $ \mathit{f}\left( {\mathit{x}, \mathit{y}} \right) = \frac{{{\rm{sin}}\sqrt {{\mathit{x}^2} + {\mathit{y}^2}} }}{{{\mathit{x}^2} + {\mathit{y}^2}}} + {{\rm{e}}^{\frac{{{\rm{cos}}2\pi \mathit{x} + {\rm{cos}}2\pi \mathit{y}}}{2}}}, - 2 < x, y < 2 $ | (15) |
函数图像如图 2所示。
|
| 图 2 测试函数图像 Fig.2 Diagram of test function |
常用的近似模型精度评价指标有均方根误差(root mean square error, RMSE)和决定系数R2, 定义如下:
| $ {\rm{RMSE = }}\frac{1}{k}\sqrt {\sum\limits_{i = 1}^k {{{\left( {{\mathit{f}_i} - {\widehat {{\mathit{f}_\mathit{i}}}}} \right)}^2}} } $ | (16) |
| $ {\mathit{R}^2} = \sum\limits_{i = 1}^k {{{\left( {{\widehat {{\mathit{f}_\mathit{i}}}} - {{\mathit{\bar f}}_\mathit{i}}} \right)}^2}/\sum\limits_{i = 1}^k {{{\left( {{\mathit{f}_i} - {{\mathit{\bar f}}_\mathit{i}}} \right)}^2}} } $ | (17) |
式中:k为样本数,fi为真实响应值,
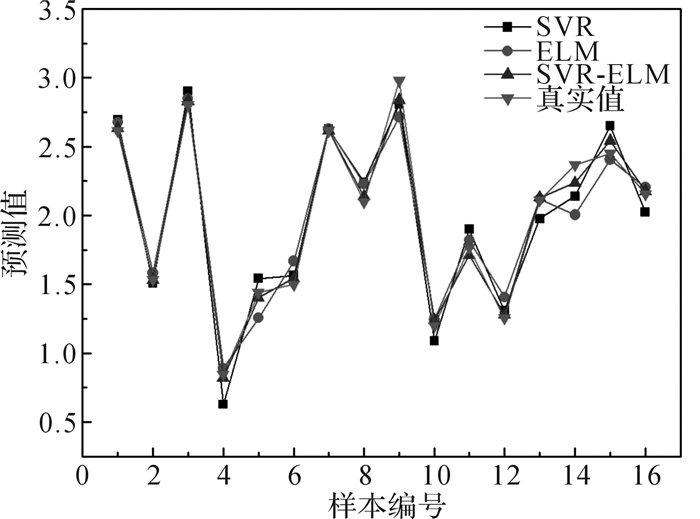
通过拉丁超立方抽样方法对测试函数随机抽样16组,分别采用SVR,ELM,SVR-ELM三种模型对样本点进行拟合。利用均方根误差RMSE与决定系数R2评价模型拟合精度,结果如表 1所示,图 3为预测结果对比。
| 近似模型 | RMSE | R2 |
| SVR | 0.025 95 | 0.868 21 |
| ELM | 0.037 81 | 0.896 76 |
| SVR-ELM | 0.001 58 | 0.998 56 |
|
| 图 3 各模型预测结果对比 Fig.3 Comparison of prediction results of each model |
测试结果表明,相比SVR,ELM两种模型,SVR-ELM混合近似模型均方根误差更小,决定系数R2更接近1,具有更好的拟合精度。
2 SVR-ELM混合近似模型在镁合金本构参数反求中的应用 2.1 有限元模型的建立与验证选取NUMISHEET2011中的Benchmark 2十字杯形件为研究对象,对镁合金AZ31B十字杯形件差温成形过程进行仿真。冲压成形的工件如图 4。

|
| 图 4 十字杯形件冲压成形示意图 Fig.4 Forming diagram of cross-shaped cup |
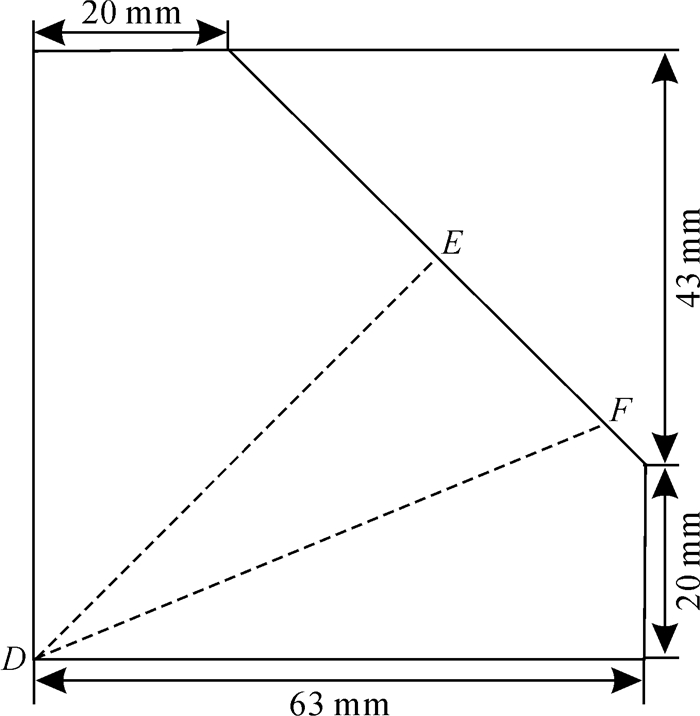
考虑到计算时间和十字杯形件的两向对称性,选取1/4杯形件,在ABAQUS中建立对称边界条件有限元模型,材料为镁合金AZ31B,板料尺寸如图 5所示,板厚为0.5 mm, 材料参数如表 2所示。
|
| 图 5 板料尺寸 Fig.5 Dimension of blank |
| 参数 | 数值 |
| 杨氏模量/GPa | 45 |
| 泊松比 | 0.35 |
| 密度/kg·m-3 | 1 770 |
| 比热/kg·J-1·℃-1 | 1 000 |
| 热传导率/W·m-1·℃-1 | 96 |
| 接触换热系数/W·m-2·℃-1 | 4 500 |
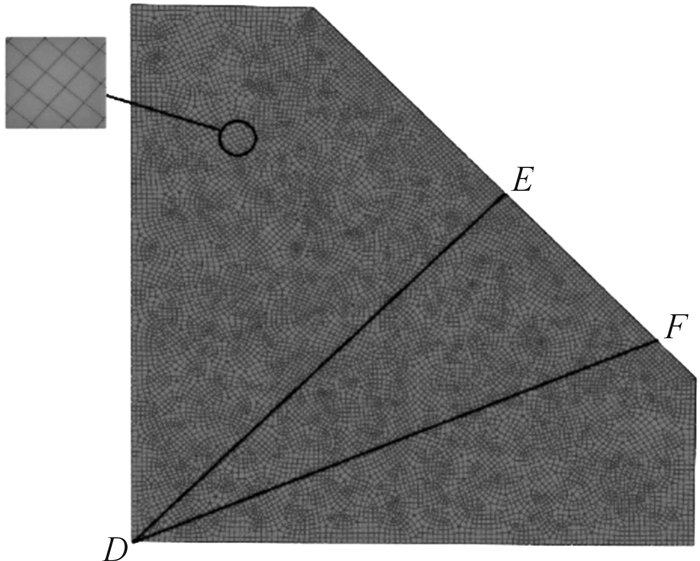
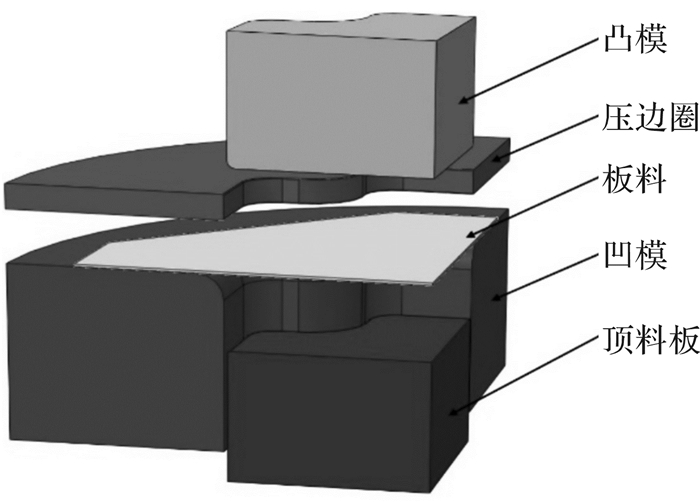
通过模具的作用使板料温度场差异化是差温成形的主要特征,将凹模和压边圈加热到250 ℃,通过热传导方式提高板料法兰部位的温度,从而降低材料流动阻力,板料、凸模和顶料板加热到100 ℃,使得处于拉深部位的板料拥有相对较低的塑性变形能力,从而有效控制该部位材料的减薄率。利用有限元软件ABAQUS进行差温成形仿真,设拉深深度为18 mm, 摩擦系数为0.05。成形仿真过程采用动力显式分析方法,温度—位移加载,板料网格划分如图 6所示,DE,DF代表截面位置,网格类型采用C3D8RT(八节点温度位移耦合减缩积分单元),沿厚度方向设置4层单元以控制沙漏问题,图 7为有限元仿真模型示意图。
|
| 图 6 板料网格划分 Fig.6 Mesh of blank |
|
| 图 7 1/4杯形件的有限元模型示意图 Fig.7 FEM diagram of 1/4 cross-shaped cup |
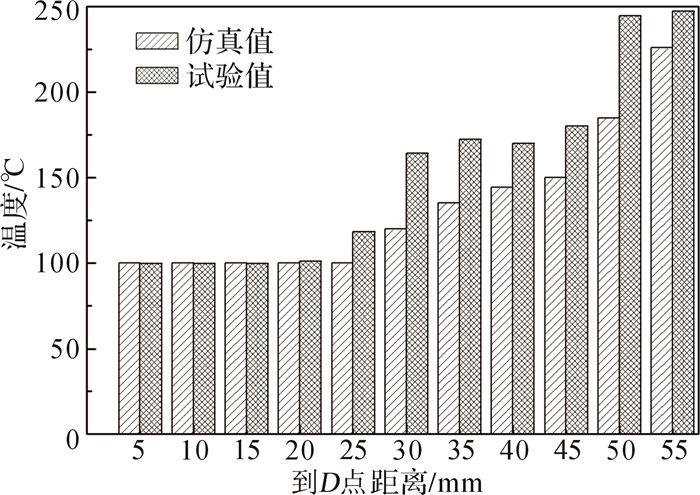
为了验证该有限元模型的有效性,利用表 3中镁合金AZ31B的Johnson-Cook本构模型关键参数[15]进行数值模拟并将仿真结果中的板料DE截面温度分布情况与试验数据进行对比,仿真结果如图 8所示,对比结果如图 9所示。
| 参数 | A | B | C | m | n |
| 数值 | 183 | 804.483 | 0.096 | 0.860 | 0.950 |

|
| 图 8 板料DE截面温度分布云图 Fig.8 Temperature distribution nephogram of DE section of blank |
|
| 图 9 板料DE截面温度分布仿真结果与试验数据对比 Fig.9 Comparison between simulation result and experimental data of temperature distribution of DE section of blank |
由图 8可知,法兰处最高温度为229.233 ℃,与试验数据相比误差为7.44%。
由图 9对比结果可知,仿真数据与试验结果基本吻合,证明建立的有限元模型有效。
2.2 Johnson-Cook本构模型Johnson-Cook本构模型(J-C模型)由应变强化项、应变率强化项和温度软化项三部分组成,它适用于描述金属材料在不同应变率、不同温度下的材料变形行为。表达式如下:
| $ \sigma = \left( {\mathit{A} + \mathit{B}{\varepsilon ^\mathit{n}}} \right)\left( {1 + \mathit{C}\cdot{\rm{ln}}\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)\left( {1 - {\mathit{T}^*}^\mathit{m}} \right) $ | (18) |
| $ {{\mathit{T}}^{*}}=\frac{\mathit{T}-{{\mathit{T}}_{\rm{room}}}}{{{T}_{\rm{melt}}}-{{\mathit{T}}_{\rm{room}}}} $ | (19) |
式中:A,B,C,m,n为待求参数;
J-C模型适用于准静态变形到大应变率的高速变形,针对不同的金属材料,一般通过准静态实验和霍普金森杆实验来获取J-C模型本构参数,但由图 9对比结果可知用此法获得的本构模型不能很好地描述AZ31B镁合金板差温成形过程。
2.3 基于SVR-ELM混合模型的本构参数反求鉴于NUMISHEET2011提供的十字杯形件试验数据,在本模型中选取沿板料DE截面方向温度最高为响应目标。以本构模型中A,B,C,m,n为设计变量,仿真值与试验值误差最小化为优化目标。使用拉丁超立方试验设计方法抽样20组,组成初始样本库,结果如表 4所示,对样本点进行仿真计算得到响应值。选取前15组数据作为训练集,后5组作为检验集。为更好地对比反求结果,分别采用SVR,ELM和SVR-ELM三种近似模型结合量子遗传算法对AZ31B差温成形的Johnson-Cook本构参数进行反求,算法最大迭代次数为50。
| 序号 | 本构参数 | ||||
| A | B | C | m | n | |
| 1 | 232.21 | 739.947 | 0.087 4 | 0.626 | 1.00 |
| 2 | 203.26 | 562.000 | 0.101 1 | 0.811 | 0.73 |
| 3 | 191.68 | 892.474 | 0.107 9 | 1.074 | 0.76 |
| 4 | 220.63 | 994.158 | 0.090 8 | 0.758 | 0.70 |
| 5 | 226.42 | 765.368 | 0.063 4 | 0.942 | 0.82 |
| 6 | 180.11 | 943.316 | 0.060 0 | 0.653 | 0.91 |
| 7 | 156.95 | 917.895 | 0.094 2 | 0.679 | 1.21 |
| 8 | 174.32 | 587.421 | 0.083 9 | 1.100 | 0.94 |
| 9 | 209.05 | 1 019.579 | 0.080 5 | 0.968 | 1.12 |
| 10 | 185.89 | 638.263 | 0.121 6 | 0.732 | 1.15 |
| 11 | 128.00 | 689.105 | 0.118 2 | 0.916 | 0.85 |
| 12 | 139.58 | 1 045.000 | 0.097 6 | 0.837 | 0.88 |
| 13 | 145.37 | 612.842 | 0.077 1 | 0.705 | 0.97 |
| 14 | 238.00 | 714.526 | 0.104 5 | 1.021 | 1.06 |
| 15 | 133.79 | 867.053 | 0.066 8 | 0.995 | 1.09 |
| 16 | 151.16 | 790.789 | 0.073 7 | 0.889 | 0.67 |
| 17 | 214.84 | 968.737 | 0.125 0 | 0.784 | 1.03 |
| 18 | 168.53 | 816.211 | 0.111 3 | 0.600 | 0.79 |
| 19 | 162.74 | 841.632 | 0.114 7 | 1.047 | 1.18 |
| 20 | 197.47 | 663.684 | 0.070 3 | 0.863 | 1.24 |
基于SVR,ELM,SVR-ELM三种不同的近似模型,通过改进的量子遗传算法寻优得到Johnson-Cook本构参数结果,如表 5所示。
| 近似模型 | A | B | C | m | n |
| SVR | 212.786 8 | 787.910 8 | 0.101 7 | 0.875 2 | 0.721 6 |
| ELM | 212.908 4 | 715.622 2 | 0.113 | 0.923 9 | 0.717 1 |
| SVR-ELM | 217.816 0 | 704.076 6 | 0.094 5 | 1.024 4 | 0.721 8 |
将基于不同近似模型反求得到的3组数据应用到十字杯形件的差温成形仿真中,成形件温度场与应力场云图分别如图 10与图 11所示。3组仿真计算得到的温度最高值与试验值对比如表 6所示。根据温度场云图显示,成形件最高温度均分布在沿DE截面方向的法兰边缘。

|
| 图 10 基于不同模型反求的本构参数获得的成形件温度分布云图 Fig.10 Temperature distribution nephogram of stamping part obtained based on constitutive parameters inversed by different models |
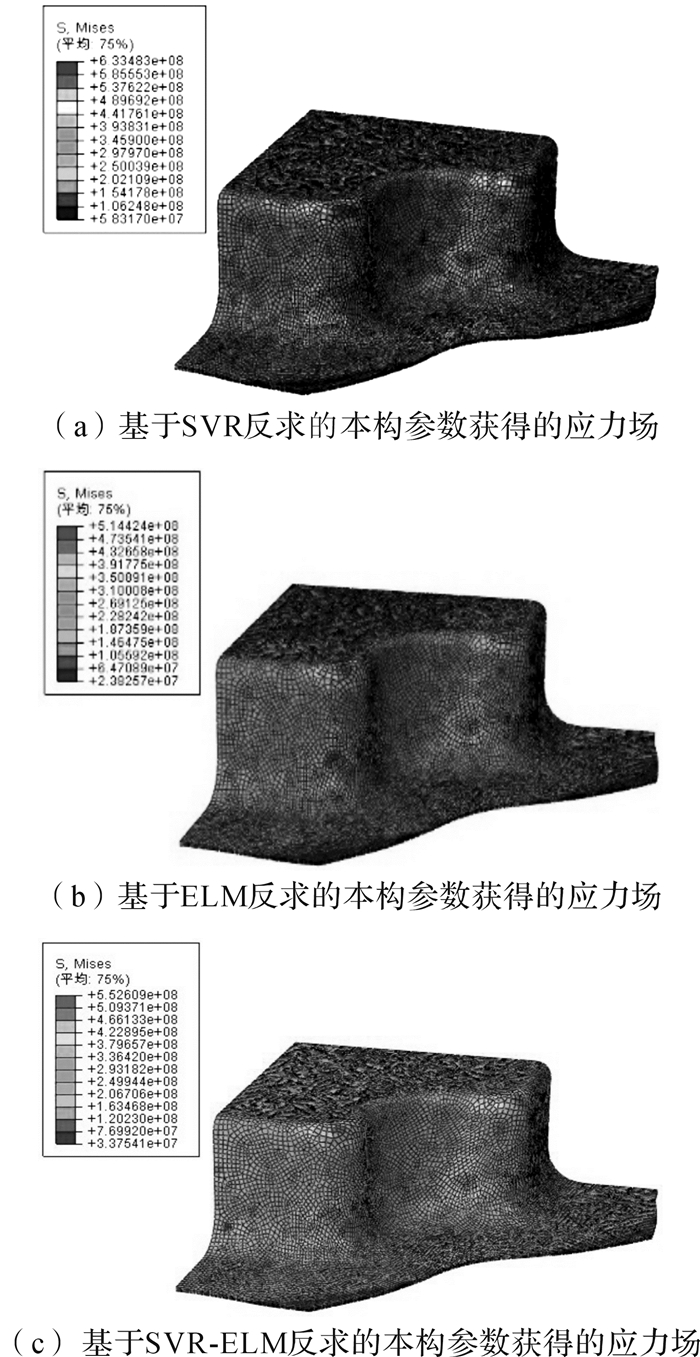
|
| 图 11 基于不同模型反求的本构参数获得的成形件应力分布云图 Fig.11 Stress distribution nephogram of stamping part obtained based on constitutive parameters inversed by different models |
| 温度最高值/℃ | SVR | ELM | SVR-ELM |
| 仿真值 | 241.033 | 242.253 | 246.688 |
| 试验值 | 247.65 | 247.65 | 247.65 |
| 误差/% | 2.67 | 2.12 | 0.39 |
结果表明在较少的算法迭代次数下,SVR-ELM混合近似模型即可获得最优解,收敛速度比2个单一近似模型快。与试验值相比,利用SVR-ELM混合近似模型反求的本构模型仿真所得的最高温度的相对误差仅为0.39%,精度最高。在基于3个不同近似模型反求的本构参数所得到的应力云图中,凹模底部圆角与侧壁半径较小的圆角附近区域应力较大,这主要是因为差温成形过程中,与凸模接触的板料部分温度较低,材料流变应力较大,随着拉深过程进行,处在圆角半径较小位置的材料还要承受较大的弯曲应力。
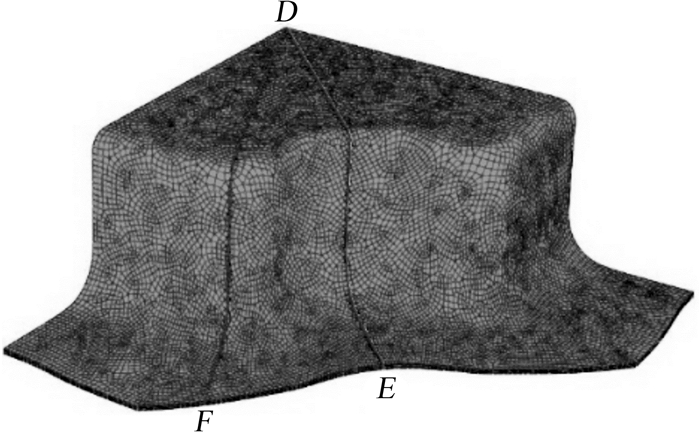
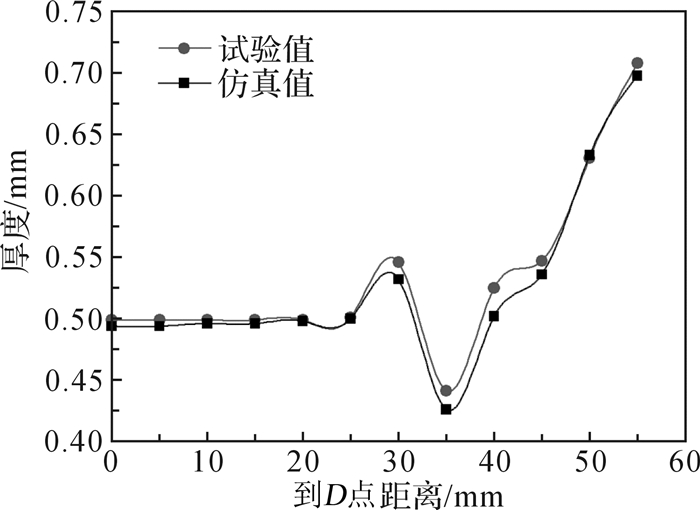
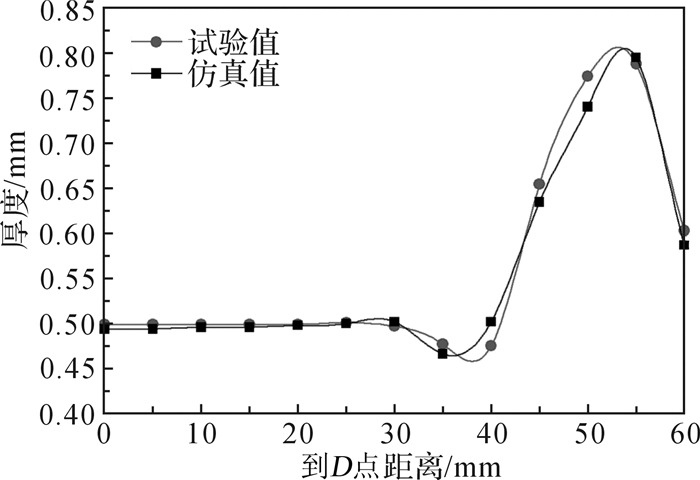
为进一步验证反求的本构参数的准确性,选取仿真结果中的DE,DF截面(如图 12所示)的厚度分布与试验数据进行对比,对比结果分别如图 13、图 14所示。
|
| 图 12 成形件中DE与DF截面位置 Fig.12 The position of DE and DF section in forming part |
|
| 图 13 DE截面厚度分布对比 Fig.13 Comparison of thickness distribution of DE section |
|
| 图 14 DF截面厚度分布对比 Fig.14 Comparison of thickness distribution of DF section |
从图 13和图 14结果可知板料在模具侧壁位置处由于拉深产生了较大的减薄,板料法兰区域DE截面位置由于材料流动不均造成材料堆积,增厚现象比较严重。
由上述结果可以看出,成形件温度场分布非常不均匀,进一步导致应力场分布不均,从而影响成形件厚度减薄率与成形质量。运用反求得到的本构方程,通过一定方法优化相关工艺,提高成形件质量是接下来的首要任务。
3 结论本文通过自适应方法更新样本库,采用SVR-ELM混合近似模型与量子遗传寻优算法建立了反求模型来求解镁合金AZ31B差温成形的Johnson-Cook本构参数。
1) 利用改进的量子遗传算法和自适应样本更新方法,提高了近似模型的拟合精度,加快了寻优算法向最优求解域收敛的速度。与采用单一近似模型相比,混合近似模型具有更好的泛化能力与更高的精度。
2) 基于NUMISHEET2011十字杯形件的差温成形有限元模型,利用SVR-ELM混合模型反求本构参数的结果误差较小,避免了常规准静态实验获得的材料参数不能很好描述冲压成形等高应变率问题,提高了镁合金差温成形数值模拟的精度,对预测成形质量具有重要的意义。
| [1] |
龙玲, 殷国富, 邹云, 等.
基于随机聚焦搜索算法的冲压成形工艺优化[J]. 计算机集成制造系统, 2012, 18(2): 314–320.
LONG Ling, YIN Guo-fu, ZOU Yun, et al. Optimization of stamping process based on stochastic focusing search algorithm[J]. Computer Integrated Manufacturing Systems, 2012, 18(2): 314–320. |
| [2] |
黄光胜, 汪凌云, 黄光杰, 等.
AZ31镁合金高温本构方程[J]. 金属成形工艺, 2004, 22(2): 41–44.
HUANG Guang-sheng, WANG Ling-yun, HUANG Guang-jie, et al. Consititutive equation of AZ31 magnesium alloy for high temperature[J]. Metal Forming Technology, 2004, 22(2): 41–44. |
| [3] |
陈荣, 卢芳云, 林玉亮, 等.
分离式Hopkinson压杆实验技术研究进展[J]. 力学进展, 2009, 39(5): 576–587.
CHEN Rong, LU Fang-yun, LIN Yu-liang, et al. A critical review of split hopkinson pressure bar technique[J]. Advances in Mechanics, 2009, 39(5): 576–587. DOI:10.6052/1000-0992-2009-5-J2008-096 |
| [4] | CLAUSEN A H, TRYLAND T, REMSETH S, et al. An investigation of material properties and geometrical dimensions of aluminium extrusions[J]. Materials and Design, 2001, 22(4): 267–275. DOI:10.1016/S0261-3069(00)00092-3 |
| [5] |
乔良, 宋小欣, 谢延敏, 等.
基于PSO-RBF代理模型的板料成形本构参数反求优化研究[J]. 中国机械工程, 2014, 25(19): 2680–2685.
QIAO Liang, SONG Xiao-xin, XIE Yan-min, et al. Reverse and optimization of sheet forming parameters based on PSO-RBF surrogate model[J]. China Mechanical Engineering, 2014, 25(19): 2680–2685. DOI:10.3969/j.issn.1004-132X.2014.19.023 |
| [6] |
李恩颖, 王琥, 李光耀.
基于支持向量机回归的材料参数反求方法[J]. 机械工程学报, 2012, 48(6): 90–95.
LI En-ying, WANG Hu, LI Guang-yao. Material parameter inverse technique based on support vector regression[J]. Journal of Mechanical Engineering, 2012, 48(6): 90–95. |
| [7] | WANG H, LI W, LI G. A robust inverse method based on least square support vector regression for Johnson-cook material parameters[J]. CMC Computers, Materials & Continua, 2012, 28(2): 121–146. |
| [8] | WANG H, ZENG Y, YU X, et al. Surrogate-assisted Bayesian inference inverse material identification method and application to advanced high strength steel[J]. Inverse Problems in Science and Engineering, 2016, 24(7): 1133–1161. DOI:10.1080/17415977.2015.1113960 |
| [9] | GOEL T, HAFTKA R T, SHY W, et al. Ensemble of surrogates[J]. Struct Multidisc Optim, 2007, 33(3): 199–216. DOI:10.1007/s00158-006-0051-9 |
| [10] | HAN K H, KIM J H. Genetic quantum algorithm and its application to combinatorial optimization problem[C]//Proceedings of IEEE Congress on Evolutionary Computation. La Jolla, CA, Jul. 16-19, 2000. |
| [11] |
谢延敏, 王新宝, 王智, 等.
基于灰色理论和GA-BP的拉延筋参数反求[J]. 机械工程学报, 2013, 4(1): 44–50.
XIE Yan-min, WANG Xin-bao, WANG Zhi, et al. Reverse of drawbead parameters based on grey theory and GA-BP[J]. Journal of Mechanical Engineering, 2013, 4(1): 44–50. |
| [12] | HUANG C, HAMI A E, RADI B. Metamodel-based inverse method for parameter identification:elastic-plastic damage model[J]. Engineering Optimization, 2016, 49(4): 633–653. |
| [13] |
李士勇, 李浩.
一种基于相位比较的量子遗传算法[J]. 系统工程与电子技术, 2010, 32(10): 2219–2222.
LI Shi-yong, LI Hao. Quantum genetic algorithm based on phase comparison[J]. Systems Engineering and Electronics, 2010, 32(10): 2219–2222. DOI:10.3969/j.issn.1001-506X.2010.10.42 |
| [14] | HUANG G B, ZHU Q Y, SIEW C, et al. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. |
| [15] |
薛翠鹤. AZ31镁合金板材温热高速率本构关系研究[D]. 武汉: 武汉理工大学材料科学与工程学院, 2010: 45-47.
XUE Cui-he. Constitutive relationship research of AZ31 magnesium alloy sheet under the HVF & warm forming condition[D]. Wuhan:Wuhan University of Technology, School of Materials Science and Engineering, 2010:45-47. http://cdmd.cnki.com.cn/Article/CDMD-10497-2010163737.htm |



