2. 华南理工大学 安全科学与工程研究所, 广东 广州 510640;
3. 江西理工大学 工程研究院, 江西 赣州 341000
2. Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640, China;
3. Engineering Institute, Jiangxi University of Science and Technology, Ganzhou 341000, China
金属矿山采空区群系统由多个相互独立又相互依存的单元采空区组成,各单元采空区内部由顶柱和间柱组成,它们共同维系着系统的稳定。“短板”单元空区是指系统中结构劣化、抗外力扰动弱、自稳熵值比较高的单元体。一旦外部荷载(爆破、机械扰动)超过其临界负荷,其自稳安全度将降低,极易造成内部结构劣化失稳,进而形成新的扰动源,诱发相邻采空区连锁反应,最终造成采空区群垮塌灾变[1-2]。
目前,地上结构物(如大跨度空间结构[3]、框架结构[4]等)“短板”结构单元甄别的研究较多,而关于地下采空区群方面的研究鲜有报道,该领域相关研究主要集中在单个采空区或采空区群整体稳定性方面[5-9]。Alcalde-Gonzalo[5]等基于双弹性理论提出了岩石质量的非线性破坏准则,确定了单元采空区的最大跨度,以判定采空区稳定性;宋卫东等[7]以石人沟铁矿为研究对象,结合FLAC3D数值分析方法,建立了三维数值计算模型,分析了采空区群的应力场、位移场分布特征;吴启红等[8]提出了数值模拟分析(整体分析)与多级模糊评判(单个分析)相结合的综合评价方法来评价采空区群的稳定性。总体来说,相关研究仅仅关注整个采空区(群)的稳定性,并未关注采空区群失稳的薄弱环节—“短板”单元空区,忽略了采空区群失稳的本源问题。因此,开展采空区群“短板”单元空区的甄别方法研究,弥补该领域研究的空白,具有十分重要的意义。
框架结构模型法主要通过分析刚节点连接的梁和柱单元杆件组成系统的结构属性来研究对象的稳定性,该方法具有计算速度快、可靠性高等特点[10]。目前,国内外尚无地下矿山大空间稳定方面的相关技术规范、采空区结构的力学计算通用模型。自稳系数法以框架结构模型法[11-13]为基础,通过构建采空区群类框架结构自稳模型,建立采空区群内部结构的典型方程组进行理论分析。鉴于采空区群是在原有岩体上开挖形成的,按照一定空间次序排列的地下空间结构体,与地表构造物在空间排列上具有一定的相似性,本文拟采用类框架结构自稳系数法,结合岩体强度理论,推导出采空区顶柱、间柱自稳系数计算式,引入顶柱、间柱重要度因子α,β,开展采空区群“短板”单元空区甄别研究,并通过现场踏勘及位移监测数据,来验证该方法分析结果的正确性。
1 采空区群类框架结构自稳模型在地下多中段开采过程中采空区没有得到及时处理,中厚矿体将遗留大量多层水平采空区,这些采空区共同组成了采空区群。
1.1 基本假设1) 采空区群赋存围岩岩体构造完整,忽略断层和节理对系统稳定性的影响;
2) 忽略大量采准、切割巷道对系统稳定性的影响;
3) 单元采空区是具有相似形状的空间结构体,暴露面积相等,顶(间)柱的几何尺寸相同;
4) 岩体为均质、各向同性的弹塑性材料,服从摩尔-库仑(Mohr-Coulomb)强度破坏准则。
1.2 模型构建采空区群是在既有地下岩体上开挖形成,主要受周边围岩约束,作用力为上覆岩层压应力和水平地应力。
1) 根据《建筑抗震设计规范》[14]的相关规定,结合结构力学分析方法,将单元采空区间柱、顶(底)柱和一定范围内的围岩,分别简化为柱单元、梁单元杆件结构,杆件之间以刚节点联接。
2) 对于浅地表采空区群而言,在垂直方向主要受岩体自重应力场作用,在水平方向主要受岩体构造应力场作用,后者远小于前者,在工程上可以忽略不计[15]。因此,在分析过程中,仅考虑垂直方向的岩体自重应力场作用。
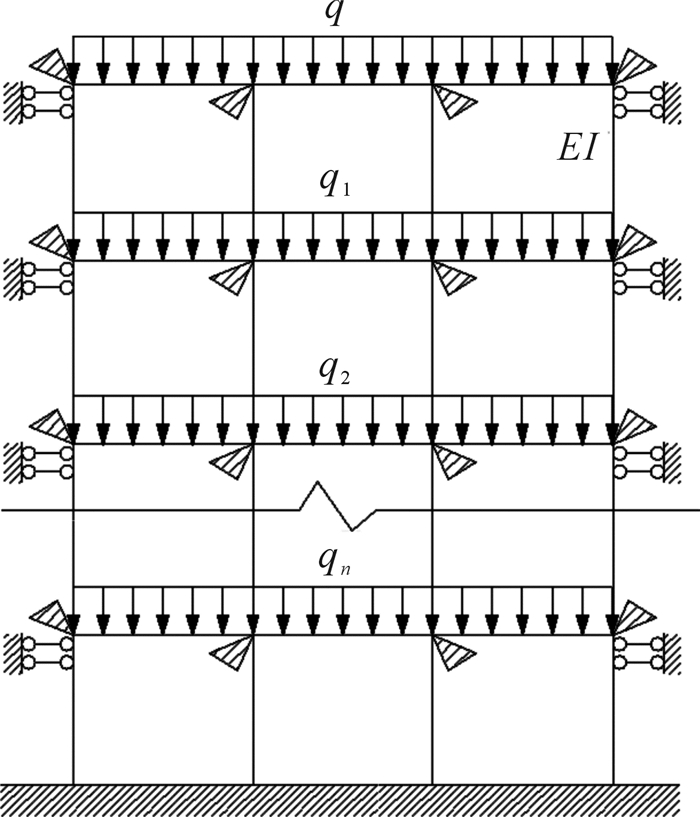
基于以上考虑,将由间柱、顶柱、空区、上覆岩层和周边围岩组成的采空区群(图 1)简化为类框架结构自稳模型(图 2),其中,q为上覆岩层及最上层顶柱自重应力的合力,q1,q2,…,qn分别为各相应中段顶(底)柱的自重应力。

|
| 图 1 采空区群力学模型 Fig.1 Mechanics model of goaf group |
|
| 图 2 采空区群类框架结构自稳模型 Fig.2 The self-stabilization model of frame structure of goaf group |
简化后的采空区群类框架结构自稳模型为无侧移刚架体,其基本体系如图 2所示。根据结构力学计算方法,采用位移法分别求解各顶柱的弯矩和间柱所受内力。该模型共有4n个结点角位移,结点线位移数量为零,基本未知量为4n。利用叠加原理可得各种荷载作用下系统位移方程式,如式(1):
| $ \left[{\begin{array}{*{20}{c}} {{\delta _{11}}}&{{\delta _{12}}}& \cdots &{{\delta _{1(4n)}}}\\ {{\delta _{21}}}&{{\delta _{22}}}& \cdots &{{\delta _{2(4n)}}}\\ \vdots & \vdots &{}& \vdots \\ {{\delta _{\left( {4n} \right)1}}}&{{\delta _{\left( {4n} \right)2}}}& \cdots &{{\delta _{\left( {4n} \right)(4n)}}} \end{array}} \right]\left\{ \begin{array}{l} {\mathit{\Delta }_1}\\ {\mathit{\Delta }_2}\\ \vdots \\ {\mathit{\Delta }_{(4n)}} \end{array} \right\} + \left\{ \begin{array}{l} {F_{{\rm{1P}}}}\\ {F_{{\rm{2P}}}}\\ \vdots \\ {F_{(4n){\rm{P}}}} \end{array} \right\}{\rm{ = }}\left\{ \begin{array}{l} 0\\ 0\\ \vdots \\ 0 \end{array} \right\} $ | (1) |
式中:δik(i,k=1, 2, 3, …, 4n)为结构的刚度系数,可由杆件的形常数求得;Δi为原结构在附加约束i处的结点位移;FiP为岩体自重应力作用下,附加约束i处产生的约束力,可由杆件的载常数求得。
对式(1) 求解,根据叠加原理可得模型各杆件所受弯矩M的表达式为:
| $ M = {{\bar M}_1}{\mathit{\Delta }_1} + {{\bar M}_2}{\mathit{\Delta }_2} + \ldots + {{\bar M}_{(4n)}}{\mathit{\Delta }_{(4n)}} + {M_{\rm{P}}} $ | (2a) |
视各杆件为隔离体,由力矩平衡求解其所受剪力(式(2b));依据静力平衡条件,可求解各杆件所受轴力(式(2c)):
| $ Q = {{\bar Q}_1}{\mathit{\Delta }_1} + {{\bar Q}_2}{\mathit{\Delta }_2} + \ldots + {{\bar Q}_{(4n)}}{\mathit{\Delta }_{(4n)}} + {Q_{\rm{P}}} $ | (2b) |
| $ {F_N} = {{\bar N}_1}{\mathit{\Delta }_1} + {{\bar N}_2}{\mathit{\Delta }_2} + \ldots + {{\bar N}_{(4n)}}{\mathit{\Delta }_{(4n)}} + {N_{\rm{P}}} $ | (2c) |
式中:Mi,Qi,Ni分别为附加约束i处发生单位角位移所产生的弯矩、剪力和轴力;MP,QP,NP分别为岩体自重应力作用下各杆件所受弯矩、剪力和轴力。
2 自稳系数法间柱和顶(底)柱两个核心要素共同决定单元采空区稳定状态[9]。因此,通过分析间柱和顶(底)柱的自稳状态可以得到单元采空区赋存状态。在类框架结构自稳系数法分析中,引入自稳系数Sd, Sj和S,分别表示顶柱、间柱和单元采空区的自稳状态值,通过比较S值的大小来判别“短板”单元空区的稳定状态。
2.1 顶柱自稳系数在自重荷载作用下,顶(底)柱产生不同程度的弯曲变形。随着弯曲变形的不断加剧,顶(底)柱上部受压应力作用、下部受拉应力作用不断增强;受拉应力作用产生的裂纹在竖直方向上不断延伸扩展,顶柱自稳系数增大。当顶柱所受拉应力逼近岩体的极限抗拉强度时,顶柱将发生失稳。这里采用自稳系数Sd来判定顶柱自稳状态。
由结构力学知,顶柱(梁)的最大弯矩Μmax出现在顶柱(梁)的中间位置。由式(3a)求解可得最大拉应力σmax为:
| $ {\sigma _{{\rm{max}}}} = \frac{{{{{M}}_{{\rm{max}}}}}}{{{W_{\rm{Z}}}}} $ | (3a) |
式中WZ为顶柱的抗弯截面系数,表达式为:
| $ {\mathit{W}_{\rm{Z}}} = \frac{{bh_1^2}}{6} $ | (3b) |
式中:b为矿房宽度, m; h1为顶(底)柱厚度, m。
由岩石强度理论知,顶柱发生拉伸破坏所承受的极限拉应力为σtm,可由式(4) 求解:
| $ \sigma _{\rm{t}}^{\rm{m}} = {C_{\rm{v}}}{\sigma _\rm{t}} $ | (4) |
式中:Cv为岩体完整性系数; σt为岩体的极限抗拉强度,MPa。
顶柱自稳系数Sd为顶柱实际所受最大拉应力σmax与顶柱发生拉伸破坏所承受的极限拉应力σtm的比值,即:
| $ {S_{\rm{d}}} = \frac{{{\sigma _{{\rm{max}}}}}}{{\sigma _\mathit{t}^{\rm{m}}}} $ | (5) |
间柱自稳状态由其受力情况决定,随着开采深度的增加,施加在间柱上的荷载将不断增加,沿间柱轴线方向的压缩变形不断扩大,间柱自稳系数也将不断增大。同理,利用自稳系数Sj来判定间柱自稳状态。
由材料力学知,间柱的轴力关系式为:
| $ {F_{\rm{N}}} = \int_\mathit{A} {} {\sigma _{\rm{c}}}{\rm{d}}A $ | (6) |
式中:FN为间柱所受的轴力;σc为间柱所受压应力;A为间柱的横截面积。
本文选取Lunder等[16]推导的矿柱强度计算公式,求解间柱的抗压强度:
| $ {\sigma _{\rm{p}}} = 0.44{\sigma _{\rm{r}}}(0.68 + 0.52{K_{\rm{a}}}) $ | (7a) |
式中:σp为矿柱抗压强度,MPa;σr为岩体单轴抗压强度,MPa;Ka为间柱摩擦系数。
| $ {K_{\rm{a}}} = {\rm{tan}}\left[{{\rm{co}}{{\rm{s}}^{-1}}\left( {\frac{{1-{C_{\rm{p}}}}}{{1 + {C_{\rm{p}}}}}} \right)} \right] $ | (7b) |
式中Cp为矿柱平均强度系数,由间柱的宽高比进行取值。
| $ {C_{\rm{p}}} = 0.46\left[{{\rm{lg}}\left( {\frac{w}{h} + 0.75} \right)} \right]\frac{{1.4h}}{w} $ | (7c) |
式中:w为间柱宽度,m;h为间柱高度,m。
间柱的自稳系数Sj为实际最大压应力σc与发生压缩破坏时所承受的极限抗压强度σp之间的比值:
| $ {S_{\rm{j}}} = \frac{{{\sigma _{\rm{c}}}}}{{{\sigma _{\rm{p}}}}} $ | (8) |
综上分析,可以得到单元采空区综合自稳系数S表达式为:
| $ S = \alpha {S_{\rm{d}}} + \beta {S_{\rm{j}}} $ | (9a) |
| $ \alpha + \beta = 1 $ | (9b) |
式中α,β分别为顶柱和间柱重要度因子,分别表示顶柱和间柱对某中段采空区稳定性的贡献率。S值越大,单元采空区稳定性越差;S值越小,单元采空区稳定性越好。此时,S值最大的单元采空区即可判断为系统中的“短板”单元空区。
目前矿业界尚无重要度因子α,β明确量化方法,本文综合文献[16-17],同时,跟踪采空区群周边残留金矿回采工程及借鉴文献[18]给出的构件(顶、间柱)损伤的方法,从构件(顶、间柱)破坏对系统(采空区)稳定性影响的角度出发,视间柱为支撑采空区稳定的关键因素,视顶柱为影响采空区结构完整性的次要因素。经综合分析校算,取α=0.3,β=0.7。
3 工程实例某大型金属矿山位于秦岭褶皱系南秦岭印支褶皱带凤县-镇安褶皱束的北缘,含金角砾岩带(AnKsb)主要分布于泥盆系中统古道岭组地层中。KT5矿体连续分布于43-77勘探线之间,矿体大致呈陡立的不规则板状体。上覆岩层及围岩主要由泥盆系中统的王家楞组(D2W)和古道岭组(D2g)的碎屑岩和碳酸岩组成。开采方法为无底柱阶段崩落法,辅以浅孔留矿法。KT5矿体经过多年开采,已经形成由多个单元采空区组成的采空区群(图 3)。

|
| 图 3 某矿山KT5矿体1 420~1 570 m中段采空区群剖面图 Fig.3 The section of goaf group of 1 420~1 570 m in KT5 ore body |
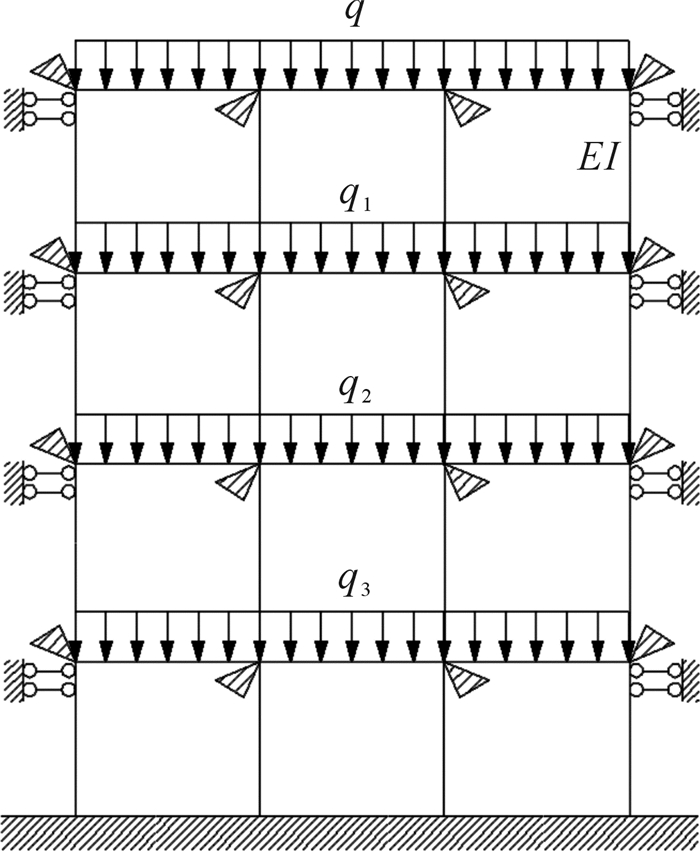
选取63-69勘探线间1 420~1 620 m中段采空区群为研究对象。构建由4个中段(1 420,1 470,1 520及1 570 m中段)12个单元采空区组成的采空区群自稳模型(图 4),各单元采空区跨度为30 m,宽度为40 m,高度为35 m,顶(底)柱厚度为15 m,间柱宽度为10 m。依据矿山实测数据,矿体、围岩的物理力学参数如表 1所示。
|
| 图 4 1 420~1 570 m中段采空区群自稳模型 Fig.4 The self-stabilization model of goaf group in 1 420~1 570 m middle section |
| 类型 | 弹性模量 /GPa |
单轴抗压强度/MPa | 抗拉强度 /MPa |
内摩擦角 /(°) |
黏聚力 /MPa |
容重/kN·m-3 | 完整性系数 | 泊松比 |
| 矿体 | 28 | 69.6 | 6.5 | 40 | 14 | 27.2 | 0.70 | 0.26 |
| 围岩 | 35 | 80.3 | 8.8 | 45 | 18 | 25.5 | 0.55 | 0.24 |
为了对比爆破前后两种情况,用自稳系数法分析结果可靠性,分别构建工况1(未考虑爆破扰动)、工况2(考虑爆破扰动)两组模型进行计算分析,来甄别该区域采空区群的“短板”单元空区。工况2中,主要考虑到采空区群长期受到爆破开采扰动的作用,导致岩体物理力学性能劣化,对岩体力学初始强度作折减处理。依照文献[19]的方法,结合Hoek-Brown破坏准则,折减系数取为1.48。
3.2 结果分析1) 顶柱。
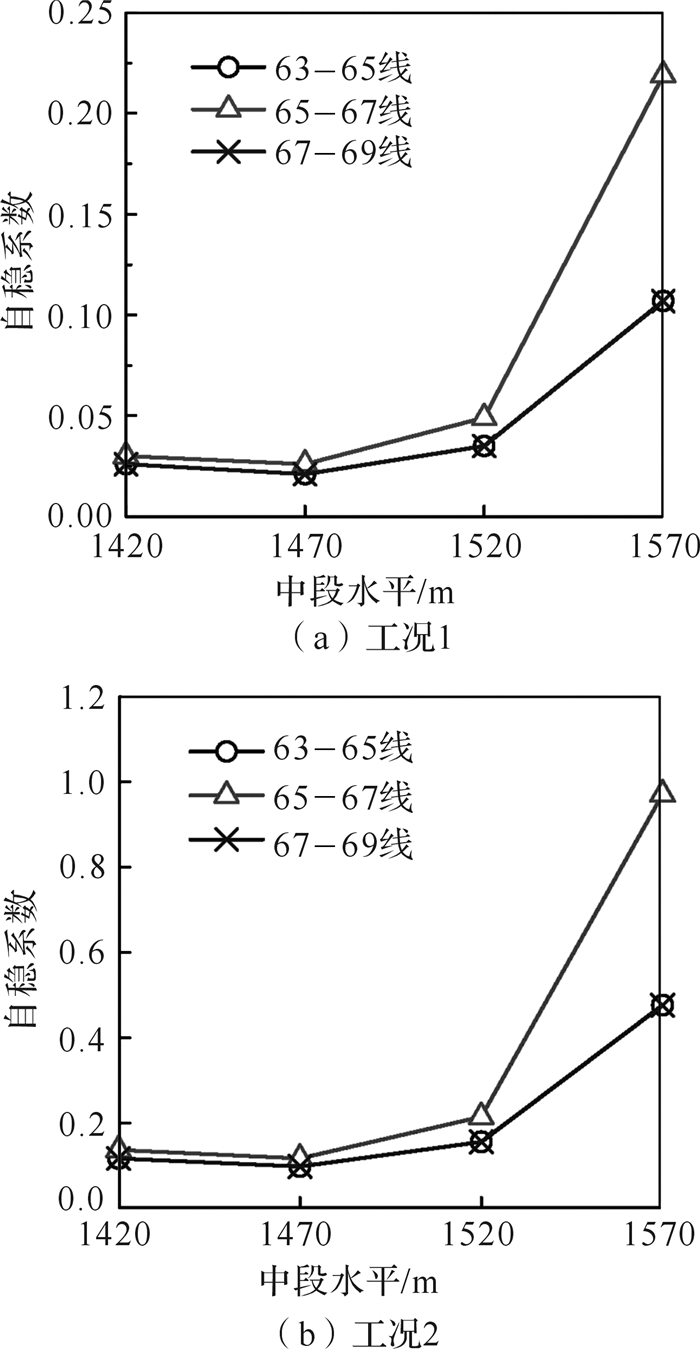
由式(3) 至式(5) 可得该系统顶柱自稳系数(图 5)。由于该采空区群呈对称分布,同一中段水平内63-65线与67-69线范围的顶柱自稳系数大小相等,在图 5中表现为相互重合。
|
| 图 5 不同中段水平顶柱的自稳系数 Fig.5 The self-stabilization coefficient of horizontal pillar in different middle sections |
由图 5可知,在同一勘探线的范围内,采空区群上部区域的1 570 m中段顶柱自稳系数最大,分别达到0.107,0.219,0.107,表明该区域顶柱的自稳性最差。这主要是在采空区群形成的初始阶段由上覆围岩压力释放造成的。1 520, 1 470, 1 420 m三个中段采空区顶柱自稳系数处于一个相对平缓的变化区间内,在1 420 m中段稍有上升。究其原因:随着赋存深度的增加,自重应力增大,顶柱所受拉应力也相应增加。
由工况2和工况1比较可知,1 570 m中段采空区顶柱自稳系数的最大增幅达344.9%,表明爆破扰动的累积损伤效应对顶柱自稳性的影响程度远高于自重应力的影响。
2) 间柱。
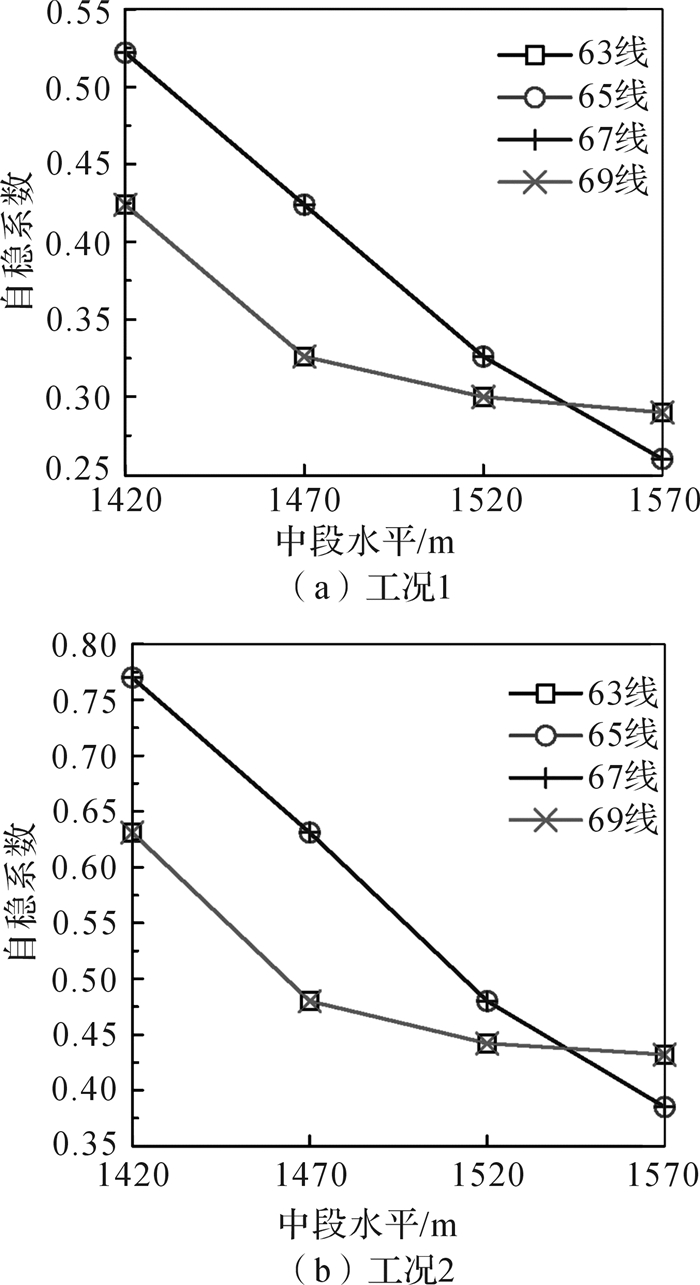
由式(6) 至式(8) 计算可得不同中段的采空区间柱自稳系数(图 6)。
|
| 图 6 不同中段水平间柱的自稳系数 Fig.6 The self-stabilization coefficient of horizontal column in different middle sections |
由图 6知,随着深度的增加,单元采空区间柱自稳系数变大,各相邻中段间柱自稳系数的增加幅值基本相同。主要原因是:① 上覆岩层压力由上部中段间柱传递到下部中段间柱;② 该中段顶柱自重应力及间柱自身重力的作用。
与周边围岩紧密接触的间柱的自稳系数,也随赋存深度的增加而变大,但总体上小于中部间柱的自稳系数,1 470~1 570 m中段间柱的自稳系数增幅趋势线平缓。究其原因:由于该区域间柱与周边围岩充分接触,周边围岩分担部分作用力,越临近地表,间柱的负荷越小。
由图 6(b)与图 6(a)比较可知,爆破扰动的累积损伤效应对间柱自稳系数有一定的影响,其中部间柱自稳系数的最大增幅达48.5%。因此,可以判断爆破荷载对顶柱的影响远大于对间柱的影响。
3)“短板”单元空区。
由式(5) 至式(9) 计算可得不同中段水平内单元采空区的自稳系数(图 7)。
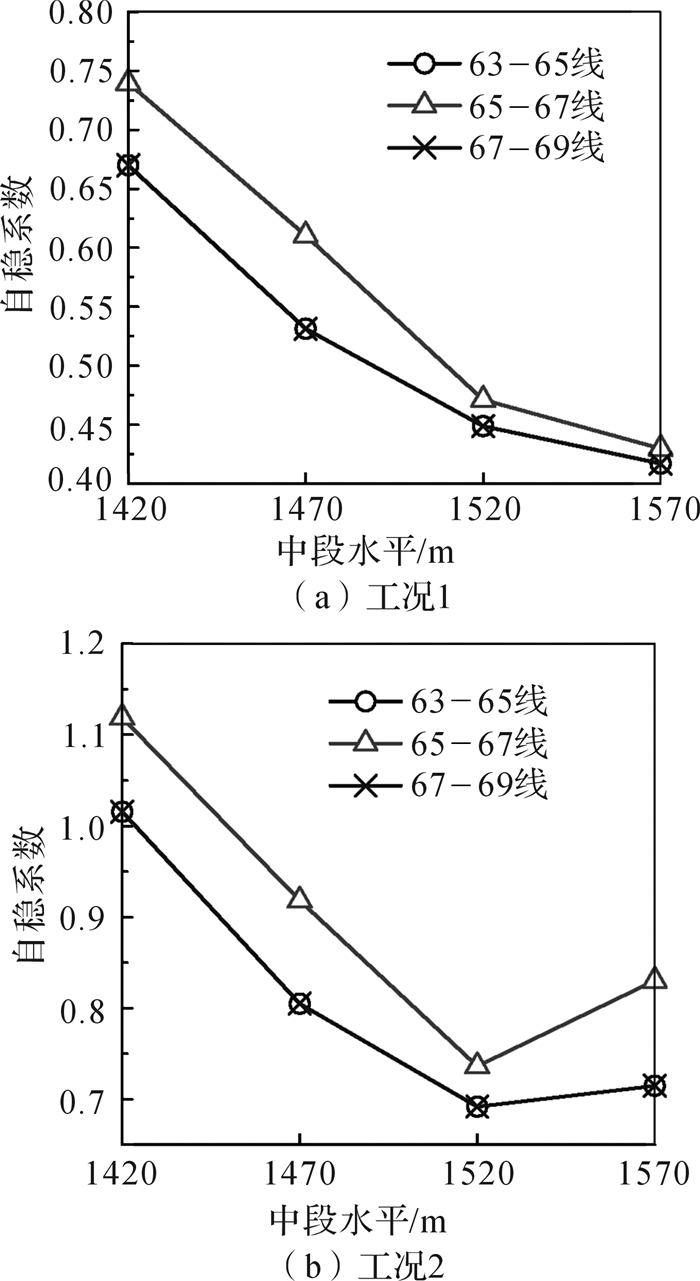
|
| 图 7 不同中段水平单元采空区的自稳系数 Fig.7 The self-stabilization coefficient of the unit gob in different middle sections |
由图 7(a)可知,在不考虑爆破扰动累积损伤效应影响的条件下,随开采深度的增加,单元采空区的自稳系数呈增加趋势,各相邻水平的单元采空区增幅大致相同。由图 7(b)可知,在爆破扰动激励下,单元采空区的自稳系数随深度增加而变大,爆破累积损伤对紧邻上覆岩层中段单元采空区的影响最为显著。究其原因:随着爆破次数的增加,上覆岩层应力充分释放,直接作用于接触的顶柱,导致该区域单元采空区的稳定性降低。
综上分析可知,不考虑爆破作用时,1 420 m中段65-67线间采空区自稳系数最大,S=0.75,即该采空区为“短板”单元空区。当受到爆破作用时,“短板”单元空区紧邻上覆岩层的采空区群中单元空区(1 570 m中段63-65线、67-69线间采空区)自稳系数显著增大,S=0.83,远小于1 420 m中段65-67线间采空区自稳系数(S=1.35),此时,“短板”单元空区仍为1 420 m中段65-67线间采空区。
3.3 现场踏勘及位移监测 3.3.1 现场踏勘图 8为1 420 m中段及1 520 m中段矿柱实景图。现场踏勘表明,1 420 m中段采空区预留矿柱破坏程度普遍大于其上部中段各矿柱;在爆破作业期间,1 420 m中段出现局部顶板脱落、矿柱剥蚀现象(图 8(a)),1 520 m中段矿柱完整性好,较为稳定(图 8(b))。现场踏勘结果与自稳系数法的计算结果基本一致。

|
| 图 8 不同中段水平矿柱实景图 Fig.8 The real-life view of horizontal pillar in different middle sections |
1) 测点布置。
本次测点共布置3个SZZX-Q200B型顶板沉降仪,记录各中段顶柱岩体的位移值,其中在1 570,1 520,1 420 m中段各布设1个,布设位置如图 9所示。记录点1,2,3分别位于不同中段顶(底)柱临空面的中部位置,记录回采过程中顶(底)柱的最大竖向变形量。需说明的是:① 为了充分利用所测数据,测点只布设在位移变形最大的65-67线顶柱中部位置的临空面;② KT5矿体采用崩落法开采,1 470 m已被所冒落的围岩封堵,考虑到监测人员及仪器的安全,未布设测点。
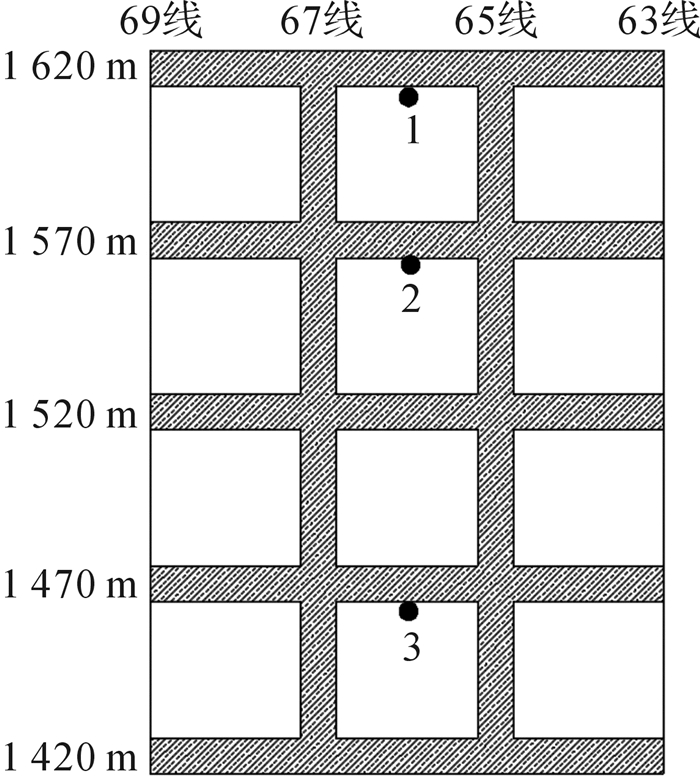
|
| 图 9 监测点布设图 Fig.9 The layout of monitoring points |
2) 测点结果分析。
现场130 d的位移监测(图 10)表明,顶柱位移变化最大的是位于1 570 m中段的测点,位移为18.82 mm,1 520 m中段位移最大值为5.64 mm,1 420 m中段顶柱位移最大值为4.02 mm。位移监测从不同维度验证了自稳系数法计算结果的准确性。
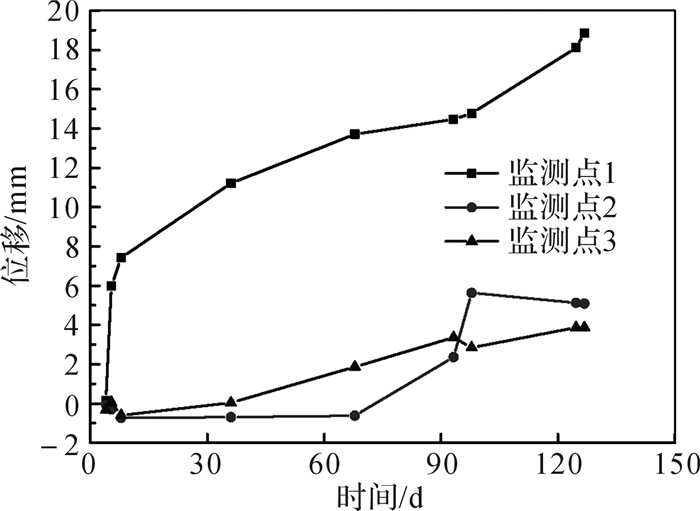
|
| 图 10 不同中段监测点位移-时间曲线图 Fig.10 The displacement-time curve of the monitoring point in different middle sections |
综上分析可知,自稳系数法基本能胜任“短板”单元空区的甄别,计算结果较准确地揭示了“短板”单元空区的分布与其赋存深度、位置的关系,反映了“短板”单元空区的分布情况。
4 结论1) 提出采空区群“短板”单元空区甄别的类框架结构自稳系数分析方法。通过构建采空区群自稳模型,建立采空区群内部结构的位移法典型方程组,结合岩石强度理论,推导出采空区顶柱、间柱自稳系数表达式,进行单元采空区的自稳系数分析,判断其自稳性状态,甄别“短板”单元空区。
2) 以某大型金属矿山4个中段12个单元采空区构成的采空区群为例,进行爆破和非爆破影响两种工况条件下采空区群“短板”单元空区的甄别分析。当采空区没有受到爆破扰动时,“短板”单元空区主要分布于底部中段的中部区域;当受到爆破扰动时,“短板”单元空区紧邻上覆岩层的采空区群中单元空区自稳系数显著增大。
3) 现场踏勘表明,1 420 m中段采空区矿柱破坏程度普遍大于其他上部中段矿柱;位移监测结果表明,位移变化最大的是位于1 570 m中段67线附近的测点,位移为18.82 mm,其余中段测点位移变化较小。验证了自稳系数法甄别结果的正确性。
4) 框架结构模型的自稳系数法为采空区群“短板”单元空区的有效甄别提供了一种新方法,为采空区失稳突变的超前防控提供依据。
| [1] |
付建新, 宋卫东, 杜建华.
金属矿山采空区群形成过程中围岩扰动规律研究[J]. 岩土力学, 2013, 34(1): 508–515.
FU Jian-xin, SONG Wei-dong, DU Jian-hua. Study of disturbance law for wall rock while goaf group formation in metal mines[J]. Rock and Soil Mechanics, 2013, 34(1): 508–515. |
| [2] |
刘长友, 杨敬轩, 于斌, 等.
多采空区下坚硬厚层破断顶板群结构的失稳规律[J]. 煤炭学报, 2014, 39(3): 395–403.
LIU Chang-you, YANG Jing-xuan, YU Bin, et al. Destabilization regularity of hard thick roof group under the multi gob[J]. Journal of China Coal Society, 2014, 39(3): 395–403. |
| [3] |
余冠群, 舒赣平, 夏乐.
大跨空间管桁架结构关键构件判别方法研究[J]. 建筑结构, 2015, 45(15): 17–21.
YU Guan-qun, SHU Gan-ping, XIA Yue. Research on the key component identification method of large-span spatial pipe truss structure[J]. Building Structure, 2015, 45(15): 17–21. |
| [4] |
安钰丰, 李威.
钢管混凝土柱-钢梁多层平面框架倒塌分析研究[J]. 工程力学, 2012, 29(Supplement 1): 115–118.
AN Yu-feng, LI Wei. Collapse analysis of concrete filled steel tubular column-steel beam planar frames[J]. Engineering Mechanics, 2012, 29(Supplement 1): 115–118. |
| [5] | ALCALDE-GONZALO J, PRENDESGERO M B, lVAREZFERNA NDEZ M I A, et al. Roof tensile failures in underground excavations[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 58: 141–148. |
| [6] | XIAO Chao, ZHENG Huai-chang, HOU Xiao-lin, et al. Stability study of goaf based on mechanical properties degradation of rock caused by rheological and disturbing loads[J]. International Journal of Mining Science and Technology, 2015, 25(5): 741–747. DOI:10.1016/j.ijmst.2015.07.007 |
| [7] |
宋卫东, 付建新, 杜建华, 等.
基于精密探测的金属矿山采空区群稳定性分析[J]. 岩土力学, 2012, 33(12): 3781–3787.
SONG Wei-dong, FU Jian-xin, DU Jian-hua, et al. Analysis of stability of goaf group in metal mines based on precision detection[J]. Rock and Soil Mechanics, 2012, 33(12): 3781–3787. |
| [8] |
吴启红, 万世明, 彭文祥.
一种多层采空区群稳定性的综合评价法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2324–2330.
WU Qi-hong, WAN Shi-ming, PENG Wen-xiang. A comprehensive evaluation method about stability of polylaminate goafs[J]. Journal of Central South University(Science and Technology), 2012, 43(6): 2324–2330. |
| [9] |
姜立春, 魏叙深, 吴爱祥.
基于动态强度折减法矿柱渐进失稳演变规律[J]. 中南大学学报(自然科学版), 2016, 47(2): 621–627.
JIANG Li-chun, WEI Xu-shen, WU Ai-xiang. Gradual evolution law of pillar based ondynamic strength reduction method[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 621–627. DOI:10.11817/j.issn.1672-7207.2016.02.036 |
| [10] |
姜立春, 肖康, 吴爱祥.
基于刚架结构模型法的采空区群失稳分析[J]. 岩石力学与工程学报, 2016, 35(Supplement 2): 4201–4210.
JIANG Li-chun, XIAO Kang, WU Ai-xiang. Goaf group instability analysis based on rigid frame structure model method[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Supplement 2): 4201–4210. |
| [11] |
李易, 陆新征, 叶列平.
钢筋混凝土框架抗连续倒塌机制研究[J]. 建筑科学, 2012, 27(5): 12–27.
LI Yi, LU Xin-zheng, YE Lie-ping. Study on the progressive collapse mechanism of RC frame structures[J]. Building Science, 2012, 27(5): 12–27. |
| [12] |
唐仁华, 陈昌富, 梁冠亭.
框架预应力锚杆挡墙的系统可靠性分析[J]. 岩石力学与工程学报, 2013, 32(12): 2520–2526.
TANG Ren-hua, CHEN Chang-fu, LIANG Guan-ting. System reliability analysis of frame prestressed anchor bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2520–2526. |
| [13] |
徐强, 马艳, 王社良.
基于构件损伤的防屈曲支撑钢框架易损性分析[J]. 四川大学学报(工程科学版), 2015, 47(4): 61–68.
XU Qiang, MA Yan, WANG She-liang. Vulnerability analysis of buckling-restrained brace frame based on the component damage[J]. Journal of Sichuan University (Engineering Editiong), 2015, 47(4): 61–68. |
| [14] |
中华人民共和国国家标准编写组. 建筑抗震设计规范: GB50011-2010[S]. 北京: 中国建筑工业出版社, 2010: 96-101.
The National Standards Compilation Group of People's Republic of China. Code for seismic design ofbuildings:GB50011-2010[S]. Beijing:China Architecture and Building Press, 2010:96-101. |
| [15] |
谭成轩, 石玲, 孙炜锋, 等.
构造应力研究[J]. 岩石力学与工程学报, 2004, 23(23): 3970–3978.
TAN Cheng-xuan, SHI Ling, SUN Wei-feng, et al. Research on tectonic stress plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(23): 3970–3978. DOI:10.3321/j.issn:1000-6915.2004.23.010 |
| [16] |
宋卫东, 曹帅, 付建新, 等.
矿柱稳定性影响因素敏感性分析及其应用研究[J]. 岩土力学, 2014, 35(Supplement 1): 271–277.
SONG We-idong, CAO Shuai, FU Jian-xin, et al. Sensitivity analysis of impact factors of pillar stability and its application[J]. Rock and Soil Mechanics, 2014, 35(Supplement 1): 271–277. |
| [17] |
张海波, 宋卫东, 付建新.
大跨度空区顶板失稳临界参数及稳定性分析[J]. 采矿与安全工程学报, 2014, 31(1): 66–71.
ZHANG Hai-bo, SONG Wei-dong, FU Jian-xin. Analysis of large-span goaf roof instability critical parameters and stability[J]. Journal of Mining & Safety Engineering, 2014, 31(1): 66–71. |
| [18] |
高扬, 刘西拉.
结构鲁棒性评价中的构件重要性系数[J]. 岩石力学与工程学报, 2008, 27(12): 2575–2584.
GAO Yang, LIU Xi-la. Importance coefficient of components in evaluation of structures robustness[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(12): 2575–2584. DOI:10.3321/j.issn:1000-6915.2008.12.027 |
| [19] |
林杭, 曹平, 赵延林, 等.
强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报(自然科学版), 2007, 38(6): 1219–1223.
LIN Hang, CAO Ping, ZHAO Yan-lin, et al. Application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University (Science and Technology), 2007, 38(6): 1219–1223. |


