2. 隆德大学 能源科学系, 瑞典 隆德 22100
2. Department of Energy Sciences, Lund University, Lund 22100, Sweden
系统分析方法是对一个物理系统进行科学分析的方法论,而工程设计在复杂物理系统的设计中则显得尤为重要。在过去许多年里,很多的科研工作者针对工程设计方法开展了诸多研究。Buede,Dennis,Haik,Pahl和Wasson等[1-5]均从系统设计和工程设计过程的角度进行了介绍,并在多个领域进行了应用。与此同时,逆向工程设计[6]、布局设计[7]、定制设计[8]和最优解设计[9-10]的新方法也在许多领域得到了实践。针对许多特定物理模型和应用场景,许多研究者开展了诸多关于具体工程应用方面的设计研究。例如:Anochie-Boateng等[11]在南非提出了一种关于路面设计的方法;陈永亮等[12]开展了关于五辊式涂布系统的设计方法研究;Lai等[13]探讨了根据随机噪声路径的一种新型鲁棒设计方法;Taibi等[14]则提出了一种紧凑型的滤波设计方法;梁松等[15]针对齿轮的辅助设计进行了程序开发;张坤等[16]则对汽车座椅的骨架构件的布局开展了相关的设计方法研究;贾丽臻等[17]结合生物技术特征类比的方法,开展了产品的概念设计研究;Song等[18]针对有机朗肯循环(organic rankine cycle, ORC)进行了参数优化设计;苏建宁等[19]开展了针对产品造型设计的方法研究;王克俭等[20]对差速螺旋啮合双转子的端面型线进行了几何设计;Coules等[21]对热冲轧试样的参数化设计开展了研究;Eltaweel等[22]总结了关于采光的几何设计研究。总之,针对机械、能源、化工、石油的各种系统,有很多关于各类型的不同设计方法的研究。一方面,这些方法对于特定的研究系统,具有比较好的实践应用;而另外一方面,一旦所研究的特定系统变了,其所提出的工程设计方法或者经验公式等往往就不适用了。随着社会的进步,尤其在信息爆炸时代,复杂物理系统日益常见,这也使传统的工程设计分析面临较大的挑战。
基于此,本文从系统分析方法角度,对弹簧滑块系统、直流电路系统、流场压降系统和平板传热热阻系统进行了阐述,归纳了4种物理系统中的重要物理量,提出了含阻系统的设想[23]。同时,本文采用含阻系统分析方法对先导式截止阀[24-30]的阀芯设计进行了研究,将分析结果与数据模拟结果进行比较,验证了含阻系统分析方法的可行性,其可以指导先导式截止阀阀芯小孔的设计。在未来海量数据积累的大数据时代,含阻系统分析方法可针对不同物理模型进行工程分析与设计,具有广阔的应用前景。
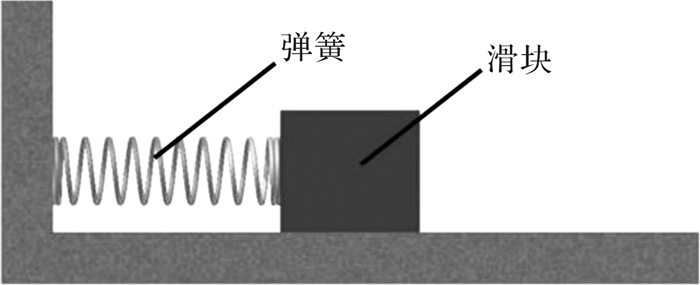
1 系统分析方法 1.1 弹簧滑块系统弹簧作为一种常见的机械弹性元件,应用于各类机械装备中,可控制机构运动、存储和释放能量、减少振动和增加缓冲,以及测量力的大小等。其在一定载荷的作用下,可以产生较大的弹性变形。根据所承受的载荷性质,弹簧可分为拉伸弹簧、压缩弹簧、弯曲弹簧和扭转弹簧等。由拉伸弹簧或压缩弹簧与一个滑块可组成一个弹簧滑块系统。图 1为最典型的处于水平方向上的弹簧滑块系统。
|
| 图 1 典型弹簧滑块系统 Fig.1 Typical spring slider system |
当系统受到一个扰动之后,滑块将产生位移变化。根据牛顿运动定律,在忽略水平面摩擦力等运动阻力的情况下,其运动规律可表示为:
| $ \left\{ \begin{array}{l} \mathit{x}{\rm{ = }}\mathit{A}{\rm{cos}}\left( {\sqrt {\mathit{kt}{\rm{/}}\mathit{m}} } \right)\\ \mathit{S}{\rm{ = 2}}\mathit{\pi }\sqrt {\mathit{m}{\rm{/}}\mathit{k}} \end{array} \right. $ | (1) |
式中:x表示滑块偏离平衡位置的位移,A表示滑块的最大位移,k表示弹簧的刚度系数,m表示滑块质量,S表示滑块的运动周期。
实际上,由于水平面摩擦力等的存在,滑块的运动会逐步衰减,因此,根据滑块的实际运动规律,需对公式(1) 进行修正,增加一个衰减函数。增加衰减函数之后的修正公式表示为:
| $ x = f\left( {\mu, m, t} \right)A{\rm{cos}}(\sqrt {\mathit{kt}{\rm{/}}\mathit{m}} ) $ | (2) |
式中f即为由滑动摩擦力主导的衰减函数,其主要与水平面摩擦系数μ和滑块质量m有关。
由此可见,在该弹簧滑块系统中,影响该系统表现(滑块的运动位移)的主要参数有:水平面的摩擦系数、滑块质量、弹簧刚度系数以及系统的输入能量。换言之,即便在复杂弹簧滑块系统中,这些因素决定了系统的属性,其他因素可视为外加的操作条件进行处理。
1.2 直流电路系统针对直流电路系统,物理学家定义了电荷、电场等概念,建立了电荷守恒定律、库伦定律等经典理论,其中:定义电荷的定向移动为电流,其方向为正电荷的定向移动方向;定义提供电动势的装置为电源;定义电源两端的势能差为电压;定义电路中负载元件阻碍电流能力的大小为电阻,其也是表征电能转化为热能等其他形式能量的物理量。
图 2为典型的简单直流电路系统,由一个电源、一个电灯泡(电阻)和若干导线构成。在该系统中,电流、电压、电阻等物理量之间的关系可表示为:
| $ \left\{ \begin{array}{l} I = U/R\\ E = {I^2}Rt = {U^2}t/R \end{array} \right. $ | (3) |

|
| 图 2 直流电路系统 Fig.2 Direct-current circuit system |
式中:I表示电流,U表示电压,R表示电阻,E表示电能转化为热能的量,t表示时间。
由此可见,在该直流电路系统中,影响该系统表现的主要参数有电源的电压和负载的电阻。换言之,即便在复杂直流电流系统中,这几个因素决定了系统属性,其他因素可视作在基础系统上的外加操作条件进行分析处理。
1.3 流场压降系统针对流场压降系统,尤其在实际工业管道等应用场合,研究主要聚焦于不可压缩黏性流体在管道中流动的能量损失。该能量损失主要由流体在管道内的摩擦阻力所引起的沿程阻力损失,管道形状变化(例如由阀门、孔板等管道元件所引起)和流动方向变化等所引起的局部阻力损失组成。
针对沿程阻力损失hl,通过量纲分析得到其与管径d、管长l、流体流速v的关系为:
| $ {{h}_{\rm{l}}}=\lambda \frac{l}{d}\frac{{{v}^{2}}}{2g} $ | (4) |
式中:g表示重力加速度;λ表示沿程阻力系数,由雷诺数Re和管道的相对粗糙度Δ/d等决定。
针对局部阻力损失hp,与沿程阻力损失类似,其可表示为:
| $ {{h}_{\rm{p}}}=\zeta \frac{{{v}^{2}}}{2g} $ | (5) |
式中:局部阻力系数ζ受管道流动截面和流动方向变化的影响,其计算相对比较复杂,主要影响因素有流动方向和流动截面积。
通过公式(4) 和公式(5) 可见,在该系统中,影响系统表现的主要参数有:管径、管截面积、管长、流体流速等。无论是在简单流阻系统还是复杂的系统中,以上因素决定了系统属性,其他复杂因素同样可视作外加操作条件。
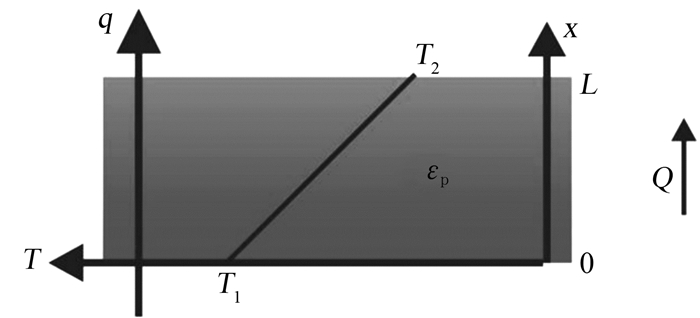
1.4 平板传热热阻系统针对平板传热热阻的研究,以稳态传热为例,其简单模型如图 3所示。假定平板的材质均匀且性能稳定,其中:板厚为L,传热系数为εp,平板的左侧高温为T1,平板的右侧低温为T2;设定高温侧的坐标位置为x=0。
|
| 图 3 平板稳态传热模型 Fig.3 Steady heat transfer model of flat plate |
由于其已处于稳定状态,即平板内部各个位置的热流密度处处相等,导热方程可表示为:
| $ \left\{ \begin{array}{l} \frac{d}{{{\rm{d}}x}}({\varepsilon _{\rm{p}}}\frac{{{\rm{d}}T}}{{{\rm{d}}x}}) = 0\\ T\left( x \right) = {T_1} + \frac{{{T_2}{\rm{ - }}{T_1}}}{L}x \end{array} \right. $ | (6) |
式中:εp表示传热系数,(T2—T1)/L表示平板上的温度梯度。它们与平板热流密度q及单位热通量Q的关系可表示为:
| $ \left\{ \begin{array}{l} q = {\rm{ - }}{\varepsilon _{\rm{p}}}\frac{{{T_2}{\rm{ - }}{T_1}}}{L}\\ Q = qC = - {\varepsilon _{\rm{p}}}C\frac{{{T_2}{\rm{ - }}{T_1}}}{L} \end{array} \right. $ | (7) |
式中C表示热流密度通过的截面面积。值得一提的是,负号表示热流密度和传热量的方向与温度梯度方向相反,即热量是由高温侧向低温侧传播的。
将公式(7) 变形成公式(3) 的形式,得到:
| $ Q = \frac{{{T_1} - {T_2}}}{{{R_{\rm{T}}}}} = \frac{{{T_1} - {T_2}}}{{L/{\varepsilon _{\rm{p}}}C}} $ | (8) |
式中:单位热通量Q可对应为电流;(T1—T2)作为温度差,可对应到直流电路系统的电压;RT表示该平板的热阻,可对应为电阻。由此可将图 3模型转化为图 4所示的直流电路问题。可以发现,用直流电路的分析方法可同样应用于热阻分析。
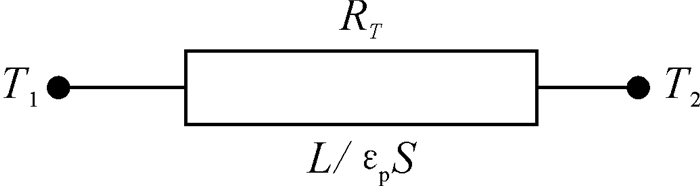
|
| 图 4 平板稳态传热模型的直流电路表达 Fig.4 Direct-current circuit model of steady heat transfer model of flat plate |
同上述系统,在平板传热热阻系统中,影响系统表现的主要参数有平板的传热系数和几何尺寸等;而这些因素就决定了系统属性,其他复杂因素可视作基础系统上的外加操作条件进行分析。
2 含阻系统分析方法 2.1 含阻系统的构成表 1是对前文提及的4个物理系统关键量的梳理结果,通过横向对比发现,其均存在一个“阻”,即存在一个量会去改变另一个既定存在:弹簧滑块系统中的摩擦系数影响其达到的最大位移,直流电路系统中的电阻改变系统的原有电压,流体压降系统中管件的沿程阻力系数和局部阻力系数改变原有水头,平板传热系统中的热阻引起不同区域的温度变化。
| 物理系统 | 公式 | 核心物理量 |
| 弹簧滑块系统 | (2) | 摩擦系数、滑块质量弹簧刚度系数、最大位移 |
| 直流电路系统 | (3) | 电压、电阻、电流 |
| 流场压降系统 | (4)(5) | 管径截面变化、管长、流体流速 |
| 平板传热热阻系统 | (8) | 平板传热系数、几何尺寸 |
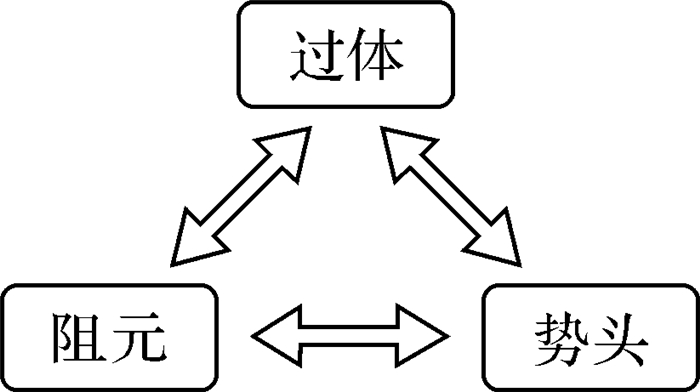
将以上阻碍系统维持现状的“改变量”、“原有量”以及两者之间的“联系量”统一起来,组成了一个新的统一物理模型,本文将其定义为含阻系统。含阻系统的实质是一种系统分析方法,如图 5所示,其由阻元、过体和势头所组成,其中“改变量”、“联系量”和“原有量”则被分别定义为阻元、过体和势头。
|
| 图 5 含阻系统的组成 Fig.5 Composition of the obstacle contained system (OCS) |
弹簧滑块系统的势头是整个系统的能量,直流电路系统的势头是电阻两端的电压,流场压降系统的势头是管程两端的压头,而平板传热热阻系统的势头则是两端的温差。阻元和势头的联系,通过过体来体现,弹簧滑块系统中的过体是滑块速度,直流电路系统中的过体是电流,流场压降系统中的过体是流体流速,平板传热热阻系统中的过体是单位热通量。
含阻系统中的3个量之间的关系若用数学模型来表达的话,可以表示为:
| $ {D_{\rm{e}}} = {f_{\rm{p}}}({O_{\rm{e}}}) $ | (9) |
式中:De表示势头(D-value element),Oe表示阻元(obstacle element),fp表示两者之间的函数关系,这个函数关系通过过体(pass body element)来具体体现。在不同的案例中,可以通过拟合等方法得到线性、几何等多种函数关系,而最需关注的是其准确性。因此,函数关系建立之后需要用大量已有的准确数据进行比较验证,从而保证含阻系统分析方法表达式的有效性。
2.2 含阻系统分析方法的优势含阻系统的实质是一种系统分析方法,通过确立阻元、过体和势头三个物理量,同时忽略系统中的其他物理量(将其他所有因素视作黑箱),建立阻元对势头的直接联系,从而做到对问题的简化。
相比目前存在的其他分析方法,含阻系统分析方法更加直接简洁。例如,计算流体力学分析方法往往需借助商业软件等进行模型建模、离散、运算等系列过程,实验分析方法则存在时间和经济性等诸多问题。相比之下,含阻系统可基于一定量的数据,通过建立阻元对势头的直接联系,得到近似且相对准确的结果。因此,含阻系统分析方法具有简单直接且相对准确的优点。
当然,值得再次强调的是,含阻系统分析方法需建立在一个具有充足数据的基础上,即被分析的系统须处于一个已经存在海量数据(大数据)的背景之下。所以,无论计算流体力学方法还是实验分析方法,都是含阻系统分析方法的基础。
3 本方法在先导阀阀芯设计中的应用 3.1 先导式截止阀及阀芯为了研究含阻系统分析方法的应用效果,采用该方法对先导式截止阀的阀芯设计进行分析。
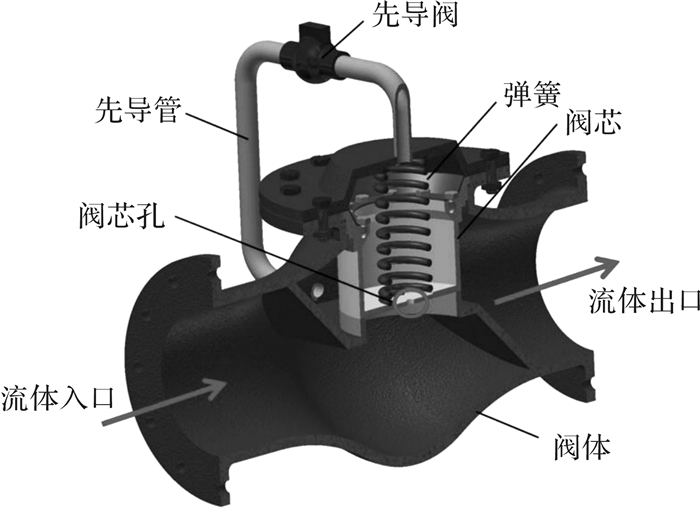
图 6是先导式截止阀的结构示意图[28],它主要由阀体、阀芯、先导管和弹簧等组成。其中阀芯为活塞式阀芯,阀芯的底部开有一个小孔,弹簧则与阀芯的底部相连,阀芯上盖接有一根先导管,先导管上装有一个先导阀(小阀),用来控制先导管的连通或关闭。该阀的工作原理可参见相关文献[24-30],本文不予具体阐述。
|
| 图 6 先导式截止阀 Fig.6 Pilot-control globe valve |
先导式截止阀活塞式阀芯底面上的小孔使流体经过时产生压差,驱动阀芯运动。因此阀芯小孔的孔径十分重要,其直接影响到压差。与此同时,阀门在节流位置由于大压降的存在,容易产生汽蚀,进而造成对阀体乃至管路系统的破坏。因此,下文将针对阀芯孔径对于压降和最大汽含率两个因素的影响,采用含阻系统分析方法进行研究。
3.2 含阻系统分析方法的压差分析应用针对先导式截止阀阀芯,在该系统中入口流速是过体,阀芯孔径是阻元,产生的压差是势头。虽然该先导式截止阀中还存在诸多其他物理量,如阀门公称直径等,但在含阻系统分析方法中,其他物理量作为黑箱处理。
通过建立数值模型,并在商业流体分析软件Fluent中进行模拟,得到阀芯孔径在不同入口流速下对于压差的影响,其具体结果如表 2所示[28]。
| 入口速度/ (m/s) |
Δp/Pa | |||||
| 2 mm | 4 mm | 6 mm | 8 mm | 10 mm | 12 mm | |
| 1.0 | 600 | 560 | 490 | 400 | 290 | 160 |
| 1.5 | 1 320 | 1 230 | 1 110 | 930 | 720 | 390 |
| 2.0 | 2 270 | 2 110 | 1 980 | 1 650 | 1 230 | 730 |
| 2.5 | 3 450 | 3 280 | 2 990 | 2 570 | 1 920 | 1 130 |
| 3.0 | 4 750 | 4 590 | 4 350 | 3 550 | 2 640 | 1 420 |
根据含阻系统分析方法,直接建立阻元(阀芯孔径)和势头(压差)的关系。换言之,不用考虑阀芯孔径与压差之间到底是什么物理关系,直接对表 2中不同入口流速下的阀芯孔径和压差进行公式拟合,得到每个速度下估算公式,具体如公式(9) 所示:
| $ \Delta p = \left\{ \begin{array}{l} - 2.72{d^2} - 6.16d + 625, v = 1{\rm{ m/s}}\\ - 6.96{d^2} + 6.64d + 1\;326, v = 1.5{\rm{ m/s}}\\ - 12.76{d^2} + 26.32d + 2\;252, v = 2{\rm{ m/s}}\\ - 20.26{d^2} + 53.75d + 3\;410, v = 2.5{\rm{ m/s}}\\ - 35.62{d^2} + 165.89d + 4\;550, v = 3{\rm{ m/s}} \end{array} \right. $ | (9) |
根据得到的拟合公式,可以计算对应速度下的压差。本文选取入口流速为1 m/s、阀芯孔径为2.5 mm和4.5 mm,进行了数值模拟和公式(9) 的计算,发现两者偏差低于1%。与此同时,计算非拟合公式对应速度下的压差,可采用不同公式间的差值进行近似。例如分析入口速度为2.1 m/s、阀芯孔径为4.5 mm的压降水平,通过公式(9) 计算入口流速为2 m/s和2.5 m/s时的压差之后,将2个压差值进行线性插值,得到其压降水平约为2 000 Pa;而通过数值模拟,得出的压差为2 019 Pa,误差小于1%。由此可见,含阻系统分析方法可较好地应用于阀芯小孔处的压差研究。值得强调的是,该方法必须基于一定准确度和数据量的数值计算结果,才能保证分析的一定精度。
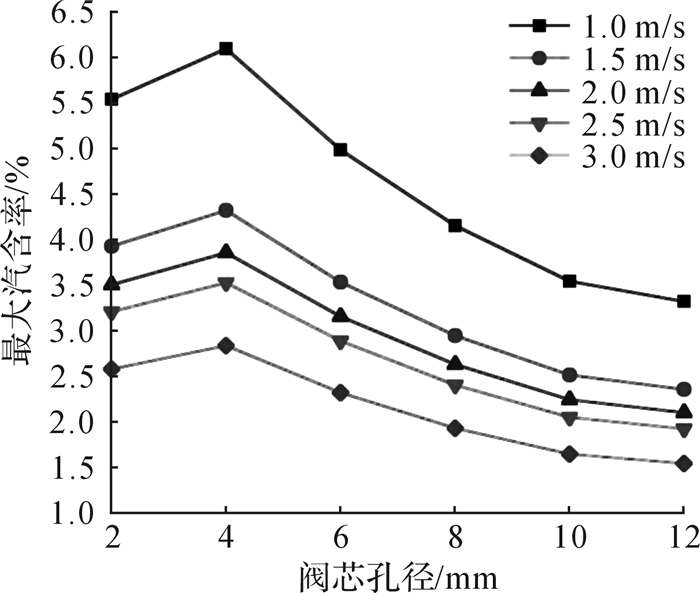
3.3 含阻系统分析方法的最大汽含率分析应用与3.2节对于阀芯小孔处的压差分析类似,通过建立两相流的先导阀数值模型,在商业软件Fluent中计算得到了在不同阀芯孔径和入口流速下阀内的最大汽含率情况,如图 7所示。
|
| 图 7 不同入口流速下阀芯孔径对最大汽含率的影响 Fig.7 Effects of orifice diameters on maximum vapor rate under different inlet speeds |
根据含阻系统分析方法,直接建立阻元(阀芯孔径)和势头(最大汽含率)的关系。与前文分析压差与阀芯孔径之间关系类似,不考虑阀芯孔径与先导式截止阀内最大汽含率之间到底是什么物理关系,直接对图 7中不同流速下的阀芯孔径和最大汽含率进行公式拟合。考虑到准确性,本次拟合采用了3次方的多项式估算公式,具体如公式(10) 所示:
| $ {C_{{\rm{max}}}} = \left\{ \begin{array}{l} 0.011\;7{d^3} - 0.25{d^2} + 1.32d + 3.90, v = 1{\rm{ m/s}}\\ 0.008\;3{d^3} - 0.18{d^2} + 0.94d + 2.76, v = 1.5{\rm{ m/s}}\\ 0.007\;4{d^3} - 0.16{d^2} + 0.84d + 2.47, v = 2{\rm{ m/s}}\\ 0.006\;8{d^3} - 0.15{d^2} + 0.76d + 2.26, v = 2.5{\rm{ m/s}}\\ 0.005\;4{d^3} - 0.12{d^2} + 0.61d + 1.81, v = 3{\rm{ m/s}} \end{array} \right. $ | (10) |
采用数值模拟和公式(10),对非拟合公式对应速度下的阀芯孔径以及最大汽含率进行计算对比发现,两者的结果差异均在2%以内,符合工程设计要求。因此,含阻系统分析方法同样可较好地应用于先导式截止阀阀内最大汽含率的研究。
4 总结本文从系统分析方法角度,对弹簧滑块系统、直流电路系统、流场压降系统和平板传热热阻系统进行了阐述,并对4种物理系统模型进行了分析与归纳,提出了含阻系统的设想,即其由阻元、过体和势头三个部分组成,可通过确立物理系统中的阻元、过体和势头,忽略其他物理量,同时建立阻元对势头的直接联系,做到对问题的简化,得到近似且相对准确的结果。采用该方法对先导式截止阀的阀芯设计进行分析发现,数值模拟和含阻系统分析方法得出的阀芯小孔处的压差和最大汽含率均在2%的误差范围内,可应用于工程实践,指导先导式截止阀阀芯小孔的设计。值得注意的是,含阻系统分析方法建立在已经具有海量数据(大数据)的基础上,目前其他物理方法得到的实际准确数据均是含阻系统分析方法的基础。在未来海量数据积累的大数据时代,含阻系统分析方法可针对物理模型进行分析,服务工程设计研究,具有广阔的应用前景。
| [1] | BUEDE D M, MILLER W D. The engineering design of systems:models and methods[M]. New Jersey: John Wiley & Sons, 2016: 112-116. |
| [2] | DENNIS A, WIXOM B H, TEGARDEN D. Systems analysis and design:an object-oriented approach with UML[M]. New Jersey: John Wiley & Sons, 2015: 341-352. |
| [3] | HAIK Y, SIVALOGANATHAN S, SHAHIN T M. Engineering design process[M]. Toronto: Nelson Education, 2015: 42-59. |
| [4] | PAHL G, BEITZ W. Engineering design:a systematic approach[M]. Berlin: Springer Science & Business Media, 2013: 296-327. |
| [5] | WASSON C S. System engineering analysis, design, and development:concepts, principles, and practices[M]. New Jersey: John Wiley & Sons, 2015: 682-689. |
| [6] | PIGGOTT A Y, LU J, LAGOUDAKIS K G, et al. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer[J]. Nature Photonics, 2015, 9(6): 374–377. DOI:10.1038/nphoton.2015.69 |
| [7] | LIM S, JEONG S, MIN S. Multi-component layout optimization method for the design of a permanent magnet actuator[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1–4. |
| [8] | DILLMAN D A, SMYTH J D, CHRISTIAN L M. Internet, phone, mail, and mixed-mode surveys:the tailored design method[M]. New Jersey: John Wiley & Sons, 2014: 221-245. |
| [9] | WEI J, LÜ C, SUN W, et al. A study on optimum design method of gear transmission system for wind turbine[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(5): 767–778. DOI:10.1007/s12541-013-0100-4 |
| [10] | HERREMA A J, WIESE N M, DARLING C N, et al. A framework for parametric design optimization using isogeometric analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 316: 944–965. DOI:10.1016/j.cma.2016.10.048 |
| [11] | ANOCHIE-BOATENG J, MAINA J. Permanent deformation testing for a new South African mechanistic pavement design method[J]. Construction and Building Materials, 2012, 26(1): 541–546. DOI:10.1016/j.conbuildmat.2011.06.055 |
| [12] |
陈永亮, 韩瑶, 刘谱, 等.
五辊式无溶剂涂布系统交叉耦合建模与设计方法[J]. 工程设计学报, 2014, 21(1): 38–42.
CHEN Yong-liang, HAN Yao, LIU Pu, et al. Mechatronic cross-coupling modeling and design method for five-rollers solventless coating system[J]. Chinese Journal of Engineering Design, 2014, 21(1): 38–42. |
| [13] | LAI X, ZHANG Y, WANG C. A new robust design method for path-generating linkages with multi-stochastic noises[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2015, 229(5): 860–869. DOI:10.1177/0954405414534435 |
| [14] | TAIBI A, TRABELSI M, SLIMANE A, et al. A novel design method for compact UWB bandpass filters[J]. IEEE Microwave and Wireless Components Letters, 2015, 25(1): 4–6. DOI:10.1109/LMWC.2014.2363016 |
| [15] |
梁松, 李海波, 张义民.
基于C和gnuplot的渐开线齿轮辅助几何设计程序开发[J]. 工程设计学报, 2014, 21(1): 80–86.
LIANG Song, LI Hai-bo, ZHANG Yi-min, et al. Development of auxiliary geometric design software for involute gear based on the C and gnuplot[J]. Chinese Journal of Engineering Design, 2014, 21(1): 80–86. |
| [16] |
张坤, 丁晓红, 倪维宇, 等.
汽车座椅骨架构件布局设计方法[J]. 工程设计学报, 2015, 22(2): 166–171.
ZHANG Kun, DING Xiao-hong, NI Wei-yu, et al. The component layout design method for automotive seat skeleton[J]. Chinese Journal of Engineering Design, 2015, 22(2): 166–171. |
| [17] |
贾丽臻, 刘伟, 檀润华, 等.
基于生物-技术特征类比的产品概念设计方法研究[J]. 工程设计学报, 2015, 22(4): 301–308.
JIA Li-zhen, LIU Wei, TAN Run-hua, et al. Research on product conceptual design based on biological-technological characteristic analogy[J]. Chinese Journal of Engineering Design, 2015, 22(4): 301–308. |
| [18] | SONG J, GU C, REN X. Parametric design and off-design analysis of organic rankine cycle (ORC) system[J]. Energy Conversion and Management, 2016, 112: 157–165. DOI:10.1016/j.enconman.2015.12.085 |
| [19] |
苏建宁, 陈肖, 张书涛, 等.
基于进化算法的产品造型创新设计方法研究[J]. 工程设计学报, 2016, 23(2): 136–142.
SU Jian-ning, CHEN Xiao, ZHANG Shu-tao, et al. Product styling innovative design method based on evolutionary algorithm[J]. Chinese Journal of Engineering Design, 2016, 23(2): 136–142. |
| [20] |
王克俭, 汪廷飞.
差速螺旋啮合双转子端面型线的统一几何设计及模拟[J]. 机械工程学报, 2017, 53(3): 51–56.
WANG Ke-jian, WANG Ting-fei. United geometrical design and simulation of sectional profiles for twin rotors in differential screw coupling[J]. Chinese Journal of Mechanical Engineering, 2017, 53(3): 51–56. |
| [21] | COULES H E, ORROCK P J, TRUMAN C E. Parametric design of scaled-down pressurised thermal shock test specimens using inelastic analysis[J]. Engineering Fracture Mechanics, 2017, 176: 308–325. DOI:10.1016/j.engfracmech.2017.03.040 |
| [22] | ELTAWEEL A, YUEHONG S U. Parametric design and daylighting:a literature review[J]. Renewable and Sustainable Energy Reviews, 2017, 73: 1086–1103. DOI:10.1016/j.rser.2017.02.011 |
| [23] |
钱锦远. 含阻系统中多孔板的流动分析及其工业应用研究[D]. 杭州: 浙江大学化学工程与生物工程学院, 2016: 17-34.
QIAN Jin-yuan. Fluid dynamic analysis on multi-stage perforated plate in obstacle contained system (OCS) and its typical industrial applications[D]. Hangzhou:Zhejiang University, College of Chemical and Biological Engineering, 2016:17-34. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016273022.htm |
| [24] | QIAN J, WEI L, JIN Z, et al. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve[J]. Energy Conversion and Management, 2014, 87: 220–226. DOI:10.1016/j.enconman.2014.07.018 |
| [25] |
钱锦远, 朱银法, 刘步展, 等.
垂直管线型先导式截止阀的阀芯运动过程数值分析[J]. 排灌机械工程学报, 2016, 34(1): 51–56.
QIAN Jin-yuan, ZHU Yin-fa, LIU Bu-zhan, et al. Transient simulation of valve core movement of pilot-control globe valve in vertical pipelines[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(1): 51–56. DOI:10.3969/j.issn.1674-8530.15.0206 |
| [26] | QIAN J, LIU B, JIN Z, et al. Numerical analysis of flow and cavitation characteristics in a pilot-control globe valve with different valve core displacements[J]. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering), 2016, 17(1): 54–64. |
| [27] | LIU B, WANG J, QIAN J, et al. Dynamic response analysis of pilot control globe valve focusing on opening and closing time of pilot valve[J]. Journal of Physics:Conference Series, 2016, 745(3): 032046. |
| [28] | QIAN J, LIU B, LEI L, et al. Effects of orifice on pressure difference in pilot-control globe valve by experimental and numerical methods[J]. International Journal of Hydrogen Energy, 2016, 41(41): 18562–18570. DOI:10.1016/j.ijhydene.2016.08.070 |
| [29] | QIAN J, GAO Z, WANG J, et al. Experimental and numerical analysis of spring stiffness on flow and valve core movement in pilot control globe valve[J]. Journal of Hydrogen Energy, 2017, 42(27): 17192–17201. DOI:10.1016/j.ijhydene.2017.05.190 |
| [30] | JIN Z, GAO Z, ZHANG M, et al. Pressure drop analysis of pilot-control globe valve with different structural parameters[J]. ASME Journal of Fluids Engineering, 2017, 139(9): 091102. DOI:10.1115/1.4036268 |



