2. 天津市生物医学检测技术与仪器重点实验室, 天津 300072;
3. 天津中医药大学 中医药工程学院, 天津 300193
2. Tianjin Key Laboratory of Biomedical Detection Technology and Instrumentation, Tianjin 300072, China;
3. School of Chinese Medicine Engineering, Tianjin University of Traditional Chinese Medicine, Tianjin 300072, China
脉象作为观察人体功能变化的重要窗口,在一定程度上能够反映人体各种生理和病理的情况。但是传统的中医脉诊需要医患双方同时在场,中医师需切身感受到患者脉象才能作出诊断。此外,传统脉诊学习中“在心易了,指下难明”的情况始终存在,很大程度上制约了脉学的传承和推广。远程医疗[1-2]和互联网+中医[3]思路下的远程脉象复放系统有效地解决了以上问题。远程脉象复放系统接收远端传来的脉象信号,经上位机对信号进行预处理后根据取脉压力浮沉情况发送相应数据到下位机,由基于“机械+液路”的复放装置进行复放,仿生手端人造脉管处便可复现出脉象,达到“面对面”脉诊的效果。
当前的脉象采集技术难以迅速准确地找到最佳取脉压力,导致无法快速获得准确的脉象信息。现有的脉象复放装置[4-6]可以分为2类。一类是依据脉象形成原理,采用液压系统来模拟血液循环,通过控制脉管内的液压及流量实现各种脉象的模拟。该过程比较繁杂,影响脉象复放效果的因素较多,如电机运转、油泵运行产生的噪音和振动等。另一类是采用磁电器件,将电磁信号转化为机械振动,还原脉搏振动,但其与传统取脉指感相差太大。脉象有“位、数、形、势”四种属性,现有脉象复放技术仅能做到对“数”(脉搏的频率和节律)和“势”(脉搏活动趋势)复放,忽略了“位”(脉位的浮沉)和“形”(静止状态下指下脉管本身的形态)。
针对上述情况,本文设计了基于STM32微处理器的机械与液路相结合的脉象复放装置;结合多传感器信息融合技术[7-9],根据不同取脉压力提取对应的脉象数据片段来复放,实现“浮、中、沉”三部九候脉诊方式[10];通过对人造脉管处液路的加、减压改变其充盈度达到对“形”的模拟;为了提高复放精度,加入基于自适应逆控制的输出补偿环节,从而实现远程脉象复放的目标。
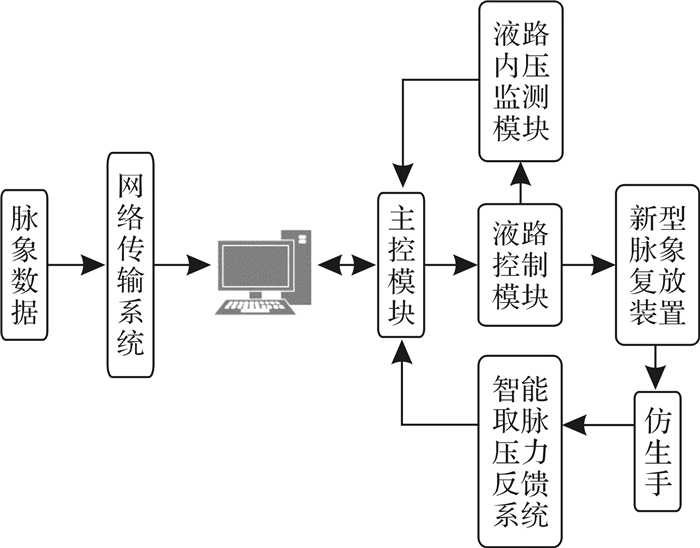
1 系统硬件设计 1.1 整体结构中医远程脉象复放系统包括网络传输系统、计算机、主控模块、液路控制模块、新型脉象复放装置、液路内压监测模块、智能取脉压力反馈系统和仿生手等。系统整体结构示意图如图 1所示。
|
| 图 1 系统整体结构示意图 Fig.1 Schematic diagram of system structure |
主控模块采用基于ARM Cortex M4内核的32位微处理器STM32F373作为主控制器,其工作主频可达72 MHz,满足系统的快速响应需求;内部USART可转换为USB与上位机通讯;自带多个定时器,便于输出多种不同频率和占空比的PWM信号对液路控制模块中的蠕动泵进行调速控制;集成4个ADC转换器满足对液路内压和取脉压力的检测;2个12位DAC转换器用于脉象的复放。
1.3 液路控制模块该模块包括1个卡默尔KPP型蠕动泵和2个电磁阀。采用ULN2803达灵顿管控制24 V电磁阀用于控制液路通断,并可在脉象复放时使仿生手位于一段封闭稳定的液路中以保证复放的准确性,采用L9110S控制蠕动泵用于驱动整个液路且可对仿生手处封闭液路时进行加减压以调节脉管的充盈度。
1.4 液路内压监测模块选用PT210B液压传感器对液路内压进行检测,传感器量程为-20~20 kPa,输出范围为0~3.3 V。经标定当检测到压力转换值大于2.8 V或小于0.8 V时判定液路有爆管或漏液危险,系统自动停止运行。
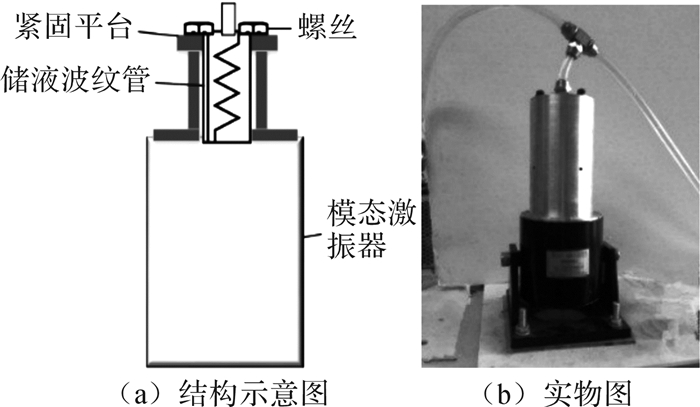
1.5 新型脉象复放装置 1.5.1 复放装置原理新型脉象复放装置结构示意图和实物图如图 2所示。新型脉象复放装置由模态激振器、传动块、紧固平台和储液波纹管组成。模态激振器基本工作原理是:载流导体在磁场中受到电磁力作用,其内部有稀土钕铁硼永磁材料提供稳定磁场,所以输入的电流方向和大小发生变化会导致作为动子的振动头产生方向和大小不同的位移。波纹管在这里起到类似心房和心室的作用,接收到由传动块传递来的模态激振器振动头的往复直线运动后,随即产生相应的压缩或拉伸形变,容积发生改变,将波纹管内所储模拟血液挤出或吸入,带动封闭液路中模拟血液运动,使封闭液路中弹性模拟脉管产生相应的膨胀或收缩,从而形成指端可以感知的脉搏搏动。利用紧固平台将模态激振器、传动块、储液波纹管等固定在一起,限定了储液波纹管运动自由度,保证其只在拉伸和压缩的方向运动,减小脉象复放误差,同时降低噪声和振动带来的影响,整体上提高系统稳定性和可靠性。
|
| 图 2 新型脉象复放装置 Fig.2 New-type pulse recurrence device |
与传统脉象模拟装置所用步进电机作为脉象发生器[11]相比,模态激振器具有位移大、出力充足、反应迅速、体积小、重量轻、频率范围宽(0~6 kHz)、结构合理、可靠性高的特点,更能满足脉象复放的要求。
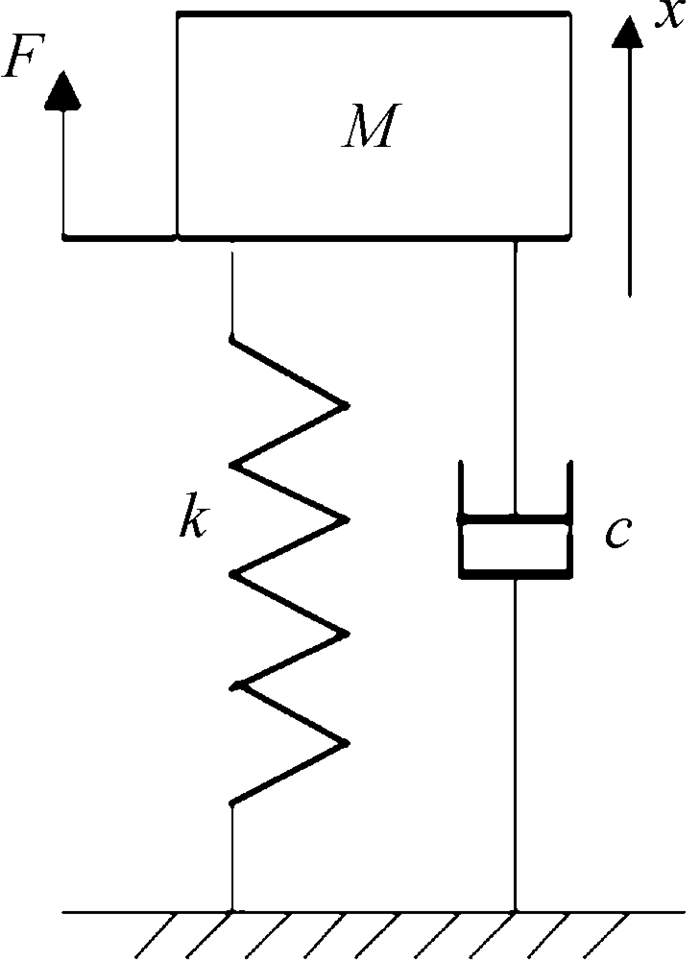
1.5.2 复放装置数学模型新型脉象复放装置动力学模型如图 3所示。
|
| 图 3 新型脉象复放装置动力学模型 Fig.3 Dynamics model of new-type pulse recurrence device |
图 3中F为激振器输出的电磁力,x为动子端位移,M为运动部分总质量,k为弹性系数,c为阻尼系数。
| $ F = BlI $ | (1) |
式中:B为磁感应强度,l为磁场中导体有效长度,I为瞬时电流。
由牛顿力学定律得复放装置动态力平衡方程:
| $ F - kx - c\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = M\frac{{{{\rm{d}}^2}x}}{{{{\rm{d}}^2}t}} $ | (2) |
设线圈两端电压为U,直流电阻为R,线圈自感系数为L,产生的反电动势为e,由基尔霍夫定律得:
| $ U = L\frac{{{\rm{d}}I}}{{{\rm{d}}t}} + RI + e $ | (3) |
| $ e = BL\frac{{{\rm{d}}x}}{{{\rm{d}}t}} $ | (4) |
联立式(1) 至式(4),经Laplace变换得系统传递函数为:
| $ G\left( s \right) = K\frac{{\omega _{\rm{n}}^2}}{{{s^2} + 2\zeta {\omega _{\rm{n}}}s + \omega _{\rm{n}}^2}} $ | (5) |
式中:
将复放装置参数代入式(5),得:
| $ G\left( s \right) = \frac{{\frac{1}{{1830}}}}{{\frac{{{s^2}}}{{25400}} + \frac{s}{{636}} + 1}} $ | (6) |
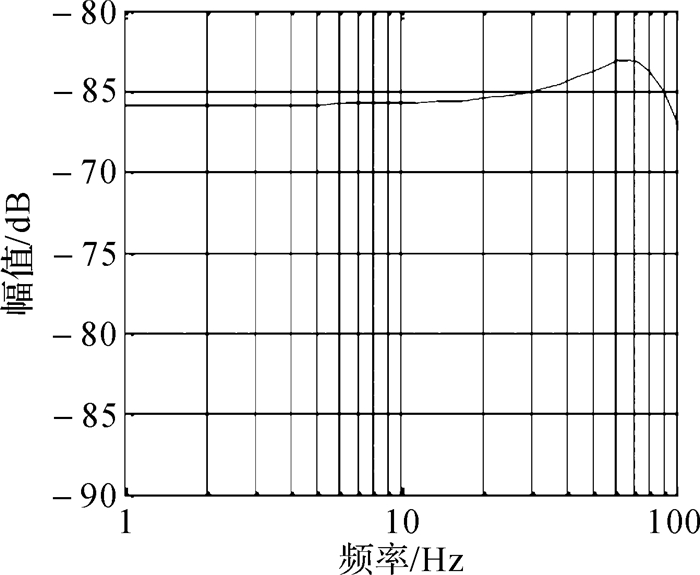
脉象信号分布的频带在10 Hz以内,正常情况下一般为1~5 Hz。由图 4知该脉象复放装置有良好的低频特性,满足脉象复放的频带要求。
|
| 图 4 复放装置幅频特性曲线 Fig.4 Amplitude-frequency curve of recurrence device |
脉象复放装置中的动力源模态激振器的活动部件顶杆的最大振幅为5 mm, 即储液波纹管的伸缩距离为-5~5 mm。为验证5 mm的振幅能否满足脉象信号振幅的要求,特进行如下计算验证。
流体在水平圆管中作层流运动时满足Poiseuille定律[12-13],公式为:
| $ Q = \frac{{{\rm{\pi }}R_1^4\Delta p}}{{8\eta {L_{\rm{y}}}}} $ | (7) |
式中:Q为体积流量;Δp是管子两端的压强差;R1为圆管半径;Ly为圆管长度:η为流体的黏滞系数。
波纹管的体积流量为:
| $ Q = \frac{1}{4}{\rm{\pi }}{D^2}\frac{d}{t} $ | (8) |
式中:D为波纹管直径;d为储液波纹管压缩距离;t为压缩距离d所用时间。
系统液路除了人造脉管外都是刚性材料,因此储液波纹管压缩排出人造血液的体积与人造脉管的膨胀体积相等,即:
| $ \frac{1}{4}{\rm{\pi }}{D^2}d = {\rm{\pi }}{L_1}{\left( {\frac{{b + \Delta b}}{2}} \right)^2} - {\rm{\pi }}{L_1}{\left( {\frac{b}{2}} \right)^2} $ | (9) |
式中:L1是脉管的长度;b为人造脉管原始直径;Δb为人造脉管膨胀后的直径增量。
可得:
| $ \Delta b = \sqrt {{b^2} + \frac{d}{{{L_1}}}{D^2}} - b $ | (10) |
综合式(7) 至式(10) 式可得人造脉管平均压强变化为:
| $ \Delta p = \frac{{32\eta {R_1}{D^2}d}}{{t{{\left( {{b^2} + \frac{d}{{{L_1}}}{D^2}} \right)}^2}}} $ | (11) |
将R1=8 mm, b=4 mm, η=100 MPa·s, D=30 mm, d=5 mm, L1=80 mm代入,计算得出:
| $ \Delta p \approx \frac{{22068.7}}{t} $ | (12) |
t为模态激振器顶杆运动5 mm所用时间,根据其响应速度,t < 1 s。因此该脉象复放装置在人造脉管端所能产生的压强变化至少有22 068.7 Pa(约为165.5 mmHg),远大于人体脉搏压强差,所以该复放装置完全满足脉象复放对于振幅的要求。
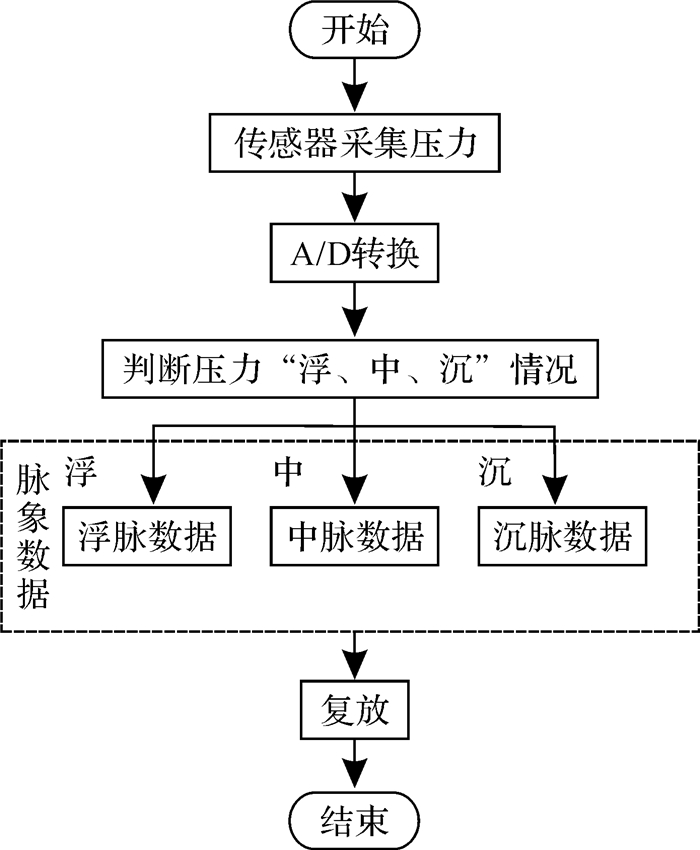
1.6 智能取脉压力反馈系统中医师在脉诊时指端会施加不同的压力来获得不同压力下的脉搏指感,从而从整体上进行诊断。在不同的取脉压力中存在一个最佳取脉压力[14], 即中医师切脉时指感最强、脉搏波最明显时指端所施加的压力。为了使中医师在实际使用该脉象复放系统时有更接近亲身为患者切脉的体验,采用智能取脉压力反馈模块实现对“浮、中、沉”不同取脉压力下不同脉象的复放。
下位机在接收到脉象数据后,根据采集过程中压力的连续线性变化规律将数据分为浮脉、中脉、沉脉三个数据片段。复放时医师指端施加的压力被FS-20压力传感器采集并转换为对应的取脉压力。根据压力的大小进行判断,若力在0~75 g之间为浮取,在75~175 g之间为中取,大于175 g则为沉取。根据判断结果复放相应的数据片段,具体流程如图 5所示。
|
| 图 5 智能取脉压力反馈流程图 Fig.5 Intelligent pulse pressure feedback process |
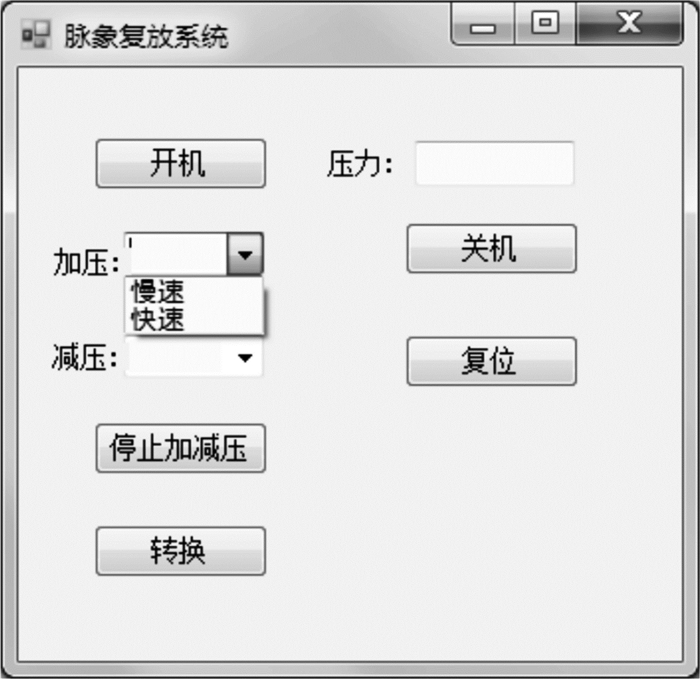
系统软件设计包括上位机软件设计和下位机软件设计。上位机软件采用C#与MATLAB混合编写,主要用于接收远程脉象数据、数据预处理、发送控制命令和接收下位机上传信息等。下位机主要执行控制命令并采集上传液路压力和取脉压力信息。具体流程图如图 6所示。图 7为上位机软件界面。

|
| 图 6 系统软件设计流程图 Fig.6 System software design flow chart |
|
| 图 7 上位机软件界面 Fig.7 Software interface of PC |
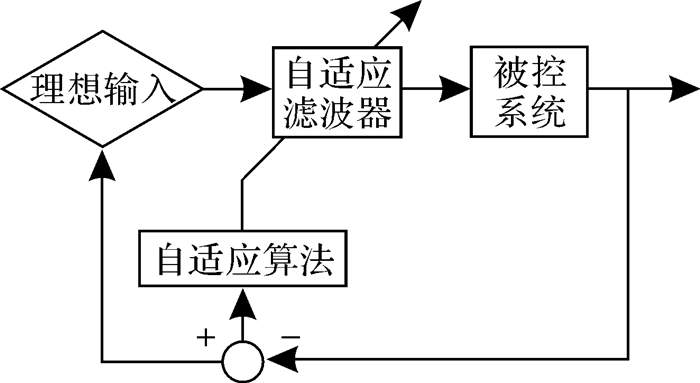
输出补偿部分采用自适应逆控制技术[15],自适应逆控制的基本思想是用一个来自控制器的信号去驱动被控系统,当控制器的传递函数收敛到被控系统传递函数的逆函数时,控制器与被控系统级联后的传递函数变为1,这样系统输出的响应信号会逼近理想的输出信号。如图 8所示,其主要有以下2个基本过程:
|
| 图 8 自适应逆控制原理图 Fig.8 Schematic diagram of adaptive inverse control |
1) 滤波过程。作为自适应模型的自适应滤波器,比较理想信号与系统输出响应信号后得出两者之间的误差,同时对理想信号进行滤波获得驱动控制信号。
采用横向滤波器作为自适应滤波器模型,输入信号分为输入信号x(n)和理想信号d(n)两路。滤波器滤波系数是延迟线抽头信号的加权系数{W1(n), W2(n), …, WM(n)}。在滤波过程中,理想信号d(n)与输入信号x(n)一同参与处理。在此情况下,对于给定的输入,横向滤波器将产生一个输出信号y(n)作为理想信号的估计。此输出信号y(n)等于输入信号x(n)和加权系数W(n)的卷积和,如下所示:
| $ \mathit{\boldsymbol{y}}\left( n \right) = \sum\limits_{a = 1}^M {{W_a}\left( n \right)\mathit{\boldsymbol{x}}\left( {n - a + 1} \right),n = 1,2, \cdots ,N} $ | (13) |
将估计误差e(n)定义为理想信号与实际滤波器输出之差,则e(n)与x(n)都被加到自适应控制部分,因此围绕抽头权值的反馈环是闭环的,加权系数W(n)将在一定的自适应算法下随e(n)进行实时更新。
2) 自适应过程。利用滤波过程得到的估计误差驱动自适应算法,通过迭代对滤波权值进行调整,使滤波器处于最佳工作状态以实现滤波过程。
该自适应算法是优化后的最陡下降法,该算法下为:
| $ \mathit{\boldsymbol{e}}\left( n \right) = \mathit{\boldsymbol{d}}\left( n \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{x}}\left( n \right) $ | (14) |
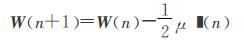
|
(15) |
式中:μ为梯度步长,▍(n)为梯度量,
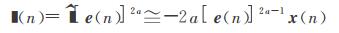
|
(16) |
由以上三式可得出:
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + \mu a{\left[ {\mathit{\boldsymbol{e}}\left( n \right)} \right]^{2a - 1}}\mathit{\boldsymbol{x}}\left( n \right) $ | (17) |
为了减少计算量, 将滤波器的输入信号x(n)截断为1或-1,同时用误差项的高阶矩作为新的误差项,该算法在实际使用时将a值取为2,则式(17) 变为:
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + 2\mu {\left[ {\mathit{\boldsymbol{e}}\left( n \right)} \right]^3} \cdot {\mathop{\rm sgn}} \left[ {\mathit{\boldsymbol{x}}\left( n \right)} \right] $ | (18) |
误差项的最高次数为3,进而达到限制迭代过程计算量的效果。
自适应算法的计算过程如下:
① 由时刻n的滤波器加权系数W(n)、输入信号x(n)以及理想信号d(n)按式(14) 计算误差信号;
② 利用式(17) 的递归算法计算滤波器权向量的更新值;
③ 将时间指数n增加1,回到步骤①,重复上述计算步骤直到达到稳态为止。
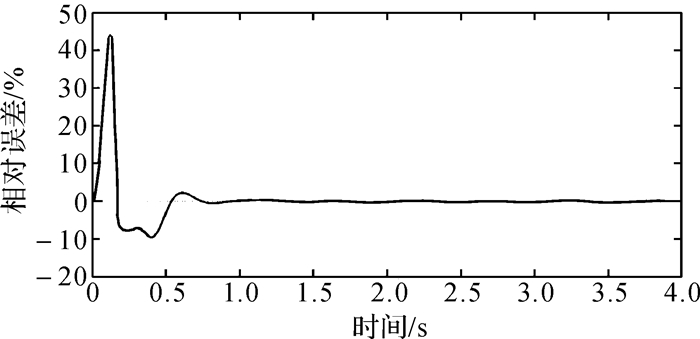
采用CLMK自适应算法,滤波器参数M=32,μ=0.01,输入2 Hz正弦信号。通过分析计算,可以得到仿真算法迭代时的跟踪相对误差曲线,如图 9所示。可以看出,该算法收敛速度快,且收敛后的稳态误差小。
|
| 图 9 CLMK算法下相对误差曲线 Fig.9 Relative error curve under CLMK algorithm |
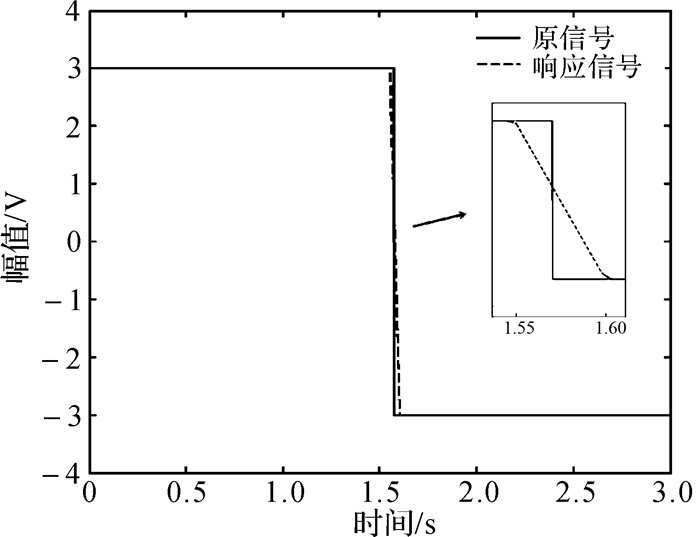
为测试闭环系统的稳定性及动态特性,向系统输入幅值为3 V的方波信号,系统响应曲线如图 10。
|
| 图 10 方波输入下响应曲线 Fig.10 Response curve with square wave input |
可以看出该系统响应速度快,动态特性好且稳态输出非常理想。
3 系统性能验证 3.1 验证实验设计实验对象:10名年龄为19~26岁的大学生。
实验设备:被试设备为本系统,检测设备为天津市天中依脉科技开发有限公司生产的脉象采集仪(津械注准20152270070)。
实验方式:1) 被试者先静坐2 min左右并保持平静心态,端坐于采集端前,手臂与心脏处于同一高度,取脉位置为受试者桡动脉关部;2) 分别由检测设备和该系统开始采集,并确定最佳取脉压力及对应脉象数据;3) 将系统脉象采集端数据传输到复放端进行复放,并由检测设备用相同的方式于仿生手桡动脉关部采集复放脉象的数据;4) 对比检测设备输出的2种脉图,并分析两者的相关性。
3.2 脉象信号处理分析 3.2.1 特征参数分析分别对采集脉象和复放脉象的10组最佳取脉压力数据进行统计分析,得到最佳取脉压力、主波幅值、降中峡幅值、重搏波幅值、升支时间、脉率等脉象特征参数,表 1以“均值±方差”的形式列出。
| 参数 | 采集脉象 | 复放脉象 |
| 最佳取脉压力/g | 110.30±12.21 | 115.10±13.42 |
| 主波幅值/mm | 21.54±12.77 | 20.99±11.87 |
| 降中峡幅值/mm | 9.94±8.96 | 12.28±8.43 |
| 重搏波幅值/mm | 13.02±7.21 | 11.04±6.78 |
| 升支时间/s | 0.095 317±0.066 3 | 0.074 813±0.060 1 |
| 脉率/(次/min) | 83.30±17.94 | 83.30±18.84 |
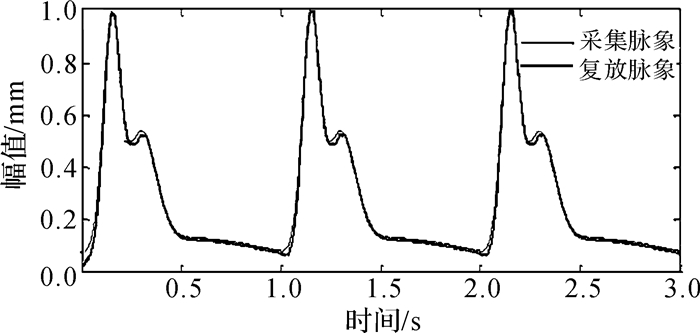
以被试者2为例,示出采集和复放脉波图对比,如图 11所示。
|
| 图 11 被试者2脉图对比 Fig.11 Comparison of No.2 testees pulse waveform |
由图 11可以直观地看出复放脉象与采集脉象相比,其还原度很高。
3.2.2 t-检验分析对上述最佳取脉压力和脉象特征参数进行双样本等方差假设的t-检验分析,结果如表 2所示。
| 参数 | P(T≤t)单尾 | P(T≤t)双尾 |
| 最佳取脉压力 | 0.479 37 | 0.935 56 |
| 主波幅值 | 0.486 54 | 0.976 62 |
| 降中峡幅值 | 0.452 14 | 0.932 56 |
| 重搏波幅值 | 0.443 28 | 0.911 31 |
| 升支时间 | 0.415 64 | 0.926 63 |
| 脉率 | 0.464 95 | 0.934 79 |
采用统计学中的Pearson系数[16]r检验复放脉象与原始脉象数据的相关性[17]。r的计算公式为:
| $ r = \frac{{\sum {\left( {X - \bar X} \right)\left( {Y - \bar Y} \right)} }}{{\sqrt {\sum {{{\left( {X - \bar X} \right)}^2}{{\left( {Y - \bar Y} \right)}^2}} } }} $ | (19) |
Pearson相关系数r的取值范围为[-1,1],其中r的正负分别表示正相关和负相关,其绝对值|r|大小表示两者相关程度的大小。|r|的取值与相关程度的关系如表 3。SPSS计算检验[18]结果见表 4。
| |r|的取值范围 | 相关程度 |
| 0.00~0.20 | 极低 |
| 0.20~0.40 | 低度 |
| 0.40~0.70 | 中度 |
| 0.70~0.90 | 高度 |
| 0.90~1.00 | 极高 |
| 被试者 | Pearson系数 |
| 被试者1 | 0.930 |
| 被试者2 | 0.931 |
| 被试者3 | 0.923 |
| 被试者4 | 0.922 |
| 被试者5 | 0.919 |
| 被试者6 | 0.933 |
| 被试者7 | 0.923 |
| 被试者8 | 0.932 |
| 被试者9 | 0.927 |
| 被试者10 | 0.929 |
由表 2知P值均大于0.05,说明采集脉象和复放脉象的最佳取脉压力及特征参数无显著性差异,且两者Pearson相关系数|r|>0.91,易知系统复放出的脉象与采集到的被试者脉象具有显著相关性。
3.3 盲测实验另邀请3名老中医对系统进行盲测,即从标准脉象数据库随机抽取脉象以供盲测,经统计3位医师盲测正确率均在93%以上。以上结果证明该系统能够以较高的准确度远程复放人体的脉象信息,可靠性也较高。
4 结束语该系统从仿生学、机械学角度出发,创新性地设计了新型脉象发生器与液压系统相结合的脉象复放系统,兼顾脉象“位、数、形、势”四种属性,加入闭环反馈机制有效修正复放误差,对脉象数据的还原度更高,使用体验更接近真实的切脉体验。在医患彼此“远在天边”的不利条件下也可实现“近在眼前”的实际诊断效果。该系统对于提高中医资源利用率、方便边远地区的群众接受较高层次的中医治疗以及传承和弘扬我国传统医学,具有重要意义。
| [1] |
孙文珊.
跨国界中医远程医疗的迫切性与可行性初探[J]. 内江科技, 2005, 20(2): 52.
SUN Wen-shan. Discussion on the urgency and feasibility of transnational traditional Chinese medicine telemedicine[J]. Neijiang Technology, 2005, 20(2): 52. |
| [2] |
侯小丽, 陈谊秋.
远程医疗的研究现状与发展前景[J]. 中国医疗器械信息, 2013, 13(7): 9–11.
HOU Xiao-li, CHEN Yi-qiu. The application and pro-gress research of tele-medicine[J]. China Medical Device Information, 2013, 13(7): 9–11. |
| [3] |
周露, 文林, 曾荣华.
互联网+中医新模式实现途径探析[J]. 亚太传统医药, 2016, 12(17): 1–2.
ZHOU Lu, WEN Lin, ZENG Rong-hua. Realization ap-proach of Chinese Medicine through Internet technology[J]. Asia-Pacific Traditional Medicine, 2016, 12(17): 1–2. |
| [4] |
汤伟昌, 孙汉钧, 徐建国, 等.
中医脉象模拟系统的研究[J]. 中国中医基础医学杂志, 2000, 6(1): 62–65.
TANG Wei-chang, SUN Han-jun, XU Jian-guo, et al. Study on pulse simulation system of traditional Chinese Medicine[J]. Chinese Journal of Basic Medicine in Tra-ditional Chinese Medicine, 2000, 6(1): 62–65. |
| [5] |
王学民, 王槿, 陈枫, 等.
中医脉象教学考试仪的研究[J]. 医疗卫生装备, 2007, 28(6): 1–2.
WANG Xue-min, WANG Jin, CHEN Feng, et al. Re-search on teaching and testing machine for traditional Chinese medicine pulse-taking[J]. Chinese Medical E-quipment Journal, 2007, 28(6): 1–2. |
| [6] |
肖香群, 王忆勤, 汤伟昌, 等.
新型中医脉象模拟系统的研制[J]. 辽宁中医杂志, 2011, 38(9): 1726–1728.
XIAO Xiang-qun, WANG Yi-qin, TANG Wei-chang, et al. New-TCM pulse condition simulation system de-velopment[J]. Liaoning Journal of Traditional Chinese Medicine, 2011, 38(9): 1726–1728. |
| [7] |
苏志毅, 赵伟, 黄松岭.
多传感器信息融合技术在现代测量领域的地位和重要作用[J]. 电测与仪表, 2013, 50(3): 1–5.
SU Zhi-yi, ZHAO Wei, HUANG Song-ling. The status and importance of multi-sensor information fusion in the field of modern measuring[J]. Electrical Measurement & Instrumentaation, 2013, 50(3): 1–5. |
| [8] |
余翀, 高翔, 邱其文.
基于多传感器数据融合的机器人里程计设计与实现[J]. 传感技术学报, 2012, 25(1): 53–57.
YU Chong, GAO Xiang, QIU Qi-wen. Design and im-plementation of robot odometer based on multisensor data fusion[J]. Chinese Journal of Sensors and Actuators, 2012, 25(1): 53–57. |
| [9] | DONG Jiang, ZHUANG Da-fang, HUANG Yao-huan, et al. Advances in multi-sensor data fusion:algorithms and applications[J]. Sensor, 2009, 9(10): 7771–7784. DOI:10.3390/s91007771 |
| [10] |
徐学军. 人体脉象建模及脉诊仿真研究[D]. 长沙: 中南大学计算机科学与技术系, 2010: 111.
XU Xue-jun.Research on modeling and simulation of pulse[D]. Changsha:Central South University, De-partment of Computer Science and Technology, 2010:111. |
| [11] |
程方荣, 刘婉华用.
Poiseuille定律探讨血液的流动特性[J]. 河南中医学院学报, 2003, 18(5): 18–19.
CHENG Fang-rong, LIU Wan-hua. A discussion on the flowing features of blood by applying the Poiseuille law[J]. Journal of Henan University of Chinese Medi-cine, 2003, 18(5): 18–19. |
| [12] |
王学民, 杨成, 陆小左, 等.
基于中医脉象的桡动脉血管模型的建立[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(6): 487–492.
WANG Xue-min, YANG Cheng, LU Xiao-zuo, et al. Model of radial artery based on human pulse[J]. Journal of Tianjin University (Science and Technology), 2013, 46(6): 487–492. |
| [13] |
王学民, 宋鹏, 周鹏, 等.
基于多传感器技术的中医脉象复放系统[J]. 传感技术学报, 2013, 26(11): 1604–1609.
WANG Xue-min, SONG Peng, ZHOU Peng, et al. System of traditional Chinese Medicine pulse replay system based on multi-sensor technology[J]. Chinese Journal of Sensors and Actuators, 2013, 26(11): 1604–1609. DOI:10.3969/j.issn.1004-1699.2013.11.024 |
| [14] |
费兆馥.
现代中医脉诊学[M]. 北京: 人民卫生出版社, 2006: 61-76.
FEI Zhao-fu. Modern TCM pulse diagnostics[M]. Bei-jing: People's Medical Publishing House, 2006: 61-76. |
| [15] |
陈浩, 吴定定, 饶国希, 等.
电动负载模拟系统自适应控制系统设计[J]. 工程设计学报, 2017, 24(2): 218–223.
CHEN Hao, WU Ding-ding, RAO Guo-xi, et al. Design of adaptive control system of electric load simu-lation system[J]. Chinese Journal of Engineering De-sign, 2017, 24(2): 218–223. |
| [16] | BLAND J M, ALTMAN D G. Statistical methods for assessing agreement between two methods of clinical measurement[J]. Lancet, 1986, 75(1): 931–936. |
| [17] |
曲淼, 唐启盛, 裴清华, 等.
运用相关性分析方法探讨抑郁症中医核心病机的研究[J]. 北京中医药大学学报, 2011, 34(8): 565–568.
QU Miao, TANG Qi-sheng, PEI Qing-hua, et al. Ker-nel TCM pathogenesis of depression investigated with correlation analysis[J]. Journal of Beijing University of Traditional Chinese Medicine, 2011, 34(8): 565–568. |
| [18] |
魏善发.
基于SPSS软件分析上海市金山区地表水污染特征[J]. 中国环境监测, 2013, 29(1): 75–81.
WEI Shan-fa. Based on SPSS software to analyze char-acteristics of surface water pollution, Jinshan District, Shanghai[J]. Environmental Monitoring in China, 2013, 29(1): 75–81. |



