高速干切滚齿工艺是一种在加工过程中不使用冷却液或润滑剂,滚刀以很高的切削速度对齿坯进行加工的方法,该工艺既绿色又高效,是未来齿轮滚切发展的重要方向[1]。相对于普通滚齿,高速干切滚齿加工并非简单地将普通滚齿机的转速提高和关断切削液系统,而需在切削加工机理、机床设计技术、刀具技术及工艺技术上加以突破改进。目前国内外针对高速干式滚齿,在切削机理、机床设计、刀具设计等方面研究较多[1-5],而对滚齿加工过程工艺优化方面研究较少。随着低碳制造这一新制造模式的提出,机床制造及齿轮加工过程碳排放量指标受到高度重视[6]。在滚齿工艺的应用中,工艺参数的决策和优化是提升齿轮滚切加工效率和工艺性能的重要措施,工艺参数如何决策和优化以达到高效低碳的目标,已成为发展和推广高速干切滚齿工艺技术必须解决的关键问题之一,本文将对高速干切滚齿加工的工艺参数低碳优化决策进行研究。
国内外研究人员提出了多种工艺参数决策和优化的方法。Cus等[7]以生产效率最大化为目标,运用改进遗传算法对切削参数进行优化。Bhushan[8]以最低能耗和最长刀具寿命为优化目标,研究了车削铝合金SiC复合材料时的切削参数优化。Yan等[9]基于加权灰色关联分析和响应面方法构建以材料去除率、表面粗糙度、能耗最小的多目标铣削参数优化模型。Lu等[10]利用灰色关联分析和主成分分析方法来获取高速端铣的粗切削的最优切削参数组合。蒋亚军等[11]利用粗糙集理论规则学习算法优化变量,采用遗传算法求解切削参数的最优值。刘海江等[12]引入协调系数构建了以最大生产率和最低生产成本为目标的优化模型,并釆用粒子群算法对模型进行寻优求解。张正旺等[13]集成主轴系统动态行为与工艺参数交互影响特性来构建模型, 采用人工蜂群算法求解,得到最优铣削工艺参数。张明树等[14]利用图论工具获取工艺实例过滤集,以加工效果相对最优为目标,通过模糊TOPSIS多属性决策获取最优高速切削工艺参数。李聪波等[15]提出一种基于田口法和响应面法的数控铣削工艺参数能效优化方法。然而,在工艺参数优化方面,上述研究大部分是针对车削、铣削及传统湿式滚齿,并以加工时间、加工质量或者加工成本等为优化目标的,少部分以能耗为优化目标;在决策方法方面,主要依靠的是工艺人员的经验和专家打分的定性方法或模糊评价法,对工艺人员和专家存在一定的主观依赖性。高速干式滚齿切削作为先进加工技术,其涉及复杂的成形运动关系及几何成形过程,与普通切削模型相比有许多不确定的因素, 且解析难度大,又缺乏有效、实用的切削参数工艺数据库,故工艺参数的拟定一般是基于原有湿式切削加工过程中的切削参数作相应的修改和调整,但是传统湿式滚齿与高速干式滚齿的加工条件不同,它的工艺参数未必适用于高速干式滚齿,且加工用时较长;或者依据工艺手册、个人经验、切削加工实验总结来实施,但易受工艺人员的加工经验和技术影响,且工艺手册数据取值保守,难以充分发挥高速干式滚齿机的加工能力。
鉴于此,本文以高速干切滚齿切削为研究对象,针对待决策工艺问题,基于高速干切滚齿工艺实例,利用BP神经网络构建加工效果评价值的预测模型。然后利用改进K-means聚类算法获取与待决策工艺问题对应的相似实例抽取集,得到相应的工艺解决方案,构建待优化工艺参数约束范围。最后运用花朵授粉算法,构建高速干切滚齿碳耗计算模型,以碳耗最小为优化目标,并以训练好的BP神经网络为目标函数变量解算器,相似实例抽取集中工艺解决方案的工艺参数值范围为约束,搜索与待决策工艺问题匹配的最优工艺参数。
1 BP神经网络预测模型的生成 1.1 问题描述将基于实例推理的工艺参数优化决策问题记为Tdec=(D, P),其中D={d1, d2, …, dq1}为高速干切滚齿加工待决策工艺问题,P={P1, P2, …, Pg}为决策所需的高速干切滚齿工艺实例集,实例集中每个工艺实例具有三大类属性集,包括工艺问题描述属性集、工艺解决方案集、加工效果评价属性集,分别记为mj={mi, 1, mi, 2, …, mi, q1},vk={vi, 1, vi, 2, …, vi, q2},en={ei, 1, ei, 2, …, ei, q3},其中:i为实例编号;j≤q1,k≤q2,n≤q3,均为正整数。
1.2 BP神经网络构建BP神经网络是目前应用广泛的一种网络模型,其具有出色的非线性逼近能力,用于预测模型的建立[16]。以待决策工艺问题为研究对象、高速干切滚齿工艺实例集为样本数据集,建立BP神经网络加工效果评价值的预测模型。
齿数、模数、齿宽、压力角、螺旋角、工件外径和切齿深度为工艺问题的描述属性,滚刀主轴转速、轴向进给速度、滚刀头数和滚刀直径为工艺解决方案中的工艺参数。以上述工艺问题描述属性值和工艺解决方案中工艺参数值为输入参数,以实例的加工效果评价值即加工时间、能源消耗为输出参数,高速干切滚齿加工的BP神经网络结构模型如图 1所示。

|
| 图 1 高速干切滚齿加工的BP神经网络结构图 Fig.1 Structure graph of BP neural networks for high-speed dry hobbing machining |
隐含层节点数由式(1)[17]计算,具体值由BP网络测试性能确定。
| $ {\rm{Imp}} = \sqrt {{\rm{Inp + Outp}}} + {\rm{Con}} $ | (1) |
式中:Imp,Inp,Outp分别为隐含层、输入层和输出层的节点数;Con为整数,1 < Con < 10。
为了保证BP网络性能的稳定性,需对样本值进行归一化处理,限定在(-1,1) 范围内,按公式(2) 进行转换[18]。
| $ d' = \frac{{d - {d_{\min }}}}{{{d_{\max }} - {d_{\min }}}} \times 0.9 + 0.05 $ | (2) |
式中:d,d′分别为转换前后的值;dmax,dmin分别为样本值转换前的最大值、最小值;0.05为避免输出量落在饱和区的常数。
2 相似实例抽取集的生成快速K中心点聚类算法[19]是一种改进的K-means算法, 计算数据集中两两样本点间的距离,选择距离较近的样本作为初始中心点,相对于K-means算法, 其避免了对初始中心点选取的过度依赖,既提高了算法的聚类效果,又缩短了计算耗时[20]。本文采用该改进的K-means算法对高速滚齿干切工艺实例集进行划分,并抽取与待决策工艺问题最相近的工艺实例抽取集。
数据集中两两样本点间的距离,即任意2个工艺实例Pi和Pj的相似程度,采用加权欧式距离定量描述,定义为:
| $ S\left( {{P_i},{P_j}} \right) = \sqrt {\sum\limits_{k = 1}^{{q_1}} {{w_k}{{\left( {{m_{ik}} - {m_{jk}}} \right)}^2}} } $ | (3) |
式中:S(Pi, Pj)为Pi和Pj的相似度,S(Pi, Pj)越小,则工艺实例Pi和Pj的相似度越大;wk是工艺实例中第k项工艺问题描述属性的权重系数,其越重要,wk越大。
针对决策所需的历史工艺实例集, 采用快速K中心点聚类算法进行聚类,抽取与待决策工艺问题匹配度最高的最近工艺实例相似组,如图 2所示快速K-means聚类抽取流程如下:

|
| 图 2 快速K-means聚类抽取流程图 Fig.2 Flow diagram of fast K-means clustering extraction |
步骤1:初始化中心点,计算工艺实例集P={P1, P2, …, Pg}中的两两实例之间的相似度S(Pi, Pj),按公式(4) 计算工艺实例集中任意一个实例Pi对应的Fi的值,按Fi值对实例进行升序排列,选择前k个实例作为初始中心点P′=Oi(i=1, 2, …, k)。
| $ {F_i} = \sum\limits_{j = 1}^g {\frac{{S\left( {{P_i},{P_j}} \right)}}{{\sum\limits_{i = 1}^g {S\left( {{P_i},{P_j}} \right)} }}} ,i = 1,2, \cdots ,g $ | (4) |
步骤2:首次聚类,对工艺实例集P中的所有Pj(j=1, 2, …, g),依次计算Pj到各簇中心Oi的距离,找到Pj关于Oi的最小距离Smin=min{S(Oi, Pj)},将Pj添加到Smin对应的类簇,形成k个工艺实例相似组G={G1, G2, …, Gk}, G∈P,并按公式(5) 计算其误差平方和:
| $ J = \sum\limits_{i = 1}^k {\sum\limits_{{G_j} \in {P_j}} {{{\left\| {{P_j} - {O_i}} \right\|}^2}} } $ | (5) |
步骤3:聚类中心点更新,针对步骤2中的k个工艺实例相似组,逐一更新其中心点。计算相似组中每一个实例与其他实例的相似度,选择相似度最高的实例作为新的中心点。
步骤4:更新实例相似组,将实例集中的实例分配到与其距离最近的聚类中心点所在的类簇中,计算误差平方和,若误差平方和与步骤2计算的误差平方和相同,则聚类结束,否则转到步骤3继续执行。
步骤5:迭代结束后,输出结果,即工艺实例相似组G={G1, G2, …, Gk}和最新的聚类中心点O′i(i=1, 2, …, k)。
步骤6:计算各聚类中心与待决策工艺问题的相似度,存在Ci使S(Ci, D)取得最小值,则Ci所在工艺实例相似组Gi为D的最近工艺实例相似组,即相似实例抽取集。
3 工艺参数低碳优化决策 3.1 花朵授粉算法花朵授粉算法[21]是剑桥大学的Yang受花朵授粉过程的启发而提出的一种具有全局收敛性的新型搜索算法,其具有参数少、操作简单、易实现、随机搜索路径和寻优能力强等优点。
花朵授粉算法是模拟自然界中显花植物花朵授粉的过程,有全局授粉和局部授粉两种方式,考虑物理上的邻近性和风等因素,花粉授粉更容易在邻近花间发生。为了有效模拟该特性,定义转换概率p∈[0, 1],由p值控制2种授粉方式之间的转换,为使选择局部授粉方式的概率大些,取初始转换概率p=0.8[22]。
全局授粉的位置变化更新算数方程式如公式(6) 所示:
| $ X_i^{t + 1} = X_i^t + \gamma L\left( \lambda \right)\left( {{g^ * } - X_i^t} \right) $ | (6) |
式中:Xit+1,Xit分别是花粉配子i在第t+1次迭代、第t次迭代的位置;γ是控制步长的比例因子;g*是当前所有迭代结果中的最优解;L是步长,携粉者如昆虫可能以各种步长移动一大段距离。
Levy飞行可以有效地模拟这种特性,L > 0, 并且符合公式(7) 所示关系:
| $ L \sim \frac{{\lambda \Gamma \left( \lambda \right)\sin \left( {{\rm{\pi }}\lambda /2} \right)}}{{\rm{\pi }}}\frac{1}{{{s^{1 + \lambda }}}}\left( {s \ge {s_0} \ge 0} \right) $ | (7) |
式中:Γ(λ)是标准的伽马函数;s指步数,s0指步数的最小值,s0=0.1。
局部授粉的位置变化更新算数方程式如公式(8) 所示:
| $ X_i^{t + 1} = X_i^t + \varepsilon \left( {X_j^t - X_k^t} \right) $ | (8) |
式中:ε为均匀分布U(0, 1) 上的随机数;Xjt,Xkt指邻近花朵配子j,k的第t次迭代的位置。
花朵授粉算法求解基本流程如图 3所示。

|
| 图 3 花朵授粉算法求解基本流程图 Fig.3 Basic flow chart of FPA solving |
在高速干切滚齿切削技术推广应用中,其工艺参数确定是一个亟待解决的难题。在工艺参数决策中,需要确定的变量有滚刀头数、滚刀直径、滚刀精度、滚刀升角、滚切方式、切削速度、轴向进给速度、滚刀主轴转速和窜刀量,其中,滚刀头数、滚刀直径、轴向进给速度、滚刀主轴转速对加工效果影响显著, 因此优化变量确定为滚刀头数、滚刀直径、轴向进给速度和滚刀主轴转速。
3.2.2 优化目标函数的确定以碳耗最小为优化目标,加工过程的碳耗从能源流和物料流的角度考虑。故高速干切滚齿工艺主要考虑的碳耗有:机床耗能、刀具损耗、原材料消耗。由于相同齿坯加工成同一成品所消耗的原材料及切削处理所产生的碳排放相同,优化变量值的不同会影响机床耗能和刀具损耗,其中机床耗能主要是电机耗能。故为简化计算,目标函数碳耗可认为是电机能耗引起的碳排放和刀具损耗引起的碳排放的总和。
1) 电机能耗引起的碳排放,包括轴向进给电机能耗、主轴电机能耗和工作台电机能耗等。高速干切滚齿加工过程由于能源消耗而引起的碳排放计算方法为:
| $ {C_{\rm{e}}} = {\rm{E}}{{\rm{F}}_{\rm{e}}} \cdot {\rm{E}}{{\rm{C}}_{\rm{e}}} $ | (9) |
式中:Ce指能源消耗引起的碳排放,kgCO2;ECe指能源消耗量,kW·h;EFe指电能的碳排放因子,kgCO2/kWh,EFe值可根据中国国家发展和改革委员会公布的2014年中国区域电网基准排放因子确定,见表 1所示。
| 区域 | EFgrid, OM,y / (tCO2/MWh) |
EFgrid, BM,y/ (tCO2/MWh) |
| 华北区域电网 | 1.058 0 | 0.541 0 |
| 东北区域电网 | 1.128 1 | 0.553 7 |
| 华东区域电网 | 0.809 5 | 0.686 1 |
| 华中区域电网 | 0.972 4 | 0.473 7 |
| 西北区域电网 | 0.957 8 | 0.451 2 |
| 南方区域电网 | 0.918 3 | 0.436 7 |
表中EFgrid, OM, y是第y年电量边际CO2排放因子,EFgrid, BM, y是第y年容量边际CO2排放因子,取EFe=
2) 刀具损耗产生的碳排放, 包括很少的直接碳排放和较多的间接碳排放。间接碳排放是在生产刀具成品中产生的。故刀具损耗产生的碳排放可以考虑其在使用过程的分摊,按公式(10) 计算:
| $ {C_t} = \frac{{{t_{\rm{c}}}}}{{{T_{\rm{t}}}}} \times {\rm{E}}{{\rm{F}}_{\rm{t}}} \times {{\rm{W}}_{\rm{t}}} $ | (10) |
式中:Ct指刀具使用产生的碳排放;tc指单件齿轮滚齿加工时间,是单件工件切削时间、快进时间、辅助时间的总和,min;Tt指所用刀具的寿命,min;EFt指所用刀具碳排放因子,kgCO2/kg;Wt指所用刀具的质量,kg。
Tt根据所用刀具类型和工厂实际使用经验取值,Wt通过实测得到。考虑刀具生产工艺过程的能耗情况,得出刀具制造过程的刀具碳排放因子为29.6 kgCO2/kg[23],本文采用此值EFt=29.6 kgCO2/kg。因此,目标函数碳耗表达式为:
| $ {C_P} = {C_{\rm{e}}} + {C_{\rm{t}}} = {\rm{E}}{{\rm{F}}_{\rm{e}}} \cdot {\rm{E}}{{\rm{C}}_{\rm{e}}} + \frac{{{t_{\rm{c}}}}}{{{T_{\rm{t}}}}} \times {\rm{E}}{{\rm{F}}_{\rm{t}}} \times {{\rm{W}}_{\rm{t}}} $ | (11) |
切削参数的取值通常受到机床、刀具、加工条件等各种技术条件的限制,且切削参数优化要考虑整个工艺系统和加工效果。对于高速切削,通常选取加工时间、产品质量、加工成本、资源消耗、环境影响作为评价整个工艺系统和加工效果的属性集[14]。加工时间的评价指标包括切削时间和辅助时间;产品质量的评价指标主要是齿轮精度;加工成本的评价指标包括刀具成本、设备成本、场地成本、能耗成本和人工成本等;资源消耗的评价指标包括原材料消耗和能源消耗等;环境影响的评价指标包括噪声、安全性、废料和废液等。由于相似实例抽取集内实例的工艺问题和待决策工艺问题相似度高,其原材料消耗相当,对资源消耗的评价就只考虑能源消耗;在同一设备和场地下,资源消耗已考虑能源消耗,故成本只考虑刀具成本;环境影响主要是废弃物的污染,由于高速干切滚齿工艺不使用切削液,环境影响较小,环境影响的评价不予考虑。
综上,将齿轮表面粗糙度、加工时间、刀具成本、能源消耗作为评价高速干切滚齿整个工艺系统加工效果的指标。由于实例是经过加工验证的,其中工艺参数设定值和加工效果评价值均满足生产要求和评价要求。故本文以相似实例抽取集中工艺解决方案中工艺参数值的范围和加工效果评价值的范围作为优化模型的约束条件。
3.3 工艺参数低碳优化模型的求解为简化问题,假设一个花粉配子对应优化问题中的一个解,将每个花朵初始化一组工艺参数,即Xi=[X1, X2, …, XD],i=1, 2, …, D,其中D表示需优化工艺参数的数量。优化变量有4个,为滚刀头数X1、滚刀直径X2、滚刀主轴转速为X3和轴向进给速度X4,其同时为上述BP神经网络模型输入层参数,对应的输出层参数有2个,设加工时间为y1、能量消耗为y2,假设gj[M, X1, X2, X3, X4]为反映BP神经网络模型输入层参数与输出层参数j的非线性映射关系函数,其中M是由描述属性下参数具体值包括齿数、模数、压力角、螺旋角、齿宽、工件外径、切齿深度七个参数构成的1×7维矩阵,BP神经网络关系函数为:
| $ \left\{ \begin{array}{l} {y^1} = {g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right]\\ {y^2} = {g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] \end{array} \right. $ | (12) |
由公式(11) 可知优化目标函数为:
综上,构建的工艺参数低碳优化的数学模型为:
| $ \begin{array}{*{20}{c}} {\min \left\{ {1.169{g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] + } \right.}\\ {\left. {29.6{g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right]\frac{{{{\rm{W}}_{\rm{t}}}}}{{{T_{\rm{t}}}}}} \right\}}\\ {{{\left( {{X_{i{P_j}}}} \right)}_{\min }} \le {X_i} \le {{\left( {{X_{i{P_j}}}} \right)}_{\max }}}\\ {{g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] \le {{\left( {{g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right]} \right)}_{{\rm{req}}}}}\\ {{g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] \le {{\left( {{g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right]} \right)}_{{\rm{req}}}}} \end{array} $ |
其中:Xi为花朵配子在种群中的位置值;(XiPj)min,(XiPj)max分别为与待决策问题对应的抽取相似实例抽取集里工艺实例Pj的工艺参数Xi的最小值、最大值;(g1[M, X1, X2, X3, X4])req,(g2[M, X1, X2, X3, X4])req为待决策工艺问题指定的最低加工要求标准对应的值。
因此,高速滚齿干切工艺参数低碳优化决策流程如图 4所示,步骤如下:

|
| 图 4 高速干切滚齿工艺参数低碳优化决策流程 Fig.4 Low carbon optimization decision flow for high-speed dry hobbing process parameters |
步骤1:待决策工艺问题任务下达,利用快速K-means聚类获取相似实例抽取集,获取相应的工艺解决方案具体值。
步骤2:以采集到的高速干切滚齿工艺实例集为样本,利用BP神经网络构建加工效果评价值预测模型。
步骤3:设定花朵授粉算法控制参数,包括种群规模N、最大迭代次数T、转换概率p和Levy飞行控制参数。
步骤4:随机初始化花朵种群初始位置,得到一个N×D维矩阵,由于优化参数有4个,故D=4;矩阵中数值在方程组(12) 约束范围内,利用碳耗表达式和调用BP神经网络模块计算目标函数值,记录种群中的最优解。
步骤5:如果rand < p,绘制一个d维矢量L,且该矢量服从Levy分布,使花粉配子通过全局授粉公式(6) 迭代;否则绘制ε,ε是在[0, 1]均匀分布的随机数,使花粉配子通过局部授粉公式(8) 进行迭代。
步骤6:位置更新后,再次调用BP神经网络模块,评测新解,如果新解好,则在种群中更新g*,从而得出一组较优的解;如果t < T, 则返回步骤3。否则,迭代结束。
步骤7:找出当前新解的最优位置g*和对应的最优值F(X)min,并输出找到的最优解Xbest,最优解即为待决策工艺问题的最优工艺参数。
4 实例验证采集某制齿机床制造企业研发的数控高速干切滚齿机YE3120CNC7的工艺实例样本,如表 2所示,实例规模为60个,齿轮精度为7级,齿轮材料为40Cr,所用滚刀为TiAIN涂层滚刀,滚刀库中滚刀参数规格包括:滚刀直径为70,75,80,85 mm;滚刀头数有1,2,3。该机床是七轴四联动环保型数控滚齿机,最大加工模数为4 mm,最大加工直径为210 mm,主轴最高转速达2000 r/min。
| 实例编号Pi | 工艺问题描述属性 | 工艺解决方案工艺参数 | 加工效果值 | ||||||||||||
| 齿轮齿数 | 齿轮模数 /mm |
齿轮压力角 /(°) |
齿轮螺旋角 /(°) |
齿宽 /mm |
工件外径 /mm |
切齿深度 /mm |
滚刀头数 | 滚刀直径 /mm |
滚刀主轴转速/(r/min) | 轴向进给速度/(mm/min) | 加工时间 /min |
能源消耗 /(kW·h) |
|||
| P1 | 51 | 1.65 | 15.5 | 31.25 | 13.0 | 101.5 | 5.42 | 3 | 80 | 680 | 88 | 0.757 7 | 0.080 1 | ||
| P2 | 48 | 2.50 | 20.0 | 17.00 | 23.0 | 131.6 | 5.60 | 2 | 85 | 700 | 73 | 0.937 6 | 0.100 9 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| P60 | 33 | 1.65 | 15.5 | 31.25 | 14.4 | 69.5 | 5.39 | 2 | 80 | 680 | 99 | 0.700 0 | 0.074 0 | ||
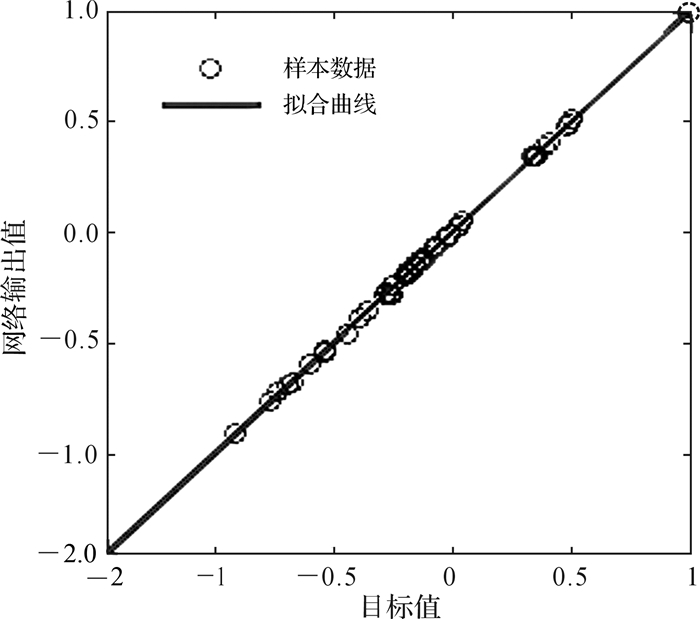
以表 2中的数据为样本,通过MATLAB语言编写程序来实现BP神经网络预测模型的构建。将50个工艺实例作为网络训练的样本,10个工艺实例作为网络检测的测试样本。此时输入层节点数为11,输出层节点数为2,根据公式(1) 可得,当取隐含层节点数为6时训练结果较好,误差曲线见图 5所示,当训练循环次数为6次时,网络收敛到预先设定的目标均方差(mean square error,MSE),为10-8,最佳验证值为0.000 712 96,图 6反映了网络输出与目标值的回归关系,二者的相关系数为0.999 88,表明训练后的神经网络具有非常好的性能,可用于预测加工效果即加工时间、能源消耗的数值。

|
| 图 5 网络训练均方差误差曲线 Fig.5 Mean square error curve of network training |
|
| 图 6 网络训练测试结果回归分析 Fig.6 Regression analysis for test result of network training |
用测试样本对训练好的网络进行测试,网络训练样本的拟合误差均在2%以内,图 7和图 8反映该BP神经网络具有较高的预测精度。

|
| 图 7 加工时间的预测 Fig.7 Processing time prediction |

|
| 图 8 能源消耗的预测 Fig.8 Energy consumption prediction |
待决策工艺问题描述属性具体值:齿数为51,齿轮模数为1.675 mm,齿轮压力角为15.5°,齿轮螺旋角为31.25°,齿宽为14.15 mm,工件外径为106 mm,切齿深度为5.6 mm。对表 2中工艺实例集采用相似实例抽取集生成方法,取k=10,形成10个相似实例组,计算待决策工艺问题与各聚类中心相似度,得到相似实例抽取集,如表 3所示。
| 实例编号Pi | 工艺问题描述属性 | 工艺解决方案工艺参数 | 加工效果值 | ||||||||||||
| 齿轮齿数 | 齿轮模数 /mm |
齿轮压力角/(°) | 齿轮螺旋角/(°) | 齿宽 /mm |
工件外径 /mm |
切齿深度 /mm |
滚刀头数 | 滚刀直径 /mm |
滚刀主轴转速/(r/min) | 轴向进给速度/(mm/min) | 加工时间 /min |
能源消耗 /(kW·h) |
|||
| P1 | 51 | 1.65 | 15.5 | 31.25 | 13.0 | 101.5 | 5.42 | 3 | 80 | 680 | 88 | 0.757 7 | 0.080 1 | ||
| P23 | 51 | 1.675 | 16 | 32 | 13.0 | 106 | 5.731 | 2 | 85 | 720 | 74 | 0.824 0 | 0.089 3 | ||
| P28 | 51 | 1.675 | 16 | 30.75 | 13.8 | 104.7 | 5.435 | 3 | 80 | 700 | 95 | 0.742 9 | 0.079 1 | ||
| P40 | 53 | 1.675 | 16 | 31.5 | 13.8 | 107.7 | 5.65 | 2 | 85 | 740 | 73 | 0.865 8 | 0.091 7 | ||
按照花朵授粉算法对工艺参数低碳优化决策中步骤方法,所用滚刀为TiAIN涂层滚刀,其刀具寿命Tt=2 880 min和刀具质量Wt=2 kg。由上述待决策工艺问题描述属性具体值可知M=[51, 1.675, 15.5, 31.25, 14.15, 106, 5.6],因此优化模型为:
| $ \begin{array}{*{20}{c}} {\min \left\{ {1.169{g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] + } \right.}\\ {\left. {0.0206{g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right]} \right\}}\\ {{X_1} \in \left\{ {2,3} \right\}{X_2} \in \left\{ {80,85} \right\}{\rm{mm}}}\\ {680 \le {X_3} \le 740{\rm{r/min}}}\\ {73 \le {X_4} \le 95{\rm{mm}}/\min }\\ {{g^1}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] \le 0.8658\min }\\ {{g^2}\left[ {\mathit{\boldsymbol{M}},{X_1},{X_2},{X_3},{X_4}} \right] \le 0.0917{\rm{kW}} \cdot {\rm{h}}} \end{array} $ |
花朵授粉算法参数设置如下:设花朵单元数(种群规模)为N=25,最大迭代数为T=100,p=0.8,γ=0.1,λ=1.5,X1,X2,X3,X4四个参数搜索范围见约束条件,且均设为正整数。采用FPA算法进行工艺参数优化, 输出找到的最优解Xbest=[80, 3, 732, 90],对应的最优值F(X)min=0.106 3,其中g1[M, Xbest]=0.732 2, g2[M, Xbest]=0.078,并作其适应度变化曲线如图 9所示,从适应度变化曲线可看出,FPA算法收敛效果好。

|
| 图 9 FPA适应度函数变化曲线 Fig.9 FPA fitness function curve |
将最优解组成的工艺解决方案(滚刀直径为80 mm,滚刀头数为3,滚刀主轴转速为732 r/min,轴向进给速度为90 mm/min),对应的加工效果和碳耗值,以及相似抽取集(表 3) 中实例结果见表 4。
| 加工效果和碳耗值 | P1 | P23 | P28 | P40 | 优化结果 |
| 加工时间/min | 0.757 7 | 0.824 | 0.742 9 | 0.865 8 | 0.732 2 |
| 能源消耗/kW·h | 0.080 1 | 0.089 3 | 0.079 1 | 0.091 7 | 0.078 0 |
| 碳耗/kgCO2 | 0.109 3 | 0.121 4 | 0.107 8 | 0.125 0 | 0.106 3 |
结果表明,将本文提出的高速干切滚齿工艺参数低碳优化决策方法得到的工艺参数应用于待决策工艺问题,所得结果相对于表 3中实例的工艺解决方案,碳耗更低,实现低碳的目标, 表明该方法是可行、有效的。
5 结束语针对高速干切滚齿加工,提出一种基于实例推理和优化算法的工艺参数低碳优化决策方法。该方法首先利用BP神经网络构建加工效果评价值的预测模型,再通过快速K-means聚类算法获取待决策工艺问题的相似实例抽取集,得到相应的工艺解决方案,构建待优化工艺参数的约束范围,最后运用花朵授粉算法,以碳耗最小为目标,以训练好的BP神经网络作为目标函数中变量值的解算器,最终得到待决策工艺问题的最优工艺参数。实例验证了该方法的可行性和有效性。结果表明:一方面,相对于单一基于实例推理的工艺参数决策方法,运用本文方法,碳耗更低,加工效果更好;另一方面,相对于单一基于优化算法的工艺参数决策方法,能够有效利用已有的知识和数据,避免工艺人员在选配工艺参数时花费大量时间去收集所需知识和数据,从而提高参数决策效率,减少了参数决策对工艺人员的依赖。该方法得到的最优工艺参数,既保证加工效果理想又使决策高效,而且有利于高速干切滚齿机的低碳运行,为机械制造企业实施低碳制造奠定了一定的理论基础。
| [1] |
陈永鹏, 曹华军, 李先广, 等.
高速干切滚齿机床热变形误差模型及试验研究[J]. 机械工程学报, 2013, 49(7): 36–42.
CHEN Yong-peng, CAO Hua-jun, LI Xian-guang, et al. Study on modeling and experiment of thermal de-formation error for high-speed dry hobbing machine[J]. Journal of Mechanical Engineering, 2013, 49(7): 36–42. |
| [2] |
周力, 曹华军, 陈永鹏, 等.
基于Deform3D的齿轮高速干式滚切过程模型及性能分析[J]. 中国机械工程, 2015, 26(20): 2705–2710.
ZHOU Li, CAO Hua-jun, CHEN Yong-peng, et al. Process simulation model and performance analysis of high-speed dry gear hobbing based on Deform3D[J]. China Me-chanical Engineering, 2015, 26(20): 2705–2710. DOI:10.3969/j.issn.1004-132X.2015.20.002 |
| [3] |
刘海江, 童荣辉.
干式滚齿刀具的参数化设计及优化[J]. 同济大学学报(自然科学版), 2008, 36(5): 651–654.
LIU Hai-jiang, TONG Rong-hui. Parameterized design of dry hob and its optimization[J]. Journal of Tongji U-niversity (Natural Science), 2008, 36(5): 651–654. |
| [4] | CLAUDIN C, RECH J. Development of a new rapid characterization method of hob's wear resistance in gear manufacturing:application to the evaluation of various cutting edge preparations in high speed dry gear hobbing[J]. Journal of Materials Processing Technology, 2009, 209(11): 5152–5160. DOI:10.1016/j.jmatprotec.2009.02.014 |
| [5] | KADASHEVICH I, BEUTNER M, KARPUSCHEWSKI B, et al. A novel simulation approach to determine thermally induced geometric deviations in dry gear hobbing[J]. Procedia CIRP, 2015(31): 483–488. |
| [6] |
李先广, 杨勇, 李聪波, 等.
面向绿色制造的干式齿轮加工过程碳排放分析[J]. 中国机械工程, 2014, 25(16): 2184–2190.
LI Xian-guang, YANG Yong, LI Cong-bo, et al. Analy-sis of carbon emission in gear dry machining process for green manufacturing[J]. China Mechanical Engineering, 2014, 25(16): 2184–2190. DOI:10.3969/j.issn.1004-132X.2014.16.010 |
| [7] | CUS F, BALIC J. Optimization of cutting process by GA approach[J]. Robotics and Computer-Integrated Manufacturing, 2003, 19(1): 113–121. |
| [8] | BHUSHAN R K. Optimization of cutting parameters for minimizing power consumption and maximizing tool life during machining of Al alloy SiC particle composites[J]. Journal of Cleaner Production, 2013, 39: 242–254. DOI:10.1016/j.jclepro.2012.08.008 |
| [9] | YAN J H, LI L. Multi-objective optimization of milling parameters:the trade-offs between energy, production rate and cutting quality[J]. Journal of Cleaner Produc-tion, 2013, 52: 462–471. DOI:10.1016/j.jclepro.2013.02.030 |
| [10] | LU H S, CHANG C K, HWANG N C, et al. Grey re-lational analysis coupled with principal component anal-ysis for optimization design of the cutting parameters in high-speed end milling[J]. Journal of Materials Pro-cessing Technology, 2009, 209(8): 3808–3817. DOI:10.1016/j.jmatprotec.2008.08.030 |
| [11] |
蒋亚军, 娄臻亮, 李明辉.
基于模糊粗糙集理论的模具数控切削参数优化[J]. 上海交通大学学报, 2005, 39(7): 1115–1118.
JIANG Ya-jun, LOU Zhen-liang, LI Ming-hui. Optimiza-tion of cutting parameters for mold NC machining based on fuzzy and rough set theory[J]. Journal of Shanghai Jiaotong University, 2005, 39(7): 1115–1118. |
| [12] |
刘海江, 黄炜.
基于粒子群算法的数控加工切削参数优化[J]. 同济大学学报(自然科学版), 2008, 36(6): 803–806.
LIU Hai-jiang, HUANG Wei. Computer numerical control machining parameter optimization based on par-ticle swarm optimization[J]. Journal of Tongji Univer-sity (Natural Science), 2008, 36(6): 803–806. |
| [13] |
张正旺, 李爱平, 鲍进, 等.
基于主轴系统动态行为的高速铣削工艺参数优化[J]. 同济大学学报(自然科学版), 2015, 43(1): 113–120.
ZHANG Zheng-wang, LI Ai-ping, BAO Jin, et al. Pa-rameters optimization of high speed milling based on the dynamic behavior of spindle system[J]. Journal of Tongji University (Natural Science), 2015, 43(1): 113–120. |
| [14] |
张明树, 阎春平, 覃斌.
基于图论和模糊TOPSIS的高速切削工艺参数优化决策[J]. 计算机集成制造系统, 2013, 19(11): 2802–2809.
ZHANG Ming-shu, YAN Chun-ping, QIN Bin. High-speed cutting parameters optimization decision based on graph theory and fuzzy TOPSIS[J]. Computer Integrated Manufacturing Systems, 2013, 19(11): 2802–2809. |
| [15] |
李聪波, 肖溱鸽, 李丽, 等.
基于田口法和响应面法的数控铣削工艺参数能效优化方法[J]. 计算机集成制造系统, 2015, 21(12): 3182–3191.
LI Cong-bo, XIAO Qin-ge, LI Li, et al. Optimization method of NC milling parameters for energy efficiency based on Taguchi and RSM[J]. Computer Integrated Manufacturing Systems, 2015, 21(12): 3182–3191. |
| [16] | SADEGHI B H M. A BP-neural network predictor model for plastic injection molding process[J]. Journal of Materials Processing Technology, 2000, 103(3): 411–416. DOI:10.1016/S0924-0136(00)00498-2 |
| [17] |
MATLAB中文论坛.
MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2010: 15-20.
MATLAB Chinese Forum. MATLAB neural networks analysis of 30 cases[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010: 15-20. |
| [18] |
董长虹M.
ATLAB神经网络与应用[M]. 北京: 国防工业出版社, 2007: 60-63.
DONG Chang-hong. MATLAB neural networks and its application[M]. Beijing: National Defense Industry Press, 2007: 60-63. |
| [19] | PARK H S, JUN C H. A simple and fast algorithm for K-medoids clustering[J]. Expert Systems with Appli-cations, 2009, 36(2): 3336–3341. DOI:10.1016/j.eswa.2008.01.039 |
| [20] |
蒋帅K. -均值聚类算法研究[D]西. 安: 陕西师范大学计算机科学学院, 2010: 9-20.
JIANG Shuai. Research on K-means clustering algorithm[D]. Xi'an:Shaanxi Normal University, School of Computer Science, 2010:9-20. |
| [21] | YANG X S.Flower pollination algorithm for global op-timization[C]//International Conference on Unconven-tional Computing and Natural Computation.Berlin, Heidelberg:Springer, 2012:240-249. |
| [22] | YANG X S, KARAMANOGLU M, HE X. Flower pollination algorithm:a novel approach for multiobjec-tive optimization[J]. Engineering Optimization, 2014, 46(9): 1222–1237. DOI:10.1080/0305215X.2013.832237 |
| [23] |
李聪波, 崔龙国, 刘飞, 等.
面向高效低碳的数控加工参数多目标优化模型[J]. 机械工程学报, 2013, 49(9): 87–96.
LI Cong-bo, CUI Long-guo, LIU Fei, et al. Multi-ob-jective NC machining parameters optimization model for high efficiency and low carbon[J]. Journal of Me-chanical Engineering, 2013, 49(9): 87–96. |



