2. 江苏海事职业技术学院, 江苏 南京 211199;
3. 江苏金冠立体停车股份有限公司, 江苏 南通 226003
2. Jiangsu Maritime Institute, Nanjing 211199, China;
3. Jiangsu Jinguan Solid Parking System Engineering Co., Ltd., Nantong 226003, China
经济快速发展、城市规模扩大、人口密度上升、汽车保有量急剧增加以及泊车位供应不足等因素致使城市交通拥堵和停车困难问题日益突出。在此背景下,如何最大限度利用有限土地资源为与日俱增的汽车提供必要的泊车位是城市规划者亟待解决的难题,而基于AGV的平面移动式智能立体停车库的出现,则很好地解决了这一难题。该智能立体停车库类似于自动仓储存储设备,通过AGV、升降电梯以及拖车板等设备协同作用来实现车辆存取及停放功能,具有占地面积少、有效停车数量多、车辆存取自动化程度高、性价比高以及安全可靠性高等优点[1]。在该智能立体停车库中,由于其运行环境复杂多变,AGV在有效避开路径资源竞争和冲突的前提下,需在较短时间内顺利完成车辆的存取及停放任务,这就涉及多AGV协同路径规划问题[2]。
针对多AGV路径规划问题,国内外学者经过多年研究,提出了多种有效方法,如模糊推理系统法[3]、Petri网法[4]、混合多目标遗传算法[5]、分散控制法[6]、时间窗法[7]以及时间窗法与其他启发式算法结合的路径规划方法[8-9]等,如:Majdi等通过引入模糊推理系统和启发式算法,不仅有效解决了多AGV在未知环境中的避障路径规划问题,同时也避免了算法陷入局部最优的问题;Nishi等提出采用Petri网分解法解决AGV系统中的多AGV路径规划问题,并通过仿真实验验证了所提方法的可行性和有效性;Krnjak等针对仓库环境中多AGV路径规划问题,提出了一种基于分散控制策略的多AGV路径规划方法,仿真实验显示,分散控制方法不仅可以有效避免潜在死锁或碰撞冲突,而且表现出较好的稳定性;Balseiro等[10]提出将蚁群算法与时间窗法进行有效结合,并将其运用到带有时间约束的车辆路径规划中,有效解决了物流配送中的车辆路径规划问题。
针对智能立体停车库中多AGV路径规划问题,采用分时利用策略,提出了一种基于动态时间窗的泊车系统路径规划方法。该方法通过将Dijkstra算法和时间窗法有效结合,按照任务优先级高低次序依次为接受任务的AGV规划最短可行路径。为测试所提方法的正确性和有效性,以AGV工作环境模型为研究对象,以安全避障和耗时最少为评价指标,以所提方法为搜索策略,在MATLAB平台上对多AGV存取车过程进行了仿真测试。
1 多AGV工作环境描述由于环境模型是研究智能立体停车库多AGV存取车路径规划问题的基础和前提,因此在研究AGV存取车路径规划过程前,需要先确定AGV的工作环境。针对环境模型,目前常用的建模方法主要有可视图法、栅格法和拓扑法。上述建模方法各有优缺点,其中:可视图法虽然可大大降低建模复杂度,但存在数据冗余度高、优化结果精确度较低等缺陷;栅格法虽然有利于提高建模精度,但存在数据存储空间大、计算程序复杂以及建模效率低等缺陷[11]。基于可视图法和栅格法的优缺点,结合拓扑法构建的模型具有结构紧凑、程序简单、数据存储占用空间小及优化结果精度高等优点,选用拓扑法作为AGV工作环境建模方法,图 1所示为采用拓扑法创建的AGV工作环境模型。P0表示车库入口,P94(与交叉口C2通道重合,此处未标出)表示车库出口,P1至P93为车库泊车位,可用于存放车辆,C1至C6表示车道交叉路口,AGV在此处可完成转向及切换车道操作。

|
| 图 1 AGV工作环境模型 Fig.1 Working environment model of AGV |
为了便于对AGV存取车路径规划过程进行研究,还需对环境模型中的交通路网和AGV作如下处理[12]:1) AGV运行车道为单道双向模式,且宽度方向仅能容纳1台AGV;2) 系统中的AGV在同一时间段内只能接受1项存取车任务,在其执行任务期间,系统分配的其他任务视为无效;3) 为避免与其他AGV发生碰撞事故,需为执行任务的AGV设定一个安全行驶区域,该安全区域可由AGV车体几何尺寸、运行速度以及运行车道几何尺寸等来确定;4) AGV在此模型内匀速行驶,且各AGV运行速度一致,忽略启动、转向、制动以及液压系统举升操作等因素导致的速度变化;5) 在某时刻或某一时间段内,路网中的任一交叉路口和任一行驶路段都只允许1台AGV使用。
2 多AGV路径规划 2.1 优先级策略在多AGV存取车路径规划中,引入优先级策略的目的在于方便系统分配任务、避免多AGV在执行存取车任务期间引发死锁或碰撞冲突以及提高停车系统整体运行效率等。根据系统和平台的不同需要,优先级制定标准有多种,如车辆存取任务的轻重缓急、车辆存取耗时的长短以及车辆存取距离的长短等。基于优先级特点,结合智能立体停车系统需要,以车辆编号大小、任务加载顺序、任务轻重缓急和距离长短为评价指标,分别为每台AGV和每项存取车任务设定优先级。对于系统中AGV的优先级,则由车辆编号大小确定,且AGV优先级高低次序与车辆编号大小成负相关;对于系统中任务的优先级,则由任务加载顺序、任务轻重缓急和距离长短等评价指标综合确定。另外,系统还规定,正在执行存取车任务的AGV的优先级高于空闲AGV的优先级[13]。
2.2 时间窗模型时间窗是指执行存取车任务的AGV从开始进入到离开某个交叉路口或某个路段的整个过程所花费的时间,其主要作用是对AGV已占用的交叉路口或行驶路段进行标记,以避免在该AGV占用的时间段内,被其他AGV使用而引发死锁或碰撞冲突[14-15]。假设系统有n台AGV,当前分配任务有m项,且m项任务需指派m台AGV完成。对于系统中的AGV、接受任务的AGV、存取车任务请求指令、优先级策略处理后的存取车任务以及任务的起点和目标点可分别用集合N、集合Q、集合M、集合A、集合S和集合R表示,即N={n1,n2,n3,…,nn},Q={q1,q2,q3,…,qm},M={m1,m2,m3,…,mm},A ={a1,a2,a3,…,am},S={s1,s2,s3,…,sm},R={r1,r2,r3,…,rm}。对于任意一项存取车任务mi,系统首先会按照优先级高低次序为其排序和分配AGV;然后调用Dijkstra算法为接受该任务的AGV(其编号可用qi表示)规划出一条距离最短的路径,该路径由一系列运行路段组成,可用有序路段集合λi表示,λi = {e1i, e2i, …, eki, …, eqi},e1i, e2i, …, eki, …, eqi ∈E,其中,eki表示路段ek在某时刻被任务mi占用,E表示路网中所有可行路段的集合;为避免执行任务mi的AGV与其他AGV因争夺路径资源而引发死锁或碰撞冲突,系统最后利用时间窗法为该可行路径上的各有序路段插入合理、连续的时间窗。在实际应用中,由于可行路径的任意有序路段ek需要被AGV分时使用,因此,有序路段ek也是由一系列时间窗组成,可用有序向量Xk={ω1k,ω2k,…,ωk}表示。另外,由于任务mi是由一系列有序路段组成的,而每条有序路段又对应着一个时间窗,因此,任务mi也可被认为是由一系列时间窗组成的,可用集合Di = {X1i, X2i, …, Xki…, Xqi}表示。
图 2所示为执行任务mi的AGV使用的交叉路口时间窗模型,图中阴影部分为AGV从驶入到离开某交叉路口所使用的时间窗,该时间窗对应的交叉路口只允许被执行任务mi的AGV使用,其他AGV只能绕行或等待,直到该时间窗被释放,其他AGV才可申请使用。与阴影部分对应的白色部分为自由时间窗,可用于规划其他AGV,亦可被其他AGV在空闲时间段内占用。

|
| 图 2 时间窗模型 Fig.2 Time window model |
多台AGV存取车路径规划中出现的冲突一般有2种,即交叉路口冲突和路径冲突,其中,路径冲突又可分为赶超冲突和相向冲突[16]。当各AGV运行速度相同时,赶超冲突不会发生,故此处不考虑赶超冲突。基于此,文中仅着重对交叉路口冲突和路径冲突中的相向冲突进行研究。
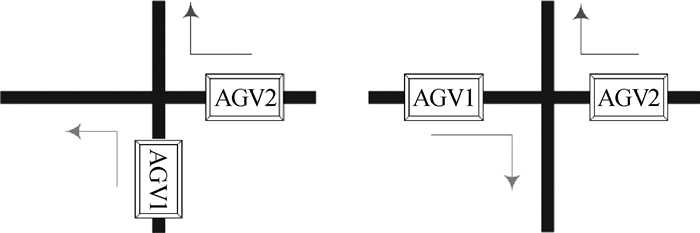
2.3.1 交叉路口冲突解决策略交叉路口冲突是指在某时刻有2台或2台以上AGV因同时共用1个交叉路口而引发的冲突[17],具体如图 3所示。对于交叉路口冲突,系统一般采用等待策略解决。当多台AGV同时到达某一交叉路口时,系统首先对各AGV优先级进行判断,然后按照优先级高低次序安排AGV通过交叉路口的先后顺序。图 4所示为采用等待策略解决交叉路口时间窗冲突前后对比图,深灰色、浅灰色和黑色矩形框分别表示AGV1注册使用的时间窗、AGV2预约申请使用的时间窗和2台AGV间的冲突时间窗。为避免AGV2在执行任务期间与AGV1发生冲突,系统会采用等待策略将AGV2在交叉路口Ci上申请的时间窗向后平移一个合理的时间,即让AGV2在进入交叉路口Ci前等待一段时间,直到交叉路口Ci被释放为止,具体如图 4(b)所示。当AGV2顺利通过交叉路口Ci时,系统自动将AGV2在交叉路口Ci的注册信息及时清除掉,从而释放该交叉路口资源,以方便其他AGV申请使用。
|
| 图 3 交叉路口冲突 Fig.3 Intersection conflict |

|
| 图 4 等待策略解决交叉路口冲突 Fig.4 Intersection conflict solved with waiting strategy |
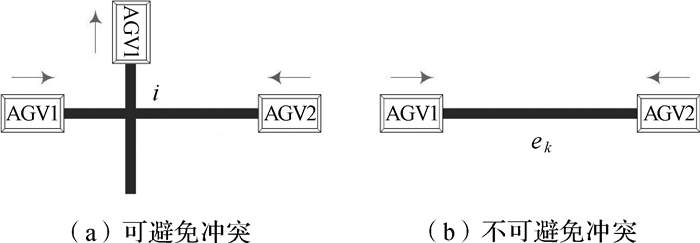
多AGV路径规划中的相向冲突又可分为可避免冲突和不可避免冲突[18],具体如图 5所示。图 5(a)所示为可避免冲突,对于此类冲突,系统可采用等待策略解决,即:将优先级低的AGV2申请使用的时间窗向后平移一段时间,直到优先级高的AGV1顺利通过交叉路口Ci后,再申请使用该交叉路口,以此避免与AGV1发生死锁或碰撞冲突,调整后的时间窗如图 6(b)所示。图 5(b)所示为不可避免冲突,对于此类冲突,最有效的解决策略是为AGV2重新规划新的可行路径。重新规划路径的具体实施步骤为:1) 系统检测多台AGV间是否出现相向冲突中的不可避免冲突;2) 对出现不可避免冲突的路段进行标记,并调用路径搜索算法重新规划路径;3) 对新搜索到的优化路径的时间窗向量表进行循环更新,直到规划出无冲突和时间最短的优化路径为止,算法搜索结束。如果算法经过多次迭代搜索(为避免程序出现死循环,程序循环搜索次数设置有最大值)仍无法找到无冲突优化路径,则算法搜索过程结束,并把此任务加载到任务序列表中,等待系统下次任务调度分配。
|
| 图 5 相向冲突 Fig.5 Opposite conflict |

|
| 图 6 等待策略解决可避免的相向冲突 Fig.6 Avoidable opposite conflict solved with waiting strategy |
采用时间窗法和Dijkstra算法,解决智能立体停车库中多AGV存取车路径规划问题的具体实施步骤为:
Step 1 初始化算法各参数,建立集合N、集合Q、集合M、集合A、集合S和集合R,分别用于表示系统中的AGV、接受任务的AGV、存取车任务请求指令、优先级策略处理后的存取车任务及任务的起点和目标点。
Step 2 将集合M中的存取车任务请求指令加载到任务序列集合A中,并按照任务优先级高低次序为其排序,处理后的序列集合A ={a1,a2,a3,…,am},其中,a1,a2,a3,…,am表示按照优先级策略处理后的任务,任务a1优先级最高,任务am优先级最低。
Step 3 根据AGV当前状态信息判断AGV工作状态。如果工作环境中有空闲AGV存在,则系统会将任务序列集合A中优先级最高的存取车任务a1分配给编号为q1(q1为集合Q中优先级最高的AGV)的空闲AGV,并在已知AGV起点位置s1、目标点位置r1及工作环境等信息的前提下,调用Dijkstra算法,为任务a1规划出一条距离最短的优化路径(该路径可用有序路段集合λ1表示,λ1 = {e11, e21, …, ek1, …, eq1},e11, e21, …, ek1, …, eq1∈E,然后转至Step 4;反之,则任务调度停止。
Step 4 计算AGV(编号为q1)在任务a1路径上各路段的驶入时间和驶出时间,初始化各路段时间窗向量表,Step 3规划的可行路径对应的时间窗向量表可用集合D1 = {X11, X21, …, Xk1…, Xq1}表示,然后转至Step 5。
Step 5 对次优任务a2的路径进行规划,转至Step 3,判断环境中是否有空闲AGV可调用,若有,则系统先将编号为q2的空闲AGV分配给次优任务a2,然后调用Dijkstra算法为任务a2规划出一条优化路径;反之,则暂停对该任务的调度,然后按照任务序列表次序依次对其他任务进行调度。
Step 6 计算AGV(编号为q2)在任务a2路径上各路段的驶入时间和驶出时间,更新各路段时间窗向量表,然后判断时间窗向量表是否存在重叠。若无重叠,则任务a2的路径规划过程结束,反之,则需检测任务a2的优化路径存在何种冲突,并根据冲突类型选用合适的冲突解决策略,如:对于交叉路口冲突和相向冲突中的可避免冲突,可采用等待策略解决;对于相向冲突中的不可避免冲突,可采用重新规划路径策略解决。
Step 7 次优任务a2的路径规划结束后,转至Step 3,然后按照任务序列表次序重复上述操作,依次完成其他任务的路径规划。
3 实例验证为了验证基于动态时间窗的泊车系统路径规划方法的有效性,以图 1所示的AGV工作环境模型为研究对象,以安全避障和耗时最少为评价指标,对多台AGV存取车路径规划过程进行测试。在规划前,需完成如下参数设置:设系统有4项存取车任务,编号分别是1,2,3和4;空闲AGV为5台,编号分别是1,2,3,4和5;按照优先级规则,任务1分配给AGV1,任务要求是将车辆从车库入口P0搬运到泊车位P6,AGV1开始执行任务的初始时间记为0 s;任务2分配给AGV2,任务要求是将车辆从泊车位P35搬运到车库入口P0,AGV2开始执行任务的初始时间记为6 s;任务3分配给AGV3,任务要求是将车辆从车库入口P0搬运到泊车位P12,AGV3开始执行任务的初始时间记为10 s;任务4分配给AGV4,任务要求是将车辆从泊车位P55搬运到车库入口P0,AGV4开始执行任务的初始时间记为13 s。
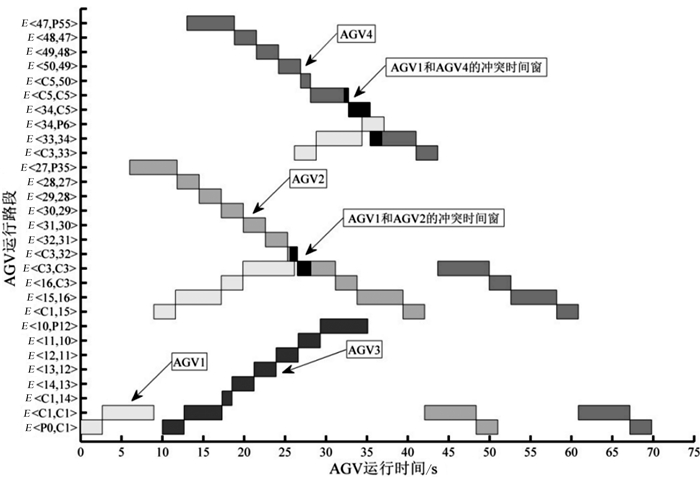
在理想条件下,AGV1,AGV2,AGV3和AGV4得到的时间窗分布结果如图 7至图 11所示。从图 7中可以看出,AGV1的可行路径为P0→C1→15→16→C3→33→34→P6;图 11中可以看出,AGV1和AGV2在交叉路口E < C3,C3 >和路段E < C3,32 >存在潜在冲突,AGV1和AGV4在交叉路口E < C5,C5 >、路段E < 34,C5 >和E < 33,34 >存在潜在冲突,冲突时间窗如图中黑色矩形框所示,冲突时间窗具体数据如表 1所示。

|
| 图 7 理想条件下AGV1可行路径时间窗分布图 Fig.7 Time window scattergram of the feasible path of AGV1 under ideal conditions |
|
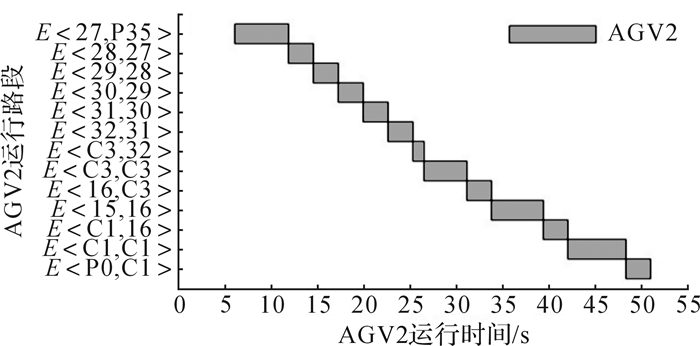
| 图 8 理想条件下AGV2可行路径时间窗分布图 Fig.8 Time window scattergram of the feasible path of AGV2 under ideal conditions |

|
| 图 9 理想条件下AGV3可行路径时间窗分布图 Fig.9 Time window scattergram of the feasible path of AGV3 under ideal conditions |

|
| 图 10 理想条件下AGV4可行路径时间窗分布图 Fig.10 Time window scattergram of the feasible path of AGV4 under ideal conditions |
|
| 图 11 理想条件下多AGV的可行路径时间窗分布图 Fig.11 Time window scattergram of the feasible paths of multiple AGV under ideal conditions |
| 冲突对象 | 冲突路段 | 冲突起始时间/s | 冲突终止时间/s |
| AGV1-AGV2 | E < C3,32> | 25.6 | 26.5 |
| E < C3,C3> | 26.5 | 28.15 | |
| AGV1-AGV4 | E < C5,C5> | 32.25 | 32.75 |
| E < 34,C5> | 32.75 | 35.4 | |
| E < 33,34> | 35.4 | 36.8 |
由图 1、图 7、图 8及图 11,结合表 1数据分析可知,AGV1和AGV2在路段E < C3, 32 >和交叉路口E < C3, C3 >处发生冲突,冲突开始时间为第25.6秒,随着时间的推移,AGV1和AGV2继续沿着各自行进方向运行,到第28.15秒时,两者间冲突刚好解除。由图 1、图 7、图 10及图 11,综合表 1数据可以看出,AGV1和AGV4在交叉路口E < C5, C5 >、路段E < 34, C5 >和路段E < 33, 34 >处发生冲突,冲突开始时间为第32.25秒,冲突刚好解除时间为第36.8秒。综上分析可知,在理想条件下,AGV1和AGV2的冲突时间窗为[25.6, 28.15]s;AGV1和AGV4的冲突时间窗为[32.25, 36.8]s。由于AGV1的优先级高于AGV2和AGV4,且AGV2和AGV4可行路径的规划是在AGV1可行路径的基础上进行的,因此,图中冲突时间窗只在AGV2和AGV4的时间窗上表示。
在基于动态时间窗的泊车系统路径规划方法下,AGV1,AGV2,AGV3和AGV4所得时间窗分布结果如图 12所示。对于AGV1,由于其优先级最高,且系统在为其规划最短路径时,各路段对应的时间窗均处于空闲状态,故AGV1的可行路径时间窗分布与理想条件下的时间窗分布相同。由图 1、图 11并综合表 1数据分析可知,AGV1和AGV2、AGV1和AGV4搜索的可行路径存在潜在冲突。根据冲突发生位置,可判断AGV1和AGV2属交叉路口冲突,AGV1和AGV4属路径相向冲突中的可避免冲突。针对这2种冲突,算法采用等待策略,按照优先级高低次序,将冲突路段E < C3, 32 >和交叉路口E < C5, C5 >的时间窗向后平移一个合适的时间段,以此解决上述冲突,平移时间窗如图 12中的黑色矩形框所示,平移时间窗的具体数据如表 2所示。由图 12并综合表 1和表 2数据分析可知,在所设计方法下,虽然AGV2和AGV4的搜索路径与AGV1的可行路径有相同运行路段,但彼此的时间窗并不存在重叠,表明等待策略能够有效解决多AGV路径规划中的交叉路口冲突和相向冲突中的可避免冲突问题。除此之外,从图 9、图 11和图 12还可看出,AGV3在本方法下得到的时间窗分布图和理想条件下的时间窗分布图相同,产生这种结果的原因在于系统为AGV3可行路径分配的时间窗与其他AGV可行路径的时间窗不存在冲突。
| 路段 | 起始时间/s | 终止时间/s |
| E < C3,32> | 25.6 | 28.3 |
| E < C5,C5> | 30.1 | 36.8 |

|
| 图 12 本算法下多AGV可行路径时间窗分布图 Fig.12 Time window scattergram of the feasible paths of multiple AGV under the proposed algorithm |
为解决多AGV存取车路径规划问题,将Dijkstra算法和时间窗法进行有效结合,提出了一种基于动态时间窗的泊车系统路径规划方法。首先利用优先级策略为加载任务排序和分配AGV;其次,采用Dijkstra算法,依次为接受任务的AGV规划最短可行路径;最后,为避免AGV间因争夺路径资源而引发死锁或碰撞冲突,利用时间窗法为各可行路径插入合理、连续的时间窗。仿真测试结果显示,该算法不仅可以为多AGV规划出全局无冲突、时间最短的优化路径,而且可以提高AGV工作效率和增强系统安全稳定性,表明该算法可行及有效。
| [1] |
王辉, 朱龙彪, 朱天成, 等.
基于粒子群遗传算法的泊车系统路径规划研究[J]. 工程设计学报, 2016, 23(2): 195–200.
WANG Hui, ZHU Long-biao, ZHU Tian-cheng, et al. Research on path planning of parking system based on PSO-genetic hybrid algorithm[J]. Chinese Journal of Engineering Design, 2016, 23(2): 195–200. |
| [2] | FAZLOLLAHTABAR H, SAIDI M M. Optimal path in an intelligent AGV-based manufacturing system[J]. Transportation Letters:the International Journal of Transportation Research, 2015, 7(4): 219–228. |
| [3] | MAJDI M, ANVAR H S, BARZAMINI R, et al.Multi AGV path planning in unknown environment using fuzzy inference systems[C]. 20083rd IEEE International Symposium on Control, Communications and Signal Processing (ISCCSP 2008).St Julians, Malta, Mar. 12-14, 2008. |
| [4] | NISHI T, MAENO R. Petri net decomposition approach to optimization of route planning problems for AGV sys-tems[J]. IEEE Transactions on Automation Science and Engineering, 2010, 7(3): 523–537. DOI:10.1109/TASE.2010.2043096 |
| [5] | UMAR U A, ARIFFIN M K A, ISMAIL N, et al. Hy-brid multi-objective genetic algorithms for integrated dy -namic scheduling and routing of jobs and automated guided vehicle (AGV) in flexible manufacturing systems (FMS) environment[J]. International Journal of Ad-vanced Manufacturing Technology, 2015, 81(9/12): 2123–2141. |
| [6] | KRNJAK A, DRAGANJAC I, BOGDAN S, et al.De-centralized control of free ranging AGVs in warehouse environments[C]. 2015 IEEE International Conference on Robotics and Automation (ICRA).Seattle, May. 26-30, 2015. |
| [7] | SMOLIĆ R N, BOGDAN S, KOVAČIĆZ, et al. Time windows based dynamic routing in multi-AGV systems[J]. IEEE Transactions on Automation Science & Engi-neering, 2010, 7(1): 151–155. |
| [8] | RAJOTIA S, SHANKER K, BATRA J L. Semi-dynamic time window constrained routeing strategy in an AGV system[J]. International Journal of Production Research, 1998, 36(1): 35–50. DOI:10.1080/002075498193921 |
| [9] | CHEN T J, SUN Y, DAI W, et al. On the shortest and conflict-free path planning of multi-AGV system based on Dijkstra algorithm and the dynamic time window method[J]. Advanced Materials Research, 2013, 645: 267–271. DOI:10.4028/www.scientific.net/AMR.645 |
| [10] | BALSEIRO S R, LOISEAUB I, RAMONET J. An ant colony algorithm hybridized with insertion heuristics for the time dependent vehicle routing prob-lem with time windows[J]. Computers & Operations Research, 2011, 38(6): 954–966. |
| [11] | GUO L X, YANG Q, YAN W J.Intelligent path plan-ning for automated guided vehicles system based on to-pological map[C]. 2012 IEEE Conference on Control, Systems and Industrial Informatics. Bandung, Indonesia, Sep.23-26, 2012. |
| [12] |
贺丽娜, 楼佩煌, 钱晓明, 等.
基于时间窗的自动导引车无碰撞路径规划[J]. 计算机集成制造系统, 2010, 16(12): 2630–2634.
HE Li-na, LOU Pei-huang, QIAN Xiao-ming, et al. Conflict-free automated guided vehicles routing based on time window[J]. Computer Integrated Manufacturing Systems, 2010, 16(12): 2630–2634. |
| [13] |
乔岩, 钱晓明, 楼佩煌, 等.
基于改进时间窗的AGVs避碰路径规划[J]. 计算机集成制造系统, 2012, 18(12): 2683–2688.
QIAO Yan, QIAN Xiao-ming, LOU Pei-huang, et al. Improved time window based conflict-free automated guided vehicle system routing[J]. Computer Integrated Manufacturing Systems, 2012, 18(12): 2683–2688. |
| [14] |
胡彬, 王冰, 王春香, 等.
一种基于时间窗的自动导引车动态路径规划方法[J]. 上海交通大学学报, 2012, 46(6): 967–971.
HU Bin, WANG Bing, WANG Chun-xiang, et al. Dy-namic routing of automated guided vehicles based on time window[J]. Journal of Shanghai Jiaotong Univer-sity, 2012, 46(6): 967–971. |
| [15] |
霍凯歌, 张亚琦, 胡志华.
自动化集装箱码头多载AGV调度问题研究[J]. 大连理工大学学报, 2016, 56(3): 244–251.
HUO Kai-ge, ZHANG Ya-qi, HU Zhi-hua. Research on scheduling problem of multi-load AGV at automated container terminal[J]. Journal of Dalian University of Technology, 2016, 56(3): 244–251. DOI:10.7511/dllgxb201603004 |
| [16] |
苏霞, 李伟光.
FMS中自动导引车路径规划[J]. 机械设计与制造, 2015(1): 201–203.
SU Xia, LI Wei-guang. Path planning of automated guided vehicles in FMS[J]. Machinery Design & Man-ufacture, 2015(1): 201–203. |
| [17] | MIYAMOTO T, INOUE K. Local and random searches for dispatch and conflict-free routing problem of capacitated AGV systems[J]. Computers & Industrial Engineering, 2016, 91: 1–9. |
| [18] | VIVALDINI K C T, ROCHA L F, BECKER M, et al.Comprehensive review of the dispatching, sched-uling and routing of AGVS[C]. Proceedings of the 11th Portuguese Conference on Automatic Control. Berlin:Springer Verlag, 2015:505-514. |


