2. 东华大学 机械工程学院, 上海 200051
2. School of Mechanical Engineering, Donghua University, Shanghai 200051, China
液压支架是机械化采煤的重要设备,它可有效支撑和控制采煤工作面的顶板并可隔离采空区以防止矸石进入工作区域和输送机内。液压支架的四连杆机构主要指的是由掩护梁、前连杆、后连杆和底座四部分组成的前后连杆双摇杆机构,杆与杆之间用销轴连接,它是液压支架的主要运动和稳定机构。四连杆机构的作用是维持支架不同方向上的稳定性,同时承受外部载荷,其设计是否合理对液压支架整体的稳定性和采煤工作的安全性至关重要。目前学者对四连杆机构的研究主要有:第1类是从运动轨迹和受力方面着手,文献[1]以连杆水平倾角为变量推导支架升降过程并根据顶梁位置来绘制运动轨迹,文献[2]使用幂函数法优化四连杆机构,文献[3-4]采用运动学和动力学方程的方法来建立四连杆多目标优化模型;第2类是从优化算法编程、机构动力学分析与参数化建模软件方面入手,文献[5-6]将四连杆机构参数化并建立四连杆运动方程并运用MATLAB来模拟四连杆运动轨迹, 文献[7-8]分别使用VC++和OpenGL对液压支架四连杆进行运动仿真和编程优化, 文献[9]根据四连杆机构定位尺寸和极限参数建立约束条件和目标函数再采用迭代搜索法进行优化, 文献[10-12]使用动力学仿真软件ADAMS对四连杆进行参数化建模、运动轨迹仿真与优化设计, 文献[13]以掩护梁与顶梁交接点的运动轨迹与给定曲线的水平差值最小为优化目标建立优化模型并使用Scilab进行优化求解,文献[14]使用Pro/E的参数化建模与基于Pro/Web.Link的液压支架动态建模流程,利用程序驱动建模和四连杆优化过程。这些研究主要是从受力、尺寸、动力学和优化算法方面进行液压支架的设计和优化研究,局限性在于:四连杆机构为空间机构,煤顶高低不均匀,因此受力较为复杂,简化计算时会产生较大误差。本文提出从四连杆机构的空间受力出发并结合支架的运动轨迹,采用粒子群优化算法对四连杆机构展开优化研究。重点研究四连杆优化设计模型的建立及求解方法。针对目前四连杆应力计算采用的二维简化模型,研究了四连杆三维空间受力分析计算模型,使四连杆力学计算更加符合实际情况。针对液压支架的稳定性要求,研究了四连杆运动轨迹的优化计算方法。在此基础上,采用粒子群优化算法并结合罚函数解决了优化模型不等式约束问题和求解问题。
1 四连杆优化模型建立及其求解方法 1.1 优化模型建立优化设计研究首先需要建立优化模型,优化模型是否合理直接关系到优化问题的解决与否。在对四连杆优化方法的研究中,选取了影响四连杆性能的几个重要参数作为优化模型参数,以三维空间力学分析代替传统的二维力学,同时考虑四连杆运动轨迹和轻量化问题。将多个优化指标融合在一个目标函数中考虑,结合相关技术规范对四连杆的技术要求,建立优化设计约束条件。通过以上研究思路,建立了比较完善的四连杆优化模型。
1) 目标函数的建立。
在建立四连杆多目标优化设计模型过程中,首先要考虑的是优化目标的选择。为了保证液压支架的工作稳定性,使其具有更好的支护性能,选取四连杆机构的运动轨迹偏移量最小作为优化设计的目标之一。为了保证四连杆机构的使用寿命,选取四连杆机构的前后连杆所受合力最小作为优化设计的目标之一。同时,为了使设计的支架减重,选取四连杆杆件总长最小作为优化的目标之一。即优化目标函数表达式为:
| $ f\left( x \right) = \min {e_{轨迹}} + \min {L_{连杆}} + \min {F_{连杆}} $ | (1) |
2) 设计变量的选择。
在进行设计变量选择的时候,一个重要的选取标准就是根据液压支架四连杆设计规范,选取那些对液压支架性能或实际需求影响较大的参数作为优化设计的变量。根据液压支架设计规范和受力分析结果以及稳定性要求,选取液压支架在最高位置时的掩护梁与水平方向的夹角θ、后连杆与水平方向的夹角φ、后连杆与掩护梁长度的比值I以及前后连杆上铰点之距与掩护梁长度的比值I1四个独立变量作为液压支架四连杆优化的设计变量。
3) 约束条件的建立。
根据液压支架的设计要求,支架在高位置时,优化模型的设计变量约束条件为:① θ的取值范围为52°~62°;② φ的取值范围为75°~85°;③ I的取值范围为0.45~0.61;④ I1的取值范围为0.22~0.30。优化的目标是使液压支架运动过程中的梁端偏移量最小。因为前后连杆的瞬心与掩护梁的连线的水平方向的夹角α即为运动轨迹与竖直方向的夹角,所以只要保证液压支架在最高位置时的α最小,也就保证了梁端轨迹的偏移量最小。根据液压支架设计技术相关规范,优化模型的状态约束条件是:① 前后连杆的比值L1/L2=0.9~1.2;② 前连杆下端的高度L6 < Hmax/5,其中Hmax为液压支架在最高位置时的高度;③ 前后连杆下端之距L7 < Hmax/4.5;④ 对于掩护式支架,有tan α < 0.16,对于支撑掩护式支架, 有tan α < 0.2。
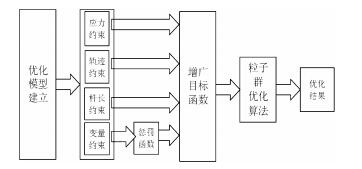
1.2 优化模型求解方法粒子群优化算法(particle swarm optimization algorithm)是Kennedy和Eberhart研发的一种进化计算方法。粒子群算法是模拟鸟群觅食行为的群体智能仿生算法。该算法在函数优化中具有收敛速度快、参数少、算法实现较为容易等优点[15]。优化过程中当粒子的飞行速度足够小或达到预设的迭代步数时,算法停止迭代,输出结果[16-17]。采用粒子群多目标优化方法将多个目标函数集中到一起使其成为多优化指标的增广函数。利用惩罚函数将变量的不等式约束转换成等式约束加入到增广函数中,通过反复迭代使结果满足约束条件为止。粒子群优化算法求解示意图如图 1所示。
|
| 图 1 粒子群优化算法求解示意图 Fig.1 Schematic diagram of solution of particle swarm optimization algorithm |
求解过程中使用惩罚函数,惩罚函数法主要是指利用添加惩罚项的办法将有约束的优化模型转化为无约束的优化模型, 罚函数法的公式为:
| $ B\left( x \right) = f\left( x \right) + \left[ {\sum {{r_i} \cdot {G_i}\left( x \right)} + \sum {{c_j} \cdot {H_j}\left( x \right)} } \right] $ | (2) |
式中:f(x)为优化目标;ri, cj为惩罚因子, 为常数;Gi(x),Hj(x)为约束函数;B(x)为增加了惩罚项的目标函数。
2 液压支架四连杆机构优化计算实例本文研究的液压支架为某公司研制的两柱支撑掩护式液压支架,该支架单根立柱的额定工作阻力为9 000 kN,最小支撑高度为2.5 m,最大支撑高度为4.5 m。顶梁、掩护梁、底座、前后连杆材料选用Q690钢板,铰接轴材料选用30CrMnTi。其中立柱和平衡千斤顶可以等效为刚性弹簧,立柱等效弹簧预压,压力大小为工作阻力的1.2倍,弹簧连接在底座柱窝球心与顶梁柱窝球心;平衡千斤顶等效为弹簧预拉,大小为1 217 kN。根据理论推导,利用C++语言编写计算程序,将液压支架初始设计参数输入,计算不同工况下液压支架的受力情况[18],进而得到液压支架初始状态参数。
1) 顶梁扭转加载工况。该工况在支架顶梁前端加方形垫块,在支架顶梁后端加长垫块,使液压支架处于偏载状态,增加液压立柱压力至额定阻力。
2) 顶梁两端加载工况。该工况在支架顶梁前端和后端均加长垫块,使液压支架处于前后两端受力状态,增加液压立柱压力至额定阻力。
利用C++语言编写计算程序,将液压支架初始设计参数输入,计算液压支架由最小高度升高到最大高度时的运动轨迹。液压支架在从2 500 mm升高到4 500 mm的过程中,液压支架的梁端轨迹的横向变化量约为73 mm,高于行业规定的最大变化量(70 mm),这对液压支架工作的整体稳定性有不利影响。液压支架通用设计标准规定液压支架的轨迹横向变化量不大于70 mm,最好小于30 mm,为了得到四连杆机构最好的运动状态,需要使用优化算法对其进行优化。
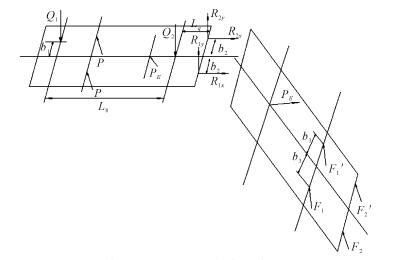
要对四连杆机构进行优化,首先要建立优化模型的数学表达式。先进行空间连杆受力计算,将连杆空间受力和连杆参数联系起来,并将其应用到四连杆的优化设计中去。对液压支架的顶梁和掩护梁分别进行受力分析,通过受力分析研究液压支架空间受力状态下前后连杆的应力状态。由于液压支架空间受力分析十分复杂,因此将对其进行简化处理。如图 2所示,取液压支架顶梁和掩护梁为分析对象,对于两柱支撑掩护式液压支架而言,在顶梁扭转加载工况下,2根液压立柱的额定工作阻力为P,顶梁前端垫块受到煤顶对其的支撑反力为Q1,垫块中心到顶梁中心线的距离为b1, 液压千斤顶作用在顶梁和掩护梁的压力为PE,顶梁后端长垫块简化为作用在顶梁后端的集中力为Q2,长垫块距顶梁后端的距离为L9,前后两个垫块之间的距离为L8,顶梁与掩护梁连接处的作用力:水平方向作用力分别为R1x,R2x,竖直方向作用力分别为R1y,R2y。液压支架前连杆对支架掩护梁的作用力:左连杆作用力为F1,右连杆为F1′;后连杆对液压支架掩护梁的作用力:左连杆作用力为F2,右连杆为F2′。连杆与掩护梁中心线的距离为b3。
|
| 图 2 液压支架顶梁和掩护梁的受力分析 Fig.2 Force analysis for top beam and shield beam of hydraulic support |
其中当支架处于最高位置、最低位置、中间位置时,掩护梁与水平方向的夹角分别为:θ1,θ2,θ3;后连杆与水平方向的夹角分别为φ1, φ2, φ3。对顶梁和掩护梁分别单独进行受力分析可知,液压支架在工作的时候要保持支顶的平衡状态,则支架的顶梁和掩护梁在脱离了连杆和底座之后的受力也是平衡的。在顶梁扭转加载工况下,分别对顶梁和掩护梁在水平方向、竖直方向的受力进行分析。
1) 对顶梁有:水平方向合力Fx=0, 竖直方向合力Fy=0, 在以x轴为旋转轴时的扭矩Mx=0, z轴为旋转轴时的扭矩Mz=0, y轴为旋转轴时的扭矩My=0, 则:
| $ \left\{ \begin{array}{l} {R_{1x}} + {R_{2x}} - 2P\sin \beta - {P_E}\cos {\alpha _5} + \left( {{Q_1} + {Q_2}} \right)f = 0\\ {R_{1y}} + {R_{2y}} - 2P\cos \beta + {P_E}\sin {\alpha _5} - \left( {{Q_1} + {Q_2}} \right) = 0\\ {Q_1}{b_1} + \left( {{R_{{1_y}}} - {R_{{2_y}}}} \right){b_2} = 0\\ {R_{1x}}{b_2} - {R_{2x}}{b_2} - {Q_1}f{b_1} = 0\\ {Q_1}{L_8} + {Q_2}{L_9} - 2P{L_5}\cos \beta - 2P\left( {{L_6} - {H_0}} \right)\sin \beta - \\ {P_E}{L_{12}}\sin {\alpha _5} - {P_E}\left( {{L_{10}} - {H_0}} \right)\cos {\alpha _5} - \left( {{Q_1} + {Q_2}} \right)f{H_0} = 0 \end{array} \right. $ | (3) |
2) 对掩护梁有:垂直方向合力Fy=0, 水平方向合力Fx=0, 在以z轴为旋转轴时的扭矩Mz=0, 在以x轴为旋转轴时的扭矩Mx=0, 在以y轴为旋转轴时的扭矩My=0, 则:
| $ \left\{ \begin{array}{l} ({R_{1x}} + {R_{2x}}{\rm{)cos}}\alpha + ({R_{1y}} + {R_{2y}}){\rm{sin}}\alpha - ({F_1} + F{\prime _1}){\rm{sin}}\left( {\alpha - {\alpha _1}} \right) - ({F_2} + F{\prime _2}){\rm{sin}}\left( {\alpha - {\alpha _2}} \right) + {P_E}{\rm{cos}}\left( {\alpha - {\alpha _5}} \right) = 0\\ - ({R_{1x}} + {R_{2x}}){\rm{sin}}\alpha - ({R_{1y}} + {R_{2y}}){\rm{cos}}\alpha + ({F_1} + F{\prime _1}){\rm{cos}}\left( {\alpha - {\alpha _1}} \right) + ({F_2} + F{\prime _2}){\rm{cos}}\left( {\alpha - {\alpha _2}} \right) + {P_E}{\rm{sin}}\left( {\alpha - {\alpha _5}} \right) = 0\\ \left( {{R_{1x}} - {R_{2x}}} \right){b_2}{\rm{sin}}\alpha + \left( {{R_{1y}} - {R_{2y}}} \right){b_2}{\rm{cos}}\alpha - \left( {{F_1} - F{\prime _1}} \right){b_3}{\rm{cos}}\left( {\alpha - {\alpha _1}} \right) - \left( {{F_2} - F{\prime _2}} \right){b_3}{\rm{cos}}\left( {\alpha - {\alpha _2}} \right) = 0\\ - \left( {{R_{1x}} - {R_{2x}}} \right){b_2}{\rm{cos}}\alpha + \left( {{R_{1y}} - {R_{2y}}} \right){b_2}{\rm{sin}}\alpha - \left( {{F_1} - F{\prime _1}} \right){b_3}{\rm{sin}}\left( {\alpha - {\alpha _1}} \right) - \left( {{F_2} - F{\prime _2}} \right){b_3}{\rm{sin}}\left( {\alpha - {\alpha _2}} \right) = 0\\ \left( {{F_1} + F{\prime _1}} \right){L_4}{\rm{cos}}\left( {\alpha - {\alpha _1}} \right) + \left( {{F_2} + F{\prime _2}} \right)({L_3} + {L_4}){\rm{cos}}\left( {\alpha - {\alpha _2}} \right) + {P_E}{L_7}{\rm{cos}}\left( {\alpha - {\alpha _5}} \right) + {P_E}{L_{11}}{\rm{sin}}\left( {\alpha - {\alpha _5}} \right) - \left( {{F_1} + F{\prime _1}} \right){L_{18}}{\rm{sin}}\left( {\alpha - {\alpha _1}} \right) = 0 \end{array} \right. $ | (4) |
式(3) 和式(4) 中:L10为前连杆与掩护梁铰接点到顶梁的距离; L12为后连杆与掩护梁铰接点到顶梁的距离; α为掩护梁与水平方向的夹角;α1为前连杆与竖直方向的夹角;α2为后连杆与竖直方向的夹角;α5为液压千斤顶与水平方向的夹角; β为液压立柱与竖直方向的夹角。
综上,结合轨迹计算方法,联立式(1) 和式(2) 可以得到液压支架的空间应力受力状态。其中,前后连杆受到的力为:
| $ {F_{总}} = \left( {{F_1} + {{F'}_1} + {F_2} + {{F'}_2}} \right) $ | (5) |
针对于该型号的液压支架,建立液压支架四连杆轨迹、受力优化模型如下(角度已转化为弧度):
| $ \left\{ \begin{array}{l} f\left( {{\theta _1},{\varphi _1},I,{I_1}} \right) = \min \left[ {{F_1} + {{F'}_1} + {F_2} + {{F'}_2}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\min \left[ {{L_1},{L_2},{L_5}} \right] + \min e\\ 0.91 \le {\theta _1} \le 1.2{\rm{rad}}\\ 1.31 \le {\varphi _1} \le 1.48{\rm{rad}}\\ 0.45 \le I \le 0.61\\ 0.22 \le {I_1} \le 0.3\\ 0.2 \times {H_1} \le D\\ {H_1}/4.5 \le E\\ 0 \le \tan \alpha = \sqrt {S/L} \le 0.2 \end{array} \right. $ | (6) |
式中:D为支架前后连杆的高度之差,E为支架前后连杆下端的水平距离。
利用粒子群优化算法对四连杆运动轨迹进行优化的时候,将惩罚函数加入优化目标函数当中,使其变为单目标无约束优化模型,这样就解决了粒子群算法只能解决单目标问题而无法用于有约束优化模型的问题。其次为了使优化函数中各个优化目标对结果的影响尽可能相近,需要将各个优化目标结果转化为同一数量级。计算程序中的目标函数写为:
| $ \begin{array}{l} {\rm{f}} = {\rm{S}}/{\rm{L}} + \left( {{\rm{fabs}}\left( {{\rm{x}}\left[ 9 \right]} \right) + {\rm{fabs}}\left( {{\rm{x}}\left[ 8 \right]} \right) + {\rm{fabs}}\left( {{\rm{x}}\left[ 7 \right]} \right) + {\rm{fabs}}} \right.\\ \left. {\left( {{\rm{x}}\left[ 6 \right]} \right)} \right)/10000 + \left( {{\rm{A}} + {\rm{C}} + {\rm{G}}} \right)/{\rm{H}}1 + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {{\rm{C}}/{\rm{A}}} \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. { - 0.9} \right)} \right)?\left( {{\rm{C}}/{\rm{A}} - 0.9} \right):0,2} \right)} \right) + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {1.2 - {\rm{C}}/} \right.} \right.} \right.} \right.\\ \left. {\left. {\rm{A}} \right)} \right)?\left. {\left. {\left( {1.2 - {\rm{C}}/{\rm{A}}} \right):0,2} \right)} \right) + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {0.2*{\rm{H}}1 - } \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. {\rm{D}} \right)} \right)?\left( {0.2*{\rm{H}}1 - {\rm{D}}} \right)/10:0,2} \right)} \right) + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {{\rm{H}}1/4.} \right.} \right.} \right.} \right.\\ \left. {\left. {5 - {\rm{E}}} \right)} \right)?\left. {\left. {\left( {{\rm{H}}1/4.5 - {\rm{E}}} \right)/10:0,2} \right)} \right) + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {{\rm{fabs}}} \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. {\left( {S/L} \right)} \right)} \right)?\left( {{\rm{fabs}}\left( {{\rm{S}}/{\rm{L}}} \right)} \right):0,2} \right)} \right) + 100*\left( {{\rm{pow}}\left( {\left( {0 - \left( {0.2 - } \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. {{\rm{fabs}}\left( {{\rm{S}}/{\rm{L}}} \right)} \right)} \right)?\left( {0.2 - {\rm{fabs}}\left( {{\rm{S}}/{\rm{L}}} \right)} \right):0,2} \right)} \right)。\end{array} $ |
其中:fabs为求绝对值函数,pow为求幂函数,?用于判断大小。
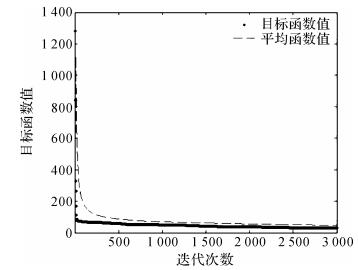
在满足以上约束条件下使用粒子群优化算法对液压支架优化模型进行求解,粒子群优化模型设置条件:维数为4维,粒子数目为30个,学习因子c1,c2均为2.0,惯性权重为0.5,粒子的最大速度为0.1,最大迭代次数为3 000次。在粒子群算法迭代进行到第20次时,目标函数值迅速下降到一个很低的水平, 为87.08,在迭代结束后,目标函数值逐渐趋于平缓,几乎不再变化,由开始时的1 281.8下降到29.023 8,说明粒子群算法已经收敛,如图 3所示。
|
| 图 3 液压支架四连杆多目标优化收敛图 Fig.3 Convergence of multi-objective optimization for four-bar mechanism of hydraulic support |
利用粒子群优化算法对液压支架四连杆机构进行优化,其优化前后各参数对比如表 1至表 3所示。
| 对比项 | θ1/(°) | φ1/(°) | I | I1 | F1/kN | F1′/kN | F2/kN | 对比项 | F2′/kN | 前连杆长/mm | 后连杆长/mm | 掩护梁长/mm | 连杆及掩护梁总长度/mm | 对比项 | 掩护梁上段长度/mm | 掩护梁下段长度/mm | 前后连杆下端水平距离/mm | 前后连杆下端高度差/mm | 轨迹偏差/mm |
| 优化前 | 0.96 | 1.293 | 0.645 | 0.199 | 685.491 | -6 269.91 | -2 697.51 | 优化前 | 7 666.65 | 1 840.0 | 1 716.0 | 2 660.0 | 6 274.0 | 优化前 | 2 130.0 | 529.7 | 850.0 | 530 | 73.17 |
| 优化后 | 0.91 | 1.336 21 | 0.61 | 0.231 927 | 397.806 | -2 176.47 | -2 222.14 | 优化后 | 4 000.4 | 1 689.5 | 1 624.3 | 2 769.8 | 6 083.6 | 优化后 | 2 127.4 | 642.4 | 851.2 | 766.1 | 20.6 |
| 对比项 | 优化前 | 优化后 |
| 顶掩铰接1处水平力R1x/kN | 108.921 | 455.441 |
| 顶掩铰接1处竖直力R1y/kN | -2 812.05 | -2 711.2 |
| 顶掩铰接2处水平力R2x/kN | -843.838 | -487.298 |
| 顶掩铰接2处竖直力R2y/kN | 1 951.75 | 2 002.5 |
| 垫块1处等效集中力Q1/kN | 4 839.41 | 4 788.51 |
| 垫块2处等效集中力Q2/kN | 13 073.4 | 13 242.8 |
| 前连杆1处受力F1/kN | 685.491 | 397.806 |
| 前连杆2处受力F′1/kN | -6 269.91 | -2 176.47 |
| 后连杆1处受力F2/kN | -2 697.51 | -2 222.14 |
| 后连杆2处受力F′2/kN | 7 666.65 | 455.441 |
| 对比项 | 优化前 | 优化后 |
| 顶掩铰接1处水平力R1x/kN | -367.458 | -15.928 8 |
| 顶掩铰接1处竖直力R1y/kN | -430.148 | -354.351 |
| 顶掩铰接2处水平力R2x/kN | -367.458 | -15.928 8 |
| 顶掩铰接2处竖直力R2y/kN | -430.148 | -354.351 |
| 垫块1处等效集中力Q1/kN | 4 839.41 | 4 788.51 |
| 垫块2处等效集中力Q2/kN | 13 073.4 | 13 242.8 |
| 前连杆1处受力F1/kN | -2 792.21 | -889.331 |
| 前连杆2处受力F′1/kN | -2 792.21 | -889.331 |
| 后连杆1处受力F2/kN | 2 484.57 | 888.128 |
| 后连杆2处受力F′2/kN | 2 484.57 | 888.128 |
从液压支架四连杆机构入手,重点研究了四连杆优化设计模型的建立过程和求解过程,并利用粒子群优化算法对ZY18000-25-45型液压支架四连杆机构进行优化。通过对比优化前后的结果,证明了四连杆多目标优化方法的可行性以及有效性,具体结论如下:
1) 液压支架的前连杆、后连杆、掩护梁长度分别由优化前的1 840,1 716,2 660 mm变化到1 689.5,1 624.3,2 769.8 mm。3类关键部件的总材料长度由优化前的6 274 mm减小到6 083.6 mm,达到了结构轻量化的目的。
2) 在连杆应力状况方面:在顶梁扭转加载工况下前连杆的应力由优化前的685.491,-6 269.91 kN分别减小到397.806,-2 176.47 kN,连杆受力减小;后连杆的应力由优化前的-2 697.51,7 666.65 kN减小到-2 222.14,4 000.4 kN,应力有所下降。结果显示优化效果良好,保证了支架的前后连杆在受力方面的均匀性,使其载荷差距减小,达到了应力优化的目的。
3) 在总体四连杆机构轨迹优化方面,四连杆机构在运动中的横向偏移量由优化前的73.17 mm减小到优化后的20.6 mm,保证其在30 mm以下,使支架在运动过程中更稳定,更安全。
| [1] |
杨磊, 王新亚, 许日成, 等.
反四连杆机构液压支架顶梁运动轨迹分析[J]. 矿山机械, 2013, 41(8): 28–30.
YANG Lei, WANG Xin-ya, XU Ri-cheng, et al. Analy-sis on motion trajectory of top beam in hydraulic support with reverse four-bar linkage[J]. Mining & Processing Equipment, 2013, 41(8): 28–30. |
| [2] |
苗耀华.
放顶煤液压支架四连杆机构优化设计[J]. 煤炭工程, 2007(6): 41–43.
MIAO Yao-hua. Optimization design of four link mecha-nism of hydraulic support for top coal caving[J]. Coal Engineering, 2007(6): 41–43. |
| [3] |
牛艳奇.
液压支架四连杆多目标优化[J]. 辽宁工程技术大学学报(自然科学版), 2015, 34(5): 628–632.
NIU Yan-qi. Hydraulic support four-bar connecting rod multi-objective optimization[J]. Journal of Liaoning Technical University (Natural Science), 2015, 34(5): 628–632. DOI:10.11956/j.issn.1008-0562.2015.05.016 |
| [4] |
韩凤霞, 胡登高, 范迅.
液压支架四连杆机构的三维建模与运动仿真[J]. 煤矿机械, 2006, 27(9): 67–68.
HAN Feng-xia, HU Deng-gao, FAN Xun. Three-di-mension model and dynamic animation of four-bar mech-anism of hydraulic support[J]. Coal Mine Machinery, 2006, 27(9): 67–68. |
| [5] |
汤卓, 刘雯雯, 王志.
基于弦截法液压支架四连杆机构运动分析[J]. 煤矿机械, 2015, 36(4): 172–174.
TANG Zhuo, LIU Wen-wen, WANG Zhi. Movement a-nalysis of hydraulic support four bar linkage based on string section method[J]. Coal Mine Machinery, 2015, 36(4): 172–174. |
| [6] |
王建国.
基于MATLAB的液压支架四连杆优化设计[J]. 煤矿开采, 2010, 15(2): 70–72.
WANG Jian-guo. Optimized design for four-bar linkage structure of powered support based on MATLAB[J]. Coal Mining Technology, 2010, 15(2): 70–72. |
| [7] |
张俊文, 董长吉.
OpenGL在煤矿液压支架四连杆机构运动仿真中的应用[J]. 矿业研究与开发, 2006, 26(1): 54–56.
ZHANG Jun-wen, DONG Chang-ji. Application of OpenGL in the motion simulation of four-bar mechanism of powered mining support[J]. Mining Research and De-velopment, 2006, 26(1): 54–56. |
| [8] |
李秋生, 王勇, 教光印.
基于VC ++液压支架四连杆机构的优化设计与分析[J]. 煤矿机械, 2010, 31(11): 23–24.
LI Qiu-sheng, WANG Yong, JIAO Guang-yin, et al. Optimization design and analysis of four-linkage mecha-nism in hydraulic support based VC ++[J]. Coal Mine Machinery, 2010, 31(11): 23–24. DOI:10.3969/j.issn.1003-0794.2010.11.011 |
| [9] |
陈亮亮.
掩护式液压支架四连杆机构的优化设计[J]. 中小企业管理与科技:上旬刊, 2012(4): 263–264.
CHEN Liang-liang. Optimum design for four-bar of coal hydraulic-support[J]. Management & Technology of SME:Early, 2012(4): 263–264. |
| [10] |
曾庆良, 戴汉政, 张鑫.
基于ADAMS的大倾角液压支架四连杆优化设计[J]. 煤炭科学技术, 2009, 37(1): 36–38.
ZENG Qing-liang, DAI Han-zheng, ZHANG Xin. Op-timized design on four linking bar of hydraulic powered support for high inclined seam based on ADAMS[J]. Coal Science and Technology, 2009, 37(1): 36–38. |
| [11] |
叶铁丽, 李民, 刘欣丽.
液压支架四连杆机构优化设计及运动仿真[J]. 煤矿机械, 2009, 30(5): 37–39.
YE Tie-li, LI Min, LIU Xin-li. Optimal design of four-bar mechanism in hydraulic support[J]. Coal Mine Ma-chinery, 2009, 30(5): 37–39. |
| [12] |
赵彬. 煤矿液压支架四连杆的遗产算法优化与软件设计[D]. 武汉: 华中科技大学机械科学与工程学院, 2011: 1-56.
ZHAO Bin.Genetic optimization and software design for four-bar of coal hydraulic-support[D]. Wuhan:Huazhong University of Science and Technology, School of Mechanical Science & Engineering, 2011:1-56. |
| [13] |
张海军, 李炳文, 姚新华, 等.
基于Scilab的液压支架四连杆优化设计[J]. 煤矿机械, 2009, 30(4): 2–4.
ZHANG Hai-jun, LI Bing-wen, YAO Xin-hua, et al. Optimal design of four-bar mechanism in hydraulic support based on Scilab[J]. Coal Mine Machinery, 2009, 30(4): 2–4. |
| [14] |
李谨, 王斌, 姚新改, 等.
基于Web的液压支架四连杆优化设计[J]. 矿山机械, 2014, 42(2): 9–12.
LI Jin, WANG Bin, YAO Xin-gai, et al. Optimization design of four-bar linkage in hydraulic support based on Web[J]. Mining Machine, 2014, 42(2): 9–12. |
| [15] |
罗润林, 阮怀宁, 朱昌星.
基于粒子群-最小二乘法的岩石流变模型参数反演[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(5): 750–753.
LUO Run-lin, RUAN Huai-ning, ZHU Chang-xing. Parameter inversion of rock creep model based on PSO -least square method[J]. Journal of Liaoning Technical University (Natural Science), 2009, 28(5): 750–753. |
| [16] |
权国通, 谭超, 侯海潮, 等.
基于粒子群三次样条优化的采煤机截割路径规划[J]. 煤炭科学技术, 2011, 39(3): 77–79.
QUAN Guo-tong, TAN Chao, HOU Hai-chao, et al. Cutting path planning of coal shearer base on particle swarm triple spline optimization[J]. Coal Science and Technology, 2011, 39(3): 77–79. |
| [17] |
黄太安, 生佳根, 徐红洋, 等.
一种改进的简化粒子群算法[J]. 计算机仿真, 2013, 30(2): 327–335.
HUANG Tai-an, SHENG Jia-gen, XU Hong-yang, et al. Improved simplified particle swarm optimization[J]. Computer Simulation, 2013, 30(2): 327–335. |
| [18] | LIU Hong-yu, LIU Jun-qing.Hydraulic support entire strength research under four kinds of typical load working conditions[C]//2011 Second International Conference on Mechanic Automation and Control Engi-neering (MACE), Hohhot, Jul 1.5-17, 2011. |



