随着世界经济的发展和人类社会对能源需求的不断增加,海上油气资源勘探活动日渐活跃。自升式海洋钻井平台以其造价低、易移动、可重复使用、抗海上恶劣作业环境能力强等优点,在浅海油气勘探开发工程中得到越来越广泛的应用。在插桩作业中,当遇到硬软土层时,平台的基础承载力会突然下降。如果采取措施不当,平台桩腿可能会突然穿透硬土层,进入下部软土层,形成“穿刺”。这轻者会导致平台倾斜,贻误工期;重者会导致平台倾覆,造成重大财产损失和人员伤亡。在海洋油气开发史上,类似的事故曾多次发生[1]。因此,对硬软双层土中平台桩靴的承载能力进行深入分析十分必要。
目前,在成层土地基承载力的计算中,主要有基于现场和模型试验结果的经验公式法[2]和基于桩-土弹塑性接触分析的有限元数值分析法[3]。1969年,Brown和Meyerhof[4]根据圆形基础的承载力试验结果,提出了著名的Brown & Meyerhof公式,该公式同时考虑了上、下层土不排水抗剪强度对基础承载力的影响,在海洋工程界得到广泛应用。1981年,Young和Focht[5]提出基础底部的压力以纵横方向3:1的比例从上部硬土层向下部软土层线性扩散,在交界面处形成一个等效基础,并将该等效基础的极限承载力作为成层土的极限承载力,人称“3:1投影面积法”。
近年来,不少国内外学者通过实验或有限元数值方法研究成层土的极限承载力。在国外,Teh等[6-7]通过离心机实验,研究砂-黏土中不同桩靴的穿透深度和失效模式,实验结果表明,砂层厚度和砂与黏土之间的承载阻力比值都会影响桩靴的极限承载力。2009年,Liu等[8]利用AFENA有限元软件包中的MIT-S1模型,对桩靴在强度各向异性土中的垂直承载力进行了数值研究,发现土的各向异性会降低桩靴的极限承载力,并揭示了土的各向异性与桩头粗糙度对承载能力的组合效应。2010年,Tho等[9]将耦合的欧拉-拉格朗日方法用于研究桩靴在海床土中的贯入过程。Henke和Qiu[10]用亚塑性本构模型模拟砂土的物理性质,利用耦合的欧拉-拉格朗日方法分析桩靴在砂-黏土中的贯入过程。2011年,Qiu和Henke[11]在假设桩-土接触面完全光滑和完全粗糙两种极端情况下计算桩靴在黏土中的极限承载力,发现其差别仅在5%以内。2012年,Yu等[12]利用大变形有限元方法研究砂-黏土中桩靴的穿透阻力,并分析了砂层厚度、内摩擦角和黏土的不排水抗剪强度对穿刺的影响。在国内,付丽娜[13]采用经典土力学极限承载力理论研究桩靴承载能力,分析了均质土(黏性土、砂性土、粉土)和成层土中桩靴承载力的计算公式,并进一步探讨了成层土地基穿刺可能性分析方法。2012年,王楠等[14]采用有限元方法,对自升式平台在上砂下软地基插桩时地基土的破坏模式和承载能力进行了大量计算和深入分析,发现当桩靴底面尺寸一定时,上部硬土层厚度是影响地基破坏模式和地基承载力的主要因素。2016年,郑刚等[15]考虑了基底粗糙度、砂土剪胀角和超载等因素,对砂-黏双层地基的极限承载力和破坏机制进行了数值研究,结果表明:基底粗糙度对极限承载力的影响随着砂土内摩擦角的增大而减小;当剪胀角较小时,剪胀角变化对承载力的影响更为明显;当下层黏土强度较小时,超载的作用更明显。
针对上硬下软双层黏土地基承载力问题,本文利用大型有限元软件ABAQUS,建立了海上自升式平台桩靴与双层黏土地基的弹塑性接触有限元模型,运用非线性有限元法计算桩靴在竖向荷载作用下地基的极限承载力。研究上层土厚度和上、下土层强度等因素对极限承载力的影响,并对硬软双层黏土地基中的穿刺现象进行分析。
1 经验计算方法土力学经典理论中有很多基础承载力的计算公式,如太沙基、汉森极限承载力公式等,但这些公式大多数是针对单一均质土地基而言的,对成层土地基并不适用。目前,成层土地基极限承载力的确定主要依靠经验公式,主要有投影面积法、Brown & Meyerhof公式和汉森加权平均法等[16]。对于双层黏土地基,通常采用投影面积法和Brown & Meyerhof公式进行计算。
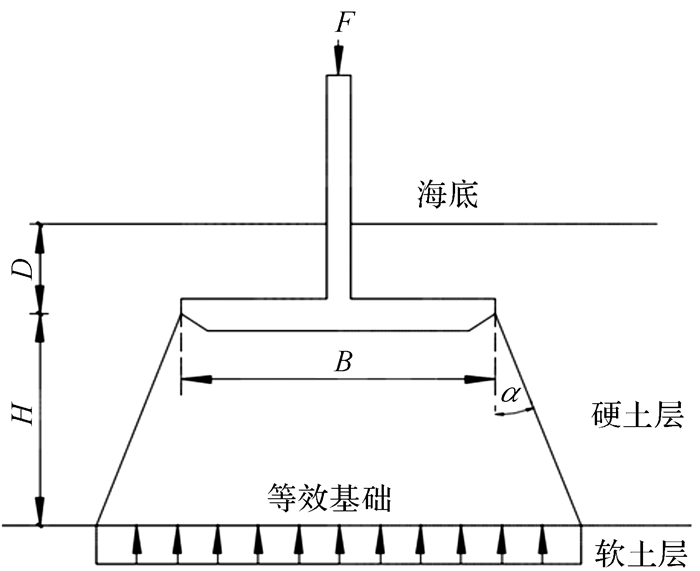
1.1 投影面积法投影面积法假定:基础底部的压力从上部硬土层向下线性扩散到下部软土层(见图 1),在土层交界面处形成一个等效基础,将这个等效基础的极限承载力作为上部硬土层基础的极限承载力,其计算公式为:
| $ \begin{align} & {{q}_{\text{u}}}=6{{S}_{\text{ub}}}\left[ \frac{1+0.2\left( D+H \right)}{\left( B+2H\text{tan}\alpha \right)} \right]\times \\ & {{(\frac{B+2H\text{tan}\alpha }{B})}^{2}}+\gamma D \\ \end{align} $ | (1) |
|
| 图 1 投影面积法示意图 Fig.1 Schematic diagram for projection area method |
式中:qu为地基极限承载力;B为基础直径;H为上层黏土厚度;D为计算断面至海底泥面的深度;γ为上层土体的有效重度;Sub为下层土不排水抗剪强度;α为扩散角。
1.2 Brown & Meyerhof公式Brown & Meyerhof公式是基于圆形基础试验数据归纳出的经验公式,它同时考虑了上层土和下层土的性状对极限承载力的影响。该公式可用于上硬下软或上软下硬土层地基极限承载力的计算。当桩靴处于双层地基的上层土中时,其极限承载力的计算公式为:
| $ {{q}_{\text{u}}}=\left( \frac{3{{S}_{\text{ut}}}H}{B}+6{{S}_{\text{ub}}} \right)+\gamma D $ | (2) |
式中Sut为上层土的不排水抗剪强度。
在对插桩作业进行工程设计时,以上2种方法具有概念简单、参数物理意义明确等优点。但由于各层土的强度、上层土厚度等因素都将对成层土地基极限承载力产生影响,而上述2种方法的适用范围和限制条件都不明确,因此,鉴于在上硬下软土层插桩时存在着“穿刺”的危险,本文对上硬下软双层黏土地基的极限承载力问题进行深入研究。
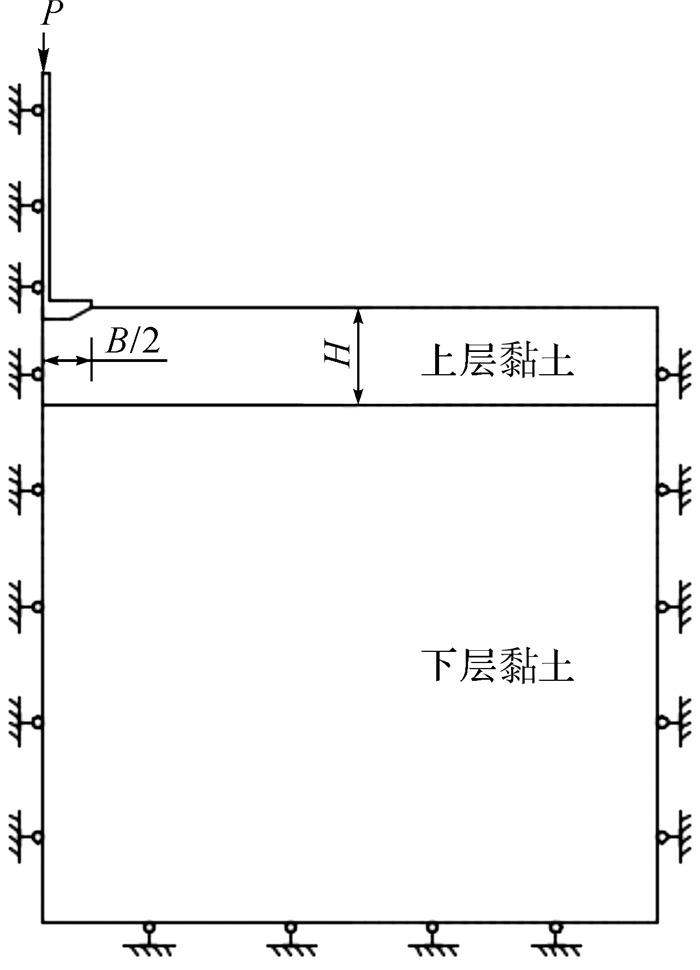
2 数值模型的建立与求解 2.1 有限元模型的建立自升式海上钻井平台的插桩过程可以看作是:在具有初始地应力的半无限弹塑性地基上,强迫圆柱形基础的埋深逐渐增加的准静态过程。插桩问题可以简化为桩靴与周围土体相互作用的弹塑性接触轴对称问题。本文在ABAQUS平台上建立了双层黏土中的桩-土耦合轴对称平面模型,如图 2所示。桩腿和周围土体都采用四节点二维轴对称单元CAX4R。桩靴与周围土体的接触定义为符合库伦摩擦定律的主从接触面接触,摩擦系数为0.3。桩腿材料为普通钢材,弹性模量为210 GPa,泊松比为0.27,桩靴直径B为8.0 m,高度为1.5 m,桩腿直径为1.0 m。黏土的弹性模量为不排水抗剪强度的500倍,泊松比为0.49,有效重度为8 kN/m3。
|
| 图 2 桩-土耦合模型 Fig.2 Pile-soil coupling model |
插桩对土体的扰动只限于桩靴附近,远处土体的应力状态和位移状态不应受到影响。为尽量消除边界效应对计算结果的影响,有限元模型的径向尺寸取50 m,深度取50 m。在土体模型的右侧施加水平方向位移约束,底面施加铅垂方向位移约束。利用模型的轴对称性,在桩腿和土体模型的中心线上(左侧边界)施加水平位移约束,土体模型顶面自由。为了减小计算误差,同时也为了缩短计算时间,桩-土接触面附近的单元网格划分得较细密,而远离接触面的土体,其网格划分相对稀疏,如图 3所示。

|
| 图 3 桩-土耦合模型网格划分 Fig.3 Mesh of pile-soil coupling model |
保持桩靴尺寸不变,通过改变上部土层厚度,上、下层土强度比值和桩靴贯入深度等物理和几何参数,依次建立有限元模型并进行计算,研究上硬下软双层黏土地基中桩靴承载力的变化情况。
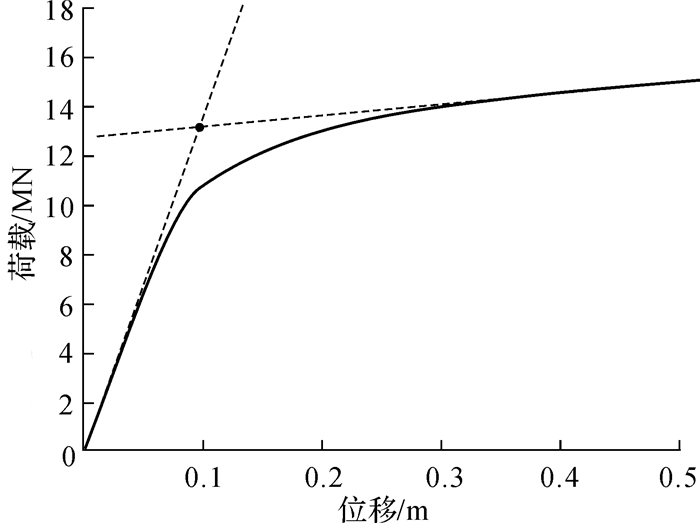
2.2 极限承载力的确定本文采用大型有限元软件ABAQUS对问题进行分析,其中土体采用Mohr-Coulomb模型,桩腿为满足MISES屈服准则的理想弹塑性模型。通过对桩腿顶端的中心节点施加不同的位移荷载,来模拟贯入深度不断增加的过程。图 4为上层土厚度与桩靴直径之比(简称为相对厚度比)H/B=1.0,上、下层黏土的不排水抗剪强度分别为60 kPa和15 kPa,位移荷载为0.5 m时得到的荷载—位移曲线。由图可以看出,在加载初期,荷载与位移呈线性关系,桩靴周围的土体呈弹性变形状态。随着荷载的增加,桩靴的贯入量亦随之增加,桩靴周围的土体逐渐进入屈服状态,导致其对桩靴贯入的阻力减小,荷载—位移曲线亦由陡变缓。这时,运用切线交汇法[17],取图中2条切线(虚线)交点对应的纵坐标值作为桩靴的极限承载力。
|
| 图 4 典型荷载—位移曲线 Fig.4 A typical curve of load-displacement |
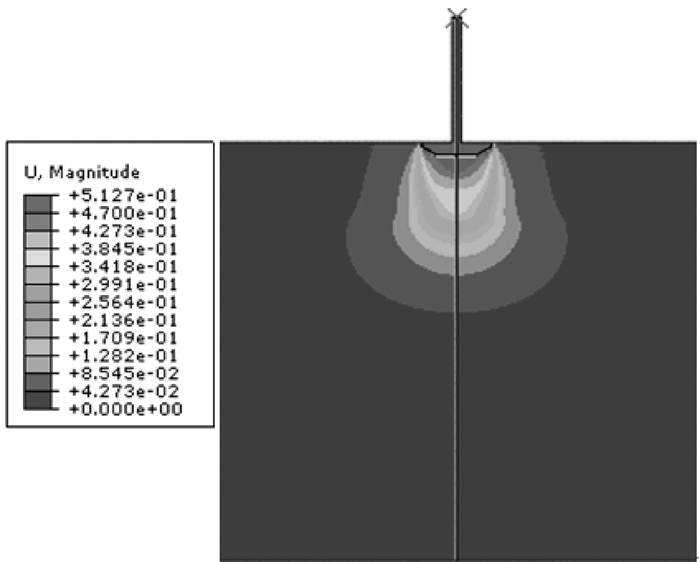
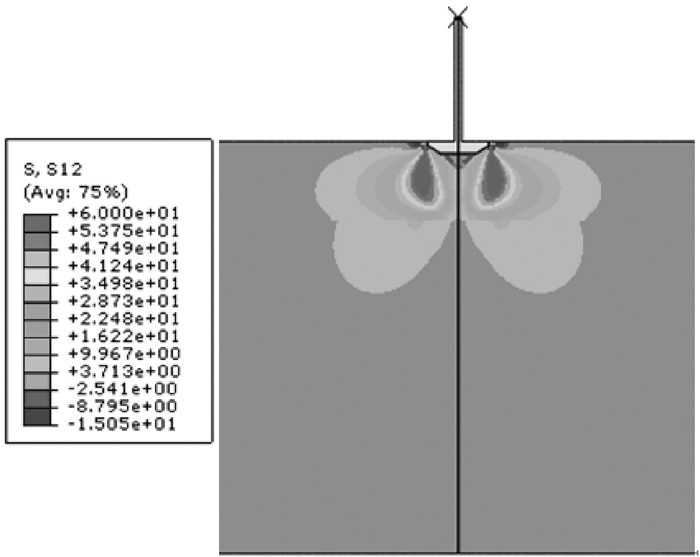
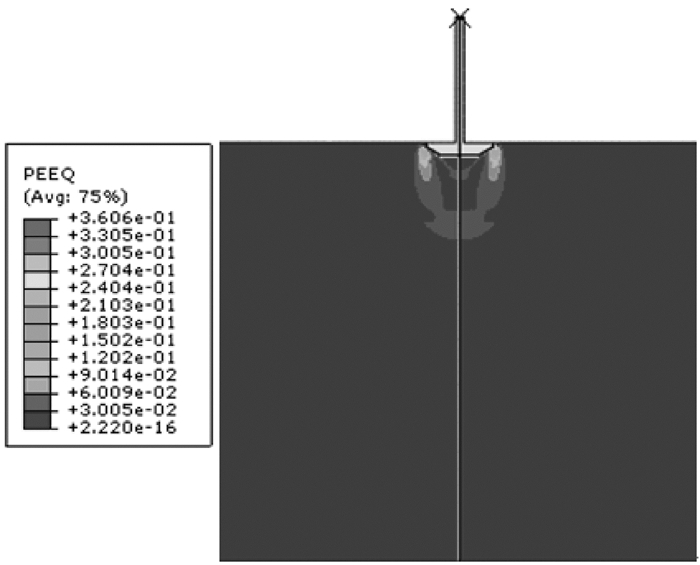
桩靴贯入0.5 m时的位移等值线如图 5所示,对应的最大剪应力等值线如图 6所示,等效塑性应变等值线如图 7所示。由图 6可以看出,桩靴边缘处土体中的最大剪应力已经达到其剪切屈服极限(60 kPa),这标志着剪切流动已经产生。由图 7可以看出,当桩靴达到极限承载力时,桩靴周围土体的塑性区已经连通成片,且已扩展至软土区,并在交界面以下的软土区出现塑性区突然增大的现象,表明交界面处具有位移连续、应变不连续的特性。
|
| 图 5 桩靴贯入0.5 m时的位移等值线 Fig.5 Displacement contour with spudcan penetration of 0.5 m |
|
| 图 6 桩靴贯入0.5 m时的最大剪应力等值线 Fig.6 Maximum shear stress contour with spudcan penetration of 0.5 m |
|
| 图 7 桩靴贯入0.5 m时的等效塑性应变等值线 Fig.7 Equivalent plastic strain contour with spudcan penetration of 0.5 m |
此情况下,由本文有限元模型计算的极限承载力为13.1 MN,而由Brown & Meyerhof公式和投影面积法得到的极限承载力分别为13.6 MN和14.1 MN,说明本文的计算模型具有足够的精度。
3 计算结果分析在自升式平台插桩作业设计中,作业现场地基极限承载力的确定一直是工程师关心的关键问题之一。在双层土地基中,极限承载力不仅与上、下层土不排水抗剪强度之比Sut/Sub(简称为上、下层土强度比)有关,还与上层土相对厚度比H/B有关[18]。本文通过基于一系列不同物理和几何参数的有限元模型,考察这2个因素对双层黏土地基极限承载力的影响,并与传统经验公式计算的结果进行对比,最后对双层黏土地基中的穿刺行为进行计算分析。
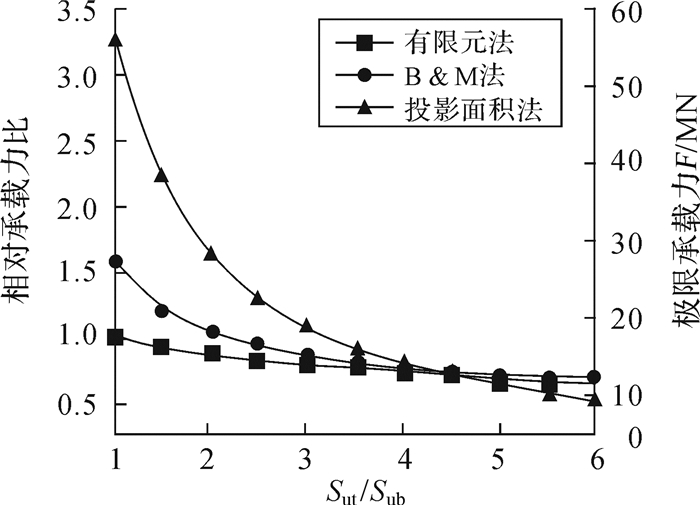
3.1 上、下层土强度比的影响上、下层土强度比Sut/Sub是影响成层土地基极限承载力的主要因素之一。本文设定上层土相对厚度比为1.0, 上层土不排水抗剪强度为60 kPa,按照表 1所示的不同上、下层土强度比考察方案,依次构建有限元模型并计算其极限承载力,考察土层强度比对极限承载力的影响,并与经验公式计算的结果进行比较,其计算结果如图 8所示。
| 方案 | Sub/kPa | Sut/Sub |
| 1 | 60.0 | 1.0 |
| 2 | 40.0 | 1.5 |
| 3 | 30.0 | 2.0 |
| 4 | 24.0 | 2.5 |
| 5 | 20.0 | 3.0 |
| 6 | 17.1 | 3.5 |
| 7 | 15.0 | 4.0 |
| 8 | 13.3 | 4.5 |
| 9 | 12.0 | 5.0 |
| 10 | 10.9 | 5.5 |
| 11 | 10.0 | 6.0 |
|
| 图 8 不同Sut/Sub时地基极限承载力曲线 Fig.8 The curves of foundation ultimate bearing capacity with different Sut/Sub |
由图 8可以看出,本文有限元计算结果和经验公式计算结果都表明,双层黏土地基的极限承载力随着上、下层土强度比的增大而减小。当Sut/Sub > 4.5时,有限元计算结果在2个经验公式结果之间,且与Brown & Meyerhof公式的结果更接近。当Sut/Sub < 4.5时,随着上、下层土强度比的降低,有限元计算结果与2个经验公式的计算结果差别越来越大。当Sut/Sub减至1.0时,双层土退化成单层土,有限元计算的相对承载力比(双层土基础极限承载力与单一上层土极限承载力之比)为1.0,而由Brown & Meyerhof公式和投影面积法计算的相对承载力比分别为1.53和3.18,表明经验公式计算结果已经严重失真。由此可见,2个经验公式更适用于软、硬差别明显的双层黏土地基承载力的计算,而对于上、下层土强度差别不大的成层土,则会产生较大的误差。在上层土相对厚度比为1.0时,用Brown & Meyerhof公式计算其极限承载力,上、下层土强度比不宜低于3.0;而由于投影面积法中没有考虑上层黏土的抗剪强度,在下层黏土强度较大时会高估其极限承载力,而在强度较低时又会低估其极限承载力,其适用于上、下层土强度比为4.0~6.0的成层土。
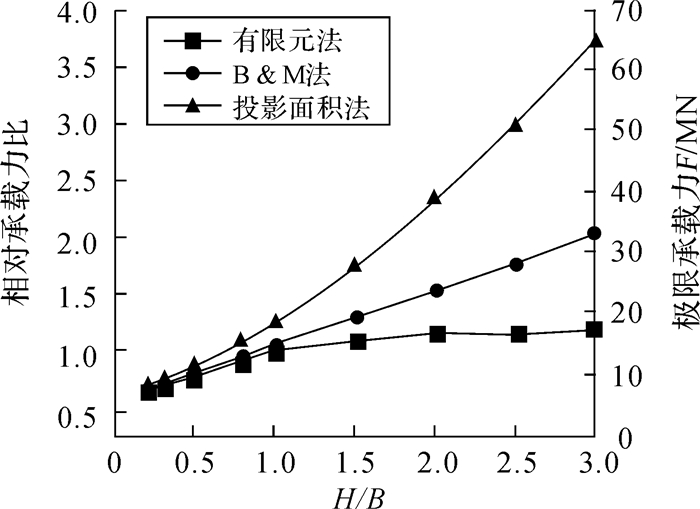
3.2 上层土相对厚度比的影响上层土相对厚度比H/B也是影响成层土地基极限承载力的重要因素。本文设定上、下层土不排水抗剪强度分别为60 kPa和20 kPa,按照表 2所示的不同上层土相对厚度比考察方案,依次构建有限元模型并计算其极限承载力,考察上层土相对厚度比对极限承载力的影响,并与经验公式计算的结果进行比较,其计算结果如图 9所示。
| 方案 | H/m | H/B |
| 1 | 2.4 | 0.3 |
| 2 | 4.0 | 0.5 |
| 3 | 6.4 | 0.8 |
| 4 | 8.0 | 1.0 |
| 5 | 12 | 1.5 |
| 6 | 16 | 2.0 |
| 7 | 20 | 2.5 |
| 8 | 24 | 3.0 |
|
| 图 9 不同H/B时地基极限承载力曲线 Fig.9 The curves of foundation ultimate bearing capacity with different H/B |
从图 9可以看出,随着上层黏土厚度的增加,地基极限承载力逐渐增大。当上层黏土厚度比H/B < 1.0时,有限元计算结果与2个经验公式计算结果非常接近;当H/B>1.0时,随着上层土厚度的增加,有限元结果和2个经验公式结果之间的差别越来越大。由有限元计算结果曲线可知:当H/B < 1.0时,荷载曲线增长较快;当H/B > 1.0时,荷载曲线渐趋平缓。这说明,随着上层黏土厚度的逐渐增加,下层软黏土对表层地基极限承载力的影响越来越小。当H/B=3.0时,双层地基的相对承载力比已经达到0.98,非常接近于单一上层土的极限承载力。反观由2个经验公式计算得到的承载力曲线,其极限承载力一直随着上层土相对厚度比的增加而增长,当H/B=3.0时,其相对承载力比分别达到1.87和3.68,已经远远超出了合理范围。由此可见,在上、下层土强度比Sut/Sub=3.0的情况下,只有在上层土相对厚度比H/B < 1.0时,由这2个经验公式得到的极限承载力才是合理的。
3.3 穿刺分析在插桩作业过程中,如果地基承载能力突然下降,加之采取措施不当,可能会引起桩靴穿刺。大量研究发现,穿刺破坏与上层土相对厚度比和上、下层土的相对强度比有直接关系。为了分析这2个因素对双层黏土地基中桩靴穿刺行为的影响,本文通过预置埋深法建立不同贯入深度(贯入深度分别为0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0 m)时的桩-土耦合有限元模型,研究插桩作业过程中桩靴贯入深度与极限承载力之间的关系。穿刺分析计算方案如表 3所示。
| 方案 | Sut/kPa | Sub/kPa | H/B |
| (a) | 60.0 | 20 | 1.5 |
| (b) | 60.0 | 20 | 1.0 |
| (c) | 60.0 | 10 | 1.0 |
其中方案(a)和(b)的设计旨在比较在上、下层土强度比相同的情况下,上层土相对厚度比对穿刺行为的影响;方案(b)和(c)的设计旨在比较在上层土相对厚度比相同的情况下,上、下层土强度比对穿刺行为的影响。计算结果如图 10所示。
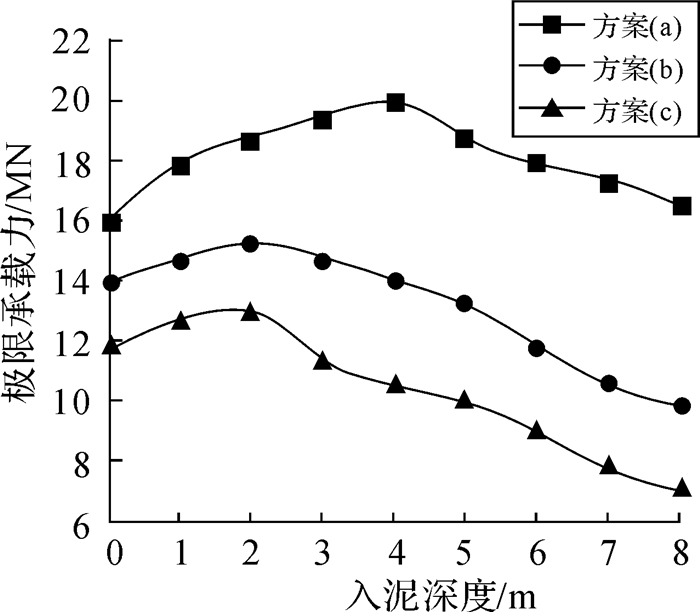
|
| 图 10 地基承载力—贯入深度曲线 Fig.10 The curves of foundation bearing capacity-penetration depth |
由图 10可以发现,在桩靴贯入初期,地基承载力随着贯入深度的增加而提高,达到峰值以后,呈现下降趋势。这是因为:刚开始贯入时,桩靴的位置离下层软土较远,地基承载力表现为类似单一土层贯入时的增长趋势;随着贯入深度的增加,桩靴向土层分界面靠近,下层软土对地基承载力的影响逐渐增强,在桩靴达到分界面之前,双层地基的极限承载力已经开始下降。由方案(a)与方案(b)的承载力曲线比较发现,2条曲线都存在峰值,即都存在着发生穿刺的可能性。在相对厚度比H/B=1.5时(方案(a)),承载力曲线在入泥深度为4 m时达到极值;在相对厚度比H/B=1.0时(方案(b)),承载力曲线在入泥深度为2 m时发生转折。由方案(b)和方案(c)的承载力曲线比较可以看出,2条曲线也都存在峰值,且随着土层强度比的增大(方案(c)较于(b)),承载力曲线达到峰值后的减幅更大。换言之,上、下层土强度比越大,发生穿刺的可能性越大。
4 结论自升式钻井平台桩靴承载力预测是插桩作业设计中的关键问题之一。上硬下软双层黏土地基极限承载力的确定是一个较为复杂的工程问题。上、下层土强度比和上层土相对厚度比对其极限承载力都有明显的影响,同时也是引起穿刺的重要因素。现有的工程实用计算方法有着各自的适用范围和限制条件,在进行工程设计时应予以考虑。本文将插桩过程视为桩靴在半无限弹塑性地基上逐渐贯入的准静态过程,将土体视为满足摩尔-库伦屈服准则的各向同性弹塑性体,定义桩-土之间的接触为满足库伦摩擦定律的主从接触面接触,在ABAQUS平台上应用非线性有限元方法,分析了上、下层土强度比和上层土相对厚度比对上硬下软双层黏土地基极限承载力的影响,并对穿刺现象进行了分析,得到了如下对自升式平台插桩作业设计和施工具有指导意义的结论:
1) 当上层土厚度比一定时,上、下层土强度比越小,双层土地基的极限承载力越大。当强度比趋于1.0时,双层黏土地基的极限承载力趋于单一上层黏土的极限承载力。Brown & Meyerhof公式和投影面积法都不能反映这一渐进特性,而只适用于硬软差别明显的双层土地基。在上层土相对厚度比为1.0时,用Brown & Meyerhof公式计算其极限承载力,上、下层土强度比不宜低于3.0;在用投影面积法计算其极限承载力时,上、下层土强度比为4.0~6.0时较为适宜。
2) 当上、下层土强度比一定时,随着上部黏土层厚度的增加,双层黏土地基的极限承载力逐渐增大。当上层土厚度增大到一定程度时(如上层土相对厚度比H/B > 3.0),下层软黏土对双层土地基极限承载力的影响可以忽略不计。在上、下层土强度比Sut/Sub=3.0的情况下,只有在上层土相对厚度比H/B < 1.0时,由Brown & Meyerhof公式和投影面积法得到的极限承载力才是合理的。
3) 穿刺破坏与上层土相对厚度比和上、下层土强度比有直接关系。上、下层土强度比越大,上层土厚度越小,就越容易发生穿刺现象,且穿刺可能在桩靴贯入双层土分界面之前发生,这是在设计自升式平台插桩作业时需要特别加以关注的。
| [1] | DIER A, CARROLL B.Guidelines for jack-up rigs with particular reference to foundation integrity[R]. Norway:Health & Safety Executive, 2004. |
| [2] | BURD H J, FRYDMAN S. Bearing capacity of plain strain footings on layered soils[J]. Canadian Geotechnical Journal, 1997, 34(2): 241–253. DOI:10.1139/t96-106 |
| [3] | LOVE J P, BURD H J, MILLIGAN G W E, et al. An-alytical and model studies of reinforcement of a layer of granular fill on a soft clay subgrade[J]. Canadian Geotechnical Journal, 1987, 24(4): 611–622. DOI:10.1139/t87-075 |
| [4] | BROWN J D, MEYERHOF G G.Experimental study of bearing capacity in layered clays[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico, Aug.25-29, 1969:45-51. |
| [5] | YOUNG A G, FOCHT J A. Subsurface hazards affect mobile jack-up rig operations[J]. Soundings, 1981, 3(2): 4–9. |
| [6] | TEH K L, CASSIDY M J, LEUNG C F, et al. Revea-ling the bearing capacity mechanisms of a penetrating spudcan through sand overlying clay[J]. Géotechnique, 2008, 58(10): 793–804. DOI:10.1680/geot.2008.58.10.793 |
| [7] | TEH K L, LEUNG C F. Centrifuge model study of spudcan penetration in sand overlying clay[J]. Géotechnique, 2010, 60(11): 825–842. DOI:10.1680/geot.8.P.077 |
| [8] | LIU J, HU Y. The effect of strength anisotropy on the bearing capacity of spudcan foundations[J]. Computers and Geotechnics, 2009, 36(1): 125–134. |
| [9] | THO K K, LEUNG C F, CHOW Y K, et al. Eulerian finite-element technique for analysis of jack-up spudcan penetration[J]. International Journal of Geomechanics, 2010, 12(1): 64–73. |
| [10] | HENKE S, QIU G. Zum absetzvorgang von offshore-hub-plattformen[J]. Geotechnik, 2010, 33(3): 284–292. |
| [11] | QIU G, HENKE S. Controlled installation of spudcan foundations on loose sand overlying weak clay[J]. Ma-rine Structures, 2011, 24(4): 528–550. DOI:10.1016/j.marstruc.2011.06.005 |
| [12] | YU L, HU Y, LIU J, et al. Numerical study of spud-can penetration in loose sand overlying clay[J]. Com-puters and Geotechnics, 2012, 46(4): 1–12. |
| [13] |
付丽娜. 自升式钻井船桩靴承载能力研究[D]. 天津: 天津大学建筑工程学院, 2008: 16-36.
FU Li-na.Research on bearing capacity of pile and shoe of self elevating drilling ship[D]. Tianjin:Tianjin Uni-versity, School of Civil Engineering, 2008:16-36. |
| [14] |
王楠, 吴建政, 徐永臣, 等.
硬土层地基破坏模式及承载能力有限元分析[J]. 海洋石油, 2012, 32(4): 88–95.
WANG Nan, WU Jian-zheng, XU Yong-chen, et al. Finite element analysis of failure modes and bearing ca-pacity of hard soil foundation[J]. Offshore Oil, 2012, 32(4): 88–95. |
| [15] |
郑刚, 周海祚, 程雪松, 等.
砂-黏土双层地基极限承载力的数值研究[J]. 岩土力学, 2016, 37(5): 1475–1485.
ZHENG Gang, ZHOU Hai-zuo, CHENG Xue-song, et al. Numerical study on the ultimate bearing capacity of sand clay layered foundation[J]. Rock and Soil Me-chanics, 2016, 37(5): 1475–1485. |
| [16] |
袁凡凡, 栾茂田, 闫澍旺, 等.
关于成层土地基极限承载力的计算方法[J]. 水利学报, 2001, 45(3): 41–45.
YUAN Fan-fan, LUAN Mao-tian, YAN Shu-wang, et al. Method for calculating the ultimate bearing ca-pacity of layered soil foundation[J]. Journal of Hydraulic Engineering, 2001, 45(3): 41–45. |
| [17] | BOUSHEHRIAN A H, HATAF N, GHAHRAMANI A. Numerical study of cyclic behavior of shallow foundations on sand reinforced with geogrid and grid-anchor[J]. World Academy of Science, Engineering and Technology, 2009, 72(58): 607–610. |
| [18] | HOSSAIN M S, RANDOLPH M F. Investigating potential for punch-though for spud foundations on layered clays[C]//Proceedings of the 17th International Offshore and Polar Engineering Conference.Lisbon, Por-tugal, Jul.1-6, 2007:1510-1517. |



