在航空领域,薄板构件应用特别多,经常需要通过各种方法进行装配,这使得螺栓连接、铆接、胶接以及焊接等各种连接技术倍受重视。在众多的连接方法中,螺栓连接因具有拆装方便、利于系统维护及成本较低等优势,其应用遍布飞机的各个部位。近年来,随着飞机朝着超大宽体的方向发展,螺栓连接的重要性更加凸显,从而使得螺栓连接件的安全可靠性成为航空领域重要的研究课题。在飞机服役过程中,连接薄板不可避免地处于各种严峻的振动环境之中,特别是当系统的外部激励频率与连接板的某一阶或几阶的模态频率一致或接近时,容易发生共振,导致螺栓连接板的可靠性倍受考验。工程设计中,影响螺栓连接板可靠性的因素有很多,比如螺栓施加的预紧力、连接板之间的摩擦系数、螺栓与孔的间隙等。对此很多学者围绕飞机结构中广泛使用的复合材料螺栓连接板的力学行为开展了研究,主要包括:螺栓连接件的动力学建模,各种参数对螺栓圆孔应力分布、螺栓孔位置裂纹萌生、裂纹扩展的影响等[1-5]。但是大多数研究所施加的载荷为静态拉伸载荷,这显然与飞机上螺栓连接板的真实载荷环境不同。因为飞机在飞行过程中,由于空-地-空载荷变化以及气流扰动等诸多因素的影响,连接板很可能处于共振环境之下。共振不仅使得螺栓松动,而且容易在螺栓孔位置引发疲劳裂纹。在振动载荷的持续作用下,结构裂纹可能扩展,并与连接板的动力学行为发生耦合,这对螺栓连接板的疲劳寿命具有不可忽视的影响[6-7]。
为了提高螺栓连接板的抗疲劳强度,研究者提出了多种抗疲劳制造与优化设计方法。这些方法的思路通常是从分析影响螺栓连接件模态频率的因素出发,通过改变连接件的质量和刚度分布来改变连接件的模态频率,从而使激励频率远离连接件模态频率,最终避免共振。比如:易济南从制造工艺与紧固件的结构形式出发,研究了一种适当降低紧固件刚度以提高螺栓连接件振动疲劳强度的设计方法[8];胡迎春等从螺栓连接件的装配方案入手,研究了一种在振动环境下提高螺栓连接系统振动疲劳寿命的策略[9];万存才则以螺栓连接件振动测试为切入点,研究了如何使弯曲模态避开激励频带,提出了一种提高弯曲模态阻尼比的抗振动疲劳设计方法[10]。此外,王崴等研究了螺栓连接件结合面间的摩擦系数对连接自松弛机理的影响,结果表明摩擦系数变化对螺栓连接件的抗振动疲劳具有明显的影响[11];张振等研究了螺栓预紧力和螺栓材料对连接件模态参数的影响[12]。
尽管国内外研究人员对螺栓连接件的静动力学问题作了大量的研究,但有关螺栓与孔间隙变化对螺栓连接板模态频率的影响研究鲜有报道。本文结合ABAQUS软件和Python编程语言,完成变通孔直径的单搭单螺栓连接板有限元建模,在此基础上探讨螺栓与孔间隙变化对螺栓连接板模态频率的影响机制,进而提出一种基于变通孔直径的螺栓连接板抗振动疲劳设计方法。
1 建模策略对于简单构件的模态频率的探讨,运用解析法便可得到系统的模态频率,进而探讨各因素对模态频率的影响。然而对于复杂的螺栓连接板多体构件而言,采用解析法进行动力学解析建模就增大了难度,而且在建模过程中,几乎不可能体现夹紧力、摩擦系数以及螺栓与孔间隙的变化对连接板系统动力学行为的影响。所以,本文借助ABAQUS软件和Python语言完成有限元动力学建模。对于任何复杂螺栓连接件而言,在不考虑阻尼的情况下,离散系统的动力学特征方程为:
| $ \mathit{\boldsymbol{K}}{{\varphi }_{i}}=\omega _{i}^{2}\mathit{\boldsymbol{M}}{{\varphi }_{i}} $ | (1) |
式中: K表示系统的刚度矩阵; M表示系统的质量矩阵;φi表示第i阶模态的振型向量; ωi表示第i阶模态频率。
求解动力学特征方程(1),就可以得到系统的模态频率和模态振型。动力学方程表明,影响模态频率的参数是系统质量和刚度分布。换言之,在螺栓连接板的动力学设计过程中,由于装配需要或者制造误差等因素的影响,通孔直径发生变化,势必影响到连接件的质量和刚度分布规律,进而也将改变螺栓连接件结合面之间的摩擦力分布。比如,通孔直径变大,系统的刚度就会变小,同时系统的质量也在变小。从影响模态频率的角度而言,刚度减小对降低系统模态频率有利,而质量减小对增加系统模态频率有利。关键问题在于,通孔直径变化所引起的刚度变化率和质量变化率并非线性关系,而且质量对系统模态频率的影响机制与刚度对系统模态频率的影响机制也不同,这种相互影响机制十分复杂。
为了探讨螺栓与孔间隙变化对螺栓连接板模态频率的影响,首要的工作是建立包含变化的螺栓与孔间隙的连接件有限元网格模型。本文采取的建模策略是借助Python语言对ABAQUS软件进行二次开发,通过Python直接与ABAQUS内核交互,编写接口命令不断调用模型对象,建立螺栓与孔间隙自动变化的计算模型[13-17]。
自动建模时,需要对结果数据库对象模型选择性提取数据,提高分析效率,建模流程如图 1所示。自动建模过程中,每修改一次通孔尺寸,就重新生成一个有限元计算模型,每一个尺寸对应一个odb文件。模态分析时,提取各通孔尺寸下各阶模态频率,并借助ABAQUS-Excel插件,生成Excel文件数据。最后,通过MATLAB编程对Excel表格数据进行处理,完成通孔直径变化对系统模态频率的影响规律分析。

|
| 图 1 含变通孔直径的连接板有限元建模流程 Fig.1 Finite element modeling flow of joint plate with varible through-hole diameter |
单搭单螺栓连接板广泛应用于飞机结构。本文以单搭单螺栓连接板为对象,建立考虑螺栓与孔间隙变化的有限元模型。
2.1 单搭单螺栓连接板试件本文设计了一种单搭单螺栓连接板试件,试件的几何形状如图 2所示。L1和L2为薄板1和薄板2的长度,t为薄板厚度,W为薄板宽度,D为板孔直径,e为板孔距板端距离。

|
| 图 2 单搭单螺栓连接板几何形状 Fig.2 The geometry of single lapped and single bolted joint plate |
算例分析中,薄板1和2的材料均采用LY12CZ铝合金,而螺栓与螺母均采用40Cr。材料40Cr的密度ρ=7 850 kg/m3,弹性模量E=210 GPa,泊松比ν=0.27。LY12CZ的密度ρ=2 740 kg/m3,弹性模量E=71.7 GPa,泊松比ν=0.33。
为探讨螺栓与孔间隙变化对连接板模态频率的影响,假定螺栓规格为M6普通螺栓,通孔直径初始值为6 mm,建模过程中通孔直径依据设定情况进行变化。连接板的形状尺寸如表 1所示。
| 参数 | L1/mm | L2/mm | t/mm | D/mm | e/D | W/D |
| 数值 | 150 | 150 | 3 | 6 | 3 | 3 |
通孔直径的大小度量采用基轴制,因为通孔直径对连接板模态频率影响的计算模型受螺栓头直径限制,并考虑到通孔过大容易导致螺栓与螺母接触面过小、易联接失效的实际情况,所以通孔直径的范围设置为6~7.8 mm。为了充分考虑螺栓与孔间隙对连接件固有频率的影响,数值分析时通孔直径变化步长设为0.01 m。
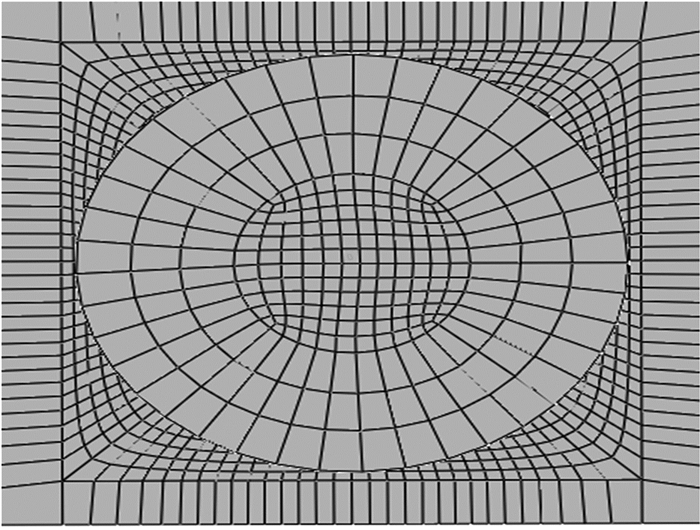
2.2 网格模型与参数设置为分析方便,将螺栓连接板的有限元网格模型简化为由2块带单孔板、1个简化的螺栓与1个简化的螺母组成。所有网格均采用C3D8R单元,孔边网格细化,有限元网格划分采用中性轴算法。为了考虑因通孔直径变化引起的各结合面之间以及板与板结合面之间摩擦力变化对模态频率的影响,板与板、板与螺栓、板与螺母结合面均定义摩擦接触,摩擦系数均设置为0.15。螺栓螺母定义为tie连接,设置分析步时用线性摄动的频率分析步。模态分析时,考虑对薄板1的左端完全固支以及薄板1左端、薄板2右端完全固支两种边界条件类型,建立的连接板有限元网格模型如图 3所示,螺栓位置网格细化的局部视图如图 4所示。

|
| 图 3 单搭单螺栓连接板有限元模型 Fig.3 Finite element model of single lapped and single bolted joint plate |
|
| 图 4 螺栓位置网格细化局部视图 Fig.4 Local view of fine mesh in bolt |
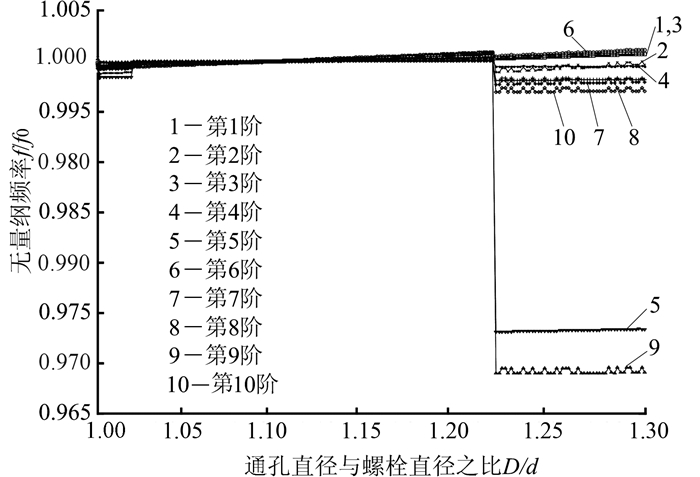
为分析方便,对通孔直径进行无量纲化,令a=D/d,其中D表示通孔直径,d表示螺栓直径。对连接板的各阶模态频率也进行无量纲化,令ξ=f/f0,其中:f表示通孔直径为D时连接板的模态频率;濮良贵等所著《机械设计》中建议螺栓连接中通孔直径D=1.1d[18],故f0表示通孔直径为1.1d时连接板的模态频率,以与经典设计方法建议尺寸的频率效应作比较。图 5与图 6表示2种边界条件下螺栓与孔间隙变化对连接件前10阶模态频率的影响计算结果。
|
| 图 5 一端固支时螺栓与孔间隙对模态频率的影响 Fig.5 Impacts of bolt-hole clearance on modal frequencies with one end fixed |
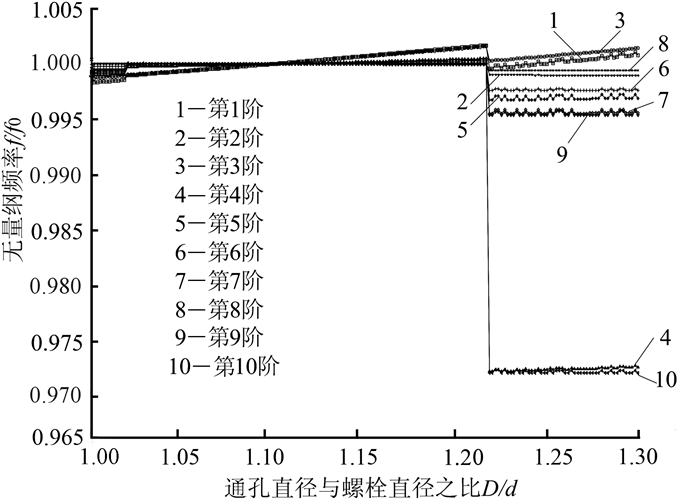
|
| 图 6 两端固支时螺栓与孔间隙对模态频率的影响 Fig.6 Impacts of bolt-hole clearance on modal frequencies with both ends fixed |
结果显示,螺栓连接板在一端固支、两端固支两种边界条件下,模态频率随通孔直径变化的关系相近,在通孔直径与螺栓直径比值为1.21~1.22时发生突变,在这个分界点前后通孔直径变化对频率有一定影响,但影响较小。对于一端固支条件下,当通孔直径处于1.1d±0.08d时,通孔直径变化对螺栓连接板各阶模态频率的影响基本上可忽略。对于两端固支边界条件下,当通孔直径处于1.1d±0.06d时,通孔直径变化对螺栓连接板各阶模态频率的影响基本上可忽略。当通孔直径大于1.21d时,通孔直径变化对连接板的各阶模态频率具有明显的影响,而且影响程度各异。根据图 5与图 6显示的结果,很容易判断通孔直径变化对螺栓连接板各阶模态频率的影响。其中,一端固支条件下,在通孔直径与螺栓直径比值为1.21~1.22时,模态频率突变最明显的是第5阶与第9阶。两端固支条件下,在通孔直径与螺栓直径比值为1.21~1.22时,模态频率突变最明显的是第4阶与第10阶。
计算结果表明螺栓与孔间隙的变化对螺栓连接板的模态频率具有明显的影响,特别是对于特定模态的频率,变化量较大,如表 2与表 3所示。
| 阶数 | 最大固有频率/Hz | 最小固有频率/Hz | 频率变化比/% |
| 1 | 28.555 | 28.518 | 0.130 |
| 2 | 175.360 | 174.971 | 0.222 |
| 3 | 192.807 | 192.566 | 0.125 |
| 4 | 534.759 | 534.448 | 0.058 |
| 5 | 671.555 | 653.314 | 2.792 |
| 6 | 1 054.007 | 1 052.023 | 0.189 |
| 7 | 1 102.197 | 1 099.335 | 0.260 |
| 8 | 1 707.036 | 1 703.731 | 0.194 |
| 9 | 2 251.284 | 2 181.088 | 3.218 |
| 10 | 2 869.845 | 2 860.859 | 0.314 |
| 阶数 | 最大固有频率/Hz | 最小固有频率/Hz | 频率变化比/% |
| 1 | 153.788 | 153.275 | 0.335 |
| 2 | 641.720 | 641.008 | 0.111 |
| 3 | 936.494 | 933.844 | 0.284 |
| 4 | 1 081.243 | 1 050.795 | 2.898 |
| 5 | 1 112.197 | 1 108.239 | 0.357 |
| 6 | 1 796.960 | 1 792.653 | 0.240 |
| 7 | 2 882.433 | 2 869.269 | 0.459 |
| 8 | 3 460.285 | 3 458.017 | 0.066 |
| 9 | 3 646.578 | 3 629.736 | 0.464 |
| 10 | 4 034.717 | 3 922.357 | 2.865 |
分析结果表明,一端固支条件下,螺栓与孔间隙变化使得连接板的第5阶模态频率改变量接近20 Hz,第9阶模态频率改变量约为70 Hz。两端固支边界下,螺栓与孔间隙变化使得连接板的第4阶模态频率改变量约为30 Hz,第10阶模态频率改变量约为110 Hz。结果说明,通孔直径的变化对特定边界条件下螺栓连接板的特定模态频率有明显的影响。因此对于连接件工况模态的模态频率对通孔直径敏感的情况,适当调整螺栓与孔的间隙对于连接板的抗共振具有非常重要的作用。
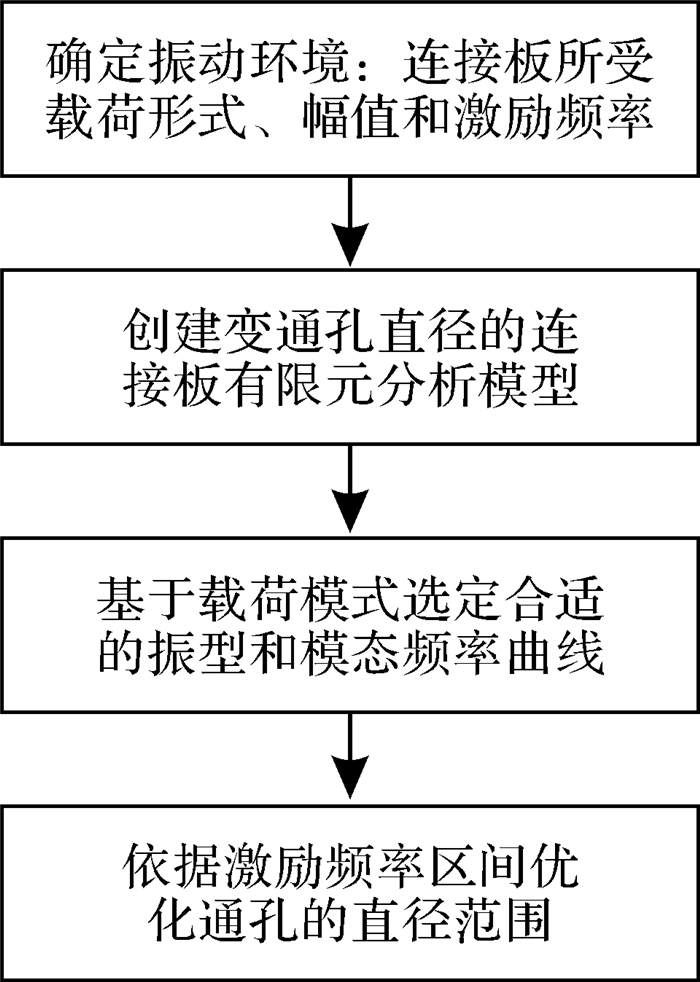
4 基于变通孔直径的连接件动力学设计对于飞机薄板螺栓连接结构而言,连接件必须在振动环境下工作,而且很可能处于宽频带激励的振动环境中。螺栓连接板的工作环境实际反映了外部激励的幅值和激励频率的大小。因此,如果已知连接板常驻的工作环境,则可为确定连接件系统的强迫共振区间提供参考。从抗振动疲劳设计的角度来看,螺栓连接件的模态频率应该避开机器的常见环境工作频率。因此,结合通孔直径对螺栓连接件模态频率的影响曲线,可以通过系统的共振区间找出避开共振区间的通孔尺寸,作为动力学设计的依据,方案如图 7示。
|
| 图 7 基于变通孔直径的连接件动力学设计方法 Fig.7 Dynamical design method of joint plate based on variable through-hole diameter |
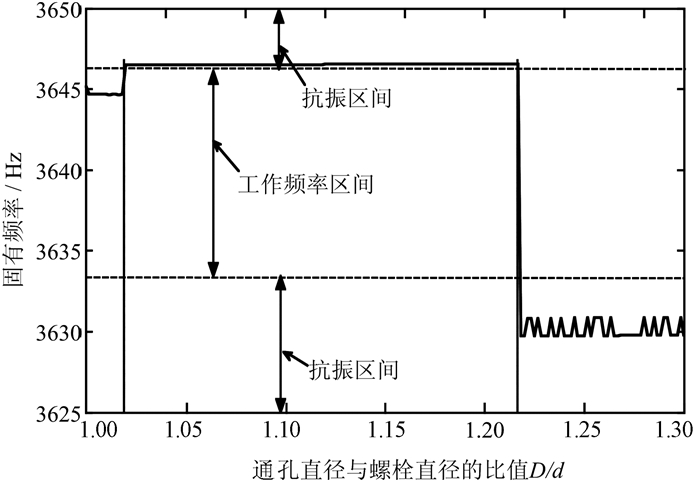
下面进一步阐述如何避免系统的共振,为螺栓连接板的动力学设计提供思路。假设螺栓连接板工作环境频率处于第9阶模态附近,并且工作频率为3 635~3 645 Hz。为了进行动力学设计,首先调出通孔直径变化对第9阶模态频率的影响曲线,划分工作频率区间,即能快速找到抗振疲劳动力学设计尺寸区间为1.02d~1.21d以及1.22d~1.3d。
如图 8所示,假设单搭单螺栓连接板所采用的螺栓直径为6 mm,通过螺栓连接板工作环境确定的设计区间,即可确定螺栓连接板通孔的抗振疲劳设计尺寸为7.12~7.26 mm以及7.32~7.8 mm。
|
| 图 8 基于变通孔直径的抗振疲劳设计应用 Fig.8 Design application of anti-vibration fatigue based on variable through-hole diameter |
这种优化可为螺栓连接件的抗振疲劳动力学设计提供一种新的思路。当然,上述针对的是对频率敏感的连接板件的设计,一般来讲,如果经典设计下的工作模态确实处于共振区间,可以加大通孔直径以降低固有频率,效果好的可以降低100 Hz以上,例如两端固支条件下,经典设计下工作模态为第10阶模态且为共振情况。
5 结语以单搭单螺栓铝合金连接板为研究对象,基于ABAQUS软件和Python语言,建立了变通孔直径的连接板有限模型。为探讨通孔直径变化对连接板模态频率的影响,通过仿真计算得到了不同通孔直径下的模态频率变化规律,并利用该规律提出了一种基于变通孔直径的连接板动力学设计方法。主要结论如下:
1) 螺栓连接板在一端固支、两端固支两种边界条件下,模态频率随通孔直径变化的关系相近,在通孔直径与螺栓直径比值为1.21~1.22时发生突变。
2) 两端固支边界条件下,当通孔直径处于1.1d±0.06d时,一端固支边界条件下,当通孔直径处于1.1d±0.08d时,通孔直径变化对螺栓连接板各阶模态频率的影响基本上可以忽略,这意味着对于经典设计中建议的1.1d孔径,从孔加工的角度分析,只要孔的误差保证在±0.06d范围内,则对动力学特性无特别影响。
3) 根据通孔直径的变化会对螺栓连接板振动特性产生影响,针对螺栓连接系统有效避开与激励载荷发生共振问题,提出了从通孔直径的角度出发,借助于有限元软件实现抗振疲劳设计的方案,为螺栓连接系统的抗振疲劳设计问题提供了思路。
4) 研究了单搭单螺栓连接系统通孔直径对螺栓连接系统固有振动频率的影响,为多螺栓、复杂分布式安装方法下螺栓连接系统的通孔直径、螺栓安装偏心位置对螺栓连接系统固有振动频率影响的分析提供了参考。
| [1] | KAPIDZIC Z, ANSELL H, SCHON J, et al. Fatigue bearing failure of CFRP composite in bolted joints ex -posed to biaxial variable amplitude loading at elevated temperature[J]. Composite Structures, 2016, 142(8): 71–77. |
| [2] | KAPIDZIC Z, ANSELL H, SCHON J, et al. Fatigue bearing failure of CFRP composite in biaxially loaded bolted joints at elevated temperature[J]. Composite Structures, 2015, 127(9): 298–307. |
| [3] | ZHOU Y, NEZHAD H Y, HOU C, et al. A three di-mensional implicit finite element damage model and its application to single-lap multi-bolt composite joints with variable clearance[J]. Composite Structures, 2015, 131(13): 1060–1072. |
| [4] | CHISHTI M, WANG C H, THOMOSON R S, et al. Experimental investigation of damage progression and strength of countersunk composite joints[J]. Composite Structures, 2012, 94(3): 865–873. DOI:10.1016/j.compstruct.2011.10.011 |
| [5] | MCCARTHY M A, MCCARTHY C T, LAWLOR V P, et al. Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints:part Ⅰ-model development and validation[J]. Composite Struc-tures, 2005, 71(2): 140–158. DOI:10.1016/j.compstruct.2004.09.024 |
| [6] |
刘文光, 陈国平, 贺红林, 等.
结构振动疲劳研究综述[J]. 工程设计学报, 2012, 19(1): 1–8.
LIU Wen-guang, CHEN Guo-ping, HE Hong-lin, et al. Review of studying on vibration fatigue[J]. Chinese Journal of Engineering Design, 2012, 19(1): 1–8. |
| [7] |
刘文光, 林炜彦, 颜龙, 等.
基于抗振动疲劳的薄板加筋设计分析[J]. 工程设计学报, 2016, 23(4): 385–390.
LIU Wen-guang, LIN Wei-yan, YAN Long, et al. A-nalysis on stiffen design of a skin plate by anti vibration fatigue[J]. Chinese Journal of Engineering Design, 2016, 23(4): 385–390. |
| [8] |
易济南.
螺栓连接件抗振性设计及制造[J]. 机械工程与自动化, 2011, 165(2): 166–167.
YI Ji-nan. Anti-vibration design of bolted joint[J]. Mechanical Engineering & Automation, 2011, 165(2): 166–167. |
| [9] |
胡迎春, 刘庚武.
螺栓组件抗拉疲劳及防松性能分析[J]. 机械制造与自动化, 2007, 36(3): 34–35.
HU Ying-chun, LIU Geng-wu. Analyze about the per-formance of tension fatigue and anti-loosen for bolt groupware[J]. Machine Building & Automation, 2007, 36(3): 34–35. |
| [10] |
万存才. G2500-2分动器螺栓振动测试与分析[D]. 大连: 大连理工大学动力工程系, 2003: 1-46.
WAN Cun-cai.Vibration test and analysis of G2500-2 transfer case bolt[D].Dalian:Dalian University of Technology, Department of Power Engineering, 2003:1-46 http://cdmd.cnki.com.cn/Article/CDMD-10141-2004021919.htm |
| [11] |
王崴, 徐浩, 马跃, 等.
振动工况下螺栓连接自松弛机理研究[J]. 振动与冲击, 2014, 33(22): 198–202.
WANG Wei, XU Hao, MA Yue, et al. Self-loosening mechanism of bolted joints under vibration[J]. Journal of Vibration and Shock, 2014, 33(22): 198–202. |
| [12] |
张振, 肖毅, 刘彦清, 等.
基于振动疲劳试验的复合材料螺栓连接预紧力松弛特性[J]. 复合材料学报, 2016, 33(1): 163–173.
ZHANG Zhen, XIAO Yi, LIU Yan-Qin, et al. Preload relaxation characteristics in composite bolted joints based on vibration fatigue test[J]. Acta Material Com-posite Serial, 2016, 33(1): 163–173. |
| [13] |
钟同圣, 卫丰, 王鸷, 等.
Python语言和ABAQUS前处理二次开发[J]. 郑州大学学报(理学版), 2006, 38(1): 60–64.
ZHONG Tong-sheng, WEI Feng, WANG Zhi, et al. Second development for fore treatment of ABAQUS u-sing Python language[J]. Journal of Zhengzhou Uni-versity (Natural Science Edition), 2006, 38(1): 60–64. |
| [14] |
张强, 马永, 李四超.
基于Python的ABAQUS二次开发方法与应用[J]. 舰船电子工程, 2011, 31(2): 131–134.
ZHANG Qiang, MA Yong, LI Si-chao. Method and application of second-developed ABAQUS based on Py-thon[J]. Ship Electronic Engineering, 2011, 31(2): 131–134. |
| [15] |
谈梅兰, 武国玉, 梁福祥.
基于ABAQUS的连杆疲劳分析[J]. 中国机械工程, 2013, 24(5): 634–637.
TAN Mei-lan, WU Guo-Yu, LIANG Fu-xiang. Fatigue analysis of connecting rods based on ABAQUS[J]. China Mechanical Engineering, 2013, 24(5): 634–637. |
| [16] |
石亦平.
ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2012: 1-393.
SHI Yi-ping. Detailed explanation of finite element a-nalysis of ABAQUS[M]. Beijing: China Machine Press, 2012: 1-393. |
| [17] |
曹金凤.
Python语言在ABAQUS中的应用[M]. 北京: 机械工业出版社, 2011: 1-356.
CAO Jin-feng. The application of python language in ABAQUS[M]. Beijing: China Machine Press, 2011: 1-356. |
| [18] |
濮良贵, 纪名刚.
机械设计[M]. 8版. 北京: 高等教育出版社, 2006: 1-424.
PU Liang-gui, JI Ming-gang. Machinery design[M]. 8th ed. Beijing: Higher Education Press, 2006: 1-424. |


