目前国内外汽车馈能研究大多数集中在汽车馈能悬架上,如对电动馈能悬架可回收路面振动能量的特性进行研究[1-3]。刘松山等对电磁馈能悬架进行了分析,其研究表明合理的开启速度能极大地改善馈能减振器的传递特性,阻尼不足区初始速度对谐波激励时的响应峰值影响并不大[4]。陈士安、王伟华等发现馈能减振器在回收振动能量的同时,其阻尼特性也与传统悬架系统接近,能够满足车辆行驶的需要[5-6]。相比于馈能悬架而言,对电机自身馈能的研究没有引起足够重视。然而,在城市道路状况下,车辆经常处于减速、下坡甚至制动行驶状态,此时若电机自身能够馈能,即可反充蓄电池,实现能量回馈。
为方便平台设计和搭建,验证本文提出的电动机馈能效率分析方案的可行性,以中小型电动机为研究对象,对电动机自身馈能进行研究,通过Simulink仿真平台建模分析并设计开发电动机馈能试验平台,进行dSPACE的硬件在环(hardware-in-the-loop, HIL)试验,通过试验与仿真数据验证馈能模型和试验平台设计的可行性,为以后电动机的馈能研究提供一些新思路与方法。
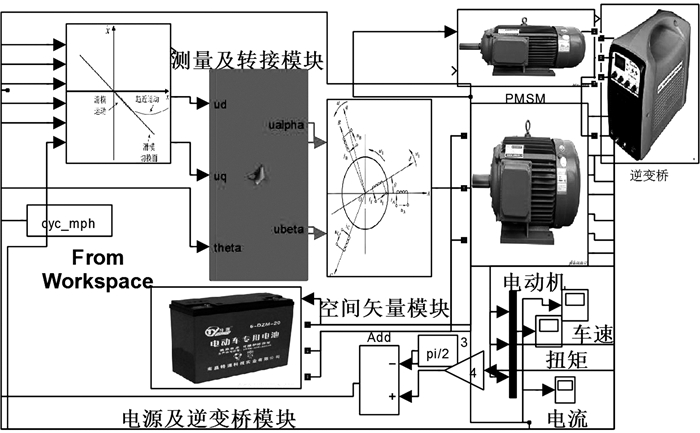
1 PMSM馈能理论建模与仿真分析本文基于Simulink软件建立的PMSM馈能系统仿真模型如图 1所示,其主要由滑模变结构控制、空间矢量、PMSM等模块组成。
|
| 图 1 PMSM馈能系统仿真模型 Fig.1 Simulation model of PMSM energy feedback system |
滑模控制算法在电动汽车动力电机控制的应用,有利于汽车动力性的提升,且以算法自身较强的鲁棒性使汽车运行更加稳定,进而有利于提高乘坐舒适性,因此该算法被广泛应用于永磁同步电动机控制领域[7-10]。永磁同步电动机在d-q坐标系中的转矩方程为:
| $ {T_{\rm{e}}} = \frac{3}{2}p{\psi _{\rm{f}}}{i_q} $ | (1) |
PMSM的直接转矩方程为:
| $ {T_{\rm{e}}} - {T_{\rm{L}}} = B\omega + \frac{J}{p}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} $ | (2) |
将式(1) 代入式(2) 得:
| $ \dot \omega = \frac{{3{p^2}}}{{2J}}{\psi _{\rm{f}}}{i_q} - \frac{p}{J}B\omega - \frac{p}{J}{T_{\rm{L}}} $ | (3) |
式中:Te为电磁转矩,N·m;TL为负载转矩,N·m;B为磁通,Wb;p为电极对数;ω为角速度, rad/s;J为转动惯量, kg·m2;iq为在d-q坐标系下的q轴电流,A;ψf为永磁体磁链峰值, Wb。
1.1.1 滑模控制器的输出函数设计为实现动力电机的控制目标要求,定义角速度跟踪误差:
| $ e\left( t \right) = {\omega _{{\rm{ref}}}} - \omega $ | (4) |
式中ωref为角速度参考值, rad/s。
积分滑模面具有平滑转矩的作用,可以很好地削弱抖动的影响,因此,在切换函数[9]中引入积分项,构造积分型滑模面:
| $ S = e\left( t \right) + {c_1}\int_0^t {e\left( t \right){\rm{d}}t} $ | (5) |
式中:c1为常数且大于0;t为时间, s。
求导可得:
| $ \dot S = - \dot \omega + {c_1}e\left( t \right) $ | (6) |
系统进入滑模面运动时:
| $ \frac{{{\rm{d}}S}}{{{\rm{d}}t}} = 0 $ | (7) |
将式(3) 代入式(6) 得:
| $ \dot S = \frac{p}{J}B\omega + \frac{p}{J}{T_{\rm{L}}} - \frac{{3{p^2}}}{{2J}}{\psi _{\rm{f}}}{i_q} + {c_1}e\left( t \right) $ | (8) |
由公式(4) 变形得:
| $ \omega = {\omega _{{\rm{ref}}}} - e\left( t \right) $ | (9) |
将式(9) 代入式(8) 得最终形式:
| $ \dot S = \left( {{c_1} - \frac{{pB}}{J}} \right)e\left( t \right) - \frac{{3{p^2}{\psi _{\rm{f}}}{i_q}}}{{2J}} + \frac{{pB{\omega _{{\rm{ref}}}} + p{T_{\rm{L}}}}}{J} $ | (10) |
为提高系统的动态响应,滑模变结构控制器采用指数趋近规律:
| $ \dot S = - \xi {\mathop{\rm sgn}} \left( S \right) - KS $ | (11) |
式中:ξ > 0,K > 0,sgn(S)为符号函数,S为滑模面。
因此,滑模控制器的输出函数:
| $ \begin{array}{l} {i_q} = \frac{{2J}}{{3{p^2}{\psi _{\rm{f}}}}}\left[ {\left( {{c_1} - \frac{{pB}}{J}} \right)e\left( t \right) + \xi {\mathop{\rm sgn}} \left( S \right) + } \right.\\ \;\;\;\;\;\;\;\left. {KS + \frac{{pB{\omega _{{\rm{ref}}}} + p{T_{\rm{L}}}}}{J}} \right] \end{array} $ | (12) |
此设计可以接受2个变量变化的影响,能够在不同的负载情况下实现转速的目标要求。
1.1.2 滑模控制系统存在性、可达性与稳定性判断汽车动力源控制系统的滑模存在性及其可达性的证明如下:
| $ S\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = S\left( { - \xi {\mathop{\rm sgn}} \left( S \right) - KS} \right) $ | (13) |
| $ S\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = - \xi \frac{{{S^2}}}{{\left| S \right|}} - K{S^2} $ | (14) |
可得
选取Lyapunov函数评价PMSM控制系统稳定性:
| $ V\left( S \right) = \frac{1}{2}{S^2} $ | (15) |
由上面滑模可达性条件:
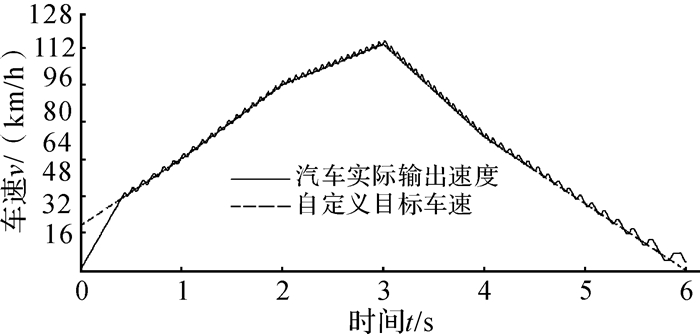
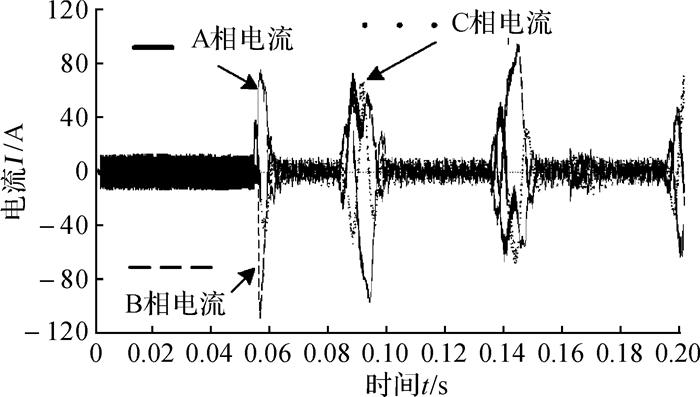
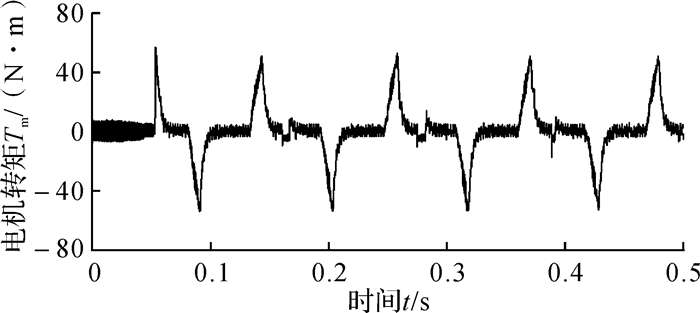
根据图 1的PMSM馈能系统仿真模型,设定0-6 s的自定义工况,进行仿真分析,结果如图 2所示。显然,启动阶段,实际车速与自定义目标车速差异较大,而较短时间后2条曲线很快就吻合,跟随性良好。因此,重点关注启动阶段电机电流和转矩变化,考虑到仿真步长与采样点限制,分析0-0.2 s内的电流变化,如图 3所示;分析0-0.5 s内的转矩变化,如图 4所示;分析0-0.2 s内的电机馈能效率,如图 5所示。
|
| 图 2 自定义工况下汽车实际车速与目标车速对比 Fig.2 Comparison of actual speed and ideal speed under custom condition |
|
| 图 3 0-0.2 s内电机电流变化 Fig.3 Variation of motor current in 0-0.2 s |
|
| 图 4 0-0.5 s内电机转矩变化 Fig.4 Variation of motor torque in 0-0.5 s |
|
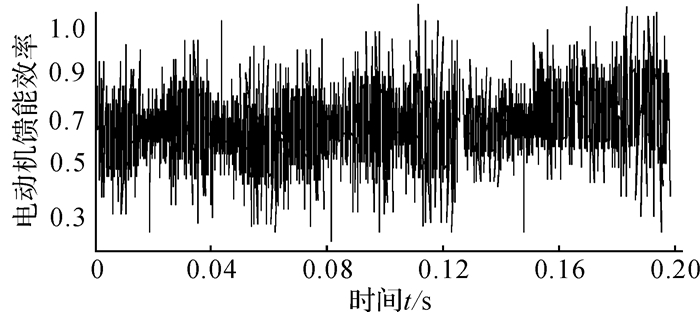
| 图 5 0-0.2 s内电动机馈能效率 Fig.5 Energy feedback efficiency of motor in 0-0.2 s |
由图 5可知电机馈能效率为70%左右,发电机的效率一般为70%~90%,故馈能有一定的可行性。
2 电机馈能系统硬件在环试验与分析为验证上述电机馈能系统理论分析结果,搭建电机馈能系统硬件在环试验平台,如图 6所示。采用dSPACE的DS2211信号采集输入板卡来采集数据、模拟数字信号以及实现通信[11]。基于dSPACE的电机馈能硬件在环试验平台,其主要包括电机控制器的数据处理单元、电动机的驱动电路、直流电动机以及用于硬件在环的dSPACE平台。采用CAN总线进行dSPACE和电动机控制器之间的数据交互[12-15]。通过ControlDesk可以对电动机控制器运行过程中的电流、电压、转速等状态变量动态监测和记录。

|
| 图 6 基于dSPACE的电机馈能系统硬件在环试验平台 Fig.6 Hardware-in-the-loop test platform for motor energy feedback system based on dSPACE |
处理器基准电压设计时需要针对系统要求,综合考虑基准源的技术指标,其主要的指标有:初始精度、输出电压温度漂移及噪声等。带12位A/D转换器的处理系统的基准电压从以下几个方面确定。
2.1.1 初始精度确定电机控制器的处理器采用n位的A/D转换器,其分辨率为1/2n,则所配的基准电压的初始精度λ为:
| $ \lambda = \frac{1}{{{2^n}}} \times {10^6} \times {10^{ - 6}} \times 100\% = \frac{1}{{{2^n}}} \times 100\% $ | (16) |
计算得到12位的转换器的初始精度为0.02%,但是考虑到其他误差的影响,实际的初始精度还要更高些,本设计按照1/2LSB的分辨率来计算,结果为0.01%。
2.1.2 温度系数确定对于n位的数据采集系统A/D转换器,基准温度计算公式:
| $ {T_{\rm{c}}} \le \frac{1}{{{2^n} \times \Delta T}} $ | (17) |
式中ΔT为工作温度变化量,通常以25 ℃作为计算基准,根据工业温度范围为-40~95 ℃,故ΔT设为70 ℃。考虑到误差的影响,实际的基准温度要比计算的小一些,因此Tc=3.48×10-6 ℃。
2.1.3 噪声校核噪声指的是电压基准输出端的电噪声,包括宽频带的热噪声和窄频带的噪声,其中热噪声可通过RC网络滤除,而窄频带噪声是内部固有的,不可滤除。对于12位分辨率的数字系统,它的1LSB值为1/4096,在满量程为2.5 V的电压下分辨的电压约为600 μV。
综合上述条件, 采用MAX6143芯片提供处理系统所需的基准电压,此款芯片温度稳定性为3×10-6/℃,初始精度为±0.05%,电压峰值3.8 μV,适用于高精度的A/D或D/A转换,工作温度范围为-40~125 ℃[16-17],满足汽车级工作要求。
2.2 功率管的选取及驱动设计 2.2.1 MOS管的选型电路设计电机的全桥驱动是电机驱动双方向旋转的电路的核心部分,驱动电路的MOS管的电源必须有足够的功率驱动能力,由驱动电路的关断电压VGEoff、导通电压VGEon、MOS管的门极电荷QG和PWM的开关频率Fs,可以计算MOS管的驱动功率Pdrv:
| $ {P_{{\rm{drv}}}} = {Q_{\rm{G}}} \times \left( {{V_{{\rm{GEon}}}} - {V_{{\rm{GEoff}}}}} \right) \times {f_{\rm{s}}} $ | (18) |
MOS管器件类型的选择方法如下:在低压侧开关中,出于对关闭或导通器件所需电压的考虑,采用N沟道MOS管;在高压侧开关中,出于对电压驱动的考虑,采用P沟道MOS管。
栅极/漏极、漏极/源极及栅极/源极的电容是影响开关性能的重要参数。由于每次开关时都要对这些电容进行充电,因此会产生开关损耗,从而降低MOS管的开关速度与效率。
即使在系统产生尖峰电流时也都要确保所选的MOS管能正常工作,因此根据各种条件下的最大电流来选择器件的额定电流。
综合考虑以上因素,本设计中的MOS管选取IRFP150N,其栅极与源极的阈值电压(threshold voltage)的范围为2~4 V,且绝对额定最大值为±20 V。
2.2.2 IR2110驱动设计9S12XS128的A/D信号采集转速信号,外接5 V的电压信号,由滑动变阻器改变输入电压的大小。在高电平为15.00 V时,导通功率管,电机开始运行,否则,电机停止运转。
选择稳压芯片L7805和稳压芯片78L15分别为IR2110外围电路提供5 V和15 V的电压。电流传感器选择ACS712芯片,该芯片的电流测量范围为-30~30 A,对应模拟量输出为66 mV/A。没有检测电流通过时,输出的电压是VCC/2,并作为基准电压,输出电压Vo=2.5+0.066×Vi, 其中Vi为输入电压,AD0脚输出模拟电压值,由处理器计算待测电流。
2.3 整体电路板设计基于Altium Designer设计电路原理图并绘制PCB板,如图 7所示。图 8为电机馈能ControlDesk工作界面。

|
| 图 7 电机控制器的PCB板 Fig.7 PCB board for motor controller |
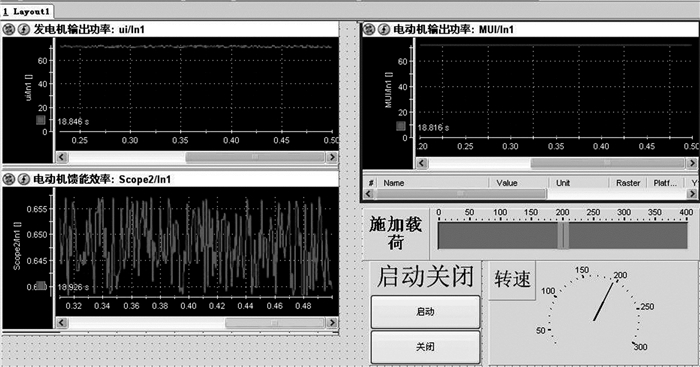
|
| 图 8 电机馈能ControlDesk工作界面 Fig.8 The ControlDesk interface for motor energy feedback |
打开ControlDesk上位机采集的波形信息,首先选取0-0.5 s时间段记录的波形(界面内如时间太长,则波形堆积显示,不利于分析波形情况)。
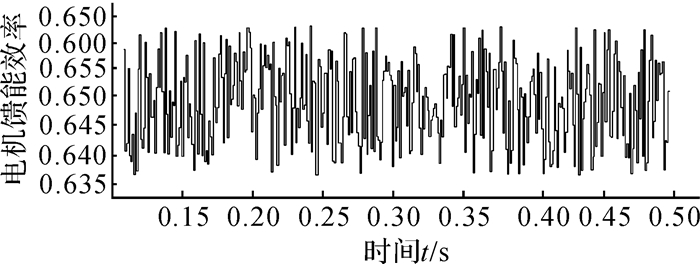
由图 9可得,硬件在环试验得到的电动机馈能效率约为64%,比前述理论计算得到的馈能效率(70%左右)略低些,主要由电机电阻、电感与电容的损耗以及设备采样精度等因素引起的,比实际的发电机效率(70%~90%)稍低。
|
| 图 9 电机馈能系统HIL试验反馈效率 Fig.9 The feedback efficiency of HIL test for motor energy feedback system |
1) 建立了包含滑模变结构控制、空间矢量、PMSM等模块的PMSM馈能系统仿真模型,进行离线仿真分析。结果表明:采用所提出的馈能方法可达到70%左右的馈能效率,具有一定的可行性。
2) 搭建了PMSM馈能系统dSPACE硬件在环试验平台,对其进行硬件在环试验验证。结果表明:电动机馈能效率在60%~80%的范围内,与离线仿真所得结果较为接近,不仅验证了所建立的馈能仿真模型的正确性,同时进一步证明纯电动汽车动力电机自身馈能在节能方面的可行性。
3) 提出的馈能方法能够为目前现有馈能方式提供更多选择以及提供一定的理论依据,对于电动汽车的电动机馈能系统的开发与研究也具有一定的借鉴意义。
| [1] |
黄昆, 张勇超, 喻凡, 等.
电动式主动馈能悬架综合性能的协调性优化[J]. 上海交通大学学报, 2009, 43(2): 226–230.
HUANG Kun, ZHANG Yong-chao, YU Fan, et al. Coordinate optimization for synthetical performance of electrical energy-regenerative active suspension[J]. Jour-nal of Shanghai Jiaotong University, 2009, 43(2): 226–230. |
| [2] |
于长淼, 王伟华, 王庆年.
电磁馈能式悬架方案设计与节能分析[J]. 汽车技术, 2010(2): 21–25.
YU Chang-miao, WANG Wei-hua, WANG Qing-nian. De-sign of electromagnetic energy regenerative suspension system and analysis of energy conservation[J]. Automobile Technology, 2010(2): 21–25. |
| [3] |
王科星.
汽车馈能式悬架技术研究[J]. 轻型汽车技术, 2010(11/12): 7–10.
WANG Ke-xing. Study on the technology of automobile energy feed suspension[J]. Light Vehicles, 2010(11/12): 7–10. |
| [4] |
刘松山, 王庆年, 王伟华.
电磁馈能悬架非线性阻尼特性仿真分析[J]. 汽车工程, 2014, 36(12): 1528–1533.
LIU Song-shan, WANG Qing-nian, WANG Wei-hua. A simulation analysis on the nonlinear damping character-istics of electromagnetic regenerative suspension[J]. Automotive Engineering, 2014, 36(12): 1528–1533. |
| [5] |
陈士安, 何仁, 陆森林.
馈能型悬架的仿真与性能评价研究[J]. 汽车工程, 2008, 28(2): 167–171.
CHEN Shi-an, HE Ren, LU Sen-lin. A study on the simulation of energy reclaiming suspension and perform -ance evaluation[J]. Automotive Engineering, 2008, 28(2): 167–171. |
| [6] |
王伟华, 李志成, 于长淼.
一种新型汽车馈能减振器的结构设计与特性分析[J]. 汽车技术, 2010(3): 44–50.
WANG Wei-hua, LI Zhi-cheng, YU Chang-miao. Struc-ture design and characteristics analysis of a new type of automotive regenerative shock[J]. Automobile Technol-ogy, 2010(3): 44–50. |
| [7] | ŠIMÁNEK J, NOVÁK J, DOLE Č EK R.Control algo-rithms for permanent magnet synchronous traction motor[C]//The International Computer Conference, Eurocon:IEEE Computer Society Press, 2007:1839-1844. |
| [8] |
刘军. 基于滑模观测器的PMSM无位置传感器矢量控制的研究[D]. 杭州: 浙江大学电气工程学院, 2014: 20-36.
LIU Jun. Research of sensorless vector control for PMSM based on sliding mode observer[D].Hangzhou:Zhejiang University, College of Electrical Engineering, 2014:20-36. http://cdmd.cnki.com.cn/article/cdmd-10335-1014193534.htm |
| [9] | PAPONEN K, KONGHIRUN M.An improved sliding mode observer for speed sensorless vector control drive of PMSM[C]//CES/IEEE 5th International Power E-lectronics and Motion Control Conference, Shanghai, Aug.14-16, 2006. |
| [10] | LIU Jia-xi, YANG Gui-jie, YAN Peng-fei.Rotor posi-tion estimation for PMSM based on sliding mode ob-server[C]//The International Conference on Mecha-tronics and Automation, Harbin, Aug.5-8, 2007. |
| [11] |
严萍, 刘国平, 李建武.
基于dSPACE平台梯形速度的PID控制模型建立及实验[J]. 机械设计与制造, 2010(9): 185–186.
YAN Ping, LIU Guo-ping, LI Jian-wu. The PID model for trapezoid speed curves design and experiment with dSPACE controller[J]. Machinery Design & Manufac-ture, 2010(9): 185–186. |
| [12] | WEI D Q, LUO X S, WANG B H, et al. Robust a-daptive dynamic surface control of chaos in permanent magnet synchronous motor[J]. Physics Letters A, 2007, 363(1/2): 71–77. |
| [13] |
周志敏.
开关电源实用技术:设计与应用[M]. 2版. 北京: 人民邮电出版社, 2007: 2-300.
ZHOU Zhi-min. Design and application of switching power supply technology[M]. 2th ed. Beijing: People's Posts and Telecommunications Press, 2007: 2-300. |
| [14] |
DARREN Ashby. 电子电气工程师必知必会[M]. 2版. 尹华杰, 译. 北京: 人民邮电出版社, 2010: 40-212.
DARREN Ashby.Electrical and electronic engineers must know[M].2th ed.Translated by YIN Hua-jie. Beijing:People's Posts and Telecommunications Press, 2010:40-212. http://www.bookask.com/book/335053.html |
| [15] |
陈南虎, 李建刚.
基于dSPACE的运动控制仿真平台设计[J]. 微计算机信息, 2008, 24(11): 258–260.
CHEN Nan-hu, LI Jian-gang. Design of a motion control simulation platform configured with dSPACE controller[J]. Microcomputer Information, 2008, 24(11): 258–260. |
| [16] | KAWAMOTO Y, SUDA Y, INOUE H, et al. Modeling of electromagnetic damper for automobile suspension[J]. Journal of System Design and Dynamics, 2007, 1(3): 524–535. DOI:10.1299/jsdd.1.524 |
| [17] |
徐琳. 汽车液电式馈能减振器研究[D]. 武汉: 武汉理工大学车辆工程学院, 2011: 10-28.
XU Lin.Study on hydraulic transmission energy-regen-erative shock absorber[D].Wuhan:Wuhan University of Technology, School of Automotive Engineering, 2011:10-28. http://cdmd.cnki.com.cn/Article/CDMD-10497-1011197098.htm |


