2. 中国石油东方地球物理勘探公司, 河北 涿州 072750
2. China Petroleum Group Oriental Geophysical Exploration Co., Ltd., Zhuozhou 072750, China
可控震源具有激发频率与振幅可控、振动连续、地震作业效率高、安全环保等优点,已成为当今油气物探作业信号激发的关键装备[1-3]。振动器作为可控震源的核心部件,其输出信号的品质越好,即输出信号的畸变越低、信噪比越高,则获得的地层资料越准确,越有利于准确判定油气藏的位置和精确地确定油气开采方案,从而大大降低油气开采成本、提高油气开发效益[4-6]。输出信号的畸变增加将降低输出信号的信噪比与分辨率,导致输出信号品质变差和不能充分利用可控震源激发地震波的能力[7]。因此,如何减小可控震源输出信号的畸变及提高信噪比,已经成为研究可控震源的热点。
提高可控震源输出信号的信噪比就是要减小畸变,找到畸变产生的原因,并针对性地采取措施,进而最大程度地提高纯净信号的比例[8]。对此,国内外学者就引起振动器输出信号畸变的原因作了一定的研究,认为源致干扰[9]、压力波动[10-11]、平板脱耦[11-14, 16]以及电液伺服阀流量—压力曲线的非线性[11, 13-16]等是导致振动器输出信号畸变高、信噪比低的主要原因,并提出了一些相应的解决措施。然而,关于振动器重锤-活塞杆动态行为规律对输出信号影响的研究却鲜有报道,而这恰恰是降低信号畸变与噪声的关键。
基于此,本文结合重锤运动轨迹检测试验,以振动器横向进油方式为基础,通过理论计算和数值模拟,开展了重锤-活塞杆动态行为规律研究,分析了横向进油方式对重锤运动与活塞杆变形的影响,找到了振动器扰动量大的直接原因;依据分析结果提出了一种竖直进油方式振动器,并与横向进油方式的结果展开对比分析,结果表明竖直进油方式能有效降低振动器扰动量。研究结果可为研制高品质、高分辨率可控震源提供指导。
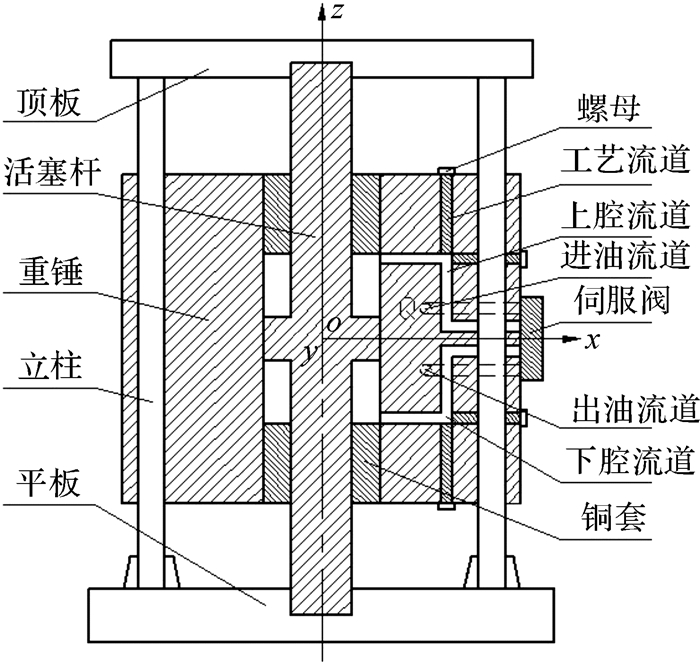
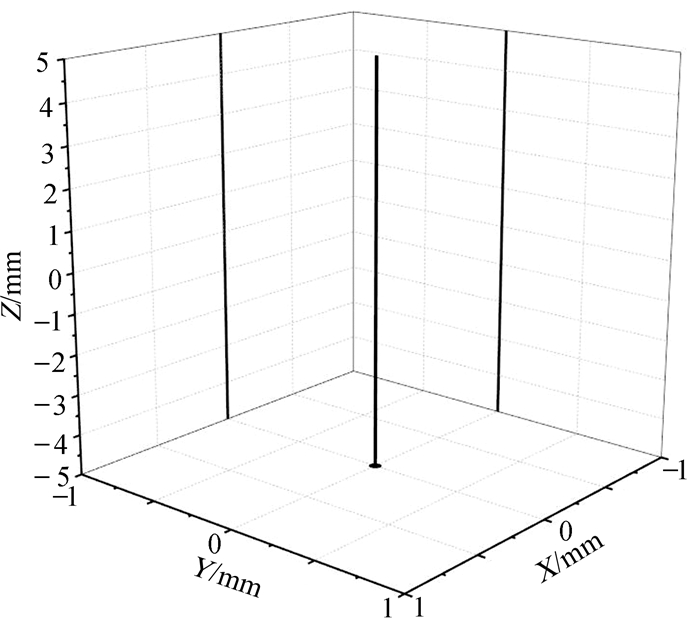
1 振动器扰动问题目前可控震源振动器多采用横向进油方式,如图 1所示。可控震源重锤上某点的理论运动轨迹为一条平行于z轴的直线,如图 2所示。
|
| 图 1 横向进油方式振动器简化结构 Fig.1 Simple structure of horizontal passageway vibrator |
|
| 图 2 横向进油方式下重锤上某点的理论运动轨迹 Fig.2 Theoretical movement path of a certain point on the reaction mass in the horizontal passageway |
重锤某点运动轨迹为一条垂直的直线或者偏离竖直方向越小,说明振动器扰动量越小,对输出信号品质的影响越小;重锤某点运动轨迹偏离竖直方向越大或者为一条空间曲线,说明振动器扰动量越大,对输出信号品质的影响越大,将导致畸变增加。
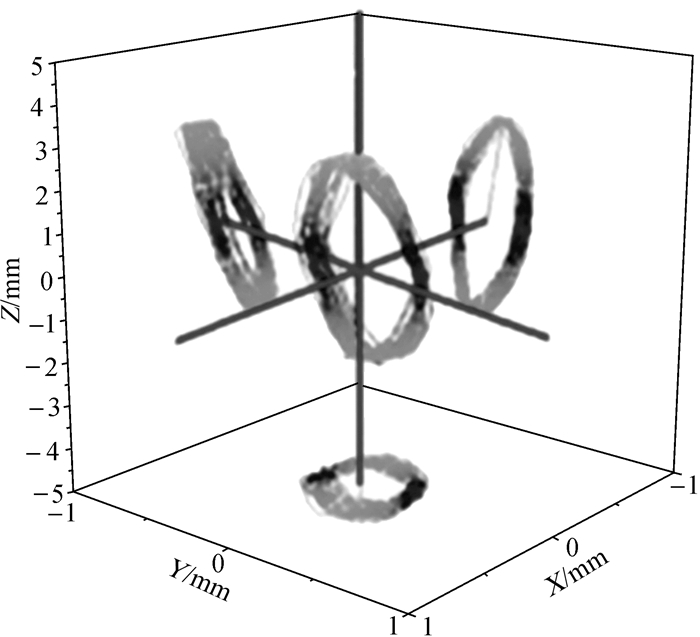
然而在可控震源的工程应用中检测出重锤上某点的实际运动轨迹如图 3所示。与图 2进行对比可以看出,重锤上某一点在水平面(即xy平面)的运动轨迹为偏离理论检测点的曲线,同样,该点在2个侧面的运动轨迹亦为偏离理论竖直方向的曲线,得到的重锤边缘点的运动轨迹为空间曲线。通过对3个投影视图的分析可知,振动器在工作过程中受x,y方向干扰,导致重锤实际运动轨迹偏离理论运动轨迹,最终表现为振动器扰动,将导致输出信号畸变剧增、品质骤降。
|
| 图 3 横向进油方式下重锤上某点的实际运动轨迹 Fig.3 Actual movement path of a certain point on the reaction mass in the horizontal passageway |
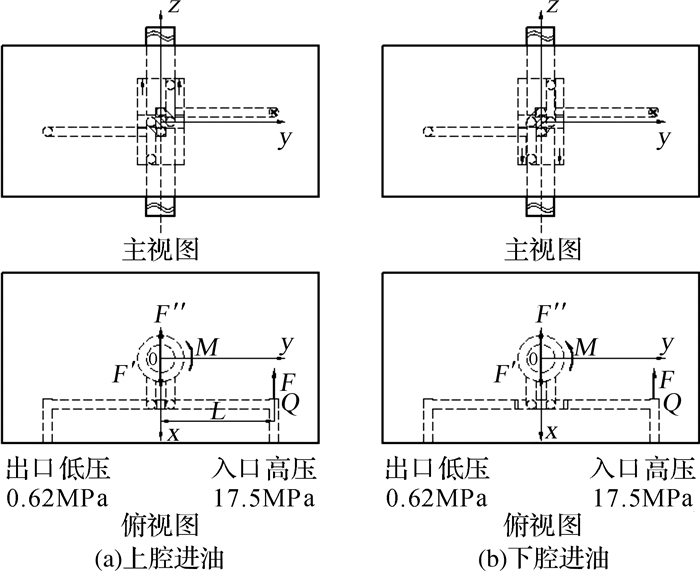
振动器工作过程中,通过伺服阀的换向,高压油液交替进入重锤上、下腔,因此重锤内的流道将有2种不同的连接形式,如图 4所示,图 4(a)为上腔进油液压流道连接形式,图 4(b)为下腔进油液压流道连接形式。振动器工作过程中使用恒压定量泵,入口压力为17.5 MPa,出口压力为0.62 MPa。
|
| 图 4 液压流道的不同连接形式 Fig.4 Different connection forms of hydraulic passageway |
从图 4可知,无论流道以哪种形式连接,由于高压油液始终经过重锤右侧,因此,在拐角Q处始终产生一个力F。根据力的平移定理,把Q处的力F平移到x轴上,此时将产生一个沿x轴负向的作用于重锤的力F″与一个绕z轴的转动力矩Mz。在重锤运动过程中,F″将对重锤产生一个水平方向的干扰,M使重锤绕活塞杆转动。
流道直径为38 mm,则Q处的作用面积:
| $ s=\frac{\text{ }\!\!\pi\!\!\text{ }{{d}^{2}}}{4}=\frac{\text{ }\!\!\pi\!\!\text{ }\times {{38}^{2}}}{4}=1\ 134.115\times {{10}^{-6}}{{\text{m}}^{\text{2}}} $ |
Q处的压力:
| $ p=\left( 17.5-0.62 \right)\times {{10}^{6}}=16.88\times {{10}^{6}}\text{Pa} $ |
Q处的作用力:
| $ F=ps=\text{ }19\ 143.861\ \text{N} $ |
绕z轴的转动力矩为:
| $ {{M}_{z}}=FL=8\ 940.183\ \text{N }\!\!·\text{m} $ |
其中L=0.467 m。
3.1.2 液压流道转动力矩仿真计算与分析1) 液压流道模型建立。
为分析横向进油方式对重锤运动的影响,建立重锤内部液压流道模型进行仿真模拟,并提取相应数据进行分析。建立的液压流道模型如图 5所示。

|
| 图 5 液压流道模型 Fig.5 Hydraulic passageway model |
2) 边界条件设置。
液压腔压力为17.5sin 2πft MPa,其中f为工作频率,压力为正值代表上腔进油,负值代表下腔进油。为实现液压腔压力变化,前半周期,流道口A为pressure-inlet,压力为17.5sin 2πft MPa,流道口B为pressure-outlet,压力为0.62 MPa; 在后半周期,流道口A为pressure-outlet,压力为0.62 MPa,流道口B为pressure-inlet,压力为17.5sin 2πft MPa。分析中取f=20 Hz。
3) 仿真结果分析。
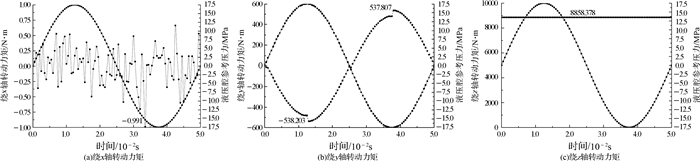
提取不同时刻绕x轴、y轴的转动力矩及压力最大时刻绕z轴的转动力矩作为整个周期下的仿真计算值,分别绘制转动力矩随时间变化的曲线,并与液压腔参考压力相比,如图 6所示,其中正弦曲线为液压腔参考压力曲线。
|
| 图 6 横向进油方式下绕x,y,z轴的转动力距变化曲线 Fig.6 The change curves of rotation torque around x, y, z axis in the horizontal passageway |
由图 6可知,振动器工作过程中,重锤受到绕x轴、y轴、z轴三个方向上的转动力矩的作用,并分别定义绕x轴、y轴、z轴的转动力矩为Mx,My,Mz。其中,由图 6(a)可知,与液压腔参考压力曲线相比,Mx曲线波动无规律,且数值很小,其最大值仅为0.991 N·m,因此对振动器的影响可忽略。
对图 6(b)进行分析可知,My曲线与液压腔参考压力曲线的波动趋势较为相似:上腔进油时,My为负值,说明此时转动力矩的方向为绕y轴顺时针方向;下腔进油时,My为正值,说明此时转动力矩的方向为绕y轴逆时针方向;在压力达到最大值时,其数值存在一定的跳跃,最大值为538.203 N·m。振动器工作过程中,My将对振动器产生影响,当液压达到最大时,转动力矩值最大,此时对振动器的影响亦最大。
根据图 6(c)可知,由于高压流道始终位于重锤右侧,因此拐角Q处始终存在一个偏心力。由力的平移定理可知,该偏心力可等效为一个作用于重锤上沿x轴负向的力与一个绕z轴的转动力矩,因此,Mz随时间变化曲线为恒定值,为8 858.378 N·m。而重锤绕z轴转动自由度未被约束,将导致重锤绕z轴转动,影响重锤运动轨迹,增大振动器的扰动量。绕z轴的转动力矩仿真计算值为8 858.378 N·m,理论计算值为8 940.183 N·m,二者的相对误差为0.915%,相对误差较小,在误差允许范围内,表明数值计算方法正确可行。通过力矩仿真值可计算出仿真力为18 968.690 N。
由上述分析可知,Mx可忽略,实际中,重锤绕y轴转动的自由度被约束,与Mz几乎恒定不变相比,其数值曲线存在波动,但其最大值为538.203 N·m,仅为Mz的6.076%,因此My对振动器的影响亦可忽略。综上,重锤主要受沿x轴负向的力与绕z轴的转动力矩作用。
3.1.3 液压流道转动力矩对振动器扰动影响分析从上述分析可知,振动器采用横向进油方式,导致重锤主要受沿x轴负向的力与绕z轴的转动力矩作用。沿x轴负向的作用力为18 968.690 N,产生水平方向的干扰,并通过重锤作用于活塞杆上,使活塞杆产生变形;绕z轴的转动力矩为8 940.183 N·m,使重锤绕z轴转动,干扰重锤的垂向振动,影响重锤运动轨迹,增大振动器的扰动量。综上,二者的耦合干扰作用极大地影响重锤运动轨迹,使振动器的扰动量急剧增加,严重影响振动器输出信号的品质。
3.2 横向进油方式对活塞杆变形的影响分析 3.2.1 活塞杆固体模型建立开展横向进油方式下活塞杆变形分析,需将流道压力作用在活塞杆上,分析流场作用下活塞杆的变形,即开展流固耦合分析。建立的活塞杆固体模型如图 7所示,活塞杆材料为40Cr。

|
| 图 7 活塞杆固体模型 Fig.7 The piston rod solid model |
由图 1可知,活塞杆上、下端分别固定在顶板与平板上,属于固定约束,因此选择fixed support;活塞杆与流体接触的面为流固耦合面;在活塞杆与重锤接触的面上施加沿x轴负向的力,其值为-18 969.690 N。
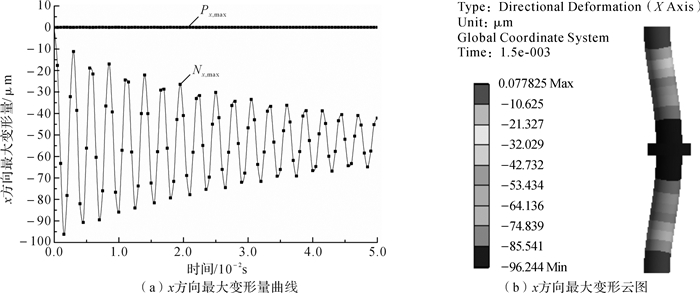
3.2.3 活塞杆变形分析提取x,y,z方向的最大变形量曲线与最大变形云图进行分析,如图 8至图 10所示,正值表示正向变形,负值表示负向变形。定义x正向最大变形量为Px, max,x负向最大变形量为Nx, max,y正向最大变形量为Py, max,y负向最大变形量为Ny, max,z正向最大变形量为Pz, max,z负向最大变形量为Nz, max。
|
| 图 8 横向进油方式下活塞杆x方向最大变形量曲线与最大变形云图 Fig.8 The maximum deformation curve and maximum deformation nephogram of piston rod in x direction in the horizontal passageway |
|
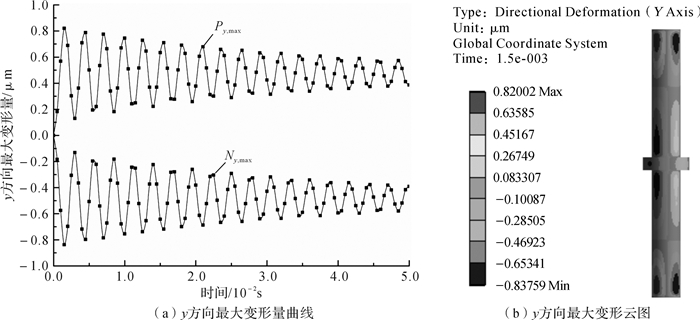
| 图 9 横向进油方式下活塞杆y方向最大变形量曲线与最大变形云图 Fig.9 The maximum deformation curve and maximum deformation nephogram of piston rod in y direction in the horizontal passageway |
|
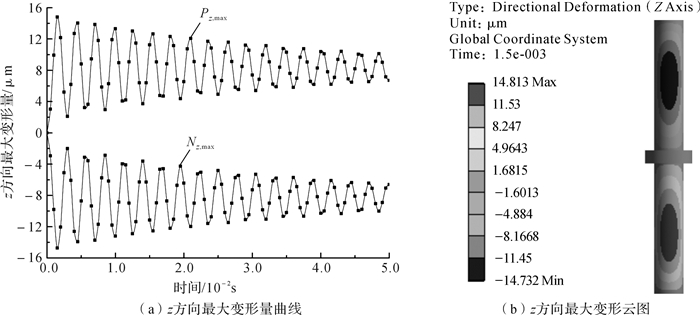
| 图 10 横向进油方式下活塞杆z方向最大变形量曲线与最大变形云图 Fig.10 The maximum deformation curve and maximum deformation nephogram of piston rod in z direction in the horizontal passageway |
图 8(a)为活塞杆x方向最大变形量随时间变化曲线,由图可知,Nx, max曲线波动趋势呈近似多周期性衰弱变化,Px, max随时间变化的曲线近似一条接近x=0的水平直线,其波动远小于Nx, max; 活塞杆x负向变形远大于x正向变形的原因是:重锤受x负向力作用,而活塞杆与重锤接触,最终x负向力作用于活塞杆上,导致活塞杆存在较大的x负向变形。图 8(b)是活塞杆x方向最大变形云图,由图中可知,活塞杆在x方向上存在明显的变形,变形主要集中在活塞杆中部,其中,Px, max的最大值为0.077 825 μm,Nx, max的最大值为96.244 μm。综上,活塞杆存在x正、负方向的变形,以x负向变形为主,在振动器工作过程中将产生x方向的干扰。
图 9为活塞杆y方向最大变形量随时间变化曲线与活塞杆y方向最大变形云图。对图 9(a)分析可知,Py, max曲线与Ny, max曲线的变化趋势大致相同,均呈近似多周期性减弱变化。由图 9(b)可知,相比活塞杆x方向的变形量,活塞杆在y方向的变形量较小,活塞杆y正向变形主要发生在活塞杆两端左侧与活塞杆中部右侧,活塞杆y负向变形主要发生在活塞杆两端右侧与活塞杆中部左侧,其中,Py, max的最大值为0.82 002 μm,Ny, max的最大值为0.837 59 μm;活塞杆存在y方向变形的主要原因是:液压油到达活塞杆圆柱面的时间、距离不同,压力损失亦不同,导致活塞杆圆柱面上液压分布不均,最终引起活塞杆变形。综上,活塞杆在y方向有变形,且存在正、负方向的变形,将对振动器产生y方向的干扰。
由图 10(a)可知,Pz, max曲线与Nz, max曲线均呈近似多周期性减弱变化趋势;对图 10(b)分析可知,活塞杆z方向的变形主要集中在活塞杆上下两部分的中间位置处,其中,Pz, max的最大值为14.813 μm,Nz, max的最大值为14.732 μm。由于重锤沿竖直方向(z方向)运动,因此活塞杆z方向的变形不会影响重锤运动,亦不会对振动器扰动产生影响。
3.2.4 活塞杆变形对振动器扰动影响分析由上述分析可知,在振动器工作过程中,活塞杆存在较大变形,而重锤环套在活塞杆上,因此活塞杆的变形运动将带动重锤一起运动,干扰重锤的垂向振动,影响重锤的运动轨迹,导致振动器扰动量增大。
3.3 振动器扰动原因分析综上,振动器工作过程中,在横向进油方式下,液压流道开设于重锤内部且呈三向非对称布置,导致重锤受沿x轴负向的力与绕z轴的转动力矩的耦合干扰作用,使重锤绕z轴转动,形成重锤扰动,同时活塞杆存在变形,干扰重锤的运动,二者相互作用,形成x,y方向的干扰,影响重锤的运动轨迹,导致重锤某点运动轨迹为空间曲线,增大了振动器的扰动量,将严重影响可控震源输出信号的品质。因此,振动器采用横向进油方式是导致振动器扰动量大的直接原因。
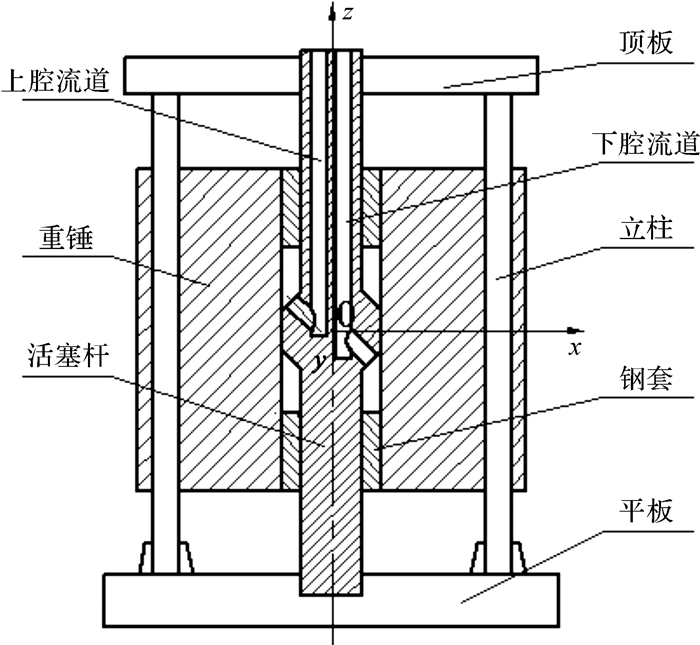
4 振动器扰动控制研究 4.1 竖直进油方式振动器由上述分析可知,横向进油方式是导致振动器扰动量大的直接原因,因此,为减小进油方式对振动器扰动的影响,对振动器进油方式进行改进,提出竖直进油方式,即液压流道竖直开设于活塞杆内部,如图 11所示。
|
| 图 11 竖直进油方式振动器简化结构 Fig.11 Simple structure of vertical passageway vibrator |
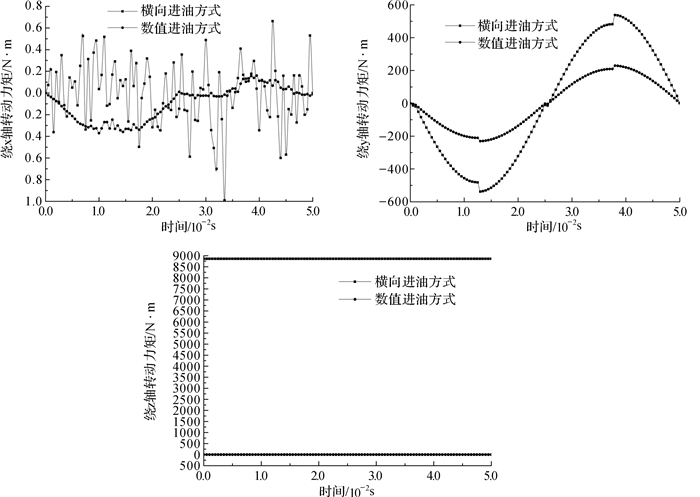
对竖直进油方式振动器采取与横向进油方式振动器相同设置并进行仿真计算,提取相关仿真结果与横向进油方式结果进行对比分析,如图 12至图 14所示。
|
| 图 12 2种进油方式的转动力矩对比 Fig.12 Comparison of rotation torque in two passageways |
|
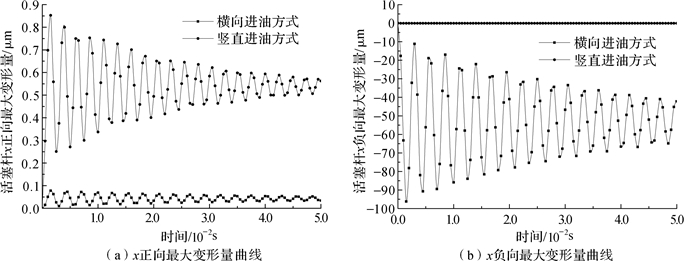
| 图 13 活塞杆x方向最大变形量对比 Fig.13 Comparison of maximum deformation of piston rod in x direction |
|
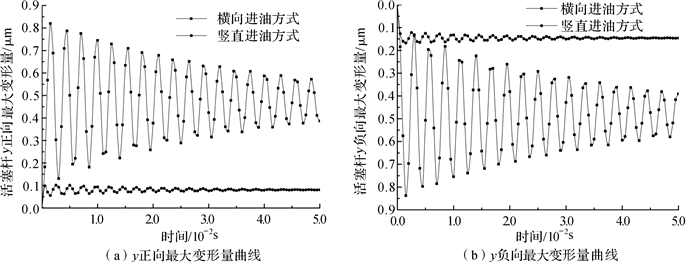
| 图 14 活塞杆y方向最大变形量对比 Fig.14 Comparison of maximum deformation of piston rod in y direction |
对图 12(a)分析可知,竖直进油方式下,Mx较横向进油时小,且波动幅度也较小,但二者结果均很小,因此Mx对重锤运动影响可忽略。
由图 12(b)可以看出,竖直进油方式下的My相比横向进油时明显降低,且由于液压流道开设于活塞杆内部,因此该转动力矩作用于活塞杆而非重锤,即不会对重锤运动产生影响。
图 12(c)中,横向进油方式下产生的Mz高达8 858.378 N·m,对重锤影响较大,而竖直进油方式下的Mz曲线近似为一条y=0的直线,因此,采用竖直进油方式后,液压流道不会使重锤绕z轴转动。
从图 13(a)可以看出,横向进油方式下活塞杆在x正向的变形量与波动幅值均小于竖直进油方式;但由图 13(b)可明显看出,竖直进油方式下活塞杆x负向变形量远小于横向进油方式下。综上,竖直进油方式下活塞杆x向等效总变形量小于横向进油方式下的活塞杆变形量。因此,采用竖直进油方式后,活塞杆x方向变形量显著降低,减小了活塞杆x方向变形对振动器的干扰。
由图 14可以明显看出,竖直进油方式下活塞杆在y正、负向的变形量均小于横向进油方式下的活塞杆变形量,且波动幅值也较缓;因此采用竖直进油方式后,减小了活塞杆y方向变形对振动器扰动的影响。
综上所述,采用竖直进油方式后,液压流道不会对重锤产生转动力矩且活塞杆变形明显减小,极大地降低了进油方式在x,y方向对重锤运动的干扰,振动器扰动将得到显著改善。
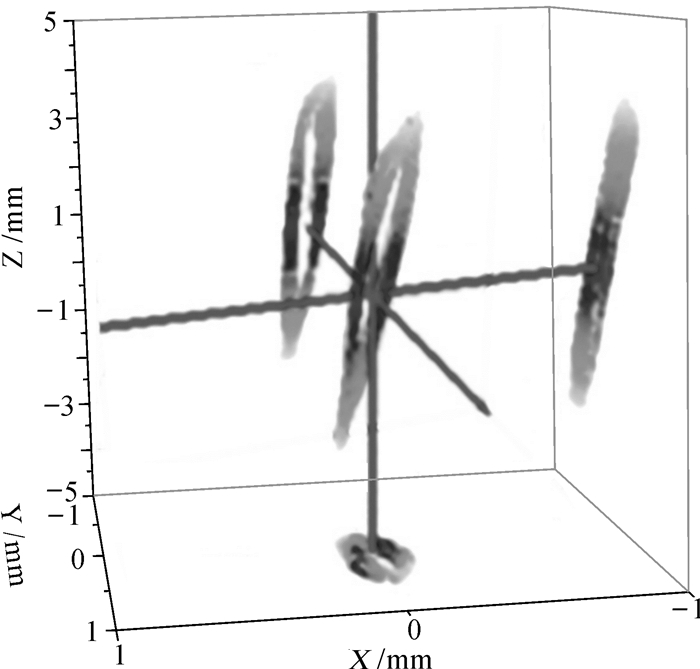
4.3 竖直进油方式振动器扰动试验验证为进一步验证竖直进油方式能减小对振动器扰动的影响,开展竖直进油方式振动器扰动试验,通过重锤运动轨迹检测试验进行验证。竖直进油方式下重锤上某点运动轨迹如图 15所示。
|
| 图 15 竖直进油方式下重锤上某点的实际运动轨迹 Fig.15 Actual movement path of a certain point on the reaction mass in the vertical passageway |
与横向进油方式下的重锤运动轨迹进行对比可明显看出,竖直进油方式下的重锤运动轨迹偏离竖直方向较小,更趋于沿竖向运动,说明振动器受x,y方向的干扰减少,这与仿真结果趋势一致。因此,振动器采用竖直进油方式后能有效减小x,y方向的干扰,明显降低了振动器扰动,有助于高品质信号的激发。
5 结论1) 横向进油方式振动器重锤运动轨迹表明,振动器受x,y方向的干扰,导致重锤运动轨迹偏离理论运动轨迹,最终表现为振动器扰动,使输出信号畸变剧增、品质骤降。
2) 横向进油方式下,振动器扰动量大、信噪比低的直接原因是振动器存在重锤转动与活塞杆变形,在x,y方向形成较大的干扰,严重影响重锤的运动轨迹,使振动器的扰动量急剧增加,最终将导致输出信号信噪比低、失真度大。
3) 采用竖直进油方式后,重锤不再受转动力矩影响且活塞杆变形得到极大改善,降低了x,y方向的干扰,结合竖直进油方式振动器扰动试验可知,振动器扰动明显减弱,有利于高品质、高分辨率信号的激发,建议在振动器的设计中采用竖直进油方式。
| [1] |
什内尔索纳. 可控震源地震勘探[M]. 李乐天, 裘恩庭, 译. 北京: 石油工业出版社, 1993: 10.
SNELL Sona.The seismic exploration of vobroseis[M]. Translated by LI Le-tian, QIU En-ting.Beijing:Petrole-um Industry Press, 1993:10 |
| [2] |
凌云, 高军, 孙德胜, 等.
可控震源在地震勘探中的应用前景与问题分析[J]. 石油物探, 2008, 47(5): 425–438.
LING Yun, GAO Jun, SUN De-sheng, et al. Analysis of vibroseis in seismic exploration and its application[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 425–438. |
| [3] |
佟训乾, 林君, 姜弢, 等.
陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912–1921.
TONG Xun-qian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Process in Geophys, 2012, 27(5): 1912–1921. DOI:10.6038/j.issn.1004-2903.2012.05.011 |
| [4] |
刘振武, 撒利明, 董世泰, 等.
中国石油物探技术发展现状与发展方向[J]. 石油勘探与开发, 2010, 37(1): 1–10.
LIU Zhen-wu, SA Li-ming, DONG Shi-tai, et al. Current situation and trend of geophysical technology in CNPC[J]. Petroleum Exploration and Development, 2010, 37(1): 1–10. |
| [5] |
撒利明, 董世泰, 李向阳.
中国石油物探新技术研究与展望[J]. 石油地球物理勘探, 2012, 47(6): 1014–1023.
SA Li-ming, DONG Shi-tai, LI Xiang-yang. Research and perspective on new geophysical technologies and methods in China[J]. Oil Geophysical Prospecting, 2012, 47(6): 1014–1023. |
| [6] |
撒利明, 甘利灯, 黄旭日, 等.
中国石油集团油藏地球物理技术现状与发展方向[J]. 石油地球物理勘探, 2014, 49(3): 611–626.
SA Li-ming, GAN Li-deng, HUANG Xu-ri, et al. The status and development direction of reservoir geophysics in CNPC[J]. Oil Geophysical Prospecting, 2014, 49(3): 611–626. |
| [7] |
LLLHEEPCOHM B, 金树堂.
可控震源信号的非线性失真和相位畸变及其校正方法[J]. 国外油气勘探, 1999, 11(4): 559–454.
LLLHEEPCOH M B, JING Shu-tang. Vibroseis signals of nonlinear distortion and phase distortion and its cor-rection methods[J]. Oil and Gas Prospecting Abroad, 1999, 11(4): 559–454. |
| [8] |
刘斌, 张志林, 赵国勇, 等.
可控震源谐波影响因素分析及对策[J]. 石油地球物理勘探, 2014, 49(6): 1053–1060.
LIU Bin, ZHANG Zhi-lin, ZHAO Guo-yong, et al. Harmonics and its attention on vibroseis data[J]. Oil Geophysical Prospecting, 2014, 49(6): 1053–1060. |
| [9] |
张宏乐.
可控震源信号中的谐波畸变影响及消除[J]. 物探装备, 2003, 13(4): 223–230.
ZHANG Hong-le. Influence of distorted harmonics in vibroseis signal and how to remove it[J]. Equipment for Geophysical Prospecting, 2003, 13(4): 223–230. |
| [10] | WEI Zhou-hong, SALLAS J J.Harmonic distortion re-duction on vibrators-Suppressing the supply pressure ripples[C], 77th SEG meeting, San Antonia, Texas, Jan 1.9, 2007. http://library.seg.org/doi/abs/10.1190/1.2792380 |
| [11] | WEI Zhou-hong, THOMAS F P. Harmonic distortion reduction in seismic vibrator[J]. The Leading Edge, 2010, 29(3): 256–261. DOI:10.1190/1.3353719 |
| [12] | CHAPMAN W L, BROWN G L, FAIR D W. The vi-broseis system:a high-frequency vibrator[J]. eophys-ical, 1991, 46(12): 1657–1666. |
| [13] |
陶知非.
可控震源输出信号畸变控制问题的研究[J]. 物探装备, 2007, 17(1): 1–13.
TAO Zhi-fei. The study on vibrator output distortion control[J]. Equipment for Geophysical Prospecting, 2007, 17(1): 1–13. |
| [14] | WEI Zhou-hong, THOMAS F P, MICHAEL A H. Fundamental discussions on seismic vibrator[J]. Geo-physics, 2010, 75(6): 13–25. |
| [15] | WEI Zhou-hong, THOMAS F P. Enhancing the low-frequency amplitude of ground force from a seismic vi-brator through reduction of harmonic distortion[J]. Geophysics, 2013, 78(4): 9–17. DOI:10.1190/geo2012-0500.1 |
| [16] |
李振春, 曲英铭, 韩文功, 等.
可控震源两种谐波产生机理与特征研究[J]. 石油物探, 2016, 55(2): 159–172.
LI Zhen-chun, QU Ying-ming, HAN Wen-gong, et al. Generation mechanism and characteristics of two kinds of harmonic waves for vibroseis[J]. Geophysical Pros-pecting for Petroleum, 2016, 55(2): 159–172. |


