2. 中国西南电子技术研究所, 四川 成都 610036
2. Institute of Electronic Technology in Southwest China, Chengdu 610036, China
波导缝隙阵天线有良好的结构和电性能,常用在机载或弹载雷达上。天线工作过程中会受到随机振动作用,随机振动不仅影响天线的结构强度和疲劳寿命,也会影响天线电性能[1-5],导致天线增益降低。
目前研究主要集中在随机振动对天线结构的位移和应力的影响[6]、天线结构疲劳寿命特性问题[7-8]以及在随机振动载荷作用下优化天线结构模型[9-10]。只有少量学者分析了随机振动对天线电性能的影响, 其中:宋立伟[11-12]通过样本生成方法计算了天线在随机振动作用下的增益损失和指向误差,在大量样本的基础上统计了天线的电性能变化,但针对每一个样本都需要计算一次电性能,所以这种方法需要大量计算;张小安等[13]运用ANSYS中随机振动谱分析工具,得到了模型随机振动响应的统计值,利用反射面天线指向精度的简化公式,通过时域近似分析方法和互相关分析方法,研究了随机振动对卡塞格伦天线指向精度的影响,但是该方法无法计算振动对天线增益的影响,而且不适用于平板缝隙天线;Schippers等[14-15]研究了振动对飞机机翼共形贴片天线的电性能影响,通过结构确定天线固有振型,利用第1阶振型模拟天线变形并分析了天线电性能的变化,但这种方法与实际情况存在较大差异。
本文利用远场方向图函数以及随机振动原理,利用宋立伟提出的随机样本生成法,忽略天线结构变形对辐射缝隙电压和指向精度的影响,提出利用位移响应的均方根计算天线增益,用均方根得到的方向图代替传统方法得到的多个方向图的均方根。论文首先对方法进行理论推导,然后利用宽边波导缝隙天线的仿真和实验对方法进行验证。
1 等效计算方法的理论推导图 1显示了波导缝隙阵天线其中一个缝隙中心和观测点P的位置关系。

|
| 图 1 观测点与缝隙中心的相对空间位置 Fig.1 The relative space position of observation point and gap center |
根据场叠加原理,在远场观测点P(θ, ϕ)处,波导缝隙阵天线的远场方向图为[16]:
| $ \mathit{\boldsymbol{E}}\left( {\theta ,\phi } \right) = \sum\limits_{n = 1}^N {{V_n}{\mathit{\boldsymbol{f}}_n}\left( {{l_n},{w_n},\theta ,\phi } \right) \cdot {{\rm{e}}^{{\rm{j}}\eta n + {\rm{j}}k{\mathit{\boldsymbol{r}}_n} \cdot \mathit{\boldsymbol{r}}}}} $ | (1) |
式中:Vn和ηn为第n个缝隙的电压幅值和相位;ln和wn为第n个缝隙的长度和宽度;θ,ϕ为点P的观测方向;fn(ln, wn, θ, ϕ)为第n个缝隙产生的单元方向图;k为传播常数;
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_n}\left( {{l_n},{w_n},\theta ,\phi } \right) = {\rm{j}}k{H_n}\left( {{l_n},{w_n},\theta ,\phi } \right)\sin \phi {\alpha _\theta } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{j}}k{H_n}\left( {{l_n},{w_n},\theta ,\phi } \right)\cos \phi {\alpha _\phi } \end{array} $ | (2) |
| $ \begin{array}{l} {H_n}\left( {{l_n},{w_n},\theta ,\phi } \right) = \frac{{\frac{{2{\rm{\pi }}}}{{{l_n}}}\cos \left( {\frac{{k{l_n}\sin \theta \cos \phi }}{2}} \right)}}{{{{\left( {\frac{{\rm{\pi }}}{{{l_n}}}} \right)}^2} - \left( {k\sin \theta \cos \phi } \right)}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sin \left( {k\sin \theta \sin \phi {w_n}/2} \right)}}{{k\sin \theta \sin \phi {w_n}/2}} \end{array} $ | (3) |
式中αθ和αϕ分别为球坐标系下θ,ϕ方向的单位矢量。
设缝隙阵天线有N个缝隙,则在有限元结构模型中,可以得到N个节点的位移响应功率谱密度矩阵Yd(ω),每个节点的自由度为3,故位移响应功率谱密度矩阵的每个子单元Yij(ω)为3×3的矩阵,Yd(ω)的维数为3N×3N[17]。
| $ {\mathit{\boldsymbol{Y}}_{\rm{d}}}\left( \omega \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{11}}\left( \omega \right)}&{{\mathit{\boldsymbol{Y}}_{12}}\left( \omega \right)}& \cdots &{{\mathit{\boldsymbol{Y}}_{1N}}\left( \omega \right)}\\ {{\mathit{\boldsymbol{Y}}_{21}}\left( \omega \right)}&{{\mathit{\boldsymbol{Y}}_{22}}\left( \omega \right)}& \cdots &{{\mathit{\boldsymbol{Y}}_{2N}}\left( \omega \right)}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{\boldsymbol{Y}}_{N1}}\left( \omega \right)}&{{\mathit{\boldsymbol{Y}}_{N2}}\left( \omega \right)}& \cdots &{{\mathit{\boldsymbol{Y}}_{NN}}\left( \omega \right)} \end{array}} \right] $ | (4) |
式中

|
(5) |
假设随机振动满足均值为零的正态随机分布,则位移响应矩阵也满足均值为零的正态随机分布,已知位移响应均方根ψiujv2和位移响应协方差σiujv2为:
| $ \psi _{{i_u}{j_v}}^2 = \frac{1}{M}\sum\limits_{m = 1}^M {\Delta {u_{im}} \cdot \Delta {v_{jm}}} $ | (6) |
| $ \sigma _{{i_u}{j_v}}^2 = \frac{1}{M}\sum\limits_{m = 1}^M {\left( {\Delta {u_{im}} - {\mu _{\Delta ui}}} \right) \cdot \left( {\Delta {v_{jm}} - {\mu _{\Delta vj}}} \right)} $ | (7) |
由于位移响应矩阵满足均值为零,所以μΔui,μΔvj为零,因此位移响应均方根等于位移响应协方差。由此得到各个节点之间满足如下关系:
| $ \left| {\frac{{\psi _{{i_u}{j_v}}^2}}{{{\psi _{{i_u}{i_u}}}{\psi _{{j_v}{j_v}}}}}} \right| = 1 $ | (8) |
式中:若i≠j或u≠v时,ψiujv为节点i在u轴方向上的分量与节点j在v轴方向上的分量的互位移响应均方根,当i=j且u=v时,ψiuiu为节点i在u轴方向上的自位移响应均方根。
在随机振动的过程中,对于天线结构的节点i来说,其位移响应的一组随机样本{Δxi, Δyi, Δzi},根据公式(6) 和公式(7) 可知,当i=j, u=v时,随机样本的方差与节点i处的位移响应均方根相等,即:
| $ D\left( {\Delta {x_i}} \right) = \psi _{{i_x}{i_x}}^2,D\left( {\Delta {y_i}} \right) = \psi _{{i_y}{i_y}}^2,D\left( {\Delta {z_i}} \right) = \psi _{{i_z}{i_z}}^2 $ | (9) |
根据位移响应的完全相关性,对于任意节点j的位移响应{Δxj, Δyj, Δzj}均可用Δxi线性表示,即:
| $ \left\{ \begin{array}{l} \Delta {x_j} = {k_{ixjx}}\Delta {x_i}\\ \Delta {y_j} = {k_{ixjy}}\Delta {x_i}\\ \Delta {z_j} = {k_{ixjz}}\Delta {x_i} \end{array} \right. $ | (10) |
式中:
因此只需生成Δxi的M个样本,即可通过公式(11) 得到其他节点的样本。根据公式(9) 可构造节点1的位移响应,在x方向分量Δx1的一组随机样本为[18]:
| $ \Delta {x_{1m}} = {\alpha _m}{\psi _{1x1x}},m = 1,2, \cdots ,M $ | (11) |
式中:αm是一组满足标准正态分布的随机数,M为该随机数列的个数。
假设只考虑随机振动对辐射缝隙中心位置的影响,则变形后第n个缝隙中心坐标为:rn+kn·Δxn, 其中:kn=(1, knxny, knxnz),Δxn=k1xnx·Δx1,n≠1。
已知波导缝隙阵天线在θ方向的方向图为[19]:
| $ \begin{array}{*{20}{c}} {{E_\theta }\left( {\theta ,\phi } \right) = \sum\limits_{n = 1}^N {{V_n}\left( {{\rm{j}}kH\left( {{l_n},{w_n},\theta ,\phi } \right)\sin \phi } \right) \cdot } }\\ {{{\rm{e}}^{{\rm{j}}\eta n + {\rm{j}}k\left( {{\mathit{\boldsymbol{r}}_n} + {\mathit{\boldsymbol{k}}_n} \cdot \Delta xn} \right) \cdot \mathit{\boldsymbol{\hat r}}}}} \end{array} $ | (12) |
对Eθ(θ, ϕ)进行如下替换:
| $ {E_\theta }\left( {\theta ,\phi } \right) = \sum\limits_{n = 1}^N {{A_n}{{\rm{e}}^{{\rm{j}}{P_n}\Delta {x_1}}}} $ | (13) |
式中:An,Pn是只关于θ和ϕ的函数,即:
| $ \left\{ \begin{array}{l} {A_n} = {V_n}\left( {{\rm{j}}kH\sin \phi } \right) \cdot {{\rm{e}}^{{\rm{j}}\eta n + {\rm{j}}k\mathit{\boldsymbol{r}}n \cdot \mathit{\boldsymbol{\hat r}}}},n = 1,2, \cdots ,N\\ {P_1} = k\left( {{\mathit{\boldsymbol{k}}_1} \cdot \mathit{\boldsymbol{\hat r}}} \right)\\ {P_n} = k{k_{{1_x}{n_x}}}\left( {{\mathit{\boldsymbol{k}}_n} \cdot \mathit{\boldsymbol{r}}} \right),n = 2,3, \cdots ,N \end{array} \right. $ | (14) |
为了方便后面的计算,首先计算方向图幅值的平方:
| $ \begin{array}{l} {\left( {{\rm{abs}}\left( {{E_\theta }\left( {\theta ,\phi } \right)} \right)} \right)^2} = \sum\limits_{n = 1}^N {A_n^2} + \\ \sum\limits_{j = n + 1}^N {\sum\limits_{n = 1}^{N - 1} {2{A_n}{A_j}\cos \left( {\left( {{P_n} - {P_j}} \right)\Delta {x_1}} \right)} } \end{array} $ | (15) |
令Δx10为随机变量Δx1的均方根, 则:
| $ \Delta {x_{10}} = \sqrt {\frac{1}{M}\sum\limits_{m = 1}^M {\Delta x_{1m}^2} } $ | (16) |
将Δx10代入公式(15),得到:
| $ \begin{array}{l} {\left( {{\rm{abs}}{{\left( {{E_\theta }\left( {\theta ,\phi } \right)} \right)}_0}} \right)^2} = \sum\limits_{n = 1}^N {A_n^2} + \\ \sum\limits_{j = n + 1}^N {\sum\limits_{n = 1}^{N - 1} {2{A_n}{A_j}\cos \left( {\left( {{P_n} - {P_j}} \right)\Delta {x_{10}}} \right)} } \end{array} $ | (17) |
若Δx1有M个值,则得到M个abs(Eθ(θ, ϕ)),这M个值的均方根为:
| $ \begin{array}{l} {\rm{RMS}}_{{E_\theta }}^2 = \sum\limits_{n = 1}^N {A_n^2} + \\ \sum\limits_{j = n + 1}^N {\sum\limits_{n = 1}^{N - 1} {2{A_n}{A_j}\left[ {\frac{1}{M}\sum\limits_{m = 1}^M {\cos \left( {\left( {{P_n} - {P_j}} \right)\Delta {x_{1m}}} \right)} } \right]} } \end{array} $ | (18) |
为方便推导,令:
| $ {P_{nj}} = {P_n} - {P_j} $ | (19) |
公式(17) 是利用位移响应均方根得到的方向图幅值的平方。公式(18) 则是利用多个样本,通过传统计算方法得到的多个方向图的均方根。将式(17) 和式(18) 中的余弦函数用泰勒展开式展开:
| $ \cos \left( {{P_{nj}}\Delta {x_{10}}} \right) = 1 - \frac{{P_{nj}^2\Delta x_{10}^2}}{{2!}} + \frac{{P_{nj}^4\Delta x_{10}^4}}{{4!}} - \cdots $ | (20) |
| $ \begin{array}{*{20}{c}} {\frac{1}{M}\sum\limits_{m = 1}^M {\cos \left( {{P_{nj}}\Delta {x_{1m}}} \right)} = 1 - \frac{1}{M}\sum\limits_{m = 1}^M {\frac{{P_{nj}^2\Delta x_{1m}^2}}{{2!}}} + }\\ {\frac{1}{M}\sum\limits_{m = 1}^M {\frac{{P_{nj}^4\Delta x_{1m}^4}}{{4!}}} - \cdots } \end{array} $ | (21) |
对比公式(20) 和(21) 可知,两式中泰勒展开式的第1项相同,将公式(21) 中的泰勒展开式第2项进行如下分解:
| $ \frac{{P_{nj}^2}}{{2!}}\frac{1}{M}\sum\limits_{m = 1}^M {\left( {\Delta x_{1m}^2} \right)} = \frac{{P_{nj}^2}}{{2!}}\Delta x_{10}^2 $ | (22) |
通过上述推导可知,
若用余弦函数泰勒展开式的前2项替代余弦函数,则当PnjΔx1m≠0时存在误差,且随着PnjΔx1m增大,误差也逐渐增大,如图 2所示,假设允许误差为5%,求得PnjΔx1m的取值范围为[-1.056 4, 1.056 4]。

|
| 图 2 余弦函数泰勒展开式误差 Fig.2 The error of cosine function's Taylor expansion |
已知PnjΔx1m满足如下关系:
| $ {P_{nj}}\Delta {x_{1m}} = {P_{nj}}{\psi _{1x1x}}{\alpha _m} $ | (23) |
式中αm为标准正态分布随机变量,均值为0,方差为1。利用3σ原则,则αm∈(-3, 3) 的概率为99.74%,那么就要求:
| $ \left| {\left( {{P_n} - {P_j}} \right){\psi _{1x1x}}} \right| \le 0.3521 $ | (24) |
把kixjx, kixjy, kixjz, kn以及
| $ \begin{array}{l} {P_n} = k\frac{{{\psi _{{n_x}{n_x}}}}}{{{\psi _{1x1x}}}}\sin \theta \cos \phi + \\ \;\;\;\;\;\;\;k\frac{{{\psi _{{n_y}{n_y}}}}}{{{\psi _{1x1x}}}}\sin \theta \sin \phi + k\frac{{{\psi _{{n_z}{n_z}}}}}{{{\psi _{1x1x}}}}\cos \theta \end{array} $ | (25) |
把公式(25) 代入公式(24),求得:
| $ \left| {k{{\left[ \begin{array}{l} {\psi _{{n_x}{n_x}}} - {\psi _{{j_x}{j_x}}}\\ {\psi _{{n_y}{n_y}}} - {\psi _{{j_y}{j_y}}}\\ {\psi _{{n_z}{n_z}}} - {\psi _{{j_z}{j_z}}} \end{array} \right]}^{\rm{T}}} \cdot \left[ {\begin{array}{*{20}{c}} {\sin \theta \cos \phi }\\ {\sin \theta \sin \phi }\\ {\cos \theta } \end{array}} \right]} \right| \le 0.3521 $ | (26) |
根据式(26) 可知,当任意2个缝隙之间位移响应均方根的差值都为零时,天线方向图函数的相位发生变化,但幅值并未改变,所以等效计算方法得到的方向图与传统随机振动方法得到的多个方向图的均方根非常匹配。当2个缝隙的位移响应均方根的差值较大时,余弦函数与其泰勒展开式的前2项之间的误差较大,从而等效计算方法得到的方向图的误差就会较大。所以在满足上述关系情况下,等效计算方法得到的方向图可以近似替代传统随机振动方法得到的多个方向图的均方根。
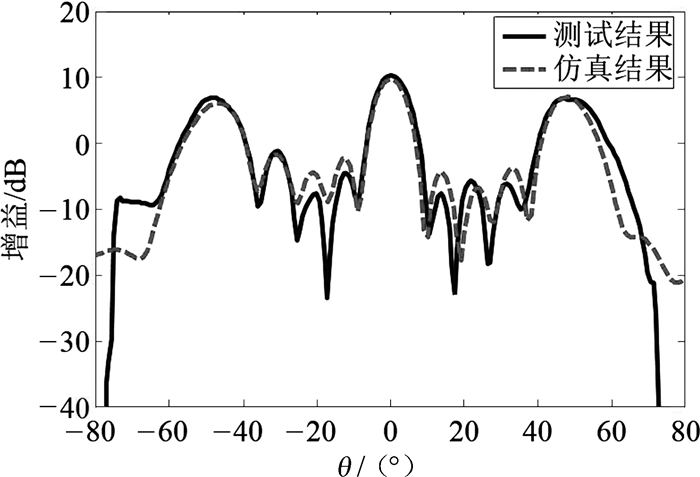
2 等效计算方法的验证本节以宽边波导缝隙阵天线为验证对象。由于ANSYS仿真随机振动过程已相当成熟,而且ANSYS仿真计算过程简单,这里没有通过实验验证ANSYS仿真结果的准确性,但HFSS仿真波导天线可能存在较大误差,而且仿真的边界设置也是至关重要的,因此需通过实验验证电磁仿真的可靠性。天线测试在微波暗室进行,采用平面近场测试。波导端口尺寸为22.86 mm×10.16 mm,天线工作频率为10 GHz,测试天线增益的实际环境如图 3所示。利用HFSS软件计算天线方向图和增益,测试与仿真结果对比如图 4所示。可以看到,主瓣和最大副瓣增益的仿真与测试结果吻合得很好,表 1中列出了主瓣和最大副瓣增益的具体值,两者误差均小于1 dB。

|
| 图 3 测试天线增益的实际环境 Fig.3 The actual environment for antenna gain test |
|
| 图 4 天线增益的仿真与测试结果对比 Fig.4 Comparison of simulation and experiment results of antenna gain |
| 对比项 | 主瓣增益/dB | 最大副瓣增益/dB |
| 测试结果 | 10.220 | 6.908 |
| 仿真结果 | 9.825 | 6.126 |
| 误差 | -0.395 | -0.782 |
验证模型为工作频率为10 GHz的缝隙天线,传播常数k=2πf/c=0.209 4 mm-1。利用ANSYS计算天线在各个方向上的位移响应均方根。由于各个方向上的位移响应均方根是在各个方向上统计的结果,不能通过简单叠加得到总的位移响应均方根,所以需要分开验证。根据式(26),推导出各个方向上的位移响应均方根需满足如下关系:
| $ \begin{array}{l} \left| {{\psi _{{n_x}{n_x}}} - {\psi _{{j_x}{j_x}}}} \right| \le 1.6815{\rm{mm}}\\ \left| {{\psi _{{n_y}{n_y}}} - {\psi _{{j_y}{j_y}}}} \right| \le 1.6815{\rm{mm}}\\ \left| {{\psi _{{n_z}{n_z}}} - {\psi _{{j_z}{j_z}}}} \right| \le 1.6815{\rm{mm}} \end{array} $ |
式中n≠j。
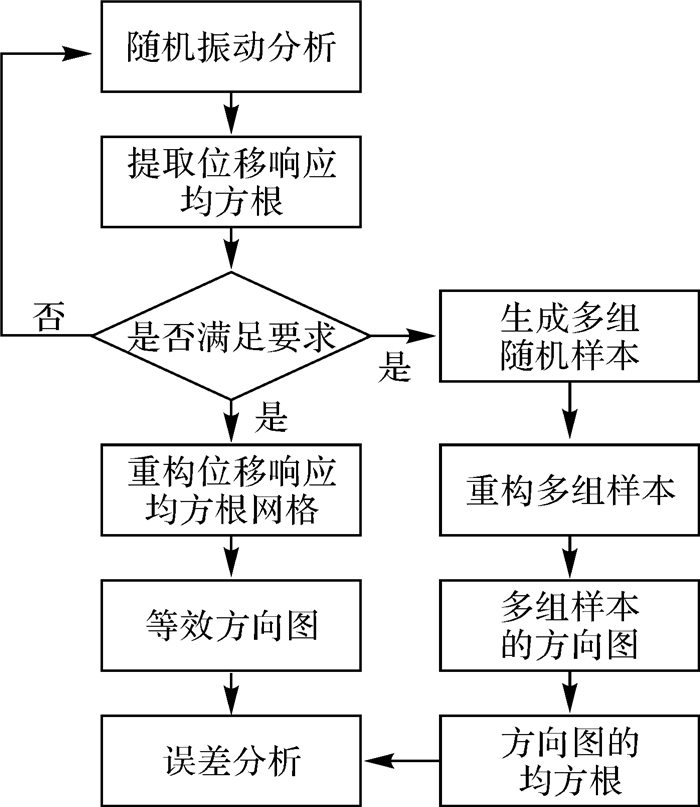
具体验证流程如图 5所示。
|
| 图 5 等效计算方法验证流程 Fig.5 The flow chart of the verification of equivalent calculation method |
随机振动分析建立在模态分析的基础上,根据公式(1) 可知,缝隙的变化是影响方向图的主要原因,因此采用波导两端固定,模态分析结果如图 6所示。

|
| 图 6 天线的前6阶固有振型 Fig.6 The first six order natural vibration modes of antenna |
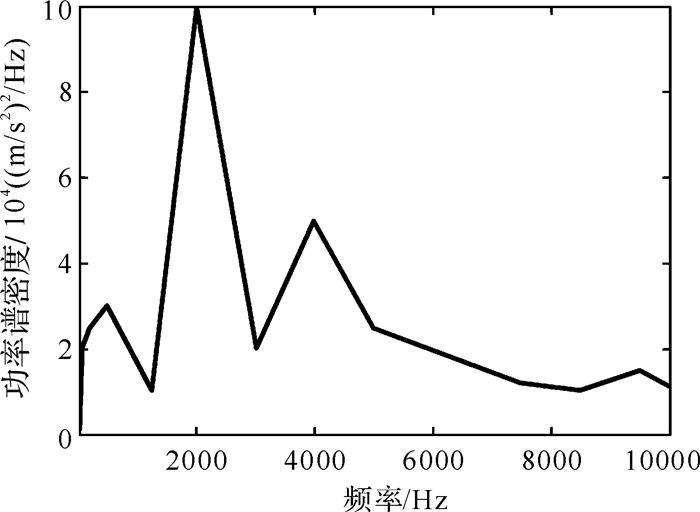
由余弦函数泰勒展开式可知,缝隙间位移响应均方根的差值越大,等效计算方法的误差越大。为了证明方法的合理性,采用较大的功率谱密度(power spectral density, PSD)值,如图 7所示,同时在X,Y,Z三个方向上施加PSD。
|
| 图 7 功率谱密度曲线 Fig.7 The power spectral density curve |
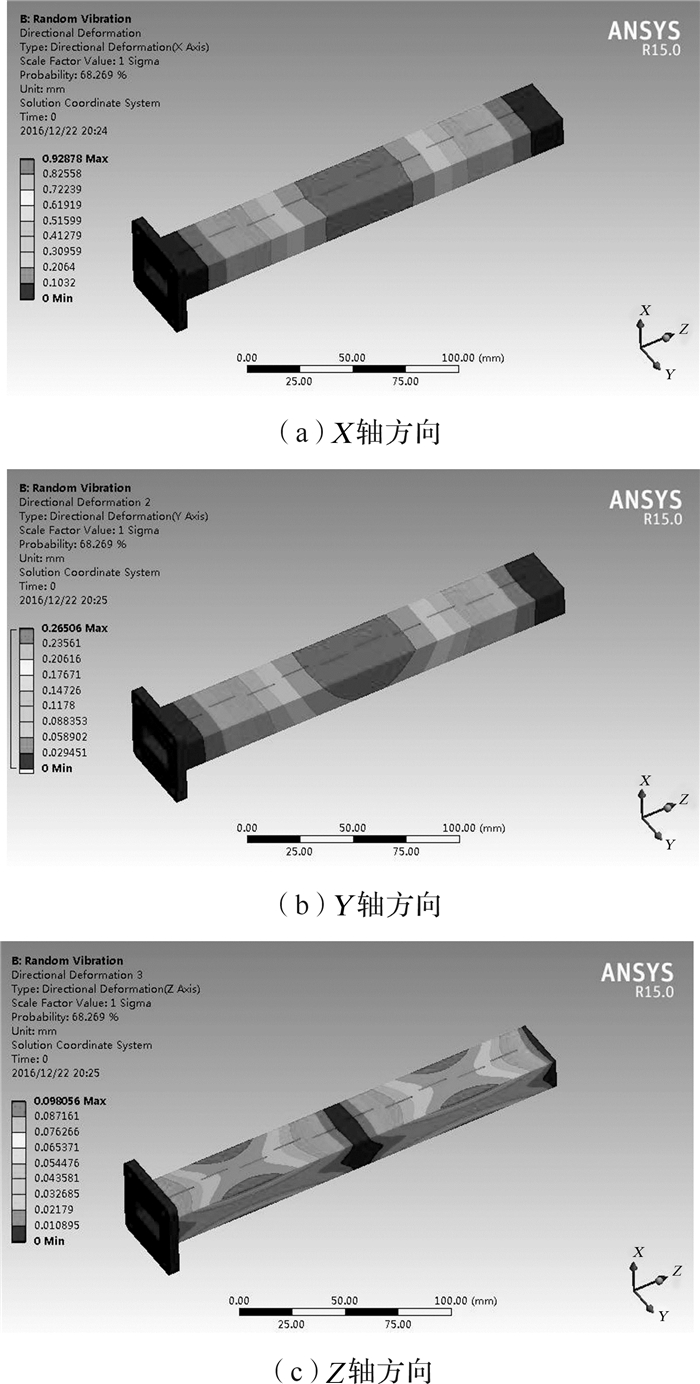
若节点位移响应均方根满足|ψmax-ψmin|≤1.681 5 mm,则缝隙中心位置的位移响应均方根一定满足|ψnxnx-ψjxjx|≤1.681 5 mm,|ψnyny-ψjyjy|≤1.681 5 mm,|ψnznz-ψjzjz|≤1.681 5 mm这些条件,所以只需要提取各个方向的位移响应均方根,并检查各方向上的位移响应均方根的最大值与最小值之差是否小于1.681 5 mm。由于有固定约束,所以位移响应均方根的最小值为0,那么要求位移响应均方根的最大值小于1.681 5 mm即可。通过仿真计算,分别得到3个方向上的位移响应均方根如图 8所示。
|
| 图 8 各个方向上位移响应均方根云图 Fig.8 Nephogram of root mean square of displacement response in each direction |
将各个方向上的位移响应均方根导出,再生成10个αm,进而得到每个方向上的10组样本,利用实体传递方法,重构变形后的模型以及变形量为位移响应均方根的模型,重构后的模型导入HFSS中,如图 9所示。
|
| 图 9 HFSS仿真模型 Fig.9 Simulation model of HFSS |
利用HFSS软件计算重构后的模型,再求每个方向上10组样本方向图的均方根,对比等效计算方法得到的方向图与传统方法得到的多个方向图的均方根,如图 10所示。
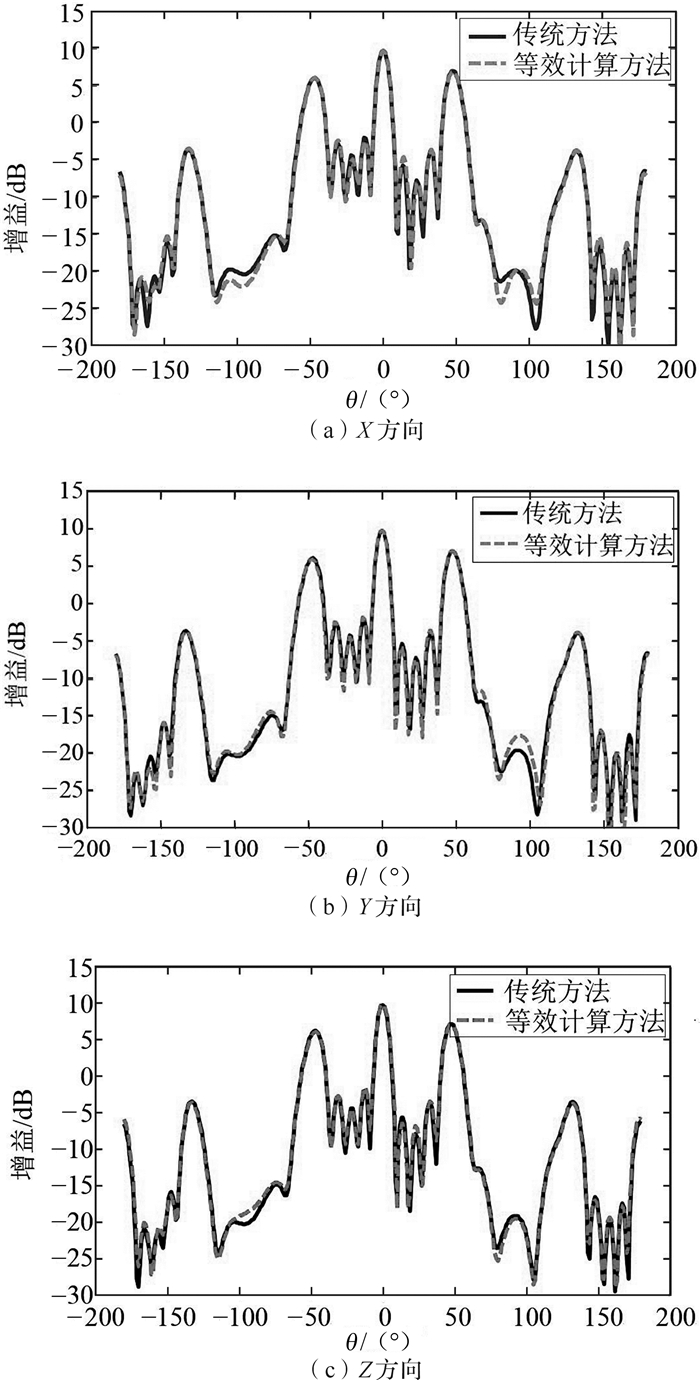
|
| 图 10 各方向上等效计算方法与传统方法得到的方向图对比 Fig.10 Comparison of the directional patterns calculated by equivalent calculation method and traditional method in each direction |
从整体来看,各个方向上利用等效计算方法得到的方向图与传统计算随机振动方法得到的多个方向图的均方根吻合得很好。方向图中的主瓣和最大副瓣的增益在表 2中列出。
| 方向 | 方法 | 主瓣增益/dB | 最大副瓣增益/dB |
| X | 传统方法 | 9.735 | 6.992 |
| 等效计算方法 | 9.686 | 6.900 | |
| 误差 | -0.049 | -0.092 | |
| Y | 传统方法 | 9.692 | 6.928 |
| 等效计算方法 | 9.709 | 6.999 | |
| 误差 | 0.017 | 0.071 | |
| Z | 传统方法 | 9.840 | 7.084 |
| 等效计算方法 | 9.743 | 7.116 | |
| 误差 | -0.097 | 0.032 |
从表 2可知,各方向上天线主瓣和最大副瓣增益的误差都小于0.1 dB,证明了利用本文方法计算的方向图可以替代传统随机振动方法得到的多个方向图的均方根。从图 10可以发现,在一些副瓣位置存在一定误差,误差来源主要有以下几点:1) 没有考虑随机振动对缝隙电压的影响;2) 没有考虑随机振动对缝隙指向精度的影响;3) 利用了余弦函数的泰勒展开式,存在截止误差。但总体而言,天线主瓣和最大副瓣增益的误差都非常小。
3 总结对于随机振动对波导缝隙阵天线增益的影响,本文提出一种等效计算方法,其主要思想是利用位移响应的均方根计算天线方向图,以替代随机振动下多组变形样本计算得到的多个方向图的均方根。根据随机振动分析得到的位移响应均方根,以及结构位移响应完全相关的特点,利用随机样本生成方法,在忽略随机振动对缝隙电压和指向精度影响情况下,从理论上验证了该方法的适用范围。只要波导缝隙阵天线的位移响应均方根与传播常数满足一定关系,即可利用该方法计算随机振动下天线增益的均方根,同时传播常数越大,位移响应均方根的范围越小。
利用样本生成的方法,重构样本模型,通过仿真计算,发现在各方向上天线主瓣和最大副瓣增益的误差都小于0.1 dB。该方法不需要计算大量样本,只需要计算随机振动作用的位移响应均方根,就可以计算出随机振动作用下波导缝隙阵天线增益的均方根。从仿真验证过程可知,传统方法需要计算M次仿真,而本方法只需进行1次仿真,本方法的计算时间是传统方法的1/M倍,可大大节约计算时间。
| [1] | ELLIOTT R S. An improved design procedure for small arrays of shunt slots[J]. IEEE Transactions on Antennas & Propagation, 1983, 31(1): 48–53. |
| [2] | ELLIOTT R S, KIM Y U. Improved design of multihole directional couplers using an iterative technique[J]. IEEE Transactions on Microwave Theory & Techniques, 1990, 38(4): 411–416. |
| [3] | YEE H Y. The design of large waveguide arrays of shunt slots[J]. IEEE Transactions on Antennas & Propagation, 1992, 40(7): 775–781. |
| [4] | SONG L, DUAN B, ZHENG F, et al. Performance of planar slotted waveguide arrays with surface distortion[J]. IEEE Transactions on Antennas & Propagation, 2011, 59(9): 3218–3223. |
| [5] |
王从思, 康明魁, 王伟.
基于阵面变形误差的有源相控阵天线电性能分析[J]. 电子学报, 2014, 42(12): 2520–2526.
WANG Cong-si, KANG Ming-kui, WANG Wei. On coupled structural-electromagnetic model of active phased array antennas with array plane structural distor-tion errors[J]. Chinese Journal of Electronics, 2014, 42(12): 2520–2526. DOI:10.3969/j.issn.0372-2112.2014.12.027 |
| [6] |
王敏, 王小静.
弹载天线随机振动的仿真分析[J]. 制导与引信, 2007, 28(2): 57–60.
WANG Min, WANG Xiao-jing. Simulation analysis in random vibration of missile-borne antenna[J]. Guidance & Fuze, 2007, 28(2): 57–60. |
| [7] |
黄莉榕. 机载环境下雷达波导的疲劳特性分析[D]. 南京: 南京理工大学机械工程学院, 2010: 69-77.
HUANG Li-rong. Analysis of fatigue property of waveguide in airborne radar environment[D].Nanjing:Nanjing University of Science & Technology, School of Mechanical Engineering, 2010:69-77. http://cdmd.cnki.com.cn/Article/CDMD-10288-2010096624.htm |
| [8] |
张瑜, 仇原鹰, 孔宪光.
基于随机分析的结构高周疲劳寿命估算[J]. 机械强度, 2009, 31(6): 999–1003.
ZHANG Yu, CHOU Yuan-ying, KONG Xian-guang. Estimation of structural life of high cycle fatigue based on random process analysis[J]. Journal of Mechanical Strength, 2009, 31(6): 999–1003. |
| [9] |
吕奇峰, 张卫红, 张桥, 等.
机振动响应下的组件结构布局优化设计[J]. 航空学报, 2010, 31(9): 1769–1775.
LU Qi-feng, ZHANG Wei-hong, ZHANG Qiao, et al. Layout design optimization of component structure with random vibration response[J]. Chinese Journal of Aero-nautics, 2010, 31(9): 1769–1775. |
| [10] |
张有为. 车辆轨道耦合系统高效随机振动分析及优化[D]. 大连: 大连理工大学工程力学系, 2013: 46-99.
ZHANG You-wei.Efficient random vibration analysis and optimization for coupled vehicle-track systems[D]. Dalian:Dalian University of Technology, Department of Engineering Mechanics, 2013:46-99. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013197985.htm |
| [11] |
宋立伟. 天线结构位移场与电磁场耦合建模及分析研究[D]. 西安: 西安电子科技大学机电工程学院, 2011: 39-80.
SONG Li-wei.Study of coupled models between fields of structural displacement and electromagnetism and their analyses of antennas[D]. Xi'an:Xidian University, School of Mechano-Electronic Engineering, 2011:39-80. http://cdmd.cnki.com.cn/Article/CDMD-10701-1011200464.htm |
| [12] |
宋立伟. 随机振动对机载雷达天线电性能的影响[C/OL]//2011年机械电子学学术会议论文集. [2016-12-07]. http://cpfd.cnki.com.cn/Area/CPFDCONFArti-cleList-GDZJ201109001h.tm.
SONG Li-wei.Effects of random vibration on airborne an-tenna performance[C/OL]//Symposium on Mechanical Electronics in 2011.[2016-12-07].http://cpfdc.nkic.om.cn/Area/CPFDCONFArticleList-GDZJ201109001h.tm. |
| [13] |
张小安, 贾建援.
火炮随机激励对天线指向精度的影响[J]. 电子机械工程, 2004, 20(4): 1–3.
ZHANG Xiao-an, JIA Jian-yuan. The effect of gun random excitation on the pointing accuracy of an antenna[J]. Electro-Mechanical Engineering, 2004, 20(4): 1–3. |
| [14] | SCHIPPERS H, Van TONGEREN J H, KNOTT P, et al.Vibrating antennas and compensation techniques re-search in NATO/RTO/SET 087/RTG 50[C]//IEEE Aerospace Conference, Big Sky, MT, Mar.3-10, 2007. |
| [15] | SCHIPPERS H, TONGEREN H V, VERPOORTE J, et al. Distortion of conformal antennas on aircraft structures[J]. Proceedings of SPIE -The International Society for Optical Engineering, 2001, 4334: 189–198. |
| [16] |
魏文元, 宫德明, 陈必森.
天线原理[M]. 北京: 国防工业出版社, 1985: 206-208.
WEI Wen-yuan, GONG De-ming, CHEN Bi-sen. An-tenna principle[M]. Beijing: National Defense Industry Press, 1985: 206-208. |
| [17] |
朱石坚.
振动理论与隔振技术[M]. 北京: 国防工业出版社, 2006: 67-98.
ZHU Shi-jian. Vibration theory and vibration isolation[M]. Beijing: National Defense Industry Press, 2006: 67-98. |
| [18] |
郭睿. 机载雷达阵列天线随机振动分析与机电综合设计[D]. 西安: 西安电子科技大学机电工程学院, 2014: 1-40.
GUO Rui.Study of random vibration and electrome-chanical integrated design of airborne radar array antenna[D]. Xi'an:Xidian University, School of Mechano-Electronic Engineering, 2014:1-40. http://cdmd.cnki.com.cn/Article/CDMD-10701-1014328400.htm |
| [19] | COETZEE J C, JOUBERT J, MCNAMARA D A. Off-center-frequency analysis of a complete planar slot-ted-waveguide array consisting of subarrays[J]. IEEE Transactions on Antennas & Propagation, 2000, 48(11): 1746–1755. |



