基于自适应Kriging代理模型的工程机械结构优化设计方法

doi:10.3785/j.issn.1006-754X.2025.05.130

基于自适应Kriging代理模型的工程机械结构优化设计方法

刘鑫^,^,, 吴青锋, 杨文广

长沙理工大学机械与运载工程学院，湖南长沙 410114

Optimization design method for construction machinery structure based on adaptive Kriging surrogate model

LIU Xin^,^,, WU Qingfeng, YANG Wenguang

College of Mechanical and Vehicle Engineering, Changsha University of Science and Technology, Changsha 410114, China

收稿日期: 2025-04-09 修回日期: 2025-07-15

基金资助:

国家自然科学基金资助项目.  52275235
湖南省杰出青年科学基金资助项目.  2021JJ10040
长沙理工大学研究生科研创新项目.  CSLGCX23047

Received: 2025-04-09 Revised: 2025-07-15

作者简介 About authors

刘　鑫（1981—），男，教授，博士，从事机械结构可靠性优化设计等研究，E-mail:lxym810205@163.com,http://orcid.org/0000-0003-4766-3517 , E-mail：lxym810205@163.com

摘要

针对工程机械优化设计问题呈现高非线性、高计算复杂度等特征及对高保真度、低成本仿真模型的需求，提出了一种基于自适应Kriging代理模型的工程机械结构优化设计方法。首先，采用泰森多边形（Voronoi diagram）方法划分工程机械结构设计变量样本空间，根据定义的样本点全局稀疏度指标（global sparsity index, GSI）找出需要加点的子空间，并根据最大最小准则在该子空间内生成全局点；其次，根据潜在最优参数定位局部加点子空间，在该子空间内产生局部点；最后，结合局部加密技术，将所得到的全局点、局部点和潜在最优解进行筛选后加入样本集以更新代理模型，从而提高代理模型的拟合精度，并将其运用于工程机械结构优化设计时代理模型的构建阶段，以大幅缩短传统高保真模型仿真时的计算时长，提升优化设计效率。数值算例验证和工程应用结果表明：与现有方法相比，在相同的加点数量下，采用所提出的方法能够使优化解更快地收敛至容许误差范围内；在臂式斗轮机上部结构和塔式起重机前臂架结构的轻量化设计中，经过1次迭代，最优解的最大相对误差分别降至0.09%和0.59%。该方法在工程机械结构优化设计中具有可行性和有效性。

关键词： 自适应代理模型 ; 工程机械结构 ; 优化设计 ; 泰森多边形 ; 遗传算法

Abstract

In view of the characteristics of high nonlinearity and high computational complexity in the optimization design of construction machinery, as well as the demand for high-fidelity and low-cost simulation models, an optimization design method for construction machinery structure based on an adaptive Kriging surrogate model was proposed. Firstly, the design variable sample space of the construction machinery structure was partitioned using the Voronoi diagram method. The global sparsity index (GSI) of the sample points was defined to identify subspaces requiring node-adding, and global points were generated within these subspaces using the max-min criterion. Next, local node-adding subspaces were identified based on the potential optimal parameters, and local points were generated accordingly. Finally, by integrating a local refinement strategy, the generated global points, local points and potential optimal solutions were filtered and incorporated into the sample set to update the surrogate model, thereby improving the fitting accuracy of the surrogate model. It was applied to the surrogate model construction phase in the construction machinery structure optimization design to significantly shorten the computational time for traditional high-fidelity model simulation and improve the efficiency of the optimization design. The numerical example verifications and engineering application results demonstrated that, compared with the existing methods, the proposed method achieved faster convergence within an acceptable error range under the same node-adding number. In the lightweight design of the upper structure of the arm-type bucket wheel reclaimer and the front boom structure of the tower crane, after only one iteration, the maximum relative errors of the optimal solution were reduced to 0.09% and 0.59% respectively. The proposed method is feasible and effective in the structural optimization design of construction machinery.

Keywords： adaptive surrogate model ; construction machinery structure ; optimization design ; Voronoi diagram ; genetic algorithm

PDF (2165KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘鑫, 吴青锋, 杨文广. 基于自适应Kriging代理模型的工程机械结构优化设计方法[J]. 工程设计学报, 2025, 32(6): 735-744 doi:10.3785/j.issn.1006-754X.2025.05.130

LIU Xin, WU Qingfeng, YANG Wenguang. Optimization design method for construction machinery structure based on adaptive Kriging surrogate model[J]. Chinese Journal of Engineering Design, 2025, 32(6): 735-744 doi:10.3785/j.issn.1006-754X.2025.05.130

在复杂工程机械结构的优化设计过程中，研究人员经常面临大规模变量空间和非线性约束优化问题。传统的优化方法通常采用高计算成本的数值仿真模型进行评估^[1-2]。尽管这些方法可以提供高精度的求解结果，但是由于单次仿真计算耗时较长，且在优化过程中需要进行大量重复仿真计算，设计效率低下。因此，为了提高优化效率并降低计算成本，采用代理模型（surrogate model）对优化问题中的目标函数和约束函数进行近似表征，在保证设计合理性的同时显著减少仿真计算量，来提升优化设计的效率。

代理模型作为一种计算高效的近似模型，能够在少量样本点的基础上构建数学近似模型，以替代昂贵的数值仿真计算，从而大幅度降低优化过程中的计算成本，因此被广泛应用于多个领域^[3]。陈一馨等^[4]将多层感知器（multilayer perceptron，MLP）作为代理模型，对挖掘机铲斗结构进行优化设计；李浩等^[5]将克里金（Kriging）模型应用于立式磨机选粉机结构的优化设计；黄文建等^[6]将代理模型运用于柔性机械臂不确定性分析。研究表明，构建高精度的代理模型能够显著提高优化设计的准确性^[7]。然而，代理模型的建模精度和优化效果在很大程度上取决于样本点的分布与选择。因此，在代理模型的构建过程中，通常会引入自适应方法，来动态优化样本点分布，提升模型的逼近精度和优化能力^[8]。

根据代理模型在优化过程中是否动态更新样本空间，基于代理模型的优化设计方法可以分为以下2类：1）静态样本空间下的直接优化方法；2）动态更新样本空间的自适应序列优化方法。在直接优化方法方面，Gu^[9]基于多项式响应面模型进行了车辆安全性分析，Li等^[10]基于二阶响应面模型进行了钣金激光焊接夹具的参数优化设计。上述研究表明，直接优化方法在工程机械的优化设计中具有一定的适用性。然而，与直接优化方法相比，序列优化方法在优化过程中能够逐步更新样本点，使得模型在局部区域的表征能力得到增强，从而更有效地提升优化精度。其中最具代表性的是Jones等^[11]提出的高效全局优化（efficient global optimization, EGO）算法。该算法结合了Kriging模型和期望改进（expected improvement, EI）准则^[12]，在全局探索与局部开发之间实现了有效平衡。随后，由于EI准则的加点效率较低，且在高维复杂优化设计中表现不佳，诸多学者对EI加点准则进行了改进，从而拓宽了EGO算法的适用范围。Wang等^[13]基于多项式响应面模型，提出了一种空间缩减策略来处理昂贵黑盒问题。魏锋涛等^[14]提出了基于多策略的改进径向基代理模型，并将其应用于减速器参数优化设计。高月华等^[15]基于Kriging模型，提出了一种加点序列优化设计方法，在一定程度上提高了加点效率。龙腾等^[16]提出了一种基于信赖域的采样空间更新策略，并结合径向基函数模型对工字梁结构进行优化设计，同时验证了该方法在处理高维工程优化问题中具有一定的优势。目前，在代理模型加点准则的设计方面取得了一定的进展，但在样本增加效率、并行采样机制、高维适应性等方面仍存在不足：大多数加点方法在每次迭代中仅能生成1个样本点来更新代理模型，这限制了加点的效率，并增大了计算资源的消耗。因此，有必要提出一种提升加点效率的方法，并实现并行加点。除此之外，在代理模型的加点过程中，必须审慎考虑新样本点之间的相似性问题。若将高相似性的样本点加入样本空间，不仅会造成不必要的计算成本的增加，还可能导致矩阵奇异问题，这会降低代理模型的预测精度，妨碍找到最优解。

本文提出了一种基于自适应Kriging代理模型的工程机械结构优化设计方法。首先，考虑到Kriging模型因其优秀的非线性拟合能力而在优化设计领域得到广泛应用^[17]，因此采用Kriging模型来近似构建工程机械结构优化问题，并利用遗传算法（genetic algorithm, GA）求解所构建的近似优化问题；其次，引入泰森多边形（Voronoi diagram）方法来划分样本空间，根据所定义的样本点全局稀疏度指标（global sparsity index, GSI）找出需要加点的子空间，并根据最大最小准则在该子空间内生成全局点；然后，根据潜在最优参数定位局部加点子空间，同样采用最大最小准则在该子空间内产生局部点；接着，结合局部加密技术，将所得到的全局点、局部点和潜在最优解进行筛选后加入样本空间以更新代理模型，从而提升优化设计效率；最后，通过数值算例来验证所提出方法的有效性，并结合工程算例进一步证明其在工程机械结构设计中的可行性与实用价值。

1 基于代理模型的优化设计基本原理

典型的优化问题的数学模型一般描述如下^[18]：

\{\begin{array}{l} m i n f (X) \\ s . t . h_{u} (X) = 0, u = 1, \dots, a \\ g_{v} (X) \leq 0, v = 1, \dots, b \\ X = (X_{1} X_{2} \dots X_{d})^{T} \end{array}

式中： X 为设计变量， $f (X)$ 为优化目标函数， $h_{u} (X)$ 为等式约束函数， $g_{v} (X)$ 为不等式约束函数, $a$ 为等式约束的个数， $b$ 为不等式约束的个数，d为设计变量的维数。

把代理模型引入优化问题，则式(1)可转变为如下近似优化问题：

\{\begin{array}{l} m i n \tilde{f} (X) \\ s . t . {\tilde{h}}_{u} (X) = 0, u = 1, \dots, a \\ {\tilde{g}}_{v} (X) \leq 0, v = 1, \dots, b \\ X = (X_{1} X_{2} \dots X_{d})^{T} \end{array}

式中： $\tilde{f} (X)$ 、 ${\tilde{h}}_{u} (X)$ 、 ${\tilde{g}}_{v} (X)$ 为各自代理模型的近似函数。

构建代理模型后，需要采用智能优化算法进行求解，以获得最优设计参数集。然而，在实际应用中，仅通过单次优化往往无法满足对误差的预定要求，因此需要采取加点策略来更新样本空间，提升代理模型的精度，从而确保最终的优化解符合设计要求。因此，合理的加点方法应兼顾全局探索与局部开发，以提高求解精度和优化效率。对此，作者提出了一种基于自适应Kriging代理模型的工程机械结构优化设计方法，来实现工程机械结构的高效优化设计。

2 基于自适应Kriging代理模型的优化设计方法

在工程机械结构的优化设计中，随着问题非线性的增强及计算复杂度的提高，为了兼顾模型精度与计算效率，采用自适应代理模型成为一种有效途径。其核心在于采取合理的样本点加点策略，动态更新代理模型，从而在有限的优化次数内实现高精度的近似优化。本文基于Voronoi diagram方法和稀疏度指标，提出一种融合全局探索与局部开发的双重加点机制，从而提升工程机械结构优化设计的效率。

2.1　Kriging代理模型构建

针对工程机械结构优化设计问题，目标函数和约束函数往往无法通过显示表达式表示出来。本文首先采用最优拉丁超立方设计（optimal Latin hypercube design, OLHD），均匀采集样本点；然后，采用Kriging模型对目标函数进行近似表征，其具体数学表达式为^[18]：

Y = f {(X)}^{T} β + z (X)

(3)

式中： $f (X)$ 为回归多项式基函数向量， $f (X) = [f_{1} (X) f_{2} (X) \dots f_{p} (X)]$ ， $p$ 为回归多项式的数量； $β$ 为回归方程的回归系数； $z (X)$ 为服从正态分布 $N (0, σ^{2})$ 的随机函数，用来表示 $Y$ 的不确定性。

2.2　全局加点方法

在对Kriging模型进行自适应优化过程中，Voronoi图可以将样本空间划分为多个不重合的子空间P_i (i=1, 2, …, N)。首先，每个子空间只包含1个初始样本点；其次，在任意一个子空间中任意一个随机点到初始样本点的距离都小于该随机点到其他子空间初始样本点的距离。n维设计空间 R 中初始样本 $X = \{X_{1}, X_{2}, \dots, X_{N}\} \subseteq R^{n}$ ，第 $i$ 个初始样本 $X_{i}$ 对应的Voronoi图子空间 $P_{i}$ 可表示为：

\begin{array}{l} P_{i} = \{X \in R^{n} | ‖X - X_{i}‖ \leq ‖X - X_{j}‖\}, \\ j = 1, 2, \dots, N, i \neq j \end{array}

(4)

式中： $‖\cdot‖$ 代表两点之间的欧式距离。

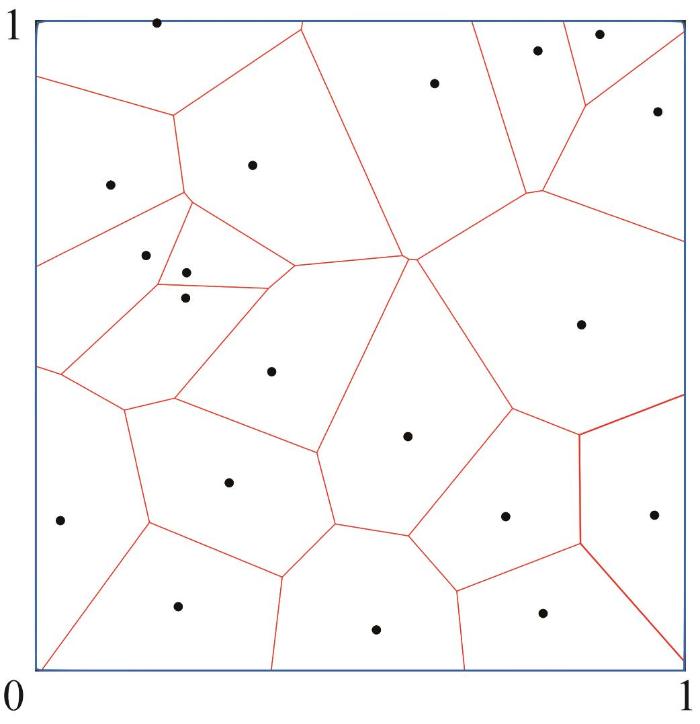
二维设计变量的Voronoi空间划分如图1所示。图中：黑色圆点代表初始样本点，红色实线所围成的区域即为每个初始样本点对应的Voronoi子空间。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 二维Voronoi图示例

Fig.1 Example of two-dimensional Voronoi diagram

高维Voronoi图呈现复杂不规则的多面体结构，难以精确描述。实践中常采用简化近似方法进行处理，具体操作流程如下：1）在设计空间内部随机生成大量的离散样本点，并计算这些随机点与初始样本点之间的欧式距离；2）与初始样本点 $X_{i}$ 距离最近的随机样本点即归属于 $X_{i}$ 所在的Voronoi子空间 $P_{i}$ ，这些大量随机样本点聚集的区域即为所要近似描述的Voronoi子空间 $P_{i}$ 。离散随机点数目 $N_{r a n d o m}$ 可通过式(5)^[19]得到：

N_{r a n d o m} = N \times n \times w

(5)

式中： $w$ 为缩放参数，其值根据具体问题而定。本文取经验值， $w$ =100。

当采用Voronoi图划分好初始样本空间后，需要计算每个样本点的全局稀疏度值V_GSI( X_i )，以衡量代理模型在不同子空间的表征性能。V_GSI( X_i )定义如下：

V_{G S I} (X_{i}) = \frac{1}{M} \sum_{j = 1}^{M} |\frac{{\tilde{F}}_{m a x} (X_{i}^{_{M, b o u n d}}) - F_{m a x} (X_{i})}{F_{m a x} (X_{i})}|

(6)

式中：M为样本点 $X_{i}$ 所归属的Voronoi子空间 $P_{i}$ 边界上的随机点数量，其值根据初始样本点数量而定，本文取经验值，M=5； $X_{i}^{M, b o u n d}$ 为样本点 $X_{i}$ 所归属的Voronoi子空间 $P_{i}$ 边界上的随机点； $F_{m a x}$ 为 $f (X)$ 、 $h (X)$ 和 $g (X)$ 中在潜在最优参数 $X^{*}$ 处的最大相对误差对应的函数类型； ${\tilde{F}}_{m a x}$ 为 $F_{m a x}$ 的代理模型。

找出最大V_GSI( X_i )值所对应的样本Voronoi子空间 $P_{i, m a x}$ ，然后在 $P_{i, m a x}$ 内部产生全局点 $X_{g l o b a l}$ 。全局点应满足最大最小距离准则，即全局点 $X_{g l o b a l}$ 与中心样本点 $X_{i}^{*}$ 之间的距离尽可能大，具体表达式为：

X_{g l o b a l} = a r g m a x (‖X_{r a n d o m} - X_{i}^{*}‖), X_{r a n d o m}, X_{i}^{*} \in P_{i, m a x}

(7)

式中： $a r g$ 表示返回当前模型最大值所对应的输入参数， X_random为 $P_{i, m a x}$ 内的随机点。

2.3　局部加点方法

采用全局加点方法可以提升代理模型的全局精度，但难以显著改善其局部精度。因此，开发一种旨在优化代理模型局部精度的局部加点方法尤为重要。

本文提出的局部加点方法如下：1）利用高效的智能优化算法求解出每一次优化迭代中的潜在最优参数 $X^{*}$ ；2）使用局部加密技术，将 $X^{*}$ 添加到样本空间中；3）找出 $X^{*}$ 所处的Voronoi子空间 $P^{*}$ ，并根据最大最小距离准则在 $P^{*}$ 内产生一个局部点 $X_{l o c a l}$ 。具体表达式为：

X_{l o c a l} = a r g m a x (‖X_{r a n d o m}^{*} - X_{j}^{*}‖)

X_{r a n d o m}^{*}, X_{j}^{*} \in P^{*}

(8)

式中： $X_{r a n d o m}^{*}, X_{j}^{*}$ 分别为 $P^{*}$ 内的随机样本点和中心样本点。

每一次优化迭代中的潜在最优参数 $X^{*}$ 包含了丰富的样本空间的局部信息，因此不仅可以利用 $X^{*}$ 进行局部开发，还可以根据 $X^{*}$ 引导代理模型局部更新的方向，从而有效提升代理模型的局部精度。

2.4　样本筛选准则

当获得全局点 $X_{g l o b a l}$ 、局部点 $X_{l o c a l}$ 和潜在最优参数 $X^{*}$ 并作为待加入样本空间的新加点后，可能会出现新加点之间距离过近或信息相似的现象，这可能导致加点策略失效，无法提升代理模型的精度，从而使优化解的误差不符合要求。因此，用最小欧式距离筛选准则来评价待加入样本空间的新加点集 $Ω_{n e w} = \{X_{g l o b a l}, X_{l o c a l}, X^{*}\}$ 。

最小欧式距离筛选准则是比较新加点之间的最小欧式距离 $d_{m i n} (Ω_{n e w})$ 和样本点之间的最小欧式距离 $d_{m i n} (X)$ ，要求 $d_{m i n} (Ω_{n e w})$ 必须大于或等于 $d_{m i n} (X)$ 。当距离不符合要求时，则需要重新挑选全局点和局部点，更新新加点集 $Ω_{n e w}$ ，直到满足准则要求。最小欧式距离筛选准则的数学描述为：

d_{m i n} (Ω_{n e w}) \geq d_{m i n} (X)

(9)

式中： $d_{m i n} (Ω_{n e w})$ 为新加点集中最小欧式距离， $d_{m i n} (X)$ 为样本点集中最小欧式距离。

通过最小欧氏距离筛选准则对样本进行筛选后，得到3个新样本点并将其加入样本空间；随后，通过真实模型计算这些新样本点的响应值，进一步更新代理模型。

本文所提出的方法实现了并行加点，在提升加点效率的同时降低了计算成本。该策略不仅平衡了全局搜索与局部开发的加点原则，而且具有较好的适用性，能够与各种代理模型和优化算法兼容，因此表现出卓越的适用性能。

2.5　求解流程

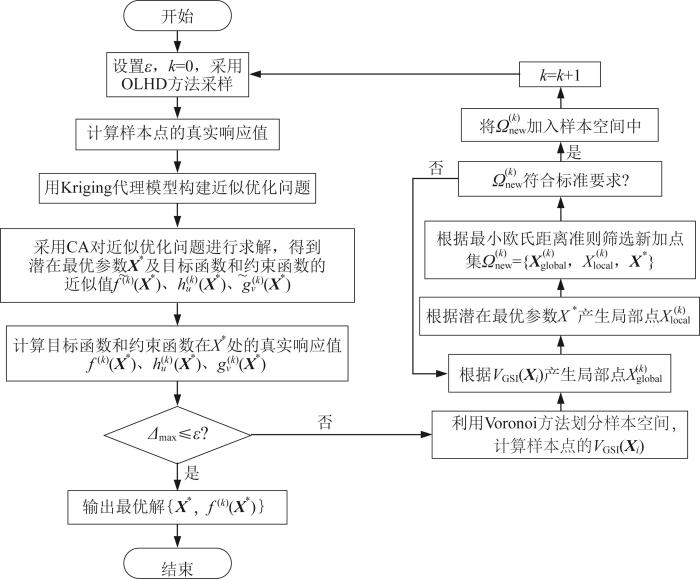
基于自适应Kriging代理模型的工程机械结构优化设计方法的流程如图2所示，其主要步骤如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于自适应Kriging代理模型的工程机械结构优化设计方法流程图

Fig.2 Flowchart of optimization design method for construction machinery structure based on adaptive Kriging surrogate model

Step 1：采用OLHD方法获得初始样本，设置容许误差 $ε$ ，循环数 $k = 0$ 。

Step 2：计算样本点的真实响应值，并用Kriging代理模型构建近似优化问题，采用GA求解得到对应的潜在最优参数 $X^{*}$ 和潜在最优解 ${\tilde{f}}^{(k)} (X^{*})$ ，以及近似约束函数值 ${\tilde{h}}_{u}^{(k)} (X^{*})$ 和 ${\tilde{g}}_{v}^{(k)} (X^{*})$ 。

Step 3：通过真实模型或数值仿真计算出潜在最优参数 $X^{*}$ 对应的真实值 $f^{(k)} (X^{*})$ 、 $h_{u}^{(k)} (X^{*})$ 和 $g_{v}^{(k)} (X^{*})$ 并计算 $Δ_{m a x}$ 的值，其中：

\begin{array}{l} Δ_{m a x} = m a x \{|\frac{f^{(k)} (X^{*}) - \tilde{f} {}^{(k)}(X^{*})}{f^{(k)} (X^{*})}|, \\ |\frac{h_{u}^{(k)} (X^{*}) - {\tilde{h}}_{u}^{(k)} (X^{*})}{h_{u}^{(k)} (X^{*})}|, |\frac{g_{v}^{(k)} (X^{*}) - {\tilde{g}}_{v}^{(k)} (X^{*})}{g_{v}^{(k)} (X^{*})}|\} \end{array}

若 $Δ_{m a x}$ < $ε$ ，则停止循环，输出最优解 $\{X^{*}, f^{(k)} (X^{*})\}$ ；否则，跳转至Step 4。

Step 4：利用Voronoi方法划分样本空间，并计算样本点的V_GSI( X_i )，找出最大V_GSI( X_i )值所对应的样本Voronoi子空间 $P_{i, m a x}$ ，在 $P_{i, m a x}$ 内产生一个全局点 $X_{_{g l o b a l}}^{(k)}$ 。

Step 5：根据潜在最优参数 $X^{*}$ 找出 $X^{*}$ 所处的Voronoi子空间 $P^{*}$ ，在 $P^{*}$ 内产生一个局部点 $X_{l o c a l}^{(k)}$ 。

Step 6：根据最小欧式距离准则筛选新加点集 $Ω_{n e w}^{(k)} = \{X_{g l o b a l}^{(k)}, X_{l o c a l}^{(k)}, X^{*}\}$ ，若 $Ω_{n e w}^{(k)}$ 符合准则要求，则加入样本空间，设置k=k+1并转至Step 2；若 $Ω_{n e w}^{(k)}$ 不符合准则要求，则跳转至Step 7。

Step 7：重新选择全局点和局部点并加入 $Ω_{n e w}^{(k)}$ ，再次采用最小欧式距离准则筛选 $Ω_{n e w}^{(k)}$ 直至满足要求。

Step 8：将更新后的 $Ω_{n e w}^{(k)}$ 加入样本空间，设置k=k+1并转至Step 2重新进行循环。

3 数值算例验证

3.1　数值算例1

本数值算例是一个常见的四维优化问题，其数学描述如下：

\{\begin{array}{l} m i n f (X) = \frac{2 X_{1} X_{2}}{{X_{4}}^{2}} + \frac{3 X_{2} X_{4}}{{X_{3}}^{2}} \\ s . t . g_{1} (X) = X_{1} X_{2} - \frac{X_{3} X_{4}}{2} - 40 \leq 0 \\ g_{2} (X) = X_{1} - \frac{X_{2}}{X_{3}} - X_{4} \leq 0 \\ g_{3} (X) = 50 - X_{2} + \frac{X_{1}}{X_{4}} - 5 X_{3} \leq 0 \\ X = (X_{1} X_{2} X_{3} X_{4})^{T} \\ 5 \leq X_{1}, X_{2}, X_{3}, X_{4} \leq 15 \end{array}

(10)

设置 $ε$ =0.1。构建Kriging代理模型，采用GA求解最优参数。GA的参数设置如下：种群规模为5，交叉概率为0.5，最大迭代次数为200。为了评估不同优化方法的性能，分别采用本文提出的方法、EI方法和概率改进（probability improvement, PI）方法对代理模型进行序列优化^[12]，并对比了该3种加点策略的收敛性能。不同加点方法下的收敛性能如表1所示，最大相对误差收敛曲线如图3所示。采用本文方法后，优化结果如表2所示。

表1 数值算例1中不同加点方法下的收敛性能

Table 1 Convergence performance under different node-adding methods in numerical example 1

方法	迭代步	新加入样本数量/个	总样本数量/个	最大相对误差/%
本文方法	Step 1	0	15	22.24
	Step 2	3	18	17.13
	Step 3	3	21	1.09
EI方法	Step 1	0	15	22.24
	Step 2	1	16	22.12
	Step 3	1	17	22.34
	Step 4	1	18	28.80
	Step 5	1	19	62.10
	Step 6	1	20	40.86
	Step 7	1	21	54.88
PI方法	Step 1	0	15	22.24
	Step 2	1	16	93.07
	Step 3	1	17	20.66
	Step 4	1	18	37.80
	Step 5	1	19	15.46
	Step 6	1	20	18.17
	Step 7	1	21	15.77

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

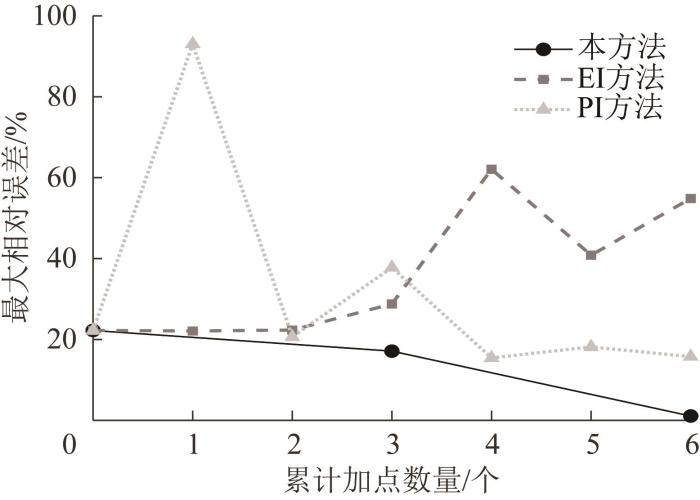
图3 数值算例1中不同加点方法下最大相对误差收敛曲线

Fig.3 Maximum relative error convergence curves under different node-adding methods in numerical example 1

表2 数值算例1中本文方法的优化结果

Table 2 Optimization results of proposed method in numerical example 1

函数	代理模型近似值	真实值	相对误差/%
X =(6.900 6 10.240 3 15.000 0 13.504 2)^T
$f (X)$	2.590 3	2.618 8	1.09
$g_{1} (X)$	71.167 7	70.617 1	0.78
$g_{2} (X)$	7.309 9	7.286 3	0.32
$g_{3} (X)$	34.916 5	34.729 3	0.54

新窗口打开| 下载CSV

由表1可知：在3种加点方法的迭代步Step 1，由于初始样本数量不足，代理模型的精度都较低，初始最大相对误差达到了22.24%；在相同加点数量的情况下，EI和PI方法由于每次只能产生1个新样本点加入样本空间，因此与本文方法相比，加点效率较低，而本文方法实现了并行加点，提高了加点效率；同时，EI和PI方法最终均未能获得满足误差要求的最优解，在迭代步Step 7时的最大相对误差分别为54.88%和15.77%，这可能是由于所选新样本与初始样本相似性较高，不能有效提升代理模型精度，需要补充更多迭代步和样本点才能满足对误差的要求，而本文方法仅经过2次加点循环便得到了满足要求的最优解。

由表2可知，采用本文方法，最优解的最大相对误差仅为1.09%，完全符合所设定的容许误差的要求。因此，本文方法在提高代理模型精度的同时，能显著降低计算成本并提升效率，具有较高的实用价值。

3.2　数值算例2

本算例也有3个不等式约束条件，数学描述如下：

\{\begin{array}{l} m i n f (X) = 5 c o s (\sqrt[]{{(\frac{X_{1} - 40}{2})}^{2} + {(X_{2} - X_{3})}^{2}}) + \\ \sqrt[]{{(\frac{X_{3} - 40}{2})}^{2} + {(X_{1} - X_{3})}^{2}} \\ s . t . g_{1} (X) = \frac{{X_{2}}^{2}}{X_{1} + 1} - \frac{{X_{1}}^{2}}{X_{3} + 1} \leq 0 \\ g_{2} (X) = X_{2} X_{3} - X_{1} X_{2} - X_{1} X_{3} \leq 0 \\ g_{3} (X) = 5 X_{1} - X_{2} X_{3} \leq 0 \\ X = (X_{1} X_{2} X_{3})^{T} \\ 0 \leq X_{1}, X_{2}, X_{3} \leq 10 \end{array}

(11)

设置容许误差 $ε$ =0.1。构建Kriging代理模型，采用GA求解最优参数。GA的参数设置如下：种群规模为5，交叉概率为0.5，最大迭代次数为200。不同加点方法下的收敛性能如表3所示，最大相对误差收敛曲线如图4所示。采用本文方法后，优化结果如表4所示。

表3 数值算例2中不同加点方法下的收敛性能

Table 3 Convergence performance under different node-adding methods in numerical example 2

方法	迭代步	新加入样本数量/个	总样本数量/个	最大相对误差/%
本文方法	Step 1	0	15	91.86
	Step 2	3	18	33.35
	Step 3	3	21	12.87
	Step 4	3	24	6.74
EI方法	Step 1	0	15	91.86
	Step 2	1	16	122.79
	Step 3	1	17	96.51
	Step 4	1	18	103.45
	Step 5	1	19	51.30
	Step 6	1	20	60.62
	Step 7	1	21	7.63
	Step 8	1	22	100.17
	Step 9	1	23	91.90
	Step 10	1	24	8.77%
PI方法	Step 1	0	15	91.86
	Step 2	1	16	70.02
	Step 3	1	17	150.01
	Step 4	1	18	39.75
	Step 5	1	19	49.35
	Step 6	1	20	40.34
	Step 7	1	21	77.75
	Step 8	1	22	41.64
	Step 9	1	23	83.66
	Step 10	1	24	4 643.46

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

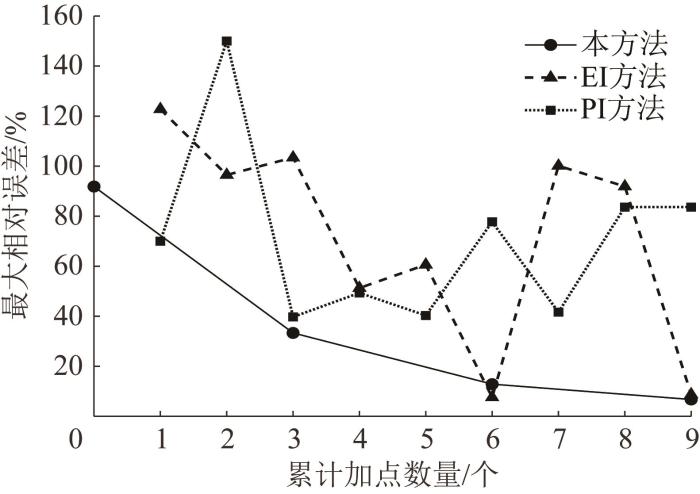
图4 数值算例2中不同加点方法下最大相对误差收敛曲线

Fig.4 Maximum relative error convergence curves under different node-adding methods in numerical example 2

表4 数值算例2中本文方法的优化结果

Table 4 Optimization results of proposed method in numerical example 2

函数	代理模型近似值	真实值	相对误差/%
X =(9.316 8.032 10.000)^T
$f (X)$	10.1979	10.1594	0.38
$g_{1} (X)$	-1.7478	-1.6375	6.74
$g_{2} (X)$	-87.3676	-87.6730	0.35
$g_{3} (X)$	-32.9077	-33.7348	2.45

新窗口打开| 下载CSV

由表3可知：在3种加点方法的迭代步Step 1，初始最大相对误差达到91.86%；EI和PI方法的加点效率较低，本文方法实现了并行加点，加点效率较高。

与此同时，在相同迭代步下，本文方法经过4个迭代步便得到了符合误差要求的最优解，具有很高的求解效率。尽管EI方法在迭代步Step 7达到了容许误差，但是相比本文方法，迭代步数明显增多，且随着迭代步数的增加，EI和PI方法优化解的最大误差有很大的起伏，并没有呈逐步下降的趋势。此外，该2种方法在迭代步Step 4时优化解的最大相对误差分别为103.45%和39.75%。出现这种情况的原因同样可能是获得的新样本与初始样本具有较高的相似性和单一性，无法有效提升代理模型的精度，需要加入更多的迭代步和样本点才有可能获得满足误差要求的最优解，而本文方法仅经过3次加点循环便得到了满足要求的最优解。采用本文方法，在迭代步Step 4时最优解的最大相对误差仅为6.74%，满足了所设置的容许误差要求。因此，本文方法能够有效提升代理模型的精度，在降低计算成本、提高计算效率的同时保证了求解准确度，具有较好的高效性和实用性。

4 工程应用

4.1　工程算例1

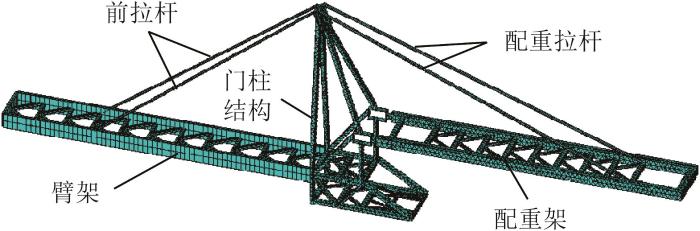
臂式斗轮机的上部结构主要由门柱结构、臂架、配重架和拉杆等部件构成。在工作过程中，斗轮机上部结构所受的实际载荷主要来自配重块自重、斗轮自重、斗轮挖掘阻力、散状物料载荷及斗轮机整个上部结构的自重。对斗轮机上部结构进行有限元建模，所建模型如图5所示。其中，门柱结构、臂架和配重架的单元类型为壳单元，前拉杆和配重拉杆为梁单元。模型的总单元数量为72 560个，总节点数量为39 189个。前拉杆和配重拉杆的材料为Q345D，其余部件的材料为Q345B。在保证斗轮机整体结构安全的前提下，以斗轮机上部结构质量 $M (X)$ 为优化目标、整体最大变形 $D (X)$ 和所承受的最大应力 $P (X)$ 为约束条件构建优化问题。优化问题的设计参数选取如下： $X_{1}$ 为前拉杆直径， $X_{2}$ 为配重拉杆直径， $X_{3}$ 为门柱结构的厚度， $X_{4}$ 为配重架厚度。该优化问题的数学模型如下：

\{\begin{array}{l} m i n M (X) \\ s . t . D (X) \leq 20 m m \\ P (X) \leq 200 M P a \\ X = (X_{1} X_{2} X_{3} X_{4})^{T} \\ 100 \leq X_{1} \leq 200 m m, 100 \leq X_{2} \leq 200 m m, \\ 9 \leq X_{3} \leq 15 m m, 9 \leq X_{4} \leq 15 m m \end{array}

(12)

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 臂式斗轮机上部结构有限元模型

Fig.5 Finite element model of upper structure of arm-type bucket wheel reclaimer

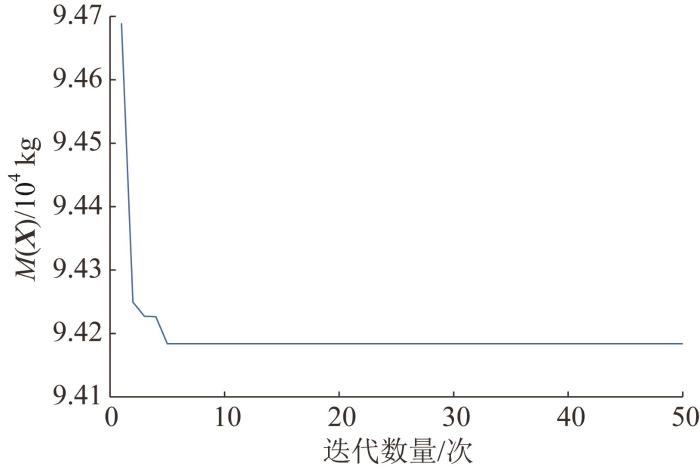
优化过程中设置初始样本数量为15个， $ε$ =0.05，采用Kriging模型来近似目标函数和约束函数，优化求解算法采用GA。GA的参数设置如下：种群规模为5，交叉概率为0.5，最大迭代次数为200。当最优个体适应度值在连续50代内的改进幅度小于1×10⁻⁶时，认为模型收敛。本文方法的迭代步及其最大误差如表5所示，优化过程中斗轮机上部结构质量的收敛曲线如图6所示，最终的优化结果如表6所示。

表5 工程算例1中本文方法的迭代步及其最大误差

Table 5 Iteration steps and their maximum errors of proposed method in engineering example 1

迭代步

新加入样本数量/个

总样本

数量/个

最大相对

误差/%

Step 1

6.02

Step 2

0.09

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 臂式斗轮机上部结构质量收敛曲线

Fig.6 Mass convergence curve of upper structure of arm-type bucket wheel reclaimer

表6 工程算例1中本文方法的优化结果

Table 6 Optimization results of proposed method in engineering example 1

函数	代理模型近似值	真实值	相对误差/%
X =(101.328 7 mm 102.6471 mm 12.1096 mm 10.1796 mm) ^T
$M (X) / k g$	94 183.846 8	94 174	0.01
$D (X) / m m$	17.073 0	17.072	0.01
$P (X) / M P a$	169.901 2	170.05	0.09

新窗口打开| 下载CSV

由表5可知，在迭代步Step 1中优化解的最大相对误差为6.02%，已经接近容许误差，因此可以推测由初始15组样本构建的Kriging模型已经具有较高的精度。在迭代步Step 2中，向样本空间加入了3个高质量样本点，最终优化解的最大相对误差仅为0.09%，完全满足对容许误差的要求。进一步分析表6中的数据可知，在满足最大应力和最大变形的约束条件下，采用本文方法能实现对斗轮机上部结构的轻量化设计。

4.2　工程算例2

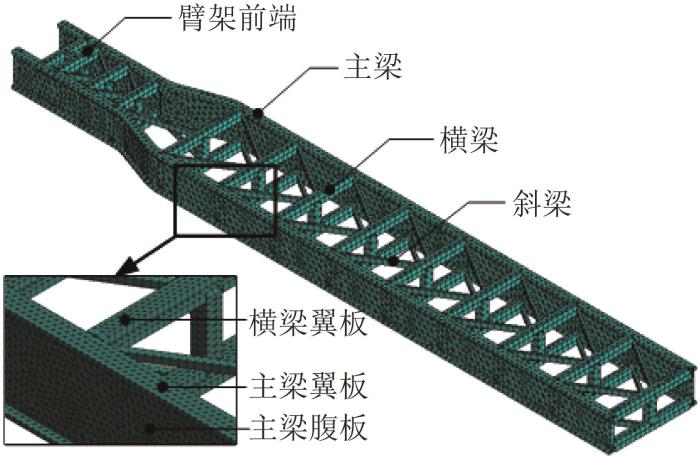
塔式起重机是建筑工地、矿山及大型工业工程项目中广泛使用的高空重物吊装设备。其前臂架结构是关键承载部件，通过在水平及垂直方向的移动，实现重物的移动与提升。前臂架结构的安全性直接影响着起重机整体的工作性能及运行稳定性。为了提升起重机的综合性能，本文基于结构优化设计方法，对其前臂架结构进行轻量化设计。起重机前臂架结构的有限元模型如图7所示。其中，前臂架结构采用壳单元建模，单元类型为shell 181，材料选用Q345，单元数量为63 788个，节点数量为34 492个。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 塔式起重机前臂架结构有限元模型

Fig.7 Finite element model of front boom structure of tower crane

前臂架结构优化问题的描述如下：

\{\begin{array}{l} m i n M (X) \\ s . t . P (X) \leq 200 M P a \\ D (X) \leq 25 M P a \\ X = {(X_{1} X_{2} X_{3} X_{4})}^{T} \\ 8 \leq X_{1}, X_{2}, X_{3}, X_{4} \leq 14 m m \end{array}

(13)

式中： $X_{1}$ 为主梁腹板厚度， $X_{2}$ 为斜梁厚度， $X_{3}$ 为横梁翼板厚度， $X_{4}$ 为主梁翼板厚度， $M (X)$ 为前臂架质量， $P (X)$ 为前臂架结构所承受的最大应力， $D (X)$ 为前臂架在垂直方向的最大位移。

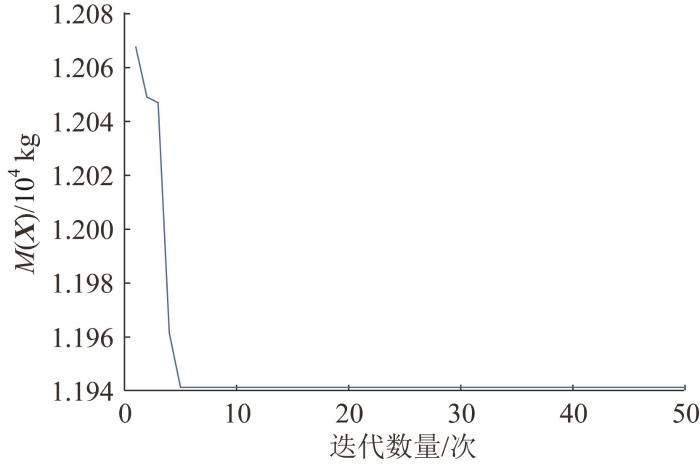
设置 $ε$ <0.05，采用Kriging模型来近似目标函数和约束函数，优化求解算法采用GA。GA的参数设置如下：种群规模为5，交叉概率为0.5，最大迭代次数为200。当最优个体适应度值在连续50代内的改进幅度小于1×10⁻⁶时，认为模型收敛。本文方法的迭代步及其最大误差如表7所示，优化过程中前臂架质量的收敛曲线如图8所示，最终的优化结果如表8所示。

表7 工程算例2中本文方法的迭代步及其最大误差

Table 7 Iteration steps and their maximum errors of proposed method in engineering example 2

迭代步

新加入样本数量/个

总样本

数量/个

最大相对

误差/%

Step 1

3.07

Step 2

0.59

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 塔式起重机前臂架质量收敛曲线

Fig.8 Mass convergence curve of front boom structure of tower crane

表8 工程算例2中本文方法的优化结果

Table 8 Optimization results of proposed method in engineering example 2

函数	代理模型近似值	真实值	相对误差/%
X =(8.207 8 mm 9.719 5 mm 8.014 9 mm 9.705 3 mm)^T
$M (X) / k g$	11 941.26	11 979.00	0.32
$D (X) / m m$	199.86	201.05	0.59
$P (X) / M P a$	20.54	20.59	0.26

新窗口打开| 下载CSV

由表7可知，在迭代步Step 1中优化解的最大相对误差为3.07%，已经小于容许误差阈值，表明由初始15组样本构建的Kriging模型具有较高的预测精度。在迭代步Step 2中向样本空间加入了3个高质量样本点，最终优化解的最大相对误差降至0.59%，完全满足对容许误差的预设要求。进一步结合表8中的数据可知，在满足最大应力及最大变形的约束条件下，采用本文方法能够实现对塔式起重机前臂架结构的轻量化设计。

综上，本文方法为工程机械结构的优化设计提供了新的设计思路和参考方案。

5 结论

1）本文基于工程机械优化问题中设计变量样本的全局及局部分布特征，提出了一种基于自适应Kriging代理模型的工程机械结构优化设计方法。该方法显著减少了对传统高保真仿真模型的依赖，缩短了计算时间。在样本数量有限的情况下，仍然能构建高精度的代理模型，从而大幅提升了代理模型的构建效率，并通过数值算例证明了方法的有效性。

2）完成了臂式斗轮机上部结构和塔式起重机前臂架结构轻量化设计中目标函数、约束函数与设计变量之间代理模型的构建，并在此基础上实现了结构的优化设计。优化结果表明，该方法在有效减小结构质量的同时，保证了工程机械结构的安全性，充分验证了所提出方法在工程机械结构优化中的可行性与工程应用价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘鑫，张远洋.

基于混合模型汽车结构耐撞性的可靠性优化设计

［J］. 长沙理工大学学报（自然科学版）， 2021， 18（1）： 95-101.