现有对于波形弹簧的研究,主要集中在力学性能分析、模态分析以及工艺研究等方面。例如:袁红彬等[3]利用Abaqus软件建立了波形弹簧的弹力试验模型,探讨了弹簧壁厚、宽度和自由高度等因素对弹力的影响规律;李双喜等[4]采用接触非线性求解方法,分析了波形弹簧外径、波厚、波宽和波高等结构参数对弹簧承载特性的影响;秦代成等[5]通过理论分析、有限元模拟及实验相结合的方法,分析了波形弹簧的力学性能,并评估了其结构尺寸对力学性能的影响;Spaggiari等[6]进行了波形弹簧多物理场建模与设计,并比较了波形弹簧与传统螺旋弹簧的优缺点;王振春等[7]对波形弹簧的加工工艺进行了研究,制定了工艺路线,并设计了相应的模具,进一步探讨了波形弹簧模具加工的关键技术。目前,对波形弹簧弹力衰减方面的研究较为短缺。在密封系统中,密封的有效性高度依赖于波形弹簧所提供的恒定轴向力,以确保密封元件如石墨环的良好接触和密封效果。此外,弹簧弹力的衰减还会削弱密封系统在不同工况下的稳定性和预测性,导致其在高温高压等极端环境下的适应能力下降,加速密封件和波形弹簧的磨损,最终增加设备的停机和维修成本[8-10]。因此,深入分析波形弹簧的弹力衰减特性对于弹簧优化设计、延长使用寿命至关重要。
作者通过设计并利用波形弹簧弹力衰减测量装置,开展了在不同温度及初始弹力下波形弹簧弹力衰减试验;基于试验数据,并结合材料蠕变理论,建立了波形弹簧弹力衰减分析模型,同时提出了一种基于Arrhenius方程的波形弹簧寿命预测方法,以期揭示温度和载荷特性对波形弹簧性能的影响,为波形弹簧在工程应用中的可靠性设计和寿命预测提供依据。
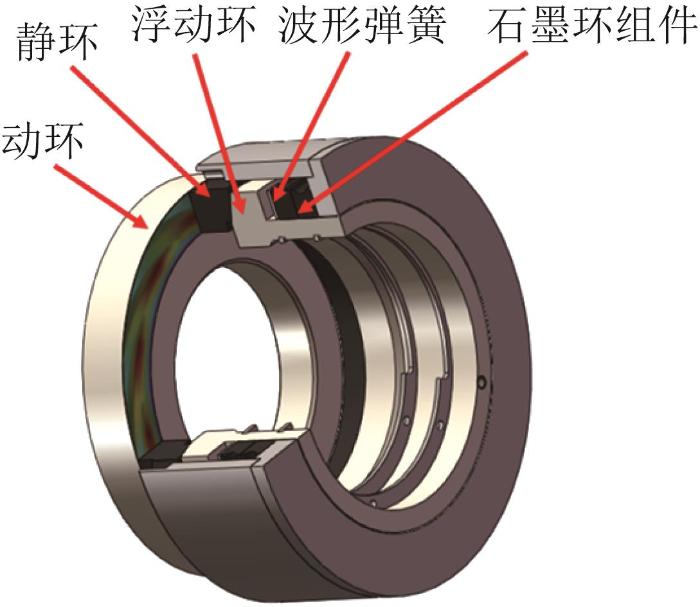
1 波形弹簧结构及弹力衰减机理
图1
图2
波形弹簧的弹力衰减主要由应力松弛和蠕变引起。在长期受力或在高温环境中,弹簧内部应力逐渐降低,导致其弹力衰减;同时,材料在高应力或高温条件下会发生蠕变,导致塑性变形积累,使弹簧难以恢复至原始形状,从而进一步加剧其弹力衰减。
2 基于蠕变模型的波形弹簧弹力衰减分析模型
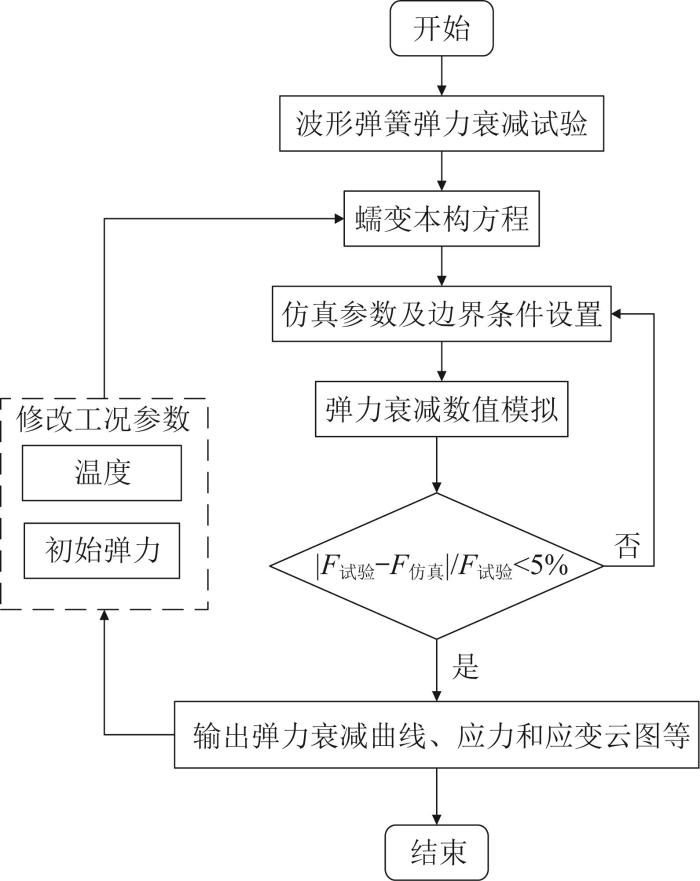
为了优化并准确预测波形弹簧的性能和使用寿命,需要建立数值模型来描述其弹力衰减行为。将波形弹簧的弹力衰减过程视为应力松弛过程。为了精确描述这一过程,引入蠕变模型。该模型能够更好地模拟波形弹簧在长期载荷下的弹力衰减特性,从而为波形弹簧的工程应用提供更加可靠的性能预测。波形弹簧弹力衰减分析流程如图3所示。图中,F为波形弹簧弹力。
图3
2.1 波形弹簧弹力衰减试验
波形弹簧的弹力通过测量压缩力得到。采用压缩试验机对波形弹簧进行持续性压缩,记录各个时间点的弹力值。压缩试验机如图4所示。在弹簧压缩过程中,弹簧位移由DR-503A微机控制电子式万能试验机控制,由高精度传感器、高精度电子引伸计、伺服电机、专用独立控制器、专用测控软件和微机等组成弹力测量装置的测量运算和自动控制系统,其可以实时显示并记录压缩位移及压缩力,并绘制压缩力曲线。温度由加热装置调节,温度变化范围为-2~2 ℃。
图4
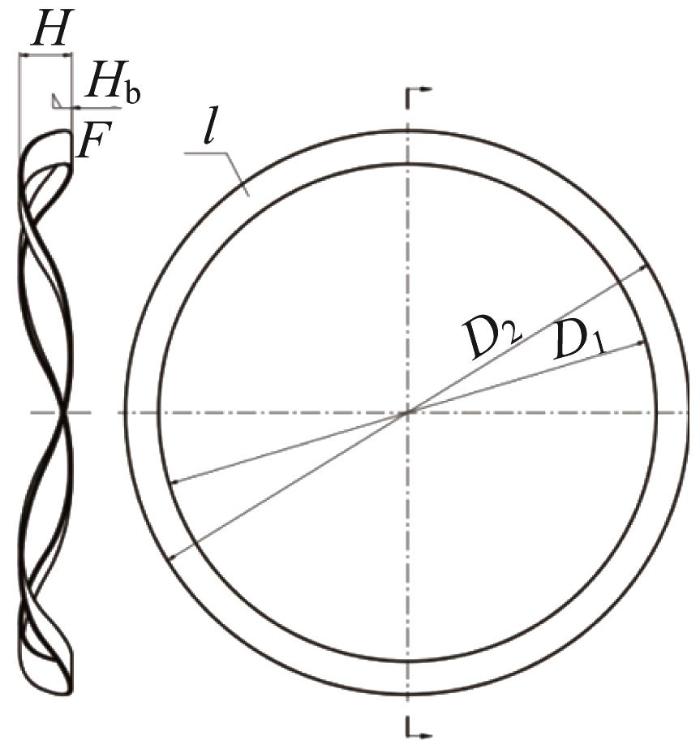
试验对象为应用于某浮环密封的波形弹簧,其结构参数如表1所示,材料为GH4145。试验前测量弹簧的初始尺寸,包括N、D2、D1、b、H和l等,并检查试验设备运转是否正常,检查温度控制系统、温度测量系统和变形量测量系统是否正常,确认设备正常后方可展开试验。将加热箱升温至试验所需的温度,并保温2~3 h,以消除试验器材受热膨胀造成的影响;然后,将波形弹簧装夹至下压板,对其加载一定的预紧力,继续保温1 h后控制上压板压缩至指定位置,记录弹力随时间的变化过程。
表1 试验用波形弹簧的结构参数
Table 1
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 正弦波形数N/个 | 4 | 自由高度H/mm | 4 |
| 外直径D2/mm | 90 | 工作高度Hb/mm | 1.54 |
| 内直径D1/mm | 81 | 压缩量f/mm | 0~3.5 |
| 宽度b/mm | 4.5 | 壁厚l/mm | 0.3 |
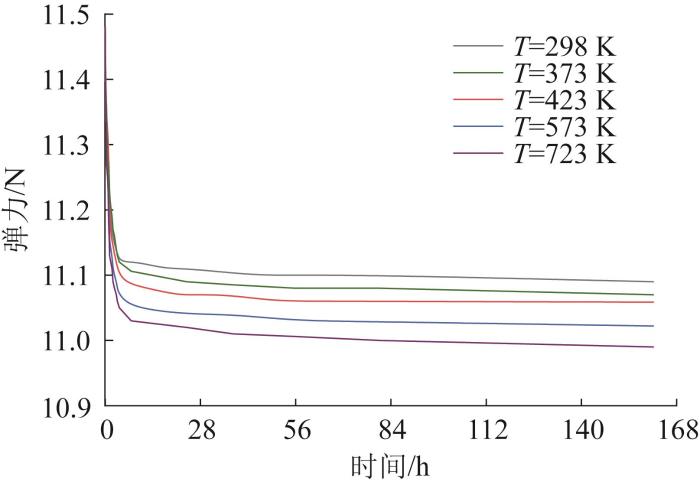
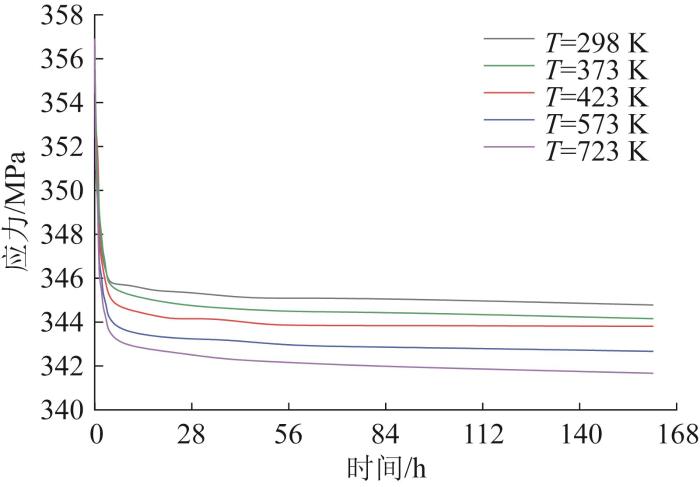
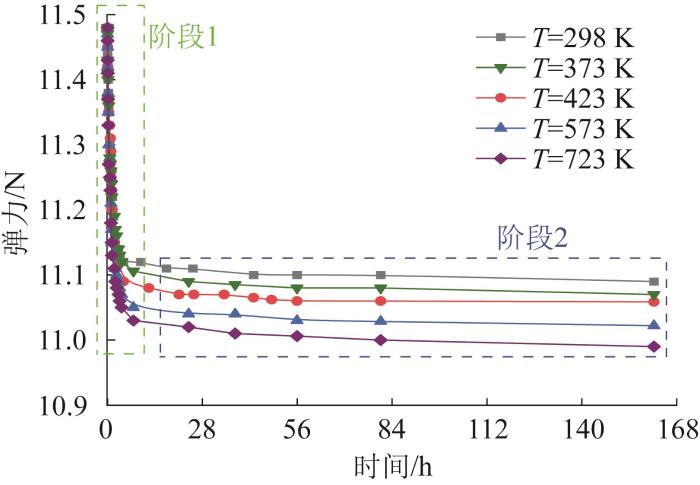
分别设置试验温度T为298、373、423、573、723 K等5个不同温度,则不同温度下波形弹簧弹力衰减试验曲线如图5所示。
图5
图5
不同温度下波形弹簧弹力衰减试验曲线
Fig.5
Test curves of wave spring elasticity decay at different temperatures
2.2 蠕变本构方程
单层封闭波形弹簧的应力计算公式为[14]:
式中:
根据
图6
在波形弹簧的应力松弛过程中,其总应变保持不变,弹性应变逐渐转化为蠕变应变,如
式中:
当温度不变时,蠕变变形与应力存在以下关系:
式中:
将
将试验结果在Origin软件中进行线性拟合,得到蠕变本构方程的参数,如表2所示。
表2 蠕变本构方程的参数
Table 2
| T/K | A | n | m |
|---|---|---|---|
| 298 | 3.899 58×10-49 | 17.938 4 | 0.075 5 |
| 373 | 1.471 43×10-42 | 15.503 6 | 0.063 3 |
| 423 | 6.449 99×10-35 | 12.348 0 | 0.059 5 |
| 573 | 1.500 00×10-26 | 9.379 3 | 0.042 1 |
| 723 | 1.298 87×10-20 | 6.731 2 | 0.035 5 |
2.3 弹力衰减数值模拟
图7
图8
在ANSYS软件中通过“几何结构”选项选定波形弹簧与上下压板的接触面,设定该区域的接触类型为无摩擦。对波形弹簧施加轴向压力,并设置边界条件以模拟压缩工况。波形弹簧在轴向移动时会产生大变形,因此启用了弱弹簧和大变形设置。在工作状态下,上下压板间距减小导致波形弹簧受到轴向压缩。对上压板的下表面施加向下的轴向位移,将下压板的上表面设置为固定边界条件。分析步骤数量设定为“2”,其中:第1步设定为上压板位移,关闭蠕变效应,时间设置为0.1 s;第2步的时间设置为576 000 s,启用蠕变效应。
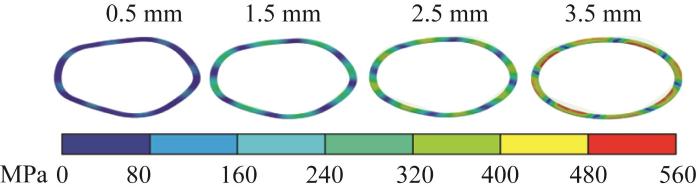
在不同压缩量下波形弹簧的应力云图如图9所示。由图可知,在压缩状态下,波形弹簧的内侧应力大于外侧应力,且由于内侧的曲率半径较小,较之外侧更容易发生应力衰减。
图9
图9
不同压缩量下波形弹簧应力分布云图
Fig.9
Stress distribution nephogram of wave spring under different compression levels
3 波形弹簧弹力衰减影响因素分析及寿命预测
3.1 弹力衰减数值模型的验证
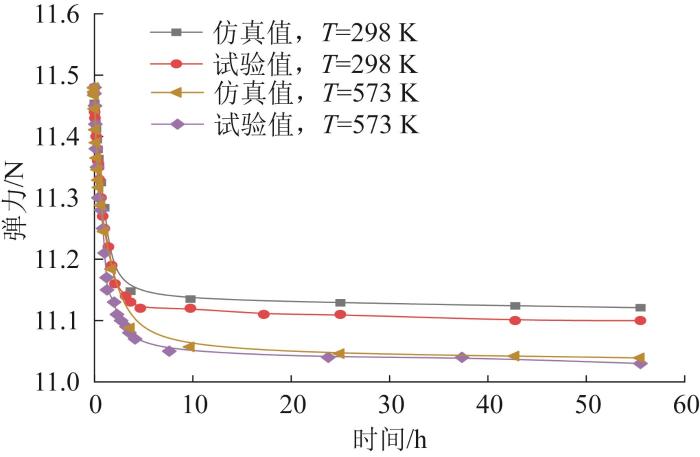
调整波形弹簧的压缩量,使其初始弹力保持在11.48 N,在298、573 K的温度下进行弹力仿真计算,则仿真与试验所得的弹力衰减曲线如图10所示。由图可知,弹力衰减曲线的变化趋势一致,其最大误差在5%以内。因此,所建立的弹力衰减数值模型可用于描述波形弹簧的弹力衰减特性。
图10
图10
仿真与试验得到的波形弹簧弹力衰减曲线
Fig.10
Elasticity decay curves of wave spring obtained through simulation and test
3.2 温度对波形弹簧弹力衰减的影响
在不同温度下波形弹簧弹力衰减仿真曲线如图11所示。由图可知,各温度下波形弹簧的弹力衰减趋势基本相同,可分为2个衰减阶段。在阶段1,弹力在短时间内快速衰减;在阶段2,弹力衰减较为平缓,衰减率趋于平稳。
图11
图11
不同温度下波形弹簧弹力衰减仿真曲线
Fig.11
Simulation curves of wave spring elasticity decay at different temperatures
分别对各温度下弹簧的弹力损失率进行计算,结果如表3所示。其中,弹力损失率
表3 不同温度下波形弹簧弹力损失率
Table 3
| T/K | F0/N | F1/N | |
|---|---|---|---|
| 298 | 11.48 | 11.09 | 3.40 |
| 373 | 11.48 | 11.07 | 3.57 |
| 423 | 11.48 | 11.05 | 3.75 |
| 573 | 11.48 | 11.02 | 4.01 |
| 723 | 11.48 | 10.99 | 4.27 |
图12
图12
弹力损失率与时间对数的关系
Fig.12
Relationship between elasticity loss rate and logarithm of time
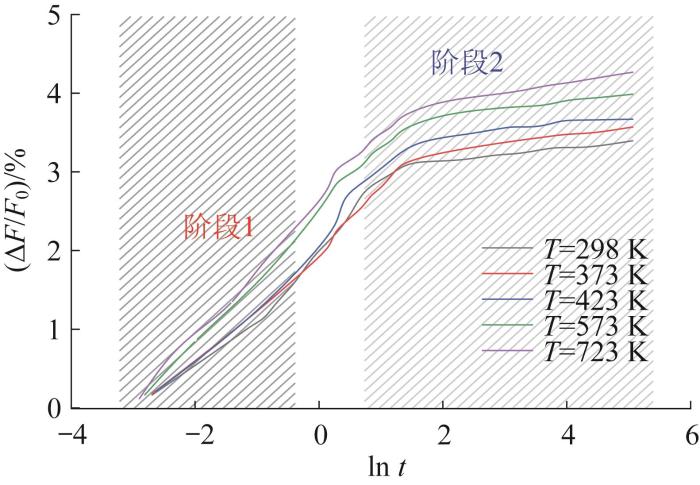
通过分析各温度下弹力损失率与时间对数,得到在各温度下弹力损失率与时间对数的线性关系,如表4所示。表中,R2为拟合相关系数。
表4 不同温度下弹力损失率与时间对数的回归方程
Table 4
| T/K | 阶段 | 回归方程 | R2 |
|---|---|---|---|
| 298 | 阶段1 | 0.981 93 | |
| 阶段2 | 0.972 22 | ||
| 373 | 阶段1 | 0.991 62 | |
| 阶段2 | 0.990 08 | ||
| 423 | 阶段1 | 0.987 76 | |
| 阶段2 | 0.920 95 | ||
| 573 | 阶段1 | 0.997 56 | |
| 阶段2 | 0.977 76 | ||
| 723 | 阶段1 | 0.997 45 | |
| 阶段2 | 0.991 48 |
由表4可知,在阶段1,弹力损失率随着温度的升高显著增大,表明弹力衰减速度对温度的变化十分敏感。在此阶段,弹簧材料快速调整其内部结构以适应新的环境应力,从而导致弹力衰减较快。经过这一调整阶段后,弹力衰减速度逐渐趋于稳定,进入弹力衰减的阶段2。在这一阶段,温度对弹力衰减的影响更加显著,高温环境下弹力衰减速度明显加快。综合来看,波形弹簧的弹力衰减过程可以分为2个阶段:初始的快速衰减阶段和后续的稳定衰减阶段,且温度对弹力衰减有显著影响。
3.3 初始弹力对波形弹簧弹力衰减的影响
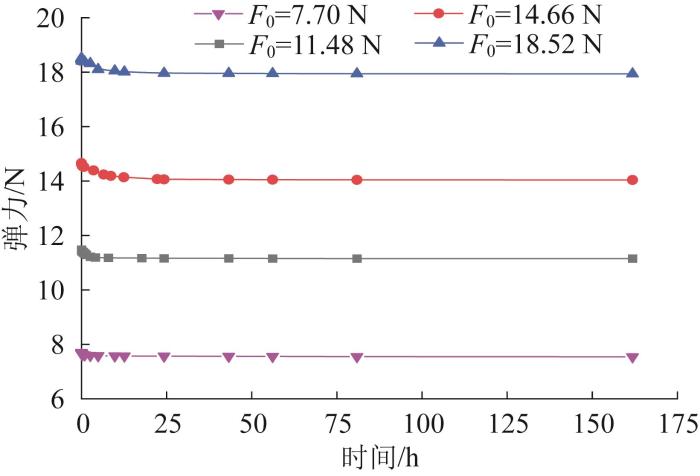
在常温(298 K)环境中,分别设置波形弹簧的初始弹力为7.70、11.48、14.66、18.52 N,得到不同初始弹力下波形弹簧弹力衰减曲线,如图13所示。
图13
图13
不同初始弹力下波形弹簧弹力衰减曲线
Fig.13
Elasticity decay curves of wave spring under different initial elasticity
由图13可知,不同初始弹力下弹簧弹力衰减过程也包含2个阶段:在阶段1,弹力迅速下降;在阶段2,弹力衰减速度变缓。
对弹力损失率进行计算,结果如表5所示。由表可知,弹簧的弹力损失率随着初始弹力的增大而显著增大。在较大初始弹力下,弹簧材料内部的应力更大,加速其内部结构的调整和变形,从而导致更明显的弹力衰减。
表5 不同初始弹力下波形弹簧弹力损失率
Table 5
| T/K | F0/N | F1/N | |
|---|---|---|---|
| 298 | 7.70 | 7.54 | 2.08 |
| 298 | 11.48 | 11.14 | 2.79 |
| 298 | 14.66 | 14.06 | 4.09 |
| 298 | 18.52 | 17.46 | 5.72 |
3.4 基于Arrhenius方程的波形弹簧寿命预测
式中:
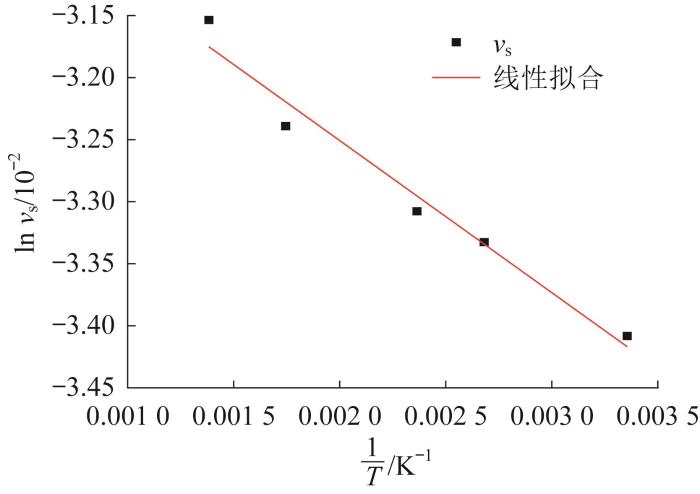
对
图14
图14
波形弹簧应力松弛率对数与温度倒数的拟合曲线
Fig.14
Fitted curve of logarithm of wave spring stress relaxation rate versus temperature inverse
则拟合方程为:
其中,拟合方程的相关系数为0.971 08。
由
应力松弛方程为[21]:
式中:C为积分常数。
当时间t=1 h时,
因此,C可看作应力松弛1 h后的弹力损失率。
将Arrhenius公式两端积分,可得:
对
根据
图15
图15
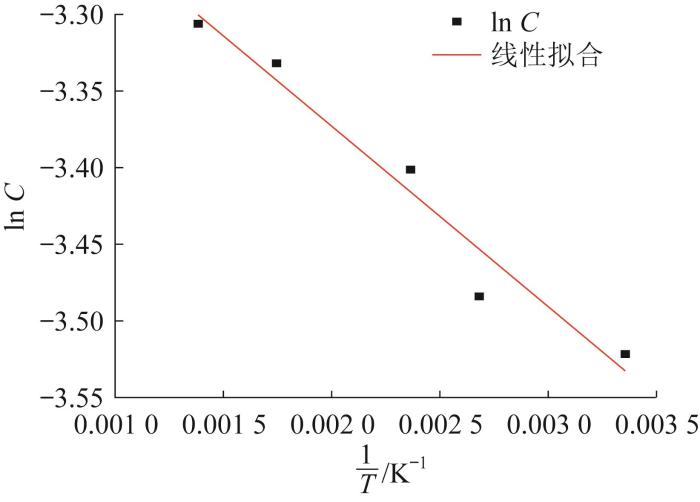
不同温度下积分常数对数与温度倒数的拟合曲线
Fig.15
Fitted curve of logarithm of integral constant versus temperature inverse at different temperatures
则拟合方程为:
其中,拟合方程的相关系数为0.936 96。
当T1=298 K时,由
在室温下使用波形弹簧过程中,常认为其弹力衰减率为40%时失效,即当
4 结 论
本文通过仿真与试验研究了波形弹簧的弹力衰减特性。基于试验数据,构建了波形弹簧弹力衰减数值分析模型,并分析了影响弹力衰减的关键因素。得到的主要结论如下:
1)通过试验数据拟合,构建了波形弹簧弹力衰减仿真模型,其能够模拟不同温度和不同初始弹力下弹力的衰减过程。仿真结果与试验结果基本吻合,最大误差不超过5%,验证了模型的有效性。该模型可预测波形弹簧在不同工况下的弹力衰减行为,为波形弹簧的设计和优化提供了重要的分析手段。
2)基于Arrhenius理论,建立了波形弹簧寿命预测模型。通过引入温度、应力等关键参数,揭示了高温环境下波形弹簧性能衰减特性。利用该模型,可以有效预测波形弹簧在不同工况条件下的服役寿命,为波形弹簧的工程设计和寿命评估提供了理论依据。
3)波形弹簧的弹力损失率随着温度的升高而显著增大,这主要由材料在高温环境下的应力松弛、蠕变效应以及微观组织变化共同导致。在高温工况下,需要特别重视材料的耐高温性能和弹力保持能力,确保波形弹簧在长期服役中的稳定性和可靠性。
4)初始弹力的大小对波形弹簧弹力衰减速度具有显著影响。较大的初始弹力会导致波形弹簧在相同压缩时间内更快地发生弹力衰减。弹力衰减过程可以分为2个阶段:在阶段1,弹力急剧减小,弹力变化率较大;在阶段2,弹力缓慢减小,直至达到稳定状态。
参考文献
石墨密封组件波形弹簧回弹仿真性能分析
[J].
Simulation performance analysis of rebound of wave spring in graphite sealing assembly
[J].
波形弹簧在传动机构中的应用探讨
[J].
Discussion on the application of wave spring in transmission mechanism
[J].
某航空密封件波形弹簧力学性能分析
[J].
Modal analysis of waveform spring of an aviation seal
[J].
结构参数对波形弹簧承载特性的影响
[J].
Effect of structural parameters on the bearing characteristics of wave spring
[J].
波形弹簧的力学性能分析
[J].
Analysis of the wave spring mechanical properties
[J].
Multiphysics modeling and design of shape memory alloy wave springs as linear actuators
[J].
波形弹簧的加工工艺及模具设计
[J].
Processing technology and die design of wave spring
[J].
波纹弹簧力学性能分析与研究
[D].
Analysis and research of wave spring mechanical properties
[D].
波形弹簧的失效分析与改进设计
[J].
Failure analysis and improvement design of wave spring
[J].
航空发动机波形弹簧弹力影响分析
[J].
Elasticity influence analysis of wave spring on aeroengine
[J].DOI:10.1016/j.commatsci.2019.04.051 [本文引用: 1]
波形弹簧的结构和设计
[J].
Structure and design of wave spring
[J].
波形弹簧性能分析及疲劳寿命预测
[D].
Performance analysis and fatigue life prediction of wave spring
[D].DOI:10.18240/ier.2020.01.12 [本文引用: 1]
prediction of wave spring
[D].DOI:10.18240/ier.2020.01.12 [本文引用: 1]
波形弹簧片结构和工艺设计的探讨
[J].
Discussion on structure and process design of wave spring leaf
[J].
基于HyperMesh和ANSYS的波形弹簧变形规律及力学性能研究
[J].
Research of deformation law and mechanical properties of wave spring based on HyperMesh and ANSYS
[J].
浮环密封中典型波形弹簧弹力影响因素及规律研究
[J/OL].
Study on influencing factors and laws of elastic force of typical wave spring in floating ring seal
[J/OL].
PFA弹簧几何结构与服役性能协同机制研究
[D].
Research on the synergistic mechanism of PFA spring geometry and service performance
[D].
不同温度条件下弹簧应力松弛的研究
[D].
Study on stress relaxation of spring under different temperature conditions
[D].
基于GTN模型的不锈钢弹簧高温失效研究
[D].
Study on high temperature failure of stainless steel spring based on GTN model
[D].
1Cr18Ni9钢螺旋压缩弹簧应力松弛机理
[J].
Stress relaxation mechanism of 1Cr18Ni9 steel helical compression spring
[J].
不锈钢弹簧蠕变与应力松弛行为研究
[J].
Study on creep and stress relaxation behavior of stainless steel spring
[J].