基于响应面法的高压共轨式超磁致伸缩喷油器响应时间优化

doi:10.3785/j.issn.1006-754X.2025.04.167

基于响应面法的高压共轨式超磁致伸缩喷油器响应时间优化

喻曹丰^,^,¹^,², 胡逸凯¹, 段永勇¹, 魏梓贤¹, 王宁¹

1.安徽理工大学机电工程学院，安徽淮南 232001

2.浙江大学流体动力基础件与机电系统全国重点实验室，浙江杭州 310027

Response time optimization of high-pressure common rail giant magnetostrictive injector based on response surface method

YU Caofeng^,^,¹^,², HU Yikai¹, DUAN Yongyong¹, WEI Zixian¹, WANG Ning¹

1.School of Mechatronics Engineering, Anhui University of Science and Technology, Huainan 232001, China

2.State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China

收稿日期: 2024-09-04 修回日期: 2024-11-14

基金资助:

国家自然科学基金资助项目.  52105042
流体动力基础件与机电系统全国重点实验室开放基金资助项目.  GZK-202302
中国博士后科学基金资助项目.  2019M652159

Received: 2024-09-04 Revised: 2024-11-14

作者简介 About authors

喻曹丰（1987—），男，副教授，博士，从事超磁致伸缩智能构件设计研究，E-mail:yucaofeng@aust.edu.cn，https://orcid.org/0000-0001-5221-8915 , E-mail：yucaofeng@aust.edu.cn

摘要

为提升高压共轨式喷油器的动态响应特性，基于超磁致伸缩材料棒及液压换向机构，设计了一种高压共轨式超磁致伸缩喷油器。在简述该喷油器整体结构设计和工作原理的基础上，考虑其驱动部分的磁滞非线性特征，基于Jiles-Atherton磁滞模型建立了其电-磁-机-液多场耦合模型。随后，搭建了完整的喷油器仿真模型，选取针阀信号作为喷油响应速度评价指标，确定了针阀弹簧预紧力的最优值。最后，采用响应面法优化了控制活塞直径、控制腔容积、进油孔直径和出油孔直径等参数，并基于拟合方程分析了优化后各参数对喷油器响应时间的影响。结果显示：相较于优化前，优化后针阀的开启延迟缩短了3.251%，开启时间缩短了1.364%，关闭延迟缩短了9.465%，关闭时间缩短了14.848%。研究表明，所采用的优化方法可有效提高针阀的响应速度，有助于提升高压共轨式喷油器的小油量喷油及多次喷油性能。

关键词： 超磁致伸缩 ; 喷油器 ; Jiles-Atherton磁滞模型 ; 响应面法 ; 参数优化

Abstract

To improve the dynamic response characteristics of high-pressure common rail injectors, a high-pressure common rail giant magnetostrictive injector was designed based on the giant magnetostrictive material rod and the hydraulic reversing mechanism. On the basis of briefly describing the overall structure design and working principle of this injector, considering the nonlinear hysteresis characteristics of its driving part, an electro-magnetic-mechanical-hydraulic multiphysics coupling model was established based on the Jiles-Atherton hysteresis model. Then, a complete simulation model of the injector was constructed. The needle valve signal was selected as the evaluation index for fuel injection response speed, and the optimal preload force of the needle valve spring was determined. Finally, the parameters such as the control piston diameter, the control cavity volume, the oil inlet diameter and the oil outlet diameter were optimized by using the response surface method, and the influence of the optimized parameters on the response time of the injector was analyzed based on the fitting equation. The results showed that compared with before optimization, the opening delay of the needle valve after optimization was reduced by 3.251%, the opening time was reduced by 1.364%, the closing delay was reduced by 9.465%, and the closing time was reduced by 14.848%. The research indicates that the adopted optimization method can effectively improve the response speed of the needle valve, which is conducive to enhancing the small-quantity fuel injection and multiple fuel injection performance of the high-pressure common rail injector.

Keywords： giant magnetostrictive ; injector ; Jiles-Atherton hysteresis model ; response surface method ; parameter optimization

PDF (3777KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

喻曹丰, 胡逸凯, 段永勇, 魏梓贤, 王宁. 基于响应面法的高压共轨式超磁致伸缩喷油器响应时间优化[J]. 工程设计学报, 2025, 32(3): 373-382 doi:10.3785/j.issn.1006-754X.2025.04.167

YU Caofeng, HU Yikai, DUAN Yongyong, WEI Zixian, WANG Ning. Response time optimization of high-pressure common rail giant magnetostrictive injector based on response surface method[J]. Chinese Journal of Engineering Design, 2025, 32(3): 373-382 doi:10.3785/j.issn.1006-754X.2025.04.167

随着全球经济的快速发展，柴油机凭借热效率高、功率范围广等优点^[1-2]，在工业、农业、国防及交通运输等领域得到了广泛应用^[3-4]。然而，伴随着柴油机的大规模应用，资源浪费与环境污染问题日益严重^[5]。2020年，我国明确提出了双碳目标，节能减排标准随之提高，这对柴油机的性能提出了更高的要求。以高喷射压力、高响应速度和高控制精度为特征的高压共轨式喷射系统是柴油机实现节能减排的关键技术之一^[6]。喷油器作为高压共轨式喷射系统的核心部件之一，对柴油机的燃烧过程、动力输出性能和废气排放性能有至关重要的影响。目前，喷油器的驱动形式主要有电磁式和压电式两种。电磁式喷油器通过改变通电线圈内的电流大小和电流启闭时间来控制衔铁的运动，但由于衔铁的吸合或断开延迟较长，电磁式喷油器的响应速度较慢^[7]。压电式喷油器利用逆压电效应制作而成，具有较快的响应速度，但存在居里温度不高、输出力较小等缺陷，且其性能难以进一步提升^[8]。

超磁致伸缩材料（giant magnetostrictive material, GMM）是一种新型的功能材料，具有应变大、居里温度高和能量转换效率高等优点^[9]，应用前景广阔。荣策等^[10]提出了以中空的GMM筒驱动T形杆来实现先导阀启闭的方案，并针对驱动结构和电源进行了设计，结果表明：所设计的方案可满足喷油器的驱动要求。Li等^[11]对GMM应用于喷油器时的驱动波形进行了研究，利用反正切函数拟合了无磁滞磁化模型，简化了模型的求解过程，并通过实验验证了所构建模型的准确性，所得结果为喷油器驱动机构的实时控制奠定了一定的理论基础。上述文献仅针对超磁致伸缩喷油器（giant magnetostrictive injector, GMI）的驱动部分进行了研究，缺少对完整GMI性能的分析。薛光明等^[12]设计了一种具有输出换向机构的GMI，其结构特点为GMM棒通过驱动螺盖和输出杆来实现输出换向，同时建立了该GMI的AMESim仿真模型并开展了实验验证，但建模时未将GMM的磁滞特性耦合到GMI模型中。综上，GMM的磁滞特性虽是重要的研究内容，但在现有的高压共轨式GMI建模分析中，将GMM磁滞模型耦合进GMI模型的研究较少，同时也缺少针对GMI喷油特性优化的研究。

为此，笔者团队拟在考虑GMM磁滞特性的基础上，采用响应面法（response surface method, RSM）对课题组前期自主研制的高压共轨式GMI^[13]的响应时间进行优化设计。RSM在机械、化工和材料等领域应用广泛^[14-15]，该方法利用多元二次回归方程来拟合设计变量与响应变量之间的函数关系，并通过分析回归方程来找到最优的参数组合，是一种有效解决多变量优化问题的统计方法。本文研究内容如下：首先，以高压共轨式GMI的整体结构为基础，建立耦合GMM磁滞特性的电-磁-机-液多场耦合模型；随后，根据单因素分析确定针阀弹簧预紧力的最优值，并采用RSM对控制活塞直径、控制腔容积、进油孔直径和出油孔直径等结构参数进行优化，以实现对GMI响应时间的优化。

1 高压共轨式GMI的结构及工作原理

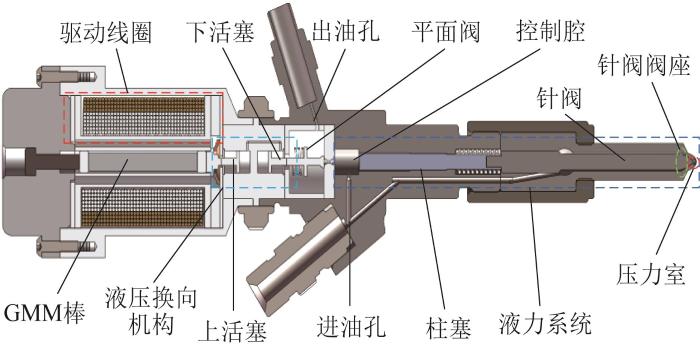
本文所研究的高压共轨式GMI的结构如图1所示，主要包括超磁致伸缩驱动部分（由驱动线圈和GMM棒组成）、液压换向机构和液力系统三部分。其中：GMM棒具有磁致伸缩效应，能够在驱动线圈产生的磁场作用下将输入的电能转化为机械能；液压换向机构由上活塞和下活塞组成，可通过改变压力来实现对活塞运动方向的转换。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 高压共轨式GMI结构示意

Fig.1 Structure diagram of high-pressure common rail GMI

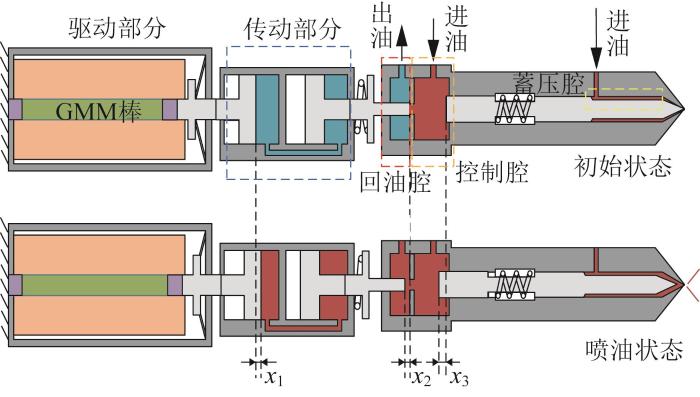
该GMI的工作原理如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 高压共轨式GMI工作原理

Fig.2 Working principle of high-pressure common rail GMI

1）初始状态下驱动部分未通电，传动部分处于低压状态，平面阀在预紧弹簧的作用下克服控制腔的液压力，关闭控制腔的出油孔。此时，控制腔与回油腔不连通，控制腔对柱塞产生的液压力与弹簧预紧力远大于针阀所受的开启液压力，故针阀被压在阀座上，不喷油。在该状态下，控制腔、蓄压腔及针阀阀座处的压强等于油路轨压。

2）当驱动部分通入电流后，传动部分的上活塞在GMM棒的推力作用下向下运动x₁，此时换向腔内压强升高，下活塞在换向腔内压强的作用下带动与其固联的平面阀克服弹簧预紧力向上运动x₂，开启控制腔的出油孔。此时，回油腔与控制腔连通，控制腔内压强降低，故控制腔对柱塞的向下液压力减小，针阀在蓄压腔、阀座处液压力的作用下向上运动x₃，开始喷油。

3）当驱动部分断电后，GMM棒恢复原始长度，换向腔内压强恢复为初始值，此时平面阀在预紧弹簧的作用下重新关闭控制腔的出油孔，随着出油量的减少，控制腔内压强逐渐升高，针阀所受的向下液压力开始增大；最后，在控制腔液压力的作用下，针阀重新落座，喷油结束，即恢复为初始状态。

2 高压共轨式GMI的电-磁-机-液多场耦合模型建立

根据高压共轨式GMI的结构和工作原理，其模型主要包括驱动线圈的电压-电流模型和电流-磁场强度模型、GMM棒的磁-机耦合模型以及针阀的机-液耦合模型。

1）电压-电流模型。

将驱动线圈简化为电阻与理想电感的串联结构，则驱动线圈的电压-电流模型可表示为：

U = L \frac{d I}{d t} + R I

式中：U为线圈电压，L为线圈电感，I为线圈电流，t为时间，R为线圈电阻。

2）电流-磁场强度模型。

驱动线圈通入电流后所产生的磁场强度可表示为：

H = f I

式中：H为线圈磁场强度，f为线圈磁场系数。

3）磁-机耦合模型。

相较于其他模型，Jiles-Atherton磁滞模型（简称J-A模型）具有物理意义明确、计算简单等优点^[16]。本文选用J-A模型来建立GMM棒的磁滞模型。根据J-A模型，驱动线圈磁场强度H与GMM棒磁化强度M之间的关系为：

\frac{d M}{d H} = [(M_{a n} - M) + c k δ \frac{d M}{d H_{c}}] / [k δ - (α + \frac{9 λ_{s} σ_{0}}{2 μ_{0} M_{s}^{2}}) (M_{a n} - M) - k δ c (α + \frac{9 λ_{s} σ_{0}}{2 μ_{0} M_{s}^{2}}) \frac{d M_{a n}}{d H_{e}}]

式中：M_an为无磁滞磁化强度，c为可逆分量系数，k为不可逆损耗系数，δ为方向系数，H_c为材料磁化强度降为0时所需的反向磁场强度，α为无磁滞磁化强度形状参数，λ_s为材料的饱和磁致伸缩系数，σ₀为预压应力，μ₀为真空磁导率，M_s为饱和磁化强度，H_s为磁性材料的有效磁场。

将GMM棒视为各向同性，基于能量的二次畴转模型计算不同磁化强度下的磁致伸缩应变λ，计算式如下：

λ = \frac{3 λ_{s}}{2 M_{s}^{2}} M^{2}

GMM棒输出力F_M的表达式为：

F_{M} = E_{M} A_{M} λ

式中：E_M为GMM棒的弹性模量，A_M为GMM棒的横截面积。

GMM棒在预应力的作用下会发生形变，即由原始长度l₁被压缩至l₀。由于预应力在GMM棒的整个工作过程中一直存在，因此可将压缩后的长度l₀视为GMM棒的原始长度，此时GMM棒与输出杆的力平衡方程可表示为：

m_{t o t} {\ddot{x}}_{s h} + c_{M} {\dot{x}}_{s h} + k_{M} x_{s h} = F_{M} - F_{u} - F_{s p r}

式中：m_tot为GMM棒与输出杆的等效质量，m_tot=m_M/3＋m_sh，其中m_M为GMM棒的质量，m_sh为输出杆的质量；x_sh为输出杆的位移；c_M为GMM棒的等效阻尼系数；k_M为GMM棒的等效刚度系数；F_spr为碟簧的预压力；F_u为换向腔对输出组件（由GMM棒和输出杆构成）的力。

4）机-液耦合模型。

根据流量连续性方程，GMI的总燃油流量Q_g可表示为：

Q_{g} = C_{d} A_{1} \sqrt[]{\frac{2}{ρ} |p_{c} - p_{g}|} + C_{d} A_{2} \sqrt[]{\frac{2}{ρ} |p_{s} - p_{g}|} + \frac{V_{g}}{E} \frac{d p_{g}}{d t}

式中：C_d为流量系数，A₁为燃油进入控制腔的截面面积，A₂为燃油进入压力室的截面面积，ρ为燃油密度，p_c为控制腔内燃油压力，p_g为高压共轨管内燃油压力，p_s为压力室内燃油压力，V_g为高压共轨管的容积，E为燃油的弹性模量。

根据流量连续性方程，控制腔内的流量方程可表示为：

\frac{V_{c}}{E} \frac{d p_{c}}{d t} + \frac{d V_{c}}{d t} = C_{d} A_{1} \sqrt[]{\frac{2}{ρ} |p_{c} - p_{g}|} - C_{d} A_{2} \sqrt[]{\frac{2}{ρ} |p_{s} - p_{g}|}

式中：V_c为控制腔容积。

根据流量连续性方程，压力室内的流量方程可表示为：

\frac{V_{s}}{E} \frac{d p_{s}}{d t} + \frac{d V_{s}}{d t} = C_{d} A_{2} \sqrt[]{\frac{2}{ρ} |p_{g} - p_{s}|} + C_{d} A_{3} \sqrt[]{\frac{2}{ρ} |p_{s} - p_{0}|}

式中：V_s为压力室容积，A₃为燃油流出压力室的截面面积，p₀为气缸内压强。

由伯努利方程可知，GMI的喷油速率q_ouk可表示为：

q_{o u k} = n C_{o u k} A_{o u k} \sqrt[]{\frac{2}{ρ} |p_{l} - p_{c}|}

式中：n为喷孔数量，C_ouk为喷孔的流量系数，A_ouk为喷孔的横截面积，p_l为油路轨压。

3 高压共轨式GMI仿真建模与分析

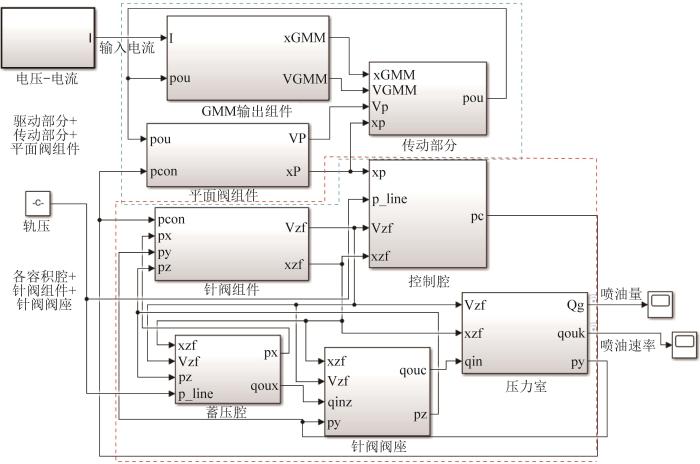
3.1　GMI仿真模型建立

基于上文建立的高压共轨式GMI的电-磁-机-液多场耦合模型，在Simulink软件中搭建其仿真模型，如图3所示。该仿真模型的输入为驱动线圈电压和油路轨压，输出为喷油量和喷油速率，其中GMI的主要参数如表1所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 高压共轨式GMI仿真模型

Fig.3 Simulation model of high-pressure common rail GMI

表1 高压共轨式GMI主要参数

Table 1 Main parameters of high-pressure common rail GMI

参数	数值
线圈电感/mH	11.2
线圈电阻/Ω	10.8
线圈磁场系数	3 180
GMM棒等效阻尼系数/(N·s/m)	3×10⁶
饱和磁致伸缩系数	1.5×10^-3
控制腔容积/mm³	30
进油孔直径/mm	0.21
出油孔直径/mm	0.27
平面阀质量/g	7.5
针阀质量/g	17.3
柱塞直径/mm	4.4
针阀直径/mm	4.0
针阀半角/(°)	29.8
喷孔数量/个	6
喷孔直径/mm	0.169

新窗口打开| 下载CSV

3.2　GMI驱动部分位移分析

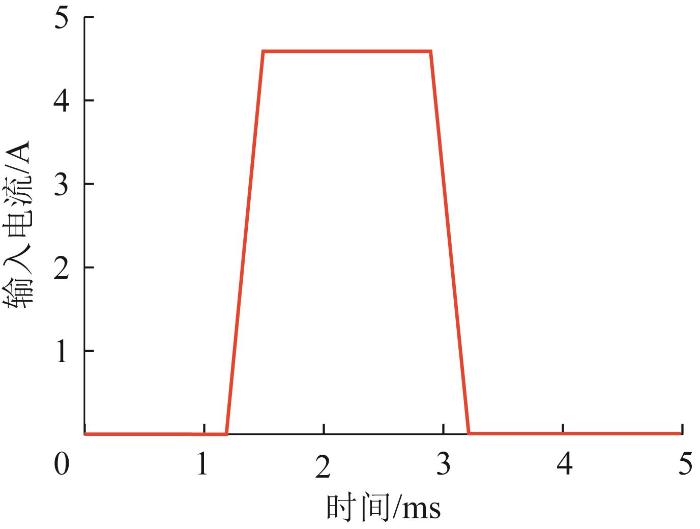
高压共轨式GMI驱动电流的波形如图4所示，电流幅值为4.6 A，持续时间为1.4 ms，整个周期的运行时间为5 ms。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 驱动电流波形

Fig.4 Driving current waveform

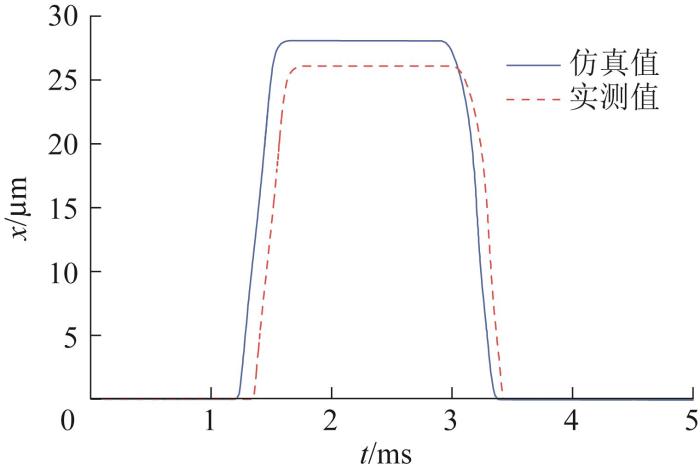
在利用Simulink软件对高压共轨式GMI驱动部分的位移进行仿真分析后，为验证仿真结果的准确性，按与仿真模型1∶1的比例搭建图5所示的GMI驱动部分的实验平台，并在驱动线圈通电后开展位移测量实验。位移传感器连接在驱动部分输出端的末端。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 GMI驱动部分位移测量实验平台

Fig.5 Experimental platform for measuring displacement of GMI driving part

将通过仿真与实验测得的GMI驱动部分的位移进行对比，结果如图6所示。由图6可知，通过实验测得的最大位移可达24.1 μm；在通电初始阶段，实测位移与仿真位移具有很高的重合度；在通电一段时间后，由于驱动线圈温度升高等因素的影响，实测位移与仿真位移存在一定误差，但两者的相关系数接近1，仍具有很高的重合度和线性度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 GMI驱动部分位移对比

Fig.6 Displacement comparison of GMI driving part

3.3　GMI喷油响应速度的评价指标选取

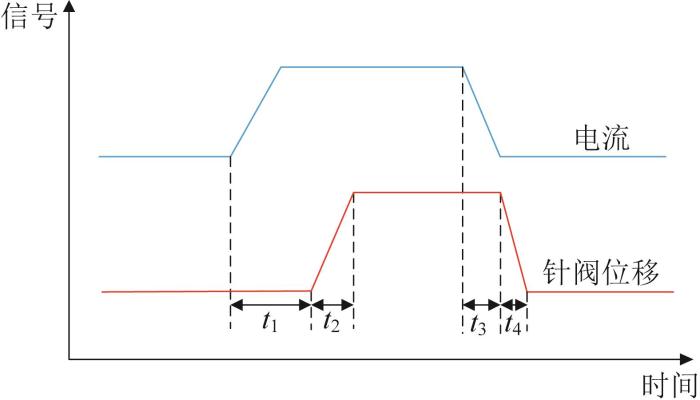
针阀作为控制喷油启闭的重要部件，其运动过程决定了高压共轨式GMI的喷油开启时间、喷油持续时间与喷油量等。针阀响应时间包括针阀开启延迟t₁、针阀开启时间t₂、针阀关闭延迟t₃和针阀关闭时间t₄，其分布情况如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 针阀响应时间分布情况

Fig.7 Distribution of response time of needle valve

考虑到喷油器需满足缓开、急关的喷油响应特性以及多次喷射的喷油要求，选择针阀的综合响应时间t_c作为高压共轨式GMI喷油响应速度的评价指标，t_c值越小，表明GMI的响应越迅速，喷油特性越好。在喷油初期，通常希望喷油速率较低，以减少氮氧化物的排放和减小噪声，则开启延迟t₁、开启时间t₂的权重可稍小；在喷油后期，通常希望针阀快速关闭，以避免雾化不良和减少颗粒物排放，则关闭延迟t₃、关闭时间t₄的权重应较高。此外，为追求矩形喷油曲线，t₂、t₄的权重应高于t₁、t₃。基于此，t₁、t₂、t₃、t₄的权重分别取0.20、0.25、0.25和0.30，由此得到t_c的表达式：

t_{c} = 0.20 t_{1} + 0.25 t_{2} + 0.25 t_{3} + 0.30 t_{4}

(11)

3.4　GMI各结构参数的重要性分析

考虑到进油孔直径、出油孔直径、控制腔容积、针阀弹簧刚度、针阀弹簧预紧力、针阀锥角以及控制活塞直径对高压共轨式GMI的喷油响应速度有影响，对各结构参数进行重要性分析，并对影响程度较大的结构参数进行优化设计。其中：控制腔出油孔的面积应小于平面阀在最大开度时的出油面积，通过计算可确定出油孔直径的上限为0.29 mm；而进油孔直径应小于出油孔直径，否则当平面阀开启时，进油孔流量大于出油孔流量，导致控制腔内压强不会降低，GMI无法正常工作；其他结构参数的取值范围选在其初始值附近。GMI各结构参数的初始值与取值范围如表2所示。

表2 GMI各结构参数的初始值与取值范围

Table 2 Initial value and value range of each structural parameter of GMI

结构参数	初始值	取值范围
进油孔直径/mm	0.21	0.20~0.23
出油孔直径/mm	0.27	0.26~0.29
控制腔容积/mm³	30	15~45
控制活塞直径/mm	4.4	4.2~4.5
针阀弹簧预紧力/N	48	38~68
针阀弹簧刚度/(N/mm)	76	60~90
针阀锥角/(°)	29.8	25~40

新窗口打开| 下载CSV

定义影响因子K，用于评价各结构参数对GMI喷油响应速度的影响程度，K表示为：

K = \frac{1}{N - 1} \sum_{s = 1}^{N - 1} \frac{(y_{s + 1} - y_{s}) / \bar{y}}{(x_{s + 1} - x_{s}) / \bar{x}}

(12)

式中：N为结构参数取值数量，N=4；x_s 、x_s₊₁分别为结构参数的第s个与第s+1个取值；y_s 、y_s₊₁分别为x_s 、x_s₊₁对应的响应值； $\bar{x}$ 为结构参数的平均值； $\bar{y}$ 为结构参数取 $\bar{x}$ 时对应的响应值。

将表2中各结构参数的值代入GMI仿真模型，通过仿真得到对应的响应时间，再利用式(12)计算得到各结构参数的重要性占比，结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

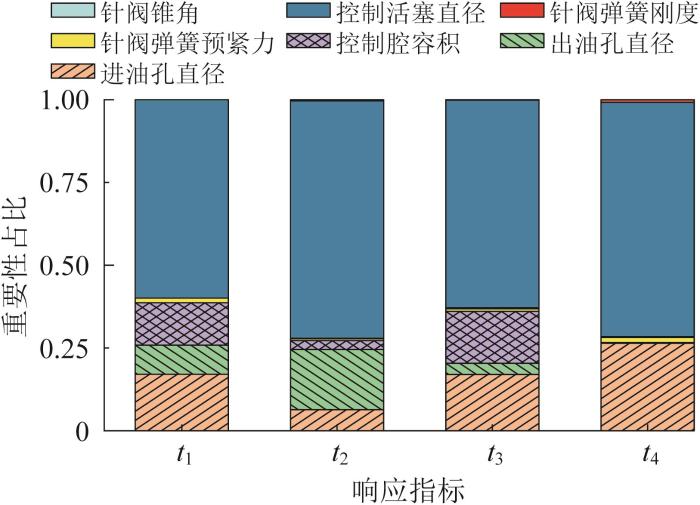
图8 GMI各结构参数的重要性占比

Fig.8 Proportion of importance of each structural parameter in GMI

由图8可知，控制活塞直径对针阀综合响应时间的影响最大，出油孔直径对针阀关闭时间t₄无影响。针阀弹簧刚度与针阀锥角对各响应时间的影响均很小，即对GMI喷油响应速度的影响可忽略不计。

考虑到针阀弹簧预紧力的影响较小，采用单因素分析法得到不同针阀弹簧预紧力下的综合响应时间，如图9所示。由图9可知，当针阀弹簧预紧力为68 N时，GMI的喷油响应速度最优，故将针阀弹簧预紧力选取为68 N。

图9

新窗口打开| 下载原图ZIP| 生成PPT

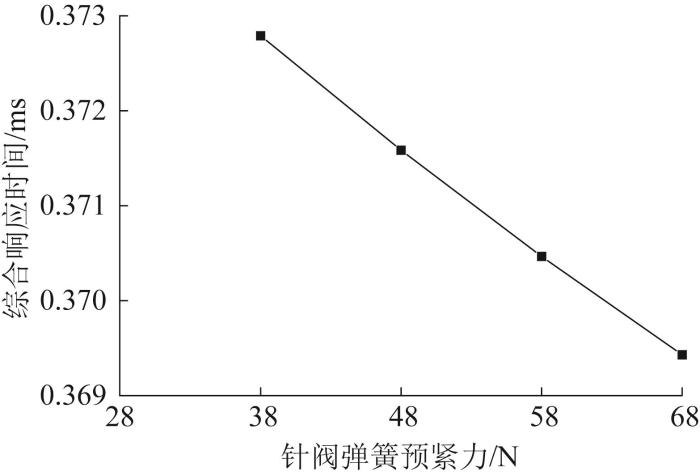
图9 针阀弹簧预紧力的单因素分析结果

Fig.9 Univariate analysis results of preload force of needle valve spring

4 基于RSM的高压共轨式GMI结构参数优化

4.1　响应面试验组

根据上文分析，选择高压共轨式GMI的控制活塞直径、控制腔容积、进油孔直径和出油孔直径作为优化变量，以GMI的响应时间（即针阀的综合响应时间t_c）为优化目标，借助Design-Expert软件，采用BBD（Box-Behnken Design）法进行四因素三水平试验设计^[15]，各因素及其水平如表3所示。

表3 GMI结构参数响应面试验的因素水平表

Table 3 Factor level table for response surface test of GMI structural parameters

水平

控制活塞

直径A/mm

控制腔容积B/mm³

进油孔直径C/mm

出油孔直径D/mm

-1

4.20

0.200

0.260

4.35

0.215

0.275

4.50

0.230

0.290

新窗口打开| 下载CSV

响应面试验所需的组数Z为：

Z = 2 k (k - 1) + z

(13)

式中：k为因素数量；z为中心点数，即各因素均取0水平时的试验点数。

工程上一般采用二次多项式回归模型进行拟合，其表达式为：

y = β_{0} + \sum_{i = 1}^{k} β_{i} x_{i} + \sum_{i = 1}^{k} β_{i i} x_{i}^{2} + \sum_{i = 1}^{k - 1} \sum_{j > i}^{k} β_{i j} x_{i} x_{j}

(14)

式中：y为预测值，β₀ 、β_i 、β_ii 、β_ij 为回归系数，x_i 、x_j 为自变量。

对于高压共轨式GMI的喷油响应速度，待优化的结构参数共有4个，中心点数选为5个，则共需进行29组试验。通过仿真得到不同结构参数组合下的GMI响应时间t_c，结果如表4所示。

表4 GMI结构参数的响应面试验结果

Table 4 Response surface test results of GMI structural parameters

试验序号	因素				t_c/ms
试验序号	A/mm	B/mm³	C/mm	D/mm	t_c/ms
1	4.50	30	0.215	0.290	0.352 905
2	4.20	30	0.230	0.275	0.351 820
3	4.35	30	0.200	0.260	0.390 330
4	4.35	30	0.215	0.275	0.360 895
5	4.35	30	0.215	0.275	0.360 895
6	4.20	30	0.200	0.275	0.393 170
7	4.20	15	0.215	0.275	0.360 630
8	4.35	30	0.230	0.260	0.359 350
9	4.35	45	0.215	0.290	0.362 490
10	4.35	30	0.200	0.290	0.374 705
11	4.35	15	0.200	0.275	0.370 000
12	4.35	15	0.230	0.275	0.339 530
13	4.35	15	0.215	0.290	0.345 120
14	4.35	45	0.200	0.275	0.391 555
15	4.20	30	0.215	0.290	0.360 895
16	4.35	30	0.215	0.275	0.360 895
17	4.35	30	0.215	0.275	0.360 895
18	4.20	30	0.215	0.260	0.376 550
19	4.35	42	0.215	0.260	0.381 485
20	4.35	30	0.230	0.290	0.338 010
21	4.50	30	0.230	0.275	0.351 150
22	4.35	30	0.215	0.275	0.360 895
23	4.35	45	0.230	0.275	0.352 550
24	4.50	15	0.215	0.275	0.353 635
25	4.50	30	0.200	0.275	0.381 005
26	4.50	45	0.215	0.275	0.374 935
27	4.35	15	0.215	0.260	0.361 295
28	4.20	45	0.215	0.275	0.380 375
29	4.50	30	0.215	0.260	0.374 075

新窗口打开| 下载CSV

4.2　响应面模型建立及其有效性分析

利用式(14)和表4数据拟合得到GMI响应时间t_c关于控制活塞直径A、控制腔容积B、进油孔直径C和出油孔直径D的响应面模型，具体为：

t_c=6.054 07-2.154 11A+0.002 674B-10.103 08C+

2.04214D+0.000 173AB+1.277 22AC-0.962 778

AD-0.009 483BC-0.003 133BD-6.350 00CD+

0.243 389A²+1.730 56×10^-6B²+12.605 56C²+5.486 11D²

(15)

对响应面模型进行有效性分析，得到其残差正态概率分布以及预测值与实际值的分布，分别如图10和图11所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

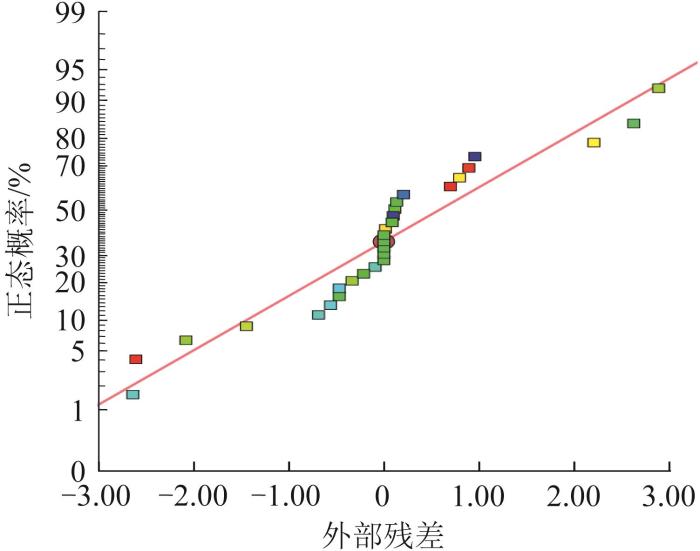
图10 响应面模型的残差正态概率分布

Fig.10 Normal probability distribution of residuals of response surface model

图11

新窗口打开| 下载原图ZIP| 生成PPT

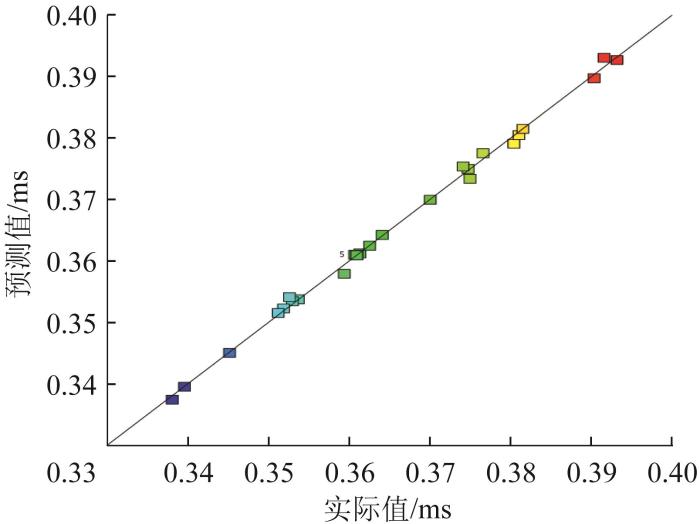
图11 GMI响应时间的预测值与实际值分布

Fig.11 Distribution of predicted and actual values of GMI response time

由图10可知，响应面模型中的残差分布大致为直线，符合正态分布，即该模型的拟合效果良好，具有统计学意义。由图11可知，预测值与实际值基本聚集在回归线附近，表明其相关性较高，说明所拟合的响应面模型中不存在明显的异常预测值。

响应面模型的误差分析结果如表5所示。其中：总方差r²越大，表明拟合效果越好；调整方差r_A²与方差r_P²的数值越大且两者的差值越小，表明拟合效果越好，一般两者差值小于0.2时，可认为拟合效果好；一般认为信噪比大于4，拟合模型即有效。综上可知，该响应面模型的拟合精度高，可用于GMI结构参数优化范围内非样本点的响应预测。

表5 响应面模型误差分析结果

Table 5 Error analysis results of response surface model

方差与信噪比	数值
r²	0.997 4
r $_{A}^{2}$	0.994 8
r $_{P}^{2}$	0.985 1
信噪比	73.245 7

新窗口打开| 下载CSV

4.3　各结构参数对响应时间的影响分析

基于上述响应面模型，分析各结构参数对GMI响应时间的影响，在分析其中2个因素对响应时间的交互影响时，其他因素保持为0水平，结果如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

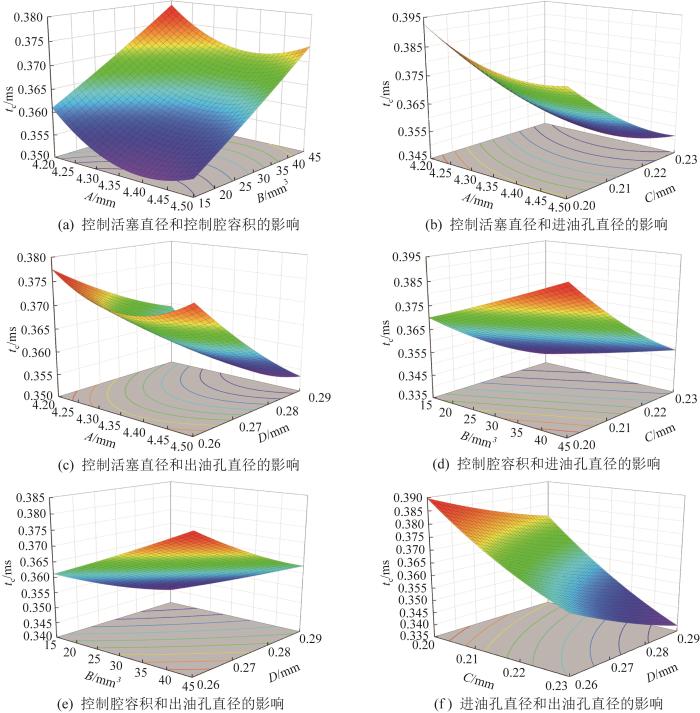
图12 各结构参数对GMI响应时间的影响

Fig.12 Influence of each structural parameter on response time of GMI

由图12(a)可知，当控制活塞直径不变时，随着控制腔容积的增大，响应时间呈上升趋势；当控制腔容积不变时，随着控制活塞直径的增大，响应时间呈先下降后上升趋势。

由图12(b)可知，当控制活塞直径不变时，随着进油孔直径的增大，响应时间呈下降趋势；当进油孔直径不变时，随着控制活塞直径的增大，响应时间呈先下降后上升趋势。

由图12(c)可知，当控制活塞直径不变时，随着出油孔直径的增大，响应时间呈下降趋势；当出油孔直径不变时，随着控制活塞直径的增大，响应时间呈先下降后上升趋势。

由图12(d)可知，当控制腔容积不变时，随着进油孔直径的增大，响应时间呈下降趋势；当进油孔直径不变时，随着控制腔容积的增大，响应时间呈上升趋势。

由图12(e)可知，当控制腔容积不变时，随着出油孔直径的增大，响应时间呈下降趋势；当出油孔直径不变时，随着控制腔容积的增大，响应时间呈上升趋势。

由图12(f)可知，当出油孔直径不变时，随着进油孔直径的增大，响应时间呈下降趋势；当进油孔直径不变时，随着出油孔直径的增大，响应时间呈下降趋势。

4.4　优化结果分析

基于RSM得到的最优结构参数如下：A=4.428 mm、B=18.756 mm³、C=0.226 mm、D=0.289 mm，结合前文选取的最优针阀弹簧预紧力，对高压共轨式GMI进行仿真分析，并将优化后的结构参数代入式(15)进行计算。通过仿真得到的优化后的响应时间为0.336 3 ms，而利用响应面模型计算得到的优化后的响应时间为0.335 9 ms，模型预测结果与仿真结果之间的相对误差仅为0.12%，由此验证了响应面模型的准确性。优化前后GMI响应时间仿真结果的对比如表6所示。与优化前相比，优化后GMI响应时间缩短了9.499%，尤其是针阀关闭速度得到了很大提升。

表6 优化前后GMI响应时间仿真结果对比

Table 6 Comparison of simulation results of GMI response time before and after optimization

对比项	t₁/ms	t₂/ms	t₃/ms	t₄/ms	t_c/ms
相对误差/%	3.251	1.364	9.465	14.848	9.499
优化前	0.292 2	0.212 6	0.439 5	0.500 4	0.371 6
优化后	0.282 7	0.209 7	0.397 9	0.426 1	0.336 3

新窗口打开| 下载CSV

为进一步验证响应时间的优化对GMI喷油响应速度的影响，对比分析了优化前后针阀的速度、位移以及GMI的喷油速率等特性，结果如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

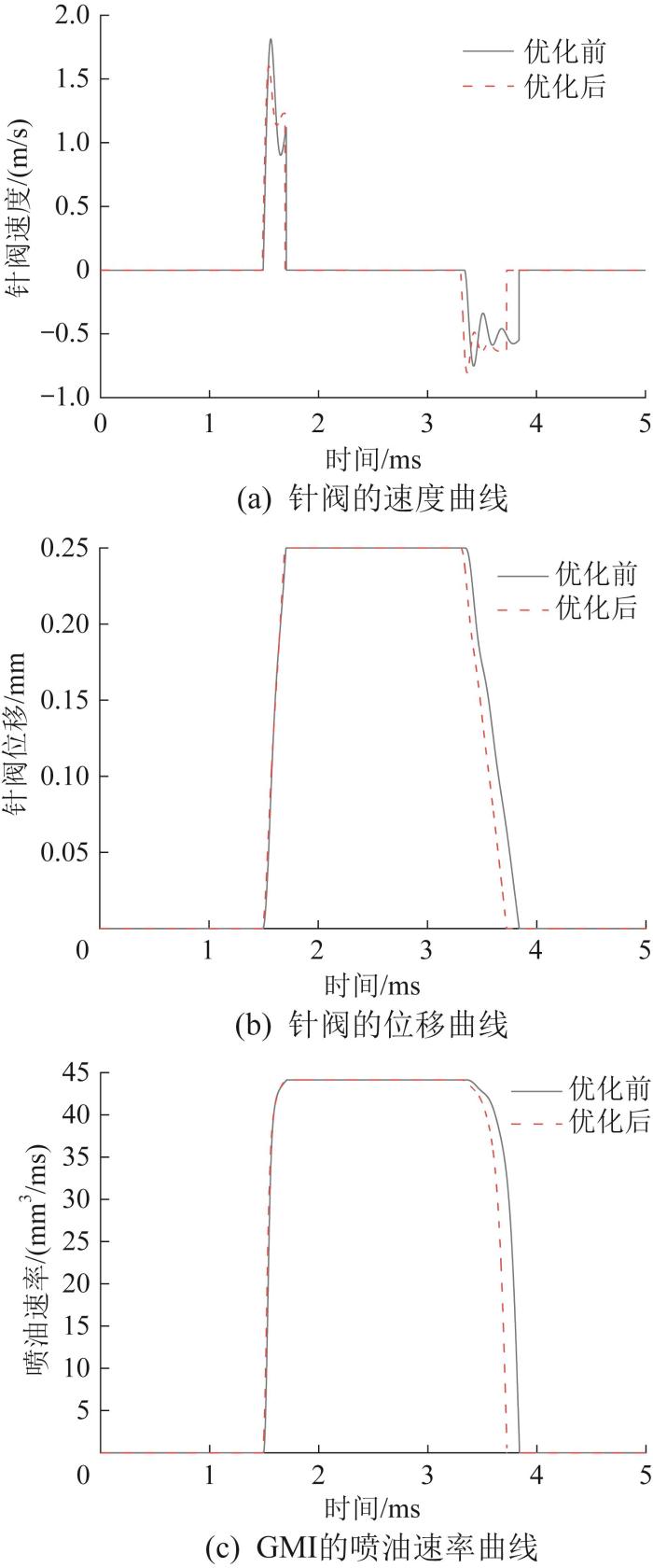
图13 优化前后针阀的速度、位移和GMI的喷油速率对比

Fig.13 Comparison of speed, displacement of needle valve and fuel injection rate of GMI before and after optimization

由图13可知，优化后针阀开启与关闭的平均速度均得到了提高；优化后针阀位移曲线左移，说明针阀响应速度得到了提升，即GMI的喷油响应速度得到了有效提升；优化后GMI的断油速度更快，即喷油特性更好。综上，通过优化响应时间，GMI的小油量喷油性能和多次喷油能力同时得到了提升，即优化后GMI具有更好的喷油能性。

5 结论

1）以针阀综合响应时间作为高压共轨式GMI喷油响应速度的评价指标，选取了控制活塞直径、控制腔容积、进油孔直径、出油孔直径、针阀弹簧预紧力、针阀弹簧刚度与针阀锥角等七个结构参数进行重要性分析，并通过单因素分析确定了最优的针阀弹簧预紧力。

2）采用RSM分析了控制活塞直径、控制腔容积、进油孔直径和出油孔直径对GMI响应时间的影响，并确定了优化后的结构参数。相较于优化前，优化后针阀的开启延迟缩短了3.251%，开启时间缩短了1.364%，关闭延迟缩短了9.465%，关闭时间缩短了14.848%。研究结果表明，针阀响应速度的提高有助于提升高压共轨式GMI的小油量喷油及多次喷油性能。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

钱德省，廖日东.

柴油机高压油泵柱塞副泄漏研究进展

［J］. 润滑与密封， 2014， 39（9）： 108-115， 118. doi：10.3969/j.issn.0254-0150.2014.09.023