机床的加工精度主要受导轨误差的影响:导轨误差映射到运动副上,运动副误差再传递至末端刀具,最终造成工件误差。研究误差传递过程有助于在机床设计阶段确定导轨刮研曲线,提高机床的加工精度。导轨误差与运动副误差的映射模型为过约束条件下的非线性模型,导轨与滑块的刚度为非线性,且滑块固定件受力存在过约束特性,模型较为复杂。对于磨削、铣削等刀具以体的形式参与的加工方式,无法通过刀尖点轨迹直接生成刀具误差与工件误差的映射模型。针对机床加工误差的传递过程,相关学者开展了大量研究。
孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型。Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响。仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型。倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模。Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模。Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型。Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数。Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应。Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型。陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测。
然而,关于考虑滑块固定件结构刚度与导轨副非线性刚度的导轨误差与运动副误差间的映射模型以及铣削、磨削工况下刀具误差与工件误差间的映射模型尚未得到深入研究,且已有研究大多针对双导轨四滑块系统,无法推广到多导轨多滑块系统。为解决上述问题,本文通过建立单滑块系统等效刚度模型、多滑块系统误差映射模型及工件加工误差预测模型,综合分析在考虑滑块固定件结构刚度与导轨副非线性刚度条件下多滑块系统中导轨误差与运动副误差间的映射关系、运动副误差与末端刀具误差间的映射关系以及刀具误差与工件误差间的映射关系,最终得到导轨误差与工件误差间的映射模型,旨在为精密机床的设计提供指导。
1 单滑块系统等效刚度模型
1.1 假设条件
当滚动导轨副产生误差时,滑块会偏离理想的运动轨迹,导致内力发生变化。为重新达到平衡状态,滑块发生偏摆,进而产生位姿误差。在进行单滑块系统静力分析时,作如下假设:
1)误差仅存在于导轨安装基面,导轨的装配误差及导轨基面误差均等效为导轨滚道面误差。
2)滚柱与滑块裙部均视为线性弹性体,导轨视为刚体。
1.2 静力分析
滚动导轨副由导轨、滑块与滚动体构成。滚动体在预紧力与外部载荷的作用下产生变形,其与导轨滚道面、滑块滚道面间的接触符合赫兹接触理论。基于赫兹接触理论,圆柱滚动体的变形量δ 与所受载荷Q 满足以下关系[20 ] :
δ = 3.81 × 2 1 - v 2 E 0.9 × Q 0.9 l 0.8 (1)
式中:v 为滚动体材料的泊松比,E 为滚动体材料的弹性模量,l 为滚动体长度。
Q = C δ 10 9 (2)
C = 3 . 81 - 10 9 × E l 8 / 9 2 1 - v 2
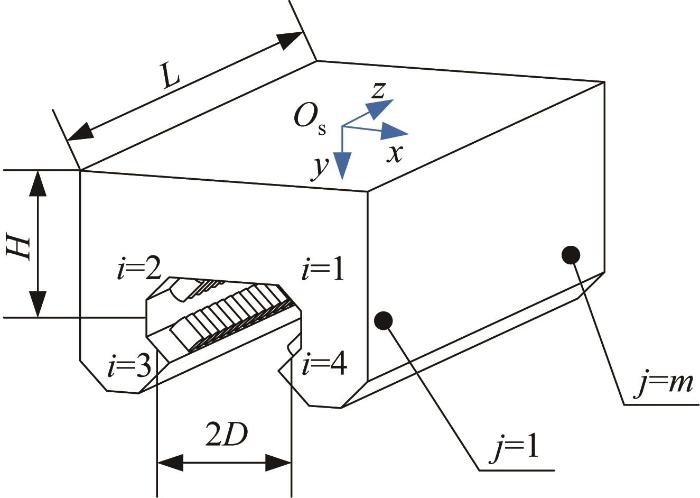
滚动导轨副中单个滑块的尺寸及滚动体的排列情况如图1 所示(坐标原点O s 位于滑块顶部平面中心)。图中:j 为滚动体所在列,j =1, 2, …, m ;i 为滚动体所在行,i =1, 2, …, 4;L 为滑块长度;D 为2行滚动体间水平距离的一半;H 为滚动体与滑块顶部平面间的垂直距离。当滑块存在相对位姿误差 e s =[δx δy δz εx εy εz ]T 时,第i 行第j 列滚动体对应的滚道面位置处会产生沿水平方向(x 向)和垂直方向(y 向)的误差分量,分别为ex , ji ey , ji
图1
图1
滑块尺寸及滚动体的排列情况
Fig.1
Size of slider and arrangement of rolling elements
令第j 列滚动体对应的滚道面在z 向上与坐标原点O s 的距离为Lj ,则有:
L j = 1 2 - j m + 1 L (3)
根据式(3),误差分量ex , ji ey , ji
e x , j i = δ x - H ε z + j m + 1 - 1 2 L ε y (4)
e y , j i = δ y + D ε z - j m + 1 - 1 2 L ε x , i = 1 , 4 δ y - D ε z - j m + 1 - 1 2 L ε x , i = 2 , 3 (5)
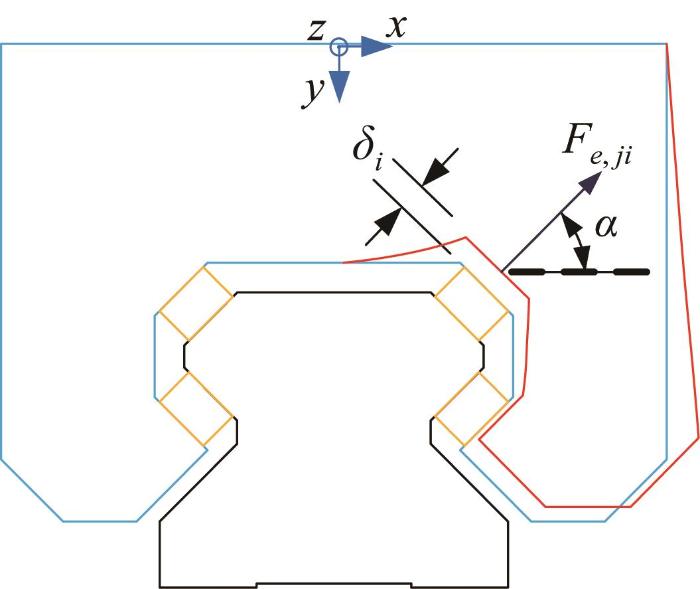
以第j 列滚动体为例,对单滑块导轨副的静力平衡状态进行受力分析,如图2 所示。假设滚动体的预压缩量为δ 0 ,初始接触角为α ,第i 行滚道面处滑块裙部的弹性系数为E h i
图2
图2
单滑块导轨副静力分析
Fig.2
Statics analysis of single-slider guide rail pair
由图2 可知,导轨与滚动体间、滚动体与滑块间各存在一对相互作用力,致使导轨、滚动体与滑块均产生变形,最终滑块变形与滚动体变形互相协调,使得导轨副达到静力平衡状态。令第i 行第j 列滚动体的变形量为δji ,第i 行滚动体处滑块裙部滚道面的变形量为δi ,第i 行第j 列滚动体的弹性力为Fe, ji 。对于第1行第j 列滚动体(初始压缩量为δ 0 ),当滚道面在x 向上存在误差ex, j 1 时,滚动体压缩量减少ex , j 1 cos α ;当滚道面在y 向上存在误差ey , j 1 时,滚动体压缩量增加ey , j 1 sin α ;当滑块裙部滚道面变形量为δ 1 时,滚动体压缩量减少δ 1 ,则可得以下静力平衡方程:
F e , j 1 = C δ 0 - e x , j 1 c o s α + e y , j 1 s i n α - δ 1 10 9 = C δ j 1 10 9 ∑ j = 1 m F e , j 1 = E h 1 δ 1 (6)
同理,分析其余3行滚动体的受力情况,可得相应的静力平衡方程:
F e , j 2 = C δ 0 + e x , j 2 c o s α + e y , j 2 s i n α - δ 2 10 9 = C δ j 2 10 9 ∑ j = 1 m F e , j 2 = E h 2 δ 2 (7)
F e , j 3 = C δ 0 + e x , j 3 c o s α - e y , j 3 s i n α - δ 3 10 9 = C δ j 3 10 9 ∑ j = 1 m F e , j 3 = E h 3 δ 3 (8)
F e , j 4 = C δ 0 - e x , j 4 c o s α - e y , j 4 s i n α - δ 4 10 9 = C δ j 4 10 9 ∑ j = 1 m F e , j 4 = E h 4 δ 4 (9)
根据方程组(6)至(9),可求解得到滑块裙部滚道面的变形量δ 1 、δ 2 、δ 3 、δ 4 ,进而计算得到各滚动体的变形量δj 1 、δj 2 、δj 3 、δj 4 及弹性力Fe , j 1 、Fe , j 2 、Fe , j 3 、Fe , j 4 。
将滚动体对滑块的作用力分解,得到滚动体对滑块的水平作用力与垂直作用力Fex , ji Fey , ji
F e x , j 1 = F e , j 1 c o s α F e y , j 1 = - F e , j 1 s i n α (10)
F e x , j 2 = - F e , j 2 c o s α F e y , j 2 = - F e , j 2 s i n α (11)
F e x , j 3 = - F e , j 3 c o s α F e y , j 3 = F e , j 3 s i n α (12)
F e x , j 4 = F e , j 4 c o s α F e y , j 4 = F e , j 4 s i n α (13)
将第i 行第j 列滚动体沿x 、y 向的分力Fex , ji Fey , ji x 向等效力Fx , ji y 向等效力Fy , ji x 向等效力矩Mx , ji y 向等效力矩My , ji z 向等效力矩Mz , ji
F x , j i = F e x , j i (14)
F y , j i = F e y , j i (15)
M x , j i = F e y , j i L j (16)
M y , j i = - F e x , j i L j (17)
M z , j i = - F e x , j i H + F e y , j i D , i = 1 , 4 - F e x , j i H - F e y , j i D , i = 2 , 3 (18)
滚动体对滑块的作用力在滑块顶部平面中心的等效合力与滑块所受的外载荷平衡,则可得滑块所受外载荷 F x 、y 、z 向的分力Fx 、Fy 、Fz 和分力矩Mx 、My 、Mz ,分别表示为:
F x = - ∑ i = 1 4 ∑ j = 1 m F x , j i = - ∑ i = 1 4 ∑ j = 1 m F e x , j i F y = - ∑ i = 1 4 ∑ j = 1 m F y , j i = - ∑ i = 1 4 ∑ j = 1 m F e y , j i F z = 0 M x = - ∑ i = 1 4 ∑ j = 1 m F ε x , j i = - ∑ i = 1 4 ∑ j = 1 m F e y , j i L j M y = - ∑ i = 1 4 ∑ j = 1 m F ε y , j i = - ∑ i = 1 4 ∑ j = 1 m F e x , j i L j M z = ∑ i = 1 4 ∑ j = 1 m F ε z , j i = - ∑ i = 1 4 ∑ j = 1 m F e x , j i H - - 1 2 i - 5 - 2 F e y , j i D (19)
由此可得到滑块相对位姿误差 e s =[δx δy δz εx εy εz ]T 与滑块所受外载荷 F Fx Fy Fz Mx My Mz ]T 之间的映射关系。
∫ 0 δ j i C δ 10 9 d δ = 9 19 C δ j i 19 9 (20)
∫ 0 δ i E h i δ d δ = 1 2 E h i δ i 2 (21)
W = ∑ i = 1 4 ∑ j = 1 m 9 19 C δ j i 19 9 + 1 2 E h i δ i 2 (22)
总势能W 为关于变量δx 、δy 、δz 、εx 、εy 、εz 的函数,记为f (δx , δy , δz , εx , εy , εz ),将其分解后可得:
W = f δ x , δ y , δ z , ε x , ε y , ε z - f 0 , δ y , δ z , ε x , ε y , ε z + f 0 , δ y , δ z , ε x , ε y , ε z - f 0 , 0 , δ z , ε x , ε y , ε z + f 0 , 0 , δ z , ε x , ε y , ε z - f 0 , 0 , 0 , ε x , ε y , ε z + f 0 , 0 , 0 , ε x , ε y , ε z - f 0 , 0 , 0 , 0 , ε y , ε z + f 0 , 0 , 0 , 0 , ε y , ε z - f 0 , 0 , 0 , 0 , 0 , ε z + f 0 , 0 , 0 , 0 , 0 , ε z - f 0 , 0 , 0 , 0 , 0 , 0 = W δ x + W δ y + W δ z + W ε x + W ε y + W ε z (23)
式中:Wδx 、Wδy 、Wδz 、Wεx 、Wεy 、Wεz 分别为由δx 、δy 、δz 、εx 、εy 、εz 引起的势能。
W δ x = ∫ 0 δ x K δ x δ d δ = 1 2 K δ x δ x 2 (24)
式中:Kδx 为单滑块导轨副对应δx 的等效刚度,Kδx 同样为关于变量δx 、δy 、δz 、εx 、εy 、εz 的函数。
同理,可得到单滑块导轨副对应δy 、δz 、εx 、εy 、εz 的等效刚度Kδy 、Kδz 、Kεx 、Kεy 、Kεz 。令 K s =diag(Kδx , Kδy , Kδz , Kεx , Kεy , Kεz ),则单滑块导轨副的总势能W 可表示为:
W = 1 2 e s T ⋅ K s ⋅ e s (25)
由此可得到单滑块导轨副对应相对位姿误差 e s 的等效六维刚度 K s 。
1.3 仿真验证
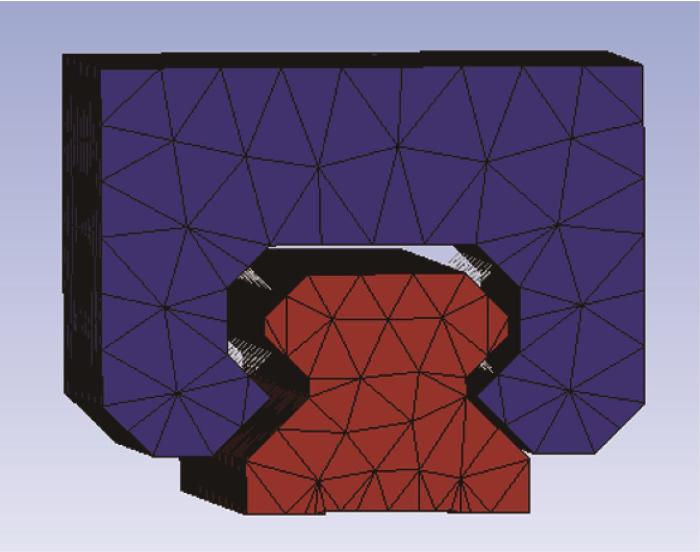
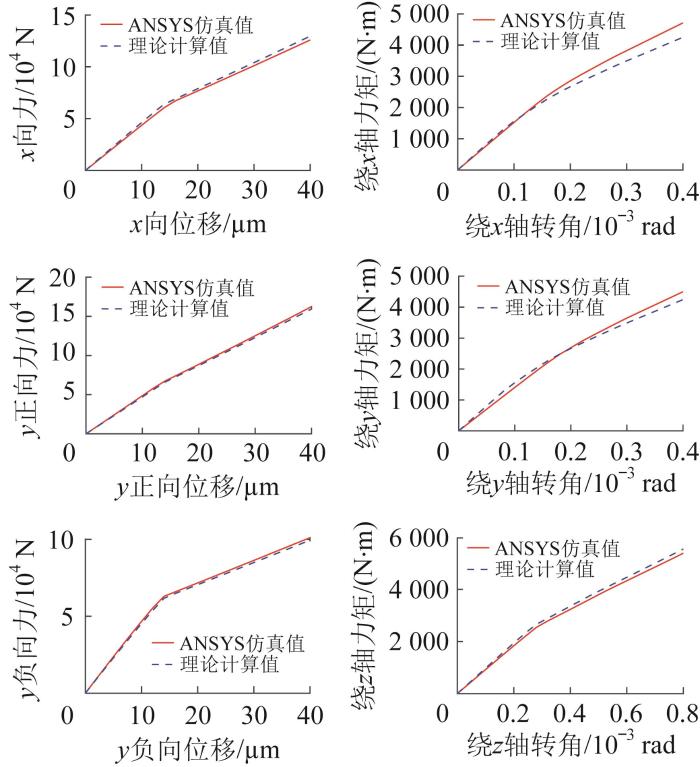
为验证上述等效刚度模型的准确性,对单滑块导轨副进行仿真验证,其仿真模型如图3 所示。将滚动体设置为非线性弹簧单元,利用ANSYS软件进行仿真,固定导轨基面,分别给滑块施加不同方向的力或力矩,获得其位移和转角,计算单滑块导轨副的等效刚度并与理论计算值进行对比,结果如图4 所示。
图3
图3
单滑块导轨副仿真模型
Fig.3
Simulation model of single-slider guide rail pair
图4
图4
单滑块导轨副等效刚度的仿真值与理论计算值对比
Fig.4
Comparison of simulation value and theoretical calculation value of equivalent stiffness of single-slider guide rail pair
由图4 可以看出,单滑块导轨副的x 向、y 正向、y 负向刚度及z 向扭转刚度的理论计算值与仿真值基本一致,而x 向、y 向扭转刚度的理论计算值与仿真值存在差异但相差较小,这是由理论建模时假设滑块裙部在各滚动体所处位置的变形相同所引起的。
2 多滑块系统误差映射模型
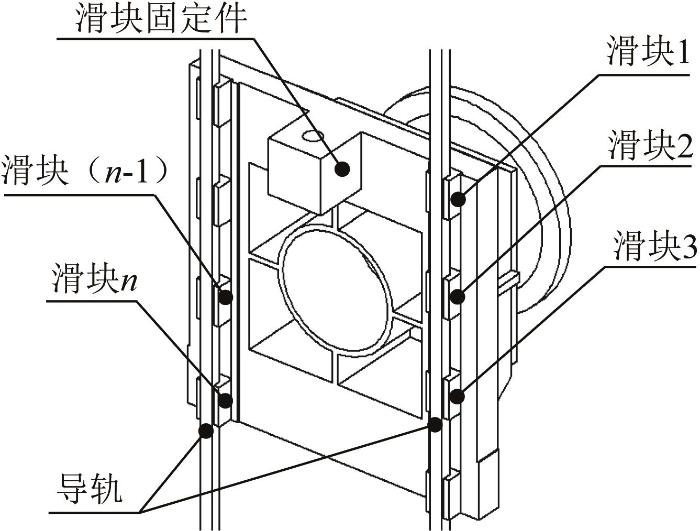
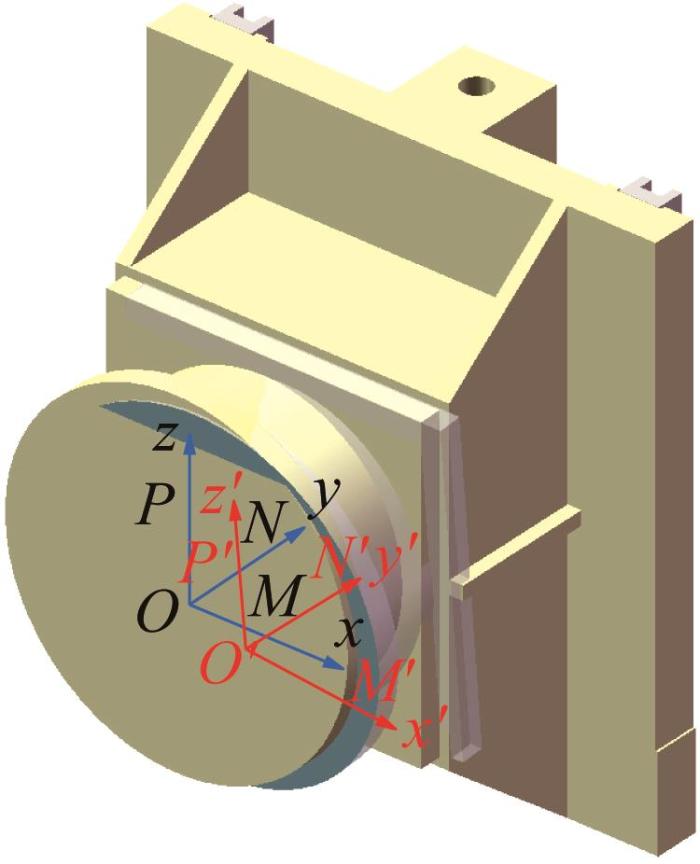
导轨误差传递到运动副的过程并不是误差直接叠加的过程,在传递过程中误差有所衰减,即存在误差均化效应。多滑块系统的结构如图5 所示,其中滑块数量为n 。导轨内部力的存在导致滚动体、滑块、导轨和滑块固定件产生弹性变形,抵消了部分导轨副误差,从而产生误差均化效应。如图6 所示,在滑块固定件上取远离滑块的一点为原点O O -xyz ),在x 、y 、z 轴上分别取点M 、 N 、 P O O ' M ' 、 N ' 、 P ' O ' M ' 、 O ' N ' 、 O ' P ' O ' - x ' y ' z '
图5
图5
多滑块系统结构示意
Fig.5
Structure diagram of multi-slider system
图6
图6
多滑块系统坐标系构建
Fig.6
Construction of coordinate system for multi-slider system
2.1 滑块固定件刚度与导轨刚度计算
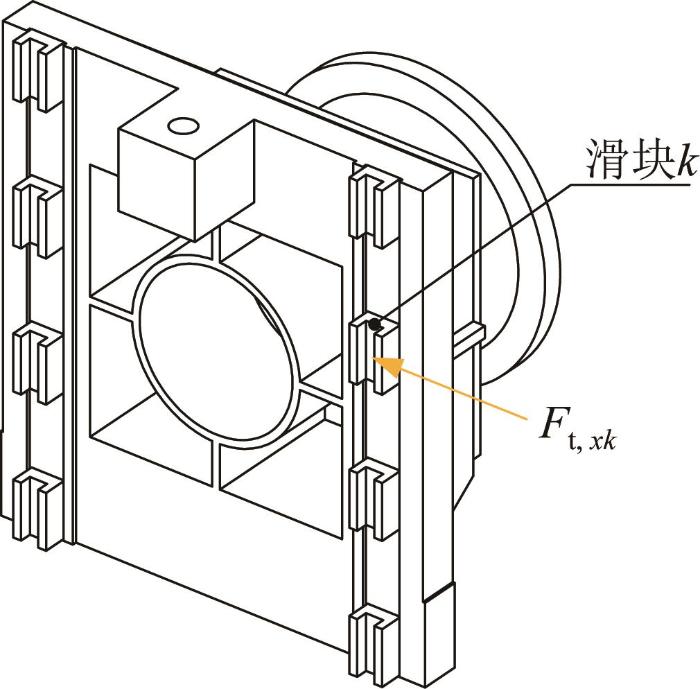
如图7 所示,在滑块k 处施加x 向单位力F t , xk n 维向量,可表示为:
e F t , x k = e F t , 1 e F t , 2 ⋯ e F t , n T (26)
e F t , s = e F t , x s e F t , y s e F t , z s e M t , x s e M t , y s e M t , z s T
式中: e F t, s s =1, 2, …, n )为单位力作用下滑块固定件在滑块s 处的六维变形量。
图7
图7
滑块固定件受力示意图
Fig.7
Force diagram of slider fastener
同理,在滑块k 处施加y 向单位力、z 向单位力、x 向单位力矩、y 向单位力矩、z 向单位力矩,可得到对应的滑块固定件各滑块位置的变形量 e F t, yk e F t, zk e M t, xk e M t, yk e M t, zk
当滑块k 处受到作用力 F k Fxk Fyk Fzk Mxk Myk Mzk ]T 时,由于线性系统具有叠加性,滑块固定件各滑块位置的变形量 eF k
e F k = F x k e F t , x k + F y k e F t , y k + F z k e F t , z k + M x k e M t , x k + M y k e M t , y k + M z k e M t , z k = E F k F k (27)
EF k e F t , xk e F t, yk e F t, zk e M t, xk e M t, yk e M t, zk
式中: EF k F k n 行6列矩阵。
由此可知,当滑块固定件受到作用力 F b = [ F 1 F 2 F n e b 为:
e b = ∑ k = 1 n e F k = ∑ k = 1 n E F k F k = E b F b (28)
根据式(28),计算得到滑块固定件柔度矩阵 E b :
E b = E F 1 E F 2 ⋯ E F n (29)
K b = E b - 1 (30)
滑块固定件柔度矩阵 E b 为其各滑块位置在单位力作用下的变形量,故固定点的选择会影响刚度矩阵 K b 。滑块固定件受力 F b 为一组平衡力,当滑块固定件在 F b 的作用下达到静力平衡后,由圣维南定理可知,在远离载荷作用的区域内,应力基本上只与所受载荷的合力和合力矩有关,即应力为0。在此区域内任意选择2个面作为固定面,由于2种情况下受力一致,最终滑块固定件的变形势能相等。由此可知,只要在远离载荷作用的区域选取固定面,滑块固定件势能就与固定面的选取无关。
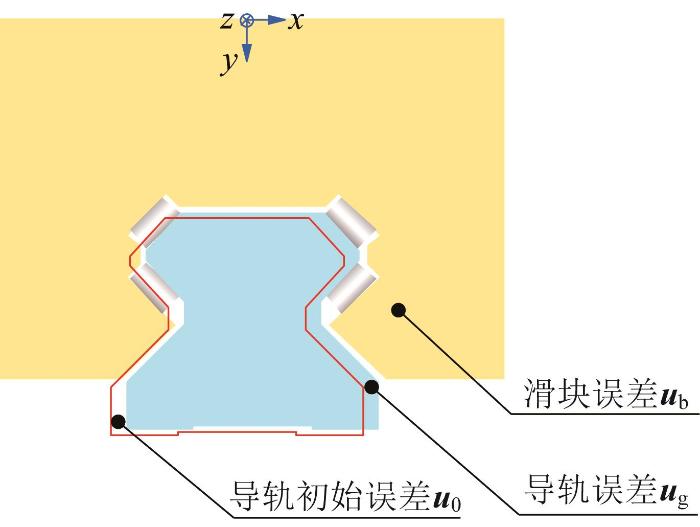
2.2 滑块固定件误差计算
图8
图8
导轨与滑块的变形示意图
Fig.8
Deformation diagram of guide rail and slider
u 0 = d x 1 d y 1 d z 1 e x 1 e y 1 e z 1 ⋯ d x n d y n d z n e x n e y n e z n T (31)
式中: u 0 为导轨初始误差,为6n 维向量;dxk 、dyk 、dzk ,exk 、eyk 、ezk 分别为导轨在滑块k 位置处的位置误差和转角误差。
当导轨副存在误差时,为了达到平衡状态,导轨产生变形 e g ,滑块相对导轨偏移 e s 。令平衡后的导轨误差为 u g ,滑块误差为 u b ,滑块固定件变形量为 e b ,其中 e g 、 e s 、 u g 、 u b 、 e b 均为6n 维向量,且满足以下关系:
e g = u g - u 0 e s = u b - u g (32)
多滑块导轨副等效刚度矩阵 K s 、滑块固定件刚度矩阵 K b 及导轨刚度矩阵 K g 均为6n 阶方阵,当多滑块系统达到静力平衡状态后,运动副的六维误差 v δx δy δz εx εy εz ]T 。
则坐标系A相对于坐标系B的坐标变换矩阵 T AB 可表示为:
T A B = 1 - ε z ε y δ x ε z 1 - ε x δ y - ε y ε x 1 δ z 0 0 0 1 (33)
设滑块1在坐标系A下的位置矩阵 H A1 (用齐次坐标表示)为:
H A 1 = X 1 Y 1 Z 1 1 T (34)
H B 1 = T A B - 1 H A 1 (35)
忽略滑块固定件变形时,滑块1的位移∆ H 1 可表示为:
Δ H 1 = H B 1 - H A 1 = - ε z Y 1 + ε y Z 1 + δ x ε z X 1 - ε x Z 1 + δ y - ε y X 1 + ε x Y 1 + δ z 1 (36)
当滑块误差为 u b ,运动副误差为 v Av e b :
e b = A v - u b (37)
A = 1 0 0 0 Z 1 - Y 1 0 1 0 Z 1 0 X 1 0 0 1 Y 1 - X 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 1 0 0 0 Z n - Y n 0 1 0 Z n 0 X n 0 0 1 Y n - X n 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1
根据滑块固定件的刚度矩阵 K b ,计算滑块固定件受力时所做的功,即可得滑块固定件的弹性势能W b :
W b = ∫ 0 e b K b ⋅ e d e = 1 2 e b T ⋅ K b ⋅ e b = 1 2 A v - u b T ⋅ K b ⋅ A v - u b (38)
根据最小势能原理[21 ] , v W b 最小,即任取 v ′ = v +v W b =W′ b -W b 应恒大于等于0,而ΔW b 可表示为:
Δ W b = 1 2 A v + Δ v - u b T ⋅ K b ⋅ A v + Δ v - u b - 1 2 A v - u b T ⋅ K b ⋅ A v - u b = A Δ v T ⋅ K b ⋅ A v - u b + A Δ v T ⋅ K b ⋅ A Δ v (39)
式(39)的后半部分可看作滑块固定件各滑块位置产生变形量 A v 式(39)的前半部分恒等于0即可满足要求,由此可得:
v = A T K b A - 1 - 1 A T K b u b (40)
e b = A v - u b = A T K b A - 1 - 1 A T K b u b - u b K b , e q u b (41)
K b , e q = A A T K b A - 1 - 1 A T K b - E
将式(41)代入式(38),可得滑块固定件的弹性势能W b :
W b = 1 2 e b T ⋅ K b ⋅ e b = 1 2 K b , e q u b T ⋅ K b ⋅ K b , e q u b = 1 2 u b T ⋅ K b , e q T K b K b , e q ⋅ u b = 1 2 u b T ⋅ K B ⋅ u b (42)
K B = K b , e q T K b K b , e q
W s = ∫ 0 e s K s ⋅ e d e = 1 2 u b - u 0 - e g T ⋅ K s ⋅ u b - u 0 - e g (43)
已知导轨变形量为 e g ,根据导轨刚度 K g 计算得到导轨受力为 K g e g ,该力所做的功即为导轨的弹性势能,可表示为:
W g = ∫ 0 e g K g ⋅ e d e = 1 2 e g T ⋅ K g ⋅ e g (44)
W t = W s + W g + W b = 1 2 u b - u 0 - e g T ⋅ K s ⋅ u b - u 0 - e g + 1 2 e g T ⋅ K g ⋅ e g + 1 2 u b T ⋅ K B ⋅ u b (45)
根据最小势能原理,滑块误差 u b 与导轨变形量 e g 的取值应令多滑块系统的总势能W t 最小,即任取 u b ′= u b + Δ u b , e g ′= e g + Δ e g 时,势能变化量ΔW t =W t ′-W t 应恒大于等于0,其中ΔW t 可表示为:
Δ W t = Δ e g T ⋅ K s ⋅ u 0 + e g - u b + 1 2 K g + K g T ⋅ e g - Δ u b T ⋅ K s ⋅ u 0 + e g - u b - 1 2 K B + K B T ⋅ u b + 1 2 Δ e g - Δ u b T ⋅ K s ⋅ Δ e g - Δ u b + 1 2 Δ e g T ⋅ K g ⋅ Δ e g + 1 2 Δ u b T ⋅ K B ⋅ Δ u b (46)
Δ W t = Δ W 1 + Δ W 2 (47)
Δ W 1 = Δ e g T ⋅ K s ⋅ u 0 + e g - u b + 1 2 K g + K g T ⋅ e g - Δ u b T ⋅ K s ⋅ u 0 + e g - u b - 1 2 K B + K B T ⋅ u b
Δ W 2 = 1 2 Δ e g - Δ u b T ⋅ K s ⋅ Δ e g - Δ u b + 1 2 Δ e g T ⋅ K g ⋅ Δ e g + 1 2 Δ u b T ⋅ K B ⋅ Δ u b
由于ΔW 2 可看作刚度为 K s 、 K g 、 K B 的滑块固定件分别在各滑块位置产生变形量(Δ e g -Δ u b )、Δ e g 、Δ u b 时的弹性势能,故ΔW 2 恒大于等于0,因此令ΔW 1 恒等于0即可满足滑块误差 u b 与导轨变形量 e g 的取值要求,使得多滑块系统的总势能W t 最小,即:
K s u 0 + e g - u b + K g e g = 0 K s u 0 + e g - u b - 1 2 K B + K B T u b = 0 (48)
u b = K s + 1 2 K s K g - 1 K B + K B T + 1 2 K B + K B T - 1 K s u 0 (49)
e g = - 2 K s K B + K B T - 1 K g + K g T + K s - 1 K s u 0 (50)
将式(49)和式(50)代入式(40),即可计算得到 v 式(32),可得:
e s = u b - u 0 - e g = K s + 1 2 K s K g - 1 K B + K B T + 1 2 K B + K B T - 1 K s u 0 - u 0 + 2 K s K B + K B T - 1 K g + K g T + K s - 1 K s u 0 (51)
式(51)为关于滑块相对导轨的偏移量 e s 的多元方程,通过解方程可求得 e s ,进而得到考虑导轨副等效刚度为非线性时的导轨误差与运动副误差间的映射模型。
2.3 仿真验证
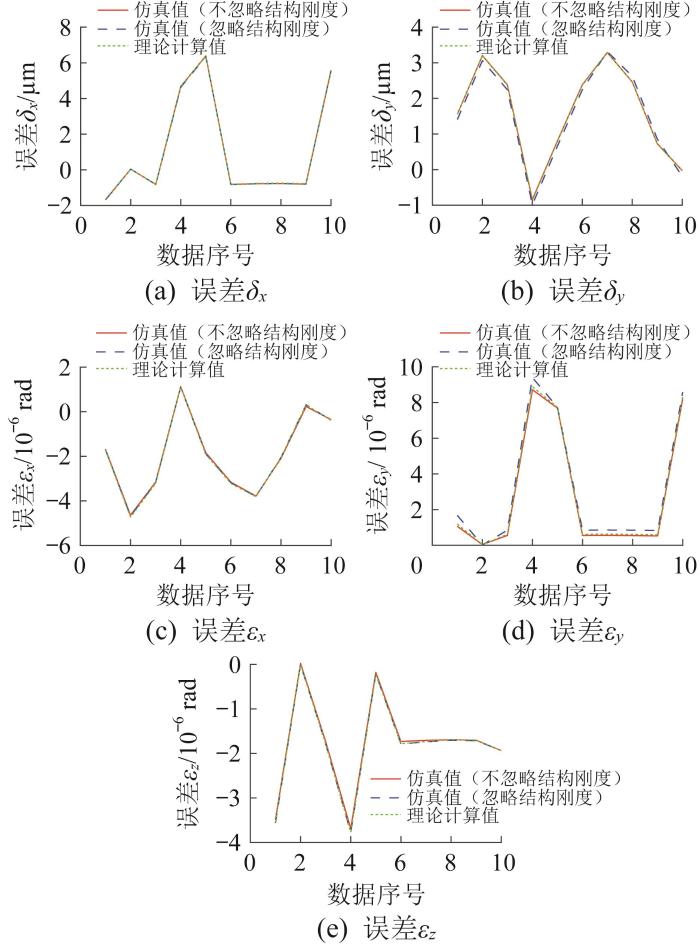
为验证上文构建的误差映射模型的准确性,以八滑块系统为例进行有限元仿真。将运动副误差的理论计算结果与仿真结果(包含忽略和不忽略滑块固定件结构刚度两种情况)进行对比,如图9 所示。
图9
图9
运动副误差的计算结果与仿真结果对比
Fig.9
Comparison between calculation results and simulation results of motion pair errors
分析图9 数据发现,基于本文方法计算得到的运动副的x 、y 向位置误差和x 、y 、z 向转角误差与原始仿真值(不忽略滑块固定件结构刚度)的相对误差最高分别为3.51%、2.46%、3.64%、11.90%、2.74%,而忽略滑块固定件结构刚度的仿真值与原始仿真值的相对误差最高分别为0.75%、17.90%、2.59%、57.30%、3.08%。由此可见,相比于传统的忽略滑块固定件弹性变形的方法,本文所提出的建模方法更贴近真实结果。
3 工件加工误差预测模型
3.1 齐次坐标变换
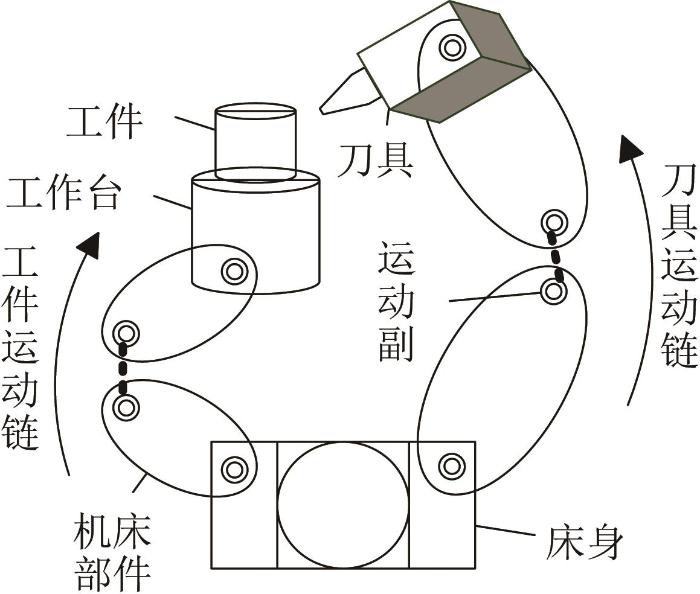
为方便计算工件的加工范围,需在工件坐标系下进行分析,因此需将末端刀具坐标系转化为工件坐标系。常见机床的拓扑结构如图10 所示,其中:工件高度为p ,刀具高度为q ,刀具半径为R 。
图10
图10
机床拓扑结构
Fig.10
Topology structure of machine tool
根据多体系统理论,刀具坐标系到工件坐标系的齐次坐标变换矩阵 T wt 可表示为:
T w t = T 1 w - 1 T 1 t (52)
式中: T 1w 、 T 1t 分别为机床坐标系到工件坐标系、刀具坐标系的齐次坐标变换矩阵。
则刀具坐标系下的齐次坐标 C t 与工件坐标系下的齐次坐标 C w 的变换公式可表示为:
C w = T w t C t (53)
刀具坐标系下刀具底面圆心位置向量 C t, c 与刀轴矢量 C t, a 可分别表示为:
C t , c = 0 , 0 , 0 , 1 T C t , a = 0 , 0 , q , 0 T (54)
联立式(52)和式(53),可得工件坐标系下刀具底面圆心位置向量 C w, c 与刀轴矢量 C w, a :
C w , c = T w t C t , c C w , a = T w t C t , a (55)
3.2 工件表面轮廓计算
刀具上的离散点满足点与刀轴矢量的距离不超过R 的条件,则有:
x t , y t , z t - D w , c × D w , a / q ≤ R (56)
式中: D w, c 、 D w, a 分别为以笛卡儿坐标表示的工件坐标系下的刀具底面圆心位置向量与刀轴矢量,由式(55)计算获得。
此外,刀具上的点在刀轴矢量上的投影位于[0,q ]内,则有:
0 ≤ x t , y t , z t - D w , c ⋅ D w , a / q ≤ q (57)
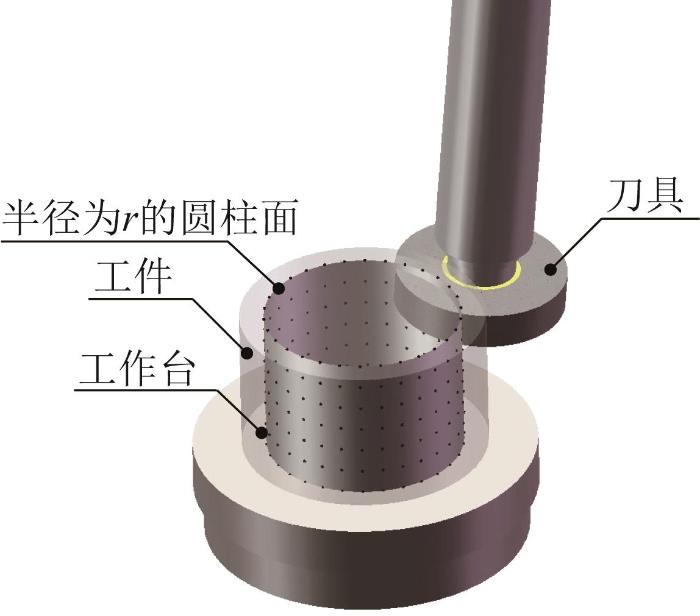
以dr 为间隔将工件离散为nr 个圆柱面,以半径r 的圆柱面为例,将柱坐标转换为笛卡儿坐标后代入式(56)与式(57),可得工件加工区域内离散点的表达式:
r c o s θ , r s i n θ , z t - D w , c × D w , a ≤ R q 0 ≤ r c o s θ , r s i n θ , z t - D w , c ⋅ D w , a ≤ q 2 0 ≤ z t ≤ p (58)
假设工件加工时间为T ,将时间离散为nt 段;将圆柱面按角度离散为nθ 段后,再将每段按高度离散为nz 个点,并将各点赋予初值1,得到nθ ×nz 阶初始加工矩阵,如图11 所示。将各点坐标与刀具位姿误差代入式(58)进行计算。若点在被加工区域内,则对应的矩阵元素赋值0,得到此时的加工矩阵。其中:1代表该位置有实体,0代表该位置被加工去除。经过nt 次重新赋值后,可得到圆柱面的最终加工矩阵,随后将矩阵内值为1的元素转化回柱坐标系,即可得到圆柱面经加工去除后的剩余实体点。将nr 个圆柱面的剩余实体点求并,即可得到最终工件实体点的分布情况。
图11
图11
刀具加工位置示意
Fig.11
Schematic diagram of tool machining position
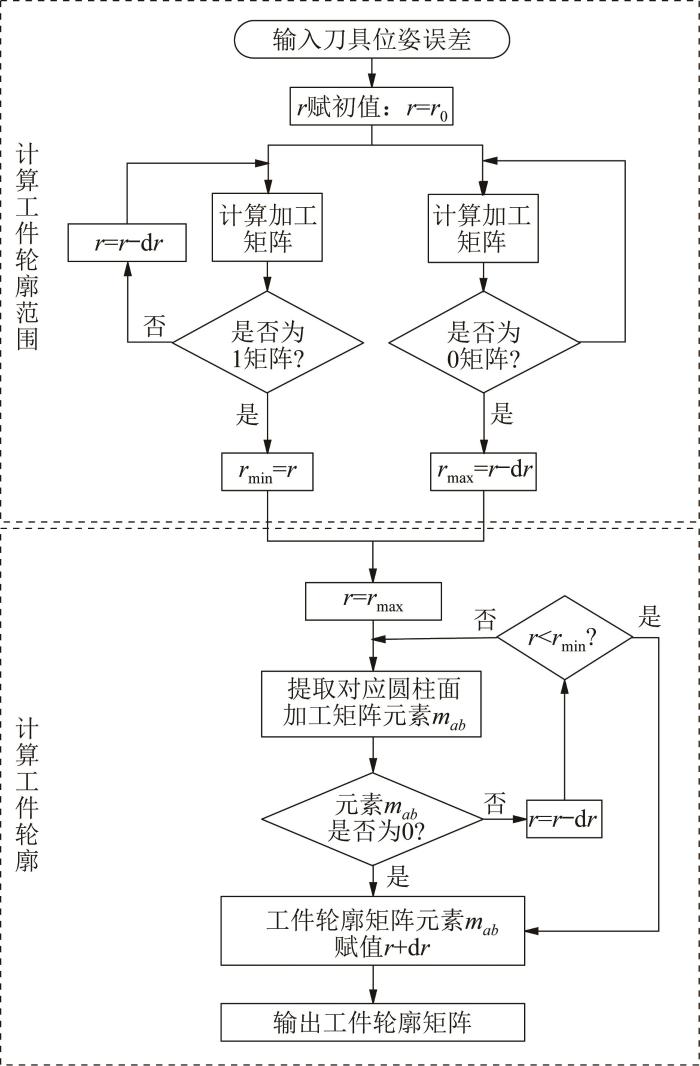
利用MATLAB软件进行拟合计算,可得到根据给定导轨误差所加工的工件表面轮廓,具体流程如图12 所示,并以此为基础计算工件的尺寸误差与圆柱度误差。
图12
图12
工件表面轮廓计算流程
Fig.12
Calculation process of workpiece surface contour
3.3 实例计算
图13
图13
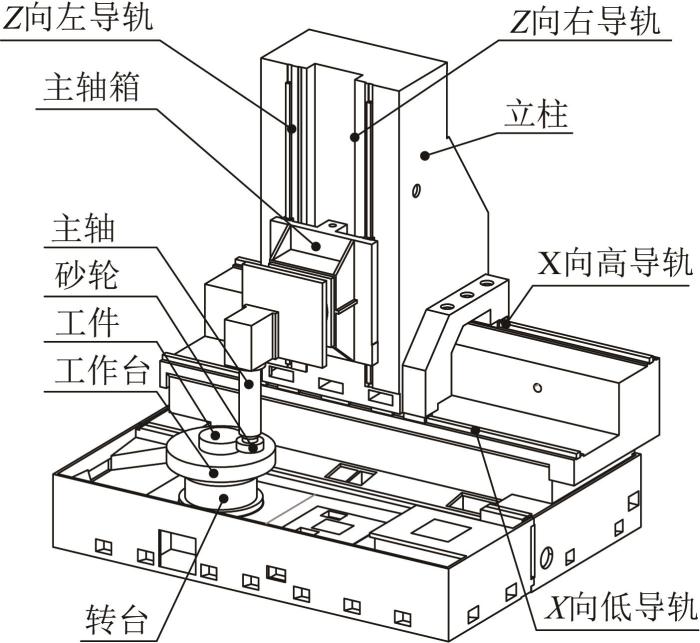
立式坐标磨床结构
Fig.13
Structure of vertical coordinate grinder
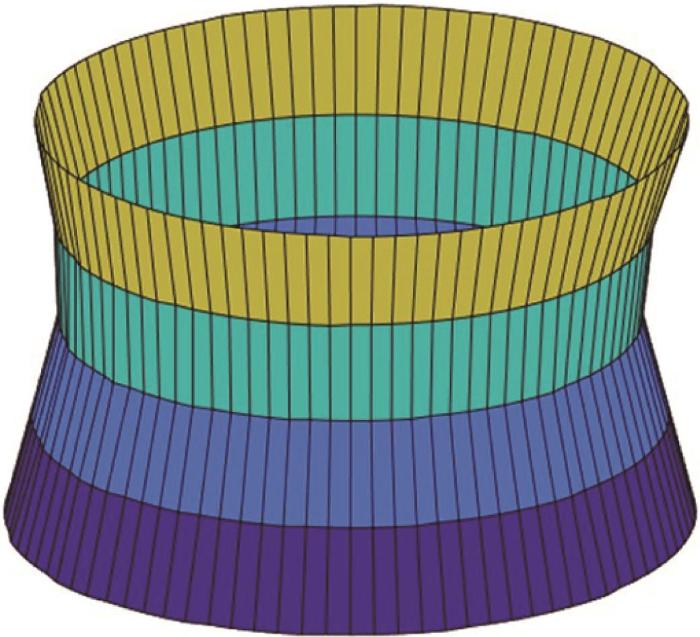
考虑到尺寸误差可通过后处理补偿,故本文重点研究圆度误差与圆柱度误差。在实际加工过程中,导轨误差除受到导轨基面误差的影响外,还受到由静力作用导致的静力变形与由加工过程生热导致的热变形的影响[22 ] 。利用激光自准直仪测量导轨基础误差,并通过有限元仿真得到导轨的静力变形量与热变形量,将三者叠加,得到导轨的综合误差。随后,利用本文所提出的方法对工件表面轮廓进行预测,结果如图14 所示。采用最小二乘法计算工件的圆柱度误差,为0.360 μm。
图14
图14
导轨误差影响下的工件表面轮廓预测结果
Fig.14
Prediction results of workpiece surface contour under influence of guide rail error
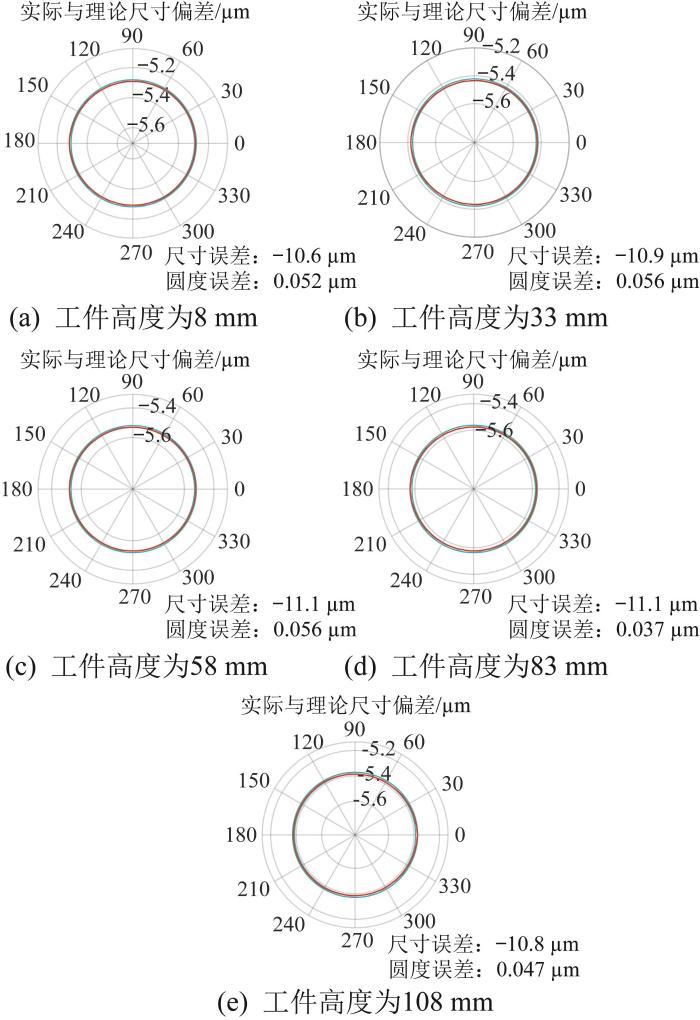
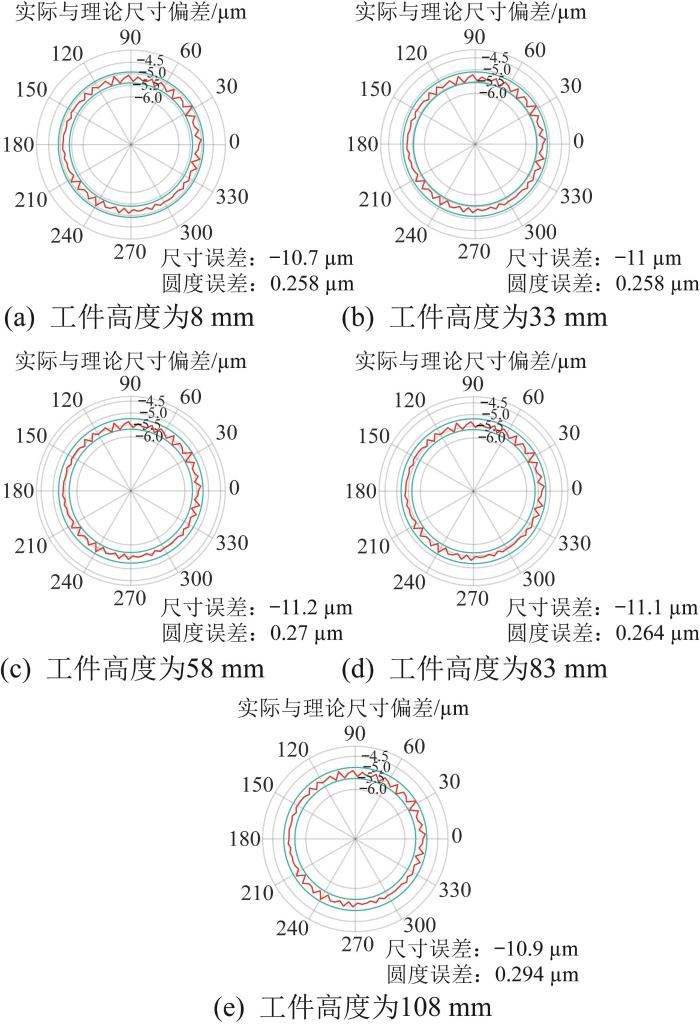
随后,采用最小二乘法分析工件上8、33、58、83、108 mm高度处圆形截面的圆度误差,结果如图15 所示。
图15
图15
导轨误差影响下的工件圆度误差
Fig.15
Workpiece roundness error under influence of guide rail error
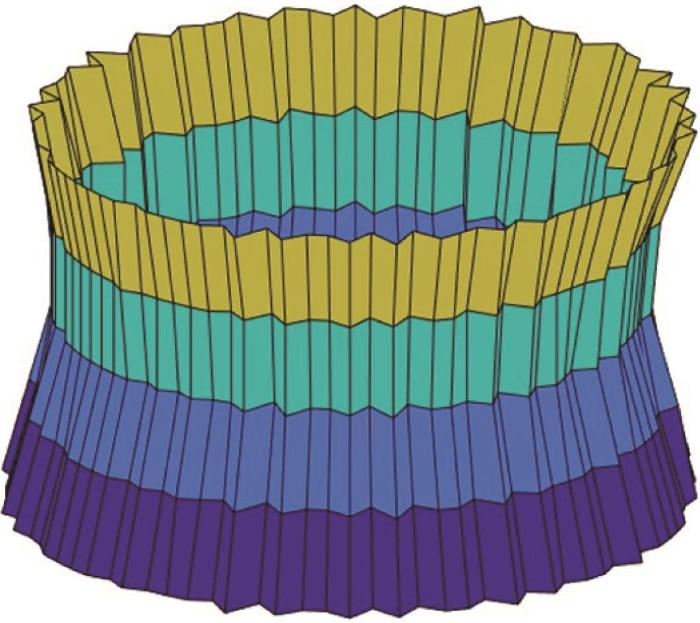
除导轨误差外,转台的跳动误差也是影响工件圆度与圆柱度的重要因素,而主轴转速远高于工作台转速,可看作其在跳动误差影响下的包络体参与加工,故主轴的跳动误差对工件的圆度误差与圆柱度误差无影响。采用电涡流传感器测量转台的径向跳动误差,并将转台径向跳动误差与导轨误差共同代入计算,得到综合误差影响下的工件表面轮廓,如图16 所示。采用最小二乘法计算工件的圆柱度误差,为0.525 μm。
图16
图16
综合误差影响下的工件表面轮廓预测结果
Fig.16
Prediction results of workpiece surface contour under influence of comprehensive error
随后,采用最小二乘法分析工件上8、33、58、83、108 mm高度处圆形截面的圆度误差,结果如图17 所示。
图17
图17
综合误差影响下的工件圆度误差
Fig.17
Workpiece roundness error under influence of comprehensive error
对比分析图14 、图15 与图16 、图17 ,发现导轨误差对工件各截面处的圆度误差影响较小,导轨误差主要影响工件不同截面处的尺寸误差,进而影响工件的圆柱度误差,而转台跳动误差显著影响工件的圆度误差,进而增大了工件的圆柱度误差。
4 结 论
1)通过对滚动导轨副进行受力分析,得到考虑滑块裙部变形与滚动体非线性刚度的导轨副等效刚度模型。根据最小势能原理,对滑块固定件结构刚度进行分析,得到考虑滑块固定件结构刚度与导轨副非线性刚度时导轨误差与运动副误差间的映射模型。与传统忽略滑块固定件结构刚度的映射模型相比,本文方法所计算的运动副误差更精确。
2)将工件离散化后,通过布尔运算得到刀具误差与工件误差间的映射关系,最终建立导轨误差与工件误差间的映射模型,可在设计阶段为导轨刮研曲线的确定提供指导,从而提高机床设计效率。
3)通过实例分析了导轨误差以及导轨误差与转台误差综合影响下的工件误差,对比发现导轨误差与转台误差对工件圆度误差与圆柱度误差的影响不同。实例结果表明,本文所提出的方法具有普适性,适用于多导轨多滑块系统。
参考文献
View Option
[1]
孙健利 直线滚动导轨机构承受垂直载荷时的刚度计算
[J]. 华中科技大学学报(自然科学版) , 1988 , 16 (5 ): 35 -40 .
[本文引用: 1]
SUN J L Stiffness calculation of linear motion guide under vertical load
[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition) , 1988 , 16 (5 ): 35 -40 .
[本文引用: 1]
[2]
孙伟 , 孔祥希 , 汪博 , 等 直线滚动导轨的Hertz接触建模及接触刚度的理论求解
[J]. 工程力学 , 2013 , 30 (7 ): 230 -234 .
[本文引用: 1]
SUN W KONG X X WANG B et al Contact modeling and analytical solution of contact stiffness by Hertz theory for the linear rolling guide system
[J]. Engineering Mechanics , 2013 , 30 (7 ): 230 -234 .
[本文引用: 1]
[3]
SHAW D SU W L Stiffness analysis of linear guideways without preload
[J]. Journal of Mechanics , 2013 , 29 (2 ): 281 -286 .
[本文引用: 1]
[4]
仇进生 , 王禹林 , 欧屹 , 等 滚动直线导轨副倾斜静刚度研究
[J]. 机床与液压 , 2018 , 46 (13 ): 14 -16 , 41 .
[本文引用: 1]
QIU J S WANG Y L OU Y , et al Research on tilting stiffness of linear rolling guideway
[J]. Machine Tool & Hydraulics , 2018 , 46 (13 ): 14 -16 , 41 .
[本文引用: 1]
[5]
倪国林 , 孙俊兰 , 姜大志 滚动直线导轨副各向载荷及刚度模型的研究
[J]. 装备制造技术 , 2011 (3 ): 6 -8 , 27 . doi:10.4028/b-j4fgts
[本文引用: 1]
NI G L SUN J L JIANG D Z The studying of the respective load and rigidity's model for linear motion ball guide
[J]. Equipment Manufacturing Technology , 2011 (3 ): 6 -8 , 27 .
DOI:10.4028/b-j4fgts
[本文引用: 1]
[6]
张巍 , 王民 , 孙乐乐 考虑预紧力和接触角变化的直线滚动导轨副刚度建模与分析
[J]. 北京工业大学学报 , 2018 , 44 (1 ): 56 -63 .
[本文引用: 1]
ZHANG W WANG M SUN L L Stiffness modeling and analysis considering influences of preload and contact angle of a linear rolling guide
[J]. Journal of Beijing University of Technology , 2018 , 44 (1 ): 56 -63 .
[本文引用: 1]
[7]
HUNG J P Load effect on the vibration characteristics of a stage with rolling guides
[J]. Journal of Mechanical Science and Technology , 2009 , 23 (1 ): 89 -99 .
[本文引用: 1]
[8]
JASTRZĘBSKI D PAWEŁKO P SZWENGIER G Modeling the effect of geometric errors on the static characteristics of guide rail systems
[J]. Advances in Manufacturing Science and Technology , 2012 , 36 (2 ): 31 -41 .
[本文引用: 1]
[9]
PAWEŁKO P BERCZYŃSKI S GRZĄDZIEL Z Modeling roller guides with preload
[J]. Archives of Civil and Mechanical Engineering , 2014 , 14 (4 ): 691 -699 .
[本文引用: 1]
[10]
WU J S CHANG J C HUNG J P The effect of contact interface on dynamic characteristics of composite structures
[J]. Mathematics and Computers in Simulation , 2007 , 74 (6 ): 454 -467 .
[本文引用: 1]
[11]
鲁明 直线滚动导轨动力学特性解析及有限元建模
[D]. 沈阳 : 东北大学 , 2011 .
[本文引用: 1]
LU M Dynamic characteristics analysis and finite element modeling of linear rolling guide
[D]. Shenyang : Northeastern University , 2011 .
[本文引用: 1]
[12]
PARK C H OH Y J LEE C H et al Theoretical verification on the motion error analysis method of hydrostatic bearing tables using a transfer function
[J]. International Journal of Precision Engineering and Manufacturing , 2003 , 4 (2 ): 64 -70 .
[本文引用: 1]
[13]
NI Y B ZHOU H Y SHAO C Y et al Research on the error averaging effect in a rolling guide pair
[J]. Chinese Journal of Mechanical Engineering , 2019 , 32 : 72 .
[本文引用: 1]
[14]
孙伟 , 汪博 , 鲁明 , 等 基于拉格朗日方程的直线滚动导轨系统解析建模
[J]. 计算机集成制造系统 , 2012 , 18 (4 ): 781 -786 .
[本文引用: 1]
SUN W WANG B LU M et al Analytical modeling of linear rolling guide system based on Lagrange equation
[J]. Computer Integrated Manufacturing Systems , 2012 , 18 (4 ): 781 -786 .
[本文引用: 1]
[15]
孙光明 , 张大卫 , 孙铭泽 , 等 精密机床直线进给系统误差均化机理研究
[J]. 工程设计学报 , 2023 , 30 (2 ): 200 -211 .
[本文引用: 1]
SUN G M ZHANG D W SUN M Z et al Research on error averaging mechanism of linear feed system for precision machine tools
[J]. Chinese Journal of Engineering Design , 2023 , 30 (2 ): 200 -211 .
[本文引用: 1]
[16]
RAHMAN M HEIKKALA J LAPPALAINEN K Modeling, measurement and error compensation of multi-axis machine tools. Part I: theory
[J]. International Journal of Machine Tools and Manufacture , 2000 , 40 (10 ): 1535 -1546 .
[本文引用: 1]
[17]
刘又午 , 章青 , 王国锋 , 等 数控机床误差补偿技术及应用发展动态及展望
[J]. 制造技术与机床 , 1998 (12 ): 5 -6 , 21 .
[本文引用: 1]
LIU Y W ZHANG Q WANG G F et al Development trend and prospect of error compensation technology and application of CNC machine tools
[J]. Manufacturing Technology & Machine Tool , 1998 (12 ): 5 -6 , 21 .
[本文引用: 1]
[18]
陈国达 , 梁迎春 , 孙雅洲 , 等 基于机床体误差模型的加工面形误差预测
[J]. 纳米技术与精密工程 , 2014 (4 ): 242 -248 .
[本文引用: 1]
CHEN G D LIANG Y C SUN Y Z et al Machined form error prediction based on volumetric error model of machine tool
[J]. Nanotechnology and Precision Engineering , 2014 (4 ): 242 -248 .
[本文引用: 1]
[19]
YU H Z JIANG L WANG J D et al Prediction of machining accuracy based on geometric error estimation of tool rotation profile in five-axis multi-layer flank milling process
[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science , 2020 , 234 (11 ): 2160 -2177 .
[本文引用: 1]
[20]
刘泽九 , 贺士荃 , 刘晖 滚动轴承应用 [M]. 北京 : 机械工业出版社 , 2007 .
[本文引用: 1]
LIU Z J HE S Q LIU H Application of rolling bearings [M]. Beijing : China Machine Press , 2007 .
[本文引用: 1]
[21]
万邦良 最小势能原理和最小余能原理的图示证明法
[J]. 力学与实践 , 1983 , 5 (4 ): 49 -50 .
[本文引用: 1]
WAN B L Graphic proof of minimum potential energy principle and minimum complementary energy principle
[J]. Mechanics and Engineering , 1983 , 5 (4 ): 49 -50 .
[本文引用: 1]
[22]
杨洪涛 , 秦鹏飞 , 李莉 , 等 数控机床移动工作台定位精度预测的建模、仿真及实验
[J]. 机电工程 , 2025 , 42 (2 ): 351 -361 .
[本文引用: 1]
YANG H T QIN P F LI L et al Modeling, simulation and experiment of positioning accuracy prediction of moving table of NC machine tool
[J]. Journal of Mechanical & Electrical Engineering , 2025 , 42 (2 ): 351 -361 .
[本文引用: 1]
直线滚动导轨机构承受垂直载荷时的刚度计算
1
1988
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
直线滚动导轨机构承受垂直载荷时的刚度计算
1
1988
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
直线滚动导轨的Hertz接触建模及接触刚度的理论求解
1
2013
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
直线滚动导轨的Hertz接触建模及接触刚度的理论求解
1
2013
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Stiffness analysis of linear guideways without preload
1
2013
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
滚动直线导轨副倾斜静刚度研究
1
2018
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
滚动直线导轨副倾斜静刚度研究
1
2018
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
滚动直线导轨副各向载荷及刚度模型的研究
1
2011
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
滚动直线导轨副各向载荷及刚度模型的研究
1
2011
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
考虑预紧力和接触角变化的直线滚动导轨副刚度建模与分析
1
2018
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
考虑预紧力和接触角变化的直线滚动导轨副刚度建模与分析
1
2018
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Load effect on the vibration characteristics of a stage with rolling guides
1
2009
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Modeling the effect of geometric errors on the static characteristics of guide rail systems
1
2012
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Modeling roller guides with preload
1
2014
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
The effect of contact interface on dynamic characteristics of composite structures
1
2007
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
直线滚动导轨动力学特性解析及有限元建模
1
2011
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
直线滚动导轨动力学特性解析及有限元建模
1
2011
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Theoretical verification on the motion error analysis method of hydrostatic bearing tables using a transfer function
1
2003
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Research on the error averaging effect in a rolling guide pair
1
2019
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
基于拉格朗日方程的直线滚动导轨系统解析建模
1
2012
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
基于拉格朗日方程的直线滚动导轨系统解析建模
1
2012
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
精密机床直线进给系统误差均化机理研究
1
2023
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
精密机床直线进给系统误差均化机理研究
1
2023
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Modeling, measurement and error compensation of multi-axis machine tools. Part I: theory
1
2000
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
数控机床误差补偿技术及应用发展动态及展望
1
1998
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
数控机床误差补偿技术及应用发展动态及展望
1
1998
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
基于机床体误差模型的加工面形误差预测
1
2014
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
基于机床体误差模型的加工面形误差预测
1
2014
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
Prediction of machining accuracy based on geometric error estimation of tool rotation profile in five-axis multi-layer flank milling process
1
2020
... 孙健利[1 ] 与孙伟等[2 ] 应用赫兹接触理论,分析了滚动直线导轨副的力学性能,并建立了其沿垂直方向的刚度模型.Shaw等[3 ] 分析了外载荷及预紧力对直线导轨接触刚度的影响.仇进生等[4 ] 推导了滚动直线导轨副在转动力矩作用下的静刚度模型.倪国林等[5 ] 与张巍等[6 ] 对整个滚动直线导轨副的力学性能进行了分析,实现了任意外载荷下滚动直线导轨副的五维静刚度建模.Hung[7 ] 、Jastrzębski等[8 ] 与Pawełko等[9 ] 将滚动体等效为单向移动的弹簧单元,采用弹簧单元法对滚动直线导轨副结合部进行了有限元建模.Wu等[10 ] 与鲁明[11 ] 利用假想材料法模拟滚柱与滚道面结合部的接触特性,并通过设置虚拟材料的弹性模量、泊松比等参数来等效滚动体,从而建立了滚动直线导轨副的有限元模型.Park等[12 ] 为探究导轨直线度误差与工作台运动误差间的映射关系,运用全解析法构建了油膜作用力与工作台运动误差间的传递模型,并定义了误差传递函数.Ni等[13 ] 、孙伟等[14 ] 与孙光明等[15 ] 采用传递函数来描述导轨直线度误差与导轨承载力之间的关系并分析了其特性,由此量化了滚动直线导轨系统的误差均化效应.Rahman等[16 ] 与刘又午等[17 ] 以多体系统理论与机床拓扑结构为基础,构建了多轴数控机床的几何误差模型.陈国达等[18 ] 与Yu等[19 ] 通过计算工件加工表面刀具接触点的分布得到了加工表面轮廓,并以此为基础开展了加工精度预测. ...
1
2007
... 滚动导轨副由导轨、滑块与滚动体构成.滚动体在预紧力与外部载荷的作用下产生变形,其与导轨滚道面、滑块滚道面间的接触符合赫兹接触理论.基于赫兹接触理论,圆柱滚动体的变形量δ 与所受载荷Q 满足以下关系[20 ] : ...
1
2007
... 滚动导轨副由导轨、滑块与滚动体构成.滚动体在预紧力与外部载荷的作用下产生变形,其与导轨滚道面、滑块滚道面间的接触符合赫兹接触理论.基于赫兹接触理论,圆柱滚动体的变形量δ 与所受载荷Q 满足以下关系[20 ] : ...
最小势能原理和最小余能原理的图示证明法
1
1983
... 根据最小势能原理[21 ] , v W b 最小,即任取 v ′ = v +v W b =W′ b -W b 应恒大于等于0,而ΔW b 可表示为: ...
最小势能原理和最小余能原理的图示证明法
1
1983
... 根据最小势能原理[21 ] , v W b 最小,即任取 v ′ = v +v W b =W′ b -W b 应恒大于等于0,而ΔW b 可表示为: ...
数控机床移动工作台定位精度预测的建模、仿真及实验
1
2025
... 考虑到尺寸误差可通过后处理补偿,故本文重点研究圆度误差与圆柱度误差.在实际加工过程中,导轨误差除受到导轨基面误差的影响外,还受到由静力作用导致的静力变形与由加工过程生热导致的热变形的影响[22 ] .利用激光自准直仪测量导轨基础误差,并通过有限元仿真得到导轨的静力变形量与热变形量,将三者叠加,得到导轨的综合误差.随后,利用本文所提出的方法对工件表面轮廓进行预测,结果如图14 所示.采用最小二乘法计算工件的圆柱度误差,为0.360 μm. ...
数控机床移动工作台定位精度预测的建模、仿真及实验
1
2025
... 考虑到尺寸误差可通过后处理补偿,故本文重点研究圆度误差与圆柱度误差.在实际加工过程中,导轨误差除受到导轨基面误差的影响外,还受到由静力作用导致的静力变形与由加工过程生热导致的热变形的影响[22 ] .利用激光自准直仪测量导轨基础误差,并通过有限元仿真得到导轨的静力变形量与热变形量,将三者叠加,得到导轨的综合误差.随后,利用本文所提出的方法对工件表面轮廓进行预测,结果如图14 所示.采用最小二乘法计算工件的圆柱度误差,为0.360 μm. ...