考虑自支撑临界角的3D打印混凝土球壳结构拆分方法与成形实验

doi:10.3785/j.issn.1006-754X.2025.04.162

考虑自支撑临界角的3D打印混凝土球壳结构拆分方法与成形实验

李胤贤^,¹, 蒋友宝^,^,², 刘艳², 高鹏翔²

1.长沙理工大学卓越工程师学院，湖南长沙 410114

2.长沙理工大学土木与环境工程学院，湖南长沙 410114

Splitting method and forming experiment of 3D printed concrete spherical shell structure considering self-supporting critical angle

LI Yinxian^,¹, JIANG Youbao^,^,², LIU Yan², GAO Pengxiang²

1.Elite Engineering School, Changsha University of Science and Technology, Changsha 410114, China

2.School of Civil and Environmental Engineering, Changsha University of Science and Technology, Changsha 410114, China

通讯作者: 蒋友宝（1982—），男，教授，博士生导师，博士，从事结构可靠性与3D打印混凝土建造技术研究，E-mail: jiangybseu@163.com，https://orcid.org/0000-0003-0276-818X

收稿日期: 2024-07-29 修回日期: 2024-09-12

基金资助:

国家自然科学基金资助项目. 52378126
湖南建工集团有限公司科技重点项目. JGJTK2022-13

Received: 2024-07-29 Revised: 2024-09-12

作者简介 About authors

李胤贤（2002—），男，硕士生，从事3D打印混凝土建造技术与无损检测技术研究，E-mail:L505175648@163.com , E-mail：L505175648@163.com

摘要

为实现3D打印混凝土球壳结构的无支撑建造，提出了一种基于自支撑临界角的结构拆分方法。该方法将结构拆分问题转化为单目标优化问题，并根据改进遗传算法和动态优化拆分策略，寻求得到较为简便、可行的球壳结构拆分方案。基于所获得的拆分方案，可将球壳结构拆分成若干个可自支撑打印的单元，对拆分单元逐一打印后完成整体结构的拼接。对于混凝土球壳结构而言，随着材料自支撑临界角的增大，拆分单元数量增加。为降低拆分单元数量过多对球壳结构后续连接及整体性能的不利影响，混凝土材料的自支撑临界角不宜过大。现场成形实验结果表明，基于所提出的方法可实现3D打印混凝土球壳结构的有效拆分，在打印过程中能够避免结构支模工作，提高了建造效率。

关键词： 3D打印混凝土 ; 球壳结构 ; 自支撑临界角 ; 遗传算法 ; 结构拆分

Abstract

In order to achieve the unsupported construction of 3D printed concrete spherical shell structures, a structure splitting method based on self-supporting critical angle is proposed. In this method, the structure splitting problem was converted into a single-objective optimization problem, and the relatively simple and feasible spherical shell structure splitting scheme was obtained by the improved genetic algorithm and dynamically optimized splitting strategy. The spherical shell structure could be split into multiple self-supporting printable units based on the obtained splitting scheme, and the whole structure could be assembled after the splitting units were printed one by one. For the concrete spherical shell structure, the number of splitting units increased with the increase of material self-supporting critical angle. To minimize the adverse effects of the number of splitting units on the subsequent connection and overall performance of the spherical shell structure, the self-supporting critical angle of the concrete material should be limited. The results of field forming experiments show that the proposed method can effectively split the 3D printed concrete spherical shell structure and avoid structural formwork during the printing process, thereby enhancing construction efficiency.

Keywords： 3D printed concrete ; spherical shell structure ; self-supporting critical angle ; genetic algorithm ; structure splitting

PDF (3689KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李胤贤, 蒋友宝, 刘艳, 高鹏翔. 考虑自支撑临界角的3D打印混凝土球壳结构拆分方法与成形实验[J]. 工程设计学报, 2025, 32(2): 151-158 doi:10.3785/j.issn.1006-754X.2025.04.162

LI Yinxian, JIANG Youbao, LIU Yan, GAO Pengxiang. Splitting method and forming experiment of 3D printed concrete spherical shell structure considering self-supporting critical angle[J]. Chinese Journal of Engineering Design, 2025, 32(2): 151-158 doi:10.3785/j.issn.1006-754X.2025.04.162

近年来，3D打印混凝土技术凭借人工成本低、建造效率高和可操作性强等优点迅速发展，逐渐成为行业热点。但由于混凝土材料具有较高的流动性，在实际打印过程中无法使结构悬垂部分一次成形，通常需要添加支撑来保证打印的连续性和完整性，这极大地增加了建造成本和施工工艺复杂度，阻碍了3D打印混凝土技术的进一步推广与应用。

为实现3D打印混凝土的无支撑或少支撑建造，蒋友宝等^[1-2]开展了3D打印混凝土圆管、3D打印预制混凝土扭曲面模壳-现浇柱的工艺参数研究，明确了材料配合比、打印路径等关键参数对混凝土曲面构件3D打印成形质量的影响规律。林晓阳等^[3]基于结构的悬垂约束提出了一种通过调整结构布局、优化几何形状来实现竖直桁架结构自支撑打印的方法，该方法可有效减小支撑结构的体积，但缺点是对壳状结构的优化效果不佳。周钰琛^[4]提出了一种通过聚类划分点云模型以将原STL（stereolithography，立体光刻）模型拆分为类似金字塔结构的分解算法，实现了简单建筑结构的初步拆分，但该方法对于造型复杂、悬垂部分较多的建筑结构存在分解效果不佳、拆分精度有限的缺陷。王铮等^[5]提出了一种基于五轴打印设备的支撑消减方案，通过调整打印方向和打印顺序来消除构件悬垂效应的影响，以减少对支撑结构的需求，但该方法对打印材料的要求较高，难以应用于混凝土结构的打印。Kontovourkis等^[6-7]提出了一种利用拓扑优化来减少3D打印壳体结构支撑材料的方法，该方法根据悬链线的参数化设计对壳体结构表面进行布局，将三角面片分区域处理以降低打印应力，并通过拓扑优化来减少支撑材料的使用量，但仍未能完全实现真正意义上的无支撑打印建造。

为此，本文以常见的3D打印混凝土球壳结构为例，提出了一种可实现无支撑打印成形的结构拆分方法。该方法根据自支撑临界角约束将混凝土球壳结构拆分成若干个可自支撑打印的单元，并利用改进遗传算法和动态优化拆分策略，以寻求得到较为简便、可行的球壳结构拆分方案。最后，通过球壳结构的打印成形实验来验证所提出的拆分方法的合理性和可行性。

1 考虑悬垂约束的结构拆分策略

1.1　悬垂效应与自支撑临界角

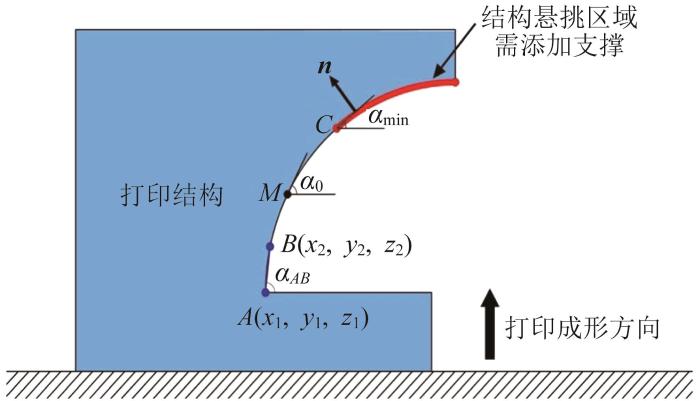
悬垂效应是指结构在自重作用下产生弯曲和形变后形成一条悬垂曲线的现象。3D打印混凝土技术的实质是通过将特殊混凝土材料层层堆积来实现结构的整体成形。对于打印结构中的部分悬挑区域，需重点考虑其悬垂角度（打印结构与水平面的夹角）对结构整体成形的影响。在自重作用下，随着悬垂角度的减小，结构成形的难度提高。当悬垂角度过小时，可能会导致已成形部分发生塌陷，从而无法继续打印工作。因此，为实现结构的一次打印成形，需建立结构悬垂效应约束模型^[3]。

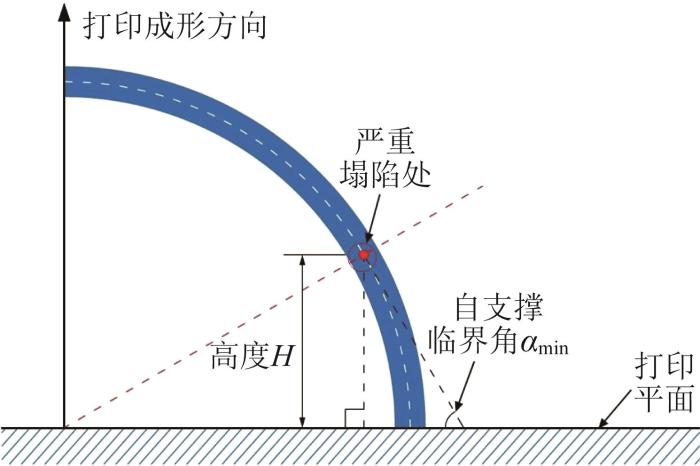
对于一般结构，某点的悬垂角度可取该点法向切线与打印起点法线的夹角。在打印过程中，当结构悬垂部分处于坍塌临界状态时，坍塌临界点的悬垂角度即为自支撑临界角。如图1所示，打印结构截面上点M的悬垂角度为 $α_{0}$ ，结构悬垂区域处打印坍塌临界点C的自支撑临界角为 $α_{m i n}$ 。自支撑临界角 $的$ 值主要与打印材料自身性质及打印参数有关，可通过相关实验测得。为实现3D打印混凝土结构的无支撑建造，需满足悬垂效应约束条件，即悬垂角度小于自支撑临界角，该约束条件可表示为：

s i n α_{m i n} - |\frac{X_{A B} d_{x}}{l_{A B}} + \frac{Y_{A B} d_{y}}{l_{A B}} + \frac{Z_{A B} d_{z}}{l_{A B}}| \leq 0

(1)

式中： $X_{A B}$ 、 $Y_{A B}$ 、 $Z_{A B}$ 分别为A（ $x_{1}$ , $y_{1}$ , $z_{1}$ ）、B（ $x_{2}$ , $y_{2}$ , $z_{2}$ ）两点连线在直角坐标系下沿各坐标轴方向的投影长度， $X_{A B} = x_{2} - x_{1}$ ， $Y_{A B} = y_{2} - y_{1}$ ， $Z_{A B} = z_{2} - z_{1}$ ； $d_{x}$ 、 $d_{y}$ 、 $d_{z}$ 为标准化成形方向向量的3个分量，分别取 $d_{x} =$ 0， $d_{y} =$ 0， $d_{z} =$ 1； $l_{A B}$ 为线段AB的长度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 结构悬挑区域示意

Fig.1 Schematic of overhanging area of structure

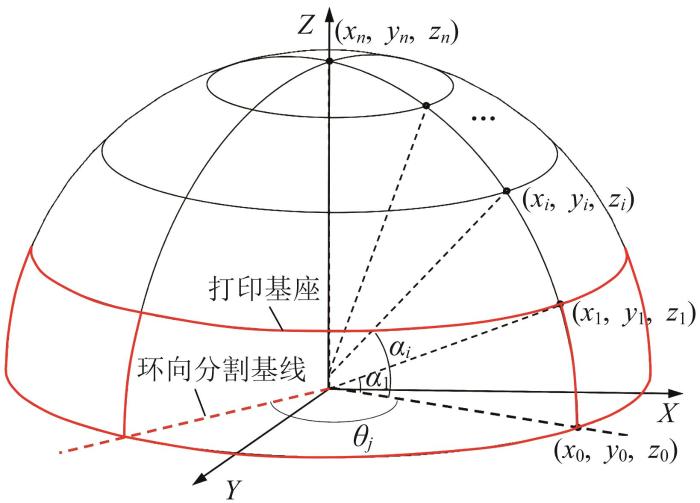
1.2　考虑悬垂效应的球壳结构拆分策略

针对球壳结构（考虑到结构对称性及实际工程中常见的混凝土壳体结构，以半球壳结构为研究对象），首先对其STL模型的所有三角面片进行初步判断，筛选出可常规打印的部分作为打印基座，并对其边缘进行优化处理^[8]。对于模型剩余的上方部分结构，根据其中心轴，采用旋转分割面对其曲面进行划分，并沿打印高度方向进行约束。打印基座的初始高度区间可取[ $z_{0}, z_{1}$ ]，最优区间旋转角度为{ $θ_{1}$ , $θ_{2}, \dots$ , $θ_{j} \dots$ , $θ_{N}$ }，θ_j 为环向拆分角度（环向分割基线与分割平面的夹角），θ_j $\in$ [0, 2π]，N为环向拆分次数。鉴于球壳结构为中心旋转对称结构，其环向旋转区间可采用等份拆分策略，即根据环向拆分次数来确定环向拆分区间，并利用改进遗传算法求解最优环向拆分次数N及高度区间[ $z_{i - 1}, z_{i}$ ]，其中i=1, 2, $\dots$ , n，n为最大分层数。球壳结构的拆分过程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 球壳结构拆分示意

Fig.2 Schematic of spherical shell structure splitting

球壳结构横断面的拆分打印过程如图3所示。根据球壳曲面旋转母线各点斜率的变化情况，将结构分为常规打印部分和考虑悬垂效应的打印部分。对于常规打印部分，可直接进行建模、切片^[9]；对于考虑悬垂效应的打印部分，要根据旋转母线凹凸性发生转变的位置进行进一步拆分，以保证每个部分的母线斜率呈单调递增或递减的状态。需要说明的是，随着拆分单元数量的增加，结构的整体性能将会受到较大影响，具体影响程度与拆分单元数量、打印材料和结构连接方式等多个因素有关，较为复杂。限于篇幅，本文仅讨论球壳结构的拆分与打印成形方法，相关力学性能的测试将在后续研究中进行完善。

图3

新窗口打开| 下载原图ZIP| 生成PPT

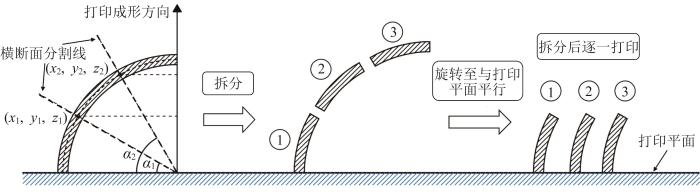
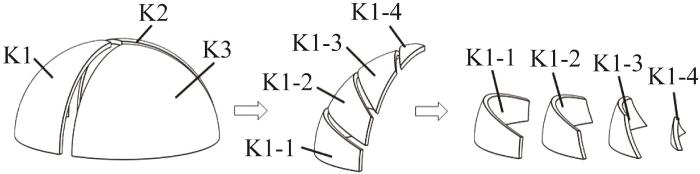
图3 球壳结构拆分打印过程

Fig.3 Splitting and printing process of spherical shell structure

2 球壳结构拆分方法

2.1　拆分问题的优化模型

混凝土材料的流动性较强，打印结构体积较小会增加后续结构整体拼接的难度，且拼接后难以保证结构的整体强度。因此，在对混凝土球壳结构进行拆分时，各拆分单元的体积不宜过大或过小，且拆分单元体积由底部向上逐级递减^[10]。针对每一个拆分单元，通过调整分割平面倾斜角度来消除悬垂效应对其打印过程的影响。考虑到拆分方案的均匀性、整体性要求以及各拆分单元能否实现自支撑等因素，可将球壳结构STL模型的拆分问题转化为多目标优化问题。

对于多目标优化问题，目前尚无较为优异的算法。在其他案例中，大多是将多目标优化问题转化为单目标优化问题^[11-12]。基于此，本文将球壳结构拆分目标组合为一个线性函数，并为每个目标变量分配不同的权重，以实现将多目标优化问题转化为单目标优化问题，对应的数学模型可表示为：

F = C_{1} F_{1} + C_{2} F_{2} + C_{3} F_{3}

(2)

其中：

F_{1} = \sum_{j = 1}^{N} \frac{g_{j}}{m_{j}}

F_{2} = \frac{\sum_{j}^{N} g_{j}}{M}

F_{3} = 1 - \frac{{|z_{i} - z_{i - 1}|}_{m a x} - {|z_{i} - z_{i - 1}|}_{m i n}}{{|z_{i} - z_{i - 1}|}_{m a x} + {|z_{i} - z_{i - 1}|}_{m i n}}

式中：F为目标函数； $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ 为各个目标对应的权重，权重值可通过熵权法确定，本文对部分初始解集进行标准化处理，计算其熵值及相关指标，最终得到 $C_{1} \in$ [0.35, 0.45]、 $C_{2} \in$ [0.2, 0.3]， $C_{3}$ 按1- $C_{1}$ - $C_{2}$ 取值； $F_{1}$ 为各环向拆分区间内满足悬垂效应的节点数与该拆分区间内总节点数的比值之和， $F_{2}$ 为所有环向拆分区间内满足悬垂效应的节点数与球壳结构STL模型总节点数的比值， $F_{3}$ 为均匀度函数；g_j 为第j个环向拆分区间内满足悬垂效应的节点数，m_j 为第j个环向拆分区间内的总节点数，M为球壳结构STL模型总节点数； $|z_{i} - z_{i - 1}|$ 为拆分层间高度，考虑到拆分单元的连接要求，分层数不宜过多。

2.2　基于遗传算法的优化求解

本文采用遗传算法求解上文所构建的优化模型。遗传算法的主要步骤包括构造初始种群和变异操作等。在构造初始种群时，考虑到球壳结构拆分方案的均匀性要求，根据初始拆分层数和环向拆分次数，在初始种群中人为构造部分均匀性较强的个体来参与对后代的遗传和变异，以提高运行效率。在拆分过程中，当达到该层最大拆分高度后，即结束本次拆分，并将本次迭代过程中的最优种群遗传至下一次迭代过程中的初始种群，以降低种群构造的随机性，从而缩短算法收敛时间。

变异操作可使部分个体产生新的染色体片段，避免陷入局部最优。但随着二进制位串长度的增加，仅依靠取反变异无法较快地跳出当前局部搜索区域。为降低编码的复杂度，根据文献[13]提出的变量微调方式进行变异操作，将二进制位串分段转化为十进制位串后，对位串中的每个变量微调0~2个步长，最后将其重新组合转化为二进制位串。该方法能够有效减少种群演化时间，加快算法的收敛速度。基于改进遗传算法的球壳结构拆分流程如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

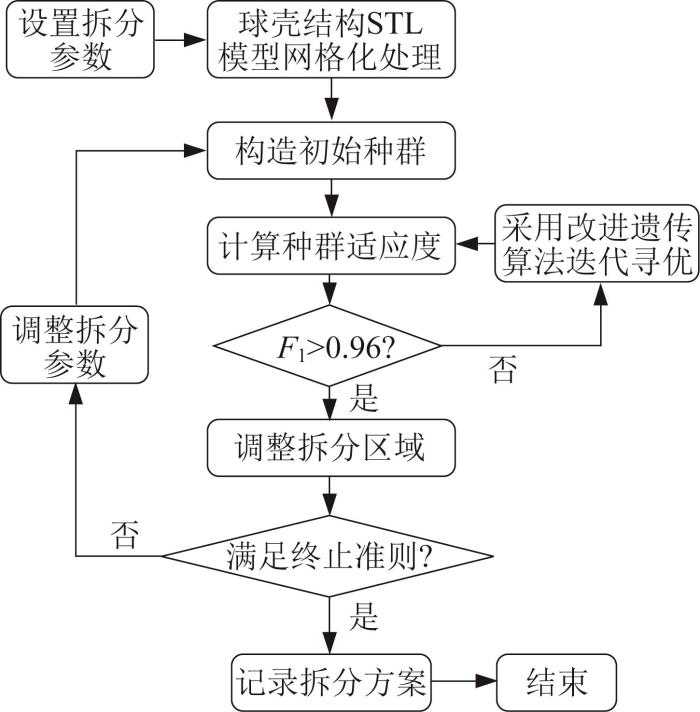
图4 基于改进遗传算法的球壳结构拆分流程

Fig.4 Splitting process of spherical shell structure based on improved genetic algorithm

球壳结构拆分的具体实施步骤如下：

步骤1：数据预处理。设置拆分参数以及遗传算法的相关参数，导入球壳结构的STL模型。

步骤2：初步筛选。根据悬垂约束条件，初步筛选出不满足悬垂效应的节点，记录其坐标及相邻节点的编号，并对剩余部分的边界进行优化处理，得到可常规打印的光滑连续基座。

步骤3：优化求解。根据拆分均匀性要求，采用一半随机解、一半均匀解的方式构造初始种群，并采用改进遗传算法进行迭代寻优，最终得到目标模型的环向拆分区间及拆分层间高度。

步骤4：迭代分层。对步骤3中的环向拆分区间进行判断，实时调整拆分区域，得到当前模型的最大层间高度，重复步骤3直至所有节点均满足要求，记录拆分方案。

步骤5：根据悬垂约束条件及步骤4得到的拆分层间高度，对球壳结构旋转母线进行拆分操作，从而得到分割平面的倾斜角度 $α_{i}$ ，拆分结束。

3 球壳结构拆分实例

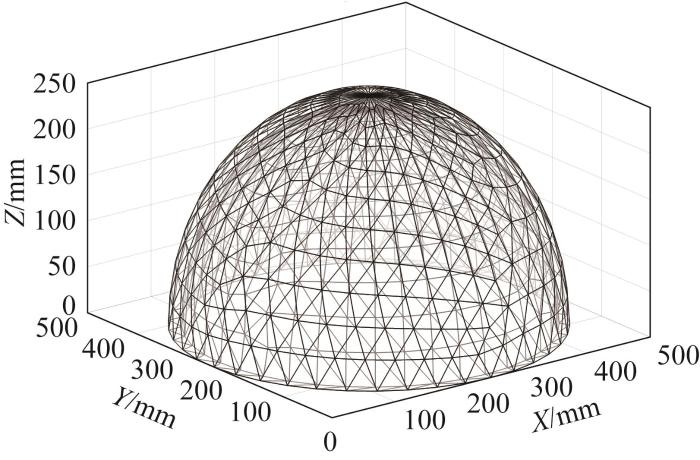
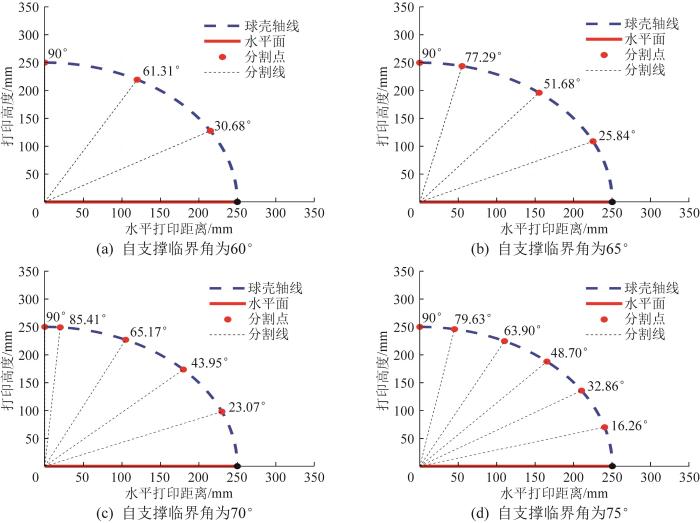
采用所提出的拆分方法，对图5所示的直径为500 mm、厚度为35 mm的球壳结构进行建模，并求解其最优拆分方案。假定混凝土材料的自支撑临界角分别为60°、65°、70°、75°，在不同悬垂约束条件下开展拆分操作。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 球壳结构示意图

Fig.5 Schematic diagram of spherical shell structure

首先，导入该球壳结构的STL模型，如图6所示。根据悬垂约束，筛选出可常规打印的球壳基座，更新打印参数后，进入迭代寻优阶段。首先，构造剩余上部结构的初始种群，并计算种群个体的适应度值。其中，各目标函数的权重 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ 分别取0.35、0.40、0.25，权重值可根据结构特征进行调整。然后，采用改进遗传算法进行迭代寻优，对当前最优环向拆分区间进行微调^[14]，即可得到当前层的拆分方案，直至达到该球壳结构的最大高度并退出迭代循环，记录球壳结构的拆分方案。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 球壳结构的STL模型

Fig.6 STL model of spherical shell structure

不同自支撑临界角下球壳结构横断面的纵向拆分情况如图7所示（图中轴线是指球壳纵向截面的中心轴线）。从图7中可以看出，当自支撑临界角为60°时，需将球壳结构拆分成3段后进行打印；当自支撑临界角为65°、70°、75°时，需将该结构分别拆分为4、5、6段进行打印。由此可知，随着自支撑临界角的不断增大，球壳结构所需拆分的段数增加，拆分单元的体积减小，这一变化趋势符合实际拆分情况^[15]，表明所提出的拆分方法具有较好的可行性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 球壳结构横断面拆分情况

Fig.7 Cross-section splitting of spherical shell structure

球壳结构的环向拆分次数一般不宜小于3，具体可根据球壳结构的几何尺寸合理设定。以自支撑临界角取65°时为例，假定球壳结构的环向拆分次数N=3, 4, 5, 6，且纵向按图7(b)所示拆分为4段，则采用不同环向拆分方案下的球壳结构拆分结果如表1所示。由表1可知，随着环向拆分次数的增加，需打印的单元数量增多，后续结构成形所需连接部分的面积也随之增大。

表1 不同环向拆分次数下球壳结构的拆分结果

Table 1 Splitting results of spherical shell structure under different circumferential splitting times

环向拆分数/次	拆分单元数量/个	连接处面积/cm²
3	12	1 232.4
4	16	1 358.1
5	20	1 483.8
6	24	1 609.5

新窗口打开| 下载CSV

假定在打印过程中，混凝土条带的宽度为35 mm，高度为10 mm。当环向拆分次数N=3时，可将球壳结构STL模型沿环向拆分为K1、K2、K3三个部分。由于球壳结构为中心对称模型，只需任选一个区域进行纵向二次拆分即可。此处选择K1部分进行纵向二次拆分，由图7(b)可知，当自支撑临界角为65°时，球壳结构纵向分割平面的倾斜角度分别为25.84°、51.68°、77.29°、90.00°，由此可将K1拆分成K1-1、K1-2、K1-3、K1-4四个部分，分别将其打印连接，打印路径可参考文献[16]设计，具体过程如图8所示。自支撑临界角为65°时球壳结构的详细拆分参数如表2所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 自支撑临界角为65°时球壳结构的拆分过程

Fig.8 Splitting process of spherical shell structure with self-supporting critical angle of 65°

表2 自支撑临界角为65°时球壳结构的拆分方案

Table 2 Splitting scheme of spherical shell structure with self-supporting critical angle of 65°

分层序号	环向拆分数N/次	环向拆分角度 $θ_{j}$ /(°)			分割点^①坐标（ $x_{i}, y_{i}$ ）/mm	分割平面倾斜角度 $α_{i}$ /(°)
分层序号	环向拆分数N/次	$θ_{1}$	$θ_{2}$	$θ_{3}$	分割点^①坐标（ $x_{i}, y_{i}$ ）/mm	分割平面倾斜角度 $α_{i}$ /(°)
1	3	60	180	300	（225，108.97）	25.84
2		60	180	300	（155，196.15）	51.68
3		60	180	300	（55，243.875）	77.29
4		60	180	300	（0，250）	90.00

①分割点为球壳结构截面中心轴线上的点。

新窗口打开| 下载CSV

同理，运用上述方法可得到其他自支撑临界角条件下的球壳结构拆分方案。由此可知，当确定材料自支撑临界角以及环向拆分次数后，本文所提出的方法能自动计算得到球壳结构的拆分方案。随后，根据拆分单元并调整其分割平面倾斜角度，即可实现各单元的自支撑打印。最后，视各拆分单元的尺寸，选择采用高性能砂浆或环氧树脂建筑结构胶等进行拼接^[17]，以实现球壳结构的免支撑打印成形。

4 实验验证

4.1　自支撑临界角测定实验

为保证3D打印混凝土材料的流动性、泵送性以及黏结强度等要求，需对其配合比进行精细化设计，以协调材料各组成部分的性能^[18]。本文选用的混凝土材料以普通硅酸盐水泥为主，掺杂部分快硬水泥，以保证打印结构的前期强度；同时，添加少量偏高岭土，以缩短混凝土材料的凝结时间以及调节混凝土材料的硬化速度，并加入一定量的硅灰来增加材料的保水性，以保证能够满足3D打印过程中的泵送要求。此外，还添加了少量纤维及纤维素醚，以提高混凝土材料的黏结能力，防止在硬化过程中产生细小裂缝，从而影响球壳结构的整体性能^[19]。混凝土材料各组成部分的质量分数如表3所示。

表3 混凝土材料各组成部分的质量分数

Table 3 Mass fraction of each component of concrete material

材料	质量分数/%
细砂	38.30
普通硅酸盐水泥	34.10
水	13.60
偏高岭土	4.80
粉煤灰	4.80
硅灰	2.40
快硬水泥	1.80
纤维	0.08
减水剂	0.01
消泡剂	0.09
纤维素醚	0.02

新窗口打开| 下载CSV

为测定混凝土材料的自支撑临界角，将半径为R的标准球壳结构（见图9）作为测试对象进行连续打印，打印过程中不设置任何支撑结构，该球壳结构的悬垂角度在0°~90°间均匀变化。在球壳结构首次出现明显塌陷的情况下记录对应的打印高度H，从而计算得到混凝土材料的自支撑临界角 $α_{m i n}$ ，计算式如下：

α_{m i n} = a r c c o s \frac{R}{H}

(3)

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 混凝土材料自支撑临界角测定原理

Fig.9 Measuring principle of self-supporting critical angle of concrete material

本实例中，混凝土打印条带宽度为15 mm，条带厚度为10 mm，室内温度为21 ℃，待打印球壳结构的直径为500 mm。混凝土材料自支撑临界角的测定现场如图10所示。多次打印实验结果显示：混凝土材料的自支撑临界角为62.76°，当打印结构的悬垂角度大于该值时，混凝土条带会出现明显的塌陷。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 混凝土材料自支撑临界角测定现场

Fig.10 Measuring site of self-supporting critical angle of concrete material

4.2　拆分打印和拼接

为保证球壳结构打印过程顺利进行，偏保守取65°作为混凝土材料的自支撑临界角。由上文分析可知，当环向拆分次数较多时，混凝土条带连接处面积较大，不利于结构的整体性能；此外，拆分单元数量较多，会极大延长最后的拼接时间。因此，本文采用环向拆分次数N=3的拆分方案进行后续实验。

经过现场实验，成功实现了球壳结构的拆分打印，实际打印过程如图11所示。其中，K1部分的各混凝土分块如图12所示，将其拼接即可得到1/3的球壳结构。如图13所示，K1部分拼接完成后的1/3球壳结构的半径为245 mm，符合结构设计要求。最后，将K1、K2、K3三部分进行拼接，即可得到完整的球壳结构，如图14所示。由图14可知，打印后拼接成形的球壳结构的外边缘直径为542.0 mm，内边缘直径为470.8 mm，平均直径为506.4 mm，打印误差为6.4 mm；实际打印条带的平均宽度为35.6 mm。在实际打印过程中，球壳结构未使用任何支撑结构即可成形，但在成形精度方面还需进一步优化。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 打印过程中的各混凝土分块

Fig.11 Each concrete block during printing

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 K1部分的各混凝土分块

Fig.12 Each concrete block of K1 part

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 拼接后的K1部分结构

Fig.13 K1 part structure after assembly

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 球壳结构及其直径

Fig.14 Spherical shell structure and its diameter

5 结论

本文考虑结构的悬垂约束条件，根据与打印材料有关的自支撑临界角对目标结构进行拆分，提出了一种适用于球壳结构无支撑打印成形的拆分方法，并通过数值计算和打印成形实验验证了所提出方法的有效性。主要结论如下：

1）将球壳结构拆分问题转化为综合拆分次数和均匀度的单目标优化问题，并通过改进遗传算法和动态优化拆分策略寻求得到合理可行的拆分方案，具有较高的效率。

2）对于混凝土球壳结构，随着材料自支撑临界角的增大，拆分单元数量增多。为降低拆分单元数量过多对结构后续连接及整体性能的不利影响，建议选取的自支撑临界角不宜过大。

3）考虑自支撑临界角的球壳结构拆分方法免除了打印过程中的支模操作。现场成形实验结果表明，所提出的拆分方案合理、可行。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蒋友宝，胡佳鑫，周浩，等.

起始点逐层等角度移动时3D打印混凝土圆管可连续打印高度

［J］. 建筑结构学报， 2022， 43（9）： 222-231.