在机械系统设计阶段,面临着多种多样不确定性因素,如几何尺寸、材料属性和外部载荷等[1 -4 ] 。这些不确定性因素的耦合作用会使系统响应出现随机偏差,难以保障其运行平稳性和工作可靠性[5 ] 。因此,准确量化机械系统参数的不确定性水平,并合理评估不确定性对系统响应的影响,对机械系统的设计与优化具有重要意义。
机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] 。其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] 。而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] 。为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] 。
非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] 。近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法。区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] 。然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费。椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况。目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等。随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况。为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量。
上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] 。为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性。Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题。Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性。上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度。
针对传统非概率凸模型在处理高维异构不确定性数据时存在的样本聚类表征能力不足的问题,本文提出了一种基于超椭球聚类算法的超椭球聚类方法(hyper-ellipsoidal clustering method, HECM),并将其应用于机械系统不确定性传播。首先,采用超椭球聚类算法获取样本聚类信息,并根据分类结果构建聚类椭球模型;其次,针对多源不确定性参数耦合现象,基于区间变量进行系统响应敏感性分析,得到多维系统参数对系统响应影响的排序;然后,采用功能度量法(performance measure approach, PMA)获取系统响应的上、下边界,实现聚类椭球不确定性传播;最后,将所提方法应用于3个数值算例和1个雷达系统工程算例,并与蒙特卡罗模拟(Monte Carlo simulation, MCS)方法进行比较,来验证所提方法的有效性。
1 基于聚类椭球模型的不确定性量化
对于工程问题中参数样本数据分组聚集现象,若采用单一椭球模型进行不确定性量化,模型内部会出现没有样本分布的空白区域,从而使不确定性量化结果过于保守。本文在度量参数不确定性时,采用超椭球聚类算法获取样本分布特征,根据聚类结果采用最小体积原则构建聚类椭球模型,实现机械系统参数不确定性量化。
1.1 聚类椭球模型构建
由于机械系统各参数表征的物理意义不同,参数数量级常存在差异。若直接使用原始数据求解样本的分布特征,会严重影响分析精度,甚至导致聚类结果出现错误。因此,在提取样本分布特征前,采用归一化方法对样本数据进行预处理,将其转换到[0, 1]区间,以消除机械系统参数数量级差异对聚类结果的影响。具体计算公式如下所示[26 ] :
u i j = x i j - x ¯ j x ¯ j - x ̲ j (1)
式中:x i j j 个参数的第i 个样本数据,u i j x ¯ j x ̲ j j 个参数的最大值和最小值。
在对数据进行聚类分析时,选择合适的距离度量方法对聚类结果的准确性至关重要。与欧氏距离相比,马氏距离能够通过协方差矩阵反映样本特征间的相关性,可以更准确地捕捉数据的内在特征[27 ] 。因此,本研究采用马氏距离度量样本的相关性。马氏距离D 可以表示为:
D x i , m k = x i - m k T Q k - 1 x i - m k (2)
式中:x i i 个样本数据,m k k 个分类的聚类中心,Q k k
超椭球聚类过程可分为获取聚类中心和求解协方差矩阵两步。
m k = ∑ i = 1 k P i k x i ∑ i = 1 k P i k (3)
式中:P i k x i k P i k = 1 P i k = 0
协方差矩阵则通过求解包络样本点的最小体积椭球获得。对于给定的样本集,存在无数个完全包含样本点的椭球。为寻找最小体积椭球,根据椭球的几何特征,构建如下优化问题[4 ] :
m i n ∏ i = 1 n λ i G s . t . x i - x C T G x i - x C ≤ 1 λ i ≥ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , n (4)
式中:λi 为椭球特征值,其乘积正比于椭球体积;G x C n
为提高计算效率,根据椭球协方差矩阵的性质对其进行特征值分解,可得到G = A T A A n 阶正定矩阵。此时椭球体积正比于d e t A - 1 式(4)可转化为[20 ] :
m i n d e t A - 1 s . t . Α x i - x C 2 ≤ 1 (5)
针对式(5)所示的优化问题,本文采用凸优化工具箱进行求解。通过对半定规划问题进行优化求解,可以保证所得椭球严格包络了所有样本点,并且该椭球具有最小体积。
1.2 聚类数自适应选取
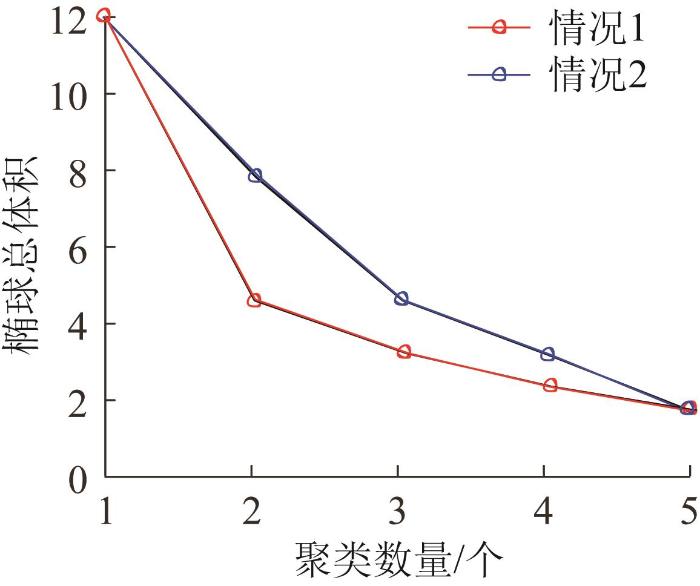
本文基于椭球模型体积变化特性,提出一种自适应选取聚类数的方法。通过分析模型总体积变化规律,判断样本数据的最佳聚类数。随着聚类数增加,椭球模型总体积会呈现不同的变化趋势,如图1 所示。
图1
图1
椭球模型总体积变化情况
Fig.1
Total volume variation of ellipsoidal model
1)情况1:随着聚类数的变化,椭球模型总体积存在较为明显的拐点,因此可以通过拐点位置选择最佳聚类数。
2)情况2:当样本点较为稀疏时,椭球模型总体积随着聚类数的增加而逐渐减小,导致难以直接判断拐点位置。
对于第1种情况,通过分析聚类椭球模型总体积的变化规律进行判断。当体积变化率δ 1 α 1 δ 2 α 2
δ 1 = V k - V k - 1 V k (6)
式中:V k k V k - 1 k - 1
δ 2 = V k - 2 - V k - 1 V k - V k - 1 (7)
采取聚类数自适应选取策略,可以在缺乏先验知识的情况下有效确定最佳聚类数。最佳聚类数选取过程如下。
步骤2:将样本集随机分为k 个聚类,设定聚类中心 m k
步骤3:以欧氏距离为度量依据,根据聚类中心 m k
步骤4:根据式(3)计算聚类中心与样本点的划分矩阵P
步骤5:根据划分矩阵P Q k
步骤6:将马氏距离作为度量依据,重新计算划分矩阵 P
步骤7:若椭球模型总体积的变化满足阈值条件,则算法停止并输出最终量化结果;否则,令k =k +1,重复步骤2到步骤6。
2 基于区间变量的系统敏感性分析
为评估不确定性参数对系统响应的影响程度,本小节采用参数的上、下边界构造区间变量,实现参数不确定性量化,并分析参数不确定性对系统响应的非概率方差贡献率。区间变量可表示为[28 ] :
x ∈ X I = X L , X U
式中:X I X L X U
当实验样本都位于区间变量 X I 内时,机械系统的不确定性可通过区间下界 X L 和区间上界 X U 来表示。为方便描述,定义区间变量中点 X C 和半径 X W 分别为[28 ] :
X C = X U + X L 2
X W = X U - X L 2
区间中点 X C 表示参数的名义值,区间半径 X W 反映参数的不确定性大小。同时定义参数X i DX 为[28 ] :
D X = X i W 2
C - 1 ( X - X C ) ≤ e
式中:C = d i a g X 1 W , X 2 W , ⋯ , X n W e = 1 , 1 , ⋯ , 1 T n
y = g X
将机械系统响应函数进行二阶泰勒展开,并忽略高阶项,则其数学表达式为[29 ] :
y = g X C + α T X - X C + X - X C β 2 ! X - X C
式中:α β
如果输入参数的区间范围已知,且机械系统响应函数在该区间内可微,则系统响应的非概率方差Dy 可以表示为:
D y = α T C C T α + 1 4 T r a c e β C C T β C C T
D y = ∑ i = 1 n ∂ g ∂ x i 2 D X i + 1 4 ∑ i = 1 n ∑ j = 1 n ∂ 2 g ∂ x i ∂ x j 2 D X i D X j
根据式(16)可知,输入参数X i D y X i ϕ i
ϕ i = ∂ g ∂ x i 2 D X i + 1 4 ∑ i = 1 n ∑ j = 1 n ∂ 2 g ∂ x i ∂ x j 2 D X i D X j
基于上述分析,输入参数X i S i
S i = ϕ i ∑ i = 1 n ϕ i
根据非概率方差贡献率定义,可知0 ≤ S i ≤ 1 S i X i
3 基于聚类椭球模型的不确定性传播
当采用聚类椭球模型度量参数不确定性时,系统响应由确定值变为多个区间变量。为实现聚类椭球模型不确定性传播,本文将聚类椭球模型分解为多个子椭球模型,并分别对每个子椭球模型进行不确定性传播,获得对应的区间变量,最终取这些区间变量的极值作为不确定性传播结果。其传播过程可表示为:
g U = m a x X g X g L = m i n X g X s . t . X r - X r C T G r X r - X r C ≤ 1 r = 1 , 2 , ⋯ , k
式中:g U 和g L 分别为系统响应的上界和下界,r
在机械系统不确定性传播前,需对每个子椭球模型进行标准化处理,将不确定域和功能函数同时映射到δ X δ [23 ] :
X = Φ T Λ 1 / 2 δ + X C
式中:正交矩阵Φ Λ Q Q = Φ T Λ Φ
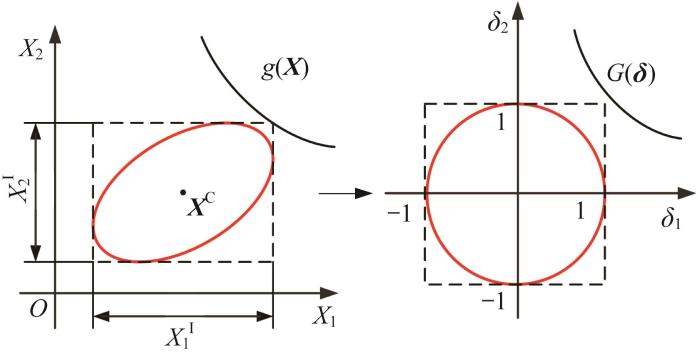
通过上述变换,n n 图2 所示。
图2
图2
椭球模型标准化过程示意图
Fig.2
Schematic diagram of standardization transformation of ellipsoidal model
PMA是一种通过给定可靠性指标求解系统响应的逆可靠度分析方法。根据凸集理论和非概率可靠性指标的几何意义,机械系统最可能失效的点与响应的极值点相同,因此可以将不确定性传播问题转化为计算最有可能失效点处的系统响应,表示为[23 ] :
m i n G δ * s . t . δ 2 = η
式中:δ * η η = 1
随后,采用序列二次规划(sequential quadratic programming, SQP)算法求解式(21)所示的优化问题,获取系统响应极值点的位置。具体步骤包括:选取初始迭代点,对约束函数进行线性化处理,对拉格朗日函数进行二次多项式近似。构建二次规划优化问题:
m i n 1 2 d T B d + ∇ G δ l T d s . t . δ l 2 + ∇ δ l 2 T ⋅ d - η = 0
式中:B d δ l l 次迭代的极值点坐标。
SQP算法通过求解二次规划子问题确定搜索方向,并基于Armijo准则计算最优步长,从而保证迭代过程的收敛性。SQP算法的计算步骤如下。
步骤1:设置初始化步长 ξ = 1 ρ , γ ∈ 0,1 ε
步骤2:求解式(22)所示的二次规划优化问题,得到搜索方向d
步骤4:采用Armijo条件计算搜索步长,如果满足G ( δ l + ξ d l ) ≤ G ( δ l ) + γ ξ ∇ G ( δ l ) T d l δ l + 1 = δ l + ξ d l ξ = ρ ξ ε
步骤5:若δ l + 1
最后,将通过SQP求得的极值点坐标由δ X k 个子响应区间,取各子响应区间的最大值为区间上边界,最小值为区间下边界。
4 算例分析
4.1 数值算例1
本算例为一个二维参数的不确定性量化问题。当样本点存在多个聚类簇时,单一椭球模型无法准确描述数据的聚集特性,降低了机械系统不确定性量化精度。为此,采用本文提出的HECM构建多个子椭球模型。不同阈值下聚类椭球模型如图3 所示。当α 1 α 2 α 1 α 2
图3
图3
算例4.1 中不同阈值下聚类椭球模型对比
Fig.3
Comparison of ellipsoidal models under different thresholds in example 4.1
当α 1 = 0.3 α 2
X 1 + 0.13 X 2 + 1.52 T 61.67 - 6.82 - 6.82 7.64 X 1 + 0.13 X 2 + 1.52 ≤ 1 X 1 + 1.41 X 2 + 0.59 T 9.06 5.11 5.11 4.63 X 1 + 1.41 X 2 + 0.59 ≤ 1 X 1 - 1.03 X 2 - 0.99 T 6.64 - 6.38 - 6.38 7.87 X 1 - 1.03 X 2 - 0.99 ≤ 1 (23)
当α 1 = 0.5 α 2
X 1 + 0.92 X 2 + 0.93 T 3.50 3.09 3.09 3.77 X 1 + 0.92 X 2 + 0.93 ≤ 1 X 1 - 1.03 X 2 - 0.99 T 6.64 - 6.38 - 6.38 7.87 X 1 - 1.03 X 2 - 0.99 ≤ 1 (24)
对于上述二维参数算例,椭球模型退化为椭圆模型。随着聚类数量的增加,模型总面积逐渐减小。不同聚类数量下模型总面积的变化情况如表1 所示。当聚类数量为3个时,δ 1
4.2 数值算例2
本算例分析一个含2维不确定性参数的系统响应函数。系统响应函数为[25 ] :
g X = X 1 s i n ω t 10 - X 2 c o s ω t (25)
图4
图4
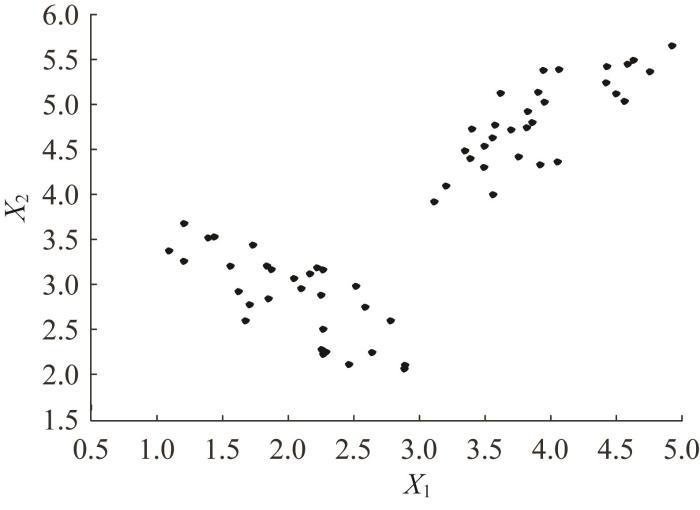
算例4.2 中不确定变量样本分布散点图
Fig.4
Scatter plot of sample distribution of uncertain variables in example 4.2
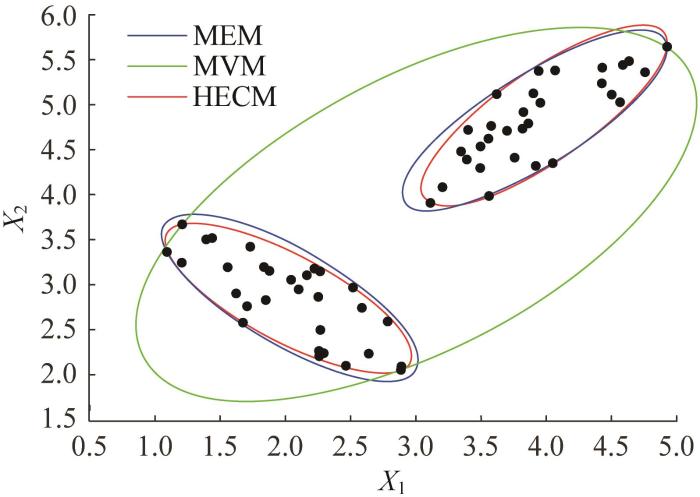
由图4 可知,样本点存在2个明显的聚类簇。为准确度量样本的不确定性,采用HECM对参数不确定性进行量化。当α 1 = 0.5 α 2
X 1 - 3.98 X 2 - 5.01 T 3.20 - 2.43 - 2.43 2.84 X 1 - 3.98 X 2 - 5.01 ≤ 1 X 1 - 2.02 X 2 - 2.98 T 2.70 2.37 2.37 3.54 X 1 - 2.02 X 2 - 2.98 ≤ 1 (26)
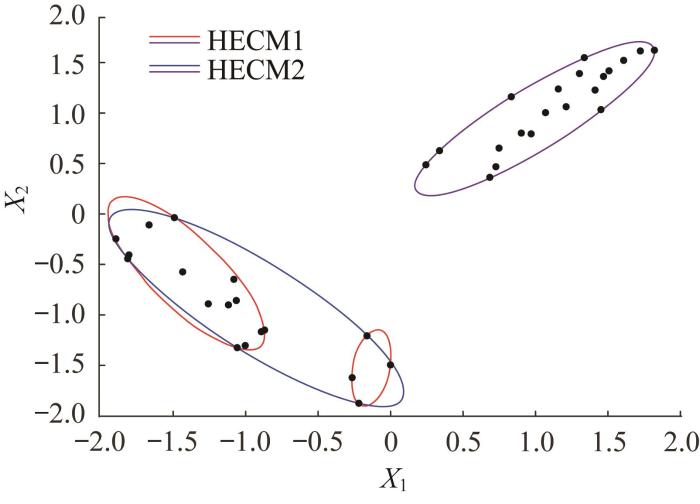
将采用HECM构造的聚类椭球模型与采用最小体积法(minimum volume method, MVM)和多模态椭球法(multimodal ellipsoid method, MEM)构建的椭球模型进行对比,结果如图5 所示。
图5
图5
算例4.2 中采用不同方法构建的椭球模型对比
Fig.5
Comparison of ellipsoid models constructed by different methods in example 4.2
基于椭球模型的特征矩阵分别计算各椭球模型总面积,结果如表2 所示。MVM在构建椭球模型时没有考虑样本分组聚集现象,提供了最保守的不确定性量化结果。MEM和HECM在处理样本聚类问题时得到了相同的分类结果,但HECM通过求解半正定规划问题构建聚类椭球模型,因此所得模型的总面积相较于MEM减少了11.04%。此算例表明采用HECM可以为分组聚集的机械系统样本提供一个准确有效的分布边界。
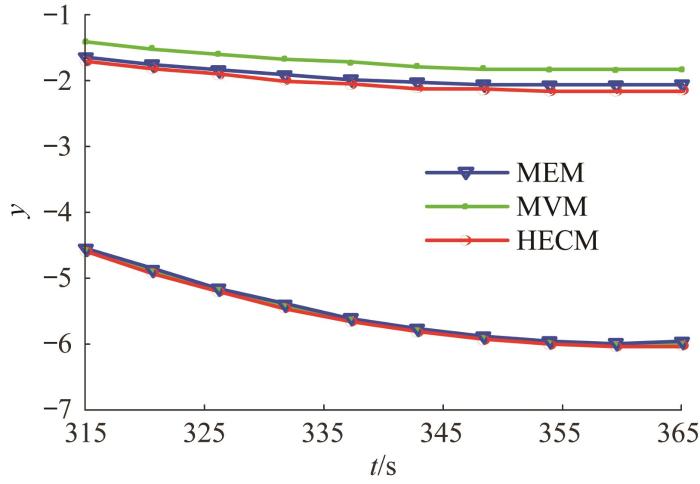
在完成参数不确定性量化后,采用PMA对所构建的椭球模型进行不确定性传播,结果如图6 所示。HECM提供了与MEM相近的区间边界,它们的不确定性传播结果均优于MVM。结果表明,在处理上述不确定性问题时,HECM和MEM具有相似的处理精度,但HECM所构建的聚类椭球模型具有更小的总面积且建模效率更高。
图6
图6
算例4.2 中不确定性传播结果
Fig.6
Uncertainty propagation results in example 4.2
4.3 数值算例3
本算例分析一个含5维不确定性参数的系统响应函数。系统响应函数为[30 ] :
g X = 31 X 1 + X 1 2 - 9 X 1 X 2 - 6 c o s X 3 + X 4 - 3 + 1 + X 2 s i n X 5 1 + 1 1 + e - X 3 / 5 - 5 X 3 2 (27)
当α 1 α 2 表3 所示。可见,针对上述5维不确定量化问题,采用HECM均得到了更加紧凑的不确定域。
完成参数不确定性量化后,基于所构建的椭球模型采用PMA进行不确定性传播,分析输入参数不确定性对系统响应的影响。为验证HECM方法的有效性,将其计算结果与MCS结果进行对比,结果如表4 所示。由表可知,PMA的不确定性传播结果与MCS结果的最大误差为1.95%,表明所提方法具有较高的计算精度。采用HECM构建的聚类椭球模型相较于MVM和MEM得到了更紧凑的响应区间,进一步说明了HECM在处理分组聚集问题时的优越性。
4.4 雷达系统工程算例
雷达系统服役环境复杂,且受多源不确定性因素的影响。这些复杂因素会干扰雷达信号的发射和接收,导致探测结果产生偏差。为评估系统参数不确定性对雷达探测性能的影响,本文采用HECM对雷达系统最大探测距离进行不确定性分析。雷达系统最大探测距离指雷达系统能发现目标的最远距离,其直接反映了雷达系统的探测能力。雷达系统最大探测距离R m a x [31 ] :
R m a x = P t ⋅ G t ⋅ G r ⋅ σ ⋅ λ 2 ⋅ τ 1.38 × 10 - 23 ⋅ 4 π 3 ⋅ T 0 ⋅ F n ⋅ L 4 (28)
式中:P t 为雷达发射功率;G t 为雷达发射增益;G r 为雷达接收增益;σ λ τ T 0 F n 为噪声系数;L
由于雷达系统存在不确定性,雷达发射的电磁信号与预设信号之间可能存在偏差。同时,电磁信号在雷达系统内部传输过程中存在损耗,导致雷达参数在一定范围内波动。雷达参数的数值区间如表5 所示[32 ] 。
为评估上述不确定性参数对雷达探测距离的影响程度,基于区间变量开展系统参数敏感性分析,计算各输入参数的非概率方差贡献率,结果如表6 所示。根据贡献率大小对输入参数进行重要性排序,即对最大探测距离的影响由大到小依次是信号频率、发射功率、综合损耗、发射增益、接收增益、脉冲宽度。采用Sobol’法计算各输入参数的敏感性指标值,得到的输入参数重要性排序与基于区间变量的敏感性分析结果一致。
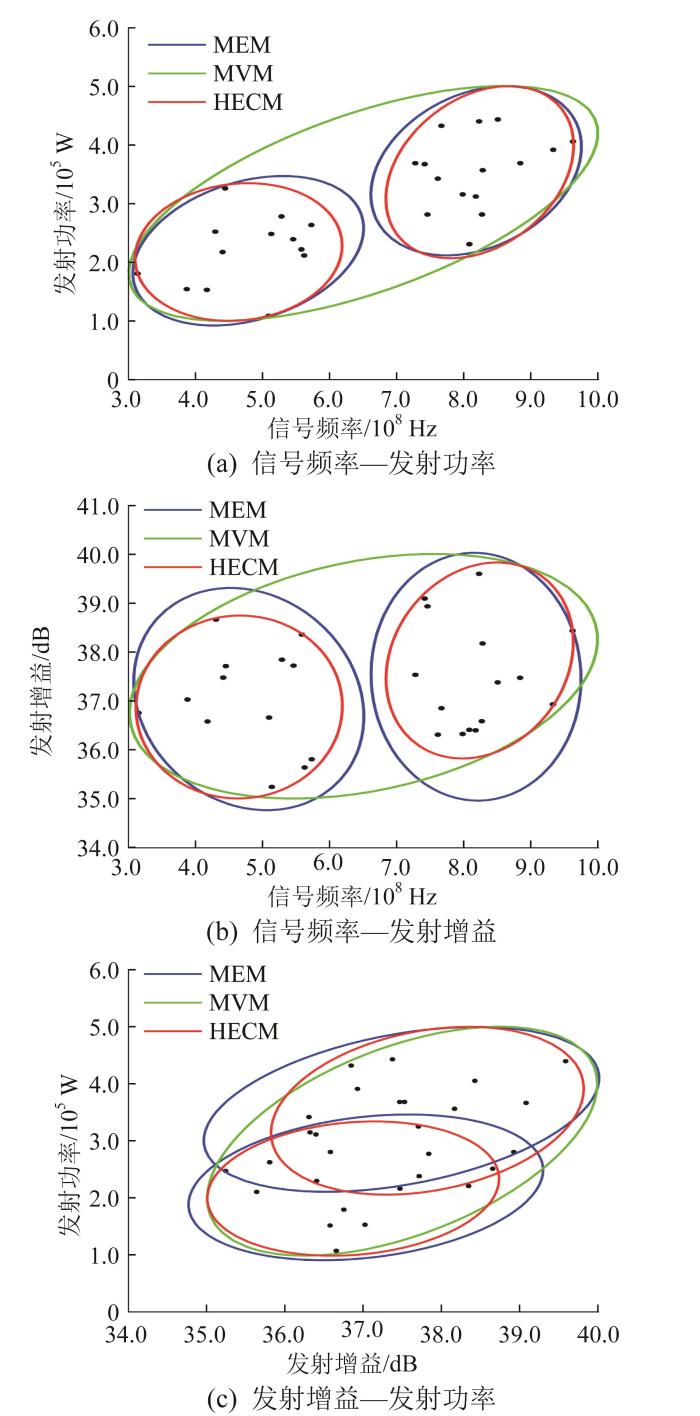
本文将信号频率、发射功率和发射增益作为雷达系统的3个不确定性输入参数,并根据样本信息构建椭球模型,结果如图7 所示。
图7
图7
雷达系统椭球模型
Fig.7
Radar system ellipsoidal models
通过比较MEM、MVM和HECM所构建的椭球模型可知,HECM充分考虑了雷达参数样本数据的分组聚集现象,得到了更紧凑的椭球模型。MEM在构建椭球模型时,采用高斯混合模型计算椭球形状矩阵,在处理小样本问题时,其计算精度无法保证,导致椭球模型的边界相对保守。采用HECM得到的椭球模型表达式为:
X 1 - 4.64 X 2 - 2.17 X 3 - 36.87 T 0.42 - 0.05 0.00 - 0.05 0.75 - 0.07 0.00 - 0.07 0.29 X 1 - 4.64 X 2 - 2.17 X 3 - 36.87 < 1 X 1 - 8.23 X 2 - 3.53 X 3 - 37.82 T 0.57 - 0.15 - 0.05 - 0.15 0.54 - 0.08 - 0.05 - 0.08 0.27 X 1 - 8.23 X 2 - 3.53 X 3 - 37.82 < 1 (29)
为评估雷达参数不确定性对最大探测距离的影响,基于上述椭球模型采用PMA计算雷达最大探测距离的区间边界,并将结果与MCS计算结果进行比较,结果如表7 所示。
对于HECM构建的聚类椭球模型,采用PMA计算得到的雷达最大探测距离的区间为[265 133, 455 757] m,与MCS计算结果相比,上边界和下边界的相对误差分别为0.02%和0.06%。采用MEM和MVM构建椭球模型时,MCS计算得到的区间分别为[250 062, 468 388] m、[257 110, 457 046] m。相较于MEM和MVM,HECM在雷达系统不确定性传播的应用中表现出更高的准确性,证明了HECM在雷达系统不确定性分析中的优势。
5 结 论
本文基于超椭球聚类算法提出了一种新的聚类椭球模型,并将其应用于雷达系统不确定性传播等算例。主要结论如下:
1)采用所提出的HECM,结合自适应聚类数选取策略,在处理小样本问题时,得到了比MEM更精准的量化结果,为后续不确定性传播提供了基础。
2)对于多源不确定性参数耦合导致不确定性传播分析效率低的问题,基于区间变量对机械系统响应进行敏感性分析,实现了多维参数对关键性能影响的重要性排序,降低了不确定性分析的复杂度。
3)采用PMA和SQP算法获取机械系统响应区间的上、下边界。对于雷达系统不确定性传播问题,采用所提出的HECM得到的不确定性传播结果与MCS计算结果相比最大误差为0.06%,表明HECM具有良好的精度和工程适用性。
参考文献
View Option
[1]
OUYANG H LIU J HAN X et al Non-probabilistic uncertain inverse problem method considering correlations for structural parameter identification
[J]. Structural and Multidisciplinary Optimization , 2021 , 64 (3 ): 1327 -1342 .
[本文引用: 1]
[2]
ZHANG D Q SHEN S S JIANG C et al An advanced mixed-degree cubature formula for reliability analysis
[J]. Computer Methods in Applied Mechanics and Engineering , 2022 , 400 : 115521 .
[3]
赵子达 , 张德权 , 欧阳衡 , 等 径向基函数-稀疏多项式混沌展开混合代理模型可靠性分析方法
[J]. 机械强度 , 2023 , 45 (5 ): 1108 -1116 .
ZHAO Z D ZHANG D Q OUYANG H et al Reliability analysis on hybrid surrogate model of radial basis function and sparse polynomial chaos expansion
[J]. Journal of Mechanical Strength , 2023 , 45 (5 ): 1108 -1116 .
[4]
JIANG C HAN X LU G Y et al Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique
[J]. Computer Methods in Applied Mechanics and Engineering , 2011 , 200 (33/34/35/36 ): 2528 -2546 .
[本文引用: 3]
[5]
刘浩 , 刘杰 , 姜潮 , 等 基于凸模型和伪概率分布的不确定性结构响应分析
[J]. 固体力学学报 , 2015 , 36 (6 ): 537 -543 .
[本文引用: 1]
LIU H LIU J JIANG C et al Uncertainty analysis of structural response based on convex model and pseudo-probability distribution
[J]. Chinese Journal of Solid Mechanics , 2015 , 36 (6 ): 537 -543 .
[本文引用: 1]
[6]
吕震宙 , 冯蕴雯 结构可靠性问题研究的若干进展
[J]. 力学进展 , 2000 , 30 (1 ): 21 -28 .
[本文引用: 1]
LÜ Z Z FENG Y W Advances in structural reliability studies
[J]. Advances in Mechanics , 2000 , 30 (1 ): 21 -28 .
[本文引用: 1]
[7]
ZHANG D Q JIA J K HAN Z H et al An efficient uncertainty quantification and propagation method through skewness and kurtosis fitting region
[J]. Structural and Multidisciplinary Optimization , 2023 , 66 (2 ): 36 .
[本文引用: 1]
[8]
ZHANG D Q ZHAO Z D OUYANG H et al An efficient reliability analysis method based on the improved radial basis function neural network
[J]. Journal of Mechanical Design , 2023 , 145 (8 ): 081705 .
[本文引用: 1]
[9]
[本文引用: 1]
YU M C LONG X Y Generalized probability and interval hybrid reliability analysis based on two-stage active learning Kriging model
[J]. Journal of Mechanical Engineering , 2022 , 58 (6 ): 274 -288 .
DOI:10.3901/jme.2022.06.274
[本文引用: 1]
[10]
NI B Y JIANG C HAN X An improved multidimensional parallelepiped non-probabilistic model for structural uncertainty analysis
[J]. Applied Mathematical Modelling , 2016 , 40 (7/8 ): 4727 -4745 .
[本文引用: 1]
[11]
WANG C QIU Z P Interval analysis of steady-state heat convection-diffusion problem with uncertain-but-bounded parameters
[J]. International Journal of Heat and Mass Transfer , 2015 , 91 : 355 -362 .
[本文引用: 1]
[12]
NI B Y JIANG C Interval field model and interval finite element analysis
[J]. Computer Methods in Applied Mechanics and Engineering , 2020 , 360 : 112713 .
[本文引用: 1]
[13]
WANG C MATTHIES H G Novel interval theory-based parameter identification method for engineering heat transfer systems with epistemic uncertainty
[J]. International Journal for Numerical Methods in Engineering , 2018 , 115 (6 ): 756 -770 .
[本文引用: 2]
[14]
BEN-HAIM Y A non-probabilistic concept of reliability
[J]. Structural Safety , 1994 , 14 (4 ): 227 -245 .
[本文引用: 1]
[15]
ZHU L P ELISHAKOFF I STARNES J H Derivation of multi-dimensional ellipsoidal convex model for experimental data
[J]. Mathematical and Computer Modelling , 1996 , 24 (2 ): 103 -114 .
[本文引用: 2]
[16]
JIANG C ZHANG Q F HAN X et al A non-probabilistic structural reliability analysis method based on a multidimensional parallelepiped convex model
[J]. Acta Mechanica , 2014 , 225 (2 ): 383 -395 .
[本文引用: 1]
[17]
王攀 , 臧朝平 改进的平行六面体凸模型识别动力学不确定参数区间的方法
[J]. 振动工程学报 , 2019 , 32 (1 ): 97 -106 .
[本文引用: 1]
WANG P ZANG C P Method of identifying dynamic uncertain parameter intervals with improved parallelepiped convex model
[J]. Journal of Vibration Engineering , 2019 , 32 (1 ): 97 -106 .
[本文引用: 1]
[18]
CAO L X LIU J XIE L et al Non-probabilistic polygonal convex set model for structural uncertainty quantification
[J]. Applied Mathematical Modelling , 2021 , 89 : 504 -518 .
[本文引用: 1]
[19]
刘杰 , 谢凌 , 卿宏军 , 等 基于主成分分析的结构不确定性建模与传播研究
[J]. 计算力学学报 , 2017 , 34 (4 ): 411 -416 .
[本文引用: 1]
LIU J XIE L QING H J et al Structural uncertainty modeling and propagation based on principal component analysis
[J]. Chinese Journal of Computational Mechanics , 2017 , 34 (4 ): 411 -416 .
[本文引用: 1]
[20]
KANG Z ZHANG W B Construction and application of an ellipsoidal convex model using a semi-definite programming formulation from measured data
[J]. Computer Methods in Applied Mechanics and Engineering , 2016 , 300 : 461 -489 .
[本文引用: 2]
[21]
JIANG C ZHANG Q F HAN X et al Multidimensional parallelepiped model: a new type of non-probabilistic convex model for structural uncertainty analysis
[J]. International Journal for Numerical Methods in Engineering , 2015 , 103 (1 ): 31 -59 .
[本文引用: 1]
[22]
LI K LIU H W Structural reliability analysis by using non-probabilistic multi-cluster ellipsoidal model
[J]. Entropy , 2022 , 24 (9 ): 1209 .
[本文引用: 1]
[23]
刘浩 , 杨开云 , 张德权 基于聚类椭球模型的不确定性传播分析
[J]. 计算力学学报 , 2018 , 35 (4 ): 431 -436 .
[本文引用: 3]
LIU H YANG K Y ZHANG D Q Uncertain propagation based on the cluster-ellipsoid model
[J]. Chinese Journal of Computational Mechanics , 2018 , 35 (4 ): 431 -436 .
[本文引用: 3]
[24]
WANG C MATTHIES H G A modified parallelepiped model for non-probabilistic uncertainty quantification and propagation analysis
[J]. Computer Methods in Applied Mechanics and Engineering , 2020 , 369 : 113209 .
[本文引用: 1]
[25]
LIU J YU Z B ZHANG D Q et al Multimodal ellipsoid model for non-probabilistic structural uncertainty quantification and propagation
[J]. International Journal of Mechanics and Materials in Design , 2021 , 17 (3 ): 633 -657 .
[本文引用: 2]
[26]
PANDA S K JANA P K Efficient task scheduling algorithms for heterogeneous multi-cloud environment
[J]. The Journal of Supercomputing , 2015 , 71 (4 ): 1505 -1533 .
[本文引用: 1]
[27]
LEE H YOO J H PARK D Data clustering method using a modified Gaussian kernel metric and kernel PCA
[J]. ETRI Journal , 2014 , 36 (3 ): 333 -342 .
[本文引用: 1]
[28]
欧阳衡 基于相关性分析的结构不确定性传播与计算反求方法研究
[D]. 长沙 : 湖南大学 , 2020 : 16 -37 .
[本文引用: 3]
OUYANG H Research on structural uncertainty propagation and computational inverse methods based on correlation analysis
[D]. Changsha : Hunan University , 2020 : 16 -37 .
[本文引用: 3]
[29]
OUYANG H WANG H Y LIU J et al Non-probabilistic sensitivity analysis method for multi-input-multi-output structures considering correlations
[J]. International Journal of Mechanical Sciences , 2024 , 271 : 109123 .
[本文引用: 1]
[30]
WANG C QIANG X FAN H R et al Novel data-driven method for non-probabilistic uncertainty analysis of engineering structures based on ellipsoid model
[J]. Computer Methods in Applied Mechanics and Engineering , 2022 , 394 : 114889 .
[本文引用: 1]
[31]
丁鹭飞 , 耿富禄 , 陈建春 雷达原理 [M]. 4版 . 西安 : 西安电子科技大学出版社 , 2020 : 163 -167 .
[本文引用: 1]
DING L F GENG F L CHEN J C Principles of radar [M]. Xi'an : Xidain University Press , 2002 : 163 -167 .
[本文引用: 1]
[32]
欧阳衡 , 高硕 , 王世涛 , 等 基于子区间的雷达探测距离和测距精度分析
[J]. 工程设计学报 , 2024 , 31 (3 ): 332 -339 .
[本文引用: 1]
OUYANG H GAO S WANG S T et al Analysis of radar detection distance and ranging accuracy based on subinterval
[J]. Chinese Journal of Engineering Design , 2024 , 31 (3 ): 332 -339 .
[本文引用: 1]
Non-probabilistic uncertain inverse problem method considering correlations for structural parameter identification
1
2021
... 在机械系统设计阶段,面临着多种多样不确定性因素,如几何尺寸、材料属性和外部载荷等[1 -4 ] .这些不确定性因素的耦合作用会使系统响应出现随机偏差,难以保障其运行平稳性和工作可靠性[5 ] .因此,准确量化机械系统参数的不确定性水平,并合理评估不确定性对系统响应的影响,对机械系统的设计与优化具有重要意义. ...
An advanced mixed-degree cubature formula for reliability analysis
0
2022
径向基函数-稀疏多项式混沌展开混合代理模型可靠性分析方法
0
2023
径向基函数-稀疏多项式混沌展开混合代理模型可靠性分析方法
0
2023
Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique
3
2011
... 在机械系统设计阶段,面临着多种多样不确定性因素,如几何尺寸、材料属性和外部载荷等[1 -4 ] .这些不确定性因素的耦合作用会使系统响应出现随机偏差,难以保障其运行平稳性和工作可靠性[5 ] .因此,准确量化机械系统参数的不确定性水平,并合理评估不确定性对系统响应的影响,对机械系统的设计与优化具有重要意义. ...
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
... 协方差矩阵则通过求解包络样本点的最小体积椭球获得.对于给定的样本集,存在无数个完全包含样本点的椭球.为寻找最小体积椭球,根据椭球的几何特征,构建如下优化问题[4 ] : ...
基于凸模型和伪概率分布的不确定性结构响应分析
1
2015
... 在机械系统设计阶段,面临着多种多样不确定性因素,如几何尺寸、材料属性和外部载荷等[1 -4 ] .这些不确定性因素的耦合作用会使系统响应出现随机偏差,难以保障其运行平稳性和工作可靠性[5 ] .因此,准确量化机械系统参数的不确定性水平,并合理评估不确定性对系统响应的影响,对机械系统的设计与优化具有重要意义. ...
基于凸模型和伪概率分布的不确定性结构响应分析
1
2015
... 在机械系统设计阶段,面临着多种多样不确定性因素,如几何尺寸、材料属性和外部载荷等[1 -4 ] .这些不确定性因素的耦合作用会使系统响应出现随机偏差,难以保障其运行平稳性和工作可靠性[5 ] .因此,准确量化机械系统参数的不确定性水平,并合理评估不确定性对系统响应的影响,对机械系统的设计与优化具有重要意义. ...
结构可靠性问题研究的若干进展
1
2000
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
结构可靠性问题研究的若干进展
1
2000
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
An efficient uncertainty quantification and propagation method through skewness and kurtosis fitting region
1
2023
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
An efficient reliability analysis method based on the improved radial basis function neural network
1
2023
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
基于两阶段主动学习Kriging模型的广义概率区间混合可靠性分析
1
2022
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
基于两阶段主动学习Kriging模型的广义概率区间混合可靠性分析
1
2022
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
An improved multidimensional parallelepiped non-probabilistic model for structural uncertainty analysis
1
2016
... 机械系统的不确定性根据其来源和性质可分为随机不确定性和认知不确定性[6 ] .其中:随机不确定性数据量大,且服从一定概率分布,常采用概率模型对该不确定性进行度量,至今已发展出一系列不确定性评估方法,如直接采样法、局部近似法和数值积分法等,来获取系统响应的统计特性[7 -8 ] .而机械系统的认知不确定性由于信息不完善、样本数据匮乏等问题,难以获取不确定性参数准确的概率分布,限制了概率模型的应用[9 ] .为了有效量化机械系统参数的认知不确定性,非概率凸模型受到了广泛关注[10 ] . ...
Interval analysis of steady-state heat convection-diffusion problem with uncertain-but-bounded parameters
1
2015
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Interval field model and interval finite element analysis
1
2020
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Novel interval theory-based parameter identification method for engineering heat transfer systems with epistemic uncertainty
2
2018
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
... [13 ].然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
A non-probabilistic concept of reliability
1
1994
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Derivation of multi-dimensional ellipsoidal convex model for experimental data
2
1996
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
... [15 ]、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
A non-probabilistic structural reliability analysis method based on a multidimensional parallelepiped convex model
1
2014
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
改进的平行六面体凸模型识别动力学不确定参数区间的方法
1
2019
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
改进的平行六面体凸模型识别动力学不确定参数区间的方法
1
2019
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Non-probabilistic polygonal convex set model for structural uncertainty quantification
1
2021
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
基于主成分分析的结构不确定性建模与传播研究
1
2017
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
基于主成分分析的结构不确定性建模与传播研究
1
2017
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Construction and application of an ellipsoidal convex model using a semi-definite programming formulation from measured data
2
2016
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
... 为提高计算效率,根据椭球协方差矩阵的性质对其进行特征值分解,可得到G = A T A A n 阶正定矩阵.此时椭球体积正比于d e t A - 1 式(4) 可转化为[20 ] : ...
Multidimensional parallelepiped model: a new type of non-probabilistic convex model for structural uncertainty analysis
1
2015
... 非概率凸模型采用参数的边界信息描述其不确定性,避免了概率模型对参数分布函数的依赖,因此在分析认知不确定性时具有明显优势[11 -12 ] .近年来,许多学者对非概率凸模型进行了研究,发展出了区间模型[13 -14 ] 、椭球模型[15 ] 、平行六面体凸模型[16 -17 ] 、多边凸集模型[18 -19 ] 等一系列方法.区间模型通过区间变量的上、下边界度量机械系统参数的不确定性[13 ] .然而,当采用区间模型处理具有相关性的不确定性参数时,可能会导致最终量化结果过于保守,从而造成资源浪费.椭球模型通过椭球的半轴长和姿态角度量参数的相关性和不确定性,更符合工程实际需求状况.目前椭球模型建模方法主要有最小体积法[15 ] 、相关性近似法[4 ] 和半定规划法[20 ] 等.随着研究的深入,相关学者发现椭球模型在处理同时包含独立参数和相关参数的工程问题时,存在无法精确度量的情况.为此,Jiang等[21 ] 提出了一种更加符合样本分布状况的平行六面体凸模型,将独立参数与相关参数纳入同一框架下进行度量. ...
Structural reliability analysis by using non-probabilistic multi-cluster ellipsoidal model
1
2022
... 上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] .为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性.Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题.Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性.上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度. ...
基于聚类椭球模型的不确定性传播分析
3
2018
... 上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] .为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性.Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题.Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性.上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度. ...
... 在机械系统不确定性传播前,需对每个子椭球模型进行标准化处理,将不确定域和功能函数同时映射到δ X δ [23 ] : ...
... PMA是一种通过给定可靠性指标求解系统响应的逆可靠度分析方法.根据凸集理论和非概率可靠性指标的几何意义,机械系统最可能失效的点与响应的极值点相同,因此可以将不确定性传播问题转化为计算最有可能失效点处的系统响应,表示为[23 ] : ...
基于聚类椭球模型的不确定性传播分析
3
2018
... 上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] .为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性.Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题.Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性.上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度. ...
... 在机械系统不确定性传播前,需对每个子椭球模型进行标准化处理,将不确定域和功能函数同时映射到δ X δ [23 ] : ...
... PMA是一种通过给定可靠性指标求解系统响应的逆可靠度分析方法.根据凸集理论和非概率可靠性指标的几何意义,机械系统最可能失效的点与响应的极值点相同,因此可以将不确定性传播问题转化为计算最有可能失效点处的系统响应,表示为[23 ] : ...
A modified parallelepiped model for non-probabilistic uncertainty quantification and propagation analysis
1
2020
... 上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] .为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性.Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题.Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性.上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度. ...
Multimodal ellipsoid model for non-probabilistic structural uncertainty quantification and propagation
2
2021
... 上述研究采用单一非概率凸模型度量参数不确定性,无法准确描述参数的分组聚集现象[22 ] .为解决这一问题,刘浩等[23 ] 提出了一种考虑参数聚类特性的不确定性分析方法,提高了不确定性量化的准确性.Wang等[24 ] 基于样本的统计特征,提出了一种子平行六面体模型,解决了平行六面体凸模型在处理分组样本时模型内部出现无样本区域的问题.Liu等[25 ] 采用高斯混合模型获取样本聚类信息,并根据聚类结果构建聚类椭球模型,以量化参数的不确定性.上述研究表明,通过引入参数聚类分组策略,可以有效提升非概率凸模型的量化精度. ...
... 本算例分析一个含2维不确定性参数的系统响应函数.系统响应函数为[25 ] : ...
Efficient task scheduling algorithms for heterogeneous multi-cloud environment
1
2015
... 由于机械系统各参数表征的物理意义不同,参数数量级常存在差异.若直接使用原始数据求解样本的分布特征,会严重影响分析精度,甚至导致聚类结果出现错误.因此,在提取样本分布特征前,采用归一化方法对样本数据进行预处理,将其转换到[0, 1]区间,以消除机械系统参数数量级差异对聚类结果的影响.具体计算公式如下所示[26 ] : ...
Data clustering method using a modified Gaussian kernel metric and kernel PCA
1
2014
... 在对数据进行聚类分析时,选择合适的距离度量方法对聚类结果的准确性至关重要.与欧氏距离相比,马氏距离能够通过协方差矩阵反映样本特征间的相关性,可以更准确地捕捉数据的内在特征[27 ] .因此,本研究采用马氏距离度量样本的相关性.马氏距离D 可以表示为: ...
基于相关性分析的结构不确定性传播与计算反求方法研究
3
2020
... 为评估不确定性参数对系统响应的影响程度,本小节采用参数的上、下边界构造区间变量,实现参数不确定性量化,并分析参数不确定性对系统响应的非概率方差贡献率.区间变量可表示为[28 ] : ...
... 当实验样本都位于区间变量 X I 内时,机械系统的不确定性可通过区间下界 X L 和区间上界 X U 来表示.为方便描述,定义区间变量中点 X C 和半径 X W 分别为[28 ] : ...
... 区间中点 X C 表示参数的名义值,区间半径 X W 反映参数的不确定性大小.同时定义参数X i DX 为[28 ] : ...
基于相关性分析的结构不确定性传播与计算反求方法研究
3
2020
... 为评估不确定性参数对系统响应的影响程度,本小节采用参数的上、下边界构造区间变量,实现参数不确定性量化,并分析参数不确定性对系统响应的非概率方差贡献率.区间变量可表示为[28 ] : ...
... 当实验样本都位于区间变量 X I 内时,机械系统的不确定性可通过区间下界 X L 和区间上界 X U 来表示.为方便描述,定义区间变量中点 X C 和半径 X W 分别为[28 ] : ...
... 区间中点 X C 表示参数的名义值,区间半径 X W 反映参数的不确定性大小.同时定义参数X i DX 为[28 ] : ...
Non-probabilistic sensitivity analysis method for multi-input-multi-output structures considering correlations
1
2024
... 将机械系统响应函数进行二阶泰勒展开,并忽略高阶项,则其数学表达式为[29 ] : ...
Novel data-driven method for non-probabilistic uncertainty analysis of engineering structures based on ellipsoid model
1
2022
... 本算例分析一个含5维不确定性参数的系统响应函数.系统响应函数为[30 ] : ...
1
2002
... 雷达系统服役环境复杂,且受多源不确定性因素的影响.这些复杂因素会干扰雷达信号的发射和接收,导致探测结果产生偏差.为评估系统参数不确定性对雷达探测性能的影响,本文采用HECM对雷达系统最大探测距离进行不确定性分析.雷达系统最大探测距离指雷达系统能发现目标的最远距离,其直接反映了雷达系统的探测能力.雷达系统最大探测距离R m a x [31 ] : ...
1
2002
... 雷达系统服役环境复杂,且受多源不确定性因素的影响.这些复杂因素会干扰雷达信号的发射和接收,导致探测结果产生偏差.为评估系统参数不确定性对雷达探测性能的影响,本文采用HECM对雷达系统最大探测距离进行不确定性分析.雷达系统最大探测距离指雷达系统能发现目标的最远距离,其直接反映了雷达系统的探测能力.雷达系统最大探测距离R m a x [31 ] : ...
基于子区间的雷达探测距离和测距精度分析
1
2024
... 由于雷达系统存在不确定性,雷达发射的电磁信号与预设信号之间可能存在偏差.同时,电磁信号在雷达系统内部传输过程中存在损耗,导致雷达参数在一定范围内波动.雷达参数的数值区间如表5 所示[32 ] . ...
基于子区间的雷达探测距离和测距精度分析
1
2024
... 由于雷达系统存在不确定性,雷达发射的电磁信号与预设信号之间可能存在偏差.同时,电磁信号在雷达系统内部传输过程中存在损耗,导致雷达参数在一定范围内波动.雷达参数的数值区间如表5 所示[32 ] . ...