工程设计学报

工程设计学报, 2024, 31(6): 810-822 doi: 10.3785/j.issn.1006-754X.2024.04.112

优化设计

基于结构功能衍生系数的桥式起重机金属结构优化设计

董青,,, 张天祥, 戚其松, 徐格宁

太原科技大学 机械工程学院，山西 太原 030024

Optimization design of metal structure of bridge crane based on structural function derivative coefficients

DONG Qing,,, ZHANG Tianxiang, QI Qisong, XU Gening

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China

收稿日期: 2024-02-19   修回日期: 2024-04-21  

基金资助: 国家自然科学基金资助项目.  52105269

First author contact: DONG Q, ZHANG T X, QI Q S, et al. Optimization design of metal structure of bridge crane based on structural function derivative coefficients[J]. Chinese Journal of Engineering Design, 2024, 31(6): 810-822.

Received: 2024-02-19   Revised: 2024-04-21  

作者简介 About authors

董青（1989—），女，副教授，博士，从事重大装备数字孪生、疲劳寿命预测、安全评估、报废决策及其相关专业软件开发等研究，E-mail:qingdong@tyust.edu.cn,https://orcid.org/0009-0004-7653-1673 , E-mail：qingdong@tyust.edu.cn

摘要

起重机是八大特种设备之一，其结构设计的合理性对于设备安全运行、提质增效至关重要。为此，提出了一种基于结构功能衍生系数的桥式起重机金属结构优化设计方法。首先，利用解释结构模型准确描述了起重机不同零部件之间的相互作用和影响关系，分析了起重机结构的复杂性，识别出对起重机金属结构强度影响较大的参数并对其进行优化设计；其次，在有限元仿真的基础上，将结构功能衍生系数与拟合函数相结合，寻找出最佳的设计参数组合；最后，以300/100 t-30 m通用桥式起重机为工程实例，通过仿真使整机的质量减小了2 035.113 kg，验证了所提方法的有效性。基于结构功能衍生系数的起重机金属结构优化设计方法，解决了传统的优化方法中忽略了起重机各零部件之间复杂的相互作用的问题，可在确保起重机服役安全性的基础上实现其金属结构的轻量化设计。

关键词： 解释结构模型 ; 结构功能衍生系数 ; 优化设计 ; 桥式起重机 ; 金属结构

Abstract

Crane is one of the eight special equipment, the rationality of its structural design is crucial for the safe operation, quality improvement, and efficiency enhancement of the equipment. Therefore, an optimization design method of metal structure of bridge crane based on structural function derivative coefficients was proposed. Firstly, the interpretive structure model was used to accurately describe the interactions and influence relationships between different parts of the crane, the structure complexity of the crane was analyzed to identify and optimize the parameters that had a significant impact on the strength of metal structure of the crane. Secondly, based on the finite element simulation, the structural function derivative coefficients were combined with fitting functions to find the optimal combination of design parameters. Finally, a 300/100 t-30 m bridge crane was taken as an engineering example, and the mass of the whole crane was reduced by 2 035.113 kg through simulation, and the effectiveness of the proposed method was verified. The optimization design method of metal structure of crane based on structural function derivative coefficients solves the problem that the complex interactions between various parts of crane is ignored in the traditional optimization method, and can realize the lightweight design of metal structure on the basis of ensuring the safety of crane service.

Keywords： interpretative structure model ; structural functional derivative coefficient ; optimization design ; bridge crane ; metal structure

PDF (3568KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

董青, 张天祥, 戚其松, 徐格宁. 基于结构功能衍生系数的桥式起重机金属结构优化设计[J]. 工程设计学报, 2024, 31(6): 810-822 doi:10.3785/j.issn.1006-754X.2024.04.112

DONG Qing, ZHANG Tianxiang, QI Qisong, XU Gening. Optimization design of metal structure of bridge crane based on structural function derivative coefficients[J]. Chinese Journal of Engineering Design, 2024, 31(6): 810-822 doi:10.3785/j.issn.1006-754X.2024.04.112

起重机械是工业、建筑等领域的关键设备，其结构设计对于整机的承载性能和安全运行至关重要。同时，随着实际工程对大吨位、高性能、小质量起重机需求的增长，起重机优化设计已成为行业关注的重点。

目前，国内外学者针对起重机结构设计及轻量化设计的研究已取得一定的成果。如：邢伟等[1]基于有限元理论和拓扑优化方法，通过理论建模、静力学计算和拓扑计算对起重机悬臂梁的质量进行优化，优化后其结构性能和经济性能都能满足工程要求；林伟等[2-4]采取改进鼠群优化等多种算法，实现了起重机主梁的轻量化设计；翁飞翔等[5-7]采取稳健优化等多种优化方法，在确保起重机结构可靠性的同时，显著减小了体积；甘盛霖等[8]的研究聚焦于改善起重机支座的应力分布；陈国雄等[9]结合有限元法与遗传算法，进行了龙门架结构多目标优化设计，取得了较高的求解效率；张磊等[10]通过Inspire和ANSYS软件对起重机伸臂上盖板和腹板的厚度进行尺寸优化；黄镇等[11-17]基于数据集训练预测模型及采用多种优化方法对起重机结构进行了优化，展现了各自方法的有效性和优越性。总体来看，这些研究为起重机结构优化设计提供了多样化的解决方案。

传统的起重机结构优化方法通常侧重于对特定设计参数的调整，而忽略了起重机各零部件之间复杂的相互作用关系。本文通过引入解释结构模型和结构功能衍生系数，提出一种能够准确捕捉起重机各零部件功能与设计参数之间关系的优化设计方法，从而求解最佳的设计参数组合，在确保起重机整机安全性的基础上，实现其金属结构的轻量化设计。

1 起重机金属结构优化设计流程

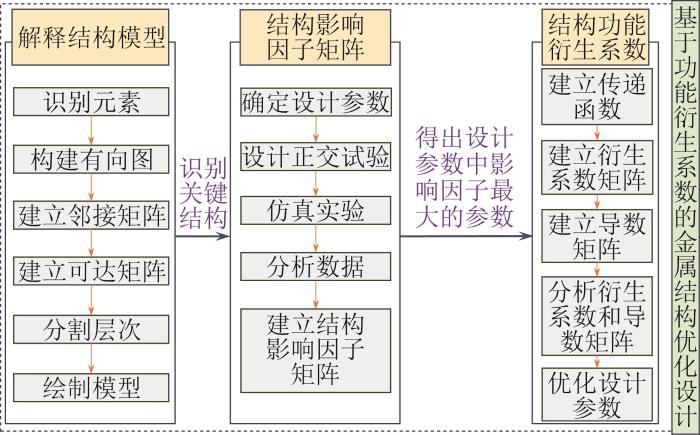
起重机金属结构设计的合理性对于设备安全运行、提质增效至关重要。为此，本文以桥式起重机（以下简称起重机）为研究对象，以轻量化其金属结构为目标，采用解释结构模型和结构耦合方法，提出基于结构功能衍生系数的起重机金属结构优化设计方法。优化设计的流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   起重机金属结构优化设计流程图

Fig.1   Optimization design flow chart of metal structure of crane


基于结构功能衍生系数的起重机金属结构优化设计流程为：首先，建立起重机的解释结构模型，分析起重机的复杂组成和运作原理，识别出影响力较大的关键结构；其次，针对关键结构进行正交试验和方差分析，建立结构影响因子矩阵，揭示不同零部件之间的耦合关系和影响程度；最后，建立传递函数，求出结构功能衍生系数，确定各个设计参数对起重机结构强度的影响趋势并进行参数优化设计，实现起重机整机的轻量化。

2 解释结构模型

起重机作为一个完整的复杂系统，由具有特定功能的机构组成，包括起升机构、运行机构、金属结构、控制系统及安全装置等，如图2所示。在整个系统中，机构内部各零部件之间存在着直接或间接的连接关系，不同的连接关系使零部件间相互依赖、相互影响、相互制约。相较于表格、文字、数学公式等描述方式，解释结构模型（interpretative structure model, ISM）具有显著优势。它以层级拓扑图的形式展示系统，具有直观性[18]。因此，从机构组成及其关联关系的角度，深入了解起重机的结构功能，可以更好地进行产品的设计和优化，在满足特定功能需求的基础上，提高起重机的安全性、可靠性，实现其绿色化。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   起重机组成

Fig.2   Composition of crane


ISM能够全面表示复杂系统的内在结构和机制，通过图形化的方式展示系统元素之间的因果关系，使得分析结果更加直观和易于理解。将系统分解为不同层次，有助于分析系统内部的层级结构和关联关系，清晰地解释系统内各元素之间的影响关系[19]。为了分析起重机零部件之间复杂的依赖关系，确定各元素之间的层次和相互影响规律，将ISM应用于起重机的结构分析上。其具体分析步骤如下：

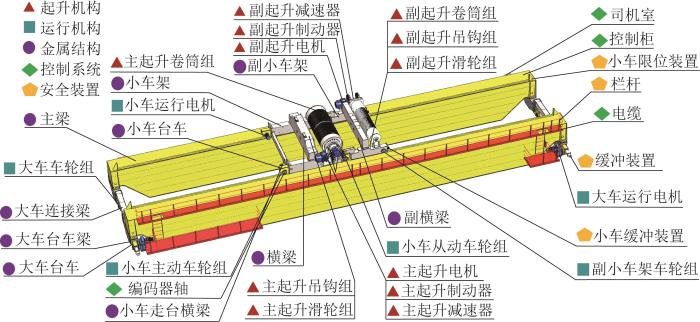
1）识别元素。识别和定义起重机相关元素，包括但不限于起升机构、大车运行机构、小车运行机构、桥架结构、小车架结构、钢丝绳、滑轮组、传动系统、控制系统和安全装置等，具体如表1所示。

表1   起重机元素

Table 1  Elements of crane

符号元素序号元素序号元素序号元素
S1主梁S8小车从动车轮组S15副横梁S22大车主起升电机
S2大车台车梁S9副小车架车轮组S16主起升定滑轮装配S23副起升定滑轮装配
S3大车连接梁S10

小车运行电机

（三合一）

S17主起升动滑轮装配S24副起升动滑轮装配
S4大车台车S18主吊钩组S25副吊钩组
S5大车车轮组S11小车台车S19

主起升卷

筒组

S26副起升卷筒组
S6

大车运行电机

（三合一）

S12小车架S27副减速器
S13副小车架S20主减速器S28副制动器
S7小车主动车轮组S14横梁S21主制动器S29大车副起升电机

新窗口打开| 下载CSV


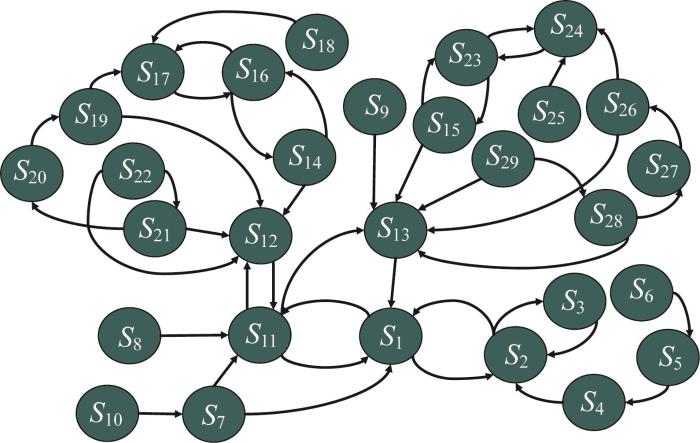
2）构建有向图。将元素成对连接来构建有向图，以此表示元素之间的相互依赖关系和影响关系，来分析系统内部结构、组织以及元素之间的相关关系。起重机初始有向图如图3所示。图中每个节点代表一个特定的元素或组件，有向边表示元素或组件之间的直接或间接关系。如：有向边从电动机指向减速器，表示电动机对减速器有直接影响。通过观察这些节点和有向边，来深入了解起重机的组织结构以及元素之间的因果关系，找到对整个系统的性能影响最大的节点，并对其进行优化设计，从而优化起重机的整体性能。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   起重机初始有向图

Fig.3   Initial digraph of crane


3）建立邻接矩阵。邻接矩阵用于表示有向图的矩阵形式。基于有向图，创建一个用于量化元素之间关联关系的矩阵，来表示每对元素之间的影响是否存在。如：起升电机对小车架和制动器有影响，则在矩阵中的相应位置标记为“1”，否则标记为“0”。起重机模型共有29个零部件，其邻接矩阵是一个29阶矩阵，即A=aij29×29，其中矩阵元素值为1的有向边集合M见式(1)，其余矩阵元素的值为0。

M=a2,1, a7,1, a11,1, a13,1, a3,2, a4,2;a2,3, a5,4, a6,5,          a10,7, a13,9, a1,11, a7,11, a8,11, a12,11, a14,12, a19,12,          a21,12, a22,12, a9,13, a11,13, a15,13, a26,13, a28,13,           a29,13, a16,14, a23,15, a14,16, a17,16, a16,17, a18,17,          a19,17, a20,19, a21,20, a22,21, a15,23, a24,23, a23,24,          a25,24, a26,24, a27,26, a28,27, a29,28=1

4）建立可达性矩阵。根据上述矩阵建立可达性矩阵，显示关系间的传递，以此显示哪些元素直接或间接地彼此影响。通过对邻接矩阵进行重复的乘法运算，逐渐扩展其路径长度，直到获得最终的可达矩阵，用于描述从一个零部件到另一个零部件是否存在路径，即是否存在一系列有向边来连接这2个零部件。若矩阵的第i行第j列的元素值为1，表示从第i个零部件到第j个零部件存在一条路径；若不存在路径，则元素值为0。可达矩阵同样是一个29阶矩阵，即B=bij29×29，其中矩阵元素值为1的有向边集合N见式(2)，其余矩阵元素的值为0，即不存在连接2个零部件的路径。

N=b1,1∼b29,1, b2,2∼b6,2, b2,3∼b6,3, b4,4∼b6,4,         b5,5, b6,5, b6,6, b7,7, b10,7, b8,8, b9,9, b13,9, b10,10,         b11,1∼b11,29, b12,1∼b12,29, b13,1∼b13,29, b9,14,         b14,14, b16,14∼b22,14, b15,15, b23,15∼b29,15, b14,16,         b16,16∼b22,16, b14,17, b16,17∼b22,17, b14,18,         b16,18∼b22,18, b19,19∼b22,19, b20,20∼b22,20,         b21,21, b22,21, b22,22, b15,23, b23,23∼b29,23, b15,24,         b24,24∼b29,24, b25,25, b26,26∼b29,26, b27,27∼b29,27,         b28,28, b29,28,b29,29=1

式中：b1,1～b29,1表示b1,1，b2,1，b3,1，…，b29,1，其他同。

5）分割层次。根据可达性和影响程度，将元素划分为不同的层次，形成层次结构，其中高层元素对低层元素具有更大的影响力。由式(2)可知不存在可划分的独立区域，即系统中各元素之间都存在着某种程度的连接或依赖关系，没有一组元素可以被单独划分出来而使得它们之间的关系相对于其他部分独立。根据系统中各元素对其他元素的影响程度划分成不同的等级层次，构建起重机系统的层次结构，这有助于识别系统中的关键零部件，在优化起重机性能时可以重点关注对整个系统有较大影响的级别较高的部件。

层次分割的步骤为：①建立可达集。可达集是指从一个零部件出发，通过有向边能够到达的所有零部件的集合。若一个零部件的可达集很大，表示它能够直接或间接影响其他许多零部件，可能在系统中具有重要的影响力或控制权。起重机元素的可达集如表2所示。②建立先行集。先行集是指一个零部件所有直接或间接前驱零部件的集合，包括其本身。通过建立先行集，可了解一个零部件对哪些零部件具有依赖关系，即哪些零部件对该零部件的行为、决策具有直接或间接的影响。若一个零部件的先行集很大，表示它依赖于许多其他结构的输入或决策。起重机元素的先行集如表3所示。③根据可达集和先行集，求出可达集与先行集的共同集。④若元素的共同集与可达集相等，则该元素为第1级元素。⑤求出第1级元素后，求出去掉第1级元素后剩余元素的可达集、先行集及共同集。⑥重复上述步骤①至⑤，直至将所有元素划分完。

表2   起重机元素的可达集

Table 2  Reachable sets of elements of crane

元素序号可达集元素序号可达集元素序号可达集
S1{S1, S2, S3, S11, S12, S13}S12{S1, S2, S3, S11, S12, S13}S21

{S1, S2, S3, S11, S12, S13, S14,

S16, S17, S18, S19, S20, S21}

S2{S1, S2, S3,S11, S12, S13}
S3{S1, S2, S3, S11, S12, S13}S13{S1, S2, S3, S11, S12, S13}S22

{S1, S2, S3, S11, S12, S13, S14,

S16, S17, S18, S19, S20, S21, S22}

S4{S1, S2, S3, S4, S11, S12, S13}S14

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18}

S23{S1, S2, S3, S11, S12, S13, S15, S23, S24}
S5{S1, S2, S3, S4, S5, S11, S12, S13}S15

{S1, S2, S3, S11, S12, S13,

S15, S23, S24}

S24{S1, S2, S3, S11, S12, S13, S15, S23, S24}
S6

{S1, S2, S3, S4, S5, S6,

S11, S12, S13}

S16

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18}

S25{S1, S2, S3, S11, S12, S13, S15, S23, S24, S25}
S7{S1, S2, S3, S7, S11, S12, S13}S17

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18}

S26{S1, S2, S3, S11, S12, S13, S15, S23, S24, S26}
S8{S1, S2, S3, S8, S11, S12, S13}S18

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18}

S27

{S1, S2, S3, S11, S12, S13, S15,

S23, S24, S26, S27}

S9

{S1, S2, S3, S9, S11, S12,

S13, S14, S16, S17, S18}

S19

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18, S19}

S28{S1, S2, S3, S11, S12, S13, S15, S23,S24, S26, S27, S28}
S10{S1, S2, S3, S7, S10, S11, S12, S13}S20

{S1, S2, S3, S11, S12, S13,

S14, S16, S17, S18, S19, S20}

S29

{S1, S2, S3, S11, S12, S13, S15, S23,

S24, S26, S27, S28, S29}

S11{S1, S2, S3, S11, S12, S13}

新窗口打开| 下载CSV


表3   起重机元素的先行集

Table 3  Preliminary sets of elements of crane

元素序号先行集元素序号先行集
S1{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S14{S9, S14, S16, S17, S18, S19, S20, S21, S22}
S15{S15, S23, S24, S25, S26, S27, S28, S29}
S2{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S16{S9, S14, S16, S17, S18, S19, S20, S21, S22}
S17{S9, S14, S16, S17, S18, S19, S20, S21, S22}
S3{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S18{S9, S14, S16, S17, S18, S19, S20, S21, S22}
S19{S19, S20, S21, S22}
S4{S4, S5, S6}S20{S20, S21, S22}
S5{S5, S6}S21{S21, S22}
S6{S6}S22{S22}
S7{S7, S10}S23{S15, S23, S24, S25, S26, S27, S28, S29}
S8{S8}S24{S15, S23, S24, S25, S26, S27, S28, S29}
S9{S9}S25{S25}
S10{S10}S26{S26, S27, S28, S29}
S11{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S27{S27, S28, S29}
S12{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S28{S28, S29}
S13{S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, S23, S24, S25, S26, S27, S28, S29}S29{S29}

新窗口打开| 下载CSV


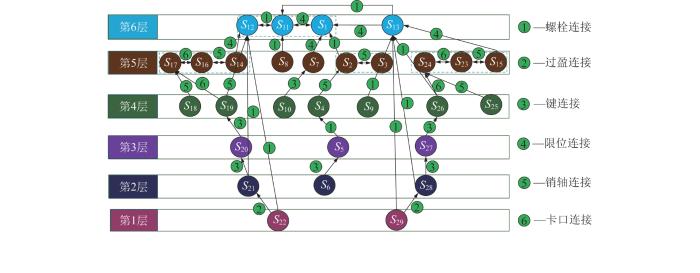
6）绘制模型。以图表或图形显示元素的层次结构和它们之间的关联关系，使系统结构的依赖关系可视化；在此基础上，建立标注连接关系代号的ISM模型，从而确定带有连接关系的有向图。基于ISM的起重机零部件层次结构及连接关系如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   基于ISM的起重机零部件层次结构及连接关系

Fig.4   Hierarchy and interconnection relationships of crane parts based on ISM


7）解释和分析。对绘制的ISM模型进行解释和分析，以识别关键元素并评估元素之间的相互影响关系。起重机零部件连接关系如表4所示。

表4   起重机零部件连接关系

Table 4  Interconnection relationships of crane parts

连接

序号

装配连接关系及尺寸符号参数传递关系符号
S22—S21主起升电机轴直径—联轴器孔径—制动器轴直径d1—Φ1—d2主起升电机输出轴转速—联轴器转速n1
S22—S12电机底座螺纹孔径—小车架固定孔径—小车架上盖板厚Φ2—Φ3—x14主起升电机转动产生力—小车架上盖板压力F1
S29—S28副起升电机轴直径—联轴器孔径—制动器轴直径d3—Φ4—d2副起升电机输出轴转速—联轴器转速n2
S29—S13电机底座螺纹孔径—小车架固定孔—小车架上盖板厚Φ5—Φ6—x14副起升电机产生的力—小车架上盖板压力F2
S21—S20联轴器孔径—减速器轴直径Φ1—d4联轴器转速—减速器输入轴转速n1
S21—S12减速器底座螺纹孔径—小车架固定孔径—小车架上盖板厚Φ8—Φ9—x14减速器转动产生的力—小车架上盖板压力F3
S6—S5大车运行电机轴直径—车轮组孔径d5—Φ10大车运行电机输出轴转速—车轮组转速n3
S28—S27副联轴器孔径—减速器孔径Φ11—Φ12副联轴器转速—减速器输入轴转速n2
S28—S13副制动器底座螺纹孔径—小车架固定孔径Φ13—Φ14副减速器转动产生的力—小车架上盖板压力F4
S20—S19主减速器输出轴直径—卷筒组孔径—卷筒轴直径d6—Φ15—d7起升减速器输出轴扭矩—卷筒扭矩M1
S5—S4大车车轮组螺纹孔直径—台车螺纹孔径—台车主副腹板厚Φ16—Φ17—x7大车车轮组支撑力—大车台车压力F5
S27—S26副减速器输出轴直径—副卷筒组孔径—副卷筒轴直径d8—Φ18—d9副起升减速器输出轴扭矩—副卷筒扭矩M2
S18—S17吊钩组孔径—主起升动滑轮组孔径—销轴直径Φ19—Φ20—d10起重量—钢丝绳抗拉强度G—σ1
S19—S17卷筒组卷筒半径—钢丝绳直经—定滑轮组滑轮半径r1—d11—r2钢丝绳上拉力—抗拉强度—抗压强度F6 —σ1—σ2
S19—S12卷筒组螺纹孔径—小车架螺纹孔径—小车架上盖板厚Φ21—Φ22—x14卷筒组压力—小车架上盖板支撑力F4
S10—S7小车运行电机轴直径—小车运行车轮组孔径d12—Φ23小车运行电机输出轴—车轮组转速n6
S4—S2大车台车连接孔径—台车梁连接孔径—销轴直径Φ24—Φ25—d13大车台车支撑力—台车梁压力F5
S9—S13副小车架车轮组螺纹孔径—副小车架螺纹孔径Φ26—Φ27副小车架车轮组支撑力—副小车架压力F7
S26—S24副卷筒组卷筒半径—钢丝绳直经—定滑轮半径r3—d14—r4副起升钢丝绳拉力—抗拉强度—卷筒抗压强度

F8—

σ3—σ4

S26—S13副卷筒组螺纹孔径—副小车架螺纹孔径Φ28—Φ29副卷筒组压力—副小车架上盖板支撑力F9
S25—S24副吊钩组孔径—副起升动滑轮组孔径—销轴直径Φ30—Φ31—d15副起重量—钢丝绳抗拉强度G2—σ3
S17—S16主起升动滑轮半径—钢丝绳直径—定滑轮半径r2—d11—r5主起升和吊钩组质量—钢丝绳抗拉强度G3—σ1
S16—S14主起升定滑轮孔径—滑轮轴直径—横梁孔径—横梁主腹板厚—横梁副腹板厚Φ32—d16—Φ33—x12—x13主起升和吊钩组滑轮组质量—钢丝绳抗拉强度—横梁抗拉强度G4—σ1—σ5
S14—S12横梁下盖板厚—小车基距—小车架上盖板厚x11—l1—x14横梁压力—小车架支撑力F10
S8—S11小车从动车轮螺纹孔径—台车螺纹孔径—台车主腹板厚Φ34—Φ35—x16小车从动车轮组支撑力—小车台车压力F11
S7—S1小车主动车轮组半径—大车主梁上盖板厚—轨距r6—x1—l2小车轮压/轨道摩擦系数—轨道摩擦力P1/u1—f
S2—S1大车台车梁螺纹孔径—大车主梁螺纹孔径—台车梁上盖板厚—主梁下盖板厚

Φ36—Φ37—

x5—x2

大车台车支撑力—主梁上产生的压力F12
S3—S2大车连接梁孔径—大车台车梁孔径—销轴直径—大车连接梁腹板厚—大车台车腹板厚

Φ38—Φ39—

d17—x7—x9

大车台车与连接梁运行过程中产生的推拉力F13
S24—S23副起升动滑轮半径—钢丝绳直径—定滑轮半径r7—d18—r8副起升和吊钩组质量—钢丝绳抗拉强度G5—σ3
S23—S15副起升定滑轮孔径—滑轮轴直径—副横梁孔径Φ40—d19—Φ41副起升量和吊钩组滑轮组质量—钢丝绳抗拉强度—横梁抗拉强度G6—σ3—σ6
S15—S13副横梁下盖板厚—小车基距—副小车架上盖板厚x11—l1—x14副横梁压力—副小车架支撑力F14
S12—S11小车架孔径—小车台车孔径—销轴直径—小车架主腹板厚—小车台车主腹板厚

Φ42—Φ43—

d20—x16—x18

小车架压力—小车台车的支撑力F15
S11—S1小车台车下盖板厚—主梁上盖板厚—轨距x17—x1—l2从动小车轮组轮压/轨道摩擦系数—小车轨道摩擦力P2/u1—f
S13—S1副小车架下盖板厚—主梁上盖板厚—轨距x15—x1—l2副小车轮组轮压/轨道摩擦系数—小车轨道摩擦力P3/u1—f
S13—S11副小车架孔径—小车台车孔径销轴直径Φ44—Φ45—d21副小车架压力—小车台车的支撑力F16

新窗口打开| 下载CSV


起重机的机构主要负责传递和转换能量，使起重机能够进行起吊、运行等动作，而其结构承受设备自身以及货物的重量，并将其传递到地基或其他支撑结构上。在某些特殊工作场合，金属结构的稳定性和抗疲劳性尤为重要。此外，结构设计时需充分考虑起重机的使用环境、工作负荷以及安全要求等因素。若结构设计不当，要么出现起重机无法承受预期的工作负荷，导致使用过程中出现损坏，影响安全运行，要么设计裕量较大，导致资源浪费及材料利用率低。因此，本文将起重机的桥架结构和小车架结构等支撑结构作为下一步研究的主体，其余零部件以表4所示的方式作用在支撑结构上，通过零部件的结构耦合进行支撑结构的综合优化，以此实现起重机的安全性及其绿色性能的提升。

3 结构耦合方法

将结构耦合理论应用到起重机结构分析中，可以更好地分析起重机内部结构之间的相互作用，为起重机的设计、运行和维护提供一个可解释的框架。因此，从结构功能耦合系统、结构影响因子矩阵和结构功能衍生系数等三方面分析起重机结构耦合模型。其中：结构功能耦合系统表示研究策略，即将起重机整体视为一个有着许多交互耦合作用的系统；结构影响因子矩阵表示研究方法，即通过正交试验和方差分析揭示起重机零部件之间的耦合规律；结构功能衍生系数表示分析与计算方法，即根据结构功能耦合系统的传递函数建立衍生系数矩阵及其导数矩阵，反映设计参数变化对起重机结构强度的影响趋势[20]。

3.1　结构影响因子矩阵

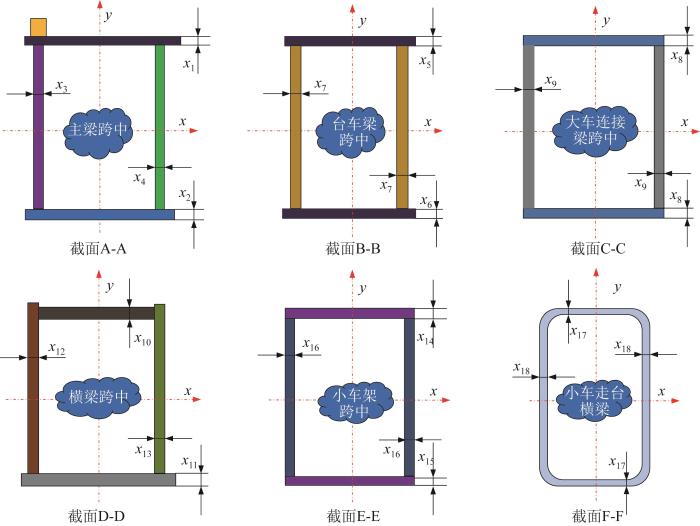
针对起重机的桥架结构、小车架结构等支撑结构，建立结构影响因子矩阵，分析各零部件之间的相互作用和影响关系。其基本流程为：1）确定设计参数。确定影响起重机结构性能和系统关键性能的设计参数。由于起重机常常由厂家根据用户需求定制，其具体结构参数如主梁跨度、起升高度、轨距和基距等都固定，故本文重点对结构截面参数进行优化设计。起重机关键结构参数如图5所示。图中：x1, x2, x3, x4分别为主梁上翼缘板厚、下翼缘板厚、主腹板厚和副腹板厚；x5, x6, x7分别为台车梁上翼缘板厚、下翼缘板厚和腹板厚；x8, x9分别为大车连接梁翼缘板厚和腹板厚；x10, x11, x12, x13分别为小车架结构横梁上翼缘板厚、下翼缘板厚、主腹板厚和副腹板厚；x14, x15, x16分别为小车架上翼缘板厚、下翼缘板厚和腹板厚；x17, x18分别为小车走台横梁翼缘板厚和腹板厚。2）设计试验计划。采用正交试验方法，设计覆盖所有设计参数组合的一系列试验，以减少试验次数，同时保证试验的全面性。3）仿真试验。进行正交试验，记录每个试验条件下起重机的结构强度。4）分析数据。采用离差平方和分析方法，计算总离差平方和TSS、组间离差平方和BSS和组内离差平方和WSS，确定试验数据中每个设计参数对系统性能的影响程度。5）建立结构影响因子矩阵，描述不同设计参数之间的相互影响。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   起重机关键结构参数示意

Fig.5   Schematic of key structural parameters of crane


TSS=∑xi-x¯2BSS=∑nj×(x¯j-x¯)2WSS=∑∑xk-x¯j2

式中：xi (i=1, 2, …, 18)为第i个数据；x¯是所有数据的均值；nj是第j组数据的个数；x¯j是第j组数据的均值；xk是第j组数据的第k个值。

影响因子矩阵 C 为：

C=V1V2⋯x1ω11ω12⋯x2ω21ω22⋯⋮⋮⋮    Vkω1kω2k⋮xiωi1ωi2  ⋯ωik

式中：V1，V2，…，Vk为参数设计的大小，即参数水平；ωik为xi 在Vk下的影响因子。

3.2　结构功能衍生系数

结构功能衍生系数用于衡量起重机各零部件之间的相互作用及其对整体功能的影响程度，即通过映射函数对上述影响因子进行量化，从而了解其对起重机系统稳定运行的影响程度[21]。若某零部件的结构功能衍生系数较大，表明其对其他零部件的影响较大。因此，应根据结构功能衍生系数的计算结果，重点关注影响力较大的零部件的结构参数。

基于结构功能衍生系数的结构参数优化步骤为：

1）建立结构功能耦合系统的传递函数。针对多因素对起重机结构强度的影响，采用多元线性回归与响应面相结合的方法进行函数拟合。将起重机结构参数xi 视为函数的自变量，结构强度作为输出结果Y。为了避免在参数优化过程中拟合阶数过高而引发振荡问题，选取阶数为2的拟合函数，在保证模型简洁性的同时，可有效捕捉系统的复杂性和非线性特征。则：

Y=b0+b1x1+b2x2+⋯+bnxi+bi+1x12+bi+2x22+⋯+b2ixi2+b2i+1x1xθ+b2i+2x2xθ+⋯+b3i-1xixθ

式中：b0, b1, …, b3i-1为各项常系数；xθ为对薄弱结构影响最大的设计参数，即影响因子最大的参数。

2）建立衍生系数矩阵。对传递函数进行偏导数计算，得到与每个起重机结构参数相关的一组多项式φij，即结构功能衍生系数[21]，并将其组成衍生系数矩阵 DCM：

DCM=φ11φ12⋯φ1nφ21ω22⋯φ2n⋮⋮⋮φm1φm2⋯φmn

3）建立衍生系数矩阵的导数矩阵。对衍生系数矩阵求导，得到其导数矩阵，以此反映设计参数变化对起重机结构强度影响的变化率。

DCM'=φ11'φ12'⋯φ1n'φ21'ω22'⋯φ2n'⋮⋮⋮φm1'φm2'⋯φmn'

4）优化设计参数。通过衍生系数及其导数矩阵，分析每个结构参数对起重机性能的影响趋势，以识别关键设计参数，并确定其优化方向。

4 工程实例

以300/100 t-30 m通用桥式起重机为研究对象，利用结构功能衍生系数对起重机金属结构（即桥架结构和小车架结构）的特征参数进行优化，来验证所提出方法的有效性和可行性。该起重机整机的性能参数如下：整机工作级别为A5，跨度为30 m，大车运行速度为4~40 m/min，结构材料为Q235-B；主起升、副起升、电葫芦的起重量分别为300，100，3 t，起升速度分别为0.3~3，3，20 m/min，起升高度分别为16，16.8，18 m；小车起升/运行工作级别为M5，小车运行速度为2~20 m/min，轨距为4 200 mm，主小车基距为4 200 mm，副小车基距为2 650 mm。起重机金属结构关键参数的设计范围如表5所示。

表5   起重机金属结构关键参数的设计范围 (mm)

Table 5  Design range of key structural parameters of metal structure of crane

结构参数初始值设计范围
桥架结构x12420~28
x22420~28
x3139~17
x4139~17
x53430~38
x62016~24
x73430~38
x8128~16
x92420~28
小车架结构x101612~20
x112016~24
x124036~44
x134036~44
x143632~40
x151612~20
x162420~28
x1753~7
x1853~7

新窗口打开| 下载CSV


以表5为基础，设计正交试验，并经过有限元静力学分析，得到不同参数组合下起重机金属结构的最大应力，结果如表6所示。表中，序号1指参数x1、x2、x3、x4发生改变，而x5、x6、…、x9均为表5所示初始值时，起重机金属结构的最大应力。其余序号类似。

表6   不同结构参数下起重机金属结构的最大应力

Table 6  Maximum stress on metal structure of crane under different structural parameters

结构序号

x1/

mm

x2/

mm

x3/

mm

x4/

mm

应力/MPa序号

x5/

mm

x6/

mm

x7/

mm

应力/MPa序号

x8/

mm

x9/

mm

应力/MPa
桥架结构1202099142.961030163096.411982098.586
220241313101.391130203498.632082498.585
32028171775.9612302438100.592182898.584
4242099135.811334163096.4422122098.578
52424131398.611434203498.6123122498.610
62428171757.1315342438100.4824122898.581
7282099139.231638163096.3225162098.595
82824131381.921738203498.5026162498.584
92828171756.5018382438100.3327162898.580
结构序号

x10/

mm

x11/

mm

x12/

mm

x13/

mm

应力/MPa序号

x14/

mm

x15/

mm

x16/

mm

应力/MPa序号

x17/

mm

x18/

mm

应力/MPa
小车架结构112163636147.8810321220158.101933131.08
212204040129.3011321624141.662035130.99
312244444149.9512322028147.742137130.79
416163636146.5013361220148.432253130.91
516204040130.5614361624130.562355130.56
616244444148.9615362028147.812457130.53
720163636145.3316401220134.682573130.85
820204040127.2617401624120.672675130.75
920244444151.9518402028147.862777130.44

新窗口打开| 下载CSV


根据表6，将设计参数设置为低水平参数V1、中间水平参数V2和高水平参数V3等3种。在不同参数水平下起重机金属结构的最大应力如表7所示。

表7   不同参数水平下起重机金属结构的最大应力 (MPa)

Table 7  Maximum stress on metal structure of crane under different parameter levels

结构参数参数水平
V1V2V3
桥架结构x1101.3998.6181.92
x2135.8198.6157.13
x3139.2381.9256.50
x4139.2381.9256.50
x598.6398.6198.50
x696.4498.61100.48
x796.3298.50100.33
x898.5898.6198.58
x998.5898.6198.58
小车架结构x10129.30130.56120.67
x11146.50130.56147.81
x12145.33127.26151.95
x13145.33127.26151.95
x14141.66130.56120.67
x15148.43130.56147.81
x16158.10141.66147.74
x17130.99130.56130.44
x18130.91130.56130.53

新窗口打开| 下载CSV


通过计算不同参数水平组合下起重机金属结构的最大应力，可得桥架结构和小车架结构上述数据的TSS、BSS、WSS分别为：10 695.697 1，3 669.084 2，7 026.6128 和2 832.043 2，557.150 4，2 274.892 8。参数组合时给出了3组参数水平V1、V2和V3，因此所建立的桥架结构和小车架结构的影响因子矩阵 C1和 C2分别如式(8)和式(9)所示。进行起重机金属结构最大应力方差分析，结果如表8所示。表中，SST为总平方和。依据上述数据建立的拟合函数表达式如式(10)和式(11)所示。

C1=V1V2V3x10.219 7%0.040 2%1.999 8%x214.135 8%0.040 2%14.527 6%x317.033 2%1.999 8%14.993 2%x417.033 2%1.999 8%14.993 2%x50.040 2%0.040 2%0.035 5%x60.000 1%0.040 2%0.144 9%x70.000 5%0.035 5%0.133 7%x80.039 3%0.040 2%0.039 3%x90.038 3%0.040 2%0.038 3%
C2=V1V2V3x102.229 8%1.578 8%9.702 7%x113.023 4%1.578 8%3.940 1%x122.307 2%3.521 6%7.633 6%x132.307 2%3.521 6%7.633 6%x140.687 8%1.578 8%9.702 7%x154.416 1%1.578 8%3.940 1%x1615.355 0%0.687 8%3.888 0%x171.382 2%1.578 8%1.635 9%x181.417 8%1.578 8%1.593 0%

表8   起重机金属结构最大应力方差分析

Table 8  Variance analysis of maximum stress on metal structure of crane

结构参数离差平方和影响因子
桥架结构x1241.70.022 6
x23099.90.289 8
x33639.50.340 1
x43639.50.340 1
x512.40.001 2
x619.812 10.001 9
x718.152 90.001 7
x812.70.001 2
x912.50.001 2
SST10 695.70
小车架结构x10372.650.131 5
x11241.920.0854
x12381.260.134 6
x13381.260.134 6
x14338.970.119 6
x15281.360.099 3
x16574.440.203 3
x17130.180.045 9
x18129.970.045 8
SST2 832.04

新窗口打开| 下载CSV


对于桥架结构，有：

 Y1=b0+b1x1+b2x2+b3x3+b4x4+b5x5+b6x6+         b7x7+b8x8+b9x9+b10x12+b11x22+b12x32+b13x42+         b14x52+b15x62+b16x72+b17x82+b18x92+b19x1x3+         b20x2x3+b21x4x3+b22x5x3+b23x6x3+b24x7x3+         b25x8x3+b26x9x3=-0.011+1.452 2x1+0.062 3x2+         0.021 6x3+0.021 6x4-0.034 3x5-0.013 2x6-         0.001 4x7-0.010 6x8-0.034 6x9-0.013 2x12+         0.538 9x22-0.132 8x32-0.132 8x42+0.066 7x52+         0.07x62+0.010 2x72+0.068 7x82+0.068 4x92-         0.245 4x1x3+0.096 4x2x3-0.132 8x4x3-         0.408 4x5x3-0.247x6x3+0.051 1x7x3-         0.141x8x3-0.274 2x9x3

由式(10)可知，x3为对结构影响最大的参数。

对于小车架结构，有：

 Y2=b0+b1x10+b2x11+b3x12+b4x13+b5x14+b6x15+        b7x16+b8x17+b9x18+b10x102+b11x112+b12x122+b13x132+        b14x142+b15x152+b16x162+b17x172+b18x182+b19x10x16+        b20x11x16+b21x12x16+b22x13x16+b23x14x16+b24x15x16+        b25x17x16+b26x18x16=-0.048 7+0.094x10-0.109 3x11+        0.049x12+0.049x13-21.516 7x14-0.036 2x15+        0.019 7x16+0.016 5x17+0.017 2x18-0.062 5x102+        0.4315x112+0.406 5x122+0.406 5x132+0.156 8x142+        0.351 5x152+0.522x162+0.174 9x172+0.137 4x182+        0.085x10x16-3.214 4x11x16-0.063 3x12x16-        0.063 3x13x16+0.579 7x14x16+0.257 4x15x16-        0.051 4x17x16-0.036 7x18x16

由式(11)可知，x16为对结构影响最大的参数。

依据函数模型，将起重机的一个结构参数视为变量，其他结构参数视为常量，来求出所有包含该变量的单项式，从而构建关于该变量的多项式，即为结构功能衍生系数。整理结构功能衍生系数，可得到衍生系数矩阵。该矩阵的因子为：

φ1=(1.452 2-0.245 4x3)x-0.013 2x2φ2=(0.062 3+0.096 4x3)x+0.538 9x2φ3=(0.021 6-0.245 4x1+0.096 4x2-0.132 8x4-0.408 4x5-0.247x6+0.051 1x7-0.141x8-0.274 2x9)x-0.132 8x2φ4=(0.021 6-0.132 8x3)x-0.132 8x2φ5=(-0.034 3-0.408 4x3)x+0.066 7x2φ6=(-0.013 2-0.247x3)x+0.07x2φ7=(-0.001 4+0.051 1x3)x+0.010 2x2φ8=(-0.010 6-0.141x3)x+0.068 7x2φ9=(-0.034 6-0.274 2x3)x+0.068 4x2
φ10=(0.094+0.085x16)x-0.062 5x2φ11=(-0.109 3-3.214 4x16)x+0.431 5x2φ12=(0.049-0.063 3x16)x+0.406 5x2φ13=(0.049-0.063 3x16)x+0.406 5x2φ14=(-21.516 7+0.579 7x16)x+0.156 8x2φ15=(-0.036 2+0.257 4x16)x+0.351 5x2φ16=(0.019 7+0.085x10-3.214 4x11-0.063 3x12-0.063 3x13+0.579 7x14+0.257 4x15-0.051 4x17-0.036 7x18)x+0.522x2φ17=(0.016 5-0.051 4x16)x+0.174 9x2φ18=(0.017 2-0.036 7x16)x+0.137 4x2

对式(12)和式(13)中的衍生系数矩阵因子求导，得到衍生系数导数矩阵因子：

φ1'=(1.452 2-0.245 4x3)-0.026 4xφ2'=(0.062 3+0.096 4x3)+1.077 8xφ3'=(0.021 6-0.245 4x1+0.096 4x2-0.132 8x4-0.408 4x5-0.247x6+0.051 1x7-0.141x8-0.274 2x9)-0.265 6xφ4'=(0.021 6-0.132 8x3)-0.265 6xφ5'=(-0.034 3-0.408 4x3)+0.133 4xφ6'=(-0.013 2-0.247x3)+0.14xφ7'=(-0.001 4+0.051 1x3)+0.020 4xφ8'=(-0.010 6-0.141x3)+0.137 4xφ9'=(-0.034 6-0.274 2x3)+0.136 8x
φ10'=(0.094+0.085x16)-0.125xφ11'=(-0.109 3-3.214 4x16)+0.863xφ12'=(0.049-0.063 3x16)+0.813xφ13'=(0.049-0.063 3x16)+0.813xφ14'=(-21.516 7+0.579 7x16)+0.313 6xφ15'=(-0.036 2+0.257 4x16)+0.703xφ16'=(0.019 7+0.085x10-3.214 4x11-0.063 3x12-0.063 3x13+0.579 7x14+0.257 4x15-0.051 4x17-0.036 7x18)+1.044xφ17'=(0.016 5-0.051 4x16)+0.349 8xφ18'=(0.017 2-0.036 7x16)+0.274 8x

在参数值按迭代步长变化时，为了使结构应力有明显的变化趋势，根据各设计参数的取值范围，设定设计参数的优化间隔为1 mm，同时优先选择结构应力影响因子大于20%的参数进行优化设计。

在初始设计参数下，桥架结构的最大应力为98.61 MPa，小车架结构的最大应力为130.56 MPa。在初始参数组合下，可求得桥架结构和小车架结构的结构功能衍生系数矩阵的导数矩阵分别为：

DCM1'=-2.371 627.182 7-34.094 6-5.157 6-0.807 9 -0.424 2     1.356 5     -0.194 8     -0.316
DCM2'=0.134-59.994 931.049 831.049 83.685 7   17.389 4     -18.369 2     0.531 9     0.510 4

其单调性矩阵M1、M2分别为：

M1=XY1x1x2x3x4x5x6x7x8x9-+----+--
M2=XY2x10x11x12x13x14x15x16x17x18+-++++-++

由式(18)、式(19)和表8可知：对于桥架结构而言，应力Y1关于x2, x7单调递增，关于x1, x3, x4, x5, x6, x8, x9单调递减，且仅有x2, x3, x4的影响因子大于0.2，故选取x2为优化参数；对于小车架结构而言，应力Y2关于x10, x12, x13, x14, x15, x17, x18单调递增，关于x11, x16单调递减，其中仅有x16的影响因子大于0.2，但是Y关于该参数为单调递减，而x10, x12, x13, x14的影响因子虽然没有超过0.2，但都超过了0.1，因此可以作为优化参数，故选取x10, x12, x13, x14作为优化参数。

在此基础上，采用结构耦合法对起重机金属结构进行优化设计，相关优化结果如表9所示。

表9   起重机金属结构优化结果

Table 9  Optimization results of metal structure of crane

结构参数第1次优化值/mm单调增减情况第2次优化值/mm单调增减情况第3次优化值/mm单调增减情况第3次优化值/mm单调增减情况
桥架结构x124-24-24-24-
x223+22+21+20+
x314-14-14-14-
x414-14-14-14-
x534-34-34-34-
x620-20-20-20-
x734+34+34+34+
x812-12-12-12-
x924-24-24-24-
ΔDCM13.567 52.489 71.411 90.334 1
Y1/MPa102.177 5104.667 2106.079 1106.413 2
小车架结构x1015+141312
x1120-202020
x1239+383736
x1339+383736
x1435+343332
x1516+161616
x1624-242424
x175+555
x185+555
ΔDCM210.863 79.86218.860 57.858 9
Y2/MPa141.423 7151.285 8160.146 3168.005 2

新窗口打开| 下载CSV


经过4次寻优后，x2, x10, x12, x13, x14的值分别为20，12，36，36，32 mm，即：优化后主梁下翼缘板厚减小了4 mm，使得桥架结构最大应力增大了7.91%；小车架结构横梁上翼缘板厚、主腹板厚、副腹板厚和小车架上翼缘板厚都减小了4 mm；小车架结构最大应力增大了28.68%，桥架质量和小车架质量分别减小了1 637.388，397.725 kg，起重机整机质量减小了2 035.113 kg。

5 结 论

在起重机结构优化设计中，传统的优化方法忽略了起重机各零部件之间复杂的相互作用。本文提出了基于结构功能衍生系数的起重机金属结构优化设计方法，在确保起重机整机安全性的基础上，实现了金属结构轻量化设计。本文重点如下：

1）建立了起重机零部件解释结构模型，引入了结构功能衍生系数，通过仿真分析，获得了不同设计参数组合下起重机金属结构的最大应力值，并以此确定了可近似描述设计参数与结构强度之间关系的拟合函数。通过衍生系数矩阵及其导数矩阵，量化了设计参数的变化对结构强度的影响。

2）以300/100 t-30 m通用桥式起重机为研究对象，根据设计参数对结构强度的影响趋势，通过参数优化，使得桥架结构的最大应力增大了7.91%，小车架结构的最大应力增大了28.68%，起重机整机质量减小了2 035.113 kg，在确保起重机金属结构承载能力的前提下，大幅度减小了整机质量。

该方法可以针对起重机不同的零部件进行具体分析，但存在一定的局限性，如衍生系数矩阵及其导数矩阵的建立需要大量试验数据。今后需进行更多的研究来突破其局限性，包括研究出更有效的方法来建立衍生系数矩阵及其导数矩阵，或者用更精准的数值模拟技术来减少对试验数据的依赖。

参考文献

邢伟， 李建阳， 谭永营， 等.

某发射塔起重机悬臂梁结构拓扑优化设计

［J］. 机床与液压， 2022， 50（21）： 120-124. doi：10.3969/j.issn.1001-3881.2022.21.022

[本文引用: 1]

XING W， LI J Y， TAN Y Y， et al.

Topological optimization design of cantilever beam structure for a transmitter tower crane

［J］. Machine Tool & Hydraulics， 2022， 50（21）： 120-124.

DOI:10.3969/j.issn.1001-3881.2022.21.022      [本文引用: 1]

林伟， 朱豪洋.

基于改进鼠群优化算法的起重机主梁轻量化设计

［J］. 机械设计， 2024， 41（4）： 131-139.

[本文引用: 1]

LIN W， ZHU H Y.

Lightweight design of crane’s main girder based on improved rat swarm optimization algorithm

［J］. Journal of Machine Design， 2024， 41（4）： 131-139.

[本文引用: 1]

李军， 周伟， 魏睿.

基于混合GSA-GA的起重机主梁优化设计

［J］. 机械设计与制造， 2021（10）： 194-197. doi：10.3969/j.issn.1001-3997.2021.10.043

LI J， ZHOU W， WEI R.

Optimization design of crane main beam based on hybrid GSA-GA

［J］. Machinery Design & Manufacture， 2021（10）： 194-197.

DOI:10.3969/j.issn.1001-3997.2021.10.043     

康振扩， 戚其松， 徐格宁， 等.

基于篮球联赛优化算法的通用桥式起重机主梁轻量化设计

［J］. 机械设计与研究， 2022， 38（3）： 222-225.

[本文引用: 1]

KANG Z K， QI Q S， XU G N， et al.

Lightweight design of main girder of an universal bridge crane based on basketball league optimization algorithm

［J］. Machine Design & Research， 2022， 38（3）： 222-225.

[本文引用: 1]

翁飞翔， 郑成， 王庆霞.

考虑可靠度的桥式起重机主梁金属结构稳健优化设计

［J］. 东华大学学报（自然科学版）， 2021， 47（5）： 74-79， 88.

[本文引用: 1]

WENG F X， ZHENG C， WANG Q X.

Robust optimization design of metal girder structure of bridge crane considering reliability

［J］. Journal of Donghua University （Natural Science）， 2021， 47（5）： 74-79， 88.

[本文引用: 1]

梁其传， 易朋兴， 邱悦.

基于稀疏网格模型与MOGA算法的起重机主梁结构优化

［J］. 现代制造工程， 2019（6）： 79-83.

LIANG Q C， YI P X， QIU Y.

Optimization of the main beam of bridge crane based on sparse grid model and MOGA algorithm

［J］. Modern Manufacturing Engineering， 2019（6）： 79-83.

刘跃昆， 朱强.

基于灵敏度分析的门式起重机结构优化设计

［J］. 现代制造工程， 2018（7）： 129-133.

[本文引用: 1]

LIU Y K， ZHU Q.

Optimization design of gantry crane structure based on sensitivity analysis

［J］. Modern Manufacturing Engineering， 2018（7）： 129-133.

[本文引用: 1]

甘盛霖， 梅益， 鄢天灿， 等.

平头塔式起重机回转总成有限元分析及结构优化

［J］. 现代制造工程， 2020（3）： 147-151， 156. doi：10.1201/9781003078548-27

[本文引用: 1]

GAN S L， MEI Y， YAN T C， et al.

Finite element analysis and structure optimum of flat-top tower cranes

［J］. Modern Manufacturing Engineering， 2020（3）： 147-151， 156.

DOI:10.1201/9781003078548-27      [本文引用: 1]

陈国雄， 曹阳， 吴家雄， 等.

焊接平台龙门架结构轻量化设计

［J］. 机械设计与制造， 2024（4）： 194-199.

[本文引用: 1]

CHEN G X， CAO Y， WU J X， et al.

Welding platform gantry structure lightweight design

［J］. Machinery Design & Manufacture， 2024（4）： 194-199.

[本文引用: 1]

张磊， 于世杰， 徐进友， 等.

面向轻量化目标的起重机伸臂结构设计及截面尺寸优化

［J］. 机械设计， 2023， 40（6）： 124-133.

[本文引用: 1]

ZHANG L， YU S J， XU J Y， et al.

Crane jib structure design and section dimension optimization for lightweight target

［J］. Journal of Machine Design， 2023， 40（6）： 124-133.

[本文引用: 1]

黄镇， 温梦珂， 李维东.

起重机主梁截面风力系数预测及结构优化设计

［J］. 哈尔滨工业大学学报， 2023， 55（12）： 123-133.

[本文引用: 1]

HUANG Z， WEN M K， LI W D.

Wind coefficient prediction and structural optimization design of crane girder section

［J］. Journal of Harbin Institute of Technology， 2023， 55（12）： 123-133.

[本文引用: 1]

LI J P， BAI L， GAO W， et al.

Reliability-based design optimization for the lattice boom of crawler crane

［J］. Structures， 2021， 29： 1111-1118.

SAVKOVIĆ M M， BULATOVIĆ R R， GAŠIĆ M M， et al.

Optimization of the box section of the main girder of the single-girder bridge crane by applying biologically inspired algorithms

［J］. Engineering Structures， 2017， 148： 452-465.

XU X， XU G X， CHEN J W， et al.

Multi-objective design optimization using hybrid search algorithms with interval uncertainty for thin-walled structures

［J］. Thin-Walled Structures， 2022， 175： 109218.

WANG X J， ZHU J Z， NI B W.

Structural reliability-based design optimization with non-probabilistic credibility level

［J］. Computer Methods in Applied Mechanics and Engineering， 2024， 418： 116489.

CARVALHO J P G， VARGAS D E C， JACOB B P， et al.

Multi-objective structural optimization for the automatic member grouping of truss structures using evolutionary algorithms

［J］. Computers & Structures， 2024， 292： 107230.

TRAN Q D， SHIN D， JANG G W.

Bayesian optimization-based topology optimization using moving morphable bars for flexible structure design problems

［J］. Engineering Structures， 2024， 300： 117103.

[本文引用: 1]

李晶， 李颖， 彭晓易.

基于矩阵自乘的一种解释结构模型改进方法

［J］. 系统科学与数学， 2021， 41（7）： 2046-2062.

[本文引用: 1]

LI J， LI Y， PENG X Y.

An improved method of interpreting structural model based on matrix self-multiplication

［J］. Journal of Systems Science and Mathematical Sciences， 2021， 41（7）： 2046-2062.

[本文引用: 1]

刘伟强， 徐立云.

基于解释结构模型和复杂网络的制造系统关键脆性因子辨识

［J］. 计算机集成制造系统， 2021， 27（11）： 3076-3092.

[本文引用: 1]

LIU W Q， XU L Y.

Identification of key brittleness factor for manufacturing system based on ISM and complex network

［J］. Computer Integrated Manufacturing Systems， 2021， 27（11）： 3076-3092.

[本文引用: 1]

汪伟.

基于零件结构耦合理论的主动再制造设计

［D］. 合肥： 合肥工业大学， 2017.

[本文引用: 1]

WANG W.

Active remanufacturing design based on coupling theory of parts structure

［D］. Hefei： Hefei University of Technology， 2017.

[本文引用: 1]

宋守许， 汪伟， 柯庆镝.

基于结构功能衍生系数的主动再制造设计

［J］. 机械工程学报， 2017， 53（11）： 175-183. doi：10.3901/jme.2017.11.175

[本文引用: 2]

SONG S X， WANG W， KE Q D.

Optimization design of predecisional remanufacturing based on structural function derivative coefficient

［J］. Journal of Mechanical Engineering， 2017， 53（11）： 175-183.

DOI:10.3901/jme.2017.11.175      [本文引用: 2]

/

〈 〉